Жесткие системы ОДУ

До сих пор мы имели дело с "хорошими" уравнениями, которые надежно решались численными методами (типа Рунге-Кутты). Однако имеется класс так называемых жестких (stiff) систем ОДУ, для которых стандартные методы практически неприменимы, поскольку их решение требует исключительно малого значения шага численного метода. Для этих систем разработаны специальные алгоритмы

Что такое жесткие ОДУ? 
Строгого общепринятого математического определения жестких ОДУ нет. В рамках этой книги будем считать, что жесткие системы - это те уравнения, решение которых получить намного проще с помощью определенных неявных методов, чем с помощью явных методов (типа тех, что были рассмотрены в предыдущих разделах). Примерно такое определение было предложено в 1950-х годах классиками в этой области Кертиссом и Хиршфельдером. Начнем разговор о жестких ОДУ с примера нежесткого уравнения, решение которого показано на рис.1. На том же графике показано решение подобного ОДУ с другим коэффициентом при правой части, равным не -10, а -30. Решение обоих уравнений не составило труда, и численный метод Рунге-Кутты дал правильный результат.


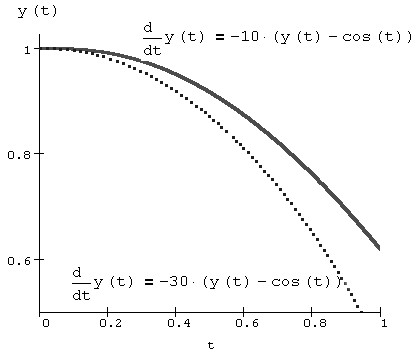
Рис. 1. Решение нежестких ОДУ методом Рунге-Кутты

На рис. 2 показано решение того же ОДУ с коэффициентом -50. Вас, несомненно, должен насторожить результат, выданный методом Рунге-Кутты. Характерная "разболтка" решения говорит о неустойчивости алгоритма. Первое, что можно сделать, - увеличить количество шагов в методе Рунге-Кутты. Можно убедиться, что при step>20 разболтка пропадает, и решение становится похожим на графики, показанные на рис. 1.

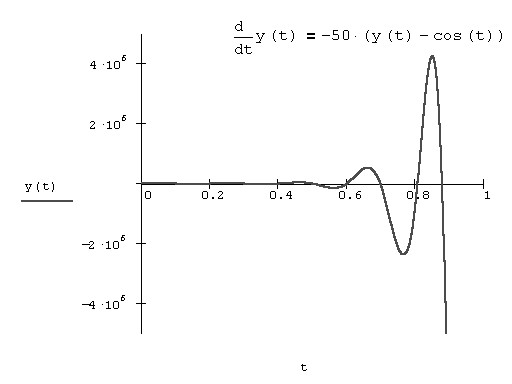
Рис. 2. Неверное решение более жесткого ОДУ методом Рунге-Кутты

Таким образом, во-первых, мы выяснили, что одни и те же уравнения (с разными параметрами) могут быть как жесткими, так и нежесткими. Во-вторых, чем жестче уравнение, тем больше шагов в обычных численных методах требуется для его устойчивого решения. С классическим примером ОДУ из листинга 11.11 все получилось хорошо, т.к. оно было не очень жестким, и небольшое увеличение числа шагов разрешило все проблемы. Для решения обычными методами более жестких уравнений требуются миллионы, миллиарды и даже большее число шагов.

Замечание Некоторые ученые замечают, что в последние годы методы Рунге-Кутты стали уступать свое главенствующее положение среди алгоритмов решения ОДУ методам, способным решать жесткие задачи.

Исторически, интерес к жестким системам возник в середине XX века при изучении уравнений химической кинетики с одновременным присутствием очень медленно и очень быстро протекающих химических реакций. Тогда неожиданно оказалось, что, как считалось, исключительно надежные методы Рунге-Кутты стали давать сбой при расчете этих задач. Рассмотрим классическую модель взаимодействия трех веществ (Робертсон, 1966), которая как нельзя лучше передает смысл понятия жесткости ОДУ.
Пусть вещество "0" медленно превращается в "1": "0"-->"1" (со скоростью 0.1), вещество "1" при каталитическом воздействии самого себя превращается очень быстро в вещество "2": "1"+"1"-->"2"+"1" (10³). И, наконец подобным образом (но со средней скоростью) реагируют вещества "2" и "1": "1"+"2"-->"0"+"2" (10²). Система ОДУ, описывающая динамику концентрации реагентов,  приведена ниже.

Бросается в глаза сильно различающийся порядок коэффициентов при разных слагаемых. Именно степень этого различия чаще всего и определяет жесткость системы ОДУ. В качестве соответствующей характеристики выбирают матрицу Якоби (якобиан) векторной функции F(t,y), т.е. функциональную матрицу, составленную из производных F(t,y). Чем вырожденнее матрица Якоби, тем жестче система уравнений. В приведенном примере определитель якобиана и вовсе равен нулю при любых значениях y₀, y₁ и y₂:

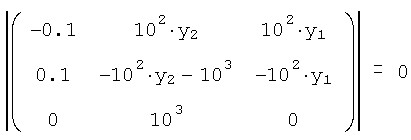
Для приведенного примера стандартным методом Рунге-Кутты все-таки удается найти решение. Однако, для этого требуется очень большое число шагов, M=20000, что делает расчеты очень медленными. При меньшем числе шагов численному алгоритму не удается найти решение. Решение данной системы ОДУ  приведено в разделе Модель химической кинетики главы Динамические системы.

В принципе, можно было бы снизить жесткость системы "вручную", применяя масштабирование. Для этого нужно искусственно уменьшить искомую функцию y₁, к примеру, в тысячу раз, разделив все слагаемые в системе ОДУ, содержащие y_1, на 1000. После масштабирования для решения полученной системы методом Рунге-Кутты будет достаточно взять всего M=20 шагов.

Однако, в последнее время для жестких систем ОДУ разработаны специальные, довольно эффективные алгоритмы.
Во-первых, можно использовать простые неявные алгоритмы, типа симметричной неявной схемы Эйлера, приведенной нами ранее;
Во-вторых, применяются более сложные неявные алгоритмы;
В-третьих, широко используются безытерационные алгоритмы, типа метода Розенброка.;