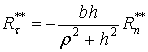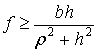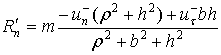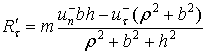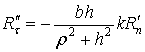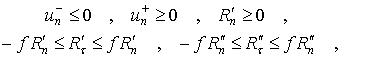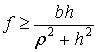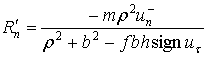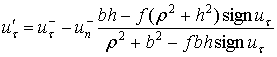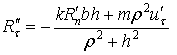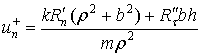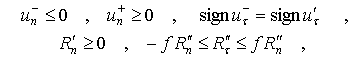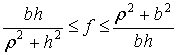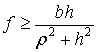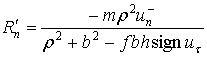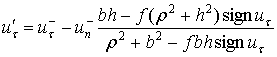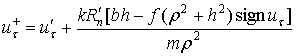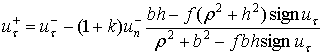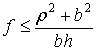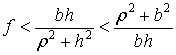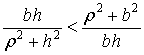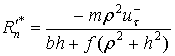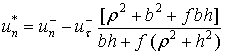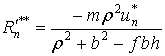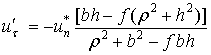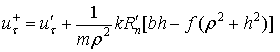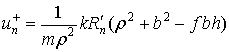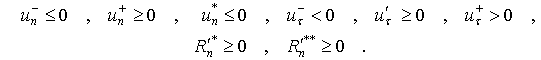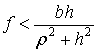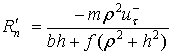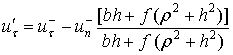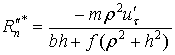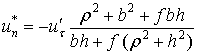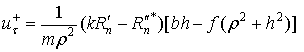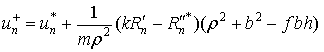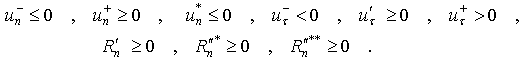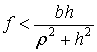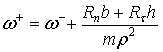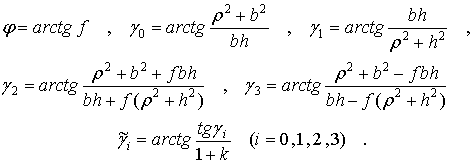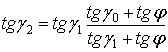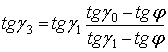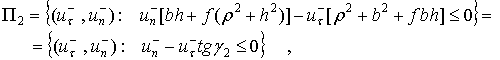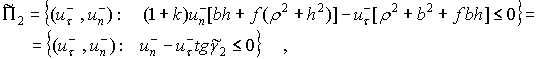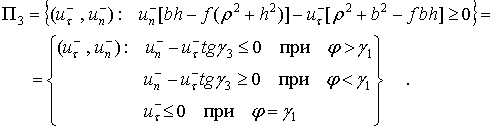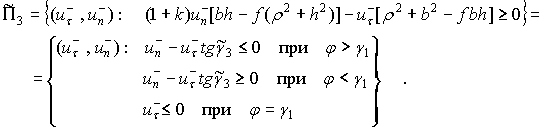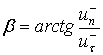Плоский удар тела о шероховатую поверхность

(A body plane collision with a rough surface
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Введение

Явление удара часто встречается при движении механических систем, в том числе при работе различных машин и механизмов. Многие (но не все) прикладные задачи могут быть исследованы в соответствии с теорией удара Ньютона [1-8].

Известно [1-2], что плоская задача удара тела о шероховатую поверхность при точечном контакте тела с поверхностью имеет корректное решение в рамках теории удара Ньютона. В этом случае однозначно определяется импульс ударной силы реакции и характер движения (скорости) тела после удара. В данной работе показано, что тип удара или характер движения точки соприкосновения в процессе удара определяется с помощью графической картины на плоскости параметров угол трения    и угол падения   (который определяет направление скорости точки соприкосновения тела с поверхностью до удара). В качестве границ, разделяющих области, соответствующие различным типам удара, выступают кривые, поведение которых зависит от положения точки соударения относительно центра масс тела, радиуса инерции тела, угла трения и коэффициента восстановления при ударе. Полученные результаты могут быть использованы в учебных курсах по теоретической механике.

Данная работа является естественным продолжением [8], в которой аналогичные результаты были получены для абсолютно неупругого удара.

§1. Исследование процесса удара

Рассмотрим плоский упругий удар тела массой  о неподвижную шероховатую поверхность (рис. 1). Пусть    –  центр масс тела,    –  точка контакта тела с поверхностью при ударе. Радиус инерции тела относительно центра масс обозначим   . Единичные вектора    и    определяют касательное и нормальное направление к поверхности в точке соударения   . Обозначим через    касательный и нормальный импульсы ударной силы реакции в точке   . Положение центра масс    относительно точки    определяется параметрами    и   . Не нарушая общности можно считать, что центр масс    лежит слева от точки соударения   

Для случая  (центр масс  лежит справа от точки соударения ), все результаты могут быть получены из соображений симметрии.

Обозначим через    касательную и нормальную скорость центра масс   ,    касательную и нормальную скорость точки соударения   ,    угловую скорость тела. За положительное примем направление угловой скорости против часовой стрелки. Скорости точек   и    связаны кинематическими соотношениями

Процесс удара разделим на две фазы: фазу деформации, в течение которой нормальная составляющая скорости точки соприкосновения уменьшается до нуля, оставаясь отрицательной, и фазу восстановления, в течение которой нормальная составляющая скорости точки соприкосновения увеличивается от нуля до некоторого положительного значения.

Значения всех скоростей до удара будем обозначать верхним индексом минус   , значения скоростей после удара верхним индексом плюс   , а значения скоростей в конце фазы деформации (или начале фазы восстановления) верхним индексом штрих ' .

Для того чтобы имел место удар в точке соприкосновения тела с поверхностью, которая является неудерживающей связью, необходимо, чтобы до удара нормальная скорость точки    была отрицательной

а нормальная составляющая импульса ударной силы реакции должна быть не отрицательной

При этом нормальная составляющая скорости точки    в конце фазы деформации равна нулю

а после удара положительна

Уравнения удара (уравнения движения центра масс и изменения кинетического момента тела относительно центра масс) в фазе деформации имеют вид

а в фазе восстановления

Здесь  – нормальные и касательные составляющие импульса ударной силы реакции соответственно в фазах деформации и восстановления. При этом для нормальных составляющих имеем [1–6]

где    –  коэффициент восстановления при ударе. Причем

Абсолютно неупругому удару соответствует , абсолютно упругому удару  .

Учитывая (2), (5) и (9), из (7) и (8) получаем соотношения для изменения скорости точки соприкосновения    в фазе деформации

и фазе восстановления

Отсюда получаем

где

Примем гипотезу Рауса [1-3] о том, что при ударе трение сводится к сухому трению с коэффициентом трения   f .

Если точка соприкосновения в процессе удара в течение некоторого (бесконечно малого) интервала времени имеет постоянное направление касательной скорости, то в этой фазе удара

В результате удара в силу (5) точка соприкосновения    может в касательном к поверхности направлении остановиться или скользить в течение всего удара и в конце удара иметь ненулевую составляющую касательной скорости. При этом если в процессе удара под действием трения касательная скорость становится равной нулю в некоторый момент времени  , то это не означает, что в дальнейшем в процессе удара она останется равной нулю. Действительно, для того, чтобы  при  должны выполняться соотношения

где  – скорость точки  соприкосновения в момент , а  –импульсы ударной силы реакции за время . Отсюда

Если условие (17) нарушено, то точка соприкосновения в силу геометрического положения тела начинает скольжение в дальнейшем в процессе удара, причем это скольжение направо или , так как при этом  и  . Таким образом в этом случае может произойти изменение направления скольжения точки соприкосновения. Сначала она скользит налево или с отрицательной скоростью, которая под действием силы трения уменьшается до нуля, а затем начинает скользить направо с увеличивающейся положительной скоростью.

Перейдем к рассмотрению различных типов удара в зависимости от того, как осуществляется скольжение в процессе удара.

1. Скольжение прекращается в фазе деформации. В этом случае

а тогда из уравнений удара (11) и (12) для фаз деформации и восстановления   получаем

Данный случай имеет место, тогда и только тогда, когда выполнены условия (3), (4), (6), .условие (15) по отдельности для фаз деформации и восстановления

и условие (17). В силу (9), (18) они равносильны условиям

2. Скольжение прекращается в фазе восстановления. В этом случае

а тогда из уравнений удара для фазы деформации и восстановления (11), (12) с учетом (9) получаем

Данный случай имеет место, тогда и только тогда, когда выполнены условия (3), (4), (6), (20), и условие(15) для фазы восстановления,

и условие (17). В силу (22) они равносильны условиям:

а) при скольжении направо

б) при скольжении налево

3. Полное скольжение (без изменения направления). В этом случае в процессе удара направление скольжения не меняется, и точка соприкосновения имеет ненулевую касательную составляющую скорости

а тогда из уравнений удара для фазы деформации и восстановления (11), (12) с учетом (9) получаем

Данный случай имеет место, тогда и только тогда, когда выполнены условия (3), (4), (6), (25)

В силу (27) они равносильны условиям:

а) при скольжении направо

б) при скольжении налево

4. Изменение направления скольжения. В процессе удара точка соприкосновения  сначала скользит налево, а затем направо (см. стр. 7). Этот случай имеет место, когда не выполнено условие (17) или

Здесь кроме (17) использовано неравенство

которое всегда справедливо. Действительно, в силу (1)    и не отрицательности   оно эквивалентно неравенству  , где радиус инерции .

Пусть  момент изменения направления скольжения в процессе удара или момент когда касательная составляющая скорости равна нулю. Возможны два подслучая.

4.1. Изменение направления скольжения в фазе деформации. Тогда  и

На первом этапе фазы деформации при  точка соприкосновения скользит налево

В этих соотношениях    – скорость точки соударения    в момент смены направления скольжения,   – импульсы ударной реакции в течение первого этапа фазы деформации.

Из уравнений удара для первого этапа фазы деформации  с учетом (33) получаем

На втором этапе фазы деформации при  точка соприкосновения скользит направо

В этих соотношениях   – импульсы ударной реакции в течение второго этапа фазы деформации.

Из уравнений удара для второго этапа фазы деформации  с учетом (35) получаем

При  точка соприкосновения скользит направо

Из уравнений удара для фазы восстановления с учетом (38) получаем

Данный случай имеет место, тогда и только тогда, когда выполнены условия (3), (4), (6), (30) и ограничения на скорости из (32), (33), (35), (37), причем условие (4) должно быть выполнено по отдельности для первого и второго этапа фазы деформации

В силу (34), (36), (39) и с учетом (30) они равносильны условиям:

4.2. Изменение направления скольжения в фазе восстановления. Тогда   и

В фазе деформации при  и на первом этапе фазы восстановления при   точка соприкосновения скользит налево

В этих соотношениях    – скорость точки соударения    в момент смены направления скольжения,   – импульсы ударной реакции в течение первого этапа фазы восстановления.

Из уравнений удара для фазы деформации  и первого этапа фазы восстановления с учетом (42) получаем

На втором этапе фазы восстановления при  точка соприкосновения скользит направо

Из уравнений удара для второго этапа фазы восстановления  с учетом (45), (46) получаем

Данный случай имеет место, тогда и только тогда, когда выполнены условия (3), (4), (6), (30) и ограничения на скорости из (41), (42), (44), (45), причем условие (4) должно быть выполнено по отдельности для первого и второго этапа фазы восстановления

В силу (43), (45), (47) и с учетом (30) они равносильны условиям:

Для всех рассмотренных выше случаев определены условия, при которых они имеют место, а также скорость точки соприкосновения    после удара и импульсы ударных сил реакции опорной поверхности для фаз деформации и восстановления. Найдем полные импульсы ударных реакций в течение всего удара

Причем, если изменяется направление скольжения точки  в фазе деформации, то . Если изменяется направление скольжения точки  в фазе восстановления, то .

Значение угловой скорости тела после удара определяется из третьего из уравнений (7), (8)

Скорость центра масс тела после удара определяется из уравнений (2)

§2. Графическая интерпретация условий, соответствующих различным типам удара

В предыдущем параграфе рассмотрены различные типы движения тела при ударе и получены условия, при которых имеет место тот или иной тип удара. Однако эти условия достаточно сложны и зависят от значений шести параметров: положения точки соударения относительно центра масс, определяемого параметрами    и   ; радиуса инерции тела относительно центра масс   ; коэффициента трения тела о поверхность    и скорости точки соприкосновения    в начале удара. Непротиворечивость этих условий и корректность модели удара (т.е. однозначность определения характеристик движения в конце удара для любого тела и любых значений скоростей в начале удара) далеко неочевидна.

Для упрощения анализа этих условий введем угол трения    и углы 

В силу (31) имеем

Из (50) следует

В силу (51) отсюда получаем

Введем следующие множества значений скорости точки соприкосновения    в начале удара 

Каждое из этих множеств является полуплоскостью. Тогда в силу условий (19), (23), (24), (28), (29),(40), (49) имеем, что:

§        в процессе удара точка соприкосновения останавливается в фазе деформации тогда и только тогда, когда

§        в процессе удара точка соприкосновения сначала скользит направо и останавливается в фазе восстановления тогда и только тогда, когда

§        в процессе удара точка соприкосновения сначала скользит налево и останавливается в фазе восстановления тогда и только тогда, когда

§        в процессе удара точка соприкосновения скользит направо (полное скольжение) тогда и только тогда, когда

§        в процессе удара точка соприкосновения скользит налево (полное скольжение) тогда и только тогда, когда

§        в процессе удара точка соприкосновения меняет направление скольжения в фазе деформации (сначала скользит налево, а затем направо) тогда и только тогда, когда

§        в процессе удара точка соприкосновения меняет направление скольжения в фазе восстановления (сначала скользит налево, а затем направо) тогда и только тогда, когда

Отметим, что характер движения точки соприкосновения    в процессе удара зависит от направления скорости этой точки до удара и не зависит от ее величины. Введем угол

который является углом падения точки   , отсчитываемым от касательного к опорной поверхности направления (рис.1). Тип удара или характер движения точки соприкосновения    в процессе удара определяется соотношением значений угла трения  , угла падения   и углов . На рис.2 приведена зависимость углов   от угла трения    и отложены по осям значения углов  .

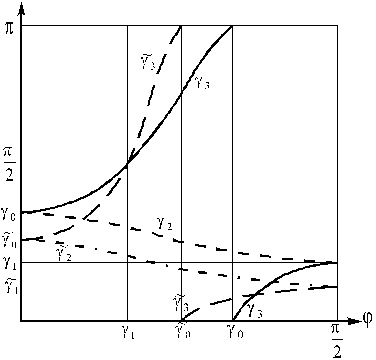
Рис. 2. Зависимость углов  от угла трения  .

Анализ с учетом рис. 2 условий (55)–(62) показывает, что некоторые из них являются избыточными. На рис. 3 показаны области значений угла трения  и угла падения , которые соответствуют различным типам ударов. В качестве границ, разделяющих эти области, выступают кривые, которые соответствуют зависимости углов   от угла трения   .

Аналитически эти условия имеют следующий вид. В процессе удара точка соприкосновения :

§        в области I      сначала скользит направо и останавливается в фазе деформации;

§        в области II      сначала скользит налево и останавливается в фазе деформации;

§        в области III      сначала скользит направо и останавливается в фазе восстановления;

§        в области IV      сначала скользит налево и останавливается в фазе восстановления;

§        в области V      и      скользит направо (полное скольжение);

§        в области VI      скользит налево (полное скольжение);

§        в области VII      меняет направление скольжения в фазе деформации (сначала скользит налево затем направо);

§        в области VIII      меняет направление скольжения в фазе восстановления (сначала скользит налево затем направо).

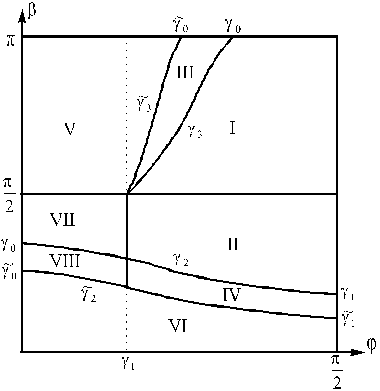
Рис. 3. Упругий удар.

Напомним, что исследование процесса удара проводилось в предположении, что центр масс    относительно точки соударения    расположен слева (рис. 1) или   . Случай    может быть исследован аналогично, либо все результаты легко получаются из соображений симметрии.

Рассмотрим также три частных случая.

Если в момент удара центр масс расположен над точкой соприкосновения    или    (этот случай имеет место при ударе осе симметричного диска о поверхность), то    ,    ,    ,  . Всегда   и зависимость типа удара от скорости точки соприкосновения до удара показана на рис.4.

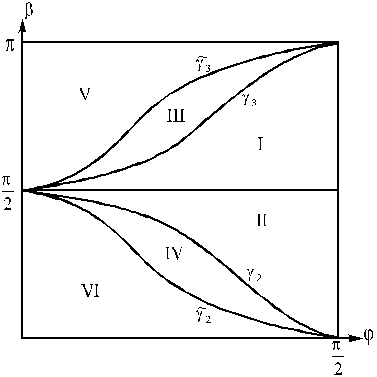
Рис. 4. Упругий удар осе симметричного диска.

В процессе удара точка соприкосновения :

§        в области I      сначала скользит направо и останавливается в фазе деформации;

§        в области II      сначала скользит налево и останавливается в фазе деформации;

§        в области III      сначала скользит направо и останавливается в фазе восстановления;

§        в области IV     сначала скользит налево и останавливается в фазе восстановления;

§        в области V      скользит направо (полное скольжение);

§        в области VI      скользит налево (полное скольжение).

В случае абсолютно неупругого удара , и в силу (50) . Области соответствующие различным типам удара показаны на рис. 5.

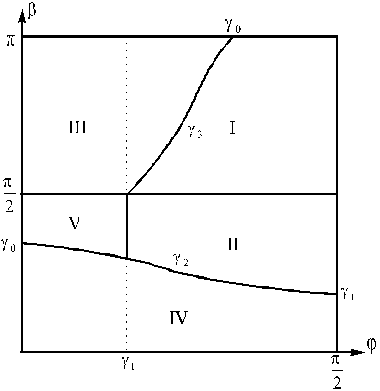
Рис. 5. Абсолютно неупругий удар.

В процессе удара точка соприкосновения :

§        в области I      сначала скользит направо, затем останавливается;

§        в области II      сначала скользит налево, затем останавливается;

§        в области III    и    скользит направо (полное скольжение);

§        в области IV      скользит налево (полное скольжение);

§        в области V      меняет направление скольжения (сначала скользит налево затем направо).

Для абсолютно шероховатой поверхности    или   . Весьма неожиданным оказывается результат (см. рис. 3), что не всегда точка  соприкосновения    останавливается в процессе удара, не смотря на бесконечно большой коэффициент трения. При малых значениях угла падения   касательная составляющая скорости не обращается в ноль. Имеет место полное скольжение налево. Этот результат особенно не очевиден для случая абсолютно неупругого удара (см. рис. 5).

Отметим также, что случай удара материальной точки о шероховатую поверхность [7] не может быть получен из приведенных в данной работе результатов предельным переходом. При этом одновременно стремятся к нулю параметры , а тогда в силу (50)  ничего нельзя сказать про углы .

Литература

1. Плявниекс В.Ю. Расчет косого удара о препятствие. В кн.: Вопросы динамики и прочности, № 18. Рига, Зинатне, 1969, с. 87-109.

2. Иванов А.П. Динамика систем с механическими соударениями. М., Международная программа образования, 1997.

3. Пановко Я.Г. Введение в теорию механического удара. М., Наука, 1977.

4. Раус Э.Дж. Динамика системы твердых тел, т.1. М., Наука, 1983.

5. Кобринский А.Е., Кобринский А.А. Виброударные системы (динамика и устойчивость). М., Наука, 1973.

6. Гольдсмит В. Удар. Теория и физические свойства соударяемых тел. М., Изд-во литературы по строительству, 1965.

7. Дубинин В.В., Гришин С.А., Лапшин В.В. Удар материальной точки о шероховатую поверхность. Препринт Ин-та прикл. мат. РАН, 1997, № 21.

8. Лапшин В.В., Дубинин В.В. Абсолютно неупругий удар тела о шероховатую поверхность. Препринт Ин-та прикл. мат. РАН, 1998, № 18.