СОДЕРЖАНИЕ

СОДЕРЖАНИЕ

Введение

1. Частотно-временные преобразования

2. Метод получение вектора свойств

3. Нейросетевое распознавние образов

4. Адаптивное преобразование Эрмита

5. Сравнение частотно-временных  векторов свойств для задачи  распозна-

     вания речи и идентификации личности в различных представлениях

Заключение

Литература

Введение

В большинстве существующих систем распознавания речи синтаксические модели строятся на основе скрытых Марковских моделей (СММ) [1]. Для улучшения вероятностных характеристик их используют совместно с искусственными нейронными сетями (ИНС) [2,3]. Вектором свойств в этих системах является одномерный частотный вектор кепструм, а также вектор, составленный из его производных [4]. Кепструм строится из последовательной частотной нормализации, логарифмирования и дискретного косинусного преобразования (ДКП) амплитудной составляющей дискретного преобразования Фурье (ДПФ). При этом ДПФ последовательно применяется к исходному звуковому сигналу в окне Хэмминга с периодичностью в 20-30 мс.

Для повышения надёжности распознавания часть нагрузки по анализу временной составляющей можно переложить из СММ в вектора свойств. Основная проблема при этом заключается в необходимости стационарной размерности и максимальной декоррелированности вектора свойств. В последние годы рассматривались несколько вариантов решения этой проблемы. Один из методов заключался в получении кепструма не из одного, а из нескольких, рядом расположенных, частотных векторов путём применения двумерного ДКП [5], что привело к значительному повышению устойчивости распознавания. В работах [6,7] рассматривается множество возможных двумерных представлений частотно-временных векторов, в том числе основанных на двумерной вейвлет-локализации. В данной работе используются двумерные вейвлет-преобразования для выделения низкочастотных компонент в частотно-временной информации, а также 3-х-слойная ИНС-сеть для итоговой классификации.

Для реализации вышеизложенной цели используется следующая последовательность алгоритмов:

·           Краткосрочный спектральный анализ

·           Алгоритм определения границ векторов свойств

·           Метод получения вектора свойств

·           Нейросетевое распознавание образов

Также рассмотрено применение изложенных технологий для задач распознавания речи и распознавания дикторов. Исследовались представления речи на основе краткосрочного преобразования Фурье и адаптивного преобразования Эрмита.

1. Частотно-временные преобразования

На вход любой системы автоматического анализа звуковой информации поступает дискретизированный по времени и квантованный по амплитуде звуковой сигнал. На Рис. 1.а изображена осциллограмма сигнала фрагмента речи, состоящего из двух слов. Применяя краткосрочный спектральный анализ к этому сигналу на основе быстрого преобразования Фурье (БПФ), получаем последовательность комплексных векторов ДПФ. Фазовая компонента содержит, в основном, информацию о пространственной ориентации источника звука. В отличие от задачи распознавания диктора, для задачи диктор-независимого распознавания речи фазовая информация не существенна и ее не рассматривают. Амплитудная составляющая этого вектора во времени - спектрограмма - может рассматриваться как обычное изображение. Известно, что наиболее информативные частоты человеческого голоса сосредоточенны в интервале 100 Гц - 5КГц, поэтому в спектрограмме оставляют только гармоники, частоты которых попадают в этот интервал. После этого, значения гармоник подвергаются амплитудному логарифмированию и частотному, так называемому мел-скейл фильтру:

                                                                                       ₍₁₎

 _{где f- частота в Гц.}

В полученной таким образом спектрограмме, изображенной на Рис 1.b, содержится большое количество шумовых эффектов, возникающих как из-за присутствующего в изначальном сигнале шума, так и из-за некоторых свойств ДПФ. Шум, возникающий при этом, можно считать нормально распределённым с нулевым математическим ожиданием. Используя то, что как частотная, так и временная размерность рассматриваемых спектрограмм является избыточной, от этого шума можно избавиться путём уменьшения изображения, с применением низкочастотного фильтра. Шум, присутствующий в изначальном сигнале, можно также разделить на две составляющие. Одна из них - стационарный шум, который можно приближенно считать аддитивным. При этом операция шумоподавления сводится к вычитанию спектра шума из частотных столбцов спектрограммы.

Полученная таким образом спектрограмма изображена на Рис. 1.с.

Рис. 1. Последовательные преобразования сигнала

a) Осциллограмма.      b) Спектрограмма (более низкие частоты расположены сверху).  

c) Спектрограмма после уменьшения размерности и шумопонижения.

2. Метод получения векторов свойств

Спектрограмма каждого слова (пример на рис. 2.a) масштабируется к квадратному виду и производится двумерное вейвлет-преобразование столько раз, сколько необходимо для получения низкочастотной матрицы TхF, где Т - временное разрешение матрицы по горизонтали, а F - частотное разрешение по вертикали. Экспериментально установленным оптимальным разрешением, с точки зрения последующего нейронного распознавания, было выбрано разрешение 8х8. Для повышения устойчивости распознавания векторов свойств, компоненты векторов нормализуются к нулевому математическому ожиданию и единичной дисперсии (рис. 2.b).

a                     b

Рис. 2. Итоговое масштабирование и нормализация

a) Спектрограмма слова.         b) Вектор свойств слова.

3. Распознавание образов

Рассмотрим простейший случай, когда речь представляет собой последовательность ограниченного количества слов. В этом случае распознавание речи сводится к классификации двухмерных векторов свойств. Каждый класс соответствует определённому слову, произнесенному различными дикторами. Конкретные двумерные векторы свойств различных слов представлены на рис. 3, где в каждом столбце представлены слова одного диктора, а в каждой строке – классы слов.

Рис. 3. Графические представления частотно-временных векторов для различных дикторов и различных слов.

Существует множество методов классификации образов с учителем. Рассмотрим основные из них: статистический, метрический и нейросетевой.

3.1. Статистический метод классификации

Обозначим:

            W[j,i,x,y]: вектор из обучающей выборки, где j -номер класса, i - номер примера, (x,y) - координаты в векторе свойств.

Х[x,y]: вектор из тестовой выборки.

P(Сj,X): вероятность принадлежности X к классу Сj при распределении вероятностей.

Тогда, функция классификации class(X) определяется следующим образом:

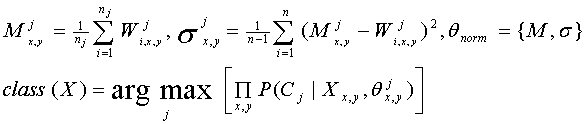 (2)

3.2. Классификация методом наименьшего расстояния

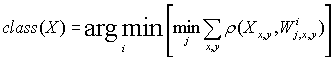                                                                   (4)

3.3. Нейросетевая классификация

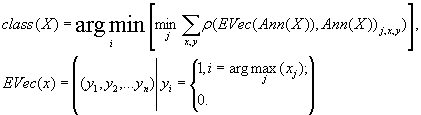                                             (5)

            где  r-евклидово расстояние, функция Ann(x) - выход нейронной сети.

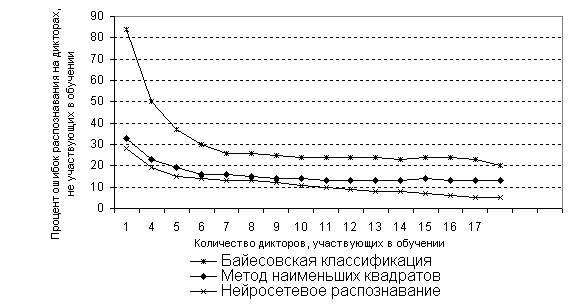
Рис 4. График зависимости процентов ошибок распознавания от метода классификации и количества дикторов, участвующих в обучении.

Из таблицы 1 и графика на рис. 4 видно, что наихудшая распознаваемость наблюдается у вероятностного подхода, основанного на двух априорных предположениях:

1)     Нормальное распределение внутриклассовых компонент вектора

2)     Статистическая независимость компонент вектора

Таблица 1. Процент ошибок распознавания в зависимости от метода классификации

Метрическое распознавание предполагает линейность вкладов каждой компоненты частотно-временного вектора в общую сумму. Единственным методом классификации, не делающим допущения о множестве векторов свойств, является нейросетевое распознавание. Известно, что 3х-слойная нейронная сеть с непрерывной сигмоидальной функцией активации может аппроксимировать любую непрерывную функцию с любой наперёд заданной точностью. Отсюда следует способность классификации любых непрерывных конечных множеств. К недостаткам нейронной сети можно отнести потенциально экспоненциальное время обучения в зависимости от количества обучающих примеров. Однако такая зависимость наблюдается в случае слабой коррелированности векторов, входящих в базовый класс. Экспериментальная зависимость количества итераций при использовании реального тестового множества приведена на Рис. 5.

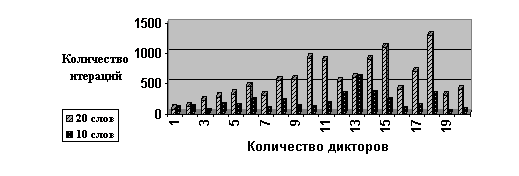
Рис 5. Зависимость количества итераций, необходимых для обучения сети, от количества дикторов и количества слов.

Основным критерием для систем распознавания речи является процент ошибки распознавания и надёжность распознавания. В таблице 2 приведены ошибки классификации нейронной сетью в зависимости от типа и интенсивности шума. Тестовая база состояла из 20-ти слов, каждое из которых было сказано 20 людьми. В качестве обучающей выборки использовались слова 17 человек, остальные слова использовались для тестирования.

_{Таблица 2.  Зависимость процента ошибок распознавания от интенсивности и типа шума}

4. Адаптивное преобразование Эрмита

Наряду с рассмотренным краткосрочным преобразованием Фурье рассмотрим альтернативное представление звукового сигнала, ориентированное непосредственно на квазипериодическую структуру речи. Это представление основано на адаптивном преобразовании Эрмита [7, 8].

Функции Эрмита образуют полную ортонормированную систему функций [9, 10] и определяются как:

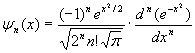
Они также могут быть определены следующими рекуррентными формулами:

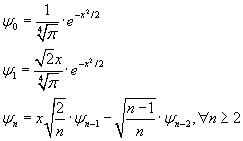
Кроме того, функции Эрмита являются собственными функциями преобразования Фурье [13]:

,

где F обозначает оператор преобразования Фурье.

Графики функций Эрмита выглядят следующим образом:

Для преобразования Эрмита мы должны определить отрезок интегрирования [14]. Если мы посмотрим на структуру речевого сигнала, то увидим, что многие участки речи зачастую имеют квазипериодическую структуру (следует подчеркнуть, что длина соседних квазипериодов, а также форма волны в соседних квазипериодах могут немного различаться):

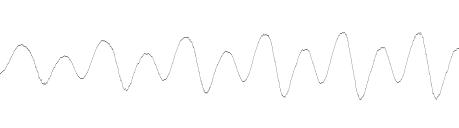
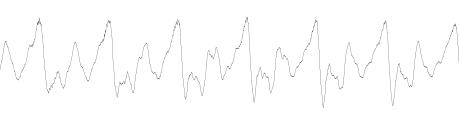
В качестве исходного отрезка будем брать поочередно каждый из таких квазипериодов. Границы будем проводить таким образом, чтобы экстремум сигнала достигался приблизительно на середине квазипериода, а значения на границах были близкими к нулю. Далее мы растягиваем наш отрезок аппроксимации [-A₀, A₀] до отрезка [-A₁, A₁], определенного по следующему критерию:

,

где n - число функций Эрмита, используемых для аппроксимации.

Затем мы раскладываем исходный сигнал в ряд Фурье по функциям Эрмита:

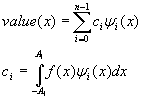
Так как функции Эрмита являются собственными функциями преобразования Фурье, то мы получаем и преобразование Фурье для данного сигнала.

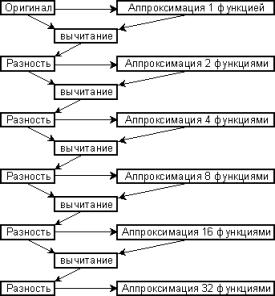Наряду с линейным кодированием можно использовать иерархическое кодирование, которое, с одной стороны,  показывает более стабильные результаты, а, с другой стороны, позволяет провести аналогию между коэффициентами Эрмита и формантами. Суть его состоит в том, что сначала квазипериод приближается одной функцией, далее находится разность, которая растягивается до нужного для аппроксимации 2 функциями отрезка и приближается уже двумя функциями и т.д. Следует подчеркнуть, что хоть такое представление и избыточно, но оно позволяет проводить полный анализ как в частотном диапазоне, так и во временном, что сказывается на возможности более тонкого анализа индивидуальных особенностей каждого человека.

5. Сравнение частотно-временных векторов свойств для задачи распознавания речи и идентификации личности в различных представлениях

Было проведено несколько тестов с использованием различных методов распознавания и классификации. Цель этих исследований заключалась в сравнении краткосрочного Фурье-анализа и адаптивного преобразования Эрмита. Сравнение проводилось на одной тестовой базе с 20 словами и 20 дикторами. Рассматривалось два критерия классификации: диктор-независимое распознавание слов и контекстно-независимое распознавание диктора.

В основе метода распознавания лежит рассматриваемый в предыдущих пунктах метод распознавания на основе двумерных частотно-временных векторов свойств. Тесты показали, что наилучший при данном подходе процент распознавания личности, равный 26%, достигается при использовании преобразования Эрмита, использующего адаптивное разложение на квазипериоды. При этом тестирование проводилось на линейном кодировании с 32 коэффициентами с последующим знаковым суммированием. Заметим, что при индексировании, основанном на иерархическом кодировании Эрмита с использованием дополнительных фильтров и ручной настройки уровня порога, точность составила 95%. Контекстно-независимое распознавание диктора существенно сложнее распознавания с использованием либо известных слов, либо известных фонем. В этом случае процент распознавания повышается до 99.5%. Наилучший процент диктор-независимого распознавания слов (96%) был достигнут при использовании фиксированных окон с Фурье базисом и логарифмическим суммированием.

Таблица 3. Сравнение правильного распознавания при использовании различных методов представления векторов свойств

Рис. 6. Лучшие (из рассмотренных) представления векторов свойств.

Полные результаты исследований приведены в Таблице 3. Эти результаты базируются на следующих особенностях методов распознавания.

Метод, основанный на адаптивных квазипериодах, содержит большее количество информации о личности диктора, чем в преобразованиях с фиксированными окнами. Связано это с сохранением фаз и сохранением частотных биений, возникающих на уровне основного тона. Именно в этой информации и хранятся индивидуальные особенности диктора. Адаптивный подбор длины и местоположения квазипероидов делают функции Эрмита более точно одновременно локализированными как в частотной, так и в пространственной области, по сравнению с косинусоидальными функциями.

Заключение

            Рассмотренные методы распознавания речи и дикторов, не уступают, а по некоторым показателям превосходят существующие подходы. К основным достоинствам метода распознавания слов, на основе двумерных векторов свойств и нейросетевой классификации, можно отнести сосредоточение наиболее существенной, шумоустойчивой частотно-временной информации в компактном частотно-временном векторе. В отличие от этого подхода, метод на основе адаптивного преобразования Эрмита работает с наиболее тонкой частотно-временной локализацией. Это представление звуковой информации является менее устойчивым к шуму, но в ней сохраняются значительно большее количество характерных особенностей голоса, чем в подходе, основанном на использовании  преобразования Фурье. Благодаря этой особенности, эта технология очень хорошо зарекомендовала себя именно в задаче распознавания голоса диктора.

            Авторы считают, что перспективным направлением в развитии диктор-независимого и диктор-адаптируемого распознавания является распознавание речи, использующее частотно-временные вектора в качестве базового элемента, ИНС формирующие на базе этих векторов вероятностные характеристики, которые в результате поступают на вход к СММ.

            Система распознавания речи и диктора могут быть объединены, используя байесовские сети. В свою очередь эта объединенная система может взаимодействовать с другими сенсорами, аудио-визуальными источниками информации, такими, например, как видеокамеры и дальномеры. Такой обмен данными между различными источниками информации может значительно увеличить как процент распознаваемости, так и надёжность распознавания аудио-визуальной информации.

            Работа выполнена при поддержке РФФИ (грант 01-01-00981) и Интел-текнолоджис.

Список литературы

[1]       Dan Tran, Michael Wagner and Tongtao Zheng. A Fuzzy approach to Statistical Models in Speech and Speaker Recognition. 1999 IEEE International Fuzzy Systems Conference Proceedings, Korea, 1275-1280.

 [2]      R.Lippmann, B.Gold "Neural classifiers useful for speech recognition" in. Proc. IEEE First Int. Conf. Neural Net., 1987. Vol. IV, pp. 417--422.

[3]       B.Gold, N.Morgan,"Speech And Audio Signal Processing" 2000.

[4]       Herve Bourlard, Nelson Morgan. Hybrid HMM/ANN Systems for Speech  Recognition: Overview and New Research Directions. http://www.tzi.org/ik98/prog/kursunterlagen/t2/bourlard.html

[5]       C.DEMARS. Two-dimensional representation of speech signal. Time-frequency representation and parametrisations. Elements of monography 1999.

http://www.limsi.fr/Individu/chrd/tablematniE2001.html.html

[6]       Speaker Identification Using Neural Networks and Wavelets. 2000 IEEE Engineering in Medicine and Biology.

[7]       C.Chan,Y.Wong,Tan.Lee,P.Ching "Two-demensional, multi-resolution analysis of speech signals and its application to speech recognition" Department of Electronic Engineering. The Chinese University of Hong Kong.1998

[8]       Gabor Szego "Orthogonal Polynomials". American Mathematical Society Colloquium Publications, vol. 23, NY, 1959.

[9]       Dunham Jeckson, "Fourier Series and Orthogonal Polynomials". Carus Mathematical Monographs, No. 6, Chicago, 1941.

[10]     Jean-Bernard Martens. "The Hermite Transform - Theory". IEEE Transactions on Acoustics, Speech and Signal Processing, vol. 38 (1990) p. 1595-1606.

[11]     Jean-Bernard Martens. "The Hermite Transform - Applications". IEEE Transactions on Acoustics, Speech and Signal Processing, vol. 38 (1990) p. 1607-1618.

[12]     Lawrence R. Rabiner, Bernard Gold. "Theory and Application of Digital Signal Processing". Prentice-Hall, Inc Englewood Cliffs, New Jersey (1975).

 [13] Andrey Krylov and Anton Liakishev. "Numerical Projection Method For Inverse Fourier Transform and its Application". Numerical Functional Analysis and optimization, vol. 21 (2000) p. 205-216.

[14]     Andrey Krylov and Danil Kortchagine "Projection filtering in image processing", Graphicon'2000 Conference proceedings, Moscow (2000) p. 42-45.