Аннотация
В работе рассматривается глобальный демографический процесс. На основе представления о
жизнесберегающих технологиях дается объяснение квадратичной зависимости скорости роста
человечества от его численности. Выводится основное уравнение теоретической демографии,
определяющее баланс между уровнем развития жизнесберегающих технологий и народонаселением.
Рассматриваются механизмы его стабилизации в быстром времени, в частности, кризис, возникающий
при демографическом перегреве. Демографический переход представляет собой результат приближения
жизнесберегающих технологий к их естественному пределу, которое сопровождается сменой
экстенсивного технологического развития интенсивным. Такой подход позволяет построить
феноменологическую модель демографического перехода, находящуюся в хорошем согласии с данными.
Abstract
The world population growth is considered. Based on the concept of life-saving technologies we
explain the squared relationship of the growth rate on the population. We derive a master
equation of the theoretical demography determining the balance between the level of life-saving
technologies and the number of people. Mechanisms of this equation stabilization in fast time,
especially a crisis emerging under demographic overheating, are considered. The demographic
transition results from life-saving technologies verging towards their natural limit. In this
connection the intensive technological development come in the stead to the extensive one.
Such approach allows constructing a phenomenological model of the demographic transition being
in a good agreement with the demographic data.
Введение
Численность биологического вида остается в
среднем постоянной на протяжении всего времени его существования. Homo Sapiens принципиально отличается от прочих видов
непрерывным увеличением своей средней численности. В этой связи изучение роста
народонаселения представляет интерес более широкий, нежели чисто
демографический, позволяя выявить популяционные различия между человеком и
животным. Понимание обуславливающих эти различия механизмов, в свою очередь,
может служить основой для рассмотрения процесса развития человечества с точки
зрения биологии.
Такой подход вполне оправдан, поскольку
люди, неуклонно увеличивающие свою численность, всего лишь решают (причем
чрезвычайно успешно) основную задачу любого вида – продолжить себя в следующих
поколениях. Определяющая роль биологии в демографических процессах явилась
отправным пунктом для возникновения теоретической демографии [1,2]. Ее основная задача – описание
демографических процессов на основе "первых принципов", т.е.
положений биологии, теории эволюции, математической экологии и прочих
"необщественных" дисциплин.
Вместе с тем, теоретическая демография
не ограничивается рассмотрением исключительно динамики народонаселения.
Сформулированный С.П. Капицей принцип демографического императива [3,4] позволяет предполагать демографическую, а
следовательно, и биологическую обусловленность многих явлений и процессов,
изучаемых общественными науками. С математической точки зрения принцип
демографического императива сводится к утверждению, что в наборе переменных,
описывающих крупномасштабные социальные, исторические, культурные,
экономические и т.п. процессы, численность народонаселения является
параметром порядка, т.е. той медленной переменной, к которой подстраиваются все
прочие.
Изучая динамику ведущих переменных, мы
можем отрешиться от многих деталей, что существенно упрощает описание. При
анализе глобального демографического процесса возрастно-половые составляющие,
пространственное распределение, а также различные факторы неравномерности
развития и миграция в первом приближении несущественны. Далее также
предполагается, что все используемые количественные характеристики являются усредненными
на временных интервалах, достаточных для устранения вызванных случайными
факторами отклонений от общего тренда.
При анализе демографических данных сразу
обращает на себя внимание произошедшая во второй половине XX века смена
характера роста народонаселения. Ускоряющийся рост сменился замедляющимся с
тенденцией к стабилизации численности человечества. Этот процесс получил
название демографического перехода. Объяснение его природы является
основной целью данной работы. Однако, прежде чем описывать, как прекращается
рост человечества, необходимо сначала понять, как он происходил.
На рис. 1 представлена зависимость
обратной численности человечества N (здесь и далее измеряется в млрд.чел.) от
времени за период с 1650 г. по 1975 г. с обратным представлением
данных по оси ординат. Как легко видеть, зависимость имеет вид прямой линии, пересекающей
ось абсцисс в момент tf » 2025 г. Таким образом, в течение указанного периода
зависимость народонаселения от времени дается формулой
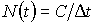 , (1) , (1)
где Dt = tf‑t – время до момента
обострения tf, а C » 200 млрд.чел.×год.
|
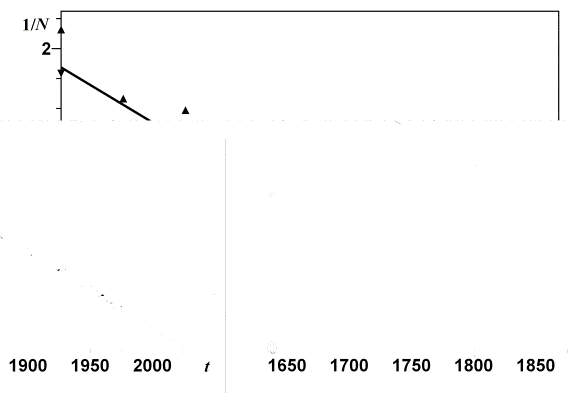
Рис. 1. Обратная численность человечества как функция
времени
Зависимость 1/N от t представляет собой линейную функцию. Если бы такой закон роста
оставался неизменным и далее, численность человечества достигла бесконечности
к 2025 г.
По данным [3,4,5,6,7].
|
Формула (1), становящаяся абсурдной при приближении t к tf, очевидно, не может быть экстраполирована в будущее. Однако ее
экстраполяция в прошлое находится в удовлетворительном согласии с демографическими
данными, как показывает рис. 2, где они дополнены оценками
антропологов и палеодемографов. В дальнейшем будем исходить из предположения,
что гиперболическая зависимость (1) справедлива на протяжении всей истории человека как
вида за исключением нескольких последних десятилетий.
Формулу (1) можно переписать в виде дифференциального уравнения
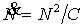 . (2) . (2)
Квадратичный вид его правой части говорит о
самоускоряющемся росте N.
|
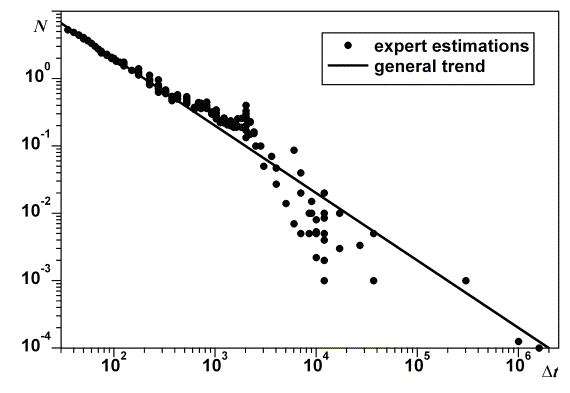
Рис. 2. Зависимость численности
человечества от времени до момента обострения tf
Прямая с наклоном ‑1 в логарифмических
координатах соответствует гиперболической зависимости.
По данным [3,4,5,6,7]. Точки представляют различные оценки численности
человечества.
|
Наряду с автономным уравнением (2) интерес представляет также эквивалентное уравнение с
зависящей от времени правой частью
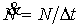 . (3) . (3)
Несмотря на то, что такая запись вряд ли может
быть физически обоснована, она является более наглядной. Формулу (3) можно рассматривать как уравнение
"мальтузианского" роста с уменьшающейся постоянной времени Dt, что позволяет
сделать вывод о сокращение масштаба времени, на котором происходят существенные
демографические изменения, т.е. об ускорении хода истории [3,4]. Вследствие этого времена, на которых необходимо проводить усреднение переменных с
целью устранения случайных отклонений,
должны быть тем больше, чем глубже в прошлое мы уходим. Отметим также, что к
настоящему моменту величина Dt стала порядка времени смены поколений, которое является характерным
временем демографических процессов, что служит дополнительным свидетельством
утраты формулой (1) применимости.
Далее
в части 1 обсуждается природа роста народонаселения и
дается объяснение квадратичного закона (2) на основе представления о жизнесберегающих
технологиях. Часть 2
посвящена обсуждению явления демографического перехода и построению его
феноменологической модели.
1. Глобальный
демографический процесс до демографического перехода
1.1. Природа роста
численности
Первый вопрос, на который необходимо
дать ответ при анализе глобального демографического процесса: а почему
численность человечества вообще увеличивается, а не остается в среднем
постоянной, как это имеет место для популяций животных?
С.П. Капица, строя
феноменологическую модель роста человечества, объясняет рост гипотетическим информационным
взаимодействием, интенсивность которого пропорциональна числу парных
отношений между людьми, что и приводит к квадратичному закону роста (2) [3,4].
К сожалению, такой подход имеет ряд неустранимых
недостатков. С одной стороны, остается непонятным, каким именно образом наличие
информационного взаимодействия приводит к росту численности человечества. С другой,
в рамках модели С.П. Капицы возникают трудности с объяснением прекращения
роста народонаселения при демографическом переходе.
Согласно высказанным в работах [3,4] идеям, демографический переход происходит, когда
прирост численности человечества за одно поколение становится сравнимым с
числом уже живущих людей. Тогда информационное взаимодействие не успевает
подстраиваться под столь стремительные изменения. Однако, как легко понять, при
этом рост населения, если он действительно обусловлен информационным
взаимодействием, должен вовсе не прекратиться (как это происходит в
действительности), а лишь замедлиться, ведь уже установившееся информационное
взаимодействие не исчезает.
Ранее нами был развит отличный подход,
основанный на представлении о демографической роли взаимопомощи и о
жизнесберегающих технологиях [1,2]. Поясним вкратце его суть.
Изменение полной численности
человечества может происходить лишь за счет процессов рождения и смерти людей.
Однако рождаемость не может быть
источником роста народонаселения, так как ее уровень обыкновенно занижен по
сравнению с предельными репродуктивными возможностями человека. Это позволяет
избежать возникновения колебаний численности, вызванных эффектами запаздывания.
Поэтому в процессе своего развития человечество выработало множество
социально-культурных и экономических ограничителей рождаемости. Среди них
религиозные ограничения свободы сексуальных отношений, установление возраста
совершеннолетия, необходимость дать приданное за невестой или уплатить за нее
калым, многоженство, эмансипация женщин, сексуальная революция и т.п.
Таким образом, единственным источником
увеличения численности человечества служит уровень смертности. Он может быть
уменьшен за счет взаимопомощи, когда действия одних людей помогают выжить
другим. В отличие от животных человек, будучи разумным, не ограничен
инстинктивными схемами коллективного поведения и может находить формы
взаимопомощи, наиболее эффективно использующие текущую численность. Уменьшение
смертности должно приводить к росту численности, которая в свою очередь
способствует дальнейшему уменьшению смертности.
Вместе с тем непосредственная
взаимопомощь возможна только в небольших популяциях и не может быть фактором
значимым для глобального демографического процесса. Чтобы одни люди могли
использовать для уменьшения смертности результаты деятельности других, необходимо
какое-то взаимодействие между различными частями человечества.
Однако люди сегодня, как и миллион лет
назад, живут весьма обособлено, занимаясь преимущественно своими делами и
уделяя мало внимания внешнему миру. Иными словами, искомое взаимодействие должно
быть очень мощным, чтобы, не затухая, преодолевать огромные пространства и
людскую замкнутость. Это означает, что его "переносчик" должен очень
легко перемещаться, не расходуясь при взаимодействии.
Таким переносчиком служат жизнесберегающие
технологии, под которыми понимаются любые знания, навыки или традиции,
которые могут быть использованы для спасения человека от смерти или продления
его жизни.
Жизнесберегающие технологии имеют
принципиальное отличие как от информации или знаний "вообще", так и
от технологий в узко-инженерном смысле этого слова. Касаясь всех и являясь
общим делом, жизнесберегающие технологии не требуют для своего создания и
распространения какого-то специального механизма. Они создаются в процессе повседневной
деятельности и распространяются путем простого копирования.
Обратим также внимание на то
обстоятельство, что любая информация постепенно утрачивается (ни люди, ни
материальные носители не вечны) и выжить во времени могут только те знания,
которые постоянно используются и возобновляются, т.е. жизненно необходимы.
Уровень развития жизнесберегающих
технологий p определяется уменьшением среднего
коэффициента смертности kd,
достигнутым благодаря их действию, т.е. p = kd ‑ kd0, где kd0 » 0,06 год‑1 коэффициент смертности первобытного человека. [1,2] Будем далее полагать, что все человечество характеризуется единым
уровнем p, т.е. что время, необходимое для распространения (или независимого
воспроизведения) новых жизнесберегающих технологий, много меньше, чем Dt.
До демографического перехода средний
коэффициент рождаемости kb можно считать приблизительно постоянным и равным kb0 » kd0. При этом скорость роста народонаселения дается формулой
 . (4) . (4)
Как уже отмечалось, жизнесберегающие
технологии создаются людьми в процессе их повседневной деятельности, т.е. на
основе уже имеющихся жизнесберегающих технологий. Соответственно, для скорости
их появления можно записать уравнение
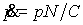 , (5) , (5)
константа C в котором определяет
трудозатраты, необходимые на увеличение p в e раз при постоянном N.
Отметим, что уравнение (4) (в отличие от уравнения (2)) линейно по N.
Поэтому оно в равной степени применимо как к человечеству в целом, так и к
отдельным народам (коль скоро мы пренебрегаем миграцией и считаем, что все
человечество имеет одинаковый уровень развития жизнесберегающих технологий).
Данное обстоятельство позволяет переносить многие результаты, относящиеся к
глобальному демографическому процессу, на "исторический" уровень, и
наоборот, распространять локальные представления на глобальный демографический
процесс.
Интегрируя систему (4)–(5), приходим к соотношению
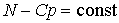 , (6) , (6)
которое в предположении нулевого
технологического уровня при отсутствии людей дает основное уравнение
теоретической демографии
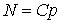 . (7) . (7)
Подстановка уравнения (7) в формулу (4) немедленно приводит к уравнению (2), ранее полученному путем анализа демографических
данных.
1.2. Основное уравнение
теоретической демографии. Представление о технологической нише
Уравнение (7), несмотря на его математическую тривиальность,
заслуживает отдельного обсуждения. Оно означает, что уровень развития жизнесберегающих
технологий p, описывающий скорость роста народонаселения,
характеризует в то же время размер экологической или, точнее говоря, технологической
ниши человечества.
В том, что увеличение уровня развития
жизнесберегающих технологий позволяет поддерживать жизнь большего числа людей,
нет ничего удивительного. В самом деле, чтобы предотвратить гибель людей, их
нужно не один раз спасти, а постоянно обеспечивать всем необходимым для жизни.
Однако обратная связь нетривиальна. Ведь
a priori нет никаких оснований
считать, что расширение занимаемой видом ниши должно приводить к изменению
относительной скорости роста его численности (за исключением, возможно,
переходного процесса, связанного с освоением новой ниши).
Представим себе, что некая неведомая
сила удвоила ареал обитания человечества, заселив новые территории точно такими
же людьми, сохранив их образ жизни и знания. Приведет ли это к удвоению
скорости роста народонаселения? Отнюдь нет. Чтобы удвоить темп прироста,
необходимо не только удвоить число людей, но и развить технологии, объединяющие
два новых независимых человечества в единое человечество удвоенной численности,
т.е. удвоить не только N, но и p.
Иначе говоря, основное уравнение (7) служит отражением существенно нелинейной природы
роста численности человечества, связанной с его целостностью.
Поскольку численность человечества и
уровень жизнесберегающих технологий совпадают с точностью до коэффициента,
процессы увеличения обеих величин эквивалентны. Соответственно, рост народонаселения
можно считать фактически единственной движущей силой развития.
В связи с центральным положением,
которое занимает уравнение (7) в теоретический демографии, весьма важным является
вопрос о его устойчивости. Любое нарушение предписанного им баланса между
уровнем жизнесберегающих технологий и населением (скажем из-за локальной
флуктуации) эквивалентно смене начальных условий системы (4)–(5). При этом на смену уравнению (7) приходит ее интеграл (6). Легко видеть, что относительная величина отклонения
будет со временем убывать из-за монотонного роста p и N. Таким образом, основное уравнение (7) устойчиво в медленном времени, т.е. на тех временах,
на которых должно проводиться усреднение демографических характеристик.
Однако оказывается, что уравнение (7) устойчиво и в быстром времени. Связано это с
динамикой быстрых переменных, неучтенных при выводе системы (4)–(5). Процессы, посредством которых происходит
восстановление баланса между численностью человечества и размером его
технологической ниши, оказываются различными в зависимости от знака отклонения,
что затрудняет их унифицированное описание.
Если из-за войн, эпидемий, стихийных
бедствий и т.п. катаклизмов население уменьшается, то включаются
популяционные (рост рождаемости, мобилизация внутренних ресурсов организмов
уцелевших особей) и социальные (усиление взаимопомощи и снятие ограничивающих
рождаемость барьеров) защитные механизмы. В результате status quo восстанавливается в течение всего лишь нескольких
поколений.
Если же, напротив, по каким-то причинам
произошло чрезмерное увеличение численности населения, не сопровождаемое
одновременным развитием технологий, то для части людей может просто не найтись
места в социальной структуре общества, которая адекватна достигнутому уровню
развития жизнесберегающих технологий. Эти люди оказываются лишними,
потребляя создаваемое другими "жизнесбережение" и не имея возможности
участвовать в его создании.
Для каждой технологии есть некоторое предельное
число рабочих рук, которые она позволяет эффективно использовать. В самом деле,
бесполезно иметь больше землепашцев, чем необходимо для обработки имеющейся
пахотной земли, или больше солдат, чем нужно для защиты от реальной военной угрозы.
Наличие
лишних людей является фактором гораздо более стойким, чем нехватка людей, так
как обычно обусловлено причинами, не являющимися чисто
случайными и, соответственно, действующими на протяжении долгого времени.
Простейшим примером может служить
увеличение урожайности сельскохозяйственных культур в результате временного
улучшения климата. В этом случае происходит ощутимое уменьшение смертности, в
первую очередь детской, приводящее вскоре к появлению людей, не востребованных
в традиционном сельскохозяйственном производстве. Причем биологические или
социальные механизмы регуляции численности могут просто не успеть включиться
из-за наличия запаздывания, связанного со сменой поколений.
Как
только относительное количество лишних людей превысит некоторый пороговый
уровень, дальнейшее стабильное развитие становится невозможным. Наличие здесь
порогового эффекта также объясняется запаздыванием, поскольку лишние люди
делаются таковыми, лишь став взрослыми. Описанное резкое изменение ситуации
представляет собой кризис – будем называть его демографическим
перегревом, – который может разрешиться только путем разделения общества.
Либо лишние люди направляется вовне в
форме колониальной экспансии, религиозных войн и т.п. процессов, которые
продолжаются до тех пор, пока избыток людских ресурсов не будет исчерпан (а
вовсе не до достижения каких-то конкретных политических или экономических
результатов), либо те же самые события происходят на месте, принимая характер
смуты, гражданской войны, геноцида. В последнем случае обыкновенно
"выбивается" значительно больше людей, чем их реально имеющийся избыток.
Дело в том, что многие технологии могут
нормально функционировать лишь в условиях стабильности, поэтому любые
потрясения уменьшают или даже сводят к нулю их применимость. Собственно говоря,
умение поддерживать стабильность и порядок также следует отнести к числу
жизнесберегающих технологий.
Поясним ситуацию вывода из употребления
жизнесберегающих технологий следующей простой моделью.
1.3. Модель развития
кризиса при демографическом перегреве
Обозначим через R число востребованных людей, т.е. размер их технологической ниши. Пусть в момент возникновения
кризиса число востребованных людей составляет R0 = Cp (далее будем полагать, что во время кризиса
новые технологии не создаются, т.е. p = const), а их полное число – N0 = R0(1+d), где d –
порог кризиса.
При малых отклонениях N от R скорость восстановления баланса между людской численностью и размером
ниши прямо пропорциональна отклонению
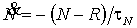 . (8) . (8)
Скорость сокращения технологической ниши,
обусловленного выводом из употребления жизнесберегающих технологий, в первом
приближении также можно считать линейно зависящей от количества лишних людей N‑R
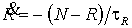 . (9) . (9)
Интегрирование системы (8)–(9) дает формулу, в соответствии с которой
восстанавливается баланс между численностью населения и размером
технологической ниши,
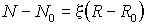 , (10) , (10)
где безразмерный параметр x = tR/tN характеризует отношение скоростей сокращения количества лишних людей и
вывода из употребления жизнесберегающих технологий. Первый процесс является
несколько более медленным. Так, характерное время разрушения экономических
связей, хозяйственной инфраструктуры, культурных стереотипов и прочих элементов
технологической ниши tR можно оценить диапазоном от нескольких лет до
нескольких десятилетий, в то время как характерное время гибели людей в
результате неестественных причин tN составляет от нескольких месяцев до
нескольких лет или (в исключительных случаях) поколения. Таким образом,
величина x варьируется единицы до нескольких десятков.
|
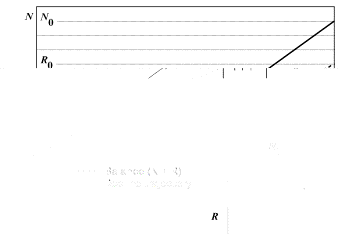
Рис. 3. Сокращение технологической
ниши и людской численности при кризисе
Из-за
вывода из употребления жизнесберегающих технологий население сокращается не
до размера технологической ниши R0, а до существенно меньшей величины N1.
График
соответствует значениям x=1,5 и d=0,3.
|
Кризис заканчивается, когда людская
численность сравняется с размером ниши, т.е. N = R, что с учетом формулы (10) дает выражение для финальной численности N1 = R0(1‑d/(x‑1)).
Фазовый портрет системы (8)–(9) представлен
на рис. 3.
В ходе кризиса людская численность
падает до величины, меньшей, нежели размер технологической ниши R0 в момент его начала. Причем
"сверхплановое" сокращение людской численности R0d/(x‑1) оказывается тем больше,
чем ближе x к единице.
Кризисы, сопровождаемые большим числом
жертв, могут возникать в случае малого времени tR (взрывное
высвобождение накопленных противоречий между различными национальностями,
конфессиями, кланами, классами, сословиями и т.п.) и значительного времени
tN (медленное вымирание
людей в результате распада привычной среды обитания или насильственная гибель
людей в сочетании с продолжающейся подпиткой молодежью).
История знает немало примеров жестоких
кризисов, которые сокращали население государств даже не на десятки процентов,
а в разы. Однако, на наш взгляд, они есть исключение, а не правило. Кризис интересен
для историка в той же мере, как болезнь для медика, но и тот, и другая
представляют собой патологии, возникающие как результат сбоя защитных механизмов.
Обществу выгоднее избежать
демографического перегрева или, в крайнем случае, сбросить избыток людской
численности вовне, нежели потом в течение десятилетий зализывать раны.
Уравнение баланса (7) останется справедливым (в среднем) в обоих случаях,
однако исторические перспективы государства, пережившего кризис, весьма
плачевны. Даже если оно не подвергается агрессии со стороны более благополучных
соседей, культура его населения претерпевает порой настолько существенные
изменения, что можно говорить о возникновении другого государства на той же
территории.
Из сказанного можно сделать простой
вывод: человечество на протяжении всей своей истории вынужденно вырабатывало
механизмы, противодействующие росту населения, опережающему развитие
жизнесберегающих технологий. В разных культурах они могли принимать различные
формы при неизменном конечном результате, сводившемся к стабилизации баланса
между численностью народонаселения и уровнем жизнесберегающих технологий.
2. Демографический
переход
Развитие жизнесберегающих технологий имеет
естественный предел, обусловленный тем, что нельзя спасти от смерти больше
людей, чем их всего живет. Это означает, что уравнение (5) справедливо лишь до определенного предела.
Сегодня средний коэффициент смертности в
наиболее развитых странах приближается к значению kd¥ » 0,01 год‑1, которое, по-видимому, определяется
биологическим пределом продолжительности человеческой жизни. Соответственно,
предельный уровень развития жизнесберегающих технологий есть p¥ = kd0‑kd¥ » 0,05 год‑1. Данное обстоятельство не означает ограниченности возможностей
технологического развития вообще. Просто создаваемые технологии становятся все
менее эффективными с точки зрения спасения жизней. Т.е. они вносят все меньший
вклад (по отношению, скажем, к их экономической значимости или инженерной
сложности) в величину p.
Как следует из формулы (7), предельная численность человечества составляет N¥ = Cp¥ » 10 млрд.чел. Это значение не может быть
превышено, поскольку избыток населения, не востребованный
жизнесберегающими технологиями, будет неизбежно уничтожен. Вместе с тем
необходимо особо отметить, что значение N¥
не связано с какими бы то ни
было ресурсными ограничениями.
Прекращение роста N носит, конечно, не
скачкообразный характер, а происходит постепенно во время демографического
перехода в результате сокращения рождаемости (при этом уравнение (4) также утрачивает применимость).
Демографический переход длится несколько поколений и за это время население
проходящих его стран возрастает в несколько раз. В ряде стран демографический
переход уже завершился, в других еще продолжается.
Явлению демографического перехода можно
дать качественное объяснение в рамках представлений о поведенческих
стратегиях, т.к. уровень рождаемости определяется преимущественно
действующими культурными нормами и стереотипами. При высокой смертности
выигрышной стратегией является рождение большого числа детей (носители
малодетной стратегии просто вымирают), а при низкой – рождение двух-трех
(носители многодетной стратегии в этом случае не просто несут неоправданно
высокие издержки по выращиванию детей, но и подвергают общество в целом риску
демографического перегрева). Социальные группы, следующие иным стратегиям,
проигрывают и не передают потомству своих стратегий.
Поскольку жизнесберегающие технологии
развиваются ускоряющимися темпами, значительное уменьшение смертности
происходит очень быстро и в какой-то момент возникает необходимость в смене
стратегии прокреативного поведения. На распространение новой стратегии и уходят
те несколько поколений, которые длится демографический переход.
Схема технологического развития также
претерпевает существенные изменения во время демографического перехода. Однако
их природа несколько иная.
Пока p << p¥, развитие жизнесберегающих технологий носит экстенсивный
характер, описываемый уравнением (5), при котором новые технологии возникают на основе уже
созданных. Однако по мере приближения p к p¥ оно должно смениться интенсивным развитием, когда новые жизнесберегающие
технологии целенаправленно "добираются" из числа еще не созданных.
При этом и скорость их появления должна уже зависеть не от достигнутого технологического
уровня p (он более
чем достаточен), а от ширины оставшегося "зазора",
т.е. от p¥‑p.
Разумной представляется гипотеза, что
скорость интенсивного развития технологий дается формулой
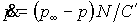 (11) (11)
с некоторым C',
вообще говоря, отличным от C.
Предположим, кроме того, что основное
уравнение (7), бывшее справедливым на протяжении всей человеческой
истории и "подкрепленное" выработанными за это время стабилизирующими
механизмами, остается таковым и во время демографического перехода (т.е. когда
система (4)–(5), из которой оно было получено, становится уже
неприменимой). Тогда для скорости роста численности человечества во время
демографического перехода вместо уравнения (2) получаем уравнение Ферхюльста
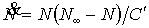 . (12) . (12)
Из формулы (12) следует, что скорость относительного прироста
народонаселения должна быть линейной функцией от его численности. Этот вывод подтверждается
рис. 4.
К сожалению, переход человечества от
закона развития (5) к закону
(11) не удается отчетливо проследить, так как ему
непосредственно предшествовала Вторая мировая война, внесшая в демографический
процесс существенные возмущения. Тем не менее, можно утверждать, что этот
переход был весьма непродолжителен во времени. Таким образом, наряду с
непрерывным демографическим переходом, связанным со сменой стратегии прокреативного
поведения, имеет место также практически скачкообразный технологический
переход, связанный с быстрым изменением стратегии технологического развития
и произошедший в начале 60‑х годов XX века. Технологический переход представляет
собой момент смены ускоряющегося роста народонаселения замедляющимся.
|
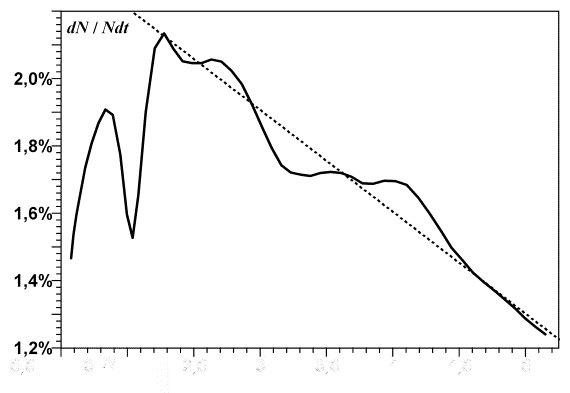
Рис. 4. Относительный годовой прирост народонаселения в
зависимости от его численности за период 1950‑2000 гг.
Резкий провал в левой части графика (1950‑1960 гг.),
по-видимому, обусловлен "большим скачком" в Китае и последствиями
Второй мировой войны. Далее устанавливается примерно линейная зависимость
темпов относительного прироста от N. Пунктирная прямая
соответствует уравнению (12) с N¥ = 10,3 млрд.чел. и C' » 330 млрд.чел.×год.
По данным [7]. Сглаженная зависимость.
|
Несмотря на различие во временной
протяженности, демографический и технологический переходы тесно взаимосвязаны и
представляют собой разные стороны одного и того же явления, которое уместно
именовать просто переходом.
Решение уравнения (12) имеет вид
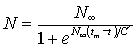 , (13) , (13)
где tm – постоянная интегрирования, определяющая момент
наибольшей скорости роста народонаселения.
Наилучшее согласие формулы (13) с демографическими данными после момента
технологического перехода (см. рис. 5) достигается при значениях N¥ = 10,7 млрд.чел. и C' = 350 млрд.чел.×год, близких к полученным ранее, и tm = 1991 г. Эта
дата также близка к 1989 г., на который реально пришелся максимум
ежегодного прироста народонаселения, составивший 87 млн.чел. при
численности человечества на тот момент в 5,20 млрд.чел. [7]. Сравнение приведенных величин со значениями N¥2/4C' » 82 млн.чел./год и Nm = N¥/2 » 5,35 млрд.чел., которые дает формула (13) при t = tm, позволяет считать точность построенной модели вполне
удовлетворительной.
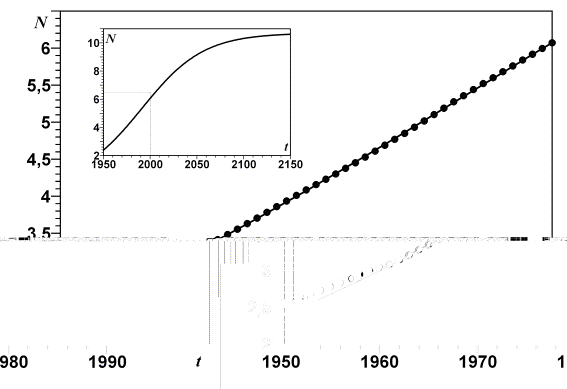
Рис. 5. Приближение графика роста
народонаселения решением уравнения (12)
Точки – реальные
демографические данные, линия – их наилучшая (при t > 1960 г.) аппроксимация формулой (13) с параметрами N¥ = 10,7 млрд.чел., C' = 350 млрд.чел.×год, tm = 1991 г.
На врезке – прогноз по формуле (13) до 2150 г.
По данным [7].
|
Выводы
Рост народонаселения обусловлен
спасением жизней людей посредством действия жизнесберегающих технологий.
Уровень развития последних прямо пропорционален числу живущих людей. Это, с одной
стороны, приводит к постоянному ускорению роста численности человечества, а с
другой, позволяет рассматривать ее в качестве меры развития последнего.
Однако та история, движущей силой
которой являлись демографические процессы, ныне подходит к концу. Приближение
уровня жизнесберегающих технологий к предельному значению привело к демографическому
переходу, результатом которого должно стать прекращение роста человечества и
стабилизация его численности на уровне предположительно в 10÷11 млрд.чел.
Тем самым завершится переходный процесс,
которым была вся предшествующая история человечества, и оно вступит в
принципиально новую фазу развития.
Литература
1. Подлазов А.В.
Теоретическая демография как основа математической истории// Препринт ИПМ им. М.В. Келдыша РАН. 2000, № 73.
2. Подлазов А.В.
Представление о жизнесберегающих и имперских технологиях в
теоретической демографии// Математическое и
компьютерное моделирование социально-экономических процессов. Материалы
российского научного симпозиума. Часть 2. М.: РГУУ, 2001.
3. Капица С.П.,
Курдюмов С.П., Малинецкий Г.Г. Синергетика и прогнозы будущего/
Сер. "Кибернетика: неограниченные возможности и возможные ограничения".
– М.: Наука, 1997. – 285 с.
4. Капица С.П.
Сколько людей жило, живет и будет жить на Земле. Очерк теории роста
человечества. – М.: Международная программа образования, 1999. –
240 с.
5. Cohen J.E.
How many people can the Earth support? W.W. Norton & Company. New York
– London. 1995.
6. http://www.census.gov/ipc/www/worldhis.html
(Historical Estimates of World Population).
7. http://www.census.gov/ipc/www/worldpop.html
(Total Midyear Population for the World: 1950‑2050).
|