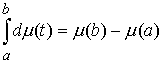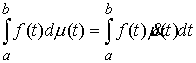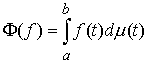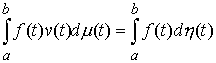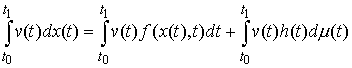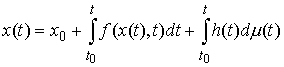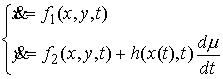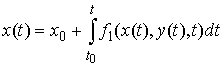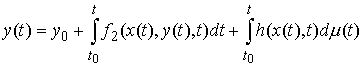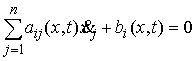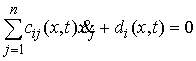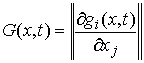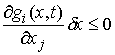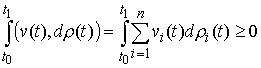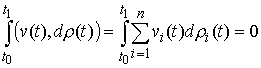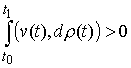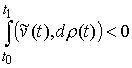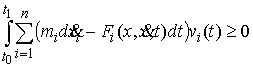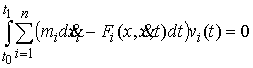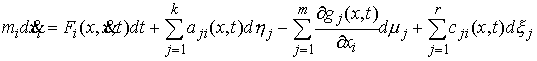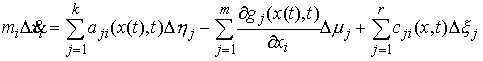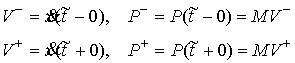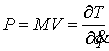Аннотация
Рассматриваются механические системы с неголономными (условными) односторонними связями.
На основе обобщенного условия идеальности связей и принципа Даламбера-Лагранжа выводятся
уравнения движения в форме уравнений Лагранжа 1-го и 2-го рода, а также в форме уравнений
Гамильтона. Формулируются основные законы движения.
Abstract
Dalamer-Lagrange principle expanded on to mechanics systems with one- sided nonholonomic
(conditional) relations. Ideal relation conditions are described. Equation of motion as
Lagrange equations of first and second kinds and Hamilton equations are derived.
Содержание
Введение.............................................................................................................. 3
1. Пространство
траекторий............................................................................. 4
2. Принцип
Даламбера-Лагранжа для условных связей................................... 8
3. Теорема
Аппеля........................................................................................... 13
4. Теоремы
Карно и непрерывность кинетической энергии.......................... 15
5. Формула
Карно............................................................................................ 17
6. Теорема
об изменении количества движения............................................. 17
7. Теорема
об изменении момента количества движения.............................. 17
8. Уравнения
Лагранжа второго рода............................................................. 17
9. Циклические
интегралы и теорема Рауса.................................................... 17
10. Преобразование
координат....................................................................... 17
11. Теорема
Нётер........................................................................................... 17
12. Примеры
задач.......................................................................................... 17
ЛИТЕРАТУРА................................................................................................... 17
Введение
В работе рассматриваются
механические системы с односторонними связями. Обзор работ по данной тематике
можно найти в [1,2]. В работах [3, 4] был рассмотрен обобщенный принцип
Даламбера-Лагранжа для систем с голономными
односторонними связями. В данной работе мы распространяем этот принцип (и
выводим уравнения движения) на системы с неголономными, т.н. условными односторонними связями.
Односторонними неголономными
связями мы называем такие ограничения, накладываемые на движение системы, которые
не представлены (и, может быть, непредставимы) в виде задания какой-либо
области в конфигурационном пространстве. Простейший вид таких ограничений – это
линейные ограничения, задаваемые неравенствами вида
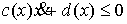 (1) (1)
Именно они возникают при описании движения одностороннего конька. Другой
вид подобных ограничений – это т.н. условные связи, возникающие, например, при
соударении абсолютно шероховатых поверхностей, которые прокатываются друг по
другу без проскальзывания. Формально подобные ограничения можно описать
системой
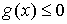 всегда, и всегда, и 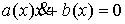 , при , при  (2) (2)
Первая часть этого условия запрещает взаимное проникновение тел, а вторая
описывает качение без проскальзывния при их соприкосновении. Подобного рода
задачи мы будем для краткости называть задачами первого вида.
Более сложные ограничения
возникают, если мы обратимся к изучению статически равновесных форм тонких
упругих стержней, стесненных пространственными ограничениями. Подобные задачи
появляются, при исследовании пространственных форм биологических макромолекул в
рамках модели тонкого упругого стержня [5]. В соответствии с аналогией Кирхгофа
– статику тонких упругих стержней можно описывать терминах движения тяжелого
твердого тела с неподвижной точкой (точнее гиростата). Стержень может быть
стеснен оболочкой, ограничивающей его предельный изгиб, и в терминах движения
гиростата это приводит к ограничениям вида (1) на возможные значения угловых
скоростей гиростата. При изучении упаковки молекул ДНК в хромосомах, возникают
ограничения на положение осевой линии стержня. В терминах движения гиростата
они описываются ограничениями на интегралы от координат направляющих векторов
сопутствующего трехгранника, т.е. имеют вид 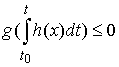 для любого для любого 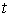 . .
В отличие от задач классической неголономной механики в задачах механики
тонких упругих стержней четко формулируется вариационный принцип – пространственная
форма стержня соответствует экстремуму упругой энергии. В терминах движения гиростата это означает, что мы
работаем в рамках т.н. вакономной механики – т.е. механики неголономных систем,
движение которых подчиняется интегральным вариационным принципам [6]. Заметим,
что отличительной особенностью вакономных систем с односторонними связями является
требование достаточной гладкости траекторий.
В настоящей работе мы
остановимся только на задачах первого вида. В разделе 1 обсуждается вопрос о
том, какую форму должны иметь уравнения движения механических систем с
односторонними и условными связями, и каково должно быть пространство
траекторий. Оказывается, что траектории движения таковы, что скорости движения
являются функциями ограниченной вариации. При этом сами траектории,
естественно, являются, по крайней мере, абсолютно непрерывными функциями. Также
рассматриваются импульсные обыкновенные дифференциальные уравнения. В разделе 2
рассматривается случай т.н. условных связей, возникающих, например, при
соударении абсолютно шероховатых поверхностей, которые прокатываются друг по
другу без проскальзывания. Формулируются условия идеальности связей и, исходя
из обобщенного принципа Даламбера-Лагранжа, выводятся уравнения движения.
В разделе 3 известная теорема Аппеля,
о сохранении составляющих импульса, касательных к поверхности удара, распространяется
на случай условных связей. Для систем с удерживающими связями эта теорема
обсуждалась в [4]. В разделах 4 и 5 известные теоремы Карно об изменении
кинетической энергии системы при ударе распространяются на случай условных
связей. Для систем с удерживающими связями эта теорема обсуждалась в [4].
Формулируется многомерный аналог третьей теоремы Карно.
В следующих двух разделах (6 и 7)
рассматриваются известные теоремы об изменении и сохранении импульса и момента
импульса для систем с условными связями. В разделах 8-11 для систем с условными
связями выводятся уравнения Лагранжа второго рода. Доказывается их
инвариантность при замене координат. Классическая теория Аппеля и Нётер о
циклических интегралах распространяется на данные системы. Для систем с удерживающими
связями эти вопросы обсуждалась в [4].
В конце работы без подробного анализа
формулируются примеры нескольких систем с условными связями, к которым
применимы методы, изложенные в данной работе.
1.
Пространство
траекторий.
В [3, 4] мы уже обсуждали вопрос о том, какую форму
должны иметь уравнения движения механических систем с односторонними связями, и
каково должно быть пространство траекторий. В системах с гладкими идеальными
удерживающими связями траектории движения – это гладкие кривые, по крайней
мере, второго порядка гладкости. Уравнения движения – это обыкновенные
дифференциальные уравнения. У систем с односторонними связями помимо гладких
движений мы можем наблюдать ещё движения, по крайней мере, двух видов.
Во-первых – это одиночный удар, когда траектория движется внутри допустимой
области, затем в какой-то момент времени ударяется о границу односторонних
связей, и потом (отскочив от границы) снова продолжает двигаться внутри
допустимой области. В момент удара скорость движения мгновенно меняется. Вторым
примером является скольжение по границе допустимой области на некотором отрезке
времени. В обоих случаях движение можно описать, добавив в правую часть
уравнений движения реакцию односторонних связей. При этом реакция не равна нулю
только в моменты движения по границе односторонних связей. В первом случае
реакция имеет импульсный вид, и ее часто описывают, используя обобщенные
функции, а во втором случае она представляет собой кусочно-непрерывную функцию.
Рассмотрим,
например, плоское движение материальной точки на, которую наложена гладкая
односторонняя связь задаваемая условием  . Уравнения её движения выглядят следующим образом . Уравнения её движения выглядят следующим образом
 , , 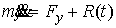 (1.1) (1.1)
где 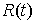 – реакция связи. Если
точка однократно сталкивается с границей односторонней связи в момент времени – реакция связи. Если
точка однократно сталкивается с границей односторонней связи в момент времени 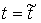 , то реакцию можно записать следующим образом: , то реакцию можно записать следующим образом: 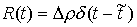 . Где . Где 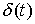 – дельта-функция
Дирака, а – дельта-функция
Дирака, а 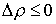 – некоторое
неположительное число. Если точка скользит по границе связи на отрезке времени – некоторое
неположительное число. Если точка скользит по границе связи на отрезке времени 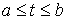 , а в остальное время находится внутри допустимой области, то , а в остальное время находится внутри допустимой области, то
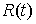 представляет собой
некоторую неположительную функцию равную нулю вне отрезка представляет собой
некоторую неположительную функцию равную нулю вне отрезка 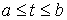 . В обоих случаях можно было бы написать . В обоих случаях можно было бы написать 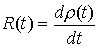 (1.2) (1.2)
где 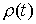 – в первом случае
представляет собой ступенчатую функцию: – в первом случае
представляет собой ступенчатую функцию:  при при 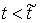 , и , и 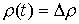 при при 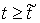 ; а во втором случае ; а во втором случае  – это кусочно-гладкая
функция, постоянная вне отрезка – это кусочно-гладкая
функция, постоянная вне отрезка 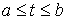 . Строго говоря, более правильно было бы равенство (1.2)
записывать как . Строго говоря, более правильно было бы равенство (1.2)
записывать как 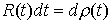 , понимая правую часть как меру Лебега-Стилтьеса с
производящей функцией , понимая правую часть как меру Лебега-Стилтьеса с
производящей функцией 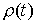 . Уравнение движения при таком описании будет выглядеть
следующим образом . Уравнение движения при таком описании будет выглядеть
следующим образом
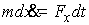 , , 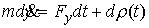
где 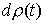 – мера
Лебега-Стилтьеса с производящей функцией – мера
Лебега-Стилтьеса с производящей функцией 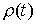 . Обсудим обоснованность такого описания движения. В обоих
случаях траектория является кусочно-гладкой функцией. Для скорости движения это
уже не так. В первом случае её можно представить в виде суммы кусочно-гладкой и
ступенчатой функций. Во втором случае скорость является просто кусочно-гладкой
функцией. . Обсудим обоснованность такого описания движения. В обоих
случаях траектория является кусочно-гладкой функцией. Для скорости движения это
уже не так. В первом случае её можно представить в виде суммы кусочно-гладкой и
ступенчатой функций. Во втором случае скорость является просто кусочно-гладкой
функцией.
Таким
образом, пространство функций, которыми мы можем описывать скорость движения
должно содержать кусочно-гладкие и ступенчатые функции, а уравнения движения
должны иметь вид, допускающий такого рода функции для скорости движения. Кроме
того, хотелось бы, чтобы уравнения движения были корректными, т.е., чтобы, при
достаточно широких предположениях, их решение существовало, и было непрерывным
по отношению к начальным условиям. Отсюда вытекает желание того, чтобы
пространство функций, описывающих положение и скорость движения, было полным,
т.е. содержало все свои предельные точки. Кроме того, из физических
соображений, оно должно быть линейным (т.е. допускать сложение скоростей).
Ступенчатыми функциями можно, с любой точностью, приблизить любую монотонную
функцию. Значит, наше пространство должно содержать монотонные функции, а также
их суммы (и разности). Простейшее функциональное пространство, содержащее
монотонные функции, а также их суммы и разности хорошо известно. Это банахово
пространство функций с ограниченной вариацией. Норма функции в нём определяется
как полная вариация функции на отрезке её определения.
Функции с
ограниченной вариацией. Пусть 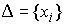 , , 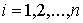 , , 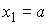 , , 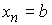 , , 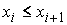 – разбиение отрезка – разбиение отрезка  . Частной вариацией конечной функции . Частной вариацией конечной функции 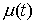 , заданной на отрезке , заданной на отрезке 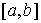 , для разбиения , для разбиения 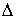 называется величина называется величина 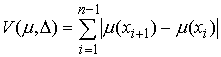 . Функция . Функция 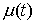 называется функцией с
ограниченной вариацией, если все ее частные вариации равномерно ограничены
сверху. Верхняя грань частных вариаций называется функцией с
ограниченной вариацией, если все ее частные вариации равномерно ограничены
сверху. Верхняя грань частных вариаций 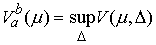 называется полной вариацией
(или просто вариацией) функции называется полной вариацией
(или просто вариацией) функции 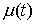 на отрезке на отрезке 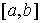 . Очевидно, что для монотонно неубывающей функции . Очевидно, что для монотонно неубывающей функции 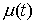 имеем имеем 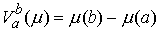 . .
Любая функция ограниченной вариации задает некую меру
Лебега-Стилтьеса. И, тем самым, определяет интеграл Лебега-Стилтьеса. Поскольку
нас будет интересовать интегрирование непрерывных функций, для которых
интегралы Стилтьеса и Лебега-Стилтьеса совпадают, то мы не будем их различать.
Дадим определение интеграла Стилтьеса. Имея некое разбиение 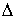 отрезка отрезка 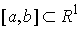 , выберем семейства
точек , выберем семейства
точек 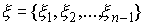 по одной в каждом
сегменте: по одной в каждом
сегменте: 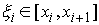 . Пусть . Пусть 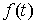 – непрерывная
функция, а – непрерывная
функция, а 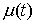 – функция ограниченной вариации на отрезке – функция ограниченной вариации на отрезке 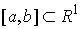 . Частной суммой для разбиения ( . Частной суммой для разбиения (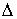 , , 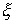 ) называется величина ) называется величина 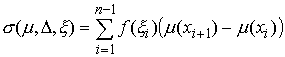 . Если эти частные суммы стремятся к конечному пределу . Если эти частные суммы стремятся к конечному пределу  при при 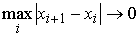 равномерно по равномерно по 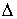 , , 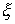 , то он называется интегралом Стилтьеса функции , то он называется интегралом Стилтьеса функции 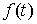 по функции по функции 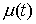 и обозначается и обозначается 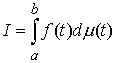 . Из определения сразу следует, что . Из определения сразу следует, что 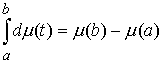 . Можно показать, что, если . Можно показать, что, если 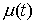 – абсолютно
непрерывна, а – абсолютно
непрерывна, а 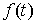 – непрерывна, то – непрерывна, то 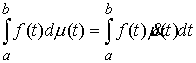 . Любая мера Лебега-Стилтьеса . Любая мера Лебега-Стилтьеса 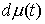 задает непрерывный
линейный функционал на пространстве задает непрерывный
линейный функционал на пространстве 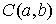 функций непрерывных
на отрезке функций непрерывных
на отрезке 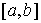 . Для . Для 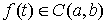 он определяется
следующим образом: он определяется
следующим образом:
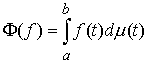 (1.3) (1.3)
Теорема
Рисса. Верно и обратное, если задан непрерывный
линейный функционал 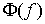 на пространстве на пространстве 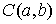 функций функций 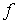 непрерывных на отрезке непрерывных на отрезке
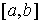 , то существует такая функция , то существует такая функция 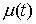 с ограниченной
вариацией, что функционал с ограниченной
вариацией, что функционал 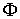 задается соотношением
(1.3). Из теоремы Рисса следует, что, если задается соотношением
(1.3). Из теоремы Рисса следует, что, если 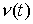 – непрерывная
функция, а – непрерывная
функция, а 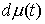 – мера Лебега-Стилтьеса, то существует мера
Лебега-Стилтьеса – мера Лебега-Стилтьеса, то существует мера
Лебега-Стилтьеса 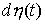 такая, что для любой
непрерывной функции такая, что для любой
непрерывной функции 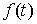 будет выполнено будет выполнено
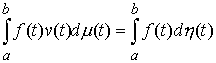 (1.4) (1.4)
Поэтому выражение 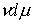 будем понимать как
соответствующую меру будем понимать как
соответствующую меру 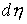 . .
Равенство мер Лебега-Стилтьеса. В свете теоремы Рисса мы будем считать две меры Лебега-Стилтьеса
совпадающими, если совпадают соответствующие им линейные функционалы. Так,
(1.4) эквивалентно записи 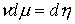 . .
Пространство траекторий.
Резюмируя сказанное, мы считаем, что траектории движения таковы, что скорости
движения являются функциями ограниченной вариации. При этом сами траектории,
естественно, являются, по крайней мере, абсолютно непрерывными функциями.
Импульсные
дифференциальные уравнения. Обсудим теперь кратко
вопрос о том, как понимать обыкновенные дифференциальные уравнения с импульсной
правой частью. Рассмотрим сначала уравнение 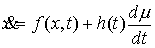 . Запишем его немного иначе: . Запишем его немного иначе:
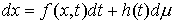 (1.5) (1.5)
где 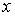 , , 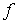 , , 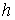  . Пусть . Пусть 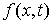 и и 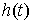 – непрерывные
вектор-функции, а – непрерывные
вектор-функции, а 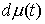 – одномерная мера
Лебега-Стилтьеса. Естественно
предположить, что решение этого уравнения мы ищем в классе вектор-функций – одномерная мера
Лебега-Стилтьеса. Естественно
предположить, что решение этого уравнения мы ищем в классе вектор-функций 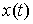 с ограниченной
вариацией. В этом случае и в левой, и в правой частях уравнения стоят векторные
меры Лебега-Стилтьеса, и само уравнение надо понимать как их совпадение. Дадим
теперь строгое определение. Пусть на отрезке с ограниченной
вариацией. В этом случае и в левой, и в правой частях уравнения стоят векторные
меры Лебега-Стилтьеса, и само уравнение надо понимать как их совпадение. Дадим
теперь строгое определение. Пусть на отрезке 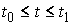 задана
вектор-функция задана
вектор-функция 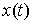 с ограниченной
вариацией. Она является решением уравнения (1.5) с начальными условиями с ограниченной
вариацией. Она является решением уравнения (1.5) с начальными условиями  , если , если 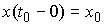 и для любой
непрерывной вектор-функции и для любой
непрерывной вектор-функции 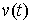 , заданной на отрезке , заданной на отрезке 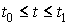 выполнено выполнено
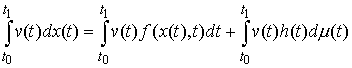
Это условие эквивалентно выполнению для каждого 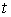 следующего уравнения следующего уравнения
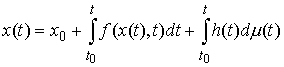
Интеграл здесь понимается, как интеграл Стилтьеса на
отрезке 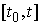 . В данной работе нас будут интересовать несколько более
сложные импульсные дифференциальные уравнения. В общем виде их можно записать
следующим образом. . В данной работе нас будут интересовать несколько более
сложные импульсные дифференциальные уравнения. В общем виде их можно записать
следующим образом. 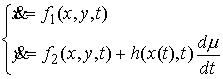
где 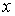 , , 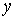 , ,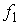 , , 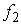 , , 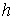 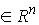 . Пусть . Пусть 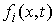 и и 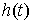 – непрерывные
вектор-функции, а – непрерывные
вектор-функции, а 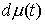 – одномерная мера
Лебега-Стилтьеса. Эта система рассматривается совершенно аналогично. Дадим
строгое определение решения. Пусть на отрезке – одномерная мера
Лебега-Стилтьеса. Эта система рассматривается совершенно аналогично. Дадим
строгое определение решения. Пусть на отрезке 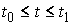 задана абсолютно
непрерывная вектор-функция задана абсолютно
непрерывная вектор-функция 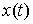 и функция с ограниченной
вариацией и функция с ограниченной
вариацией 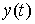 . Они являются решением приведенной выше системы уравнений с
начальными условиями . Они являются решением приведенной выше системы уравнений с
начальными условиями 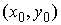 , если , если 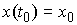 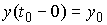 и для любого и для любого 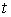 на отрезке на отрезке 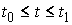 выполнено выполнено
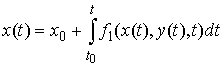
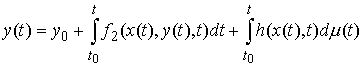
В частном случае, когда 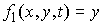 , эта система может быть записана более кратко следующим
образом: , эта система может быть записана более кратко следующим
образом: 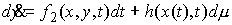
2.
Принцип
Даламбера-Лагранжа для условных связей.
В этом разделе мы рассмотрим случай т.н. условных
связей. Начнем с примера. Рассмотрим следующую механическую систему. Пусть по
гладкой плоскости скользит массивный диск радиуса 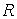 . Введем на плоскости декартову систему координат . Введем на плоскости декартову систему координат 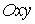 , а на ободе диска отметим какую-нибудь точку , а на ободе диска отметим какую-нибудь точку 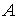 . Положение диска можно описать тремя параметрами . Положение диска можно описать тремя параметрами 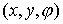 , где , где 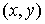 – координаты центра
диска, а – координаты центра
диска, а 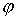 – угол между осью – угол между осью 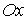 и радиусом диска,
идущим из центра в точку и радиусом диска,
идущим из центра в точку 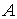 . Пусть движение диска ограничено полуплоскостью . Пусть движение диска ограничено полуплоскостью 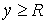 . При выходе на границу ограничений, т.е. на прямую . При выходе на границу ограничений, т.е. на прямую 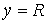 обод диска касается
прямой обод диска касается
прямой 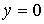 . Предположим, что контакт диска с этой прямой является
абсолютно шероховатым. Это означает, что, как бы ни были слабы силы,
прижимающие диск к граничной прямой, диск катается по ней без проскальзывания.
Такое свойство можно записать в следующем виде. . Предположим, что контакт диска с этой прямой является
абсолютно шероховатым. Это означает, что, как бы ни были слабы силы,
прижимающие диск к граничной прямой, диск катается по ней без проскальзывания.
Такое свойство можно записать в следующем виде.
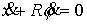 , при условии, что , при условии, что 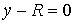 (2.1) (2.1)
Связи, аналогичные (2.1) будем называть условными.
Для рассмотрения уравнений движения в подобных
случаях несколько обобщим этот пример,
рассмотрев механическую систему общего вида с одной группой условных связей.
Рассмотрение систем с большим числом групп условных связей может быть
произведено аналогично. Как и в [3, 4] рассмотрим систему из 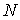 материальных точек,
перемещающихся в пространстве под действием приложенных к ним сил. Координаты
точек объединим в один вектор материальных точек,
перемещающихся в пространстве под действием приложенных к ним сил. Координаты
точек объединим в один вектор 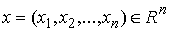 , где , где 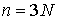 . В отсутствие связей движение системы описывается вторым
законом Ньютона . В отсутствие связей движение системы описывается вторым
законом Ньютона
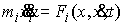 , , 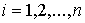 (2.2) (2.2)
где 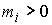 – массы точек, а – массы точек, а 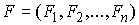 – вектор сил,
действующих на точки системы. Наложим на систему семейство – вектор сил,
действующих на точки системы. Наложим на систему семейство 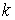 линейных, идеальных
удерживающих связей: линейных, идеальных
удерживающих связей: 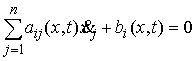 , , 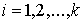 , где , где 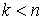 – число связей. Или в
матричной форме. – число связей. Или в
матричной форме.
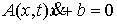 (2.3) (2.3)
где 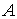 – матрица – матрица 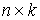 , , 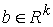 . Добавим семейство
односторонних голономных связей . Добавим семейство
односторонних голономных связей
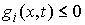 , , 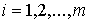 (2.4) (2.4)
Добавим также одну группу условных связей:
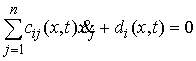 , , 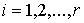 , при , при 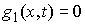
где 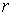 – число условных
связей в группе связей. Или в матричной форме – число условных
связей в группе связей. Или в матричной форме
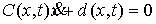 , при , при 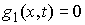 (2.5) (2.5)
где 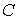 – матрица – матрица 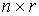 , , 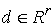 . Условные связи независимы, если . Условные связи независимы, если 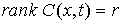 всюду. всюду.
Конфигурационное пространство. Множество точек 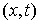 , удовлетворяющих связям (2.3-2.5) будем называть расширенным
конфигурационным пространством или, иногда, для краткости просто
конфигурационным пространством. Внутренностью
конфигурационного пространства будем называть множество точек , удовлетворяющих связям (2.3-2.5) будем называть расширенным
конфигурационным пространством или, иногда, для краткости просто
конфигурационным пространством. Внутренностью
конфигурационного пространства будем называть множество точек 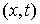 , в которых , в которых
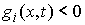 , , 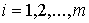 (2.6) (2.6)
Границей конфигурационного пространства или поверхностью удара будем называть
множество точек 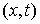 , удовлетворяющих хотя бы одному уравнению , удовлетворяющих хотя бы одному уравнению
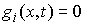 , , 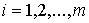
Мы будем предполагать, что все функции,
описывающие связи, являются непрерывными по 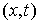 , а те, что описывают односторонние связи, являются гладкими
по , а те, что описывают односторонние связи, являются гладкими
по 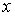 – первого класса
гладкости, так, что в каждой точке – первого класса
гладкости, так, что в каждой точке 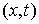 конфигурационного
пространства можно определить пространство возможных перемещений. Возможным перемещением удерживающих
связей в точке конфигурационного
пространства можно определить пространство возможных перемещений. Возможным перемещением удерживающих
связей в точке 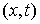 называется любой
вектор называется любой
вектор 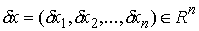 удовлетворяющий
условию удовлетворяющий
условию
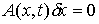 . .
Эти возможные перемещения образуют линейное пространство 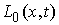 (размерности (размерности 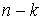 , если связи независимы). Возможным
перемещением односторонних голономных связей в точке , если связи независимы). Возможным
перемещением односторонних голономных связей в точке  называется любой
вектор называется любой
вектор 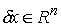 удовлетворяющий
условию удовлетворяющий
условию
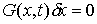 . (2.7) . (2.7)
где 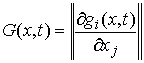 – якобиева матрица системы тех функций – якобиева матрица системы тех функций 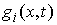 , для которых , для которых 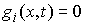 . Эти возможные перемещения образуют линейное пространство . Эти возможные перемещения образуют линейное пространство 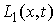 . Его размерность
зависит от числа независимых функций . Его размерность
зависит от числа независимых функций 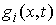 , удовлетворяющих условию , удовлетворяющих условию 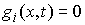 и всегда не меньше,
чем и всегда не меньше,
чем 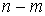 . Во внутренней точке конфигурационного пространства, там,
где выполнены неравенства (2.6), это пространство совпадает с . Во внутренней точке конфигурационного пространства, там,
где выполнены неравенства (2.6), это пространство совпадает с 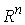 . .
Допустимым перемещением односторонних голономных связей в точке 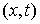 называется любой
вектор называется любой
вектор 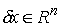 , удовлетворяющий условию , удовлетворяющий условию
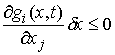 для тех функций для тех функций 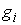 , для которых , для которых 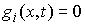 (2.8) (2.8)
Эти вектора образуют некий конус 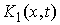 . Во внутренней точке конфигурационного пространства, там,
где выполнены неравенства (2.6), этот конус совпадает с . Во внутренней точке конфигурационного пространства, там,
где выполнены неравенства (2.6), этот конус совпадает с 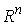 . Он представляет собой замыкание конуса перемещений, сдвигаясь
вдоль которых локально мы остаемся внутри области, допустимой односторонними
связями (2.4). Заметим, что, поскольку из (2.7) следует (2.8), то . Он представляет собой замыкание конуса перемещений, сдвигаясь
вдоль которых локально мы остаемся внутри области, допустимой односторонними
связями (2.4). Заметим, что, поскольку из (2.7) следует (2.8), то
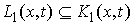 (2.9) (2.9)
Возможным перемещением условных
связей в точке 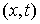 такой, что такой, что 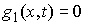 называется любой
вектор называется любой
вектор 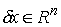 удовлетворяющий
условиям удовлетворяющий
условиям
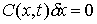 и и 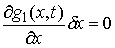
Во всех других точках 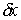 – это любой вектор из – это любой вектор из
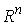 . Эти возможные перемещения образуют линейное пространство . Эти возможные перемещения образуют линейное пространство 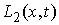 . .
Возможные перемещения. Пространство возможных перемещений
в точке 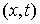 обозначается обозначается 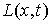 . Оно определяется
как пересечение всех указанных выше пространств возможных перемещений . Оно определяется
как пересечение всех указанных выше пространств возможных перемещений 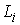 : :
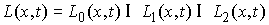
Конус допустимых направлений. Мы также будем предполагать,
что в каждой точке поверхности удара можно определить конус 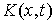 допустимых
направлений. Он представляет собой пересечение конуса допустимых направлений
односторонних связей и пространства возможных перемещений удерживающих связей: допустимых
направлений. Он представляет собой пересечение конуса допустимых направлений
односторонних связей и пространства возможных перемещений удерживающих связей: 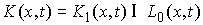 . Используя (2.9), несложно убедиться, что пространство
возможных перемещений лежит в конусе допустимых направлений . Используя (2.9), несложно убедиться, что пространство
возможных перемещений лежит в конусе допустимых направлений 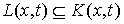 (2.10) (2.10)
Перейдём теперь к определению пространства
возможных вариаций. Мы будем рассматривать движение на некотором отрезке
времени 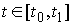 . Вариацией кривой . Вариацией кривой
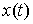 будем называть
непрерывную вектор-функцию будем называть
непрерывную вектор-функцию 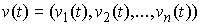 . Возможные вариации
Вариацию . Возможные вариации
Вариацию 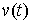 кривой кривой 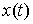 будем называть
возможной, если будем называть
возможной, если 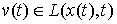 для всех для всех 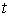 , т.е. вектор , т.е. вектор 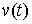 является возможным
перемещением в точке является возможным
перемещением в точке 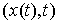 . Допустимые
вариации. Вариацию . Допустимые
вариации. Вариацию 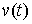 кривой кривой 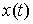 будем называть
допустимой, если будем называть
допустимой, если 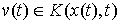 для всех для всех 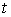 (т.е. вектор (т.е. вектор 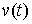 является допустимым
перемещением в точке является допустимым
перемещением в точке 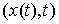 ). Отличие от определения возможной вариации состоит в том, что во всех точках ). Отличие от определения возможной вариации состоит в том, что во всех точках 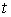 , в которых кривая , в которых кривая 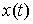 выходит на границу
односторонних и условных связей, вектор выходит на границу
односторонних и условных связей, вектор 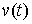 лежит в конусе
допустимых направлений лежит в конусе
допустимых направлений 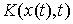 . Поскольку конус допустимых перемещений содержит
пространство возможных перемещений (2.10), то любая возможная вариация является
допустимой. . Поскольку конус допустимых перемещений содержит
пространство возможных перемещений (2.10), то любая возможная вариация является
допустимой.
Идя по традиционной схеме рассуждений, уравнения
движения мы будем строить исходя из следующих принципов.
Принцип освобождения от связей. Пусть 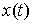 – траектория движения
системы со связями (2.3-2.5). Тогда
систему можно освободить от связей и добавить некую силу – реакцию
связей – траектория движения
системы со связями (2.3-2.5). Тогда
систему можно освободить от связей и добавить некую силу – реакцию
связей 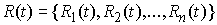 таким образом, что
кривая таким образом, что
кривая 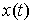 останется траекторией
освобожденной системы. При этом компоненты реакции связей представляют собой
меры Лебега-Стилтьеса останется траекторией
освобожденной системы. При этом компоненты реакции связей представляют собой
меры Лебега-Стилтьеса 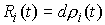 , имеющие особенности, сосредоточенные на множестве тех моментов
времени, в которые траектория , имеющие особенности, сосредоточенные на множестве тех моментов
времени, в которые траектория 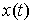 выходит на
односторонние ограничения. Траектория системы представляет собой такую
дифференцируемую функцию выходит на
односторонние ограничения. Траектория системы представляет собой такую
дифференцируемую функцию 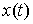 , производная которой, , производная которой, 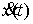 является функцией с
ограниченной вариацией. При этом будут
справедливы следующие уравнения. является функцией с
ограниченной вариацией. При этом будут
справедливы следующие уравнения.
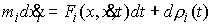 , , 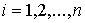 (2.11) (2.11)
Идеальность связей (полная). Связи (2.3-2.5) называются (вполне) идеальными, если для любой траектории
системы 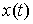 , и для любой её допустимой
вариации , и для любой её допустимой
вариации 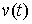 интегральная
элементарная работа сил реакции связей неотрицательна, т.е. интегральная
элементарная работа сил реакции связей неотрицательна, т.е.
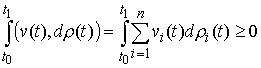 (2.12) (2.12)
Это условие означает, что, при выходе действительной траектории системы на
границу удерживающих связей, реакция связей направлена внутрь области, допустимой
этими связями.
Двусторонняя идеальность связей. Связи (2.3-2.5) называются
двусторонне идеальными, если для любой траектории движения системы 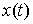 и для любой ее возможной вариации и для любой ее возможной вариации 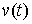 интегральная
элементарная работа сил реакции односторонних связей равна нулю, т.е. интегральная
элементарная работа сил реакции односторонних связей равна нулю, т.е.
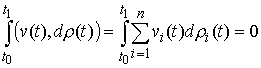 (2.13) (2.13)
Из полной идеальности связей вытекает их двусторонняя идеальность. Допустим
противное. Тогда существует возможная (и, значит, допустимая) вариация 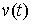 такая, что такая, что 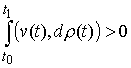 . Взяв возможную (и, следовательно, допустимую) вариацию . Взяв возможную (и, следовательно, допустимую) вариацию 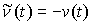 получим получим 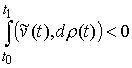 , что противоречит (2.12). , что противоречит (2.12).
Найдя 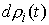 из (2.11) и подставив
в (2.12) получим эквивалентную форму записи условия полной идеальности связей. Для любой допустимой вариации из (2.11) и подставив
в (2.12) получим эквивалентную форму записи условия полной идеальности связей. Для любой допустимой вариации 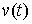 должно выполняться должно выполняться
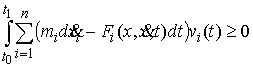 (2.14) (2.14)
Аналогично для условия двусторонней идеальности связей (2.13). Для любой
допустимой вариации 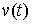 должно выполняться должно выполняться
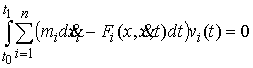 (2.15) (2.15)
Принцип Даламбера-Лагранжа. Пусть непрерывная кривая 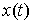 удовлетворяет уравнениям
связей (2.3, 2.4, 2.5), а ее производная существует почти всюду и является
функцией ограниченной вариации. Кривая удовлетворяет уравнениям
связей (2.3, 2.4, 2.5), а ее производная существует почти всюду и является
функцией ограниченной вариации. Кривая 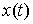 является траекторией
движения системы с идеальными связями (2.3, 2.4, 2.5) тогда и только тогда,
когда для любой допустимой вариации является траекторией
движения системы с идеальными связями (2.3, 2.4, 2.5) тогда и только тогда,
когда для любой допустимой вариации 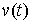 выполнены соотношения
(2.14) и, следовательно, для любой возможной вариации, соотношения (2.15). выполнены соотношения
(2.14) и, следовательно, для любой возможной вариации, соотношения (2.15).
Исходя из этого принципа в
[3] были получены уравнения Лагранжа первого рода для односторонних и
удерживающих связей. Без особых изменений повторив рассуждения раздела 8 этой
работы, мы получим уравнения Лагранжа 1-го рода для нашего случая. Кривая 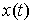 является траекторией
движения системы с идеальными связями
(2.3-2.5) тогда и только тогда, когда найдутся такие векторные меры
Лебега-Стилтьеса является траекторией
движения системы с идеальными связями
(2.3-2.5) тогда и только тогда, когда найдутся такие векторные меры
Лебега-Стилтьеса 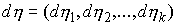 , , 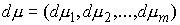 и и 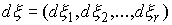 , что , что
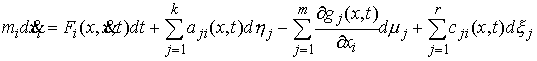 (2.16) (2.16)
При этом каждая мера 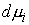 неотрицательна и
сосредоточена на множестве моментов
времени, в которые неотрицательна и
сосредоточена на множестве моментов
времени, в которые 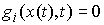 . Каждая мера . Каждая мера 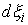 сосредоточена на
множестве моментов времени, в которые сосредоточена на
множестве моментов времени, в которые 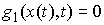 . .
Матричная форма уравнений. Пусть 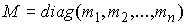 – диагональная
матрица, с элементами – диагональная
матрица, с элементами 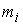 на диагонали, на диагонали, 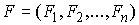 – сводный вектор сил,
тогда уравнения (2.16) можно записать в
более компактной форме – сводный вектор сил,
тогда уравнения (2.16) можно записать в
более компактной форме
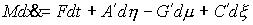 (2.17) (2.17)
где знак 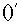 означает
транспонирование матриц. означает
транспонирование матриц.
Гладкий случай. В [3] было показано, что, если связи имеют
второй класс гладкости, то скорость движения раскладывается на две составляющие
– абсолютно непрерывную функцию и функцию скачков. Т.е. сингулярная непрерывная
составляющая отсутствует. Эти же рассуждения, без особых изменений, можно
повторить и в нашем случае.
Замечание о скачках. Любая функция ограниченной вариации есть сумма непрерывной функции и
функции скачков представляющей собой ступенчатую функцию с не более чем счетным
числом ступеней. В точках скачка функций 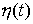 , , 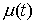 , и , и 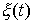 (и только в них)
траекторная скорость (и только в них)
траекторная скорость 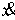 также может иметь
скачок. Обозначим эти скачки соответственно также может иметь
скачок. Обозначим эти скачки соответственно 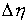 , , 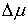 , , 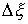 и и  . В силу (2.16) они связаны следующим соотношением . В силу (2.16) они связаны следующим соотношением
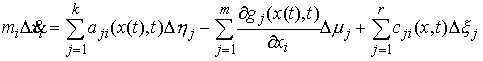
или, более кратко 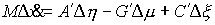 . Отсюда, заметив, что
во все время движения выполнены уравнения удерживающих связей (2.3),
т.е. . Отсюда, заметив, что
во все время движения выполнены уравнения удерживающих связей (2.3),
т.е. 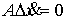 , получаем , получаем
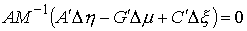 (2.18) (2.18)
Таким образом, скачки 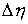 , , 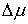 и и 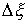 не являются
независимыми. Они связаны системой не являются
независимыми. Они связаны системой 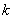 линейных соотношений. линейных соотношений.
3.
Теорема
Аппеля.
Для систем с односторонними связями известна
теорема Аппеля о сохранении обобщенных импульсов в касательной плоскости
поверхности удара [5, 6]. В [4] она была выведена из уравнений движения систем
с идеальными односторонними связями. Здесь мы распространим её на случай
условных связей. Рассуждения будем вести по схеме [4], основываясь на
уравнениях Лагранжа первого рода. "
Кинетической метрикой " будем называть Риманову метрику, порождаемую
матрицей масс  . В этой метрике кинетическая энергия системы . В этой метрике кинетическая энергия системы 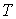 выражается формулой выражается формулой 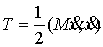 . Это половина
квадрата нормы вектора скорости системы. Вектором
импульса механической системы называется сводный вектор импульсов всех
ее точек . Это половина
квадрата нормы вектора скорости системы. Вектором
импульса механической системы называется сводный вектор импульсов всех
ее точек 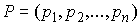 , где , где 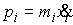 . Кратко это можно записать следующим образом . Кратко это можно записать следующим образом
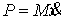 (3.1) (3.1)
При движении системы вектор импульса представляет собой вектор-функцию
ограниченной вариации. Ее можно представить в виде суммы двух составляющих 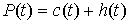 , где , где 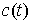 - непрерывная
функция, а - непрерывная
функция, а 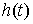 - функция скачков
(кусочно-постоянная вектор-функция с не более чем счетным числом точек
разрыва). Пусть система двигается по траектории - функция скачков
(кусочно-постоянная вектор-функция с не более чем счетным числом точек
разрыва). Пусть система двигается по траектории 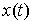 и и 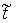 - точка скачка вектора импульса. Будем
называть ее точкой удара. Обозначим - точка скачка вектора импульса. Будем
называть ее точкой удара. Обозначим
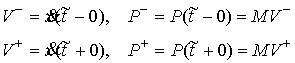 (3.2) (3.2)
Для функции с ограниченной вариацией эти величины всегда определены. Точка 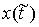 лежит на границе
односторонних связей, т.е. лежит на границе
односторонних связей, т.е. 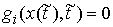 для некоторых для некоторых 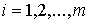 . Здесь мы рассмотрим случай, когда точка удара лежит также и
на границе условных связей, т.е. . Здесь мы рассмотрим случай, когда точка удара лежит также и
на границе условных связей, т.е. 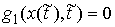 . Условие скачка скорости в точке удара (2.18) в терминах
импульса системы выглядит следующим образом . Условие скачка скорости в точке удара (2.18) в терминах
импульса системы выглядит следующим образом 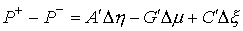 (3.3) (3.3)
Касательной плоскостью удара 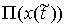 (или просто
плоскостью удара) назовем линейное пространство возможных перемещений в точке
удара (или просто
плоскостью удара) назовем линейное пространство возможных перемещений в точке
удара 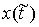 . Это множество векторов . Это множество векторов 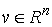 , касающихся удерживающих связей и тех односторонних и
условных связей, которые вышли на ограничение, т.е. векторов, для которых
выполнено , касающихся удерживающих связей и тех односторонних и
условных связей, которые вышли на ограничение, т.е. векторов, для которых
выполнено  , и , и 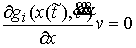 , для тех , для тех 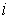 , для которых , для которых 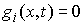 , а также , а также 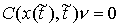 , если , если 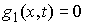 . Не нарушая общности, для краткости записи, будем считать,
что в точке удара все односторонние и условные связи выходят на ограничение.
Тогда плоскость удара . Не нарушая общности, для краткости записи, будем считать,
что в точке удара все односторонние и условные связи выходят на ограничение.
Тогда плоскость удара 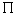 задается системой
соотношений задается системой
соотношений
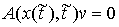 , , 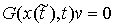 , , 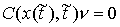 (3.4) (3.4)
где 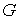 - матрица Якоби
односторонних связей (2.7). - матрица Якоби
односторонних связей (2.7).
Теорема Аппеля.
Возьмем 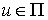 - любой вектор в
плоскости удара. Тогда из (3.3, 3.4) имеем - любой вектор в
плоскости удара. Тогда из (3.3, 3.4) имеем 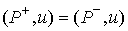 . Т.е. сохраняются проекции вектора импульса системы на
плоскость касательную поверхности удара. По-другому это равенство можно
записать следующим образом . Т.е. сохраняются проекции вектора импульса системы на
плоскость касательную поверхности удара. По-другому это равенство можно
записать следующим образом
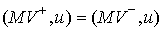 (3.5) (3.5)
Оно означает, что в кинетической метрике сохраняются проекции скорости
системы на плоскость удара.
Нормальная плоскость удара. Введем вектора 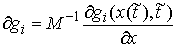 , и , и 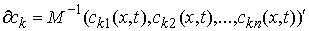 . Это "градиенты односторонних и условных связей" в
кинетической метрике. Плоскостью . Это "градиенты односторонних и условных связей" в
кинетической метрике. Плоскостью 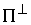 , нормальной к плоскости удара , нормальной к плоскости удара  будем называть
линейное пространство, натянутое на вектора будем называть
линейное пространство, натянутое на вектора 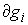 и и 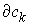 в пересечении с
линейным пространством в пересечении с
линейным пространством 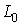 возможных перемещений
удерживающих связей (1.7). возможных перемещений
удерживающих связей (1.7).
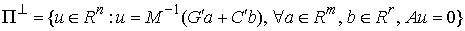 (3.6) (3.6)
Нетрудно видеть, что  и и 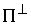 взаимно ортогональны
в кинетической метрике и их линейная оболочка совпадает с взаимно ортогональны
в кинетической метрике и их линейная оболочка совпадает с 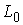 . Таким образом, . Таким образом, 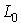 есть прямая сумма касательной
и нормальной плоскостей есть прямая сумма касательной
и нормальной плоскостей 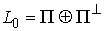 . В соответствии с этим скорости . В соответствии с этим скорости 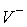 и и 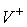 однозначно
раскладываются на касательную однозначно
раскладываются на касательную 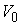 и нормальную и нормальную 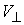 составляющие. составляющие.
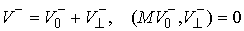 , , 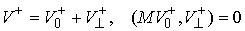 (3.7) (3.7)
Причем 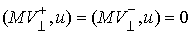 для любого вектора для любого вектора 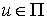 из касательной
плоскости удара. Тогда из (3.5, 3.7) получаем из касательной
плоскости удара. Тогда из (3.5, 3.7) получаем 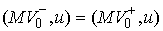 , т.е. теорема Аппеля означает, что сохраняется проекция
скорости на касательную плоскость удара в кинетической метрике. , т.е. теорема Аппеля означает, что сохраняется проекция
скорости на касательную плоскость удара в кинетической метрике.
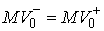 , , 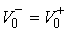 (3.8) (3.8)
Отсюда следует, что 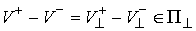
Замена координат. Естественно, все указанные соотношения сохраняются при замене координат и,
в частности, при интегрировании части связей и переходе к обобщенным
координатам. Вектор импульса при этом определяется соотношением  . .
4.
Теоремы
Карно и непрерывность кинетической энергии.
В [4], с помощью уравнений Лагранжа первого рода,
было показано, что известные теоремы Карно (см., например, [7]) выводятся из
уравнений движения систем с идеальными односторонними связями. В данном разделе
мы распространим их действие на системы с условными связями. Здесь, так же как
и для односторонних связей, для однозначного определения движения необходимы
дополнительные гипотезы о перераспределении энергии при ударах. Точнее
необходим выбор той или иной модели связей (принято говорить о выборе модели
реализации связей [1, 6]). В данном разделе, при изложении третьей теоремы
Карно, мы будем рассматривать свойства движения в предположении, что все
рассматриваемые односторонние и условные связи порождены едиными причинами и,
поэтому, при ударе может происходить перераспределение энергии между ними. Для
модели абсолютно упругих соударений это приводит к сохранению полной энергии
системы даже в случае "абсолютно шероховатых" условных связей. Другие модели
могут накладывать условие полной или частичной зависимости связей. Они могут
быть рассмотрены аналогичным образом. Впрочем, сказанное касается только
третьей теоремы Карно. Первые две не зависят от способа реализации связей. В
теоремах Карно рассматривается поведение кинетической энергии в точках скачка
скорости (точках удара). Здесь мы рассмотрим случай, когда точка удара  лежит не только на
границе односторонних связей, но также и на границе условных связей, т.е. лежит не только на
границе односторонних связей, но также и на границе условных связей, т.е.  . .
При
формулировке теорем Карно используются следующие термины.
Потерянные скорости - это
компоненты вектора приращения скорости при ударе:  . Из (3.8) следует, что . Из (3.8) следует, что
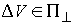 , т.е. что вектор потерянных скоростей лежит в нормальной
плоскости удара. Кинетическая энергия
потерянных скоростей - это кинетическая энергия системы , т.е. что вектор потерянных скоростей лежит в нормальной
плоскости удара. Кинетическая энергия
потерянных скоростей - это кинетическая энергия системы 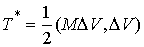 , которую она имела бы, двигаясь с потерянной скоростью. Из
(3.7, 3.8) следует, что , которую она имела бы, двигаясь с потерянной скоростью. Из
(3.7, 3.8) следует, что 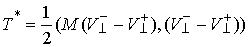 (4.1) (4.1)
Потерянная кинетическая
энергия определяется
как разность кинетических энергий до и после удара: 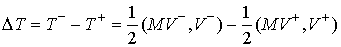 . Из (3.7, 3.8) следует, что . Из (3.7, 3.8) следует, что
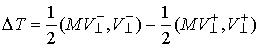 (4.2) (4.2)
Первая теорема Карно обычно формулируется как явление, происходящее при внезапном наложении
удерживающих связей. В нашей терминологии она звучит следующим образом. Если
сразу после удара траектория касается границы удерживающих и условных связей
(т.е. 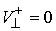 ), то потерянная при ударе кинетическая энергия равна
кинетической энергии потерянных скоростей (т.е. ), то потерянная при ударе кинетическая энергия равна
кинетической энергии потерянных скоростей (т.е. 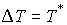 ). Это утверждение сразу вытекает из (4.1, 4.2). ). Это утверждение сразу вытекает из (4.1, 4.2).
Вторая теорема Карно обычно формулируется как явление, происходящее при внезапном снятии
удерживающих связей. При этом потерянные скорости и энергия называются
приобретенными. В нашей терминологии она звучит следующим образом. Если в
точности перед ударом траектория касалась границы удерживающих и условных
связей (т.е. 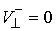 ), то приобретенная при ударе кинетическая энергия равна
кинетической энергии приобретенных скоростей (т.е. ), то приобретенная при ударе кинетическая энергия равна
кинетической энергии приобретенных скоростей (т.е. 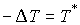 ). Это утверждение также сразу вытекает из (4.1, 4.2). ). Это утверждение также сразу вытекает из (4.1, 4.2).
Нормальное пространство скольжения. Нормальную плоскость
удара можно разложить на две составляющие. Нормальным пространством скольжения 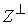 будем называть
линейное пространство, натянутое на вектора будем называть
линейное пространство, натянутое на вектора 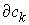 (градиенты условных
связей) в пересечении с линейным пространством (градиенты условных
связей) в пересечении с линейным пространством 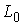 возможных перемещений
удерживающих связей (1.7). возможных перемещений
удерживающих связей (1.7).
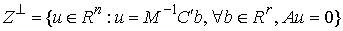 (4.3) (4.3)
Из (3.6) нетрудно видеть, что 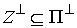 . Обозначим . Обозначим 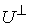 - ортогональное (в кинетической
метрике) дополнение к - ортогональное (в кинетической
метрике) дополнение к 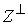 в в 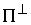 . Тогда . Тогда 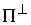 есть прямая сумма
нормального пространства скольжения и его ортогонального дополнения есть прямая сумма
нормального пространства скольжения и его ортогонального дополнения 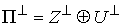 . В соответствии с этим, нормальные составляющие скорости . В соответствии с этим, нормальные составляющие скорости 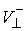 и и 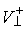 однозначно
раскладываются на нормальную скорость скольжения однозначно
раскладываются на нормальную скорость скольжения 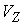 и её ортогональное дополнение и её ортогональное дополнение
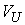
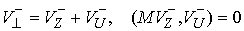 , , 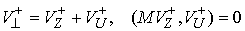 (4.4) (4.4)
В этих терминах кинетическая энергия потерянных скоростей (4.1) определяется
следующим соотношением 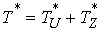 , где , где
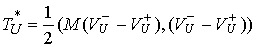 , , 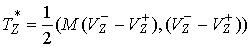 (4.5) (4.5)
А потерянная кинетическая энергия (4.2) определяется следующим соотношением: 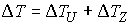 (4.6) (4.6)
где
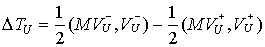 , , 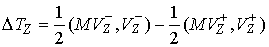 (4.7) (4.7)
Третья теорема Карно формулируется для случая, когда удар не является условно кратным, т.е.
траектория выходит на ограничение ровно одной условной связи. Если при этом
градиент односторонней связи и градиент условной связи линейно независимы, то 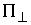 представляет собой
двухмерное пространство. В этом случае представляет собой
двухмерное пространство. В этом случае 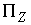 и и 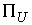 представляют собой одномерные пространства и поэтому. представляют собой одномерные пространства и поэтому.
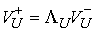 , , 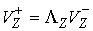 (4.8) (4.8)
где 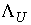 , , 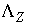 - некоторые числа
(если, конечно, - некоторые числа
(если, конечно, 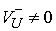 и и 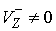 ) )
Формулировка теоремы. Третья теорема Карно формулируется следующим образом. Потерянная кинетическая
энергия равна доле кинетической энергии потерянных нормальных скоростей,
вычисляемой по формуле
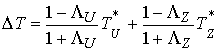 (4.9) (4.9)
Доказательство. Подставив (4.8) в (4.5) и в (4.7) получим 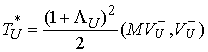 и и 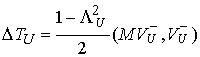 . Отсюда следует, что . Отсюда следует, что
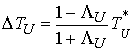 (4.10) (4.10)
Аналогичными рассуждениями получаем, что
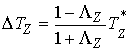 (4.11) (4.11)
Подставив (4.10-11) в (4.6) сразу получаем (4.9). Доказательство закончено.
Обсудим теперь вопрос
определения скалярных множителей 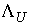 , , 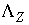 в (4.8) (как мы уже
говорили, решение этого вопроса зависит от выбора модели односторонних и
условных связей). в (4.8) (как мы уже
говорили, решение этого вопроса зависит от выбора модели односторонних и
условных связей).
Коэффициент восстановления. Нормальная составляющая скорости 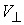 не обязана
сохраняться при ударе. Для определения её изменения необходимы дополнительные
предположения о природе связей наложенных на систему. Если связи не зависят от
времени, одна из возможных моделей - это линейная взаимозависимость величин
нормальной составляющей скорости до и после удара, задаваемая т.н.
коэффициентом восстановления. Более подробную информацию об этом можно найти в
[2]. Коэффициентом восстановления не обязана
сохраняться при ударе. Для определения её изменения необходимы дополнительные
предположения о природе связей наложенных на систему. Если связи не зависят от
времени, одна из возможных моделей - это линейная взаимозависимость величин
нормальной составляющей скорости до и после удара, задаваемая т.н.
коэффициентом восстановления. Более подробную информацию об этом можно найти в
[2]. Коэффициентом восстановления 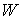 называется
неотрицательная величина, определяемая следующим образом называется
неотрицательная величина, определяемая следующим образом
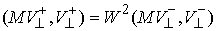 (4.12) (4.12)
Если 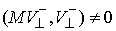 , то , то 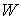 - это отношение
модуля нормальной составляющей скорости - это отношение
модуля нормальной составляющей скорости 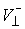 (до удара) к модулю
нормальной составляющая скорости (до удара) к модулю
нормальной составляющая скорости 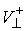 (после удара) в
кинетической метрике. (после удара) в
кинетической метрике.
Коэффициент скольжения. Скорость нормального скольжения 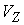 также не обязана
сохраняться при ударе. Для определения её изменения необходимы дополнительные
предположения о природе связей наложенных на систему. Если связи не зависят от
времени, одна из возможных моделей - это линейная взаимозависимость величин
скорости скольжения до и после удара, задаваемая т.н. коэффициентом скольжения.
Коэффициентом скольжения также не обязана
сохраняться при ударе. Для определения её изменения необходимы дополнительные
предположения о природе связей наложенных на систему. Если связи не зависят от
времени, одна из возможных моделей - это линейная взаимозависимость величин
скорости скольжения до и после удара, задаваемая т.н. коэффициентом скольжения.
Коэффициентом скольжения 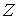 назовём величину, определяемую
следующим образом назовём величину, определяемую
следующим образом
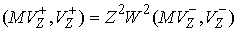 (4.13) (4.13)
при этом знак 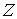 выбирается равным
знаку величины выбирается равным
знаку величины 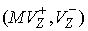 . Вычитая (4.13) из (4.12)
и, подставляя (4.4) получаем . Вычитая (4.13) из (4.12)
и, подставляя (4.4) получаем
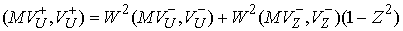 (4.14) (4.14)
Если  , то , то 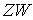 - это отношение модуля
скорости скольжения - это отношение модуля
скорости скольжения 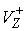 (до удара) к модулю
скорости скольжения (до удара) к модулю
скорости скольжения 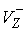 (после удара) в
кинетической метрике. Качественно говоря, величина импульса нормального
скольжения (после удара) в
кинетической метрике. Качественно говоря, величина импульса нормального
скольжения 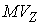 характеризует
"нормальное давление" на границу условных связей. А коэффициент скольжения
описывает "шероховатость" условных связей. Значение характеризует
"нормальное давление" на границу условных связей. А коэффициент скольжения
описывает "шероховатость" условных связей. Значение 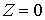 соответствует
абсолютно шероховатым условным связям. Значение соответствует
абсолютно шероховатым условным связям. Значение 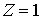 соответствует
абсолютно гладким условным связям - т. е., означает, что фактически они
отсутствуют. Величина соответствует
абсолютно гладким условным связям - т. е., означает, что фактически они
отсутствуют. Величина 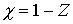 называется коэффициентом мгновенного трения [9]. называется коэффициентом мгновенного трения [9].
Задание коэффициентов восстановления и скольжения
позволяет определить 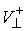 по по 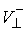 , если удар не является условно кратным, т.е. мы вышли на ограничение
ровно одной условной связи. Если при этом градиент односторонней связи и
градиент условной связи линейно независимы, то , если удар не является условно кратным, т.е. мы вышли на ограничение
ровно одной условной связи. Если при этом градиент односторонней связи и
градиент условной связи линейно независимы, то 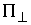 представляет собой
двухмерное пространство. Поэтому, как уже говорилось представляет собой
двухмерное пространство. Поэтому, как уже говорилось 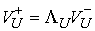 , , 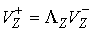 . Где . Где 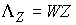 , а , а 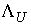 определяется
соотношением (4.14) определяется
соотношением (4.14)
Абсолютно упругий удар. Остановимся более подробно на случае абсолютно упругих соударений (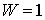 ). В этом случае ). В этом случае 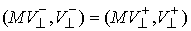 и из (3.7) следует,
что кинетическая энергия сохраняется, несмотря на скачок скорости. и из (3.7) следует,
что кинетическая энергия сохраняется, несмотря на скачок скорости.
Приведенные рассуждения можно резюмировать в следующем утверждении.
Непрерывность кинетической энергии. В случае абсолютно упругих соударений
кинетическая энергия системы является непрерывной функцией времени. Если связи
гладкие (класса два), то, как было показано в [3], скорость является суммой
абсолютно непрерывной составляющей и функции скачков (непрерывная сингулярная
составляющая отсутствует). Тогда из непрерывности кинетической энергии следует
ее абсолютная непрерывность.
Закон сохранения энергии. Если связи стационарны, и силы потенциальны, то непрерывность кинетической
энергии немедленно влечет за собой закон сохранения энергии. В самом деле,
пусть 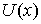 - силовая функция.
Тогда полная энергия - силовая функция.
Тогда полная энергия 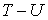 - это непрерывная
функция. На каждом открытом отрезке, не содержащем скачков она постоянна в силу
обычных законов сохранения для удерживающих связей (на участках, когда
траектория выходит на границу односторонних и условных ограничений, их можно
рассматривать как удерживающие). Но, поскольку множество скачков не более чем
счетно, то полная энергия постоянна на всем отрезке времени. - это непрерывная
функция. На каждом открытом отрезке, не содержащем скачков она постоянна в силу
обычных законов сохранения для удерживающих связей (на участках, когда
траектория выходит на границу односторонних и условных ограничений, их можно
рассматривать как удерживающие). Но, поскольку множество скачков не более чем
счетно, то полная энергия постоянна на всем отрезке времени.
5.
Формула Карно.
Обобщив рассуждения, проведенные в
предыдущем разделе можно получить формулу, которую естественно назвать формулой
Карно. Пусть в точке удара нормальное пространство 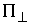 имеет размерность имеет размерность  . Выберем любой ортонормированный (в кинетической метрике)
базис . Выберем любой ортонормированный (в кинетической метрике)
базис 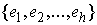 в в 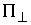 , и разложим по нему нормальные составляющие скоростей
движения до и после удара , и разложим по нему нормальные составляющие скоростей
движения до и после удара 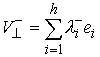 , , 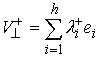 . Обозначим . Обозначим 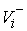 и и 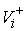 - проекции скоростей
на оси нашего базиса - проекции скоростей
на оси нашего базиса
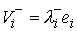 , , 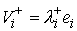 (5.1) (5.1)
Поскольку 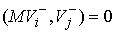 , , 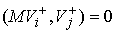 , и , и 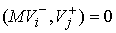 при при 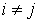 , то кинетическая энергия потерянных скоростей (4.1) может
быть представлена суммой , то кинетическая энергия потерянных скоростей (4.1) может
быть представлена суммой
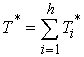 (5.2) (5.2)
где 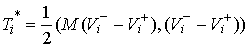 (5.3) (5.3)
А потерянная кинетическая энергия (4.2) определяется следующим соотношением 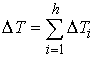 (5.4) (5.4)
где 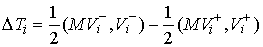 (5.5) (5.5)
Если все коэффициенты второго разложения в (5.1) отличны от нуля, т.е. 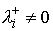 , то , то 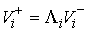 , где , где 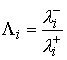 (5.6) (5.6)
Подставив (5.6) в (5.3) и (5.5)
получим 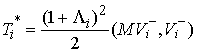 и и 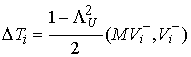 . Отсюда следует, что . Отсюда следует, что 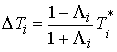 . .
Формула Карно.
Подставляя последнее соотношение в (5.4) получаем
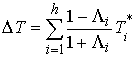 (5.7) (5.7)
Эту формулу можно трактовать следующим образом. Потерянная кинетическая
энергия равна доле кинетической энергии нормальных компонент потерянных
скоростей, вычисляемой по формуле (5.7). Заметим, что формула Карно остаётся
справедливой и при обращении в нуль некоторых 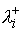 . В этом случае коэффициент при . В этом случае коэффициент при  нужно положить равным
минус единице. Доказательство является очевидным, если переписать (5.7) в
следующей форме нужно положить равным
минус единице. Доказательство является очевидным, если переписать (5.7) в
следующей форме
 (5.8) (5.8)
Выберем теперь базис  таким образом, чтобы
вектор таким образом, чтобы
вектор  был направлен вдоль
нормальной скорости при подходе к точке удара. Тогда был направлен вдоль
нормальной скорости при подходе к точке удара. Тогда 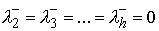 , и из (5.8) получим , и из (5.8) получим 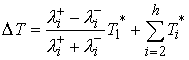 . Добавив . Добавив 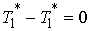 к правой части этого
соотношения и воспользовавшись (5.2), получим к правой части этого
соотношения и воспользовавшись (5.2), получим
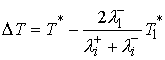 (5.9) (5.9)
Распространим определение коэффициента
восстановления на наш многомерный случай следующим образом. Назовём
коэффициентом восстановления  отношение модуля
нормальной составляющей скорости отношение модуля
нормальной составляющей скорости 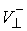 (до удара) к проекции
на неё нормальной составляющей скорости (до удара) к проекции
на неё нормальной составляющей скорости  (после удара) в кинетической
метрике: (после удара) в кинетической
метрике: 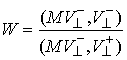 . Тогда . Тогда 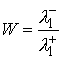 и из (5.9) получаем и из (5.9) получаем
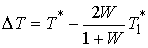 (5.10) (5.10)
Величину  естественно называть
кинетической энергией скоростей потерянных вдоль направления удара. Теперь
третью теорему Карно можно сформулировать следующим образом. естественно называть
кинетической энергией скоростей потерянных вдоль направления удара. Теперь
третью теорему Карно можно сформулировать следующим образом.
Теорема Карно для кратного удара. Потерянная кинетическая энергия равна
кинетической энергии потерянных скоростей за вычетом доли кинетической энергии
скоростей потерянных вдоль направления удара, вычисляемой по формуле (5.10).
6.
Теорема об
изменении количества движения.
Для систем с идеальными удерживающими связями
среди основных законов динамики формулируются теоремы об изменении количества
движения системы и о движении ее центра
масс (см., например, [8]). В [4], с помощью уравнений Лагранжа первого рода,
было показано, что они справедливы и при наличии идеальных односторонних
связей. В данном разделе, следуя [4], мы распространим их действие на условные
связи.
Количество движения системы. Это трехмерный вектор 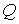 равный сумме
количеств движений всех составляющих систему точек. Количество движения
материальной точки - это трехмерный вектор равный сумме
количеств движений всех составляющих систему точек. Количество движения
материальной точки - это трехмерный вектор 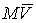 , где , где 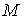 - масса точки, а - масса точки, а 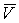 - трехмерный вектор
ее скорости: - трехмерный вектор
ее скорости: 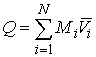 . Выше мы использовали сводный вектор координат точек
системы . Выше мы использовали сводный вектор координат точек
системы 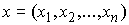 и сводный вектор сил и сводный вектор сил 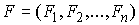 , , 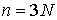 . И в этих терминах были выписаны уравнения Лагранжа первого
рода (2.17). Кроме того, мы ввели вектор импульса системы . И в этих терминах были выписаны уравнения Лагранжа первого
рода (2.17). Кроме того, мы ввели вектор импульса системы 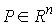 (3.1). В этих обозначениях (3.1). В этих обозначениях 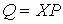 , где , где 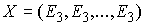 - матрица - матрица 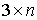 , составленная из , составленная из 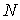 экземпляров трехмерных
единичных матриц экземпляров трехмерных
единичных матриц 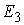 . Мы будем использовать и то и другое описание, понимая, что
они эквивалентны. . Мы будем использовать и то и другое описание, понимая, что
они эквивалентны.
Теорема об изменении количества движения. Если удерживающие, односторонние и условные
связи, наложенные на систему, идеальны и допускают поступательный сдвиг всех
точек системы как твердого тела вдоль какого-нибудь направления 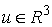 постоянного во
времени, то проекция количества движения системы на это направление постоянного во
времени, то проекция количества движения системы на это направление 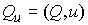 является абсолютно
непрерывной функцией и скорость ее изменения равна является абсолютно
непрерывной функцией и скорость ее изменения равна 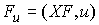 , т.е. равна суммарной проекции на это направление вектора
активных сил: , т.е. равна суммарной проекции на это направление вектора
активных сил: 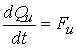 . Эта теорема непосредственно вытекает из аналогичного
утверждения для сводных векторов системы. . Эта теорема непосредственно вытекает из аналогичного
утверждения для сводных векторов системы.
Теорема об изменении вектора импульса. Если удерживающие,
односторонние и условные связи, наложенные на систему, идеальны и допускают поступательный
сдвиг всех точек системы как твердого тела вдоль какого-нибудь направления 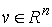 постоянного во
времени, то проекция вектора импульса на это направление постоянного во
времени, то проекция вектора импульса на это направление 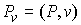 является абсолютно
непрерывной функцией и скорость ее изменения равна является абсолютно
непрерывной функцией и скорость ее изменения равна 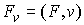 , т.е. равна проекции на это направление сводного вектора
активных сил , т.е. равна проекции на это направление сводного вектора
активных сил
 (6.1) (6.1)
Доказательство. Возьмем какую-либо траекторию движения
системы 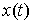 , , 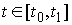 . Для нее выполнены уравнения Лагранжа первого рода (2.17).
Используя вектор импульса системы . Для нее выполнены уравнения Лагранжа первого рода (2.17).
Используя вектор импульса системы 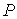 их можно переписать
следующим образом их можно переписать
следующим образом
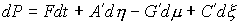 (6.2) (6.2)
Условие теоремы означает, что в каждой точке конфигурационного пространства
вектор 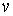 является возможным
перемещением, т.е. является возможным
перемещением, т.е. 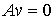 во все время
движения. Далее, во все время
движения. Далее, 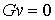 в тех точках
траектории, которые расположены на границе односторонних связей, т.е. в тех
точках, в которых сосредоточена мера в тех точках
траектории, которые расположены на границе односторонних связей, т.е. в тех
точках, в которых сосредоточена мера 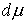 . И, кроме того, . И, кроме того, 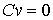 в тех точках
траектории, которые расположены на границе условных связей, т.е. в тех точках,
в которых сосредоточена мера в тех точках
траектории, которые расположены на границе условных связей, т.е. в тех точках,
в которых сосредоточена мера 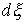 . Отсюда следует, что во все время движения . Отсюда следует, что во все время движения 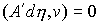 , , 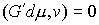 и и 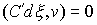 . Заметим, что эти равенства, как и (6.2), надо понимать как
равенство мер Лебега-Стилтьеса. Домножив обе части (6.2) на . Заметим, что эти равенства, как и (6.2), надо понимать как
равенство мер Лебега-Стилтьеса. Домножив обе части (6.2) на 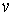 получаем получаем
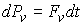 (6.3) (6.3)
Поскольку 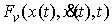 есть функция
ограниченной вариации, то есть функция
ограниченной вариации, то 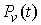 явля-ется абсолютно
непрерывной функцией и выполнено (6.1). Доказательство за-кончено. явля-ется абсолютно
непрерывной функцией и выполнено (6.1). Доказательство за-кончено.
Возьмем 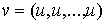 , т.е. составим вектор , т.е. составим вектор 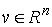 из из 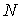 экземпляров вектора экземпляров вектора 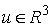 . Если домножить теперь (6.3) слева на . Если домножить теперь (6.3) слева на 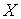 , то получим (6.1). Это доказывает теорему об изменении
количества движения. , то получим (6.1). Это доказывает теорему об изменении
количества движения.
Обычными рассуждениями из
теоремы об изменении количества движе-ния выводится следующие утверждения.
Пусть выполняются указанные выше предположения о связях тогда:
Закон сохранения количества движения. Если суммарная
проекция всех активных сил на направление 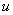 равна нулю, то во все
время движения сохра-няется значение проекции количества движения системы на
это направление. равна нулю, то во все
время движения сохра-няется значение проекции количества движения системы на
это направление.
Теорема о движении центра масс. Движение центра масс системы
в про-екции на ось 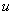 совпадает с движением
свободной от связей точки, масса кото-рой
равна суммарной массе всех точек системы, и к которой приложена сила, равная
сумме всех активных сил, действующих на точки системы. Следствие. Если суммарная проекция всех активных сил на
направление совпадает с движением
свободной от связей точки, масса кото-рой
равна суммарной массе всех точек системы, и к которой приложена сила, равная
сумме всех активных сил, действующих на точки системы. Следствие. Если суммарная проекция всех активных сил на
направление 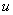 равна нулю, то центр
масс системы в проекции на эту ось двигается с посто-янной скоростью. равна нулю, то центр
масс системы в проекции на эту ось двигается с посто-янной скоростью.
7.
Теорема об
изменении момента количества движения.
Для систем с идеальными удерживающими связями помимо
теорем об изменении количества движения
формулируются теоремы об изменении мо-мента количества движения (см.,
например, [8]). В [4], с помощью уравнений Лагранжа первого рода, было
показано, что они справедливы и при наличии идеальных односторонних связей. В
данном разделе, следуя [4], мы распро-страним их действие на условные связи. Не
нарушая общности, мы будем рас-сматривать случай, когда все оси проходят через
начало системы координат и все моменты вычисляются также относительно начала
координат.
Момент количества движения системы относительно начала координат - это трехмерный
вектор 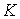 равный сумме моментов
количества движения всех составляющих систему точек. Момент количества движения
материаль-ной точки равный сумме моментов
количества движения всех составляющих систему точек. Момент количества движения
материаль-ной точки 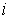 относительно начала
координат - это трехмерный вектор относительно начала
координат - это трехмерный вектор 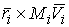 , где , где 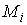 - масса точки, а - масса точки, а 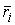 и и  - ее трехмерный
радиус-вектор, и вектор скоро-сти: - ее трехмерный
радиус-вектор, и вектор скоро-сти: 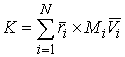 . Момент сил системы
относительно начала координат - это трехмерный вектор . Момент сил системы
относительно начала координат - это трехмерный вектор 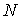 равный сумме моментов
всех активных сил системы. Момент силы равный сумме моментов
всех активных сил системы. Момент силы 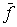 относительно начала
координат - это трехмерный вектор относительно начала
координат - это трехмерный вектор 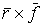 , где , где 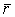 - трехмерный
радиус-вектор точки системы, к которой приложена сила: - трехмерный
радиус-вектор точки системы, к которой приложена сила: 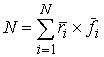 . .
Так же, как и выше мы будем использовать сводные
вектора координат точек системы 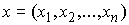 , сил , сил 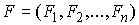 , , 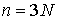 , импульса сис-темы , импульса сис-темы 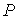 и т.п. Вектор момента импульса.
Введем сводный вектор и т.п. Вектор момента импульса.
Введем сводный вектор 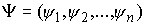 моментов количества
движения системы (или моментов импульса) относи-тельно начала координат
следующим образом. Координаты вектора моментов количества
движения системы (или моментов импульса) относи-тельно начала координат
следующим образом. Координаты вектора 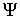 естест-венным образом
разбиваются на тройки естест-венным образом
разбиваются на тройки 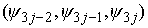 , , 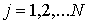 . Каждая тройка соответствует материальной точке . Каждая тройка соответствует материальной точке 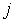 системы. Координаты
ее момента количества движения системы. Координаты
ее момента количества движения 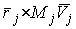 и есть значения координат
в тройке и есть значения координат
в тройке 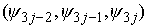 . Вектор моментов
сил. Аналогично вводится сводный вектор . Вектор моментов
сил. Аналогично вводится сводный вектор 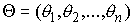 моментов сил системы
относительно начала координат. Каж-дая тройка его координат равна тройке
координат момента силы моментов сил системы
относительно начала координат. Каж-дая тройка его координат равна тройке
координат момента силы 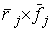 . В этих терминах . В этих терминах 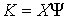 , , 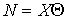 , где , где 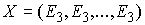 - матрица - матрица 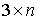 , составленная из , составленная из 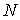 экземпляров трех-мерных
единичных матриц экземпляров трех-мерных
единичных матриц 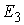 . .
Сводным векторным произведением векторов 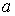 , , 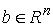 будем называть вектор будем называть вектор
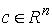 , определяемый по следующему правилу. Пусть , определяемый по следующему правилу. Пусть 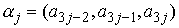 , , 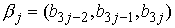 , , 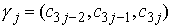 - трехмерные вектора,
составленные из троек координат векторов - трехмерные вектора,
составленные из троек координат векторов 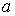 , , 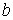 и и 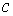 , как и выше. То-гда , как и выше. То-гда 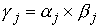 , где " , где "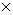 " означает обычное векторное произведение. Сводное векторное
произведение будем обозначать знаком " " означает обычное векторное произведение. Сводное векторное
произведение будем обозначать знаком "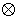 ". Таким образом, ". Таким образом, 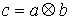 . Заметим, что для сводного векторного произведения
справедливы те же утверждения, что и для обычного векторного произведения в
трехмерном пространстве, в частности, верна формула смешанного произведения: . Заметим, что для сводного векторного произведения
справедливы те же утверждения, что и для обычного векторного произведения в
трехмерном пространстве, в частности, верна формула смешанного произведения: 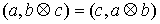 . Во введенных обозначениях можно записать . Во введенных обозначениях можно записать
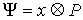 , , 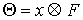 (7.1) (7.1)
Теорема об изменении момента количества движения. Если
удержи-вающие, односторонние и условные связи, наложенные на систему, идеальны
и допускают поворот всех точек системы как твердого тела вокруг какой-нибудь
постоянной оси с направляющим вектором 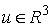 и проходящей через
начало координат, то проекция момента количества движения системы на эту ось и проходящей через
начало координат, то проекция момента количества движения системы на эту ось 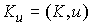 является абсолютно
непрерывной функцией и скорость ее измене-ния равна является абсолютно
непрерывной функцией и скорость ее измене-ния равна 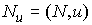 , т.е. равна суммарной проекции на это направление век-торов
моментов активных сил: , т.е. равна суммарной проекции на это направление век-торов
моментов активных сил: 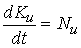 . Эта теорема непосредственно вытекает из аналогичного
утверждения для сводных векторов системы. . Эта теорема непосредственно вытекает из аналогичного
утверждения для сводных векторов системы.
Поворот. Поворотом сводного
пространства 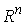 координат точек системы
вокруг оси с направляющим вектором координат точек системы
вокруг оси с направляющим вектором 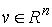 , и проходящей через начало координат, будем называть
однопараметрическую группу ортогональных пре-образований , и проходящей через начало координат, будем называть
однопараметрическую группу ортогональных пре-образований 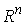 с собственным
вектором с собственным
вектором 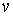 . При этом каждая естественная тройка координат одной
материальной точки системы преобразуется ортого-нально опять в естественную
тройку координат той же точки. Это означает, что соответствующие ортогональные
матрицы преобразований пространства . При этом каждая естественная тройка координат одной
материальной точки системы преобразуется ортого-нально опять в естественную
тройку координат той же точки. Это означает, что соответствующие ортогональные
матрицы преобразований пространства 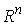 являются блочными
диагональными матрицами. На диагонали расположены ортогональные матрицы являются блочными
диагональными матрицами. На диагонали расположены ортогональные матрицы 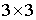 , у которых собственным вектором является век-тор, координаты
которого являются соответствующей тройкой координат на-правляющего вектора , у которых собственным вектором является век-тор, координаты
которого являются соответствующей тройкой координат на-правляющего вектора 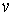 . Пусть у нас есть поворот в исходном трехмерном пространстве
всех точек системы как твердого тела вокруг какой-нибудь постоянной оси с
направляю-щим вектором . Пусть у нас есть поворот в исходном трехмерном пространстве
всех точек системы как твердого тела вокруг какой-нибудь постоянной оси с
направляю-щим вектором 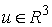 и проходящей через
начало координат. Ему соответст-вует поворот в сводном пространстве координат
точек системы и проходящей через
начало координат. Ему соответст-вует поворот в сводном пространстве координат
точек системы 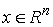 с на-правляющим
вектором с на-правляющим
вектором 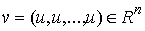 , координаты которого составлены из , координаты которого составлены из 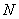 экземпляров координат
вектора экземпляров координат
вектора 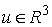 . .
Теорема об изменении вектора моментов импульса. Если удерживаю-щие,
односторонние и условные связи, наложенные на систему, идеальны и допускают
поворот всех точек системы как твердого тела вокруг какой-нибудь постоянной оси
с направляющим вектором 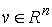 и проходящей через
начало координат, то проекция сводного вектора моментов импульса системы на эту
ось и проходящей через
начало координат, то проекция сводного вектора моментов импульса системы на эту
ось 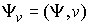 является абсолютно
непрерывной функцией и скорость ее изменения равна является абсолютно
непрерывной функцией и скорость ее изменения равна 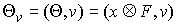 , т.е. равна проекции на это направление сводного вектора
моментов активных сил. , т.е. равна проекции на это направление сводного вектора
моментов активных сил.
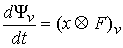 (7.2) (7.2)
Доказательство. Возьмем любую траекторию движения системы 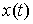 . Для нее выполнены уравнения Лагранжа первого рода (6.2).
Условие теоремы означает, что в каждой точке конфигурационного пространства и в
любой момент времени возможным перемещением является вектор . Для нее выполнены уравнения Лагранжа первого рода (6.2).
Условие теоремы означает, что в каждой точке конфигурационного пространства и в
любой момент времени возможным перемещением является вектор 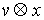 , т.е. , т.е. 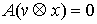 . А также . А также 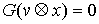 в тех точках траектории,
которые расположены на границе односторонних связей, т.е. в тех точках, в
которых сосредоточена мера в тех точках траектории,
которые расположены на границе односторонних связей, т.е. в тех точках, в
которых сосредоточена мера 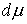 . И, кроме того, . И, кроме того, 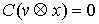 в тех точках
траектории, которые расположены на границе условных связей, т.е. в тех точках,
в которых сосредоточена мера в тех точках
траектории, которые расположены на границе условных связей, т.е. в тех точках,
в которых сосредоточена мера 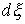 . Отсюда следует, что во все время движения . Отсюда следует, что во все время движения 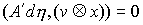 , , 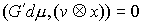 , и , и 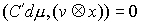 . Эти равенства надо понимать как равенства мер
Лебега-Стилтьеса. Домножив обе части (6.2) на . Эти равенства надо понимать как равенства мер
Лебега-Стилтьеса. Домножив обе части (6.2) на 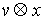 , получаем , получаем 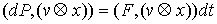 , или , или
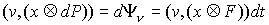 (7.3) (7.3)
Поскольку 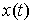 - абсолютно
непрерывна, то применима формула Лейбница для мер Лебега-Стилтьеса [3]. Значит - абсолютно
непрерывна, то применима формула Лейбница для мер Лебега-Стилтьеса [3]. Значит 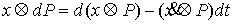 . Но . Но 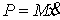 и и 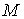 - диагональная матрица масс размером - диагональная матрица масс размером 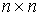 , у которой на диагонали расположены тройки одинаковых чисел
(массы соответствующих точек системы). Поэтому , у которой на диагонали расположены тройки одинаковых чисел
(массы соответствующих точек системы). Поэтому 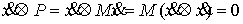 и, значит, и, значит, 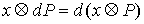 . Тогда из (7.3) . Тогда из (7.3) 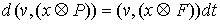 , или , или 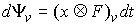 . Поскольку . Поскольку 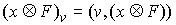 есть функция
ограниченной вариации, то есть функция
ограниченной вариации, то 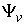 является абсолютно
непрерывной функцией и выполнено (7.2). Доказательство закончено. является абсолютно
непрерывной функцией и выполнено (7.2). Доказательство закончено.
Обычными рассуждениями из теоремы
об изменении момента количества движения выводится Закон сохранения момента количества движения. Пусть
выполняются указанные выше предположения о связях. Если суммарная проекция
на направление 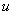 векторов моментов
активных сил равна нулю, то во все время движения сохраняется значение проекции
момента количества движения системы на это направление. векторов моментов
активных сил равна нулю, то во все время движения сохраняется значение проекции
момента количества движения системы на это направление.
8.
Уравнения
Лагранжа второго рода.
В [3] были выведены уравнения
движения механических систем с идеальными односторонними связями в форме
уравнений Лагранжа второго рода. В данном разделе мы повторим этот вывод для
систем с идеальными условными связями. Такие уравнения можно получить, обычным образом, если удерживающие
и односторонние связи голономны. Пусть 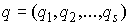 обобщенные координаты
тогда обобщенные координаты
тогда
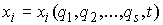 , , 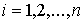 (8.1) (8.1)
Мы считаем, что функции 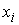 имеют, по крайней
мере, второй класс гладкости. Тогда траектория движения имеют, по крайней
мере, второй класс гладкости. Тогда траектория движения 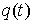 - это абсолютно
непрерывная вектор-функция, производная которой - это абсолютно
непрерывная вектор-функция, производная которой 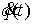 является функцией
ограниченной вариации. Односторонние связи в обобщенных координатах задаются
системой неравенств является функцией
ограниченной вариации. Односторонние связи в обобщенных координатах задаются
системой неравенств 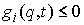 , , 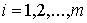 (8.2) (8.2)
Группа условных связей задается системой условий
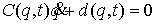 , при , при 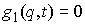 (8.3) (8.3)
где матрица 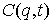 размером размером 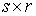 , и вектор , и вектор 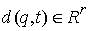 получаются из (2.5): получаются из (2.5): 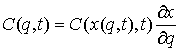 , , 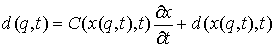 . Из (8.1) получаем . Из (8.1) получаем
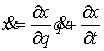 , откуда , откуда 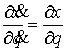 (8.4) (8.4)
Кроме того
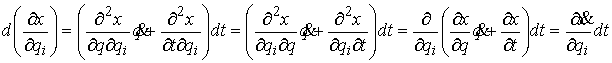
или, в матричной форме 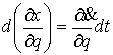 . Подставив (8.4) в уравнения удерживающих связей (2.3)
получим систему . Подставив (8.4) в уравнения удерживающих связей (2.3)
получим систему 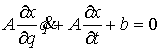 , которая должна тождественно выполняться при всех , которая должна тождественно выполняться при всех 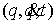 . Отсюда . Отсюда 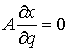 . Воспользуемся матричной формой уравнений Лагранжа 1-го рода
(2.17). Домножив обе части (2.17) слева на матрицу . Воспользуемся матричной формой уравнений Лагранжа 1-го рода
(2.17). Домножив обе части (2.17) слева на матрицу 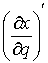 получим получим
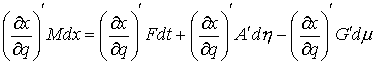 (8.5) (8.5)
Матрица  абсолютно непрерывна
поэтому, используя формулу Лейбница для мер Лебега-Стилтьеса [3], получаем на
действительной траектории абсолютно непрерывна
поэтому, используя формулу Лейбница для мер Лебега-Стилтьеса [3], получаем на
действительной траектории 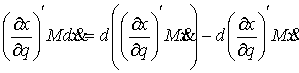 . Использовав (8.4-5) выводим отсюда . Использовав (8.4-5) выводим отсюда 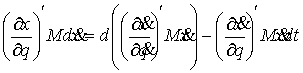 . Введем кинетическую энергию системы . Введем кинетическую энергию системы 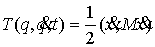 . Тогда . Тогда 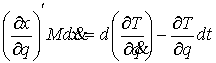 . Как обычно, обозначим . Как обычно, обозначим 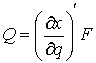 вектор обобщенных сил вектор обобщенных сил
 , , 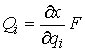 , , 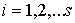 . Далее, в силу . Далее, в силу 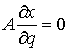 имеем имеем 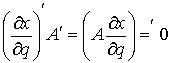 . Обозначим . Обозначим 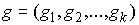 тогда тогда 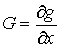 и и 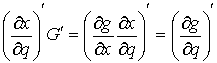 . Обозначим также . Обозначим также 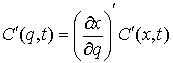 . Подставив эти обозначения
в (2.17) получим . Подставив эти обозначения
в (2.17) получим
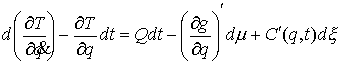 (8.6) (8.6)
или, в
покоординатном виде
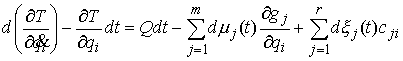 (8.7) (8.7)
Заметим, что по форме уравнения (8.7) совпадают с
уравнениями Аппеля для систем с непроинтегрированными связями.
Потенциальный случай. Если силы имеют силовую функцию 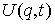 , то введем, как обычно, функцию Лагранжа , то введем, как обычно, функцию Лагранжа  . И уравнения движения приобретут форму . И уравнения движения приобретут форму 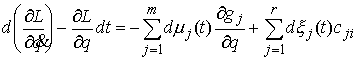 . Здесь везде . Здесь везде 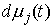 - неотрицательные
меры Лебега-Стилтьеса, каждая из которых сосредоточена на множестве моментов
времени, в которые траектория движения выходит на границу соответствующего
одностороннего ограничения - неотрицательные
меры Лебега-Стилтьеса, каждая из которых сосредоточена на множестве моментов
времени, в которые траектория движения выходит на границу соответствующего
одностороннего ограничения 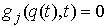 . А меры . А меры 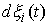 сосредоточенны там,
где траектория выходит на границу условных связей сосредоточенны там,
где траектория выходит на границу условных связей 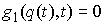 . В матричной записи эти уравнения выглядят следующим образом . В матричной записи эти уравнения выглядят следующим образом
 (8.8) (8.8)
9.
Циклические
интегралы и теорема Рауса.
В [4], было показано, что теория Рауса
игнорирования циклических координат справедлива при наличии идеальных
односторонних связей. В данном разделе, следуя [4], мы распространим её
действие на системы с условными связями. Рассмотрим голономную механическую
систему, которая в локальных координатах 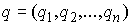 описывается лагранжианом описывается лагранжианом 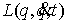 . Пусть на систему
наложены односторонние и условные связи (8.2, 8.3). Тогда уравнения движения
будут иметь вид (8.8). Далее рассуждаем по обычной схеме. . Пусть на систему
наложены односторонние и условные связи (8.2, 8.3). Тогда уравнения движения
будут иметь вид (8.8). Далее рассуждаем по обычной схеме.
Циклические координаты. Обобщенная координата 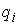 называется циклической,
если она не входит явно в функцию Лагранжа называется циклической,
если она не входит явно в функцию Лагранжа 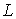 и в неравенства односторонних
и условных связей, т.е. и в неравенства односторонних
и условных связей, т.е.
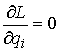 , , 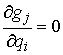 , ,  , , 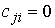 , , 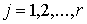 (9.1) (9.1)
Не циклические координаты называются позиционными.
Циклические интегралы. В силу уравнений (8.8) и условий (9.1) для циклической координаты 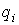 выполнено выполнено 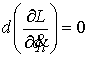 . Значит, величина . Значит, величина 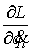 остается постоянной,
т.е. является первым интегралом уравнений движения, который называется циклическим
интегралом. остается постоянной,
т.е. является первым интегралом уравнений движения, который называется циклическим
интегралом.
Циклическую координату 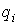 назовём отделяющейся, если помимо (9.1)
выполняется условие назовём отделяющейся, если помимо (9.1)
выполняется условие 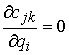 , , 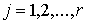 , , 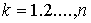 . Функция Рауса.
Пусть координаты . Функция Рауса.
Пусть координаты 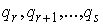 являются
отделяющимися циклическими. Им соответствуют циклические интегралы: являются
отделяющимися циклическими. Им соответствуют циклические интегралы: 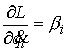 , , 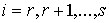 , где , где 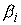 - константы
интегралов. Циклические координаты в эти уравнения не входят. Будем считать,
что они функционально независимы и, следовательно, разрешимы относительно
циклических скоростей, и мы можем найти последние как функции позиционных
координат - константы
интегралов. Циклические координаты в эти уравнения не входят. Будем считать,
что они функционально независимы и, следовательно, разрешимы относительно
циклических скоростей, и мы можем найти последние как функции позиционных
координат 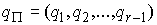 , позиционных скоростей , позиционных скоростей 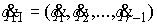 , констант циклических интегралов , констант циклических интегралов 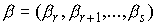 и времени: и времени: 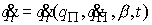 , ,  (9.4) (9.4)
Составим функцию Рауса
 (9.5) (9.5)
Здесь всюду вместо циклических скоростей подставлены их выражения (9.4).
Теорема Рауса. Пусть  - траектория движения
нашей системы, тогда для позиционных координат выполнены уравнения Лагранжа
второго рода, в которых в качестве функции Лагранжа берется функция Рауса
(9.5). - траектория движения
нашей системы, тогда для позиционных координат выполнены уравнения Лагранжа
второго рода, в которых в качестве функции Лагранжа берется функция Рауса
(9.5).
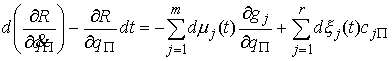 (9.6) (9.6)
Доказательство. Для краткости записи введем вектор
циклических скоростей 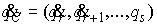 . Повторяя дословно рассуждения [4], получим, что во всех точках траектории движения
выполняются соотношения . Повторяя дословно рассуждения [4], получим, что во всех точках траектории движения
выполняются соотношения 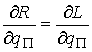 , , 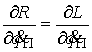 , , 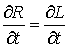 , , 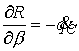 . Подставляя их в уравнения (8.8) получаем для позиционных
координат уравнения (9.6). Доказательство закончено. . Подставляя их в уравнения (8.8) получаем для позиционных
координат уравнения (9.6). Доказательство закончено.
10.
Преобразование
координат.
Известно, что уравнения Лагранжа второго рода инвариантны относительно замены координат. В
[4] было показано, что это справедливо и в случае односторонних связей. Это
остается справедливым и при наличии условных связей. Рассмотрим голономную
механическую систему, которая в локальных координатах 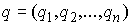 описывается лагранжианом описывается лагранжианом 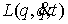 . Пусть на систему
наложены односторонние и условные связи (8.2, 8.3). Далее рассуждаем по обычной
схеме. Пусть . Пусть на систему
наложены односторонние и условные связи (8.2, 8.3). Далее рассуждаем по обычной
схеме. Пусть 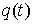 , , 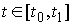 - траектория движения нашей системы. Тогда
для нее выполнены уравнения Лагранжа второго рода (8.8). Пусть мы переходим от
старых координат - траектория движения нашей системы. Тогда
для нее выполнены уравнения Лагранжа второго рода (8.8). Пусть мы переходим от
старых координат 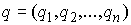 к новым к новым 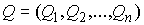 , причем функции перехода , причем функции перехода 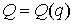 и и 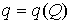 принадлежат второму
классу гладкости и преобразование невырожденное, т.е. принадлежат второму
классу гладкости и преобразование невырожденное, т.е. 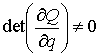 . Обозначим . Обозначим 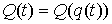 , , 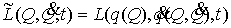 , , 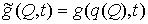 , , 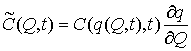 . Ясно, что . Ясно, что 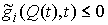 . Повторяя
дословно рассуждения [4], получим, что во всех точках траектории движения
выполняются . Повторяя
дословно рассуждения [4], получим, что во всех точках траектории движения
выполняются 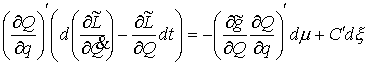 , откуда сразу следуют
требуемые соотношения , откуда сразу следуют
требуемые соотношения 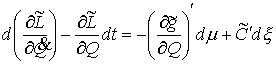 . .
11.
Теорема
Нётер.
В [4], было показано, что теорема
Нётер о существовании первых интегралов лагранжевых систем справедлива при
наличии идеальных односторонних связей. В данном разделе, следуя [4], мы
распространим действие этой теоремы на условные связи. Как и в предыдущих
разделах, наши рассуждения почти дословно повторяют традиционные (см.,
например, [9]). Мы будем проводить их в локальных координатах, понимая, что
значение нётерова интеграла не зависит от выбора последних [10]. Рассмотрим
голономную механическую систему, которая в локальных координатах 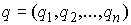 описывается лагранжианом описывается лагранжианом
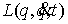 . Пусть на систему наложены односторонние и условные связи
(8.2, 8.3). Рассмотрим однопараметрическую группу . Пусть на систему наложены односторонние и условные связи
(8.2, 8.3). Рассмотрим однопараметрическую группу 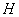 диффеоморфизмов
нашего конфигурационного пространства. Локально действие группы можно описать
векторным полем диффеоморфизмов
нашего конфигурационного пространства. Локально действие группы можно описать
векторным полем 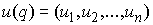 . Пусть . Пусть 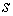 - групповой параметр,
а - групповой параметр,
а 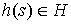 соответствующее ему
преобразование. Будем считать, что значение соответствующее ему
преобразование. Будем считать, что значение 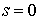 соответствует
тождественному преобразованию. Действие группы соответствует
тождественному преобразованию. Действие группы 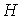 можно описать
функционально можно описать
функционально 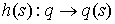 . При этом функции . При этом функции 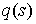 удовлетворяют
следующим уравнениям удовлетворяют
следующим уравнениям
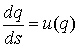 (11.1) (11.1)
Мы будем
требовать, чтобы в рассматриваемой координатной окрестности действие группы
было свободным, т.е., чтобы 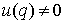 . Пусть . Пусть 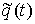 - траектория движения
нашей системы. Тогда для нее выполнены уравнения Лагранжа второго рода (8.8).
Пусть - траектория движения
нашей системы. Тогда для нее выполнены уравнения Лагранжа второго рода (8.8).
Пусть 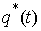 любая гладкая кривая.
Применив к ней преобразования любая гладкая кривая.
Применив к ней преобразования 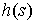 , мы получим однопараметрическое семейство кривых , мы получим однопараметрическое семейство кривых 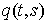 . При этом . При этом 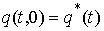 . Обозначим . Обозначим 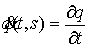 . Тогда . Тогда 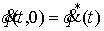 . .
Инвариантность лагранжиана. Будем говорить, что лагранжиан 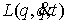 инвариантен
относительно действия группы инвариантен
относительно действия группы 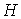 , если для любой гладкой кривой , если для любой гладкой кривой 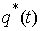 и любых и любых 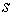 и и 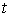 выполнено выполнено 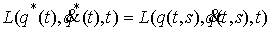 . .
Инвариантность односторонних связей. Будем говорить, что односторонние голономные
связи (8.2) инвариантны относительно действия группы 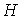 , если в любой момент времени инвариантна их граница, т.е. , если в любой момент времени инвариантна их граница, т.е. 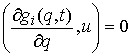 , для любых , для любых 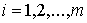 таких, что таких, что 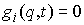 . .
Инвариантность условных связей. Будем говорить, что условные связи (8.3)
инвариантны относительно действия группы  , если в любой момент времени инвариантна их граница, т.е.
при , если в любой момент времени инвариантна их граница, т.е.
при 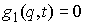 выполнено выполнено 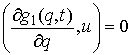 и и 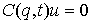 . .
Теорема Нётер.
Пусть лагранжиан нашей системы, односторонние и условные связи инвариантны
относительно гладкого (класса два) свободного действия группы  , определённой выше, тогда для любой траектории движения
системы , определённой выше, тогда для любой траектории движения
системы  выполнено выполнено 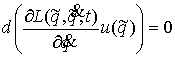 , т.е. система допускает первый интеграл движения , т.е. система допускает первый интеграл движения 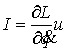 (11.2) (11.2)
Доказательство.
Возьмем любую точку траектории  . В соответствии с теоремой о
выпрямлении для обыкновенных дифференциальных уравнений [11], в некоторой
окрестности этой точки систему (11.1) можно "выпрямить". Это означает, что
существует такое (гладкое класса два) преобразование от старых координат . В соответствии с теоремой о
выпрямлении для обыкновенных дифференциальных уравнений [11], в некоторой
окрестности этой точки систему (11.1) можно "выпрямить". Это означает, что
существует такое (гладкое класса два) преобразование от старых координат  к новым к новым 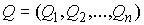 , при котором уравнения действия группы (8.2) примут
простейший вид: , при котором уравнения действия группы (8.2) примут
простейший вид: 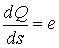 , где , где 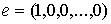 - постоянный
единичный вектор. Несложно убедиться, что - постоянный
единичный вектор. Несложно убедиться, что
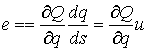 (11.3) (11.3)
Как было
показано в предыдущем разделе, в новой системе координат траектории движения
нашей системы будут удовлетворять уравнениям Лагранжа второго рода для нового
лагранжиана 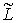 , получающегося из старого подстановкой координатных функций.
При этом , получающегося из старого подстановкой координатных функций.
При этом 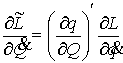 (11.4) (11.4)
Инвариантность
лагранжиана и односторонних связей при действии группы  сохранится и в новой
системе координат. И условия инвариантности в ней становятся очень простыми.
Они означают, что координата сохранится и в новой
системе координат. И условия инвариантности в ней становятся очень простыми.
Они означают, что координата  - циклическая и
выполняются условия теоремы Рауса (п.9). Значит, величина - циклическая и
выполняются условия теоремы Рауса (п.9). Значит, величина 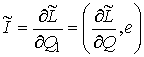 является первым
интегралом движения. Подставив сюда (11.3, 11.4) и сравнив с (11.2) убеждаемся,
что является первым
интегралом движения. Подставив сюда (11.3, 11.4) и сравнив с (11.2) убеждаемся,
что  . Теорема доказана. . Теорема доказана.
12.
Примеры
задач.
Не давая подробного анализа, приведем несколько примеров механических
систем с условными связями, для которых применимы результаты, изложенные в
данной работе.
Пример 1. По гладкой
вертикальной плоскости скользит массивный шероховатый диск радиуса  . Движение диска ограничено полуплоскостью . Движение диска ограничено полуплоскостью 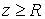 . При выходе на границу ограничений, т.е. на прямую . При выходе на границу ограничений, т.е. на прямую 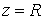 обод диска касается
прямой обод диска касается
прямой 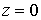 . Контакт диска с этой прямой является абсолютно шероховатым.
Это система с тремя степенями свободы. Однако, наличие циклического интеграла
позволяет свести задачу к двухмерному биллиарду. . Контакт диска с этой прямой является абсолютно шероховатым.
Это система с тремя степенями свободы. Однако, наличие циклического интеграла
позволяет свести задачу к двухмерному биллиарду.
Пример 2. Массивный шероховатый диск в круге, на
горизонтальной плоскости. Это система с тремя степенями свободы. Однако,
наличие циклического интеграла позволяет свести задачу к двухмерному биллиарду.
Пример 3. Два массивных шероховатых диска в гладком
круге на горизонтальной плоскости. Это система с шестью степенями свободы.
Однако, наличие двух циклических интегралов позволяет свести задачу к четырем
степеням свободы.
Пример 4. Массивный шероховатый диск в круге, квадрате,
между двумя прямыми и т.п.
Пример 5. Тяжёлый
шероховатый шар, движение которого ограничено наклонной плоскостью.
ЛИТЕРАТУРА
1.
Козлов В.В.,
Трещев Д.В. Биллиарды. Генетическое введение в динамику систем с ударами. М.,
МГУ, 1991 - 168с.
2.
Иванов А.П.
Динамика систем с механическими соударениями. М., "Международная программа
образования", 1997 - 336с .
3.
Кугушев
Е.И., Сорокина О.В. Принцип Даламбера-Лагранжа в механических системах с
односторонними связями. Препринт ИПМ им. М.В. Келдыша РАН, 2002 - 32с.
4.
Кугушев
Е.И., Сорокина О.В. Закономерности движения механических система с
односторонними связями. Препринт ИПМ им. М.В. Келдыша РАН, 2002 - 28с.
5.
Козырева
Е.Е., Кугушев Е.И. Краевые задачи при исследовании пространственных структур
РНК. Препринт ИПМ им. М.В. Келдыша РАН, N 74, 2002 - 32с.
6.
Козлов В.В.
Динамика систем с неинтегрируемыми связями I-V. Вестник МГУ, сер. мат.-мех., 1982, N 3, с.92-100, 1982, N 4, с.70-76, 1983, N 3, с.102-111, 1987, N 5, с.76-83, 1988, N 6, с.51-54.
7.
Маркеев А.П.
Теоретическая механика. "Регулярная и хаотическая динамика", 1999 - 569с.
8.
Березкин
Е.Н. Курс теоретической механики. М., МГУ, 1974 - 646с.
9.
Голубев Ю.Ф.
Основы теоретической механики. М., МГУ, 2000 - 719с.
10.
Арнольд В.И.
Математические методы классической механики. М., Эдиториал УРСС, 2000 - 408с.
|
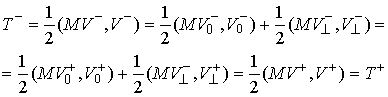
![]() - силовая функция.
Тогда полная энергия
- силовая функция.
Тогда полная энергия ![]() - это непрерывная
функция. На каждом открытом отрезке, не содержащем скачков она постоянна в силу
обычных законов сохранения для удерживающих связей (на участках, когда
траектория выходит на границу односторонних и условных ограничений, их можно
рассматривать как удерживающие). Но, поскольку множество скачков не более чем
счетно, то полная энергия постоянна на всем отрезке времени.
- это непрерывная
функция. На каждом открытом отрезке, не содержащем скачков она постоянна в силу
обычных законов сохранения для удерживающих связей (на участках, когда
траектория выходит на границу односторонних и условных ограничений, их можно
рассматривать как удерживающие). Но, поскольку множество скачков не более чем
счетно, то полная энергия постоянна на всем отрезке времени.![]() имеет размерность
имеет размерность ![]() . Выберем любой ортонормированный (в кинетической метрике)
базис
. Выберем любой ортонормированный (в кинетической метрике)
базис ![]() в
в ![]() , и разложим по нему нормальные составляющие скоростей
движения до и после удара
, и разложим по нему нормальные составляющие скоростей
движения до и после удара 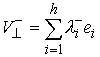 ,
, 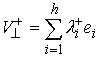 . Обозначим
. Обозначим ![]() и
и ![]() - проекции скоростей
на оси нашего базиса
- проекции скоростей
на оси нашего базиса![]() ,
, ![]() (5.1)
(5.1)![]() ,
, ![]() , и
, и ![]() при
при ![]() , то кинетическая энергия потерянных скоростей (4.1) может
быть представлена суммой
, то кинетическая энергия потерянных скоростей (4.1) может
быть представлена суммой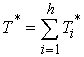 (5.2)
(5.2)![]() (5.3)
(5.3)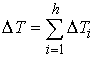 (5.4)
(5.4)![]() (5.5)
(5.5)![]() , то
, то ![]() , где
, где 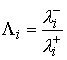 (5.6)
(5.6)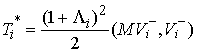 и
и 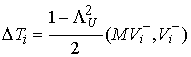 . Отсюда следует, что
. Отсюда следует, что 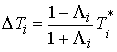 .
.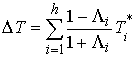 (5.7)
(5.7)![]() . В этом случае коэффициент при
. В этом случае коэффициент при ![]() нужно положить равным
минус единице. Доказательство является очевидным, если переписать (5.7) в
следующей форме
нужно положить равным
минус единице. Доказательство является очевидным, если переписать (5.7) в
следующей форме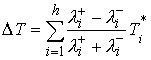 (5.8)
(5.8)![]() таким образом, чтобы
вектор
таким образом, чтобы
вектор ![]() был направлен вдоль
нормальной скорости при подходе к точке удара. Тогда
был направлен вдоль
нормальной скорости при подходе к точке удара. Тогда ![]() , и из (5.8) получим
, и из (5.8) получим 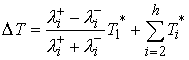 . Добавив
. Добавив ![]() к правой части этого
соотношения и воспользовавшись (5.2), получим
к правой части этого
соотношения и воспользовавшись (5.2), получим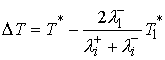 (5.9)
(5.9)![]() отношение модуля
нормальной составляющей скорости
отношение модуля
нормальной составляющей скорости ![]() (до удара) к проекции
на неё нормальной составляющей скорости
(до удара) к проекции
на неё нормальной составляющей скорости ![]() (после удара) в кинетической
метрике:
(после удара) в кинетической
метрике: 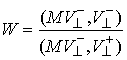 . Тогда
. Тогда 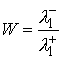 и из (5.9) получаем
и из (5.9) получаем![]() (5.10)
(5.10)![]() естественно называть
кинетической энергией скоростей потерянных вдоль направления удара. Теперь
третью теорему Карно можно сформулировать следующим образом.
естественно называть
кинетической энергией скоростей потерянных вдоль направления удара. Теперь
третью теорему Карно можно сформулировать следующим образом.![]() равный сумме
количеств движений всех составляющих систему точек. Количество движения
материальной точки - это трехмерный вектор
равный сумме
количеств движений всех составляющих систему точек. Количество движения
материальной точки - это трехмерный вектор ![]() , где
, где ![]() - масса точки, а
- масса точки, а ![]() - трехмерный вектор
ее скорости:
- трехмерный вектор
ее скорости: 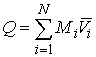 . Выше мы использовали сводный вектор координат точек
системы
. Выше мы использовали сводный вектор координат точек
системы ![]() и сводный вектор сил
и сводный вектор сил ![]() ,
, ![]() . И в этих терминах были выписаны уравнения Лагранжа первого
рода (2.17). Кроме того, мы ввели вектор импульса системы
. И в этих терминах были выписаны уравнения Лагранжа первого
рода (2.17). Кроме того, мы ввели вектор импульса системы ![]() (3.1). В этих обозначениях
(3.1). В этих обозначениях ![]() , где
, где ![]() - матрица
- матрица ![]() , составленная из
, составленная из ![]() экземпляров трехмерных
единичных матриц
экземпляров трехмерных
единичных матриц ![]() . Мы будем использовать и то и другое описание, понимая, что
они эквивалентны.
. Мы будем использовать и то и другое описание, понимая, что
они эквивалентны.![]() постоянного во
времени, то проекция количества движения системы на это направление
постоянного во
времени, то проекция количества движения системы на это направление ![]() является абсолютно
непрерывной функцией и скорость ее изменения равна
является абсолютно
непрерывной функцией и скорость ее изменения равна ![]() , т.е. равна суммарной проекции на это направление вектора
активных сил:
, т.е. равна суммарной проекции на это направление вектора
активных сил: ![]() . Эта теорема непосредственно вытекает из аналогичного
утверждения для сводных векторов системы.
. Эта теорема непосредственно вытекает из аналогичного
утверждения для сводных векторов системы.![]() постоянного во
времени, то проекция вектора импульса на это направление
постоянного во
времени, то проекция вектора импульса на это направление ![]() является абсолютно
непрерывной функцией и скорость ее изменения равна
является абсолютно
непрерывной функцией и скорость ее изменения равна ![]() , т.е. равна проекции на это направление сводного вектора
активных сил
, т.е. равна проекции на это направление сводного вектора
активных сил![]() (6.1)
(6.1)![]() ,
, ![]() . Для нее выполнены уравнения Лагранжа первого рода (2.17).
Используя вектор импульса системы
. Для нее выполнены уравнения Лагранжа первого рода (2.17).
Используя вектор импульса системы ![]() их можно переписать
следующим образом
их можно переписать
следующим образом![]() (6.2)
(6.2)![]() является возможным
перемещением, т.е.
является возможным
перемещением, т.е. ![]() во все время
движения. Далее,
во все время
движения. Далее, ![]() в тех точках
траектории, которые расположены на границе односторонних связей, т.е. в тех
точках, в которых сосредоточена мера
в тех точках
траектории, которые расположены на границе односторонних связей, т.е. в тех
точках, в которых сосредоточена мера ![]() . И, кроме того,
. И, кроме того, ![]() в тех точках
траектории, которые расположены на границе условных связей, т.е. в тех точках,
в которых сосредоточена мера
в тех точках
траектории, которые расположены на границе условных связей, т.е. в тех точках,
в которых сосредоточена мера ![]() . Отсюда следует, что во все время движения
. Отсюда следует, что во все время движения ![]() ,
, ![]() и
и ![]() . Заметим, что эти равенства, как и (6.2), надо понимать как
равенство мер Лебега-Стилтьеса. Домножив обе части (6.2) на
. Заметим, что эти равенства, как и (6.2), надо понимать как
равенство мер Лебега-Стилтьеса. Домножив обе части (6.2) на ![]() получаем
получаем![]() (6.3)
(6.3)![]() есть функция
ограниченной вариации, то
есть функция
ограниченной вариации, то ![]() явля-ется абсолютно
непрерывной функцией и выполнено (6.1). Доказательство за-кончено.
явля-ется абсолютно
непрерывной функцией и выполнено (6.1). Доказательство за-кончено.![]() , т.е. составим вектор
, т.е. составим вектор ![]() из
из ![]() экземпляров вектора
экземпляров вектора ![]() . Если домножить теперь (6.3) слева на
. Если домножить теперь (6.3) слева на ![]() , то получим (6.1). Это доказывает теорему об изменении
количества движения.
, то получим (6.1). Это доказывает теорему об изменении
количества движения. ![]() равна нулю, то во все
время движения сохра-няется значение проекции количества движения системы на
это направление.
равна нулю, то во все
время движения сохра-няется значение проекции количества движения системы на
это направление.![]() совпадает с движением
свободной от связей точки, масса кото-рой
равна суммарной массе всех точек системы, и к которой приложена сила, равная
сумме всех активных сил, действующих на точки системы. Следствие. Если суммарная проекция всех активных сил на
направление
совпадает с движением
свободной от связей точки, масса кото-рой
равна суммарной массе всех точек системы, и к которой приложена сила, равная
сумме всех активных сил, действующих на точки системы. Следствие. Если суммарная проекция всех активных сил на
направление ![]() равна нулю, то центр
масс системы в проекции на эту ось двигается с посто-янной скоростью.
равна нулю, то центр
масс системы в проекции на эту ось двигается с посто-янной скоростью.![]() равный сумме моментов
количества движения всех составляющих систему точек. Момент количества движения
материаль-ной точки
равный сумме моментов
количества движения всех составляющих систему точек. Момент количества движения
материаль-ной точки ![]() относительно начала
координат - это трехмерный вектор
относительно начала
координат - это трехмерный вектор ![]() , где
, где ![]() - масса точки, а
- масса точки, а ![]() и
и ![]() - ее трехмерный
радиус-вектор, и вектор скоро-сти:
- ее трехмерный
радиус-вектор, и вектор скоро-сти: 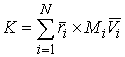 . Момент сил системы
относительно начала координат - это трехмерный вектор
. Момент сил системы
относительно начала координат - это трехмерный вектор ![]() равный сумме моментов
всех активных сил системы. Момент силы
равный сумме моментов
всех активных сил системы. Момент силы ![]() относительно начала
координат - это трехмерный вектор
относительно начала
координат - это трехмерный вектор ![]() , где
, где ![]() - трехмерный
радиус-вектор точки системы, к которой приложена сила:
- трехмерный
радиус-вектор точки системы, к которой приложена сила: 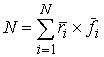 .
. ![]() , сил
, сил ![]() ,
, ![]() , импульса сис-темы
, импульса сис-темы ![]() и т.п. Вектор момента импульса.
Введем сводный вектор
и т.п. Вектор момента импульса.
Введем сводный вектор ![]() моментов количества
движения системы (или моментов импульса) относи-тельно начала координат
следующим образом. Координаты вектора
моментов количества
движения системы (или моментов импульса) относи-тельно начала координат
следующим образом. Координаты вектора ![]() естест-венным образом
разбиваются на тройки
естест-венным образом
разбиваются на тройки ![]() ,
, ![]() . Каждая тройка соответствует материальной точке
. Каждая тройка соответствует материальной точке ![]() системы. Координаты
ее момента количества движения
системы. Координаты
ее момента количества движения ![]() и есть значения координат
в тройке
и есть значения координат
в тройке ![]() . Вектор моментов
сил. Аналогично вводится сводный вектор
. Вектор моментов
сил. Аналогично вводится сводный вектор ![]() моментов сил системы
относительно начала координат. Каж-дая тройка его координат равна тройке
координат момента силы
моментов сил системы
относительно начала координат. Каж-дая тройка его координат равна тройке
координат момента силы ![]() . В этих терминах
. В этих терминах ![]() ,
, ![]() , где
, где ![]() - матрица
- матрица ![]() , составленная из
, составленная из ![]() экземпляров трех-мерных
единичных матриц
экземпляров трех-мерных
единичных матриц ![]() .
.![]() ,
, ![]() будем называть вектор
будем называть вектор
![]() , определяемый по следующему правилу. Пусть
, определяемый по следующему правилу. Пусть ![]() ,
, ![]() ,
, ![]() - трехмерные вектора,
составленные из троек координат векторов
- трехмерные вектора,
составленные из троек координат векторов ![]() ,
, ![]() и
и ![]() , как и выше. То-гда
, как и выше. То-гда ![]() , где "
, где "![]() " означает обычное векторное произведение. Сводное векторное
произведение будем обозначать знаком "
" означает обычное векторное произведение. Сводное векторное
произведение будем обозначать знаком "![]() ". Таким образом,
". Таким образом, ![]() . Заметим, что для сводного векторного произведения
справедливы те же утверждения, что и для обычного векторного произведения в
трехмерном пространстве, в частности, верна формула смешанного произведения:
. Заметим, что для сводного векторного произведения
справедливы те же утверждения, что и для обычного векторного произведения в
трехмерном пространстве, в частности, верна формула смешанного произведения: ![]() . Во введенных обозначениях можно записать
. Во введенных обозначениях можно записать ![]() ,
, ![]() (7.1)
(7.1)![]() и проходящей через
начало координат, то проекция момента количества движения системы на эту ось
и проходящей через
начало координат, то проекция момента количества движения системы на эту ось ![]() является абсолютно
непрерывной функцией и скорость ее измене-ния равна
является абсолютно
непрерывной функцией и скорость ее измене-ния равна ![]() , т.е. равна суммарной проекции на это направление век-торов
моментов активных сил:
, т.е. равна суммарной проекции на это направление век-торов
моментов активных сил: ![]() . Эта теорема непосредственно вытекает из аналогичного
утверждения для сводных векторов системы.
. Эта теорема непосредственно вытекает из аналогичного
утверждения для сводных векторов системы.![]() координат точек системы
вокруг оси с направляющим вектором
координат точек системы
вокруг оси с направляющим вектором ![]() , и проходящей через начало координат, будем называть
однопараметрическую группу ортогональных пре-образований
, и проходящей через начало координат, будем называть
однопараметрическую группу ортогональных пре-образований ![]() с собственным
вектором
с собственным
вектором ![]() . При этом каждая естественная тройка координат одной
материальной точки системы преобразуется ортого-нально опять в естественную
тройку координат той же точки. Это означает, что соответствующие ортогональные
матрицы преобразований пространства
. При этом каждая естественная тройка координат одной
материальной точки системы преобразуется ортого-нально опять в естественную
тройку координат той же точки. Это означает, что соответствующие ортогональные
матрицы преобразований пространства ![]() являются блочными
диагональными матрицами. На диагонали расположены ортогональные матрицы
являются блочными
диагональными матрицами. На диагонали расположены ортогональные матрицы ![]() , у которых собственным вектором является век-тор, координаты
которого являются соответствующей тройкой координат на-правляющего вектора
, у которых собственным вектором является век-тор, координаты
которого являются соответствующей тройкой координат на-правляющего вектора ![]() . Пусть у нас есть поворот в исходном трехмерном пространстве
всех точек системы как твердого тела вокруг какой-нибудь постоянной оси с
направляю-щим вектором
. Пусть у нас есть поворот в исходном трехмерном пространстве
всех точек системы как твердого тела вокруг какой-нибудь постоянной оси с
направляю-щим вектором ![]() и проходящей через
начало координат. Ему соответст-вует поворот в сводном пространстве координат
точек системы
и проходящей через
начало координат. Ему соответст-вует поворот в сводном пространстве координат
точек системы ![]() с на-правляющим
вектором
с на-правляющим
вектором ![]() , координаты которого составлены из
, координаты которого составлены из ![]() экземпляров координат
вектора
экземпляров координат
вектора ![]() .
.![]() и проходящей через
начало координат, то проекция сводного вектора моментов импульса системы на эту
ось
и проходящей через
начало координат, то проекция сводного вектора моментов импульса системы на эту
ось ![]() является абсолютно
непрерывной функцией и скорость ее изменения равна
является абсолютно
непрерывной функцией и скорость ее изменения равна ![]() , т.е. равна проекции на это направление сводного вектора
моментов активных сил.
, т.е. равна проекции на это направление сводного вектора
моментов активных сил.![]() (7.2)
(7.2)![]() . Для нее выполнены уравнения Лагранжа первого рода (6.2).
Условие теоремы означает, что в каждой точке конфигурационного пространства и в
любой момент времени возможным перемещением является вектор
. Для нее выполнены уравнения Лагранжа первого рода (6.2).
Условие теоремы означает, что в каждой точке конфигурационного пространства и в
любой момент времени возможным перемещением является вектор ![]() , т.е.
, т.е. ![]() . А также
. А также ![]() в тех точках траектории,
которые расположены на границе односторонних связей, т.е. в тех точках, в
которых сосредоточена мера
в тех точках траектории,
которые расположены на границе односторонних связей, т.е. в тех точках, в
которых сосредоточена мера ![]() . И, кроме того,
. И, кроме того, ![]() в тех точках
траектории, которые расположены на границе условных связей, т.е. в тех точках,
в которых сосредоточена мера
в тех точках
траектории, которые расположены на границе условных связей, т.е. в тех точках,
в которых сосредоточена мера ![]() . Отсюда следует, что во все время движения
. Отсюда следует, что во все время движения ![]() ,
, ![]() , и
, и ![]() . Эти равенства надо понимать как равенства мер
Лебега-Стилтьеса. Домножив обе части (6.2) на
. Эти равенства надо понимать как равенства мер
Лебега-Стилтьеса. Домножив обе части (6.2) на ![]() , получаем
, получаем ![]() , или
, или ![]() (7.3)
(7.3) ![]() - абсолютно
непрерывна, то применима формула Лейбница для мер Лебега-Стилтьеса [3]. Значит
- абсолютно
непрерывна, то применима формула Лейбница для мер Лебега-Стилтьеса [3]. Значит ![]() . Но
. Но ![]() и
и ![]() - диагональная матрица масс размером
- диагональная матрица масс размером ![]() , у которой на диагонали расположены тройки одинаковых чисел
(массы соответствующих точек системы). Поэтому
, у которой на диагонали расположены тройки одинаковых чисел
(массы соответствующих точек системы). Поэтому ![]() и, значит,
и, значит, ![]() . Тогда из (7.3)
. Тогда из (7.3) ![]() , или
, или ![]() . Поскольку
. Поскольку ![]() есть функция
ограниченной вариации, то
есть функция
ограниченной вариации, то ![]() является абсолютно
непрерывной функцией и выполнено (7.2). Доказательство закончено.
является абсолютно
непрерывной функцией и выполнено (7.2). Доказательство закончено.![]() векторов моментов
активных сил равна нулю, то во все время движения сохраняется значение проекции
момента количества движения системы на это направление.
векторов моментов
активных сил равна нулю, то во все время движения сохраняется значение проекции
момента количества движения системы на это направление.![]() обобщенные координаты
тогда
обобщенные координаты
тогда ![]() ,
, ![]() (8.1)
(8.1)![]() имеют, по крайней
мере, второй класс гладкости. Тогда траектория движения
имеют, по крайней
мере, второй класс гладкости. Тогда траектория движения ![]() - это абсолютно
непрерывная вектор-функция, производная которой
- это абсолютно
непрерывная вектор-функция, производная которой ![]() является функцией
ограниченной вариации. Односторонние связи в обобщенных координатах задаются
системой неравенств
является функцией
ограниченной вариации. Односторонние связи в обобщенных координатах задаются
системой неравенств ![]() ,
, ![]() (8.2)
(8.2)![]() , при
, при ![]() (8.3)
(8.3)![]() размером
размером ![]() , и вектор
, и вектор ![]() получаются из (2.5):
получаются из (2.5): 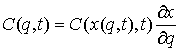 ,
, ![]() . Из (8.1) получаем
. Из (8.1) получаем 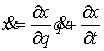 , откуда
, откуда 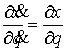 (8.4)
(8.4)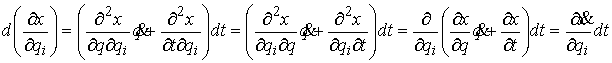
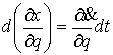 . Подставив (8.4) в уравнения удерживающих связей (2.3)
получим систему
. Подставив (8.4) в уравнения удерживающих связей (2.3)
получим систему 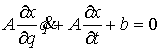 , которая должна тождественно выполняться при всех
, которая должна тождественно выполняться при всех ![]() . Отсюда
. Отсюда 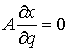 . Воспользуемся матричной формой уравнений Лагранжа 1-го рода
(2.17). Домножив обе части (2.17) слева на матрицу
. Воспользуемся матричной формой уравнений Лагранжа 1-го рода
(2.17). Домножив обе части (2.17) слева на матрицу ![]() получим
получим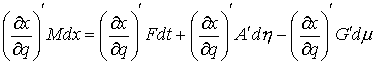 (8.5)
(8.5)![]() абсолютно непрерывна
поэтому, используя формулу Лейбница для мер Лебега-Стилтьеса [3], получаем на
действительной траектории
абсолютно непрерывна
поэтому, используя формулу Лейбница для мер Лебега-Стилтьеса [3], получаем на
действительной траектории 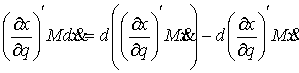 . Использовав (8.4-5) выводим отсюда
. Использовав (8.4-5) выводим отсюда 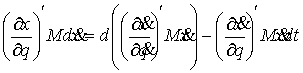 . Введем кинетическую энергию системы
. Введем кинетическую энергию системы ![]() . Тогда
. Тогда 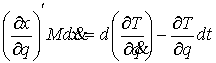 . Как обычно, обозначим
. Как обычно, обозначим 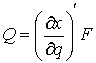 вектор обобщенных сил
вектор обобщенных сил
![]() ,
, 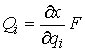 ,
, ![]() . Далее, в силу
. Далее, в силу 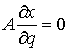 имеем
имеем 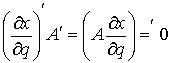 . Обозначим
. Обозначим ![]() тогда
тогда ![]() и
и 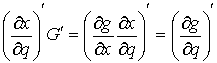 . Обозначим также
. Обозначим также 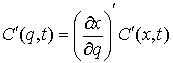 . Подставив эти обозначения
в (2.17) получим
. Подставив эти обозначения
в (2.17) получим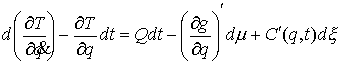 (8.6)
(8.6)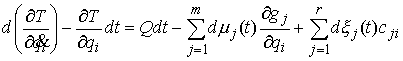 (8.7)
(8.7)![]() , то введем, как обычно, функцию Лагранжа
, то введем, как обычно, функцию Лагранжа ![]() . И уравнения движения приобретут форму
. И уравнения движения приобретут форму 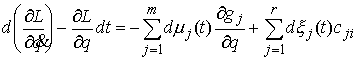 . Здесь везде
. Здесь везде ![]() - неотрицательные
меры Лебега-Стилтьеса, каждая из которых сосредоточена на множестве моментов
времени, в которые траектория движения выходит на границу соответствующего
одностороннего ограничения
- неотрицательные
меры Лебега-Стилтьеса, каждая из которых сосредоточена на множестве моментов
времени, в которые траектория движения выходит на границу соответствующего
одностороннего ограничения ![]() . А меры
. А меры ![]() сосредоточенны там,
где траектория выходит на границу условных связей
сосредоточенны там,
где траектория выходит на границу условных связей ![]() . В матричной записи эти уравнения выглядят следующим образом
. В матричной записи эти уравнения выглядят следующим образом (8.8)
(8.8)![]() описывается лагранжианом
описывается лагранжианом ![]() . Пусть на систему
наложены односторонние и условные связи (8.2, 8.3). Тогда уравнения движения
будут иметь вид (8.8). Далее рассуждаем по обычной схеме.
. Пусть на систему
наложены односторонние и условные связи (8.2, 8.3). Тогда уравнения движения
будут иметь вид (8.8). Далее рассуждаем по обычной схеме.![]() называется циклической,
если она не входит явно в функцию Лагранжа
называется циклической,
если она не входит явно в функцию Лагранжа ![]() и в неравенства односторонних
и условных связей, т.е.
и в неравенства односторонних
и условных связей, т.е.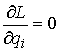 ,
, 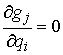 ,
, ![]() ,
, ![]() ,
, ![]() (9.1)
(9.1)![]() выполнено
выполнено 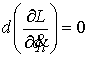 . Значит, величина
. Значит, величина ![]() остается постоянной,
т.е. является первым интегралом уравнений движения, который называется циклическим
интегралом.
остается постоянной,
т.е. является первым интегралом уравнений движения, который называется циклическим
интегралом. ![]() назовём отделяющейся, если помимо (9.1)
выполняется условие
назовём отделяющейся, если помимо (9.1)
выполняется условие 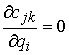 ,
, ![]() ,
, ![]() . Функция Рауса.
Пусть координаты
. Функция Рауса.
Пусть координаты ![]() являются
отделяющимися циклическими. Им соответствуют циклические интегралы:
являются
отделяющимися циклическими. Им соответствуют циклические интегралы: 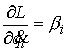 ,
, ![]() , где
, где ![]() - константы
интегралов. Циклические координаты в эти уравнения не входят. Будем считать,
что они функционально независимы и, следовательно, разрешимы относительно
циклических скоростей, и мы можем найти последние как функции позиционных
координат
- константы
интегралов. Циклические координаты в эти уравнения не входят. Будем считать,
что они функционально независимы и, следовательно, разрешимы относительно
циклических скоростей, и мы можем найти последние как функции позиционных
координат ![]() , позиционных скоростей
, позиционных скоростей ![]() , констант циклических интегралов
, констант циклических интегралов ![]() и времени:
и времени: ![]() ,
, ![]() (9.4)
(9.4) (9.5)
(9.5)![]() - траектория движения
нашей системы, тогда для позиционных координат выполнены уравнения Лагранжа
второго рода, в которых в качестве функции Лагранжа берется функция Рауса
(9.5).
- траектория движения
нашей системы, тогда для позиционных координат выполнены уравнения Лагранжа
второго рода, в которых в качестве функции Лагранжа берется функция Рауса
(9.5).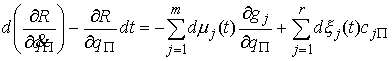 (9.6)
(9.6)![]() . Повторяя дословно рассуждения [4], получим, что во всех точках траектории движения
выполняются соотношения
. Повторяя дословно рассуждения [4], получим, что во всех точках траектории движения
выполняются соотношения 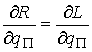 ,
, 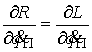 ,
, ![]() ,
, 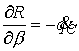 . Подставляя их в уравнения (8.8) получаем для позиционных
координат уравнения (9.6). Доказательство закончено.
. Подставляя их в уравнения (8.8) получаем для позиционных
координат уравнения (9.6). Доказательство закончено.![]() описывается лагранжианом
описывается лагранжианом ![]() . Пусть на систему
наложены односторонние и условные связи (8.2, 8.3). Далее рассуждаем по обычной
схеме. Пусть
. Пусть на систему
наложены односторонние и условные связи (8.2, 8.3). Далее рассуждаем по обычной
схеме. Пусть ![]() ,
, ![]() - траектория движения нашей системы. Тогда
для нее выполнены уравнения Лагранжа второго рода (8.8). Пусть мы переходим от
старых координат
- траектория движения нашей системы. Тогда
для нее выполнены уравнения Лагранжа второго рода (8.8). Пусть мы переходим от
старых координат ![]() к новым
к новым ![]() , причем функции перехода
, причем функции перехода ![]() и
и ![]() принадлежат второму
классу гладкости и преобразование невырожденное, т.е.
принадлежат второму
классу гладкости и преобразование невырожденное, т.е. 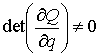 . Обозначим
. Обозначим ![]() ,
, ![]() ,
, ![]() ,
, 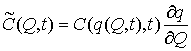 . Ясно, что
. Ясно, что ![]() . Повторяя
дословно рассуждения [4], получим, что во всех точках траектории движения
выполняются
. Повторяя
дословно рассуждения [4], получим, что во всех точках траектории движения
выполняются 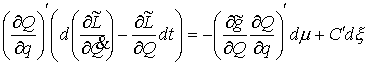 , откуда сразу следуют
требуемые соотношения
, откуда сразу следуют
требуемые соотношения 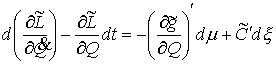 .
. ![]() описывается лагранжианом
описывается лагранжианом
![]() . Пусть на систему наложены односторонние и условные связи
(8.2, 8.3). Рассмотрим однопараметрическую группу
. Пусть на систему наложены односторонние и условные связи
(8.2, 8.3). Рассмотрим однопараметрическую группу ![]() диффеоморфизмов
нашего конфигурационного пространства. Локально действие группы можно описать
векторным полем
диффеоморфизмов
нашего конфигурационного пространства. Локально действие группы можно описать
векторным полем ![]() . Пусть
. Пусть ![]() - групповой параметр,
а
- групповой параметр,
а ![]() соответствующее ему
преобразование. Будем считать, что значение
соответствующее ему
преобразование. Будем считать, что значение ![]() соответствует
тождественному преобразованию. Действие группы
соответствует
тождественному преобразованию. Действие группы ![]() можно описать
функционально
можно описать
функционально ![]() . При этом функции
. При этом функции ![]() удовлетворяют
следующим уравнениям
удовлетворяют
следующим уравнениям![]() (11.1)
(11.1)![]() . Пусть
. Пусть ![]() - траектория движения
нашей системы. Тогда для нее выполнены уравнения Лагранжа второго рода (8.8).
Пусть
- траектория движения
нашей системы. Тогда для нее выполнены уравнения Лагранжа второго рода (8.8).
Пусть ![]() любая гладкая кривая.
Применив к ней преобразования
любая гладкая кривая.
Применив к ней преобразования ![]() , мы получим однопараметрическое семейство кривых
, мы получим однопараметрическое семейство кривых ![]() . При этом
. При этом ![]() . Обозначим
. Обозначим ![]() . Тогда
. Тогда ![]() .
. ![]() инвариантен
относительно действия группы
инвариантен
относительно действия группы ![]() , если для любой гладкой кривой
, если для любой гладкой кривой ![]() и любых
и любых ![]() и
и ![]() выполнено
выполнено ![]() .
.![]() , если в любой момент времени инвариантна их граница, т.е.
, если в любой момент времени инвариантна их граница, т.е. 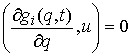 , для любых
, для любых ![]() таких, что
таких, что ![]() .
.![]() , если в любой момент времени инвариантна их граница, т.е.
при
, если в любой момент времени инвариантна их граница, т.е.
при ![]() выполнено
выполнено 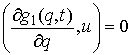 и
и ![]() .
.![]() , определённой выше, тогда для любой траектории движения
системы
, определённой выше, тогда для любой траектории движения
системы ![]() выполнено
выполнено 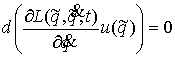 , т.е. система допускает первый интеграл движения
, т.е. система допускает первый интеграл движения 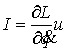 (11.2)
(11.2)![]() . В соответствии с теоремой о
выпрямлении для обыкновенных дифференциальных уравнений [11], в некоторой
окрестности этой точки систему (11.1) можно "выпрямить". Это означает, что
существует такое (гладкое класса два) преобразование от старых координат
. В соответствии с теоремой о
выпрямлении для обыкновенных дифференциальных уравнений [11], в некоторой
окрестности этой точки систему (11.1) можно "выпрямить". Это означает, что
существует такое (гладкое класса два) преобразование от старых координат ![]() к новым
к новым ![]() , при котором уравнения действия группы (8.2) примут
простейший вид:
, при котором уравнения действия группы (8.2) примут
простейший вид: ![]() , где
, где ![]() - постоянный
единичный вектор. Несложно убедиться, что
- постоянный
единичный вектор. Несложно убедиться, что 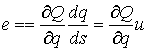 (11.3)
(11.3)![]() , получающегося из старого подстановкой координатных функций.
При этом
, получающегося из старого подстановкой координатных функций.
При этом 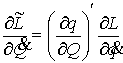 (11.4)
(11.4)![]() сохранится и в новой
системе координат. И условия инвариантности в ней становятся очень простыми.
Они означают, что координата
сохранится и в новой
системе координат. И условия инвариантности в ней становятся очень простыми.
Они означают, что координата ![]() - циклическая и
выполняются условия теоремы Рауса (п.9). Значит, величина
- циклическая и
выполняются условия теоремы Рауса (п.9). Значит, величина 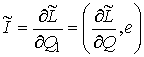 является первым
интегралом движения. Подставив сюда (11.3, 11.4) и сравнив с (11.2) убеждаемся,
что
является первым
интегралом движения. Подставив сюда (11.3, 11.4) и сравнив с (11.2) убеждаемся,
что ![]() . Теорема доказана.
. Теорема доказана.![]() . Движение диска ограничено полуплоскостью
. Движение диска ограничено полуплоскостью ![]() . При выходе на границу ограничений, т.е. на прямую
. При выходе на границу ограничений, т.е. на прямую ![]() обод диска касается
прямой
обод диска касается
прямой ![]() . Контакт диска с этой прямой является абсолютно шероховатым.
Это система с тремя степенями свободы. Однако, наличие циклического интеграла
позволяет свести задачу к двухмерному биллиарду.
. Контакт диска с этой прямой является абсолютно шероховатым.
Это система с тремя степенями свободы. Однако, наличие циклического интеграла
позволяет свести задачу к двухмерному биллиарду.