Аннотация
Теорема Биркгофа о существовании периодических движений в математических биллиардах с двумя
степенями свободы распространяется на механические системы с односторонними связями и
динамические биллиарды. Рассматривается также существование условно-периодических движений в
системах более высокой размерности.
Abstract
The Birkhoff theorem about periodic trajectories of mathematical billiards on plane is expanded
on to mechanic systems with one-sided relations and dynamic billiards. Also existence of almost
periodic motions is investigated for systems of higher dimension.
Содержание
Введение.............................................................................................................. 3
1. Метрика
Мопертюи....................................................................................... 4
2. Теорема
Биркгофа для динамических биллиардов....................................... 7
3. Условия
строгой выпуклости....................................................................... 9
4. Строгая
выпуклость в двухмерном случае................................................. 13
5. Биллиард
в однородном поле тяжести........................................................ 14
6. Биллард
в ньютоновом поле........................................................................ 16
7. Условно-периодические
движения при понижении порядка по Раусу...... 17
8. Плоское
тело с полостью............................................................................ 18
9. Плоское
тело в круге................................................................................... 23
10. Несвязная
граница..................................................................................... 25
ЛИТЕРАТУРА................................................................................................... 28
В работе рассматриваются
вопросы существования периодических и условно-периодических движений в
механических системах с односторонними связями и в динамических биллиардах.
Обзор работ по данной тематике можно найти в [1-3]. С общих позиций биллиардные
задачи можно рассматривать как часть теории механических систем с
односторонними связями. Тем не менее, принято выделять два специальных класса
задач – математические биллиарды и динамические биллиарды.
Математический биллиард (или биллиард Биркгофа [4])
это механическая система, представляющая собой материальную точку, движущуюся в
отсутствии внешних сил по плоскости или в многомерном евклидовом пространстве
внутри некоторой связной области. Граница области считается кусочно-гладкой, а
удары о границу считаются абсолютно упругими.
Другой класс систем – это натуральные механические
системы с односторонними связями и абсолютно упругими соударениями. В таких
системах выполняется закон сохранения энергии. При заданном значении уровня энергии
движение такой системы можно рассматривать как движение материальной точки в
римановом пространстве по геодезическим метрики Якоби. Простейшим примером
здесь является математический биллиард, на который наложено потенциальное
силовое поле. По всей видимости, в работах [5-6] впервые такие системы были
названы динамическими биллиардами.
В данной работе мы расширим рамки, и не будем
различать понятие динамического биллиарда и натуральной лагранжевой
механической системы с односторонними связями. Однако, мы будем требовать,
чтобы лагранжиан системы не зависел от времени, и, чтобы удары были абсолютно
упругими. Это обеспечит нам существование интеграла энергии (или, точнее,
интеграла Якоби).
Перейдем теперь к содержанию работы. В первом
разделе описываются известные понятия лагранжевой механики, позволяющие
рассматривать траекторию движения системы как геодезическую римановой метрики
Якоби или, в более общем случае, метрики Мопертюи, при фиксированном значении
обобщенного интеграла энергии.
Во втором разделе показывается (без строгого
доказательства), что теорему Биркгофа о существовании периодических движений
можно распространить на случай динамических биллиардов со строго выпуклой
областью возможного движения в метрике
Мопертюи.
В третьем разделе
формулируются необходимые и достаточные условия строгой выпуклости области
возможного движения для динамических биллиардов с любым числом степеней свободы. Они выводятся, основываясь не на геометрическом аппарате, а
на аппарате лагранжевой механики. Для строгой выпуклости необходимо, чтобы граничное движение не
сходило с границы связи и достаточно, чтобы на границе одностороннего
ограничения реакция связи нигде не обращалась в ноль. В отличие от
математических биллиардов здесь строго выпуклая область может иметь
многосвязную границу. В качестве иллюстрации приводится пример динамического
биллиарда с двумя степенями свободы, у которого биллиардная область строго
выпукла, и имеет три компоненты связности.
В четвертом разделе формулируются условия строгой
выпуклости для систем с двумя степенями свободы. В пятом и шестом разделах эти
условия применяются к плоскому биллирду в однородном и ньютоновском поле сил
тяжести. В качестве примера даются условия строгой выпуклости для эллиптического
биллиарда в однородном поле и для кругового в ньютоновском.
В седьмом разделе делается замечание, касающееся
наличия условно-периодических движений в системах, обладающих циклическими
интегралами, если в приведенной по Раусу системе существуют периодические
движения. В восьмом и девятом разделе даются примеры таких систем.
В восьмом разделе рассматривается движение
плоского тела с полостью. На плоскости движения расположен неподвижный “столбик”.
В начальный момент тело расположено так, что этот столбик попадает внутрь
полости тела. Тело двигается так, что граница полости ударяется о столбик.
Производится понижение порядка системы по Раусу, и находятся достаточные
условия существования периодических решений в приведенной системе.
В девятом разделе аналогичным образом
рассматривается движение плоского тела внутри круговой области.
В десятом разделе приводятся достаточные условия
существования двухзвенных периодических движений у динамических биллиардов с
несвязной границей. В качестве иллюстрации приводятся два примера. Первый
– движение тяжелого твердого тела с
неподвижной точкой, ударяющегося о две твердые, гладкие поверхности. Второй –
это система из трех или четырех физических маятников в каком-либо поле сил,
расположенных таким образом, чтобы никакие три из них не могли соударяться
одновременно.
Пусть динамический биллиард имеет 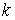 степеней свободы. В
локальных координатах степеней свободы. В
локальных координатах 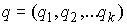 лагранжиан такой
системы представляет собой квадратичную функцию скоростей лагранжиан такой
системы представляет собой квадратичную функцию скоростей
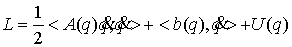 (1.1) (1.1)
где  – положительно
определенная матрица – положительно
определенная матрица 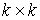 , и , и 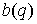 – – 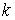 -мерный вектор. Силовое поле обладает силовой функцией -мерный вектор. Силовое поле обладает силовой функцией  . На движение системы наложено гладкое одностороннее
ограничение . На движение системы наложено гладкое одностороннее
ограничение 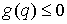 , удар о которое считается абсолютно упругим. , удар о которое считается абсолютно упругим.
В [7-8] показано, что движение
такой системы можно описать, используя т.н. уравнения с мерами. Если 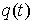 является движением
нашей системы, то найдется такая неотрицательная мера Лебега-Стилтьеса является движением
нашей системы, то найдется такая неотрицательная мера Лебега-Стилтьеса  , сосредоточенная в точках выхода траектории на границу, т.е.
там, где , сосредоточенная в точках выхода траектории на границу, т.е.
там, где  , что будут выполнены следующие уравнения Лагранжа с мерами , что будут выполнены следующие уравнения Лагранжа с мерами
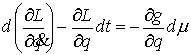 (1.2) (1.2)
В метрике кинетической энергии 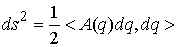 закон отражения при
единичном ударе о границу означает, что касательная составляющая скорости
сохраняется, а нормальная составляющая меняет свой знак. Более подробно с этими вопросами можно
ознакомиться в [2, 8-10]. закон отражения при
единичном ударе о границу означает, что касательная составляющая скорости
сохраняется, а нормальная составляющая меняет свой знак. Более подробно с этими вопросами можно
ознакомиться в [2, 8-10].
В такой системе выполняется
обобщенный закон сохранения энергии
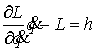 (1.3) (1.3)
Если члены линейные по скорости отсутствуют в лагранжиане (т.е. 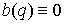 ), то, в соответствии с принципом Мопертюи-Лагранжа, выбрав
какое-либо значение константы ), то, в соответствии с принципом Мопертюи-Лагранжа, выбрав
какое-либо значение константы 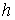 , мы можем свести движение нашей системы на этом уровне
энергии к движению точки с единичной скоростью по геодезическим линиям Римановой
метрики (метрики Якоби) , мы можем свести движение нашей системы на этом уровне
энергии к движению точки с единичной скоростью по геодезическим линиям Римановой
метрики (метрики Якоби)
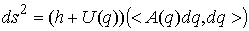 (1.4) (1.4)
Эта метрика отличается от метрики кинетической энергии только множителем,
поэтому закон отражения при единичном ударе о границу при таком рассмотрении не
меняется.
Если линейные по скорости члены присутствуют в
Лагранжиане, то мы можем ввести функционал действия по Мопертюи и метрику
Мопертюи в конфигурационном пространстве. Зафиксируем какое-либо значение
интеграла энергии 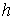 . Гладкая кривая . Гладкая кривая 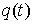 , на которой выполняется закон сохранения энергии (1.2) с
этой константой называется изоэнергетической.
Величина , на которой выполняется закон сохранения энергии (1.2) с
этой константой называется изоэнергетической.
Величина
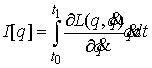 (1.5) (1.5)
для изоэнергетической кривой называется функционалом действия Мопертюи.
Безударные участки траекторий нашей системы являются экстремалями этого
функционала при фиксированном значении константы интеграла энергии и свободном
значении начального и конечного времени. Начальная и конечные точки при этом
тоже фиксируются. Более подробно этот вопрос освещен, например, в [11]. Выбрав
в конфигурационном пространстве две точки 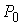 и и 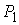 , мы можем поставить вопрос о нижней границе функционала действия
Мопертюи на множестве изоэнергетических кривых, соединяющих эти точки. , мы можем поставить вопрос о нижней границе функционала действия
Мопертюи на множестве изоэнергетических кривых, соединяющих эти точки.
Поскольку матрица кинетической
энергии положительно определена, то при фиксированном положении 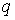 и произвольных
скоростях и произвольных
скоростях 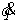 величина лагранжиана величина лагранжиана 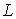 ограничена снизу.
Верхнюю границу этого ограничения (т.е. минимум ограничена снизу.
Верхнюю границу этого ограничения (т.е. минимум  ) обозначим ) обозначим 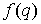 . Нетрудно получить, что она достигается при . Нетрудно получить, что она достигается при  . Подставив . Подставив 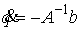 в (1.1) получаем в (1.1) получаем
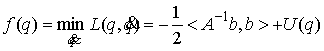
Таким образом, 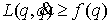 (1.6) (1.6)
В данной работе мы ограничимся случаем, когда константа интеграла энергии 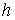 настолько велика, что
для некоторого настолько велика, что
для некоторого 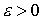 всюду в
конфигурационном пространстве выполняется неравенство всюду в
конфигурационном пространстве выполняется неравенство
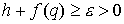 (1.7) (1.7)
Если линейные по скорости члены отсутствуют в лагранжиане, то 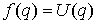 и это условие
совпадает с обычным условием невырожденности метрики Якоби (1.4) и это условие
совпадает с обычным условием невырожденности метрики Якоби (1.4) 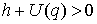 (1.8) (1.8)
Пользуясь тем, что на изоэнергетических кривых выполнено
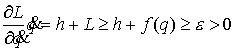 (1.9) (1.9)
Получаем, что нижняя граница функционала действия Мопертюи конечна и строго
положительна, при 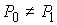 . Обозначим ее . Обозначим ее 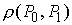 и назовем расстоянием
в метрике Мопертюи. и назовем расстоянием
в метрике Мопертюи.
Скорости изоэнергетических кривых ограничены по
модулю. Используя теоремы Хелли несложно показать, что на самом деле нижняя
граница функционала Мопертюи достигается на изоэнергетической кривой,
представляющей собой абсолютно непрерывную функцию, скорость которой ограничена
по модулю. Такие кривые будем называть минимальными.
На тех участках, где кривая не выходит на границу односторонних связей, она
представляет собой гладкую функцию, удовлетворяющую уравнения Лагранжа второго
рода. В общем случае она удовлетворяет уравнениям Лагранжа с мерами (1.2)
Из минимальности функции 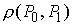 следует неравенство
треугольника: для любых точек следует неравенство
треугольника: для любых точек 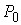 , , 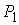 , , 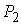 выполнено выполнено
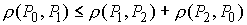 (1.10) (1.10)
В самом деле. Если бы было 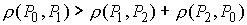 , то, склеив минимальные кривые, соединяющие пары точек , то, склеив минимальные кривые, соединяющие пары точек 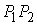 и и 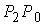 мы построим изоэнергетическую
кривую, соединяющую пару точек мы построим изоэнергетическую
кривую, соединяющую пару точек 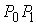 , на которой действие по Мопертюи меньше, чем , на которой действие по Мопертюи меньше, чем 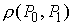 . .
Покажем, что локально неравенство треугольника является строгим. Мы будем понимать под
этим следующее. Пусть 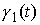 и и 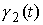 – две различные минимальные
кривые, исходящие из точки – две различные минимальные
кривые, исходящие из точки 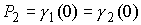 . Причем на границе области лежит разве что только точка . Причем на границе области лежит разве что только точка 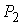 . Остальные точки этих кривых лежат внутри области. Тогда
можно подобрать такие малые положительные величины . Остальные точки этих кривых лежат внутри области. Тогда
можно подобрать такие малые положительные величины 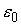 и и  , что неравенство (1.10) будет строгим , что неравенство (1.10) будет строгим
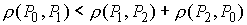 (1.11) (1.11)
здесь  , , 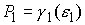 . .
Приведем схему доказательства.
В соответствии с принципом Мопертюи-Лагранжа-Якоби минимальные кривые
удовлетворяют уравнениям Лагранжа второго рода, т.е. являются траекториями
движения нашей механической системы. Константа интеграла энергии выбрана нами
настолько большой, что во время движения скорость нигде не обращается в ноль.
Поэтому для каждого положения 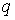 существуют ровно одна
минимальная кривая исходящая из существуют ровно одна
минимальная кривая исходящая из 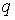 в данном направлении.
Значит, если две минимальные кривые соприкасаются и скорости у них направлены в
одну сторону, то эти кривые совпадают. в данном направлении.
Значит, если две минимальные кривые соприкасаются и скорости у них направлены в
одну сторону, то эти кривые совпадают.
Возьмем такую малую
окрестность точки 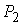 , чтобы в ней любую пару точек соединяла только одна
минимальная кривая (более подробно о существовании такой окрестности см. в
п.3). Тогда минимальная кривая, соединяющая , чтобы в ней любую пару точек соединяла только одна
минимальная кривая (более подробно о существовании такой окрестности см. в
п.3). Тогда минимальная кривая, соединяющая
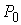 и и 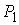 , будет подходить к кривым , будет подходить к кривым 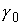 и и 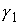 под ненулевым углом.
В окрестности точки под ненулевым углом.
В окрестности точки 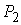 сделаем замену
координат таким образом, чтобы в этой точке матрица кинетической энергии стала
единичной. Тогда в окрестности точки сделаем замену
координат таким образом, чтобы в этой точке матрица кинетической энергии стала
единичной. Тогда в окрестности точки 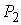 метрика будет
евклидовой с точностью до малых первого порядка по координатам. А при
интегрировании функционала действия отклонение будет иметь уже второй порядок
по координатам. Для евклидовой метрики неравенство треугольника будет строгим,
а величина рассогласования в неравенстве будет малой первого порядка по
координатам. Значит, рассогласование сохранится и в неевклидовом случае в
достаточно малой координатной окрестности. метрика будет
евклидовой с точностью до малых первого порядка по координатам. А при
интегрировании функционала действия отклонение будет иметь уже второй порядок
по координатам. Для евклидовой метрики неравенство треугольника будет строгим,
а величина рассогласования в неравенстве будет малой первого порядка по
координатам. Значит, рассогласование сохранится и в неевклидовом случае в
достаточно малой координатной окрестности.
Заметим, что если кривые 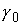 и и 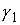 совпадают, строгость
неравенства треугольника является очевидной. Поскольку действие на кривой,
соединяющей совпадают, строгость
неравенства треугольника является очевидной. Поскольку действие на кривой,
соединяющей 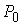 и и 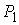 будет просто частью
одного из слагаемых в правой части (1.11) будет просто частью
одного из слагаемых в правой части (1.11)
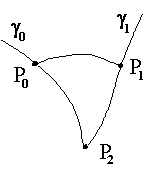
Рис.1.1. Если выбрать точки 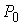 и и 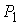 близкими к точке близкими к точке 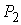 , то неравенство треугольника станет строгим , то неравенство треугольника станет строгим 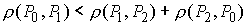
Мы будем в основном
рассматривать биллиарды с двумя степенями свободы, хотя многие рассуждения
проходят и в случае более высоких размерностей. Как уже говорилось в предыдущем
разделе, константу 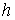 интеграла энергии
возьмем настолько большой, чтобы всюду было интеграла энергии
возьмем настолько большой, чтобы всюду было  . Это означает, что движение может происходить во всей
области . Это означает, что движение может происходить во всей
области 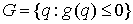 . Причем скорость движения нигде не обращается в ноль. В этом
случае любые две точки конфигурационного пространства можно соединить
изоэнергетической кривой, и, значит, и минимальной кривой. . Причем скорость движения нигде не обращается в ноль. В этом
случае любые две точки конфигурационного пространства можно соединить
изоэнергетической кривой, и, значит, и минимальной кривой.
Область 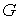 выпукла, если в
метрике Мопертюи для любых двух точек, лежащих в выпукла, если в
метрике Мопертюи для любых двух точек, лежащих в 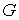 , кратчайшая линия, соединяющая их, не выходит на границу , кратчайшая линия, соединяющая их, не выходит на границу 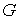 нигде, кроме, может
быть самих этих точек. нигде, кроме, может
быть самих этих точек.
Определение.
Область 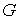 будем называть строго
выпуклой, если выполнены следующие два условия: будем называть строго
выпуклой, если выполнены следующие два условия:
·
В метрике
Мопертюи для любых двух точек, лежащих в 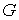 , кратчайшая линия, соединяющая их, не выходит на границу , кратчайшая линия, соединяющая их, не выходит на границу 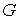 нигде, кроме, может
быть самих этих точек. нигде, кроме, может
быть самих этих точек.
·
Если
начальная или конечная точка лежит на границе 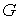 , то кратчайшая не касается границы в этой точке. , то кратчайшая не касается границы в этой точке.
Заметим, что для евклидовой метрики это
определение строгой выпуклости эквивалентно обычному.
Для математических биллиардов
со строго выпуклой областью движения известна теорема Биркгофа о существовании
периодических решений. Подробное ее доказательство для случая двух степеней
свободы можно найти в [1]. Для натуральных механических систем, у которых в
лагранжиане отсутствуют члены линейные по скоростям теорема Биркгофа, почти в
неизменном виде может быть распространена на случай со строго выпуклой областью
возможного движения. Нестрого обосновать это можно, например, следующим образом.
Доказательство, приведенное в [1], использует только локальные утверждения.
Однако локально в окрестности данной точки можно выбрать такие координаты, в
которых метрическая матрица в данной
точке будет единичной. Кроме того, производные функции расстояния по
координатам будут отличаться от евклидового случая на бесконечно малую величину.
Теорема Биркгофа. Эту теорему мы формулируем, почти дословно повторяя [1]. Пусть область
возможного движения 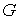 динамического
биллиарда является гладким компактным двухмерным многообразием с краем и строго
выпукла. Тогда для каждой связной компоненты границы и любых натуральных динамического
биллиарда является гладким компактным двухмерным многообразием с краем и строго
выпукла. Тогда для каждой связной компоненты границы и любых натуральных 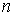 и и 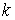 ( (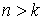 ) существуют по крайней мере две геометрически различные
периодические траектории динамического биллиарда, имеющие ) существуют по крайней мере две геометрически различные
периодические траектории динамического биллиарда, имеющие 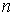 звеньев и совершающие звеньев и совершающие
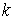 оборотов вокруг
данной компоненты границы. Для одной из этих траекторий соответствующая
замкнутая оборотов вокруг
данной компоненты границы. Для одной из этих траекторий соответствующая
замкнутая 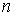 -звенная ломаная имеет максимальную длину среди всех близких
замкнутых -звенная ломаная имеет максимальную длину среди всех близких
замкнутых 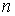 -звенных ломаных. Если этот максимум – изолированная
критическая точка функции длины ломаной на множестве -звенных ломаных. Если этот максимум – изолированная
критическая точка функции длины ломаной на множестве  -звенных ломаных, то ломаная, соответствующая другой периодической
траектории, изолированным максимумом функции длины не является. -звенных ломаных, то ломаная, соответствующая другой периодической
траектории, изолированным максимумом функции длины не является.
Замечание 2.1. В
отличие от математических биллиардов, в случае динамических биллиардов строго
выпуклая область возможного движения 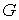 может иметь границу,
состоящую из нескольких связных компонент. В двухмерном случае каждая
компонента диффеоморфна окружности. Траектория может переходить от компоненты к
компоненте. В связи с этим Теорема Биркгофа может быть дополнена. Например, в
частном случае, когда траектория переходит от компоненты может иметь границу,
состоящую из нескольких связных компонент. В двухмерном случае каждая
компонента диффеоморфна окружности. Траектория может переходить от компоненты к
компоненте. В связи с этим Теорема Биркгофа может быть дополнена. Например, в
частном случае, когда траектория переходит от компоненты 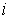 к компоненте к компоненте 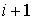 ровно один раз на периоде. ровно один раз на периоде.
Дополнение к Теореме Биркгофа. Пусть область возможного движения 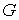 имеет имеет 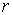 связных компонент.
Перенумеруем их в произвольном порядке. Выберем связных компонент.
Перенумеруем их в произвольном порядке. Выберем 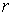 пар натуральных чисел пар натуральных чисел
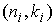 , , 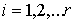 , , 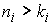 . Тогда существуют по крайней мере две геометрически
различные периодические траектории динамического биллиарда, имеющие . Тогда существуют по крайней мере две геометрически
различные периодические траектории динамического биллиарда, имеющие 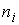 звеньев на компоненте звеньев на компоненте
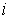 и совершающие и совершающие 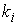 оборотов вокруг
данной компоненты границы. оборотов вокруг
данной компоненты границы.
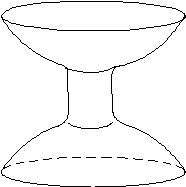
Рис.2.1 Пример строго выпуклой области, граница
которой имеет две компоненты связности.
Замечание 2.2 По всей видимости теорема Биркгофа верна и в
общем случае, для геодезических в метрике Мопертюи. Это будет предметом рассмотрения
отдельной работы. Здесь мы только отметим, что из неравенства треугольника,
справедливого для метрики Мопертюи, очевидным образом вытекает существование по
крайней мере 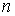 -звенных периодических траекторий максимальной длины,
совершающих один оборот. -звенных периодических траекторий максимальной длины,
совершающих один оборот.
В этом
разделе мы сформулируем необходимые и достаточные условия строгой выпуклости
области возможного движения для динамических биллиардов с любым числом степеней
свободы. Мы будем выводить их, основываясь не на геометрическом аппарате, а на
аппарате лагранжевой механики. При этом мы будем пользоваться следующим
замечательным фактом. Следуя [12], откалибруем лагранжиан сдвинув силовую
функцию на величину константы интеграла энергии: 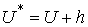 . Для нового лагранжиана можно считать, что . Для нового лагранжиана можно считать, что 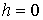 . Оставив старые обозначения мы можем написать, пользуясь
(1.3) . Оставив старые обозначения мы можем написать, пользуясь
(1.3) 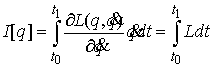
Это означает, что длина изоэнергетической кривой в метрике Мопертюи совпадает
с функционалом действия.
Кроме того, мы будем использовать то,
что на траекториях натуральных механических систем на достаточно малых
интервалах времени функционал действия достигает минимума на единственной
траектории. В самом деле. Расширим конфигурационное пространство, добавив еще
одну координату – время. Возьмем начальную точку 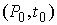 , Испустим из нее траектории нашей системы со всевозможными
скоростями. Они удовлетворяют уравнениям Лагранжа второго рода и, в силу
теоремы о выпрямлении для обыкновенных дифференциальных уравнений (см,
например, [13]) заполнят без взаимных пересечений некоторую окрестность
начальной точки. Через каждую ее точку будет проходить ровно одна траектория. С
другой стороны каждая точка этой окрестности может быть соединена с начальной
точкой кратчайшей кривой, которая тоже удовлетворяет тем же уравнениям Лагранжа
второго рода. Значит, решения же этих уравнений являются не только экстремалями,
но и минимальными кривыми. Более подробно этот вопрос рассмотрен, например, в [14]. , Испустим из нее траектории нашей системы со всевозможными
скоростями. Они удовлетворяют уравнениям Лагранжа второго рода и, в силу
теоремы о выпрямлении для обыкновенных дифференциальных уравнений (см,
например, [13]) заполнят без взаимных пересечений некоторую окрестность
начальной точки. Через каждую ее точку будет проходить ровно одна траектория. С
другой стороны каждая точка этой окрестности может быть соединена с начальной
точкой кратчайшей кривой, которая тоже удовлетворяет тем же уравнениям Лагранжа
второго рода. Значит, решения же этих уравнений являются не только экстремалями,
но и минимальными кривыми. Более подробно этот вопрос рассмотрен, например, в [14].
Рассмотрим движение механической системы,
соответствующей нашему динамическому биллиарду при фиксированной константе
интеграла энергии.
Утверждение 3.1
(Необходимое условие строгой выпуклости) Если биллиардная область 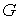 строго выпуклая, то
любое движение системы начавшееся на ее границе с начальной скоростью,
касающейся границы, остается на границе все время. В частности, для
динамического биллиарда с двумя степенями свободы граница строго выпуклая, то
любое движение системы начавшееся на ее границе с начальной скоростью,
касающейся границы, остается на границе все время. В частности, для
динамического биллиарда с двумя степенями свободы граница 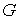 является одномерной
и, достаточное условие означает, что система может двигаться по границе все
время, не сходя с нее. является одномерной
и, достаточное условие означает, что система может двигаться по границе все
время, не сходя с нее.
Доказательство.
Допустим противное, что 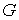 строго выпуклая
область, и строго выпуклая
область, и 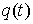 , , 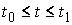 – траектория системы
до некоторого момента – траектория системы
до некоторого момента 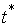 лежащая на границе лежащая на границе 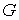 , а, начиная с этого момента, расположенная внутри , а, начиная с этого момента, расположенная внутри 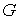 . Поскольку граница предполагается гладкой, то в момент . Поскольку граница предполагается гладкой, то в момент 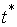 траектория касается
ее. Рассмотрим теперь отрезок траектории на интервале траектория касается
ее. Рассмотрим теперь отрезок траектории на интервале  , где , где 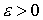 выбирается столь
малым, чтобы на нашей траектории функционал действия достигал минимума. Этой
траектории будет соответствовать кривая минимальной длины в метрике
Мопертюи-Лагранжа, которая вся, кроме начальной точки, лежит внутри выбирается столь
малым, чтобы на нашей траектории функционал действия достигал минимума. Этой
траектории будет соответствовать кривая минимальной длины в метрике
Мопертюи-Лагранжа, которая вся, кроме начальной точки, лежит внутри 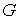 , а в начальной точке касается границы , а в начальной точке касается границы 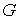 . Это противоречит строгой выпуклости . Это противоречит строгой выпуклости 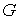
Определение.
Движение нашей механической системы будем называть граничным, если его
траектория все время остается на границе области 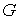 . .
Рассмотрим
теперь достаточное условие строгой выпуклости. Пусть 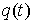 , , 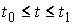 – траектория системы,
лежащая на границе – траектория системы,
лежащая на границе 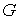 . Граница области . Граница области 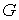 задается (локально)
уравнением задается (локально)
уравнением 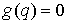 и в каждый момент
времени система двигается под воздействием обобщенной реакции связи и в каждый момент
времени система двигается под воздействием обобщенной реакции связи 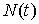
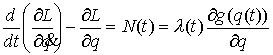 (3.1) (3.1)
Для того, чтобы траектория не сходила с границы, необходимо, чтобы реакция
не была направлена наружу области 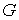 , т.е. чтобы в любой момент времени было , т.е. чтобы в любой момент времени было 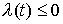 . .
Определение. Одностороннее
ограничение 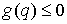 назовем невырожденным,
если всюду на поверхности назовем невырожденным,
если всюду на поверхности 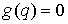 , кроме, может быть, счетного числа точек выполняется условие , кроме, может быть, счетного числа точек выполняется условие
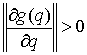 . .
Мы рассматриваем только
невырожденные односторонние ограничения.
Утверждение 3.2
(Достаточное условие строгой выпуклости) Пусть одностроннее ограничение
невырождено и пусть любое движение системы начавшееся на границе с начальной
скоростью, касающейся границы, остается на границе все время (т.е. является
граничным). Если на любом граничном движении системы обобщенная реакция связи
направлена внутрь области 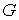 и нигде не обращается
в ноль (т.е. и нигде не обращается
в ноль (т.е. 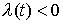 ), то область возможного движения системы ), то область возможного движения системы 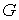 является строго выпуклой. является строго выпуклой.
Доказательство.
Допустим, что какая-либо кратчайшая кривая выходит на границу в своей
внутренней точке. Тогда она должна подходить по касательной к границе в этой
точке. В самом деле. Допустим, что траектория подходит к границе не по
касательной, тогда в этой точке скорость должна претерпевать скачок (в
противном случае будет протыкание границы). Траектория терпит излом и в его
окрестности по строгому неравенству треугольника (см. п.1) длину кратчайшей
можно было бы уменьшить.
Первое условие доказываемого утверждения означает,
что, если кратчайшая касается границы области 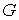 в какой-точке, то она
все время остается на границе, т.е. является граничной траекторией. Значит
минимальные кривые не могут выходить на границу в своей внутренней точке, если
начальная или конечная точка не лежит на ней. в какой-точке, то она
все время остается на границе, т.е. является граничной траекторией. Значит
минимальные кривые не могут выходить на границу в своей внутренней точке, если
начальная или конечная точка не лежит на ней.
Пусть теперь 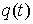 , , 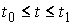 – граничная траектория
системы. Покажем, что она не является кратчайшей, т.е. не минимизирует (даже
локально) функционал действия. Построим кривую с теми же граничными условиями,
на которой функционал действия будет меньше. Возьмем гладкую функцию – граничная траектория
системы. Покажем, что она не является кратчайшей, т.е. не минимизирует (даже
локально) функционал действия. Построим кривую с теми же граничными условиями,
на которой функционал действия будет меньше. Возьмем гладкую функцию  , , 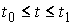 , обращающуюся в ноль на концах и положительную внутри интервала
(например, , обращающуюся в ноль на концах и положительную внутри интервала
(например, 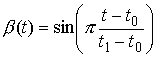 ). Рассмотрим семейство кривых ). Рассмотрим семейство кривых 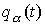
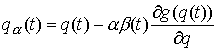 (3.2) (3.2)
Для достаточно малых неотрицательных
значений параметра 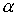 все эти кривые будут
лежать в все эти кривые будут
лежать в 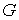 и, кроме того, и, кроме того, 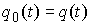 . Обозначим . Обозначим 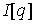 – функционал действия – функционал действия
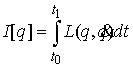 . Тогда, разлагая . Тогда, разлагая 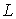 в ряд и, пользуясь
остаточным членом в форме Лагранжа, получаем при в ряд и, пользуясь
остаточным членом в форме Лагранжа, получаем при 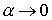
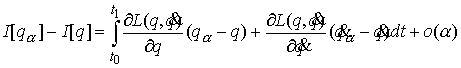
Используя, как обычно формулу
интегрирования по частям получаем
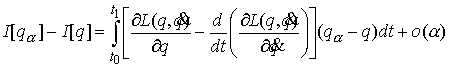
Применив (3.1-2) получим
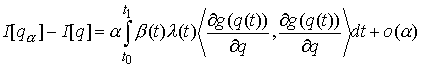
Втрое условие нашего утверждения означает, что  . Отсюда следует, что для малых значений . Отсюда следует, что для малых значений 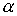 будет будет 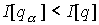 , т.е. функционал действия на кривой , т.е. функционал действия на кривой 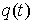 не минимален. Это
завершает доказательство утверждения 3.2. не минимален. Это
завершает доказательство утверждения 3.2.
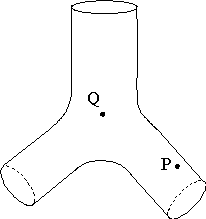
Рис.
3.1. Пример строго выпуклой области биллиарда с тремя связными компонентами
границы. В центре располагается положительный заряд 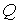 . Такой же заряд размещается на материальной точке . Такой же заряд размещается на материальной точке 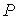 , движущейся по поверхности, склеенной из трех цилиндров. , движущейся по поверхности, склеенной из трех цилиндров.
Пример. Можно
сразу привести пример системы, для которой выполнены достаточные условия строгой выпуклости. Рассмотрим поверхность,
склеенную из трех цилиндров. В центре располагается положительный заряд 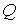 . Такой же заряд размещается на материальной точке . Такой же заряд размещается на материальной точке 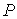 , движущейся по поверхности. Граница биллиардной области
состоит из трех окружностей. Электростатическая сила отталкивания обеспечит
отрицательную реакцию связи при движении по граничным окружностям с любой
скоростью. Значит, биллиардная область является строго выпуклой при любой
положительной константе интеграла энергии, достаточной для перехода от одной
граничной окружности к любой другой. , движущейся по поверхности. Граница биллиардной области
состоит из трех окружностей. Электростатическая сила отталкивания обеспечит
отрицательную реакцию связи при движении по граничным окружностям с любой
скоростью. Значит, биллиардная область является строго выпуклой при любой
положительной константе интеграла энергии, достаточной для перехода от одной
граничной окружности к любой другой.
Следствие 3.1
Рассмотрим множество 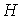 значений константы
интеграла энергии значений константы
интеграла энергии 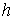 , для которых выполнены условия утверждения 3.2 и,
следовательно, область возможного движения , для которых выполнены условия утверждения 3.2 и,
следовательно, область возможного движения 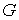 является строго
выпуклой. Если область является строго
выпуклой. Если область 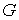 компактна, то
множество компактна, то
множество 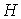 открыто на числовой
прямой. Это следствие того, что множитель открыто на числовой
прямой. Это следствие того, что множитель  в реакции однозначно
и гладко зависит от параметров движения (см., например [11]). Поэтому, при
компактном в реакции однозначно
и гладко зависит от параметров движения (см., например [11]). Поэтому, при
компактном  , минимальное возможное по модулю значение множителя , минимальное возможное по модулю значение множителя 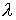 отлично от нуля и
достаточные условия продолжают выполняться при малых шевелениях параметров
системы. отлично от нуля и
достаточные условия продолжают выполняться при малых шевелениях параметров
системы.
Следствие 3.2
Если область движения математического биллиарда строго выпукла, то она
останется таковой и при наложении любого не слишком большого силового поля.
Следствие 3.3. Из
утверждения 3.2 виден способ проверки строгой выпуклости областей движения для
динамических биллиардов с двумя степенями свободы. В компактном случае граница
области топологически представляет собой семейство одномерных окружностей. При
некоторых значениях константы интеграла энергии 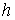 по всем этим
окружностям может происходить граничное движение. Это является необходимым
условием строгой выпуклости области движения. Если это имеет место для
изолированного значения по всем этим
окружностям может происходить граничное движение. Это является необходимым
условием строгой выпуклости области движения. Если это имеет место для
изолированного значения 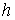 , то, как это видно из предыдущего следствия, область
возможного движения не является строго выпуклой. Если это происходит на целом
отрезке значений , то, как это видно из предыдущего следствия, область
возможного движения не является строго выпуклой. Если это происходит на целом
отрезке значений 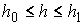 , то для значений , то для значений 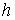 , лежащих внутри этого интервала имеет смысл проверить
величину реакции односторонней связи. , лежащих внутри этого интервала имеет смысл проверить
величину реакции односторонней связи.
Замечание 3.1
Проверку знака множителя 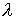 в реакции удобно
производить следующим образом. Домножив обе части (3.1) на в реакции удобно
производить следующим образом. Домножив обе части (3.1) на 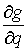 получим, что знак получим, что знак 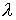 совпадает со знаком
величины совпадает со знаком
величины  . Отметим сразу, . Отметим сразу,  является ковектором,
поэтому для получения формы, не зависящей от выбора системы координат,
необходимо умножать на вектор является ковектором,
поэтому для получения формы, не зависящей от выбора системы координат,
необходимо умножать на вектор 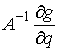 . Здесь . Здесь 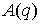 – положительно
определенная симметричная матрица кинетической энергии, значит – положительно
определенная симметричная матрица кинетической энергии, значит 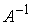 тоже является
симметричной, положительно определенной и знак тоже является
симметричной, положительно определенной и знак 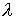 совпадает со знаком
величины совпадает со знаком
величины
 (3.3) (3.3)
который должен быть отрицательным.
Рассмотрим более подробно случай двух степеней
свободы. Обозначим для краткости локальные координаты координаты  , тогда имеем , тогда имеем
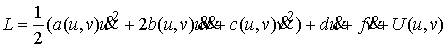
Уравнения Лагранжа второго рода имеют вид
(*) 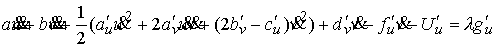 (4.1) (4.1)
(**) 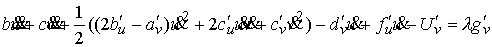 (4.2) (4.2)
Проделав с ними следующую линейную комбинацию
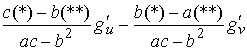 (4.3) (4.3)
получим в левой части в точности выражение (3.3). Оно будет иметь вид
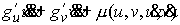 (4.4) (4.4)
где  – функция,
квадратичная по скоростям. Знак этой величины должен быть отрицательным. Для
граничного движения имеем – функция,
квадратичная по скоростям. Знак этой величины должен быть отрицательным. Для
граничного движения имеем 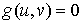 . Значит . Значит
 , , 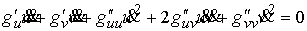 (4.5) (4.5)
Исключив из (4.4) члены с ускорениями получим, что нам необходимо выполнение
неравенства
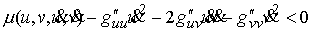 (4.6) (4.6)
Далее, интеграл энергии имеет вид
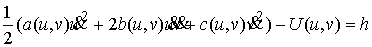 (4.7) (4.7)
Пусть, например, 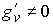 , тогда существует , тогда существует 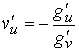 и, из интеграла
энергии получаем и, из интеграла
энергии получаем  , , 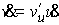 . Введя величину . Введя величину 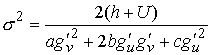 (4.8) (4.8)
эти выражения можно привести к симметричному виду
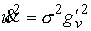 , , 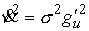 (4.9) (4.9)
Отсюда и из первого уравнения (4.5) получаем
 (4.10) (4.10)
При помощи этих выражений мы можем исключить скорости из (4.6) и у нас
получится условие строгой выпуклости, содержащее только координаты
Для
плоских биллиардов в потенциальном силовом поле проверку отрицательности
реакции граничного движения можно проводить, пользуясь очевидными механическими
соображениями. Следующая формула дает выражение для центробежной силы: 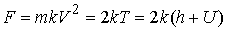 , где , где 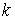 – кривизна граничной
кривой, – кривизна граничной
кривой, 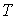 – кинетическая
энергия точки. Эта сила должна быть больше, чем проекция активной силы на
нормаль к кривой – кинетическая
энергия точки. Эта сила должна быть больше, чем проекция активной силы на
нормаль к кривой
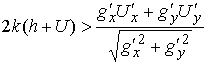
Рассмотрим движение
материальной точки единичной массы в плоскости  в однородном поле
тяжести в однородном поле
тяжести 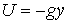 . Пусть движение ограничено областью . Пусть движение ограничено областью  . Выведем условия строгой выпуклости этой области. Воспользуемся
сначала полным методом. В данном случае . Выведем условия строгой выпуклости этой области. Воспользуемся
сначала полным методом. В данном случае 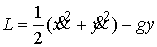 . Уравнения Лагранжа второго рода для граничной траектории
имеют вид . Уравнения Лагранжа второго рода для граничной траектории
имеют вид
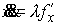 , , 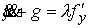
Нас интересует выполнение неравенства
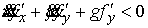
Используя второе уравнение (3.8) получаем
 (5.1) (5.1)
В нашем случае 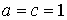 , , 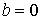 , поэтому формулы (4.8) дают , поэтому формулы (4.8) дают
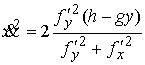 , , 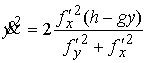 (5.2) (5.2)
Отсюда сразу видно, что необходимо, чтобы было 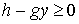
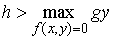 (5.3) (5.3)
Из соотношений (5.2) и первого уравнения (4.5) получаем 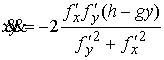 . Подставив все это в (5.1) получаем следующее условие
строгой выпуклости . Подставив все это в (5.1) получаем следующее условие
строгой выпуклости
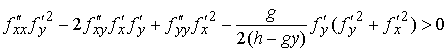 (5.4) (5.4)
Заметим, что это условие фактически определяет знак геодезической кривизны
границы области биллиарда в метрике Якоби.
Таким образом условие
строгой выпуклости области движения плоского биллиарда в однородном поле
тяжести дают условия (5.3-4).
Возьмем в качестве примера эллиптический биллиард,
для которого 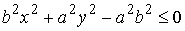 . Условие (5.3) дает здесь . Условие (5.3) дает здесь 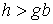 . Условия (5.4) выглядит следующим образом . Условия (5.4) выглядит следующим образом
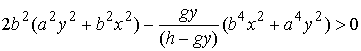
Это неравенство должно выполняться на
границе области, т.е., в точках, где 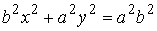 . Поэтому его можно упростить . Поэтому его можно упростить
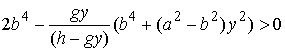 , , 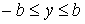
Из качественных соображений ясно, что реакция связи минимальна, когда точка
находится в верхнем положении, т.е. при 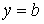 . В этом случае наше неравенство принимает следующий вид . В этом случае наше неравенство принимает следующий вид
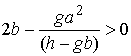 или или 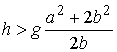
В данном случае результат можно было бы
получить из простых соображений. При движении по эллипсу реакция минимальна в
его верхней точке. Для того, чтобы реакция не обращалась в ноль в верхней точке
эллипса, центростремительное ускорение должно превышать ускорение силы тяжести,
т.е., 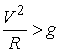 , где , где 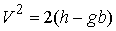 – квадрат скорости в
верхней точке эллипса, а – квадрат скорости в
верхней точке эллипса, а 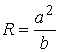 – радиус кривизны
эллипса в этой точке. Таким образом, необходимо, чтобы было – радиус кривизны
эллипса в этой точке. Таким образом, необходимо, чтобы было
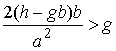 , или , или 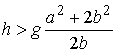
Мы получили тот же результат.
Рассмотрим движение материальной точки единичной
массы в плоскости 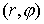 (в полярных координатах)
в ньютоновском поле сил (в полярных координатах)
в ньютоновском поле сил 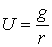 . Пусть движение ограничено областью . Пусть движение ограничено областью 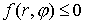 . Выведем условия строгой выпуклости этой области. В данном
случае . Выведем условия строгой выпуклости этой области. В данном
случае 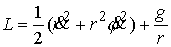 . Уравнения Лагранжа второго рода для граничной траектории
имеют вид . Уравнения Лагранжа второго рода для граничной траектории
имеют вид
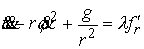 , , 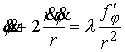
Нас интересует выполнение неравенства 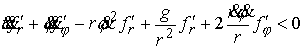 . В простейшем случае, когда граница представляет собой
окружность . В простейшем случае, когда граница представляет собой
окружность 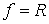 , это неравенство выглядит так: , это неравенство выглядит так: 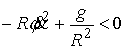 , или , или 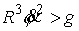 . К нему надо добавить закон сохранения энергии для
граничного движения . К нему надо добавить закон сохранения энергии для
граничного движения  , откуда , откуда 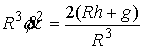 . Поэтому условие строгой выпуклости можно переписать так: . Поэтому условие строгой выпуклости можно переписать так: 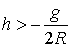 . .
Рассмотрим теперь общий случай. Используя второе
уравнение (4.5) получаем 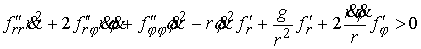 (6.1) (6.1)
В нашем случае 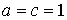 , , 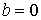 , поэтому формулы (4.8) дают , поэтому формулы (4.8) дают
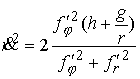 , , 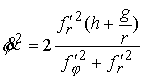 (6.2) (6.2)
Отсюда сразу видно, что необходимо, чтобы было 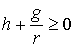 , т.е. , т.е.
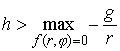 (6.3) (6.3)
Из соотношений (6.2) и первого уравнения (4.5) получаем
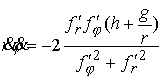 (6.4) (6.4)
Подставив все это в (6.1) получаем следующее условие строгой выпуклости
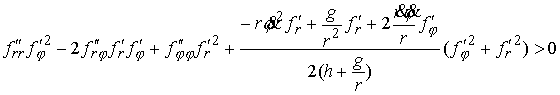 (6.5) (6.5)
Заметим, что это условие фактически определяет знак геодезической кривизны
границы области биллиарда в метрике Якоби.
Таким образом, условие
строгой выпуклости области движения плоского биллиарда в ньютоновском поле сил
дают условия (6.3, 6.5).
В данном разделе мы сделаем одно замечание,
касающееся возникновения условно-периодических движений. Пусть система
лагранжева система без односторонних ограничений обладает круговой симметрией и
ей соответствует циклическая координата  и циклический интеграл. и циклический интеграл.
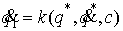 (7.1) (7.1)
где 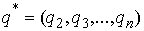 – позиционные
координаты, а – позиционные
координаты, а 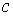 – константа интеграла. – константа интеграла.
Произведем понижение ее
порядка по Раусу. Пусть приведенная система имеет периодическое решение 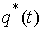 с периодом с периодом 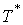 . Тогда исходная система имеет двухчастотное движение
периодическое, или условно-периодическое. При изменении начального значения
координаты . Тогда исходная система имеет двухчастотное движение
периодическое, или условно-периодическое. При изменении начального значения
координаты  все такие решения
заметут в фазовом пространстве инвариантный двухмерный тор. все такие решения
заметут в фазовом пространстве инвариантный двухмерный тор.
Точно такая же ситуация имеет
место и для динамических биллиардов. Это лагранжева система с односторонними
ограничениями 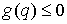 . Если эти
ограничения допускают ту же круговую симметрию, в системе так же можно
произвести понижение порядка по Раусу (подробнее этот вопрос рассматривается в [9-10]). Возьмем два экземпляра фазового
пространства нашего биллиарда и склеим их по границе так, чтобы траектории
биллиарда стали непрерывными. Это означает, что граничная точка . Если эти
ограничения допускают ту же круговую симметрию, в системе так же можно
произвести понижение порядка по Раусу (подробнее этот вопрос рассматривается в [9-10]). Возьмем два экземпляра фазового
пространства нашего биллиарда и склеим их по границе так, чтобы траектории
биллиарда стали непрерывными. Это означает, что граничная точка 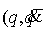 ) склеивается с граничной точкой ) склеивается с граничной точкой 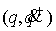 таким образом, чтобы
для скоростей таким образом, чтобы
для скоростей 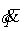 и и 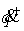 выполнялся закон абсолютно
упругого соударения. В получившемся удвоенном пространстве мы получим
инвариантный двухмерный тор с условно-периодическим движением. Однако движение
будет кусочно-гладким. выполнялся закон абсолютно
упругого соударения. В получившемся удвоенном пространстве мы получим
инвариантный двухмерный тор с условно-периодическим движением. Однако движение
будет кусочно-гладким.
Если система обладает не одной, а несколькими
круговыми симметриями, то, естественно, мы будем получать многочастотные
условно-периодические движения и многомерные инвариантные торы.
В следующих разделах мы приведем
несколько примеров указанного рода.
Рассмотрим плоское тело, свободно двигающееся по
гладкой плоскости. Внутри тела вырезана связная некая область 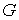 . Пусть в плоскости задана абсолютная система координат . Пусть в плоскости задана абсолютная система координат 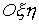 и в точке и в точке 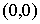 установлен “столбик”. В начальный момент тело расположено так, что
этот столбик попадает внутрь области установлен “столбик”. В начальный момент тело расположено так, что
этот столбик попадает внутрь области 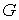 . На движение тела наложена односторонняя связь, состоящая в
том, что “столбик” не выходит за пределы области . На движение тела наложена односторонняя связь, состоящая в
том, что “столбик” не выходит за пределы области 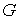 в теле. Толщину “столбика” считаем нулевой. Говоря другими словами, тело
двигается так, что граница области в теле. Толщину “столбика” считаем нулевой. Говоря другими словами, тело
двигается так, что граница области 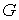 ударяется о точку ударяется о точку 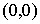 . .
Дадим формальное описание этой системы. Свяжем с
телом систему координат 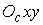 , начало которой , начало которой 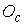 совпадает с центром
тяжести тела. Будем считать, что область совпадает с центром
тяжести тела. Будем считать, что область 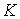 в теле задается
неравенством в теле задается
неравенством
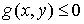 (8.1) (8.1)
где 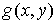 – гладкая функция,
градиент которой не обращается в ноль нигде на границе области – гладкая функция,
градиент которой не обращается в ноль нигде на границе области 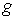 , т.е. в точках , т.е. в точках 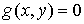 . Мы будем также считать, что центр тяжести тела не лежит на
границе области . Мы будем также считать, что центр тяжести тела не лежит на
границе области 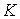 , т.е. что , т.е. что 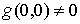 . .
Положение
тела можно было бы описывать тройкой координат 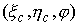 , где , где  – координаты центра
масс тела – координаты центра
масс тела  в абсолютной системе,
а в абсолютной системе,
а 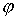 – угол наклона оси – угол наклона оси  связанной системы
координат по отношению к оси связанной системы
координат по отношению к оси 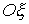 абсолютной системы.
Однако, мы будем использовать тройку абсолютной системы.
Однако, мы будем использовать тройку 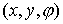 , где , где 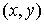 – координаты начала
абсолютной системы координат – координаты начала
абсолютной системы координат  в связанной системе. в связанной системе.
Переход от связанной системы
координат к абсолютной производится поворотом на угол 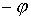 относительно относительно 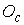 и сдвигом на вектор и сдвигом на вектор 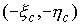 . Поэтому первая и вторая тройки координат связаны соотношениями . Поэтому первая и вторая тройки координат связаны соотношениями
 , , 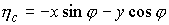 (8.2) (8.2)
а их скорости
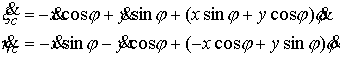
Обозначим 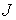 – центральный момент
инерции тела, а его массу – центральный момент
инерции тела, а его массу 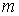 , для краткости записи, будем считать равной единице , для краткости записи, будем считать равной единице 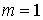 . По теореме Кенига кинетическая энергия тела . По теореме Кенига кинетическая энергия тела 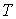 выражается соотношением выражается соотношением
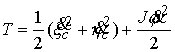 (8.3) (8.3)
или, в координатах 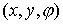
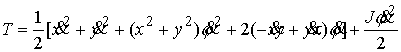
Для краткости записи перейдем к полярным координатам 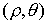 в системе связанной с
телом в системе связанной с
телом
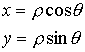 , , 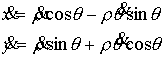 , , 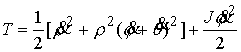
Сохраним обозначение односторонней связи: 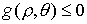 . .
Поскольку координата 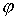 не входит в
кинетическую энергию и в описание односторонней связи, то она является
циклической (в смысле систем с односторонними связями [9]). Циклический интеграл имеет вид не входит в
кинетическую энергию и в описание односторонней связи, то она является
циклической (в смысле систем с односторонними связями [9]). Циклический интеграл имеет вид

Проводя исключение циклической координаты и
понижение порядка системы по Раусу, получаем
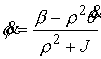 , , 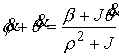
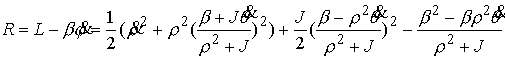
или
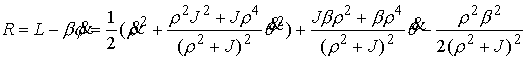
Координата  не входит в функцию
Рауса. Однако, она не является циклической, поскольку в общем случае входит в
уравнение границы односторонней связи не входит в функцию
Рауса. Однако, она не является циклической, поскольку в общем случае входит в
уравнение границы односторонней связи  . .
Найдем условия, при которых область движения
приведенной системы будет строго выпуклой. Воспользуемся результатами раздела 4
для систем с двумя степенями свободы. В обозначениях этого раздела имеем
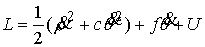 , , 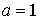 , , 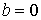 , , 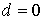 , ,
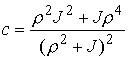 , , 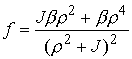 , , 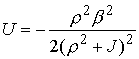
Интеграл энергии имеет вид 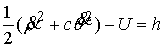 . Уравнения граничного движения приводятся к виду . Уравнения граничного движения приводятся к виду
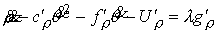 , , 
Значит

и нам надо исследовать выполнение неравенства
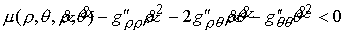 (8.4) (8.4)
Выражения (4.8-10) дают нам
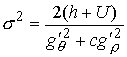 , , 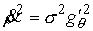 , , 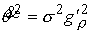 , , 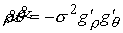 (8.5) (8.5)
Рассмотрим простой случай, когда граница
биллиардной области 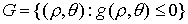 представляет собой
искаженную окружность представляет собой
искаженную окружность 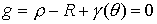 , где , где 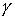 – – 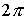 -периодическая функция и -периодическая функция и 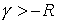 . Последнее неравенство гарантирует отсутствие точек
самопересечения границы. Мы будем считать, что . Последнее неравенство гарантирует отсутствие точек
самопересечения границы. Мы будем считать, что 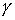 дважды непрерывно
дифференцируемая функция. Это возможно только в том случае, когда любой малый
отрезок границы виден из центра тяжести под ненулевым углом. Отсюда следует,
что центр тяжести тела лежит внутри области дважды непрерывно
дифференцируемая функция. Это возможно только в том случае, когда любой малый
отрезок границы виден из центра тяжести под ненулевым углом. Отсюда следует,
что центр тяжести тела лежит внутри области 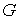 . В противном случае из центра тяжести можно провести
касательную к некоторой точке границы и в ней будет . В противном случае из центра тяжести можно провести
касательную к некоторой точке границы и в ней будет 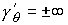 . Кроме того, область . Кроме того, область 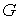 должна быть
звездчатой, т.е. каждая точка границы должна быть видна из центра тяжести. Обозначим должна быть
звездчатой, т.е. каждая точка границы должна быть видна из центра тяжести. Обозначим 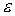 , , 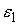 , , 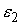 максимальные значения
модулей величин максимальные значения
модулей величин 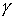 , , 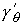 и и 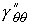 соответственно на
периоде соответственно на
периоде 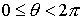 . .
В данном случае (8.5) выглядят следующим образом
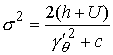 , ,  , , 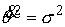 , , 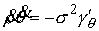
а неравенство (8.4) становится таким:
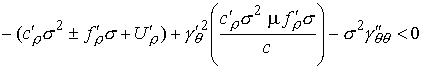 (8.6) (8.6)
или 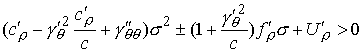 (8.7) (8.7)
Для краткости записи введем величину
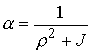 , , 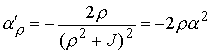 (8.8) (8.8)
Имеем
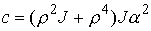 , , 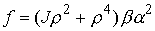 , , 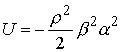
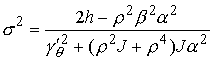 , , 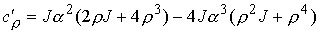 , ,
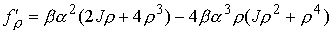 , , 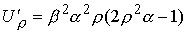
Заметим, что из выражения для 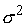 видно, что должно
быть видно, что должно
быть 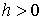 . .
Рассмотрим выполнение
неравенства (8.7) когда 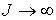 . При этом . При этом 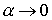 и и 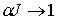 . С точностью до малых первого порядка имеем . С точностью до малых первого порядка имеем
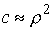 , , 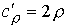 , , 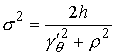 , , 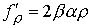 , , 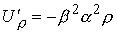
Подставив это в (8.7) получим, что, при больших 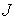 , для строгой выпуклости биллиардной области достаточно
выполнение неравенства , для строгой выпуклости биллиардной области достаточно
выполнение неравенства
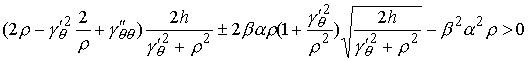
Поскольку при больших 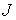 величина величина 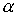 становится сколь
угодно малой, то для выполнения этого неравенства достаточно выполнение
неравенств становится сколь
угодно малой, то для выполнения этого неравенства достаточно выполнение
неравенств
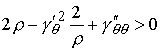 и и 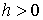
Первое неравенство должно выполняться на границе, т.е. при 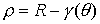 . .
Окончательно получаем, следующее утверждение.
Пусть нам заданы положительная
константа интеграла энергии 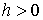 и любое значение
константы циклического интеграла и любое значение
константы циклического интеграла 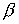 . Тогда при достаточно больших значениях момента инерции . Тогда при достаточно больших значениях момента инерции 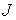 для строгой
выпуклости биллиардной области достаточно выполнения неравенства для строгой
выпуклости биллиардной области достаточно выполнения неравенства
 (8.9) (8.9)
В простейшем случае, когда область в теле представляет собой окружность с
центром в центре масс, имеем  , (8.9) становится тривиальным ( , (8.9) становится тривиальным ( ) и всегда выполняется. ) и всегда выполняется.
а)
б)
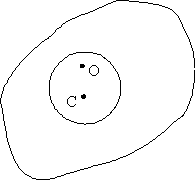
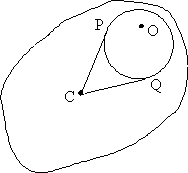
Рис.
8.1 Плоское тело с полостью. 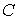 – центр тяжести тела. – центр тяжести тела.
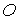 – неподвижный столбик
в плоскости движения тела. Граница тела упруго ударяется о столбик. а)Центр
тяжести находится внутри полости – возможна строгая выпуклости движения. б)
Центр тяжести находится внутри полости – возможна строгая выпуклости движения. – неподвижный столбик
в плоскости движения тела. Граница тела упруго ударяется о столбик. а)Центр
тяжести находится внутри полости – возможна строгая выпуклости движения. б)
Центр тяжести находится внутри полости – возможна строгая выпуклости движения.
Замечание. Мы
разобрали случай, когда центр тяжести находится внутри вырезанной в теле
области, как на рис 8.1-a). В
случае, же когда центр тяжести находится вне вырезанной в теле области (см.
рис. 8.1-b) мы фактически показали, что при тех же условиях область движения не
является строго выпуклой. В самом деле, проведем из центра тяжести касательную
к некоторой точке 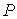 границы. В
окрестности этой точки величина границы. В
окрестности этой точки величина 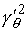 будет сколь угодно
большой. Поэтому неравенство поменяет знак и будет будет сколь угодно
большой. Поэтому неравенство поменяет знак и будет 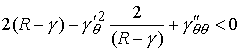 . В этом случае реакция связи для граничного движения в
окрестности точки . В этом случае реакция связи для граничного движения в
окрестности точки  будет направлена
наружу исходной области. И, значит, в исходной задаче граничное движение не
может продолжаться по всей границе, и будет с нее сходить по крайней мере в
окрестности точки будет направлена
наружу исходной области. И, значит, в исходной задаче граничное движение не
может продолжаться по всей границе, и будет с нее сходить по крайней мере в
окрестности точки  . Это и означает, что область не является строго выпуклой. . Это и означает, что область не является строго выпуклой.
 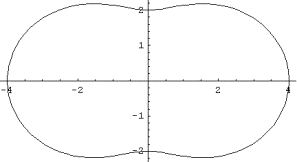
k=1 k=2
 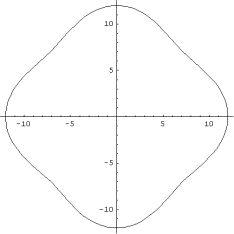
k=3 k=4
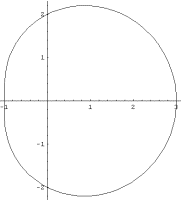
Рис. 8.2. Полости  в плоском теле. При заданном уровне энергии движения они становятся
строго выпуклыми при больших моментах инерции. в плоском теле. При заданном уровне энергии движения они становятся
строго выпуклыми при больших моментах инерции.
Пример.
Рассмотрим теперь один конкретный пример. Пусть  , где , где 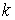 – натуральное число.
Поскольку – натуральное число.
Поскольку  и и 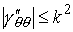 , из (8.8) вытекают следующие достаточные условия строгой
выпуклости: , из (8.8) вытекают следующие достаточные условия строгой
выпуклости:
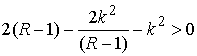 , или , или 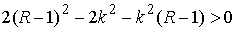
Значит, если 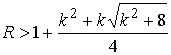 , то область возможного движения биллиарда строго выпукла
(для , то область возможного движения биллиарда строго выпукла
(для 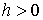 и больших значений и больших значений 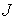 ). Приведем небольшой перечень приблизительных значений: ). Приведем небольшой перечень приблизительных значений:
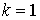 , , 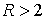 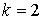 , , 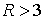 , ,  , , 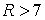
В общем случае, при 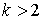 , заменив , заменив 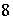 на на 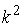 , получим следующую оценку , получим следующую оценку
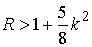
Рассмотрим плоское тело, свободно двигающееся по
гладкой плоскости внутри круга  радиуса радиуса 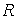 . В плоскости задана абсолютная система координат . В плоскости задана абсолютная система координат 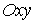 . Центр круга . Центр круга 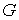 расположен в точке расположен в точке 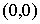 . Положение тела будем описывать полярными координатами его
центра тяжести . Положение тела будем описывать полярными координатами его
центра тяжести 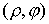 . Свяжем с телом какую-либо прямую, проходящую через его
центр тяжести. Ориентацию тела будем задавать углом . Свяжем с телом какую-либо прямую, проходящую через его
центр тяжести. Ориентацию тела будем задавать углом 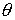 между этой прямой и
лучом, идущим из начала абсолютной системы координат в центр тяжести тела.
Граница тела имеет некоторую форму. Тело двигается так, что его граница не
выходит за пределы круга между этой прямой и
лучом, идущим из начала абсолютной системы координат в центр тяжести тела.
Граница тела имеет некоторую форму. Тело двигается так, что его граница не
выходит за пределы круга 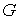 . Для выбранного способа описания ориентации тела это
ограничение не зависит от полярного угла . Для выбранного способа описания ориентации тела это
ограничение не зависит от полярного угла 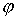 . Рассмотрим случай, когда тело не слишком большое по
размерам и ограничение можно описать одним неравенством . Рассмотрим случай, когда тело не слишком большое по
размерам и ограничение можно описать одним неравенством
 (9.1) (9.1)
где 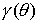 – гладкая функция. – гладкая функция.
Обозначим 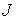 – центральный момент
инерции тела, а его массу – центральный момент
инерции тела, а его массу 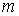 , для краткости записи, будем считать равной единице , для краткости записи, будем считать равной единице 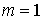 . По теореме Кенига кинетическая энергия тела . По теореме Кенига кинетическая энергия тела 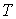 выражается соотношением выражается соотношением
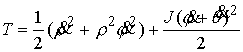
Поскольку координата 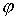 не входит в
кинетическую энергию и в описание односторонней связи, то она является
циклической (в смысле систем с односторонними связями [9]). Циклический интеграл имеет вид не входит в
кинетическую энергию и в описание односторонней связи, то она является
циклической (в смысле систем с односторонними связями [9]). Циклический интеграл имеет вид
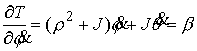
Проводя исключение циклической координаты и
понижение порядка системы по Раусу, получаем
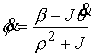 , , 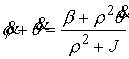
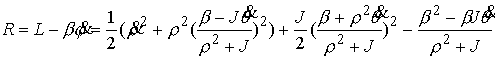
или
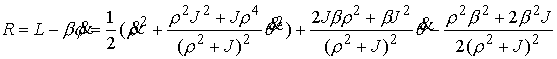
Координата 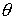 не входит в функцию
Рауса. Однако, она не является циклической, поскольку в общем случае входит в
уравнение границы односторонней связи не входит в функцию
Рауса. Однако, она не является циклической, поскольку в общем случае входит в
уравнение границы односторонней связи 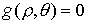 . Дальнейшие рассуждения почти дословно повторяют предыдущий
раздел. Найдем условия, при которых область движения приведенной системы будет
строго выпуклой. Воспользуемся результатами раздела 4 для систем с двумя
степенями свободы. В обозначениях этого раздела имеем . Дальнейшие рассуждения почти дословно повторяют предыдущий
раздел. Найдем условия, при которых область движения приведенной системы будет
строго выпуклой. Воспользуемся результатами раздела 4 для систем с двумя
степенями свободы. В обозначениях этого раздела имеем
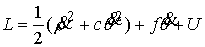 , , 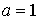 , , 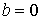 , , 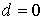 , ,
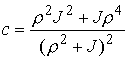 , , 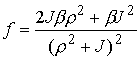 , , 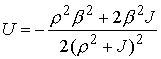
Интеграл энергии имеет вид 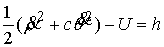 . Уравнения граничного движения приводятся к виду . Уравнения граничного движения приводятся к виду
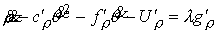 , , 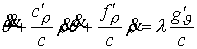
Значит 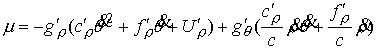 и нам надо исследовать выполнение неравенства и нам надо исследовать выполнение неравенства
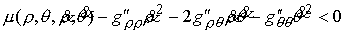 (9.4) (9.4)
Выражения (4.8-10) дают нам
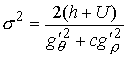 , , 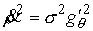 , , 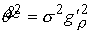 , , 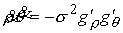 (9.5) (9.5)
а неравенство (9.4) становится таким:
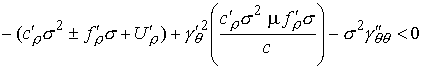 (9.6) (9.6)
или 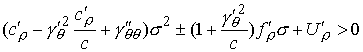 (9.7) (9.7)
Для краткости записи опять введем величину 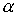 (8.8). Имеем (8.8). Имеем
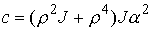 , , 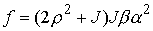 , , 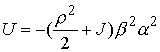 , ,
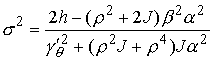 , , 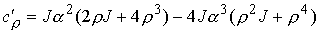 , ,
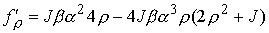 , , 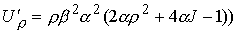
Заметим, что из выражения для 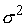 видно, что должно
быть видно, что должно
быть 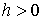 . .
Рассмотрим выполнение
неравенства (8.7) когда 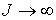 . При этом . При этом 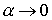 и и 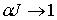 . С точностью до малых первого порядка имеем . С точностью до малых первого порядка имеем
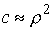 , , 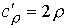 , , 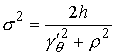 , , 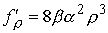 , , 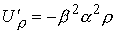
Подставив это в (8.7) получим, что, при
больших 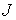 , для строгой выпуклости биллиардной области достаточно
выполнение неравенства , для строгой выпуклости биллиардной области достаточно
выполнение неравенства
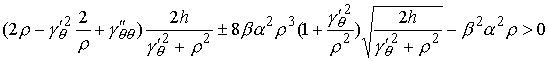
Поскольку при больших 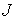 величина величина 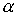 становится сколь
угодно малой, то для выполнения этого неравенства достаточно выполнение
неравенств становится сколь
угодно малой, то для выполнения этого неравенства достаточно выполнение
неравенств
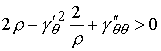 и и 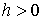
Первое неравенство должно выполняться на границе, т.е. при 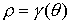 . .
Окончательно получаем,
следующее утверждение. Пусть нам заданы
положительная константа интеграла энергии 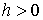 и любое значение
константы циклического интеграла и любое значение
константы циклического интеграла 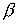 . Тогда при достаточно больших значениях момента инерции . Тогда при достаточно больших значениях момента инерции 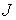 для строгой
выпуклости биллиардной области достаточно выполнения неравенства для строгой
выпуклости биллиардной области достаточно выполнения неравенства 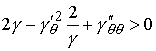 (9.8) (9.8)
В простейшем случае, когда в тело представляет
собой окружность радиуса  , имеем , имеем 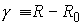 , (9.8) становится тривиальным ( , (9.8) становится тривиальным (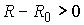 ) и всегда выполняется. ) и всегда выполняется.
В данном разделе мы рассмотрим аналоги теоремы
Биркгофа о существовании двухзвенных периодических движений для некоторых невыпуклых биллиардов.
Рассуждения, проводимые здесь, аналогичны тем, что использовались в [15] для натуральных механических систем при
поиске двухзвенных движений между точками границы области возможного движения.
Такие движения были названы либрациями. Рассмотрим сначала математический биллиард
на плоскости с невыпуклой областью движения 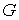 . Границу . Границу 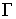 области будем считать
гладкой, класса области будем считать
гладкой, класса 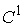 , а саму область – компактной. Пусть граница , а саму область – компактной. Пусть граница 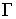 имеет две компоненты
связности. имеет две компоненты
связности.
Двухзвенное движение. Покажем, что всегда существует по крайней мере одно двухзвенное периодическое движение. Это означает, что на
границе области движения найдутся две точки 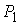 и и 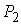 такие, что
внутренность отрезка такие, что
внутренность отрезка 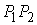 не имеет общих точек
с границей не имеет общих точек
с границей 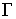 , а сам отрезок ортогонален границе в своих конечных точках.
Двухзвенное движение – это периодическое движение по отрезку , а сам отрезок ортогонален границе в своих конечных точках.
Двухзвенное движение – это периодическое движение по отрезку 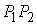 между его граничными
точками. между его граничными
точками.
Доказательство.
Обозначим 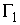 и и 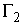 компоненты связности
границы и компоненты связности
границы и 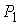 , , 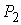 – такие точки,
лежащие на них, расстояние между которыми минимально. Очевидно, что отрезок – такие точки,
лежащие на них, расстояние между которыми минимально. Очевидно, что отрезок 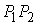 не имеет других общих
точек с границей, кроме своих концов. Кроме того, в этих точках он ортогонален
границе. В самом деле. Допустим, касательный вектор к границе в точке не имеет других общих
точек с границей, кроме своих концов. Кроме того, в этих точках он ортогонален
границе. В самом деле. Допустим, касательный вектор к границе в точке 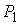 имеет ненулевую
проекцию на отрезок имеет ненулевую
проекцию на отрезок 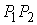 . Тогда мы можем немного сместиться по границе так, что
расстояние до точки . Тогда мы можем немного сместиться по границе так, что
расстояние до точки 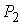 уменьшится. Если при
смещении появятся дополнительные точки пересечения с границей, то расстояние
тем более станет меньше. уменьшится. Если при
смещении появятся дополнительные точки пересечения с границей, то расстояние
тем более станет меньше.
Если граница имеет 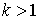 компонент связности,
то указанные выше рассуждения без существенных изменений можно провести для
каждой ее связной компоненты и ближайшей к ней другой компоненты. Для каждой
связной компоненты границы найдется двухзвенное периодическое движение, начинающееся
на ней и имеющее минимальную длину. Если мы возьмем любую пару компонент, то
между ними можно провести двухзвенник минимальной длины. Однако, он может
пересекаться с другими компонентами границы и, поэтому не будет двухзвенной
периодической траекторией. Покажем, что общее число двухзвенных периодических
траекторий не менее, чем компонент связности,
то указанные выше рассуждения без существенных изменений можно провести для
каждой ее связной компоненты и ближайшей к ней другой компоненты. Для каждой
связной компоненты границы найдется двухзвенное периодическое движение, начинающееся
на ней и имеющее минимальную длину. Если мы возьмем любую пару компонент, то
между ними можно провести двухзвенник минимальной длины. Однако, он может
пересекаться с другими компонентами границы и, поэтому не будет двухзвенной
периодической траекторией. Покажем, что общее число двухзвенных периодических
траекторий не менее, чем 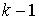 . .
Составим граф, вершины которого соответствуют
компонентам связности границы, а ребра – минимальным по длине двухзвенным
движениям. Покажем, что этот граф является связным. Допустим, что это не так, и
существует две группы вершин, между которыми нет ребра графа. Тогда компоненты
связности границы разбиваются на два множества соответствующих двум компонентам
нашего графа. Минимальный двухзвенник, соединяющий два этих множества, не может
иметь внутренних точек, попадающих на границу. Иначе он не был бы минимальным.
Значит, он должен присутствовать в графе и соединять обе его компоненты. Мы
пришли к противоречию. Поскольку граф связен и число его вершин равно 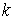 , то число ребер (т.е. двухзвенных периодических траекторий )
не может быть меньше, чем , то число ребер (т.е. двухзвенных периодических траекторий )
не может быть меньше, чем 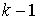 . .
Пример 10.0. В
качестве возможного примера двухзвенных движений упомянем о движении тяжелого
твердого тела вокруг неподвижной точки.
Тело имеет произвольную (гладкую) форму. Его движение ограничено двумя какими-либо
гладкими поверхностями  и и  . Тело может двигаться с одной или другой стороны от
поверхностей . Тело может двигаться с одной или другой стороны от
поверхностей  так, чтобы
поверхность тела не проходила через них. Удары считаем абсолютно упругими. Это
– динамический биллиард с тремя степенями свободы. В соответствии с доказанным
утверждением, если константа интеграла энергии такова, что область возможного
движения связна и содержит границу, то существует по крайней мере одно двухзвенное
периодическое движение. Например, при движении по инерции такое имеет место всегда. так, чтобы
поверхность тела не проходила через них. Удары считаем абсолютно упругими. Это
– динамический биллиард с тремя степенями свободы. В соответствии с доказанным
утверждением, если константа интеграла энергии такова, что область возможного
движения связна и содержит границу, то существует по крайней мере одно двухзвенное
периодическое движение. Например, при движении по инерции такое имеет место всегда.
Пример 10.1. Другой пример – это система из трех или
четырех физических маятников в каком-либо поле сил, расположенных таким
образом, чтобы никакие три из них не могли соударяться одновременно (см. Рис.
10.1). В этом случае граница биллиардной области имеет две компоненты
связности, и, значит, возможно, по крайней мере, одно двухзвенное периодическое
движение. Заметим, что здесь, конечно, еще надо доказывать гладкость границы.
Она заведомо будет, если тела маятников имеют строго выпуклую гладкую форму. В
плоском случае – это система с тремя или четырьмя степенями свободы, а в
пространственном – с девятью или двенадцатью.
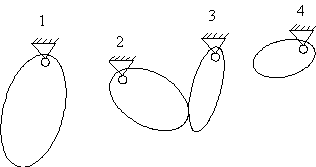
Рис. 10.1. Система из четырех физических
маятников, никакие три из которых не могут столкнуться одновременно. Силовое
поле – любое. При достаточно большой константе интеграла энергии можно так
распределить энергию между маятниками, и подобрать их начальные положения, что будет происходить двухзвенное
периодическое движение. На этом движении будет ровно два соударения. Одно –
маятников 2 и 3, а другое – маятников 1
и 2 или (и) 3 и 4
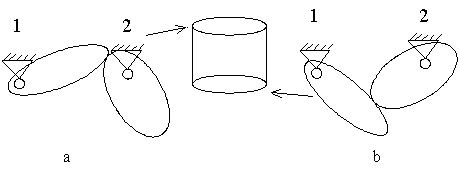
Рис. 10.2 Система
из двух маятников – большого (1) и малого (2). Конфигурационноое пространство –
цилиндр. Граница области возможного движения – это две окружности в основании и
вверху цилиндра. Силовое поле – любое. При достаточно большой константе
интеграла энергии можно так распределить энергию между маятниками, и подобрать
их начальные положения, что будет
происходить двухзвенное периодическое движение. На этом движении будет ровно
два соударения. Одно (a) в на верхней
компоненте границы, а другое (b) на нижней.
Пример 10.2. Еще
пример – два маятника (рис 10.2) с цилиндрическим конфигурационным
пространством. Габариты маятников таковы, что маятник  может совершать
полные обороты, а маятник может совершать
полные обороты, а маятник  – нет. – нет.
Пример 10.3. Связка из двух спутников
на орбите вокруг Земли. Форма спутников произвольна. Длина, соединяющих из
троса велика настолько, чтобы спутники могли быть разведены при любой
ориентации. Силовое поле – центральное. Граница имеет по крайней мере две
компоненты связности. Одна – соответствует натянутому тросу. Другая –
соприкосновению поверхностей спутников. Методом понижения порядка по Раусу
получаем двухчастотное условно периодическое движение.
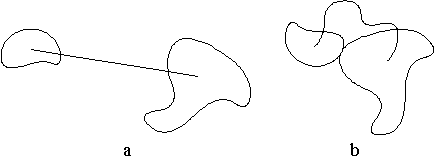
Рис. 10.3 Система
из двух спутников, связанных длинным тросом. Силовое поле – центральное.
Граница области допустимого движения имеет не менее двух компонент связности.
При достаточно большой константе интеграла энергии можно так распределить
энергию между телами, и подобрать их начальные положения, что будет происходить двухчастотное двухзвенное
условно периодическое движение. На этом движении будет ровно два соударения.
Одно (a) с натянутым тросом, а другое (b) столкновение тел. Компактность здесь обеспечивается на поверхности
уровня интегралов момента и энергии.
Благодарности. Авторы весьма признательны
В.В. Козлову, Д.В. Трещеву и М.В. Дерябину за советы и полезные обсуждения
данной работы.
[1] Козлов В.В., Трещев Д.В. Биллиарды.
Генетическое введение в динамику систем с ударами. М., МГУ, 1991 – 168с. [2]Brogliato
B. Nonsmooth Impact Mechanics. Springer-Verlag
London Limited 1996, p. 400. [3]Иванов А.П. Динамика систем с механическими соударениями. М., “Международная программа образования”, 1997 – 336с . [4]Биркгоф Д. Динамические системы. Изд.
Регулярная и хаотическая динамика. 1999 – 407с. [5]Белецкий В.В., Панкова
Д.В. Связка двух тел на орбите как
динамический биллиард. Препринт
ИПМ им. М.В. Келдыша
РАН , N 7, 1995 – 32с. [6] V.V.Beletsky,
G.V.Kasatkin and E.L.Starostin. The Pendelum as a Dynamical Billiard.
Chaos, Solitons & Fractals, v.7 N 8
1995 – pp1145 - 1178. [7]Buttazzo G., Percivale D. On the approximation of the
elastic bounce problem on Riemanian manifolds. Journal of Differential
equations, 1983, 47, 227-275. [8] Сорокина О.В., Кугушев Е.И. Принцип Даламбера-Лагранжа в
механических системах с односторонними связями. Препринт ИПМ им. М.В. Келдыша
РАН, N 14, 2002 – 32с. [9] Сорокина О.В., Кугушев Е.И. Закономерности движения
механических систем с односторонними связями. Препринт ИПМ им. М.В. Келдыша
РАН, N 15, 2002 – 28с. [10] Березинская С.
Н. , Кугушев Е.И. Об
уравнениях движения механических систем с условными односторонними связями. Препринт
ИПМ им. М.В. Келдыша РАН, N 16, 2002 – 32с. [11] Голубев Ю.Ф.
Основы теоретической механики. М., МГУ, 2000 – 719с. [12] Арнольд В.И.,
Козлов В.В., Нейштадт А.И. Математические аспекты классической и небесной
механики. М., Эдиториал УРСС, 2002 – 416с. [13] Арнольд В.И. Обыкновенные дифференциальные
уравнения. М., Наука, 1984 – 272с. [14] Янг. Л. Лекции по вариационному исчислению
и теории оптимального управления. М., Мир, 1974 – 488с. [15] Козлов В.В.
Методы качественного анализа в динамике твердого тела. М., МГУ, 1980 – 231с.
|