Аннотация
Рассматриваются инвариантные многообразия уровня интеграла энергии и линейных по скоростям
интегралов механических систем. Даются условия, при которых они диффеоморфны конфигурационному
пространству. Приводятся примеры: волчок Эйлера с эксцентриком, симметричный конек на гладкой
поверхности.
Abstract
Mechanic system invariant manifolds of energy and linear integrals are investigated. In some
cases such manifolds are diffeomorphic to qonfiguration space. Some examples are given: Euler
rigid body with excentric, symmetric sky on smooth surface.
Содержание
Введение
1. Интегралы
линейные по скоростям.
2. Волчок
Эйлера с эксцентриком
3. Симметричный
конек на поверхности.
4. Симметричный
конек на поверхности вращения.
5. Симметричный
конек на цилиндрической поверхности.
6. Волчок
Лагранжа на поверхности вращения.
ЛИТЕРАТУРА
В данной работе
рассматриваются инвариантные многообразия уровня интеграла энергии и линейных по
скоростям интегралов механических систем. Если интегралы находятся в инволюции
и независимы, то тип многообразий уровня в компактном случае устанавливает
теорема Лиувилля [1], в соответствии с которой, они являются торами. Если
интегралы не находятся в инволюции, то тип многообразия уровня приходится
устанавливать специальным образом. Полезным в этом случае является известное
утверждение из дифференциальной геометрии о накрытиях [2].
Пусть
у нас есть два гладких замкнутых компактных n-мерных многообразия 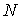 и и 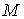 . Рассмотрим гладкое отображение . Рассмотрим гладкое отображение  . Если это отображение всюду регулярно, то оно является
накрытием с конечным числом листов. . Если это отображение всюду регулярно, то оно является
накрытием с конечным числом листов.
Пусть
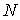 связно. Если накрытие
однолистно, то связно. Если накрытие
однолистно, то 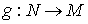 является диффеоморфизмом. является диффеоморфизмом.
В первом разделе работы это утверждение
прилагается к случаю, когда система с 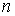 степенями свободы
имеет интеграл энергии и степенями свободы
имеет интеграл энергии и 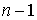 соотношений линейных
по скоростям и независимых. Соотношения могут быть первыми интегралами системы
или непроинтегрированными дифференциальными связями. Показывается, что в
компактном случае из того, что область возможного движения покрывает все
ориентируемое конфигурационное пространство (с ненулевым запасом по уровню
энергии) следует, что многообразие уровня имеет две связные компоненты
диффеоморфные конфигурационному пространству. В неориентируемом случае
компонента связности одна, и многообразие уровня диффеоморфно многообразию, ориентирующему
конфигурационное пространство. Это утверждение является развитием аналогичных
рассуждений, приведенных в [3]. соотношений линейных
по скоростям и независимых. Соотношения могут быть первыми интегралами системы
или непроинтегрированными дифференциальными связями. Показывается, что в
компактном случае из того, что область возможного движения покрывает все
ориентируемое конфигурационное пространство (с ненулевым запасом по уровню
энергии) следует, что многообразие уровня имеет две связные компоненты
диффеоморфные конфигурационному пространству. В неориентируемом случае
компонента связности одна, и многообразие уровня диффеоморфно многообразию, ориентирующему
конфигурационное пространство. Это утверждение является развитием аналогичных
рассуждений, приведенных в [3].
В следующих разделах приводятся примеры
систем, обладающих требуемой системой линейных соотношений.
Во втором разделе рассматривается волчок
Эйлера с эксцентриком, т.е. материальной точкой, свободно вращающейся вокруг
главной оси инерции тела. Конфигурационное многообразие системы – это 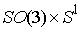 . Три интеграла
сохранения момента количества движения в абсолютных осях высекают и интеграл
энергии высекают в фазовом пространстве инвариантное многообразие уровня,
каждая из двух связных компонент которого диффеоморфна конфигурационному
многообразию. . Три интеграла
сохранения момента количества движения в абсолютных осях высекают и интеграл
энергии высекают в фазовом пространстве инвариантное многообразие уровня,
каждая из двух связных компонент которого диффеоморфна конфигурационному
многообразию.
В третьем разделе рассматривается
неголономная система – симметричные сани Чаплыгина, или, иначе говоря, конек,
скользящий по гладкой поверхности. Эта задача рассматривалась ранее в [4], где
были выведены уравнения движения для общего случая и рассмотрены частные случаи
некоторых поверхностей вращения. В данной работе показывается, что для
симметричного конька всегда существует первый интеграл движения линейный по
скоростям. Вместе с неголономной связью он образует систему независимых
линейных интегралов. Поэтому здесь применима теория, развитая в первом разделе.
В компактном случае инвариантное многообразие уровня имеет две компоненты,
каждая из которых диффеоморфна конфигурационному многообразию.
В четвертом разделе рассматривается
движение симметричного конька по поверхности вращения. Показывается, что задача
редуцируется к фазовому потоку на двухмерном многообразии. Приводятся частные
случаи интегрируемости системы.
В пятом разделе рассматривается движение
симметричного конька по цилиндрической поверхности общего вида. Оказывается,
что в этом случае конек всегда вращается с постоянной угловой скоростью. Если
силовое поле направлено поперек образующей, то система интегрируется в квадратурах.
В последнем, шестом, разделе
рассматривается задача перемещения волчка Лагранжа по гладкой поверхности
вращения. Он скользит по поверхности так, что ось динамической симметрии все
время совпадает с нормалью к поверхности. Показывается, что система
интегрируется в квадратурах. И в случае тороидального конфигурационного
пространства имеет два независимых линейных по скоростям первых интеграла.
Отсюда вытекает, что многообразие уровня, при достаточно большой энергии
диффеоморфно объединению двух торов.
Рассмотрим механическую систему с гладким
замкнутым компактным 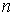 -мерным
конфигурационным многообразием -мерным
конфигурационным многообразием 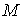 . Фазовое пространство в этом случае представляет
собой . Фазовое пространство в этом случае представляет
собой 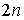 -мерное касательное расслоение -мерное касательное расслоение 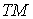 .
Пусть система обладает семейством .
Пусть система обладает семейством 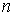 гладких функционально
независимых первых интегралов гладких функционально
независимых первых интегралов
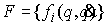 , , 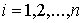
Здесь
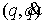 – локальные
координаты. Для вектора – локальные
координаты. Для вектора 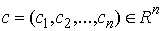 введем введем 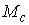 – многообразие уровня
системы – многообразие уровня
системы 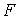
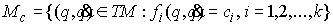
Естественная
проекция 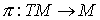 , суженная на , суженная на 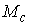 , дает отображение , дает отображение 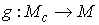 . Как уже говорилось во введении, в компактном случае, для
того, чтобы . Как уже говорилось во введении, в компактном случае, для
того, чтобы 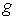 было конечнолистным накрытием
достаточно, чтобы оно было регулярным в каждой точке было конечнолистным накрытием
достаточно, чтобы оно было регулярным в каждой точке 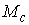 . В [3] , был отмечен тот простой факт, что регулярность . В [3] , был отмечен тот простой факт, что регулярность 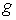 эквивалентна условию
невырожденности якобиевой матрицы первых интегралов по скоростям, т.е. условию эквивалентна условию
невырожденности якобиевой матрицы первых интегралов по скоростям, т.е. условию
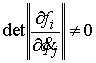 (1.1) (1.1)
Для полноты изложения докажем это. Будем
обозначать вектора касательные к  приставкой приставкой  . Они определяются в локальной системе координат . Они определяются в локальной системе координат 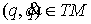 системой уравнений системой уравнений
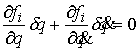 , , 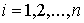 (1.2) (1.2)
Введём
вектора
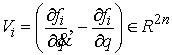 , , 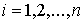
Они
удовлетворяют (1.2) и, поэтому касаются 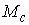 , т.е. , т.е. 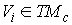 . Поскольку первые интегралы движения функционально
независимы, то система векторов . Поскольку первые интегралы движения функционально
независимы, то система векторов  линейно независима.
Поэтому их линейная оболочка совпадает с пространством линейно независима.
Поэтому их линейная оболочка совпадает с пространством 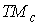 в каждой точке в каждой точке 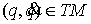 . При естественной проекции эти вектора проектируются в
вектора . При естественной проекции эти вектора проектируются в
вектора 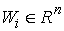 , касательные к конфигурационному многообразию в точке , касательные к конфигурационному многообразию в точке 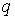 . В указанной локальной системе координат имеем . В указанной локальной системе координат имеем 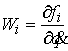 . Условие регулярности отображения . Условие регулярности отображения 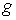 означает, что
линейная оболочка векторов означает, что
линейная оболочка векторов 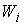 совпадает со всем
касательным пространством, и это эквивалентно условию (1.1). Доказательство
закончено. совпадает со всем
касательным пространством, и это эквивалентно условию (1.1). Доказательство
закончено.
Рассмотрим теперь консервативную
механическую систему с гладким замкнутым компактным 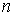 -мерным
конфигурационным многообразием -мерным
конфигурационным многообразием 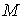 . Пусть в локальных обобщенных координатах лагранжиан системы
имеет вид . Пусть в локальных обобщенных координатах лагранжиан системы
имеет вид
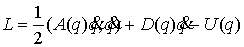 (1.3) (1.3)
Где 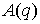 – невырожденная
симметрическая положительно определённая – невырожденная
симметрическая положительно определённая 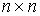 матрица, матрица, 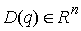 , а , а 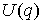 – потенциальная
энергия. Все функции предполагаем гладкими. Интеграл энергии имеет вид – потенциальная
энергия. Все функции предполагаем гладкими. Интеграл энергии имеет вид
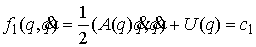 (1.4) (1.4)
Допустим,
что у системы есть 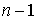 первых интегралов
линейных по скоростям. Локально, в любой координатной окрестности они имеют вид первых интегралов
линейных по скоростям. Локально, в любой координатной окрестности они имеют вид
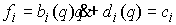 , , 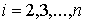 (1.5) (1.5)
где 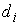 – гладкие функции, и – гладкие функции, и 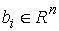 – гладкие
вектор-функции, которые можно рассматривать как поля ковекторов на – гладкие
вектор-функции, которые можно рассматривать как поля ковекторов на 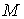 . Введем также векторные поля . Введем также векторные поля
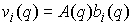 , (1.6) , (1.6)
Если
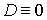 и и 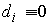 , то , то
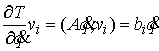
т.е.
интегралы (1.5) являются Нётеровыми для полей симметрии 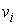 . .
Линейные по скоростям интегралы будем
называть невырожденными, если всюду на конфигурационном многообразии 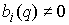 , или, что то же самое, , или, что то же самое, 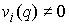 . Будем называть эти интегралы независимыми, если всюду на
конфигурационном многообразии линейно независимы ковекторы . Будем называть эти интегралы независимыми, если всюду на
конфигурационном многообразии линейно независимы ковекторы 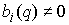 , или, что то же самое, поля , или, что то же самое, поля 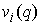 . Очевидно, что из независимости полей вытекает их невырожденность. . Очевидно, что из независимости полей вытекает их невырожденность.
Ориентирующее накрытие. Для формулировки основного утверждения нам
понадобится еще одно понятие. Известно, что для всякого неориентируемого
многообразия 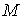 существует
двухлистное накрытие существует
двухлистное накрытие 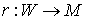 , где , где 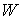 – ориентируемое
многообразие. Это т.н. ориентирующее накрытие [5]. Многообразие – ориентируемое
многообразие. Это т.н. ориентирующее накрытие [5]. Многообразие  будем называть
ориентирующим. Его точками являются следующие классы эквивалентных путей. Пусть будем называть
ориентирующим. Его точками являются следующие классы эквивалентных путей. Пусть
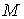 связно, и связно, и 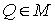 – некая отмеченная
точка. Для любой точки – некая отмеченная
точка. Для любой точки 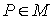 , обозначим , обозначим 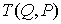 – множество гладких
путей из – множество гладких
путей из  в в 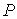 . Оно разбивается на два класса эквивалентных путей . Оно разбивается на два класса эквивалентных путей 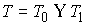 так, что для любой
пары путей так, что для любой
пары путей 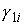 , , 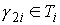 , , 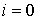 , ,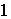 путь путь 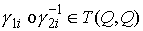 сохраняет ориентацию,
и для любой пары путей сохраняет ориентацию,
и для любой пары путей 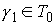 , ,  путь путь 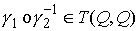 изменяет ориентацию. изменяет ориентацию.
Утверждение
1.1 Пусть конфигурационное многообразие 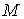 компактно, и
интегралы (1.5) являются независимыми. Тогда, при заданных значениях констант
линейных интегралов компактно, и
интегралы (1.5) являются независимыми. Тогда, при заданных значениях констант
линейных интегралов 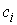 , , 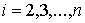 , найдется достаточно большое число , найдется достаточно большое число 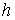 такое, что для любых
значений константы интеграла энергии, превышающих его такое, что для любых
значений константы интеграла энергии, превышающих его 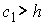 , многообразие уровня , многообразие уровня
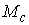 интегралов (1.4-5)
обладает следующими свойствами интегралов (1.4-5)
обладает следующими свойствами
a) Если 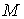 ориентируемо, то ориентируемо, то 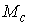 имеет две компоненты
связности, каждая из которых диффеоморфна конфигурационному мнгогообразию имеет две компоненты
связности, каждая из которых диффеоморфна конфигурационному мнгогообразию  . .
b) Если 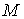 неориентируемо, то неориентируемо, то 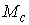 имеет одну компоненту
связности, и диффеоморфно
ориентирующему мнгогообразию имеет одну компоненту
связности, и диффеоморфно
ориентирующему мнгогообразию 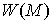 . .
Доказательство.
Пусть 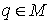 – любая точка
конфигурационного многообразия. Если – любая точка
конфигурационного многообразия. Если 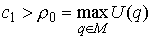 , то в касательном пространстве скоростей , то в касательном пространстве скоростей 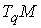 уравнение интеграла энергии (1.4) высекает некий эллипсоид уравнение интеграла энергии (1.4) высекает некий эллипсоид 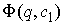 . Вследствие этого многообразие уровня компактно. Поскольку . Вследствие этого многообразие уровня компактно. Поскольку 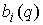 линейно независимы,
то система линейных уравнений (1.4)
задает в этом же пространстве некую прямую линейно независимы,
то система линейных уравнений (1.4)
задает в этом же пространстве некую прямую  . Если начать увеличивать константу интеграла энергии . Если начать увеличивать константу интеграла энергии 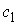 , то, начиная с некоторого ее значения , то, начиная с некоторого ее значения 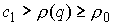 , прямая , прямая 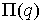 будет пересекать
эллипсоид будет пересекать
эллипсоид 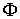 в двух точках. Функция в двух точках. Функция
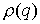 , по крайней мере, непрерывна. Возьмем , по крайней мере, непрерывна. Возьмем 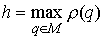 и покажем, что эта
величина удовлетворяет условиям нашего утверждения. и покажем, что эта
величина удовлетворяет условиям нашего утверждения.
Пусть  . Рассмотрим параметрическое семейство линейных уравнений для . Рассмотрим параметрическое семейство линейных уравнений для
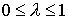 : :
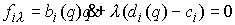 , , 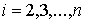 (1.7) (1.7)
Ему
будет отвечать семейство многообразий уровня 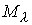 . При . При 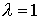 мы получаем исходное
семейство уравнений, т.е. мы получаем исходное
семейство уравнений, т.е. 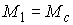 . При . При 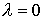 мы получим
многообразие мы получим
многообразие 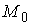 уровня интеграла
энергии (1.3) и системы уравнений уровня интеграла
энергии (1.3) и системы уравнений
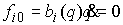 , , 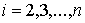 (1.8) (1.8)
Эллипсоид
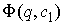 не зависит от не зависит от 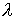 , а прямая , а прямая 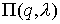 с уменьшением с уменьшением 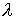 будет приближаться к
нулевому вектору будет приближаться к
нулевому вектору 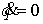 . Поэтому не только при . Поэтому не только при 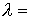 , но и при всех значениях , но и при всех значениях  она будет иметь две
точки пересечения с эллипсоидом. Обозначим их она будет иметь две
точки пересечения с эллипсоидом. Обозначим их
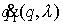 , ,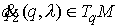 . Тогда . Тогда 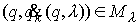 , ,  . В этих точках нормаль к эллипсоиду, т.е. . В этих точках нормаль к эллипсоиду, т.е.  (или (или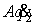 ) и ковекторы ) и ковекторы 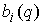 линейно независимы.
Это означает, что якобиева матрица функций уровня по скоростям невырождена и,
значит, на линейно независимы.
Это означает, что якобиева матрица функций уровня по скоростям невырождена и,
значит, на 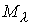 функционально
независимы интеграл энергии и функции (1.7). Отсюда следует, что все
многообразия функционально
независимы интеграл энергии и функции (1.7). Отсюда следует, что все
многообразия 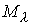 диффеоморфны между
собой (см., например [6]). Поэтому достаточно доказать утверждение теоремы для
случая диффеоморфны между
собой (см., например [6]). Поэтому достаточно доказать утверждение теоремы для
случая 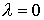 . .
Рассмотрим теперь случай 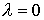 . Введем якобиеву
матрицу функций (1.4, 1.8) по скоростям . Введем якобиеву
матрицу функций (1.4, 1.8) по скоростям
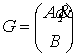
где 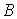 – матрица, строками
которой являются ковекторы – матрица, строками
которой являются ковекторы 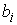 , , 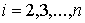 .
Условием регулярности отображения проекции .
Условием регулярности отображения проекции  является условие является условие 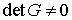 . Как уже говорилось, оно выполняется в силу того, что прямая
(1.8) имеет с эллипсоидом (1.4) две точки пересечения. . Как уже говорилось, оно выполняется в силу того, что прямая
(1.8) имеет с эллипсоидом (1.4) две точки пересечения.
Таким образом, проекция 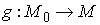 всюду регулярна.
Значит, она является конечнолистным накрытием. Число листов здесь равно двум по
той же причине – эллипсоид (1.4) и прямая (1.8) имеют ровно две точки
пересечения. Отметим, что в силу однородности уравнений (1.8) скорости в этих
точках противоположны. всюду регулярна.
Значит, она является конечнолистным накрытием. Число листов здесь равно двум по
той же причине – эллипсоид (1.4) и прямая (1.8) имеют ровно две точки
пересечения. Отметим, что в силу однородности уравнений (1.8) скорости в этих
точках противоположны.
Ориентируемый
случай. Рассмотрим сначала случай, когда  является
ориентируемым многообразием. Покажем, что накрывающее пространство является
ориентируемым многообразием. Покажем, что накрывающее пространство 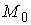 имеет две компоненты
связности. Допустим противное. Пусть точки имеет две компоненты
связности. Допустим противное. Пусть точки 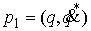 и и 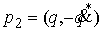 лежат на двух листах
нашего накрытия и соединяются гладким путем лежат на двух листах
нашего накрытия и соединяются гладким путем 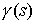 , ,  , лежащим на , лежащим на 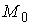 . Поскольку путь . Поскольку путь 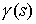 лежит в касательном
расслоении к лежит в касательном
расслоении к 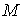 , то его можно представить в виде , то его можно представить в виде 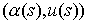 , где , где 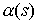 – проекция пути – проекция пути 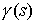 на на 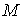 , а , а 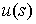 – векторное поле
вдоль – векторное поле
вдоль 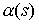 . По построению . По построению
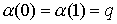 , , 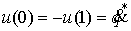 (1.9) (1.9)
и из
(1.8)
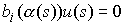 , , 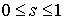 , ,  (1.10) (1.10)
По
условию утверждения, векторные поля 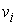 , , 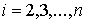 линейно независимы в
каждой точке линейно независимы в
каждой точке 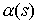 . Пусть . Пусть 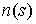 – единичный вектор
ортогональный всем – единичный вектор
ортогональный всем 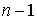 векторам векторам 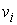 в римановой метрике
на в римановой метрике
на 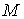 , задаваемой матрицей кинетической энергии, т.е. , задаваемой матрицей кинетической энергии, т.е.
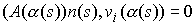 , , 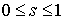 , , 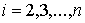 (1.11) (1.11)
Направление
вектора 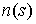 выбираем таким, чтобы
ориентация репера выбираем таким, чтобы
ориентация репера  совпадала с
ориентацией совпадала с
ориентацией 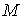 . Поскольку поля . Поскольку поля 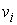 гладкие, то и гладкие, то и 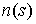 гладко зависит от гладко зависит от 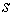 . .
В силу (1.6) условие (1.10) выглядит
следующим образом:
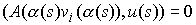
Это
означает, что вектор 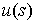 ортогонален всем
векторам ортогонален всем
векторам 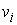 при всех при всех 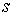 . Из (1.7) следует, что везде . Из (1.7) следует, что везде 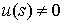 . Поэтому при всех . Поэтому при всех 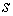 вектор вектор  имеет ненулевую
проекцию на вектор имеет ненулевую
проекцию на вектор 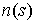 , т.е. , т.е.
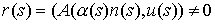 , , 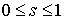
Однако,
из (1.9) мы получаем, что 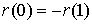 , что невозможно в силу непрерывности функции , что невозможно в силу непрерывности функции 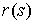 . .
Мы пришли к противоречию. Значит,
накрывающее пространство 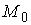 двухлистно и имеет
две компоненты связности. Сужение проекции двухлистно и имеет
две компоненты связности. Сужение проекции 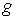 на каждую компоненту
дает однолистное накрытие и, значит, является диффеоморфизмом этой компоненты и
конфигурационного многообразия на каждую компоненту
дает однолистное накрытие и, значит, является диффеоморфизмом этой компоненты и
конфигурационного многообразия 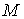 . Доказательство в ориентируемом случае закончено. . Доказательство в ориентируемом случае закончено.
Неориентируемый случай. Рассмотрим теперь случай, когда конфигурационное
многообразие системы 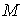 неориентируемо. Как и
в ориентируемом случае, мы можем утверждать, что естественная проекция
многообразия уровня является двухлистным накрытием, однако число компонент
связности многообразия уровня остается пока неизвестным. неориентируемо. Как и
в ориентируемом случае, мы можем утверждать, что естественная проекция
многообразия уровня является двухлистным накрытием, однако число компонент
связности многообразия уровня остается пока неизвестным.
Решить этот вопрос можно следующим
образом. Пусть 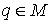 – любая точка, и – любая точка, и 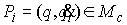 , , 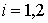 – накрывающие ее
точки на многообразии уровня. Построим путь на – накрывающие ее
точки на многообразии уровня. Построим путь на 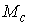 , соединяющий , соединяющий 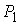 и и 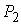 . Для этого возьмем замкнутый путь . Для этого возьмем замкнутый путь 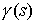 , , 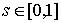 на на 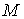 , исходящий из точки , исходящий из точки 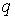 , и возвращающийся в нее со сменой ориентации. В соответствии
с леммой о поднятии пути [2], его можно поднять на , и возвращающийся в нее со сменой ориентации. В соответствии
с леммой о поднятии пути [2], его можно поднять на 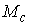 и построить путь и построить путь 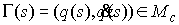 , проектирующийся в , проектирующийся в 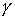 . Далее, действуя по той же схеме, что и для ориентируемого
случая, показываем, что вектора скорости . Далее, действуя по той же схеме, что и для ориентируемого
случая, показываем, что вектора скорости 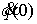 и и 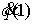 ориентированы одинаково,
по отношению к ориентированы одинаково,
по отношению к 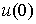 и и 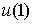 . Но, из-за смены ориентации, . Но, из-за смены ориентации,  . Значит, вектора скорости . Значит, вектора скорости 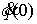 и и  не совпадают. Отсюда
следует, что не совпадают. Отсюда
следует, что 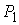 и и 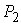 принадлежат разным
листам накрытия. Следовательно многообразие принадлежат разным
листам накрытия. Следовательно многообразие 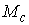 связно. Докажем
теперь, что оно диффеоморфно ориентирующему мнгогообразию связно. Докажем
теперь, что оно диффеоморфно ориентирующему мнгогообразию 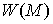 . .
Многообразия 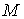 и и 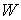 связаны двухлистным
накрытием связаны двухлистным
накрытием 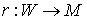 . Несложно убедиться, что касательные расслоения . Несложно убедиться, что касательные расслоения 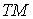 и и 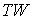 также будут связаны
двухлистным накрытием также будут связаны
двухлистным накрытием 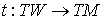 , где , где  . .
Рассмотрим механическую систему с
конфигурационным многообразием 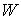 и всеми
характеристиками взятыми с и всеми
характеристиками взятыми с 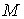 . Такую систему можно назвать поднятием механической системы
с . Такую систему можно назвать поднятием механической системы
с 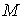 на на 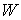 . У поднятой системы также, как и у исходной, будет иметься . У поднятой системы также, как и у исходной, будет иметься 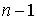 независимых, линейных
по скоростям первых интегралов. Многообразие уровня независимых, линейных
по скоростям первых интегралов. Многообразие уровня 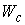 будет двухлистно
накрывать многообразие будет двухлистно
накрывать многообразие 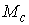 : : 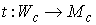 .
Поскольку .
Поскольку 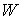 ориентируемо, то
многообразие уровня ориентируемо, то
многообразие уровня 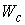 будет иметь две
связные компоненты, диффеоморфные будет иметь две
связные компоненты, диффеоморфные 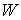 . Как и в ориентируемом случае, сужение проекции . Как и в ориентируемом случае, сужение проекции 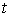 на каждую компоненту
дает однолистное накрытие и, значит, является диффеоморфизмом этой компоненты
и многообразия уровня на каждую компоненту
дает однолистное накрытие и, значит, является диффеоморфизмом этой компоненты
и многообразия уровня 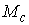 . Значит . Значит 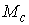 также диффеоморфно также диффеоморфно 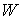 . Что и требовалось показать. . Что и требовалось показать.
Доказательство утверждения 3.1 закончено.
Отметим, что рассмотрение аналогичного
утверждения в однородном случае было проведено ранее в [3].
Замечание 1.1 Об области возможного движения. Эллипсоид интеграла энергии растет в
размерах монотонно с ростом константы 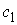 . Поэтому, если . Поэтому, если  , то найдется такая точка , то найдется такая точка 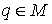 , что эллипсоид интеграла энергии (1.4) и прямая линейных
интегралов не будут иметь общих точек. Это означает, что область возможного
движения системы не будет совпадать со всем конфигурационным многообразием , что эллипсоид интеграла энергии (1.4) и прямая линейных
интегралов не будут иметь общих точек. Это означает, что область возможного
движения системы не будет совпадать со всем конфигурационным многообразием 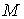 . Следовательно, утверждение 1.1 можно сформулировать
следующим образом: . Следовательно, утверждение 1.1 можно сформулировать
следующим образом:
При
заданных значениях констант линейных интегралов. Если константа интеграла
энергии больше значения, необходимого для того, чтобы область возможного
движения занимала все конфигурационное многообразие, то многообразие уровня 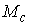 интегралов (1.4-5) в
ориентируемом случае имеет две компоненты связности, каждая из которых
диффеоморфна конфигурационному мнгогообразию интегралов (1.4-5) в
ориентируемом случае имеет две компоненты связности, каждая из которых
диффеоморфна конфигурационному мнгогообразию 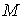 . .
В неориентируемом случае многообразие уровня
 является связным и
диффеоморфно ориентирующему многообразию
является связным и
диффеоморфно ориентирующему многообразию
 . .
Замечание 1.2 Об однородных интегралах. Если линейные интегралы однородны, т.е.  , то прямая, высекаемая ими, проходит через , то прямая, высекаемая ими, проходит через  , и всегда пересекает эллипсоид интеграла энергии в двух
точках, если, конечно, он не вырожден. Значит, область возможного движения
определяется только значением константы интеграла энергии и можно брать , и всегда пересекает эллипсоид интеграла энергии в двух
точках, если, конечно, он не вырожден. Значит, область возможного движения
определяется только значением константы интеграла энергии и можно брать 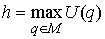 . В этом случае утверждение 1.1 выглядит следующим образом. . В этом случае утверждение 1.1 выглядит следующим образом.
В
однородном случае, если уровень энергии превышает минимальный, при котором
движение возможно на всем конфигурационном пространстве, то при любых значениях
констант линейных интегралов многообразие уровня 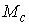 интегралов (1.4-5) в
ориентируемом случае имеет две компоненты связности, каждая из которых
диффеоморфна конфигурационному мнгогообразию интегралов (1.4-5) в
ориентируемом случае имеет две компоненты связности, каждая из которых
диффеоморфна конфигурационному мнгогообразию 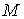 . В неориентируемом случае многообразие уровня . В неориентируемом случае многообразие уровня 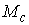 является связным
и диффеоморфно ориентирующему
многообразию является связным
и диффеоморфно ориентирующему
многообразию 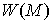 . .
Замечание 1.3 О движении по инерции. В однородном случае, если движение
происходит по инерции, т.е. 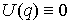 , то область возможного движения либо пуста (для
отрицательных значений энергии), либо занимает все конфигурационное
пространство. Для положительных значений энергии выполняется утверждение 1.1, а
для нулевого значения, очевидно, что все точки многообразия уровня будут
состоять из положений равновесия, и оно будет диффеоморфно конфигурационному
пространству. Значит, утверждение 1.1 можно сформулировать здесь следующим
образом: , то область возможного движения либо пуста (для
отрицательных значений энергии), либо занимает все конфигурационное
пространство. Для положительных значений энергии выполняется утверждение 1.1, а
для нулевого значения, очевидно, что все точки многообразия уровня будут
состоять из положений равновесия, и оно будет диффеоморфно конфигурационному
пространству. Значит, утверждение 1.1 можно сформулировать здесь следующим
образом:
В
однородном случае, если движение происходит по инерции, то для любых значений
констант линейных интегралов имеем следующее. Если энергия положительна, то
многообразие уровня 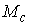 интегралов (1.4-5) в
ориентируемом случае имеет две компоненты связности, каждая из которых диффеоморфна
конфигурационному многообразию интегралов (1.4-5) в
ориентируемом случае имеет две компоненты связности, каждая из которых диффеоморфна
конфигурационному многообразию 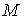 . В неориентируемом случае многообразие уровня . В неориентируемом случае многообразие уровня 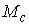 является связным
и диффеоморфно ориентирующему
многообразию является связным
и диффеоморфно ориентирующему
многообразию 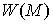 . .
В обоих случаях, если энергия нулевая, то оно имеет одну
компоненту связности диффеоморфную конфигурационному многообразию. Если энергия
отрицательна, то многообразие уровня пусто.
Замечание 1.4 О неголономных связях и частных интегралах. При доказательстве утверждения 1.1 мы не
использовали тот факт, что функции уровня представляют собой первые интегралы
механической системы. Это могут быть любые функции. Отсюда следует, например,
что в качестве линейных по скоростям функций можно брать непроинтегрированные
(или неголономные) дифференциальные связи. Также утверждение 1.1 применимо к
частным линейным по скоростям интегралам системы, существующим только при
некоторых значениях своих констант.
Замечание
1.5 О полной системе линейных интегралов. Если у нас имеется не 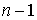 , а ровно , а ровно 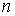 независимых
интегралов линейных по скоростям, то они также высекают инвариантное
многообразие уровня. Невырожденная линейная (по скоростям) система уравнений
имеет ровно одно решение. Значит, естественная проекция является однолистным
накрытием и, следовательно, инвариантное многообразие уровня диффеоморфно
конфигурационному пространству. независимых
интегралов линейных по скоростям, то они также высекают инвариантное
многообразие уровня. Невырожденная линейная (по скоростям) система уравнений
имеет ровно одно решение. Значит, естественная проекция является однолистным
накрытием и, следовательно, инвариантное многообразие уровня диффеоморфно
конфигурационному пространству.
Примером такой системы является волчок
Эйлера. Три интеграла сохранения момента количества движения в абсолютных осях
высекают в фазовом пространстве многообразие диффеоморфное конфигурационному
пространству  . .
Замечание 1.6 О фазовом потоке. Напомним, что при естественной проекции
фазовый поток на многообразии уровня механической системы проектируется в
фазовый поток на конфигурационном пространстве. В ориентируемом случае на нем
возникнет два потока, соответствующих двум компонентам связности многообразия
уровня. Векторные поля, соответствующие этим потокам будут линейно независимы в
каждой точке конфигурационного пространства.
Возьмём волчок Эйлера, т.е. твёрдое тело с неподвижной
точкой, в отсутствии моментов силы тяжести. Добавим к нему эксцентрик –
материальную точку массы 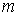 , вращающуюся вокруг первой главной оси инерции тела на
расстоянии , вращающуюся вокруг первой главной оси инерции тела на
расстоянии  от неё в плоскости, и
отстоящей от начала координат на расстоянии от неё в плоскости, и
отстоящей от начала координат на расстоянии 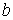 . Конфигурационное многообразие нашей системы – это . Конфигурационное многообразие нашей системы – это 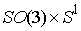 . Помимо углов Эйлера . Помимо углов Эйлера 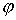 , , 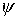 , , 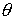 ,
определяющих ориентацию твердого тела, введём также угол ,
определяющих ориентацию твердого тела, введём также угол 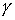 , задающий положение точки эксцентрика , задающий положение точки эксцентрика 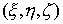 в подвижной системе координат: в подвижной системе координат:
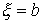 , , 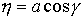 , ,  (2.1) (2.1)
Пусть 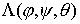 – матрица перехода от
подвижных осей твёрдого тела к неподвижным. Тогда – матрица перехода от
подвижных осей твёрдого тела к неподвижным. Тогда
 (2.2) (2.2)
где 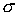 – вектор момента
количества движения в проекции на подвижные оси. Он представляет собой сумму
момента количества движения твердого тела и момента количества движения точки
эксцентрика: – вектор момента
количества движения в проекции на подвижные оси. Он представляет собой сумму
момента количества движения твердого тела и момента количества движения точки
эксцентрика:
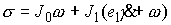 (2.3) (2.3)
здесь
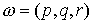 – вектор мгновенной
угловой скорости твердого тела в проекции на подвижные оси, – вектор мгновенной
угловой скорости твердого тела в проекции на подвижные оси, 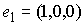 – направляющий вектор
первой главной оси инерции твёрдого тела в подвижных осях, – направляющий вектор
первой главной оси инерции твёрдого тела в подвижных осях, 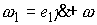 – вектор мгновенной угловой
скорости вращения эксцентрика в проекции на подвижные оси, – вектор мгновенной угловой
скорости вращения эксцентрика в проекции на подвижные оси, 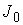 и и 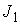 – матрицы тензоров
инерции твёрдого тела и эксцентрика в подвижных осях – матрицы тензоров
инерции твёрдого тела и эксцентрика в подвижных осях
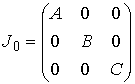 , , 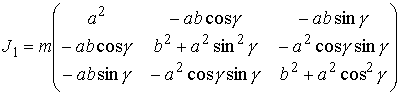 (2.4) (2.4)
Кинетическая
энергия системы также представляет собой сумму кинетических энергий твёрдого
тела и точки эксцентрика:
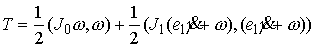 (2.5) (2.5)
Система
допускает четыре первых интеграла движения
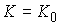 , , 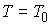 (2.6) (2.6)
В [3] многообразие уровня этой системы
интегралов исследовалось прямым способом. Применим здесь к ней утверждение 1.1.
Интегралы сохранения моментов количества движения линейны по скоростям и
однородны. Их Нетеровы поля 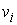 представляют собой
поля поворотов вокруг абсолютных осей. В любой точке конфигурационного
многообразия они независимы. Движение происходит по инерции. представляют собой
поля поворотов вокруг абсолютных осей. В любой точке конфигурационного
многообразия они независимы. Движение происходит по инерции.
Применяя замечание 1.3, получаем
следующее. Для любых значений констант 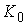 интегралов моментов
при движении с положительной энергией интегралов моментов
при движении с положительной энергией 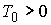 многообразие уровня
интегралов (2.6) имеет две компоненты связности, каждая из которых диффеоморфна
конфигурационному многообразию многообразие уровня
интегралов (2.6) имеет две компоненты связности, каждая из которых диффеоморфна
конфигурационному многообразию 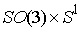 .
Для нулевого уровня энергии это многообразие имеет одну компоненту связности
также диффеоморфную .
Для нулевого уровня энергии это многообразие имеет одну компоненту связности
также диффеоморфную 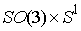 . .
Рассмотрим
движение однородного круглого плоского диска, который в своем центре все время
касается гладкой, компактной, замкнутой, связной поверхности 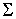 . Пусть на поверхности локально задана какая-либо
ортогональная сеть координат . Пусть на поверхности локально задана какая-либо
ортогональная сеть координат  . Обозначим . Обозначим  – радиус-вектор точки
поверхности в абсолютном пространстве. Тогда – радиус-вектор точки
поверхности в абсолютном пространстве. Тогда
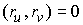 (3.1) (3.1)
Мы считаем, что координаты невырождены,
т.е.
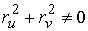 (3.2) (3.2)
Свяжем
с диском сопутствующую систему координат с началом в центре диска и
направляющими векторами 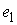 , , 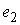 , ,  . Вектора . Вектора 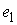 и и 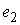 лежат
в плоскости диска, а вектор лежат
в плоскости диска, а вектор 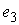 совпадает
с нормалью к поверхности совпадает
с нормалью к поверхности 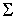 . .
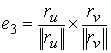 (3.3) (3.3)
В силу симметрии диска, оси сопутствующей
системы являются его главными центральными осями инерции. Рассматриваемая
система имеет три степени свободы. Локально положение системы описывается
тройкой 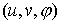 , где , где 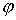 – угол поворота вектора – угол поворота вектора
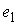 относительно
координатного вектора относительно
координатного вектора 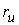 . .
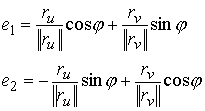 (3.4) (3.4)
Конфигурационное пространство представляет
собой сферическое расслоение поверхности 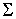 , т.е. касательное расслоение, в котором высечено
многообразие, соответствующее касательным векторам единичной длины. Будем обозначать
его , т.е. касательное расслоение, в котором высечено
многообразие, соответствующее касательным векторам единичной длины. Будем обозначать
его 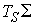 . Очевидно, что группа поворотов диска по углу . Очевидно, что группа поворотов диска по углу 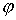 оставляет кинетическую
энергию системы неизменной. Ниже мы покажем это непосредственно. оставляет кинетическую
энергию системы неизменной. Ниже мы покажем это непосредственно.
На
движение диска наложена следующая дополнительная неголономная связь. Поместим в
центр диска конёк, который двигается по поверхности  . Мы будем считать, что линия скольжения конька направлена по . Мы будем считать, что линия скольжения конька направлена по
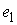 . Условие скольжения состоит в том, что скорость центра диска . Условие скольжения состоит в том, что скорость центра диска
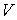 должна быть
направлена по линии скольжения должна быть
направлена по линии скольжения 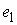 , т.е., должно быть выполнено , т.е., должно быть выполнено 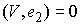 и и  . Поскольку скорость . Поскольку скорость 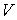 касается поверхности касается поверхности 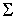 , а , а 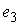 нормален к ней, то
последнее равенство выполняется автоматически, поэтому остаётся только условие нормален к ней, то
последнее равенство выполняется автоматически, поэтому остаётся только условие 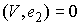 . Используя (3.1, 3.4) в локальных координатах связь можно
записать следующим образом . Используя (3.1, 3.4) в локальных координатах связь можно
записать следующим образом
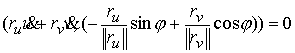
или
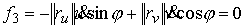 (3.5) (3.5)
Система
допускает интеграл энергии
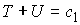
где  – кинетическая, а – кинетическая, а 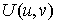 – потенциальная
энергия системы. Массу диска будем считать единичной. Выразим кинетическую
энергию в обобщенных координатах. Главные моменты инерции диска обозначим ( – потенциальная
энергия системы. Массу диска будем считать единичной. Выразим кинетическую
энергию в обобщенных координатах. Главные моменты инерции диска обозначим (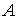 , , 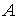 , , 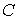 ). По теореме Кёнига ). По теореме Кёнига
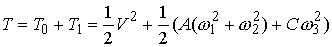 (3.6) (3.6)
где первое слагаемое – это кинетическая
энергия центра масс.
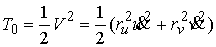
Второе слагаемое в (3.5) – это
кинетическая энергия вращения диска вокруг центра масс. В нём 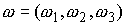 – мгновенная угловая
скорость диска в проекции на подвижные оси: – мгновенная угловая
скорость диска в проекции на подвижные оси:
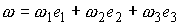
Умножая  , ,  скалярно на скалярно на 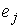 , , 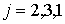 , получим известное соотношение , получим известное соотношение
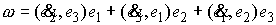
или
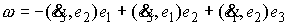
Значит,
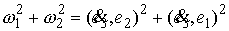
Используя то, что 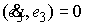 , получаем отсюда , получаем отсюда
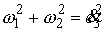
и
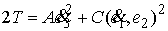
Из (3.4) имеем
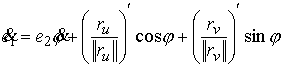
Здесь
и далее 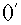 означает производную
по времени. Поскольку вектора означает производную
по времени. Поскольку вектора 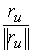 , и , и 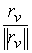 – единичные и
ортогональные, то – единичные и
ортогональные, то
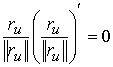 , , 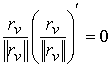 , ,  (3.7) (3.7)
Используя
это и (3.1) находим 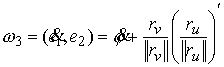 . Окончательно получаем . Окончательно получаем
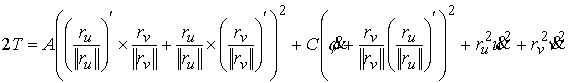
У системы есть интеграл энергии
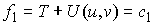 (3.8) (3.8)
Мы предполагаем, что поле сил является
однородным, и потенциальная энергия зависит только от положения центра тяжести
диска. Координата  является циклической,
т.к. она не входит в кинетическую и потенциальную энергии, а её скорость не
входит в уравнение неголономной связи (3.5). Ей соответствует циклический
интеграл момента собственного вращения является циклической,
т.к. она не входит в кинетическую и потенциальную энергии, а её скорость не
входит в уравнение неголономной связи (3.5). Ей соответствует циклический
интеграл момента собственного вращения
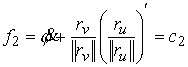 (3.9) (3.9)
В
соответствии с замечанием (1.4) в качестве третьей функции уровня возьмем
неголономную связь (3.5). Для краткости будем называть ее также линейным
интегралом. Исследуем независимость линейных интегралов. Интеграл (3.5) невырожден
в силу (3.2). Интеграл (3.9) невырожден в силу того, что коэффициент при  равен единице.
Поскольку равен единице.
Поскольку  не входит в (3.5), то
интегралы независимы. Следовательно применимо утверждение 1.1. не входит в (3.5), то
интегралы независимы. Следовательно применимо утверждение 1.1.
В
нашем случае линейные интегралы однородны. Применяя замечание 1.2, получаем следующее. Если уровень энергии
превышает минимальный, при котором движение возможно на всем конфигурационном
пространстве, то при любых значениях константы 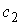 линейного интеграла
(3.9) многообразие уровня линейного интеграла
(3.9) многообразие уровня 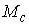 интегралов (3.5,
3.8-9) имеет две компоненты связности, каждая из которых диффеоморфна
конфигурационному многообразию интегралов (3.5,
3.8-9) имеет две компоненты связности, каждая из которых диффеоморфна
конфигурационному многообразию 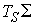 . .
Если
силовое поле отсутствует и движение происходит по инерции, то, применяя
замечание 1.3, получаем следующее. Для любых значений константы 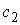 интеграла (3.9) при
движении с положительной энергией многообразие уровня интегралов (3.5, 3.8-9)
имеет две компоненты связности, каждая из которых диффеоморфна
конфигурационному многообразию интеграла (3.9) при
движении с положительной энергией многообразие уровня интегралов (3.5, 3.8-9)
имеет две компоненты связности, каждая из которых диффеоморфна
конфигурационному многообразию 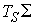 . Для нулевого уровня энергии это многообразие имеет одну
компоненту связности также диффеоморфную . Для нулевого уровня энергии это многообразие имеет одну
компоненту связности также диффеоморфную 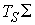 . .
Возьмем
симметричный конек, рассмотренный в предыдущем разделе, но будем считать, что
поверхность 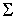 , по которой он перемещается, является поверхностью вращения , по которой он перемещается, является поверхностью вращения
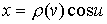 , ,  , , 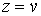
Мы по-прежнему считаем, что поверхность
гладкая, компактная связная и замкнутая (т.е., не имеет границы). В этом случае
топологически она представляет собой двухмерную сферу 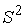 или тор или тор 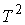 . Конфигурационное пространство, соответственно, . Конфигурационное пространство, соответственно, 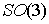 или или 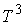 . Будем считать, что силовое поле симметрично: . Будем считать, что силовое поле симметрично: 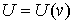 . Несложно убедиться, что у системы есть группа
симметрий – вращение вдоль параметра . Несложно убедиться, что у системы есть группа
симметрий – вращение вдоль параметра 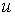 . Систему можно редуцировать к фазовому потоку на двухмерной
сфере . Систему можно редуцировать к фазовому потоку на двухмерной
сфере 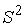 или двухмерном торе или двухмерном торе 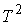 . Произведем прямые выкладки для такой редукции. . Произведем прямые выкладки для такой редукции.
Имеем
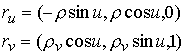 (4.1) (4.1)
Находим отсюда неголономную связь (3.4)
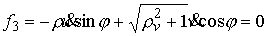 (4.2) (4.2)
Для краткости записи обозначим
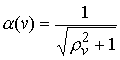 , ,
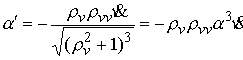
Далее находим
 , , 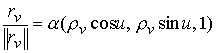
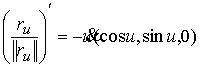 , , 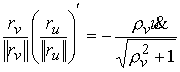
Линейный интеграл (3.9) имеет вид
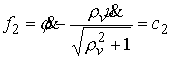 (4.3) (4.3)
Теперь находим
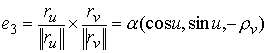 , ,
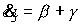
где
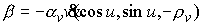 , ,

Имеем
 , ,
 , ,
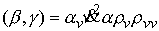
Откуда
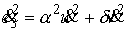 (4.4) (4.4)
где
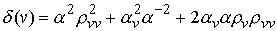
Используя (4.3) найдем кинетическую
энергию
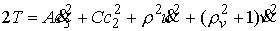
Переобозначив константы, выпишем интеграл
энергии
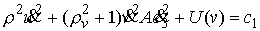 (4.5) (4.5)
или
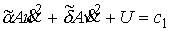 (4.6) (4.6)
где
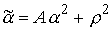 , , 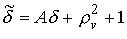
В некритическом случае, когда 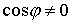 имеем из (4.2) имеем из (4.2)
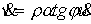 (4.7) (4.7)
подставив
это в (4.6) получаем
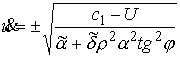 (4.8) (4.8)
подставив (4.8) в (4.7, 4.3) находим
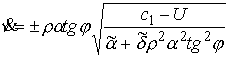 (4.9) (4.9)
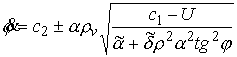 (4.10) (4.10)
Система уравнений (4.8-10) имеет следующий
вид
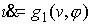 , , 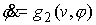 , , 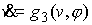
Два последних уравнения отделяются. Они
определяют фазовый поток редуцированной системы.
Заметим,
что, если 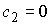 , то система интегрируется в квадратурах, поскольку из
(4.9-10) получаем , то система интегрируется в квадратурах, поскольку из
(4.9-10) получаем
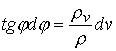
откуда находим первый интеграл
 . .
Очевидно
также, что система интегрируется и в случае вертикальной круговой
цилиндрической поверхности 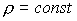 . Здесь . Здесь
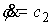 , и , и  . .
Возьмем
симметричный конек, рассмотренный в разделе 4, но будем считать, что
поверхность  , по которой он перемещается, является цилиндрической , по которой он перемещается, является цилиндрической
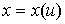 , , 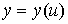 , , 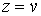
В этом случае
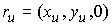 , , 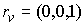 (5.1) (5.1)
Для краткости записи обозначим
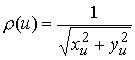
Находим неголономную связь (3.4)
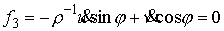 (5.2) (5.2)
Имеем
 , , 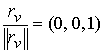
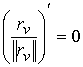 , , 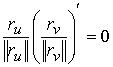
Линейный интеграл (3.9) имеет вид
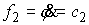 (5.3) (5.3)
Это означает, что при движении по
цилиндрической поверхности симметричный конек вращается с постоянной скоростью.
Теперь находим
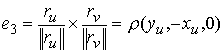 , ,
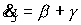
где
 , ,
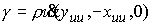
получаем
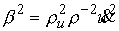 , ,
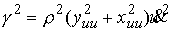 , ,
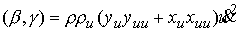
Откуда
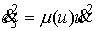 (5.4) (5.4)
где
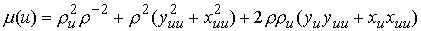
Используя (5.3) найдем кинетическую
энергию

Переобозначив константы, выпишем интеграл
энергии
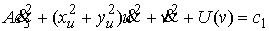 (5.5) (5.5)
или
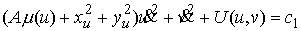 (5.6) (5.6)
В некритическом случае, когда 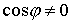 имеем из (5.2) имеем из (5.2)
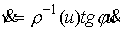 (5.7) (5.7)
Если силовое поле горизонтально, т.е. 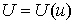 , то система интегрируется в квадратурах. Имеем из (5.6) , то система интегрируется в квадратурах. Имеем из (5.6)

Для интегрирования (5.7) подставляем в
него результаты интегрирования этого уравнения и, из (5.3), 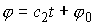
Откажемся
теперь от неголономной связи. Рассмотрим движение однородного круглого плоского
диска, который в своем центре все время касается гладкой, компактной,
замкнутой, связной поверхности 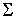 . Будем считать, что поверхность . Будем считать, что поверхность 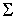 , по которой он перемещается, является поверхностью вращения , по которой он перемещается, является поверхностью вращения
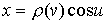 , , 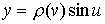 , , 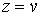
Мы по-прежнему считаем, что поверхность
гладкая, компактная связная и замкнутая (т.е., не имеет границы). В этом случае
топологически она представляет собой двухмерную сферу 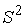 или тор или тор 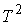 . Конфигурационное пространство, соответственно, . Конфигурационное пространство, соответственно, 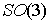 или или  . Будем считать, что силовое поле симметрично: . Будем считать, что силовое поле симметрично: 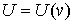 . Воспользовавшись обозначениями раздела 4, получаем линейный интеграл . Воспользовавшись обозначениями раздела 4, получаем линейный интеграл
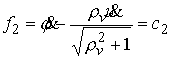 (6.1) (6.1)
Интеграл энергии
 (6.2) (6.2)
Координата 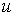 является циклической.
Ей соответствует линейный первый интеграл является циклической.
Ей соответствует линейный первый интеграл
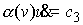 (6.3) (6.3)
Подставив это в (4.6) получаем
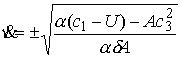
Система интегрируется в квадратурах.
Если
движение происходит по тороидальной поверхности вращения, то координаты не
вырождаются. И мы имеем семейство двух независимых линейных интегралов (6.2-3).
Поверхность уровня здесь, при достаточно больших значениях энергии является
объединением двух трехмерных торов 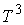 . .
Несложно
убедиться, что линейные интегралы в данной задаче находятся в инволюции.
Поэтому, полученный результат полностью соответствует теореме Лиувилля о
системе интегралов в инволюции.
Благодарности. Авторы весьма признательны В.В. Козлову, и Я.В. Татаринову и Д.В.
Трещеву за советы и полезные обсуждения данной работы.
1.
Арнольд В.И.
Математические методы классической механики. М., Эдиториал УРСС, 2000 – 408с.
2.
Дубровин
Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия. М., Эдиториал УРСС,
2001, т.2 – 293с.
3.
Орешкина
Л.Н. Некоторые обобщения задачи о санях Чаплыгина. Механика твердого тела.
Донецк, вып. 19, 1986, с. 34-39.
4.
Мельдианова
В.С., Кугушев Е.И. Об инвариантных многообразиях механических систем. Препринт
ИПМ им. М.В. Келдыша РАН, N 14 , 2002 – 32с.
5.
Рохлин В.А.,
Фукс Д.Б. Начальный курс топологии. Геометрические главы. М., Наука, 1977 –
488с.
6.
Милнор Дж.
Теория Морса. М., Мир, 1971.
|