О движении тела в газе, реагирующем с его поверхностью. Вывод уравнений динамики
|
|
(3) |
|
Здесь ![]() - равнодействующая всех сил,
- равнодействующая всех сил, ![]() - сумма всех моментов, действующих на тело.
- сумма всех моментов, действующих на тело.
Как
изменится эта динамическая система при появлении взаимодействия тела с газом?
Тогда,
во-первых, среди сил и моментов появятся слагаемые, связанные с суммарным
импульсом и кинетическим моментом, передаваемым молекулами газа телу при
столкновениях.
Также,
когда поток вещества, поглощенный (или испускаемый телом) столь значителен, что
следует учесть и изменение геометрии масс тела, к системе следует присоединить
уравнение:
(3’) ![]() ,
,
И сделать поправку в первом уравнении
основной системы:
(3”) ![]() .
.
Здесь поправка к скорости ![]() учитывает смещение
центра масс, а
учитывает смещение
центра масс, а ![]() - поток массы, возникающие за счет поглощения (или
испускания) телом вещества.
- поток массы, возникающие за счет поглощения (или
испускания) телом вещества.
Одновременно сильная
анизотропия поглощения молекул газа поверхностью может привести к изменению
геометрии масс. Учет изменения формы тела аналогичным способом[3]
связан с определенными затруднениями, которые уже упоминались во введении.
Подход, позволяющий их избежать, будет изложен далее.
§2 Вычисление потоковых
величин
Из чего
складываются и, соответственно, как вычисляются потоковые члены: сила – поток
импульса, момент – поток кинетического момента, массовый поток и все остальные?
Очевидно,
что силы складываются из микроскопических изменений импульса в отдельных
соударениях. Для их нахождения необходимо найти эти микроскопические изменения
импульса для каждого и проинтегрировать по всей поверхности по всем
соударениям. Если имеют место несколько разных типов взаимодействия молекул
газа с телом, например, зеркальное отражение и поглощение, каждое со своей
вероятностью. Тогда локальные потоки, полученные для каждого типа, следует
сложить с соответствующими весами, и, потом проинтегрировать по поверхности.
Аналогично
поступим и с остальными потоками.
Далее будет подробно
рассмотрено три важнейших типа взаимодействия молекул газа с поверхностью –
зеркальное или упругое отражение, диффузное отражение и сорбция. Будем
обозначать слагаемые, соответствующие каждому типу взаимодействия индексами ![]() (elastic)- зеркальный тип,
(elastic)- зеркальный тип, ![]() (diffuse)- диффузный тип,
(diffuse)- диффузный тип, ![]() (sorption) - сорбция.
Соответствующие потоковые величины определим следующим образом:
(sorption) - сорбция.
Соответствующие потоковые величины определим следующим образом:
|
(4) |
|
Здесь функции ![]() ,
, ![]() и есть веса,
указывающие относительную долю соударений каждого типа, они должны
удовлетворять условиям:
и есть веса,
указывающие относительную долю соударений каждого типа, они должны
удовлетворять условиям: ![]() ,
, ![]() и
и ![]() . Аргументами весовых функций
. Аргументами весовых функций ![]() могут быть координата
поверхности
могут быть координата
поверхности ![]() , относительная скорость
, относительная скорость ![]() и нормаль
и нормаль ![]() к поверхности в точке
падения молекулы газа:
к поверхности в точке
падения молекулы газа: ![]() .
.
Величины ![]() ,
, ![]() ,
, ![]() и т.д. - микроскопические изменения соответствующих величин
при единичном акте взаимодействия заданного типа.
и т.д. - микроскопические изменения соответствующих величин
при единичном акте взаимодействия заданного типа. ![]() - дифференциальная
частота столкновений, выражение для нее будет представлено ниже.
- дифференциальная
частота столкновений, выражение для нее будет представлено ниже.
§3 К вычислению потоков.
Дифференциальная частота.
Дифференциальная
частота столкновений молекул газа с телом есть число молекул в элементарном фазовом объеме падающих за
единицу времени на тело извне его границы. Она
определяется выражением:
(5) ![]() .
.
где ![]() - внутренняя нормаль в точки поверхности тела
- внутренняя нормаль в точки поверхности тела ![]() , а
, а ![]() - относительная скорость:
- относительная скорость: ![]() . Дифференциальное сечение столкновений
. Дифференциальное сечение столкновений ![]() для твердых шаров
есть:
для твердых шаров
есть: ![]() , где
, где ![]() - радиус шара. Эта
формула может быть обобщена на случай тела с выпуклой границей, заданной
уравнением
- радиус шара. Эта
формула может быть обобщена на случай тела с выпуклой границей, заданной
уравнением ![]() , где
, где ![]() - кусочно-гладкая функция в
- кусочно-гладкая функция в ![]() . Тогда сечение может быть записано в виде:
. Тогда сечение может быть записано в виде:
(6) ![]() .
.
Таким образом, для вычисления потока
какой-либо величины, передаваемой молекулами газа телу, необходимо взять
изменение этой величины в единичным столкновении и проинтегрировать по ![]() . А интеграл по
. А интеграл по ![]() от единицы даст
просто полную частоту столкновений молекул газа с телом.
от единицы даст
просто полную частоту столкновений молекул газа с телом.
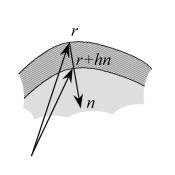
Рис.1
Для тел с гладкой
границей можно аналитически учесть изменение формы в сечении столкновений.
Пусть ![]() - толщина слоя
адсорбированного вещества в точке поверхности
- толщина слоя
адсорбированного вещества в точке поверхности ![]() (Рис. 1). Очевидно, прирост этой величины будет равен объему
вещества адсорбированного на единичной площади за единицу времени, а объем, в
свою очередь есть масса адсорбированных молекул, отнесенная к плотности вещества
(Рис. 1). Очевидно, прирост этой величины будет равен объему
вещества адсорбированного на единичной площади за единицу времени, а объем, в
свою очередь есть масса адсорбированных молекул, отнесенная к плотности вещества ![]() :
:
(7) ![]()
Теперь для тела с
гладкой границей можно легко установить зависимость функции ![]() от времени, установив
по координате сдвиг на глубину
от времени, установив
по координате сдвиг на глубину ![]() вдоль нормали
вдоль нормали ![]() :
:
(8) ![]() .
.
Здесь через ![]() обозначен момент времени, когда толщина слоя считалась
нулевой, а
обозначен момент времени, когда толщина слоя считалась
нулевой, а ![]() - время роста слоя.
- время роста слоя.
§4 Динамика столкновений
для различных типов взаимодействия.
В этом параграфе будет
рассмотрены все три типа взаимодействий: упругое и диффузное отражение, а также
сорбция; для каждого из них будет рассчитана динамика отдельного столкновения.
Будем использовать следующие обозначения (Рис. 2):
![]() - внутренняя нормаль поверхности тела в точке соударения,
- внутренняя нормаль поверхности тела в точке соударения,
![]() - относительная скорость,
- относительная скорость,
![]() - скорость поверхности в точке соударения
- скорость поверхности в точке соударения ![]() .
.
Тильдами будем обозначать величины после столкновения.
4.1 Зеркальное отражение.
При зеркальном или идеально
упругом взаимодействии выполнены все законы сохранения механики: импульса,
энергии и кинетического момента. Динамика упругого столкновения двух тел
изучалась еще Максвеллом [10].
Запишем законы сохранения
для упругого столкновения твердого тела с точечной массой в виде:
|
(9) |
|
Разрешим эти тождества
относительно ![]() и
и ![]() , и полагая, что сила взаимодействия сталкивающихся частиц
направлена по нормали к поверхности в точке соударения. Из закона сохранения
импульса имеем:
, и полагая, что сила взаимодействия сталкивающихся частиц
направлена по нормали к поверхности в точке соударения. Из закона сохранения
импульса имеем:
|
(10) |
|
где ![]() -некоторая скалярная величина, имеющая размерность импульса.
Подставив полученные выражения импульсов после столкновения
-некоторая скалярная величина, имеющая размерность импульса.
Подставив полученные выражения импульсов после столкновения
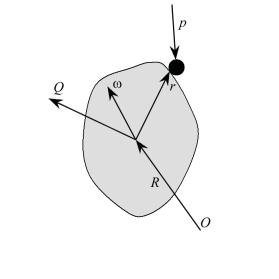
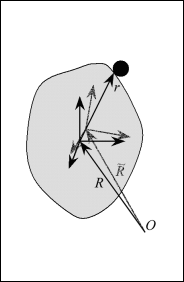
рис. 2 рис. 3
в закон сохранения
кинетического момента, получим:
(10’) ![]()
Теперь коэффициент ![]() можно найти из закона сохранения энергии:
можно найти из закона сохранения энергии:
(11) 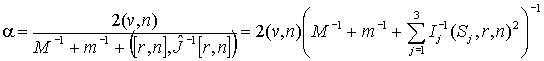
Итак, изменения импульса и кинетического
момента будут иметь вид:
|
(12) |
|
Ни масса, ни геометрия тела при упругом
взаимодействии, очевидно, не меняются.
4.2 Диффузное отражение.
Диффузное отражение
можно представить в виде последовательной сорбции и десорбции с максвелловским
распределением, соответствующем температуре поверхности. При этом скорости
молекул, покидающих поверхность, считаются не зависимыми от их скоростей перед
столкновением с поверхностью, а лишь подчиняющимися распределению:
(13) 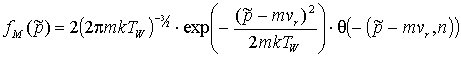
При диффузном отражении в отдельном
соударении энергия не сохраняется[4].
Имеют место лишь законы сохранения импульса и кинетического момента:
|
(14) |
|
откуда легко получить, что:
![]() ,
,
![]() .
.
Найдем средний импульс отлетающей молекулы:
![]()
Итак, в среднем по распределению отраженных
молекул найдем:
|
(15) |
|
Ни масса, ни геометрия тела при диффузном взаимодействии,
так же как и в упругом случае, очевидно, не меняется.
4.3 Сорбция.
Под сорбцией, не вдаваясь в
конкретные физико-химичесские механизмы, будем понимать такое соударение, при
котором молекула газа поглощается и далее движется с телом как одно целое. Это
взаимодействие неупругое, поэтому механическая энергия не сохраняется. Остаются
законы сохранения импульса, кинетического момента и, что здесь уже играет свою
роль, закон сохранения массы:
|
(16) |
|
Заметим, что в этом случае ![]() , поскольку при присоединении молекулы центр масс смещается.
Смещение запишем в виде:
, поскольку при присоединении молекулы центр масс смещается.
Смещение запишем в виде:
(17) ![]() .
.
Из законов сохранения найдем:
![]()
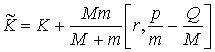
Соответственно получим:
|
(18) |
|
4.4 Учет изменения геометрии масс при сорбции.
Изменение
геометрии масс стоит обсудить особо. В этом параграфе будет показано
преимущество описания меняющейся геометрии масс в терминах тензора инерции, а
не главных осей и моментов инерции.
Найдем, как меняется тензор
инерции при единичном акте поглощения точечной массы поверхностью тела (Рис.
3).
По определению тензора
инерции:
(19) ![]()
После столкновения центр инерции «нового»
тела сместится в точку ![]() , поэтому тензор его инерции будет суммой момент тензора
инерции «старого» относительно точки
, поэтому тензор его инерции будет суммой момент тензора
инерции «старого» относительно точки ![]() и тензора инерции
поглощенной молекулы:
и тензора инерции
поглощенной молекулы:
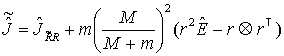 .
.
Найдем смещенный момент «старого» тела:
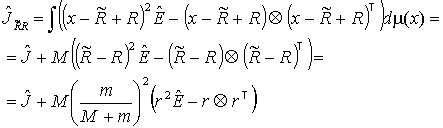
Итак, тензор инерции «нового» тела:
(20) ![]() ,
, 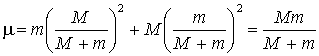
И можно записать:
(21) ![]()
Рассмотрим теперь возможность расчета
изменений ортов главных осей и главных моментов инерции. Вообще говоря, вектора
![]() ,
,![]() ,
,![]() и главные моменты инерции
и главные моменты инерции ![]() , находятся решением задачи на собственные векторы и числа
для тензора
, находятся решением задачи на собственные векторы и числа
для тензора
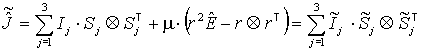 .
.
И в общем случае решение может быть найдено с
помощью такого подхода. Преобразование от старого собственного базиса {![]() ,
,![]() ,
,![]() } к новому {
} к новому {![]() ,
,![]() ,
,![]() } имеет вид:
} имеет вид:
![]() , где
, где 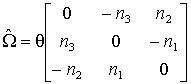 , так что
, так что ![]()
Тогда получим, что:
(22) ![]() ;
;
(23) ![]()
(24) ![]() ,
, ![]()
Подстановкой (22) в
(24) получим три уравнения на ![]() ,
, ![]() . А по ним уже найдутся и главные моменты инерции из (23).
. А по ним уже найдутся и главные моменты инерции из (23).
Найдем достаточное условие,
при котором угол поворота собственного базиса
при присоединении молекулы малой массы (по сравнению с массой тела)
может считаться также малой величиной. Это необходимо для того, что бы изменения
от отдельных соударений можно было бы проинтегрировать в соответствующую
потоковую величину.
Если
угол ![]() мал, то в линейном
приближении
мал, то в линейном
приближении ![]() , откуда получаем, что:
, откуда получаем, что:
|
(25) |
|
где: 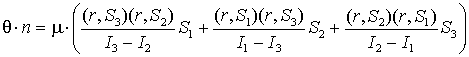 .
.
Но последнее выражение имеет смысл
только, когда ![]() и верно неравенство:
и верно неравенство:
(26) ![]()
Действительно, если полученное неравенство не
выполнено, то значение угла ![]() не являться малым,
что делает неприменимым использованное приближение.
не являться малым,
что делает неприменимым использованное приближение.
Итак, неравенство (26) и
есть искомое условие малости угла поворота. В тех случаях, когда оно не
выполняется (или точность приближения малых углов по каким-либо причинам
оказывается неудовлетворительной) необходимо решать задачу на собственные
векторы и собственные значения для «нового» тензора инерции нужно решать либо
способом (22-24), либо явно, находя корни характеристического уравнения и т.д.
Но в любом из этих случаев результат для конечных приращений оказывается довольно
громоздким, содержащим, в частности кубические радикалы, согласно формуле
Кардано. Тем более затруднительно становится интегрирование по отдельным
изменениям главных осей и моментов инерции даже в тех случаях, когда они малы.
§5 Особенности динамики
твердого тела с переменной геометрией масс.
Итак, на основании уже
рассмотренной динамики столкновений в случае сорбции предлагается отвергнуть
естественный, на первый взгляд, путь учета в динамике твердого тела изменения
массы за счет сорбирующегося вещества – ввести поправки в уравнения,
описывающие вращение ортов главных осей и дополнить систему уравнениями на
главные моменты инерции. Поскольку этот путь таит в себе трудности, которые,
помимо громоздкости выражений, связанны с тем, что если условие (26)
нарушается, то изменение направлений главных осей не является квазинепрерывным[5].
Если при присоединении молекул в некоторый момент времени возникает, а затем
разрушается динамическая симметрия, то базис главных осей скачкообразно
поворачивается на угол, который может принимать совсем не малые значения [2].
Но сам тензор инерции при
этом останется квазинепрерывным: каждый его элемент в координатном
представлении при присоединении молекулы (масса которой мала по сравнению с
массой тела) будет меняться на малую величину.
Поэтому предлагается
описывать динамику твердого тела в терминах тензора инерции.
Утверждение 1. При движении
твердого тела без изменения геометрии масс зависимость тензора инерции от
времени описывается уравнением:
(27) 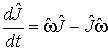 ,
,
где 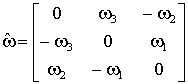 - объект дуальный к вектору угловой частоты.
- объект дуальный к вектору угловой частоты.
Пользуясь тем, что каждая точка твердого тела
движется вокруг центра масс по закону ![]() , докажем утверждение 1 с помощью выкладки:
, докажем утверждение 1 с помощью выкладки:
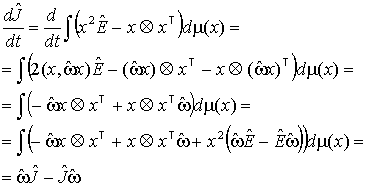
Для описания динамики твердого тела система с
(27) дополняется уравнениями:
(28) ![]() .
.
В нашем случае правая часть уравнения для
тензора инерции должна быть дополнена потоковой величиной, интегрирующей
изменения от отдельных столкновений:
(29) 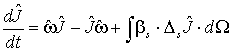 .
.
где ![]() дается выражением
(21).
дается выражением
(21).
По-видимому,
именно тензор инерции, а не главные оси и главные моменты инерции будут
«правильными» переменными при численном моделировании динамики твердого тела с
переменной геометрией масс. При этом, хотя предлагаемое описание, по сути,
эквивалентно традиционно используемым способам, и является избыточным для
стандартных задач без изменения массы и формы тела, оно является
предпочтительным для решения задач с потоками вещества, квазинепрерывно
меняющими и массу, и форму тела.
§6 Основная система уравнений
Теперь можно записать итоговую систему
уравнений. В общем случае
|
(30) |
|
где 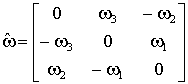 - объект дуальный к вектору угловой частоты, а
микроскопические изменения величин сведены в таблицу 1. Замыкается система
уравнениями, описывающими изменение частоты столкновений вместе с геометрической
формой тела (5-8).
- объект дуальный к вектору угловой частоты, а
микроскопические изменения величин сведены в таблицу 1. Замыкается система
уравнениями, описывающими изменение частоты столкновений вместе с геометрической
формой тела (5-8).
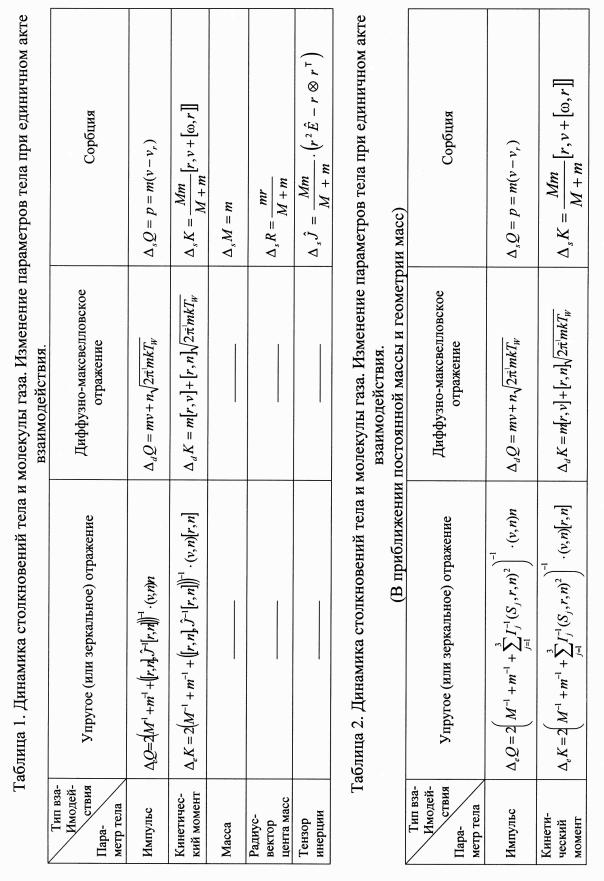
В некоторых случаях, когда
изменение геометрической формы и массы незначительны, допустимо пользоваться
соответствующим приближением.
Итак, в приближении постоянной массы и
геометрии масс динамическую систему удобно записать в виде:
|
(31) |
|
Где соответствующие приращения сведены в
таблице 2. Дифференциальная частота столкновений в этом случае полагается постоянной.
§7 Границы применимости и связь с кинетикой газа
Применимость
представленного подхода вычисления
потоковых величин (сил, моментов, потока массы, и т.д.) ограничивается
тем условием, что частота столкновений молекул газа с поверхностью тела должна
быть столь достаточно велика, так чтобы интегрирование (а не суммирование) по
отдельным столкновениям было оправданным. Это условие эквивалентно тому, что
число столкновений за минимальное характерное время должно быть на несколько
порядков больше единицы. К характерным временам относятся период вращения
вокруг своей оси, время прохождения одного витка при движении по спирали,
характерные времена релаксации, т.е. величины, обратные коэффициентам в первых
членах разложения диссипативных сил и моментов, а также, возможно, времена,
определяемые спецификой конкретной задачи.
Также
за рамками рассмотрения пока оставался вопрос влияния движущегося тела на
функцию распределения газа. Этим влиянием можно пренебречь, если длина
свободного пробега молекул газа велика по сравнению с размером тела
(свободномолекулярное обтекание). В этом случае функция распределения молекул
газа будет определяться согласно конкретной постановке задачи (4).
В тех случаях, когда влияние
движение тела на газ оказывается существенным, в принципе можно рассмотреть
согласованное с полученной динамической системой кинетическое уравнение,
например, уравнение Больцмана [5]:
(32) 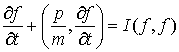
Здесь пространственная переменная определена
вне области пространства занимаемой телом. На границе нужно поставить условия
согласования с уравнениями динамики [8, 9]:
(33) ![]()
Ядра взаимодействия молекул газа с
поверхностью могут быть легко получены из уже рассмотренной динамики
столкновений (12, 13):
|
(34) |
|
Однако в настоящее время получение не только
аналитического, но и численного решения этого уравнения в окрестности
движущегося тела с указанными условиями на поверхности тела существуют
непреодоленные затруднения.
В
случае, когда длина свободного пробега много меньше линейного размера
(гидродинамическое обтекание) тела возможно рассмотрение соответствующего
гидродинамического приближения уравнений (33-34).
Более
подробный анализ влияния движения тела на газ выходит за рамки этой работы,
хотя и представляет значительный интерес.
Заключение
Полученная система уравнений
(30), по сути, является заготовкой для получения моделей для конкретных задач.
Кроме того, она может оказаться пригодной и для исследований общих
закономерностей движения твердых тел в газе. Но это – уже предмет будущих
исследований.
Автор благодарит В. В.
Веденяпина, М. В. Масленникова и Ю. Н. Орлова, чьи советы и замечания в
значительной мере содействовали этой работе, а также И. В. Мелихова и А. Я.
Горбачевского за интересные и полезные обсуждения.
Литература
[1] Арнольд В. И., Козлов В. В., Нейштадт А. И.
Математические аспекты классической и небесной механики. – М: Эдиториал
УРСС, 2002.
[2] Арнольд В. И. Математические методы классической
механики. – М: Эдиториал УРСС, 2000.
[3] Батищева Я. Г., Веденяпин В. В., Мелихов И. В., Горбачевский А.
Я., О движении твердого тела в газе с неоднородными поверхностными
химическими процессами. // Мат.моделирование, 2003г. №5.
[4] Белецкий В. В., Яншин А. М., Влияние аэродинамических сил на
вращательное движение спутников. – Киев, Наукова думка, 1984.
[5] Борисов А. В., Мамаев И. С. Динамика
твердого тела. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001.
[6] Веденяпин В. В., Кинетические уравнения
Больцмана и Власова. – М.: Физматлит, 2001.
[7] Мелихов И. В., Симонов Е. Ф., Ведерников А. А., Хемореактивное
движение частиц катализатора в газовой среде при гетерогенном катализе
// Ж. Физ. Хим., 1998, т 72, №12, с.
2300 - 2306.
[8] Пярнпуу А. А., Взаимодействие газов с
поверхностями. – М., "Наука", 1974.
[9] Черчиньяни К., Теория и приложение
уравнения Больцмана. – М., "Мир", 1978.
[10] Maxwell J. C. Illustration of the Dynamical Theory of
Gases. // Philosophical Magazine. 1860. Vol. 1. P. 377-409
[11] J. Willneff, H.-G. Maas, Design
and calibration of four-headed camera system for use in microgravity
research.// IAPRS, Vol. XXXIII, Amsterdam, 2000.
[1] Указанной неприятной особенностью обладают и другие переменные, связанные с главными осями инерции, например углы Эйлера.
[2] Здесь под тензорным
произведением двух векторов ![]() и
и ![]() подразумевается
объект:
подразумевается
объект:![]() , который в координатном представлении имеет вид:
, который в координатном представлении имеет вид:
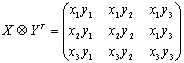
![]()
[3] С помощью дополнительных уравнений: ![]() ,
, ![]() я поправки в
четвертом уравнении основной системы.
я поправки в
четвертом уравнении основной системы. ![]() ,
, ![]() , где добавка
, где добавка ![]() к мгновенной угловой
частоте учитывает поворот базиса собственной системы за счет изменения формы
тела, а потоки
к мгновенной угловой
частоте учитывает поворот базиса собственной системы за счет изменения формы
тела, а потоки ![]() - изменения моментов инерции.
- изменения моментов инерции.
[4] Тем не менее, может быть выполнен интегральный закон сохранения энергии, если, например, температура поверхности равна температуре газа, и стенка неподвижна.
[5] Строго говоря, при поглощении отдельных молекул любой параметр либо не меняется, либо меняется на конечную величину. Условие же
квазинепрерывности некоторого параметра означает, что при присоединении частицы
(молекулы газа) малой массы (![]() ) изменение этого параметра имеет тот же порядок малости, что
и отношение масс:
) изменение этого параметра имеет тот же порядок малости, что
и отношение масс: ![]() . Условие квазинепрерывности является необходимым для
правомерности того, чтобы описывать эволюцию параметра соответствующей
потоковой величиной.
. Условие квазинепрерывности является необходимым для
правомерности того, чтобы описывать эволюцию параметра соответствующей
потоковой величиной.
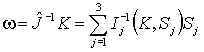 ,
, 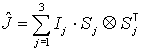 .
.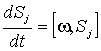 ,
,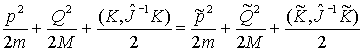
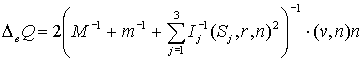
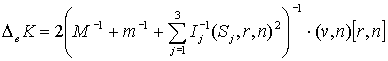
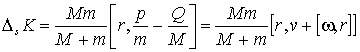 ,
,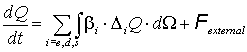 ,
,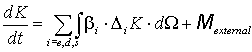
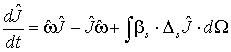
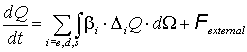 ,
,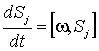 ,
,  .
.