Периодические колебания оси симметрии спутника под действием гравитационного и аэродинамического моментов

( Periodic oscillations of the satellite symmetry axis under the action of gravitational and aerodynamic torques
Preprint, Inst. Appl. Math., the Russian Academy of Science)

1. Уравнения вращательного движения спутника. Рассмотрим искусственный спутник Земли, представляющий собой динамически симметричное твердое тело, центр масс которого движется по неизменной круговой орбите. Для записи уравнений движения спутника вокруг центра масс введём две правые декартовы системы координат – орбитальную  и образованную главными центральными осями инерции спутника . Точка  – центр масс спутника, ось  направлена вдоль геоцентрического радиуса-вектора этой точки, ось  направлена по вектору кинетического момента орбитального движения спутника,  – ось динамической симметрии спутника.

Положение системы координат  относительно орбитальной сис­темы будем задавать углами ,  и , которые введем следующим условием. Система  переводится в систему  тремя последовательным поворотами: 1) на угол  вокруг оси , 2) на угол  вокруг новой оси , 3) на угол  вокруг новой оси , совпадающей с осью . Таким образом,  – угол между осью  и плоскостью ,  – угол между проекцией оси  на плоскость  и осью . Эти два угла задают направление оси  в орбитальной системе координат.

Действие на спутник гравитационного и восстанавливающего аэродинамического моментов приводит к движению оси , описываемому уравнениями

       (1.1)

Здесь , ,   – компоненты абсолютной угловой скорости спутника в системе , точкой обозначено дифференцирование по времени , – отношение осевого и экваториального главных центральных моментов инерции спутника,  – параметр аэродинамического момента. При записи уравнений (1.1) в качестве единицы измерения времени принята величина, обратная орбитальной угловой скорости спутника. В этом случае период орбитального движения равен . Использованные в (1.1) выражения для аэродинамического момента получены в предположении, что внешняя оболочка спутника представляет собой сферу с центром на оси , атмосфера неподвижна в абсолютном пространстве и ее плотность неизменна вдоль орбиты.

Уравнения (1.1) получены следующим образом. Величины , ,  представляют собой проекции абсолютной угловой скорости спутника на оси Резаля, совпадающие при  с осями ,  и . Уравнения вращательного движения, спутника, записанные в переменных , , , ,  и , разбиваются на две подсистемы. Одна из них образована уравнениями (1.1) и описывает движение оси  относительно орбитальной системы координат, другая образована уравнениями для ,  и описывает движения спутника вокруг этой оси. Вследствие динамической симметрии спутника компонента угловой скорости  является первым интегралом его уравнений движения, и система (1.1) не содержит угла . Если интересоваться только движением оси , то уравнение для  можно не рассматривать, а величину  считать параметром.

Физически допустимые значения параметра  лежат в интервале . Эти неравенства следуют из неравенств «треугольника» для момен­тов инерции спутника.

Уравнения (1.1) допускают первый интеграл (обобщенный интеграл энергии)

                  (1.2)

инвариантны относительно преобразования переменных

,   ,                                     (1.3)

и допускают стационарные решения

,   ,  ,                               (1.4)

где  – корень уравнения

                              (1.5)

Уравнения (1.1) инвариантны также относительно преобразования переменных и параметра

,   ,   ,                            (1.6)

Ниже значительное внимание уделяется случаю , когда аэродинамический момент отсутствует. В этом случае преобразование (1.6) сводится к преобразованию переменных , , . Уравнение (1.5) при  имеет корень , которому отвечает стационарное решение

,   ,   ,                                    (1.7)

Это решение описывает движение спутника, в котором ось  совпадает с осью  (нормалью к плоскости орбиты). Используя первый интеграл (1.2) в качестве функции Ляпунова, можно найти [1] достаточные условия устойчивости решения (1.7)

,                                      (1.8)

Необходимые условия его устойчивости получаются из анализа характеристического уравнения системы, полученной линеаризацией уравнений (1.1) при  в окрестности (1.7). Это характеристическое уравнение имеет вид

                                              (1.9)

,  

Оно биквадратное, поэтому решения линеаризованной системы ограниченны только в том случае, когда все корни уравнения (1.9) – чисто мнимые и простые, т. е. в случае

,   ,                                      (1.10)

Последние неравенства выражают необходимые условия устойчивости решения (1.7). Ниже уравнения (1.1) рассматриваются при . В этом случае условия (1.8) выполнены при , условия (1.10) – при  и .

2. Периодические решения Ляпунова. Исследование периодических движений оси  начнем с построения решений Ляпунова уравнений (1.1), существующих в окрестности указанных выше стационарных решений. Для сокращения записи будем использовать векторные обозначения. Введём вектор  и определим функцию  так, чтобы записать систему (1.1) в виде

                                               (2.1)

В силу инвариантности уравнений (1.1) относительно преобразования (1.3) система (2.1) обладает свойством Е [2] по отношению к матрице , т. е. имеет место соотношение

                                  (2.2)

Инвариантность уравнений (1.1) относительно преобразования (1.6) выражается соотношением

                          (2.3)

где , . Первый интеграл (1.2) запишем в виде . Справедливы равенства

, 

Сначала рассмотрим решения Ляпунова в случае . Стационарное решение (1.7) обозначим . Пусть в некоторой области  уравнение (1.9) имеет простой корень ,  и не имеет корней вида  для любого целого . Тогда [3, 4] при  в окрестности стационарного решения  система

                                                    (2.4)

допускает семейство периодических решений Ляпунова

                                         (2.5)

где  и  – произвольные постоянные, , ,  – некоторое положительное число,  и  – аналитические функции своих аргументов, , , . В силу свойств симметрии системы (2.4) (ср. тождества (2.2) и (2.3) при ) и ее первого интеграла  функцию  можно выбрать удовлетворяющей соотношениям [4]

,   

Положим . Эта функция – периодическая с периодом  и удовлетворяет условиям

,                         (2.6)

скалярная форма которых

,  ,   ,   

,   

,   

Положив в выписанных соотношениях , найдем краевые условия, определяющие решение . Векторная форма этих условий

,                                 (2.7)

скалярная форма

Пусть  – решение краевой задачи (2.4),(2.7). Продолжим его на всю действительную ось как решение уравнения (2.4). Можно доказать, что это решение удовлетворяет соотношениям (2.6) и вследствие этих соотношений соотношению

Таким образом, функция  является -антипериодической, а функция  – -периодической. Численное решение краевой задачи (2.4), (2.7) позволяет построить решение (2.5) в явном виде и продолжить его за пределы малой окрестности стационарной точки .

        Перейдем к случаю . Стационарное решение (1.4), (1.5), переходящее при  в (1.7), обозначим . В этом решении , . Рассмотрим характеристическое уравнение системы (2.1), линеаризованной в окрестности : . Здесь  – единичная матрица порядка 4. Это уравнение так же, как и уравнение (1.9), – биквадратное. Пусть в некоторой области  оно имеет простой корень ,  и не имеет корней вида  для любого целого . Тогда [3, 4] при  в окрестности стационарного решения  система (2.1) допускает семейство периодических решений Ляпунова

                           (2.8)

где  и  – произвольные постоянные, , ,  – положительное число,  и  – аналитические функции своих аргументов, , ,  . В силу свойств симметрии системы (2.1), выражаемых тождествами (2.2) и (2.3), и аналогичных свойств ее первого интеграла функции  и  можно выбрать удовлетворяющими соотношениям

При  такие функции  и  совпадают с функциями и  в решении (2.5). В этом смысле решение (2.8) является продолжением решения (2.5) системы (2.1) из точки  в окрестность последней.

Пусть . Эта функция – периодическая с периодом  и удовлетворяет соотношениям

,                               (2.9)

Положив здесь , найдем краевые условия, определяющие решение . Векторная форма этих условий

,                                    (2.10)

скалярная форма

Можно доказать, что всякое решение краевой задачи (2.1), (2.10), продолженное на всю действительную ось как решение уравнения (2.1), удовлетворяет соотношениям (2.9) и, следовательно, является -периодическим. Решая численное эту задачу, можно продолжить решение (2.8) за пределы малой окрестности стационарной точки .

        В общем случае каждая из систем (2.1) и (2.4) имеет два семейства решений Ляпунова, отвечающих разным парам комплексно-сопряженных корней соответствующих характеристических уравнений. В частности, при выполнении условий (1.8) корни уравнения (1.9) имеют вид , , где  и ,   при . Семейство решений с меньшим периодом будем называть короткопериодическим, другое семейство – длиннопериодическим.

3. Численное построение периодических решений. В силу инвариантности уравнений (1.1) относительно преобразования (1.6) их периодические решения достаточно вычислить при . Численное построение периодических решений (2.5) и (2.8) проводилось методом продолжения по параметру. Параметром служил период  или угловая скорость . Использовался вариант метода, описанный в [5]. Он основан на решении краевых задач (2.4), (2.7) и (2.1), (2.10) методом стрельбы. При построении им решения краевой задачи (2.4), (2.7) начальные условия ,  и параметр  (или ) считались неизвестными, краевые условия (2.7) в точке  служили уравнениями для их определения. Поскольку неизвестных здесь на единицу больше, чем уравнений, удобно считать, что уравнения задают кривую  в пространстве .

Для успешной работы алгоритма продолжения по параметру необходимо, чтобы почти во всех точках кривой  матрица

                       (3.1)

имела полный ранг. Эта матрица многократно используется в алгоритме. Для вычисления ее первых двух столбцов интегрируются соответствующие уравнения в вариациях, последний столбец – значение правых частей второго и третьего уравнений системы (2.4) на вычисляемом решении в точке .

К сожалению, к числу точек кривой , в которых ранг матрицы (3.1) меньше 2, принадлежит точка [, , ], отвечающая стационарному решению . Поскольку это – единственная наперед известная точка кривой, именно ее хотелось бы использовать в качестве начальной точки при работе алгоритма. Указанная трудность преодолевается с использованием следующего замечания. Если  – решение краевой задачи (2.4), (2.7), то его производная  является решением уравнения в вариациях

                                         (3.2)

и удовлетворяет соотношениям (ср.(2.6))

,   

Функция  имеет иные свойства симметрии, чем функция . Положив в последних соотношениях , найдем краевые условия, определяющие решение :

,                                    (3.3)

Пусть   – решения уравнения (3.2) с начальными условиями , . Оба эти решения и, следовательно, их произвольная линейная комбинация , где ,  – const, удовлетворяет первому условию (3.3). Подстановка такой линейной комбинации во второе условие приводит к линейной системе относительно  и

,    

Чтобы выписанная система имела нетривиальное решение, ее определитель должен равняться нулю:

Можно показать, что краевая задача (2.4), (2.7) в окрестности решения  эквивалентна краевой задаче

                                  (3.4)

для системы (2.4), (3.2), причем матрица

                                               (3.5)

имеет в точке  полный ранг. Аналогичным образом вместо краевой задачи (3.4) можно рассматривать краевую задачу

Вычисление решения (2.5) проводилось следующим образом. Для определения первых нескольких точек кривой  использовалась стартовая процедура, в которой методом продолжения по параметру решалась краевая задача (2.4), (3.2), (3.4). Начальной точкой служила точка . Затем начинала работать основная процедура, решавшая задачу (2.4), (2.7). Быстродействие стартовой процедуры было несколько ниже, чем основной, поскольку расчет матрицы (3.5) выполнялся численным дифференцированием.

После построения некоторого отрезка кривой  при фиксированном значении , вычислялись отрезки аналогичных кривых в пространстве  при фиксированном значении . В результате находилась зависимость решения (2.5) от двух параметров.

По такой же схеме осуществлялось построение решений краевой задачи (2.1), (2.10). Начальные условия ,  и параметр  (или ) считались неизвестными, краевые условия (2.10) в точке  служили уравнениями для их определения. Эти уравнения задают некоторую кривую  в пространстве , причем точка [, , ], отвечающая стационарному решению , лежит на этой кривой. В точке  уравнения, задающие кривую , имеют особенность, и в её окрестности построение  сводилось к решению более сложной, чем (2.1), (2.10), краевой задачи. Новая задача ставилась на основании следующего наблюдения. Если  – решение задачи (2.1), (2.10), то ее производная  является решением уравнения в вариациях

                                           (3.6)

и удовлетворяет соотношениям (ср.(2.9))

,   

Положив в последних соотношениях , найдем краевые условия, определяющие решение :

,                                   (3.7)

Пусть теперь   – решения уравнения (3.6) с прежними значениями . Задача (3.6), (3.7) имеет нетривиальные решения в том и только том случае, когда

Можно показать, что краевая задача (2.1), (2.10) в окрестности решения  эквивалентна краевой задаче

                                   (3.8)

для системы (2.1), (3.6), причем новая задача не имеет особенностей в точке . Аналогичным образом вместо краевой задачи (3.8) можно рассматривать краевую задачу

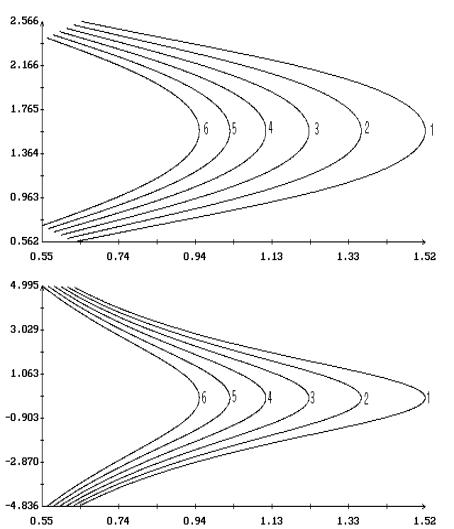
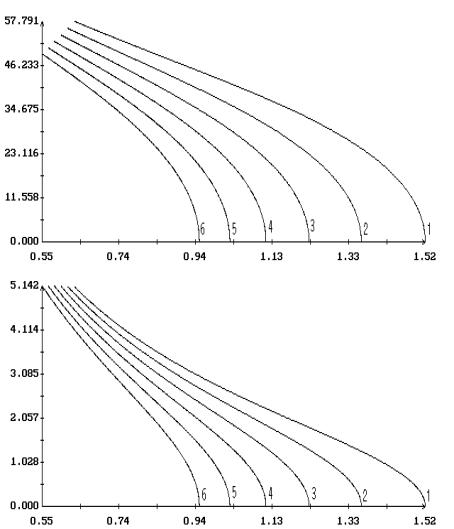
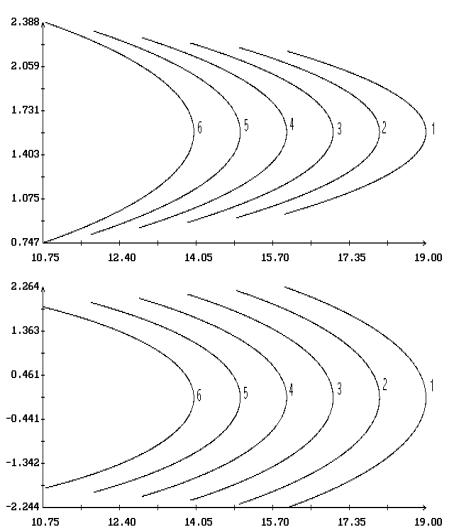
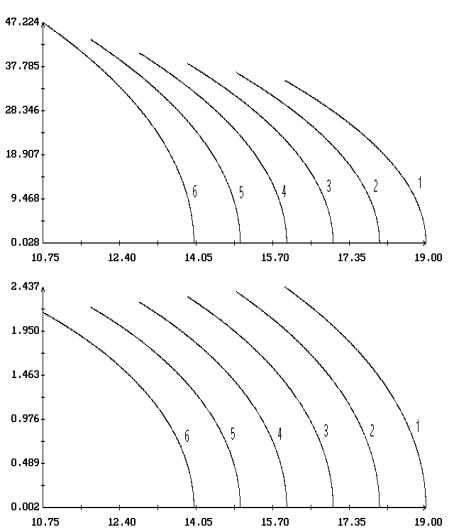
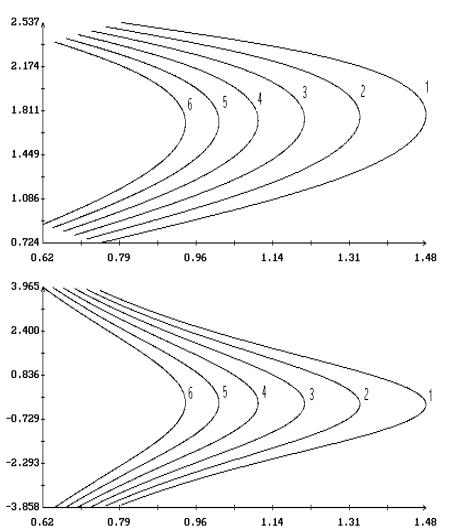
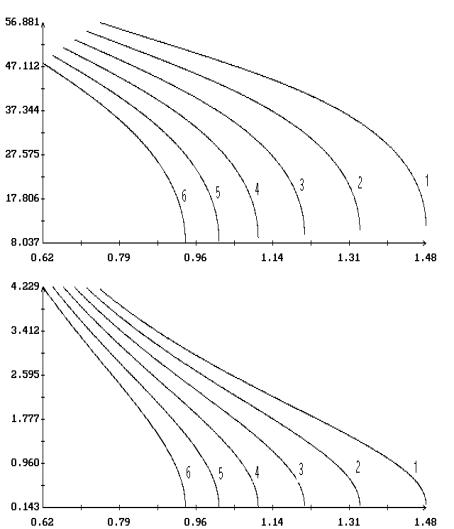
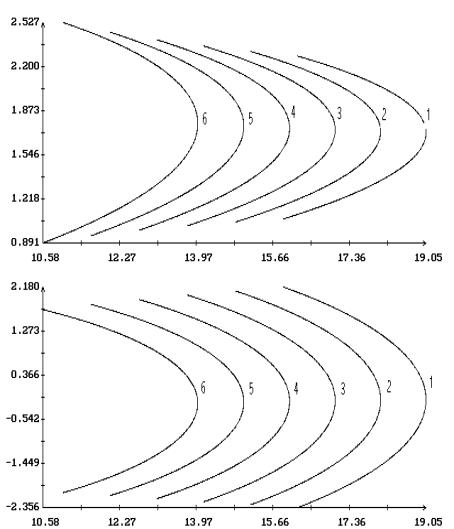
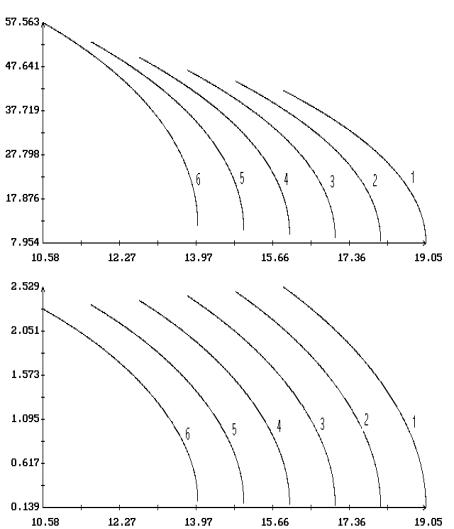
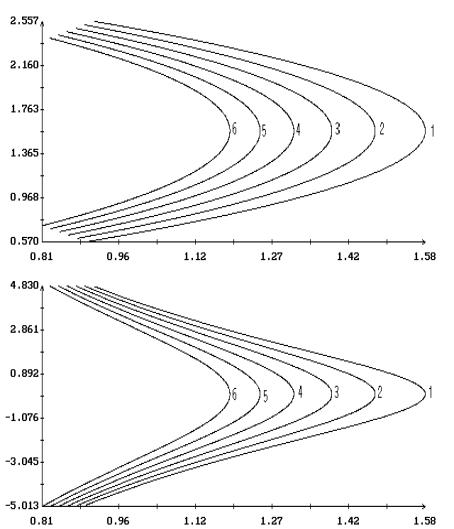
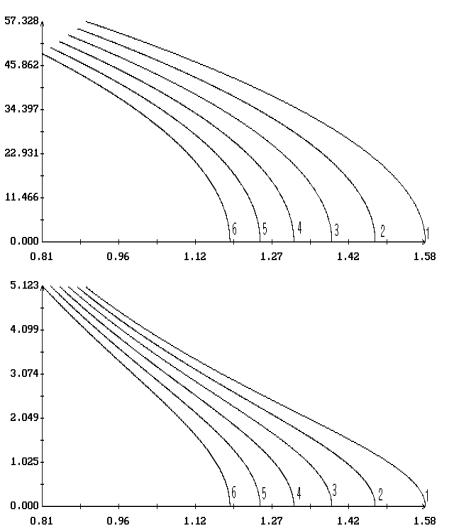
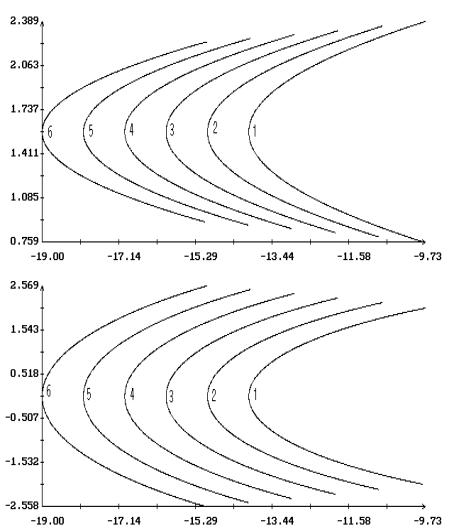
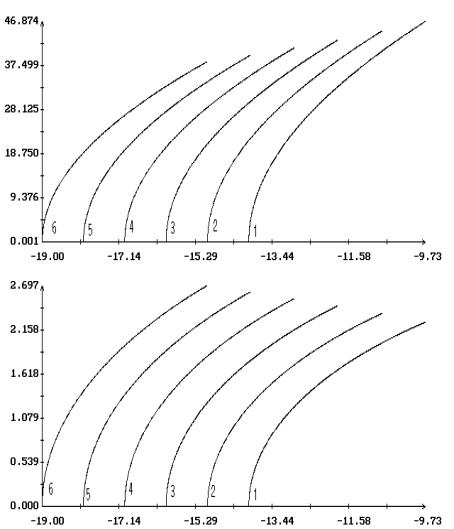
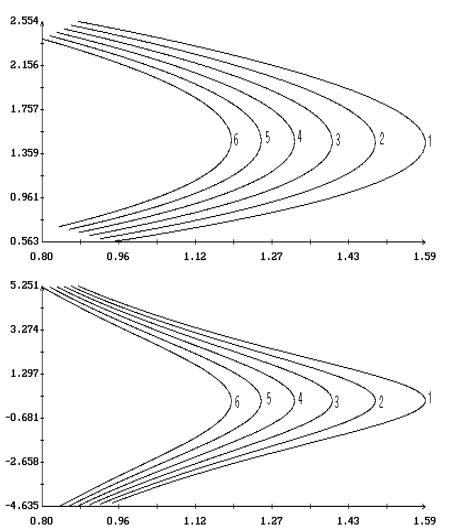
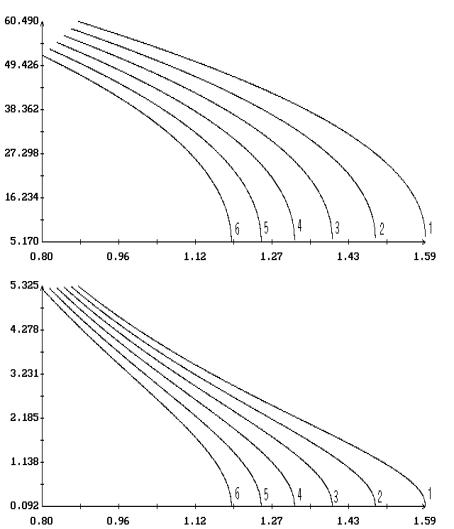
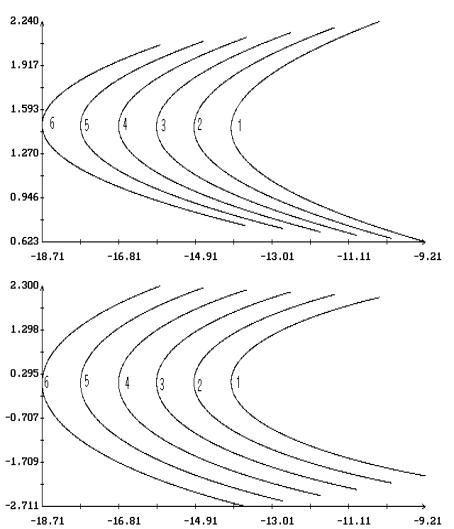
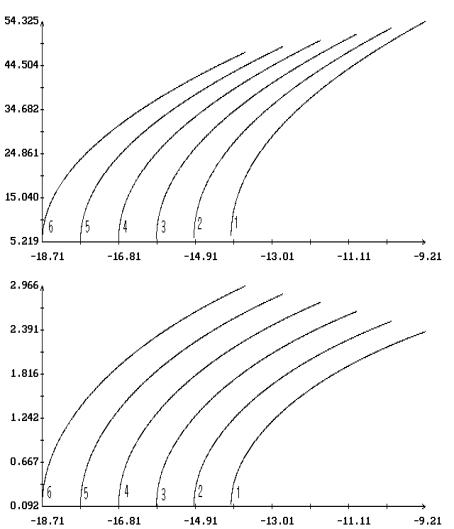
Примеры продолжения короткопериодических решений Ляпунова по параметрам  и  в случае ,  и  приведены на рис. 1. – 8. Здесь результаты продолжения представлены графиками зависимости ненулевых начальных условий решений краевых задач (2.4), (2.7) и (2.1), (2.10) от одного из этих параметров при фиксированном значении другого. Кроме того, на этих рисунках для вычисленных решений приведены аналогичные графики максимального угла  между осями  и  и максимальной проекции  угловой скорости оси  на плоскость . Указанные величины определены соотношениями

,   

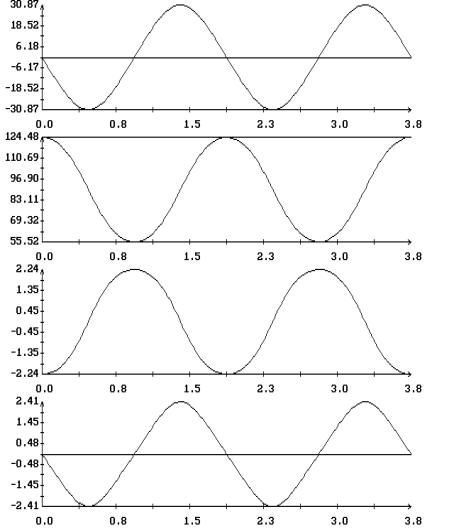
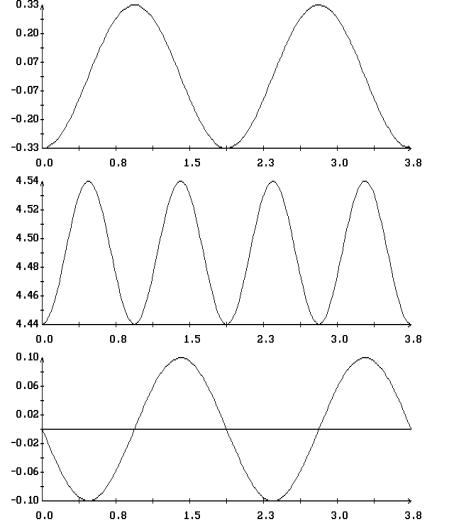
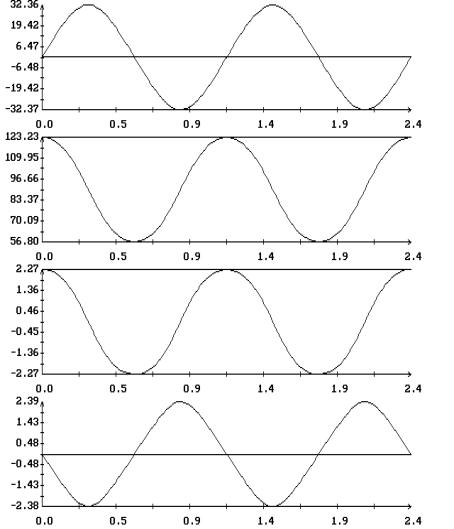
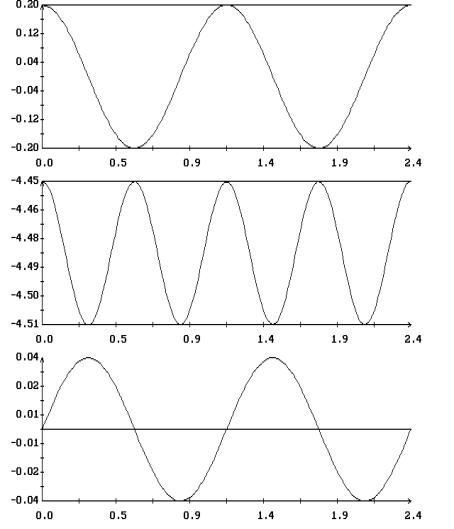
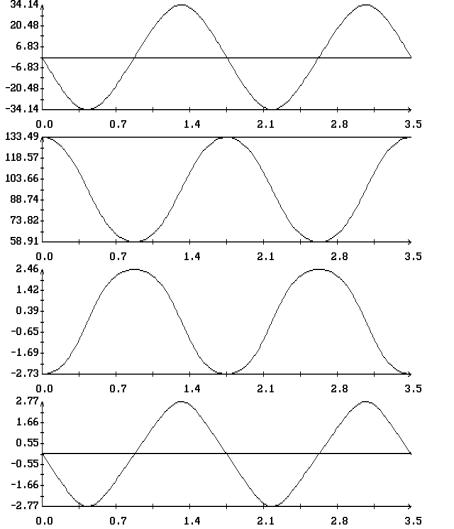
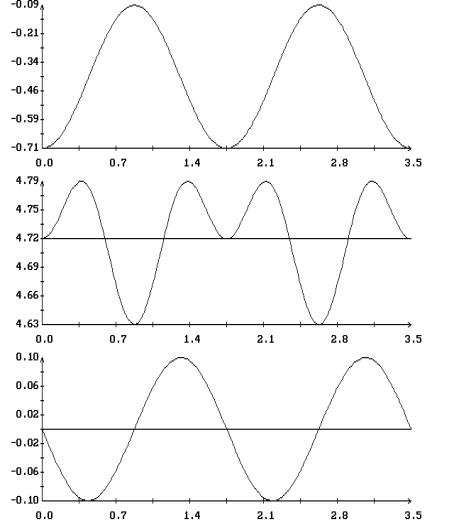
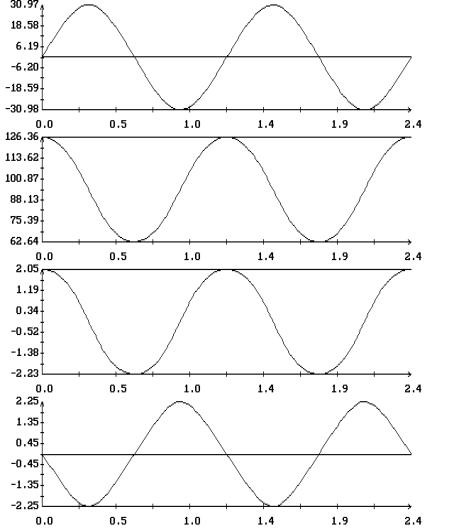
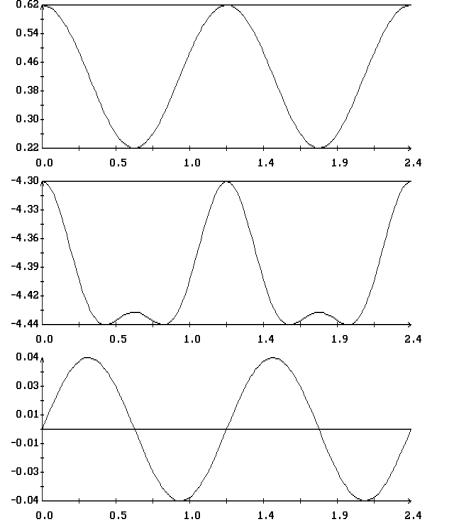
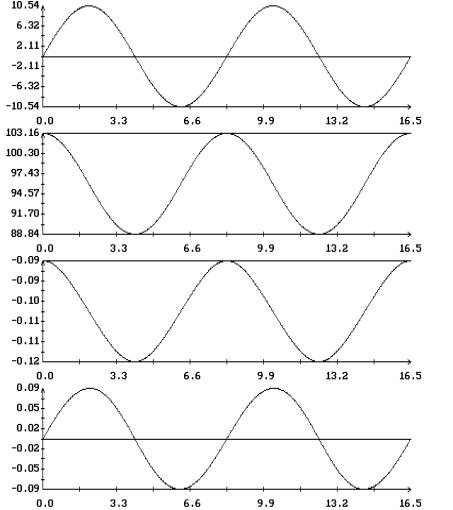
Примеры найденных периодических решений приведены на рис. 9 – 12 . Решения построены на отрезках  и представлены графиками зависимости от времени переменных уравнений (1.1) и компонент безразмерного кинетического момента спутника в орбитальной системе координат

,

,

.

        Графики зависимости от  или  начальных условий  и  на рис. 1 – 8 выглядят симметричными соответственно относительно прямых  и , но точная симметрия имеет место только в случае . Отвечающие симметричным точкам на этих графиках (точнее, точкам с одинаковыми абсциссами) периодические решения получаются одно из другого сдвигом по  на половину периода. Следовательно, такие симметричные точки задают одно и то же периодическое решение, и каждой паре симметричных точек на графиках начальных условий отвечает одна точка на графике величины  или .

        Как показывает анализ рис. 9 – 12, при ,  в найденных периодических решениях , . В переменных ,  последние соотношения имеют вид , . Эти соотношения характерны для движений спутника, близких регулярной прецессии Эйлера динамически симметричного твердого тела. Таким образом, при указанных значениях  и  короткопериодические решения уравнений (1.1) описывают слабо возмущенную регулярную прецессию Эйлера. Собственный кинетический момент спутника в этих решениях практически не меняется (ср. графики функций  на рис. 9 – 12). Колебания его абсолютной величины составляют не более нескольких процентов от ее максимального значения, а направление вектора собственного кинетического момента с погрешностью в несколько градусов совпадает с направлением оси  (нормали к плоскости орбиты) или противоположно ей.

        4. Устойчивость периодических решений. Для исследования устойчивости периодических решений вычислялись их мультипликаторы – собственные числа матриц монодромии уравнений в вариациях (3.2) и (3.6). Свойства симметрии исследуемых решений позволяют установить специальные свойства этих матриц. Рассмотрим сначала задачу (2.1), (2.10). Пусть  – решение этой задачи, продолженное на всю действительную ось как решение уравнения (2.1). Уравнение в вариациях для  имеет вид (3.6). Матрица этого уравнения – периодическая с периодом и в силу соотношений (2.2) и (2.9) при любом  удовлетворяет равенству

                         (4.1)

        Обозначим через  матрицу фундаментальной системы решений уравнения (3.6) с начальным условием . Вследствие (4.1)

                                               (4.2)

        Матрица монодромии уравнения (3.6)  обладает следующим свойством:  при любом . Взяв , получим . В силу (4.2) . Таким образом,  и, следовательно, . Используя последнее равенство, можно доказать, что характеристическое уравнение матрицы  – возвратное [2]. Кроме того, в силу автономности системы (2.1) это уравнение имеет корень, равный 1. С учетом сделанных замечаний характеристическое уравнение матрицы монодромии имеет вид

                                            (4.3)

где  – коэффициент. Если , то все корни уравнения (4.3) лежат на ок­ружности  и выполнены необходимые условия орбитальной устойчивости исследуемого периодического решения. В противном случае это реше­ние орбитально неустойчиво.

        Приведенные соотношения и утверждения справедливы для решений краевой задачи (2.4), (2.7), но в случае этой задачи расчет мультипликаторов проводился иначе. Пусть теперь  – решение задачи (2.4), (2.7), продолженное на всю действительную ось как решение уравнения (2.4). Уравнение в вариациях для  имеет вид (3.2). Матрица этого уравнения в силу соотношения (2.3) при  и соотношения (2.6) удовлетворяет равенству

где  – любое число. Вследствие этого равенства и равенства (4.1) (при ) матрица уравнения (3.2) является периодической с периодом . Матрица монодромии уравнения (3.2) равна , ее характеристическое уравнение имеет вид (4.3).

        В процессе продолжения по параметру решений краевых задач (2.4), (2.7) и (2.1), (2.10) в каждой вычисленной точке кривых, задающих эти решения в трехмерных пространствах начальных условий и параметра (см. п. 3) вычислялась соответствующая матрица монодромии, ее собственные числа (мультипликаторы периодического решения) и коэффициент  в уравнении (4.3). Вычисление собственных чисел и коэффициента проводилось независимо. Собственные числа находились с помощью стандартных программ линейной алгебры, коэффициент  вычислялся по следу матрицы монодромии и сумме ее диагональных миноров второго порядка – согласно (4.3) эти два числа равны соответственно  и . Как показали расчеты, неустойчивость вычисленных решений имеет место лишь на весьма узких интервалах изменения параметров  и .

        5. Вращательное движение спутника «Фотон-12». При  и  уравнения (1.1) можно считать простой, но содержательной моделью вращательного движения спутников «Фотон» [6,7]. В частности, построенные периодические решения достаточно похоже описывают установившийся режим вращательного движения «Фотона-12», возникший через несколько суток после начала его неуправляемого полета [7]. Режим характеризовался значениями параметров , , . Движение в этом режиме продолжалось примерно неделю – до окончания полета. Режим медленно эволюционировал, и, разумеется, его нельзя описать периодическими решениями с большой точностью, но примерно в течение одних суток 19.09.99 согласие с предложенным описанием было очень точным. В указанные сутки было , , .

        Эволюция режима движения спутника «Фотон-12» была связана, в основном, с изменением направления вектора его собственного кинетического момента. 19.09.99 этот вектор был направлен практически по нормали к плоскости орбиты. Его отклонения от нормали не превышало . В периодических решениях на рис. 9 и 11этот вектор отклоняется от нормали не более чем на . Указанный факт объясняет повышенную точность описания движения спутника короткопериодическими решениями уравнений (1.1).

6. Периодические решения при . Длиннопериодические решения системы (1.1) можно исследовать точно также, как были исследованы ее короткопериодические решения, но можно воспользоваться другим способом. При  система (1.1) допускает формальное решение, в котором

                                                   (6.1)

 и  определяются уравнениями

,                                            (6.2)

Эти уравнения допускают первый интеграл . Их общее решение представим в виде

,                     (6.3)

Здесь  и  – произвольные постоянные, , , . Для решения (6.3) орт оси  в орбитальной системе координат имеет компоненты . Следовательно, ось  в этой системе движется по конусу с углом полураствора  и осью . В абсолютном пространстве ось  неподвижна.

        Решения (6.1), (6.3) и систему (6.2) будем называть вырожденными. Исследуем вопрос о существовании периодических решений системы (1.1), определенных при достаточно больших значениях  и близких указанным вырожденным решениям. Этот вопрос можно решить с помощью теоремы, доказанной в [8]. Теорему [8] можно было бы непосредственно применить в данном случае, если бы уравнения в вариациях для вырожденной системы (6.2) имели единственное (с точностью до постоянного множителя) нетривиальное периодическое решение. В случае системы (6.2) и ее решения (6.3) это условие не выполнено – частные производные выражений (6.3) по  и  задают линейно независимые периодические решения уравнений в вариациях для (6.2).

        Чтобы удовлетворить указанному условию, сделаем в системе (1.1) замену независимой переменной. Введем вместо  переменную , определив ее соотношением . В результате такой замены вырожденная система принимает вид

,                             (6.4)

        Здесь штрихом обозначено дифференцирование по . Общее решение уравнений (5.4) выражается через эллиптические функции Якоби

,              (6.5)

с модулем ,  – произвольная постоянная. Решение (6.5) – периодическое с периодом .

Уравнения движения спутника, получившиеся из (1.1) переходом к независимой переменной , запишем в виде

,                   (6.6)

,  ,  , 

,  , 

, 

Здесь использованы обозначения работы [8]. Первый интеграл (1.2) в этих обозначениях можно представить так . Здесь  – известная функция.

        В новых обозначениях вырожденная система (5.4) принимает вид

                                                  (6.7)

Ее решение (6.5) при  обозначим . Это решение будем рассматривать при значениях параметра  из отрезка , принадлежащего интервалу  или интервалу . Чтобы сформулировать теорему о периодических решениях системы (6.6), существующих при достаточно больших значениях  и близких к вырожденному решению , , следует заметить, что

и по вырожденной системе (6.7), ее решению  и функциям  и  построить некоторую функцию . Алгоритм построения этой функции описан в [8]. Параметры  и , число  и функция  выступают в данном случае в роли параметров ,  и функций ,  из [8]. Зададимся произвольным числом  и введём в плоскости  множество . Оказывается, существуют такие положительные числа ,  и , что при ,  система (6.6) имеет -периодическое решение , , удовлетворяющее соотношениям

,   

Чтобы можно было говорить о единственности этого решения, следует уточнить главный член разности . В частности, единственность имеет место при условии, что решение , , удовлетворяет краевым условиям (2.10). В случае  эти условия можно заменить условиями (2.7) и взять более широкое множество .

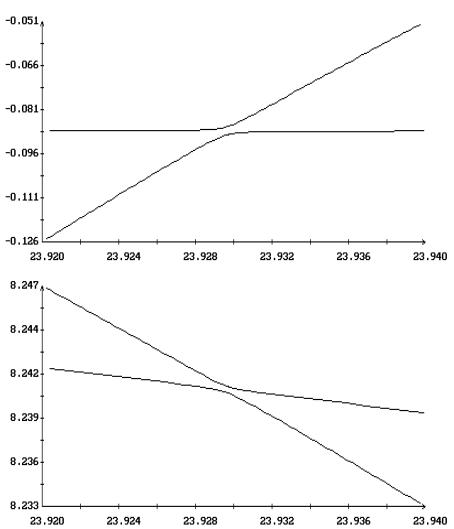
        Решая численно краевую задачу (2.1), (2.10), можно построить решение ,  в явном виде. Примеры вычисления этого решения приведены на рис. 13, 14. На рис. 13 представлены графики зависимости начального условия  и периода  этого решения от  при фиксированном значении начального условия . Фиксация этого начального условия эквивалентна фиксации параметра . На рис. 14 приведены примеры найденных периодических решений. Решения построены на отрезках . Указанные решения задачи (2.10) при  совпадают с решениями, полученными продолжением по  длиннопериодических решений Ляпунова.

        Кривые, приведенные в левой части рис. 13, состоят их отдельных гладких кусков. При выбранном масштабе рисунка разрывы между кусками незаметны и для наглядности обозначены маркерами. Якобиан

для решений задачи (2.10), принадлежащих одному и тому же куску, имеет одинаковый знак. При переходе на соседний кусок знак якобиана меняется. Поведение вычисленных решений в окрестности разрыва при  показано в правой части рис. 13. Как видно из рисунка, разрывы вызваны ветвлением этих решений. Зоны разрывов на оси  определяются соотношением , поэтому решению ,  отвечают отрезки кривых в левой части рис. 13, расположенные вне этих зон.

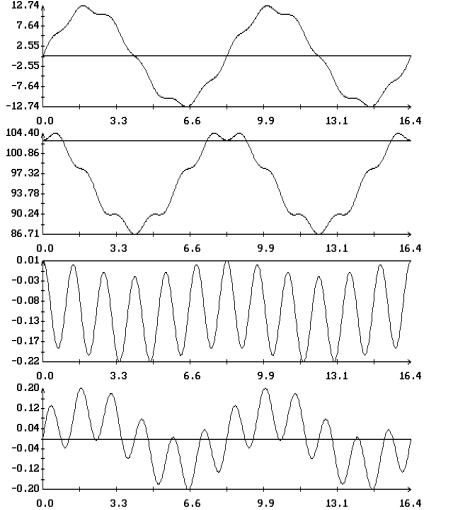
        Левые графики на рис. 14 иллюстрируют решение задачи (2.10), которое можно отождествить с решением , , правые графики относятся к решению, начальные условия которого лежат на кривых, выходящих из зоны разрыва при . Сравнение рисунков показывает, что обнаруженное ветвление обусловлено резонансами между быстрыми и медленными движениями спутника. Введенное выше условие  существования решения ,  служит для исключения таких резонансов.

        Вычисление мультипликаторов рассматриваемых решений задачи (2.10) позволило обнаружить их неустойчивость только на участках кривых начальных условий, отвечающих резонансным решениям.

        В случае  решение ,  можно использовать для приближенного описания прецессии оси вращения Земли под действием Луны или Солнца, но при учете только одного из этих тел. Рассматривая уравнения (1.1) в случае действия Луны, последнюю следует считать притягивающим центром, а Землю – ее спутником, движущемся по круговой селеноцентрической орбите.

        Данная работа выполнена при поддержке РФФИ (проект 02-01-00323).

Список литературы

1.     Черноусько Ф.Л. Об устойчивости регулярной прецессии спутника // ПММ. 1964. Т. 28. Вып. 1. С. 155-157.

2.     Хейл Дж. Колебания в нелинейных системах. М.: Мир, 1966. 230 с.

3.     Малкин И.Г. Некоторые задачи теории нелинейных колебаний. М.: ГИТТЛ, 1956. 491 с.

4.     Сазонов В.В., Сарычев В.А. Периодические решения систем обыкновенных дифференциальных уравнений, близких автономным. Препринт Института прикладной математики АН СССР № 90. М, 1997. 59 с.

5.     Сарычев В.А., Сазонов В.В., Мельник Н.В. Пространственные периодические колебания спутника относительно центра масс // Космические исследования. 1980. Т. 18. Вып. 5. С. 659-677.

6.     Сазонов В.В., Чебуков С.Ю., Абрашкин В.И. и др. Анализ низкочастотных микроускорений на борту ИСЗ «Фотон-11» // Космические исследования. 2001. Т. 39. № 4. С. 419-435.

7.     Абрашкин В.И., Балакин В.Л., Белоконов И.В. и др. Неуправляемое вращательное движение спутника “Фотон-12” и квазистатические микроускорения на его борту // Космические исследования.2003. Т. 41. № 1. С. 45-56.

8.      Воронин А.А., Сазонов В.В. Периодические движения гироскопических систем // ПММ. 1988. Т. 55. Вып. 5. С. 719-729.

Приложение