Аннотация
Исследованы задачи многокомпонентной двухфазной фильтрации в условиях течений с фазовым
переходом. Процесс извлечения флюида из подземного пласта характеризуется малой величиной
потока из скважины. Кроме того, в задаче существует еще один малый параметр, определяемый
отношением плотностей и вязкостей газообразной и жидкой фаз. Система с малыми параметрами
представляет собой сингулярно возмущенную систему. Исследование показывает, что весьма
быстро формируется автомодельный режим с максимально допустимыми значениями газонасыщенности
вблизи скважин. Кроме того, в согласии с теорией сингулярно возмущенных уравнений существует
пограничный по времени и пространству слой, где формируется неавтомодельный режим течения.
Abstract
The multi-component two-phase filtration flow has been considered. The production process is
characterized with the low depression. Besides there is a small parameter determined with
the ratio of the densities and viscosity coefficients. The small parameter system is
a singularly perturbed one. As a result of the investigation it is established the self-similar
regime near the well with a maximal possible value of the gas saturation has been formed
during the short time. The theory of the singularly perturbed equations had resulted
in the existence of the boundary layers both in the space and the time domain where
the flow is not self-similar one.
ВВЕДЕНИЕ
Многие процессы в
гидрологии и нефтяной инженерии приводят к задачам двухфазного течения с "распределенными"
в пространстве фазовыми переходами в пористой среде, происходящими не на
отдельной поверхности, как, например, в классической задаче Стефана, а в
пространственной области. Это имеет место всегда, когда флюид состоит из
нескольких химически различных компонентов, находящихся в различных агрегатных
состояниях. Типичными примерами является выделение газа при течении насыщенной
нефти, углеводородного конденсата при течении природного газа, образование
твердой серы при фильтрации сероводородсодержащего газа, выделение кислых газов
при течении минерализованных растворов подземной воды.
Формирование двухфазных течений весьма
характерно для процессов нефте- и газодобычи. Подобные течения формируются,
во-первых, в тех случаях, когда происходит высвобождение растворенного газа,
во-вторых, когда происходит естественное или искусственное вытеснение
углеводородов. Обычно вытесняющим агентом служит вода, а сам процесс называется
заводнением. Подвижность нефти в пласте во многом зависит от количества растворенного
в ней газа. Растворимость же газа в нефти определяется давлением (и
температурой как постоянным пластовым параметром, но не параметрами процесса
течения). Для того, чтобы поддержать пластовое давление и, как следствие, удержать газ, присутствующий в нефтяных или
водных подземных резервуарах, на практике широко применяется метод заводнения.
По этой причине возникает потребность в математическом моделировании процессов
вытеснения двух несмешивающихся
жидкостей. Одной из первых моделей,
описывающих двухфазные течения, явилась одножидкостная модель “разноцветных
жидкостей” [Герольд С.П., 1932]. В рамках подобных моделей
предполагалось, что область фильтрационного течения полностью заполнена
однородной жидкостью с неизменными характеристиками, например, такими же, как у
вытесняемой жидкости – нефти. Вытесняющая и вытесняемая жидкости отличаются при
этом только цветом, т.е. фактически прослеживается перемещение первоначальной
границы раздела жидкостей при известном поле давлений.
В работах [Куфарев П.П.,
1948] эта модель усовершенствована путем пренебрежения зависимостью от давления
плотности воды и предположения полного взаимного вытеснения жидкостей. Модели
подобного рода называются моделями “поршневого” вытеснения.
Одномерная модель фильтрации
с использованием фазовых проницаемостей и в предположении несжимаемости флюида
была исследована Бакли и Левереттом [Buckley S.E., Leverett M.C., 1942], которые
выявили наличие скачка насыщенности на фронте вытесняющей жидкости, что
указывало на гиперболическую природу уравнений для насыщенности. Классические
модели двухфазной фильтрации, такие как модели Бакли-Леверетта и
Раппопорта-Лиса [Rappoport L.A., Leas W.I., 1953] предполагают
зависимость функций фазовых проницаемостей и капиллярного давления только от насыщенности.
Уравнения течения неоднородных жидкостей в общих предположениях
были даны М. Маскетом и М. Мересом [Chungshiang P.P., 1990],
рассматривающих изотермические процессы при
наличии 3-х фаз (вода, жидкость, газ), находящихся в фазовом равновесии.
Система настолько сложна, что решения могут быть получены, как правило, только
численными методами. Модели, основанные на уравнениях Маскета-Мереса, принято
называть моделями черной нефти (black oil model). Их применение в
некоторых случаях, например, при истощении газоконденсатных месторождений,
невозможно, поскольку возникают эффекты фазовых переходов, существенно
зависящие от компонентного состава углеводородной фазы и термобарических
условий фильтрации.
Для этой цели используют так
называемые композиционные модели, использующие сложные уравнения состояния
смеси и коэффициенты распределения (константы фазового равновесия) [Николаевский В.Н., 1996]. В случае двухфазной фильтрации, уравнения баланса
масс каждого компонента записываются
для каждой фазы отдельно. При этом, в рамках использования методов термодинамики
необратимых процессов, уравнения содержат источники, пропорциональные разности
химических потенциалов компонент в различных фазах. Если устанавливается равенство
химических потенциалов компонент, присутствующих в обеих фазах, то это значит,
что система пришла в термодинамическое равновесие.
Пусть система состоит
из k компонент и j фаз. Тогда, полное число переменных
является суммой числа концентраций j(k-1), числа насыщенностей фаз j-1 плюс два: j(k-1)+(j-1) + 2 = jk+1. Две дополнительные переменные учитывают давление и
температуру в пласте. В условиях локального термодинамического равновесия эти
переменные взаимосвязаны равенствами химических потенциалов компонент
присутствующих в фазах. Всего таких равенств будет k(j-1). При этом число необходимых уравнений баланса масс
компонент, содержащихся в смеси уменьшается и равно просто числу компонент k. Таким образом,
число независимых переменных, соответствующих системе уравнений баланса масс
компонентов, равно разности полного числа переменных и числа равенств
химических потенциалов компонент присутствующих в фазах, т.е. (jk+1)-k(j-1) = k+1, что соответствует
добавлению еще одного уравнения – баланса тепла. В изотермическом случае, когда
T=const, число независимых переменных равно k, т.е. соответствует числу
необходимых уравнений баланса масс компонент, содержащихся в смеси.
ПОСТАНОВКА ЗАДАЧИ
В задаче двухфазной фильтрации для изначально однофазной смеси
рассматриваются уравнения сохранения массы и импульса каждого химического
компонента, которые, при допущениях о химической нейтральности компонент и
изотермичности процесса имеют вид закона Дарси. Уравнения фильтрации
представляют собой уравнения баланса для каждой компоненты, записанные в
дивергентной форме относительно молярных плотностей:
для однофазной области
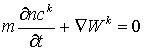 , где , где 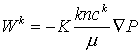 , (1) , (1)
здесь Wk
и ck - фильтрационный
поток и молярная концентрация k-ой компоненты в однофазной смеси; m, K
– пористость и проницаемость среды; t,
P, n, m , k – размерные
время, давление, молярная плотность, динамическая вязкость и относительная
фазовая проницаемость смеси,
и двухфазной области
 (2) (2)
 , ,  (3) (3)
Здесь 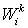 и и  - фильтрационный поток
и молярная концентрация k-ой компоненты в i-й
фазе двухфазной смеси, s – объемная
насыщенность пор фазой B, т.е.
объемная концентрация фазы B. Верхний
индекс "k" используется для k-ой химической компоненты, и нижний
индекс "i" для i-й фазы (i = A, B). Остальные величины с индексами
относятся соответственно к фазам A и В. - фильтрационный поток
и молярная концентрация k-ой компоненты в i-й
фазе двухфазной смеси, s – объемная
насыщенность пор фазой B, т.е.
объемная концентрация фазы B. Верхний
индекс "k" используется для k-ой химической компоненты, и нижний
индекс "i" для i-й фазы (i = A, B). Остальные величины с индексами
относятся соответственно к фазам A и В.
Система уравнений (1) – (3) описывает
эволюцию N-компонентной двухфазной смеси. При этом предполагается, что смесь
находится в состоянии локального термодинамического равновесия. Поскольку
процесс предполагается изотермическим, т.е. Т=const., то система (1) – (3) должна
описывать изменения во времени и пространстве значений порового давления P и концентраций  в смеси каждой из
компонент. Если первоначально система находится в однофазном состоянии, то в смеси каждой из
компонент. Если первоначально система находится в однофазном состоянии, то 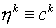 , т.е. , т.е.  есть концентрации
компонент смеси, когда смесь находится в однофазном состоянии, в данном случае
в состоянии A. Равновесные концентрации
компонент в обеих фазах зависят от давления и концентраций, и удовлетворяют
следующим условиям: есть концентрации
компонент смеси, когда смесь находится в однофазном состоянии, в данном случае
в состоянии A. Равновесные концентрации
компонент в обеих фазах зависят от давления и концентраций, и удовлетворяют
следующим условиям:
 , i = A,B (4) , i = A,B (4)
Эти концентрации
связаны соотношениями, вытекающими из условий термодинамического равновесия –
равенства химических потенциалов. Количество этих соотношений равно количеству
компонент смеси:
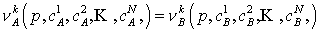 , k=1,..., N (5) , k=1,..., N (5)
где 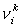 - химический
потенциал k-ой компоненты в i-й фазе. При этом концентрации, как
сказано выше, удовлетворяют условиям
(4). - химический
потенциал k-ой компоненты в i-й фазе. При этом концентрации, как
сказано выше, удовлетворяют условиям
(4).
Для молярной плотности смеси n и полной молярной концентрации k-ой
компоненты смеси ck справедливо соотношение:
 (6) (6)
Здесь  - молярная плотность флюида. Рассматриваемый
процесс – есть процесс выпадения фазы B из фазы A, где величина насыщенности s фазы B определяется соотношением (6). - молярная плотность флюида. Рассматриваемый
процесс – есть процесс выпадения фазы B из фазы A, где величина насыщенности s фазы B определяется соотношением (6).
Начальное состояние системы предполагается
однофазным (состояние A), но для любого t>0 система находится
в двухфазном состоянии, т.е. описывается системой уравнений (2), (3) плюс
условия нормировки концентраций (4) и условия фазового равновесия.
Если просуммировать систему (2), то можно
получить уравнение для полной молярной плотности флюида:
 . .
Для
известных уравнений состояния nA, nB соотношения (6) могут быть
использованы для определения 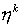 , s. , s.
Для того чтобы перейти к весовой плотности смеси r, умножим молярную
плотность каждой фазы на ее молярную массу:
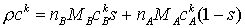 (7) (7)
В итоге получаем соотношение для весовых плотностей
фаз:
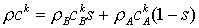 (8) (8)
Уравнения изотермической фильтрации примут вид:
1)
для однофазной области:
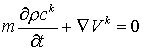 , где , где 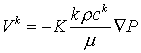 (9) (9)
2)
для двухфазной области:
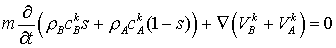 (10) (10)
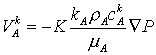 , , 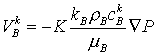 (11) (11)
Здесь Vik -
поток фильтрации весовой концентрации k-ой компоненты в i-ой фазе смеси. Подстановка
(8) в (10) дает:
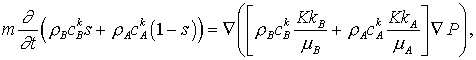 k=1,...,N (12) k=1,...,N (12)
После приведения к
безразмерной форме уравнения сохранения (12) в новых обозначениях примут вид:
 k=1,..., N (13) k=1,..., N (13)
Здесь  , где L –
характерный линейный размер области, а индекс “o” ассоциирован с начальным
состоянием системы: , где L –
характерный линейный размер области, а индекс “o” ассоциирован с начальным
состоянием системы:
 , , 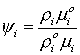 , ,  , , 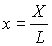 , , 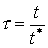 , , 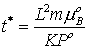 , , 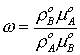 , ,
где 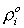 - начальная плотность, вязкости - начальная плотность, вязкости 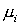 предполагаются
зависимыми от давления, предполагаются
зависимыми от давления,  - безразмерные
плотности, t*- минимальное,
характерное время эволюции, соответствующее менее вязкой среде. - безразмерные
плотности, t*- минимальное,
характерное время эволюции, соответствующее менее вязкой среде.
Для определенности считаем процесс выпадения фазы B из фазы A основным направлением фазового перехода.
Уравнения (13) можно
упростить, если учесть описанные ранее свойства смеси. Просуммируем (13) по
всем компонентам:
 (14) (14)
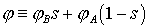 , , 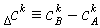 . .
Умножив
(14) на 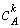 , вычтем полученный результат из k-го уравнения системы (13) и просуммируем полученные уравнения по
всем A-образующим компонентам: , вычтем полученный результат из k-го уравнения системы (13) и просуммируем полученные уравнения по
всем A-образующим компонентам:
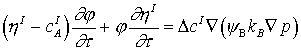 + + (15) (15)
Для упрощения модели
используем свойство контрастности течения. При малых значениях s справедливо разложение: 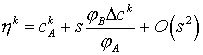 . С учетом свойства (5),
модель контрастного течения многокомпонентной смеси в радиальной системе
координат имеет вид двух уравнений относительно давления p и насыщенности s: . С учетом свойства (5),
модель контрастного течения многокомпонентной смеси в радиальной системе
координат имеет вид двух уравнений относительно давления p и насыщенности s:
 (16) (16)
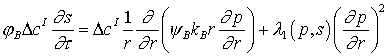 (17) (17)
Величина 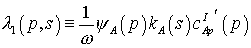 характеризует
интенсивность фазового перехода за счет изменения давления. С учетом (5) эта
система замкнута. характеризует
интенсивность фазового перехода за счет изменения давления. С учетом (5) эта
система замкнута.
Рассмотрим одномерную задачу
возмущения изначально однофазного флюида, соответствовавшего фазе A, в цилиндрической области толщиной H. Однофазный флюид, соответствующий
фазе A, характеризуется массовым
расходом  , где , где 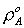 - весовая плотность
фазы A; - весовая плотность
фазы A;  - оценка скорости
движения фазы A; - оценка скорости
движения фазы A;  , ,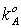 - динамическая вязкость и фазовая проницаемость фазы A; - динамическая вязкость и фазовая проницаемость фазы A;  – начальное давление
в пласте; – начальное давление
в пласте; 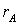 , Н –
соответственно радиус и глубина скважины. , Н –
соответственно радиус и глубина скважины.
Для исключения давления
достаточно пренебречь производной в правой части, которая имеет порядок w:
 , p=1, s=0, (t=0, r®1), , p=1, s=0, (t=0, r®1),
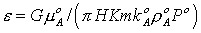 . .
В последнем условии
отброшены малые члены порядка w. Параметр e характеризует интенсивность возмущения
пласта.
Процесс извлечения нефти
характеризуется малыми градиентами давления, т.е. можно считать 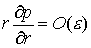 . Разлагая давление р
в асимптотический ряд по параметрам e и w, имеем: . Разлагая давление р
в асимптотический ряд по параметрам e и w, имеем:
 , где , где 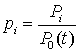
Полагая
при этом 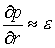 , задачу для насыщенности можно представить в следующем виде: , задачу для насыщенности можно представить в следующем виде:  (18) (18)
Интенсивность фазового перехода l считаем постоянной.
Задача
Коши (18) для уравнения конвективного переноса с затуханием рассмотрена при
следующих аппроксимациях фазовых проницаемостей:
kA=1-s, kB»Lsb, s®0; b>1.
Так как s
= 0 при t = 0, то в начальный
момент времени можно считать, что sb=f(e), где f(e) ® 0 при e ® 0. Если провести анализ
величин в полученных уравнениях, то в области r~e при условии, что sb~e, можно доказать
существование пограничного по времени слоя для t~e1/b. Уравнения,
описывающие процесс на начальном этапе, будут рассмотрены ниже. Уравнение (18),
получено преобразованием системы уравнений (16)-(17), которая обладает
автомодельными решениями, зависящими от переменной 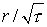 , поскольку уравнения (16)-(17) параболического типа. Можно
ожидать, что уравнение (18) так же обладает решениями подобного типа. , поскольку уравнения (16)-(17) параболического типа. Можно
ожидать, что уравнение (18) так же обладает решениями подобного типа.
В переменной  уравнение (18) примет
вид: уравнение (18) примет
вид:
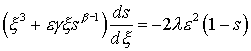 (19) (19)
xÎW={x>0}; s(¥)=0; b>1, где w=Lb
Здесь s=s(x) – монотонная, убывающая
функция, с непрерывной первой производной при x>0. Для исследования автомодельного решения s=s(x), перепишем уравнение (19)
в виде: 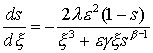 . Рассмотрим . Рассмотрим  . Имеем: . Имеем:  . .
В зависимости от поведения 1-s,
имеем следующие ситуации:

Таким образом, поведение 1-s
означает, что не существует ограниченного решения, для которого в нуле функция s
принимает значение  . .
В
дальнейшем будет показано, что существует единственная функция s(x)®0, если x®¥ и для этой функции s(0)=1. Точка x =0 – точка ветвления, т.е. существуют другие решения, равные 1 в этой
точке. Например, решение s º1 так же является
решением рассматриваемого уравнения. Но существует только единственное решение s(x) такое, что s(x)®0, если x®¥.
Итак, задача Коши для
уравнения (19) принимает окончательный вид:
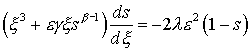
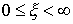 ; ; 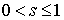 ; ;  (20) (20)
ПОСТРОЕНИЕ АВТОМОДЕЛЬНОГО РЕШЕНИЯ
Построим асимптотическое
разложение решения задачи (20) при e®0. Решение будем искать в
виде ряда:  . Разложение при e®0, x=O(1) назовем внешним (индекс ex); разложение при e®0, x®0 назовем внутренним, или
разложением в промежуточном слое (индекс in).
Обычная техника метода возмущений дает: . Разложение при e®0, x=O(1) назовем внешним (индекс ex); разложение при e®0, x®0 назовем внутренним, или
разложением в промежуточном слое (индекс in).
Обычная техника метода возмущений дает:
 (21) (21)
Функция (21) – удовлетворяет условию задачи
Коши на бесконечности, но коэффициенты sn(x) имеют нарастающие
особенности при x®0, следовательно, обычный
ряд возмущений сходится неравномерно.
В соответствии с общим
принципом приступим к построению внутреннего разложения в окрестности точки x=0. Главный член
внутреннего разложения в окрестности нуля ведет себя как:
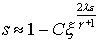 , при x®0, "e (22) , при x®0, "e (22)
Таким образом, решение
задачи (20) при x=0 имеет точку ветвления,
оставаясь к тому же ограниченным. Формальное разложение по степеням параметра e имеет вид (21) со
следующим пределом:
 , e®0, x = O(1) (23) , e®0, x = O(1) (23)
Функция (23) определена во всей области W, а точка x=0 является для нее
полюсом. В итоге смена последовательности предельных переходов приводит к
перерождению типа особенности решений. Точка ветвления для s(x;e) при переходе e®0, x®0 переходит в полюс при
переходе x®0, e®0.
Таким образом, условие
задачи Коши (20) можно сформулировать так: из всевозможных кривых (22) в
окрестности x=0 необходимо выбрать ту,
которая согласуется с формальным решением в области x =O(1). Это утверждение справедливо лишь в том
случае, если выполняется следующая теорема существования и единственности
решения.
Теорема: существует единственное решение автомодельного
уравнения (19) удовлетворяющее условию: 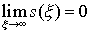 и это решение sº1 в окрестности нуля. и это решение sº1 в окрестности нуля.
Доказательство. Запишем исходное уравнение (19) в виде: 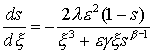 . Выполнив несложные преобразования, получим: . Выполнив несложные преобразования, получим:
 . .
Рассмотрим выражение в скобках для значений x®¥. Оно ограничено, т.е. его значение можно положить
равным  . Откуда следует, что: . Откуда следует, что:
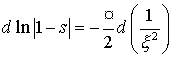 , т.е. , т.е.  . .
Итак,
решение уравнения (2.12) имеет вид:
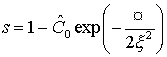 , где , где 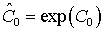 . .
Рассмотрим это выражение более детально. Нетрудно
заметить, что если x®¥, то экспоненциальный множитель стремится к единице.
Следовательно, для выполнения условия 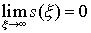 , необходимо чтобы
константа , необходимо чтобы
константа  . .
Таким образом, условие на бесконечности  , выбором константы , выбором константы 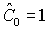 , единственным образом определяет решение тождественно равное
1 в окрестности нуля. Теорема доказана, т.е. действительно формальное
разложение в области x=O(1) единственным образом определяет из всего
множества решений в окрестности нуля то, для которого s º1. ▄ , единственным образом определяет решение тождественно равное
1 в окрестности нуля. Теорема доказана, т.е. действительно формальное
разложение в области x=O(1) единственным образом определяет из всего
множества решений в окрестности нуля то, для которого s º1. ▄
Итак, для решения s(x,e) задачи (20)
построены внешнее разложение (21), внутреннее разложение (22) и рассмотрены
поведения коэффициентов при значении x®0 и при значениях x®¥ соответственно. Нетрудно
заметить, что ряды между собой не согласованы. Начиная с главных членов,
слагаемые в разложениях отличаются зависимостью от малого параметра e: во внешнем
разложении эта зависимость степенная, тогда как во внутреннем – показательная.
Как следует из работ Ломова С.А. [Ломов
С.А., 1981], составное
асимптотическое разложение сходится неравномерно, поэтому задача бисингулярно возмущена. Это наводит на мысль о том, что
существует еще один масштаб и еще одно асимптотическое разложение решения s(x,e) в области,
промежуточной между значениями  и значениями и значениями  . .
Масштаб промежуточного слоя 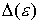 может быть найден
следующим путем. Если x®0, то слагаемое x3s/ является главным в левой части (19), тогда
как в формальном разложении (21) главным будет слагаемое egxsb-1s/. Поэтому, разложение (23) становится
некорректным, начиная с зоны, где оба слагаемых в левой части (19) оказываются
одного порядка. Размер этой зоны и является размером промежуточного слоя. может быть найден
следующим путем. Если x®0, то слагаемое x3s/ является главным в левой части (19), тогда
как в формальном разложении (21) главным будет слагаемое egxsb-1s/. Поэтому, разложение (23) становится
некорректным, начиная с зоны, где оба слагаемых в левой части (19) оказываются
одного порядка. Размер этой зоны и является размером промежуточного слоя.
Для построения разложения в
промежуточном слое, используется метод растяжения переменой 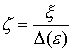 в этой области. При
этом масштаб новой переменной определяется условием равенства порядков
слагаемых уравнения (19) в
промежуточном слое. Главный член промежуточного разложения ищем в виде: s(z×D) » d(e) s1(z), откуда получим: D3 = Dedb-1. в этой области. При
этом масштаб новой переменной определяется условием равенства порядков
слагаемых уравнения (19) в
промежуточном слое. Главный член промежуточного разложения ищем в виде: s(z×D) » d(e) s1(z), откуда получим: D3 = Dedb-1.
Заметим, что внешнее разложение соответствует
тому, что главным в уравнении (19) является слагаемое egxsb-1s/, а разложение в промежуточном слое означает
уравнивание порядков обеих частей уравнения. Таким образом, второе необходимое
условие вытекает, если приравнять порядок левой и правой частей в (19): D2d =e2. Два уравнения
содержат два неизвестных параметра, D и d: D(e)=e1-1/2b, d(e)=e1/b.
Характерный размер области
растяжения переменной является нетривиальной дробно-степенной функцией
параметра возмущения.
Уравнение (19), записанное
через новые переменные, приводится к виду уравнения Бернулли относительно
обратной функции z(s1), которое имеет аналитическое решение:
 , Q=g/(lb) (24) , Q=g/(lb) (24)
Константа
C может быть определена из условия
сращивания промежуточного и внешнего разложений. Для этого вводится
"промежуточная" функция s = s/Y(e), где e2<Y<e1/b, которая по порядку
величины соответствует зоне перехода от промежуточной области к внешней
области. Такая перенормировка означает, что рассматривается промежуток, где
функция s меняется от e1/b до e2. Естественно, что
эта область примыкает к внешней асимптотике, так как s(¥)=0. Разложения
(23), (24), для обратных функций xex(s) и xin(s),
записанные через промежуточную переменную в переходной зоне должны совпадать,
тогда C=0.
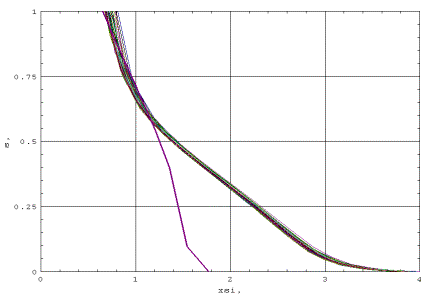
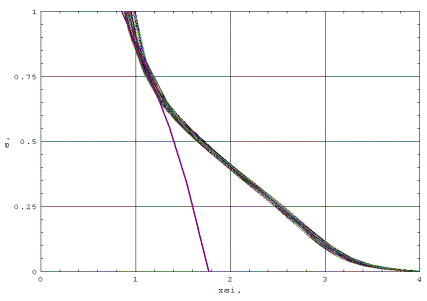
Кривая 3 на фиг. 1
иллюстрирует поведение внутреннего разложения. Характер точного решения 1,
внешнего разложения 2, разложения в промежуточном слое 3 и их сращивание
представлены на фиг. 2.
В работах Вазова В. [Вазов В., 1968] и Евграфова М.А. [Евграфов
М.А., 1979], интеграл в
(3.b.4) может быть представлен в виде следующего разложения приx®0:
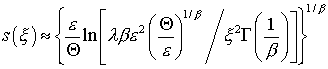 (25) (25)
Это
соотношение показывает, что в промежуточном слое решение ведет себя как дробная
степень логарифмической функции: s » A(elne)1/b , где A константа.
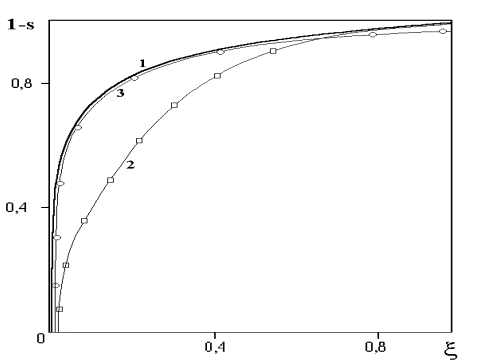
ФИГ. 1 Кривая 3 иллюстрирует поведение внутреннего
разложения.

ФИГ. 2 Показан характер
точного решения 1, внешнего разложения 2, разложения в промежуточном слое 3 и
их сращивание.
НЕАВТОМОДЕЛЬНОЕ РЕШЕНИЕ
Вернемся
к исходной задаче насыщенности (18) с учетом аппроксимаций фазовых
проницаемостей kA=1-s, kB»Lsb, где b>1:
 (26) (26)
Как указывалось выше, параметр e характеризует интенсивность возмущения пласта. Возмущение
считается малым, поэтому e <<1.
Поскольку начальное условие
для насыщенности 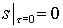 , то для малых времен можно предположить, что s=O(ea) и насыщенность отлична от нуля для малых значений r. Перенормируем
уравнение (26) следующим образом. Для этого, как было проделано ранее, искомую
функцию s представим в виде s=e1/bs1(z)+O(e2/b) и введем новую
переменную , то для малых времен можно предположить, что s=O(ea) и насыщенность отлична от нуля для малых значений r. Перенормируем
уравнение (26) следующим образом. Для этого, как было проделано ранее, искомую
функцию s представим в виде s=e1/bs1(z)+O(e2/b) и введем новую
переменную 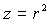 . Тогда, для переменной t находим: t = te2-1/b и уравнение (26)
примет вид: . Тогда, для переменной t находим: t = te2-1/b и уравнение (26)
примет вид:
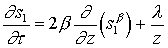 (27) (27)
В силу предположения, что
при малых временах s<<1 для второго слагаемого в
правой части (27) справедлива оценка:  . Тогда интенсивность источника, характеризующую величину
потока флюида к центру области, определяем, как интеграл от функции . Тогда интенсивность источника, характеризующую величину
потока флюида к центру области, определяем, как интеграл от функции 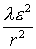 по области,
ограниченной окружностями с радиусами ro и R – соответственно,
внутренней и внешней границами области, деленный на ее площадь: по области,
ограниченной окружностями с радиусами ro и R – соответственно,
внутренней и внешней границами области, деленный на ее площадь:
  . .
Здесь ro<<1, поэтому интеграл
положителен: 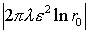 , а соответственно, площадь области: , а соответственно, площадь области:  . Откуда следует: . Откуда следует:  ® ®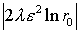 . .
Таким образом, уравнение (27)
можно рассматривать как уравнение с
источником. Предполагая, что источник постоянен на начальном этапе процесса,
приходим к гиперболическому уравнению с константой в правой части:
 (28) (28)
Здесь 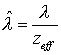 - среднее значение источника. Выписав характеристическое
уравнение, находим уравнения характеристик: - среднее значение источника. Выписав характеристическое
уравнение, находим уравнения характеристик:
 и и 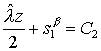 (29) (29)
Соответственно, общее решение запишем в виде:
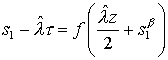 или или  (30) (30)
Решение s находим, используя начальное и граничное условия из (26):
для
начального условия t = 0 Þ s1 = 0, f = 0. Тогда s1 = 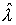 t. t.
для
граничного условия z = 1 Þ s1 = 0, 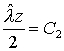 . Тогда . Тогда 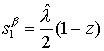
Откуда следует соотношение для переменной по
времени: 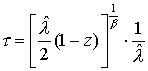 . .
Поясним полученные результаты. В начальный
момент насыщенность новой фазы в нуле мала, т.е. имеет порядок e1/b и отлична от нуля
только для достаточно малых значений z. Далее происходит
нарастание насыщенности в нуле и соответственно ее профиль смещается к границе
области z=1. Это нарастание происходит до момента времени  . При этом для малой интенсивности фазового перехода . При этом для малой интенсивности фазового перехода 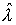 характерное время
нарастания может быть достаточно большим. Как только значение насыщенности
становится максимальным, характер поведения решения принципиально меняется. характерное время
нарастания может быть достаточно большим. Как только значение насыщенности
становится максимальным, характер поведения решения принципиально меняется.
Когда значение насыщенности
максимально smax=1, то решение становится автомодельным, т.е. для
времен  профиль насыщенности
остается постоянным, смещаясь к границе области z=1. По сути, автомодельное
решение представляет собой волну, движущуюся из центра координат к границе
области, где значение насыщенности равно нулю. профиль насыщенности
остается постоянным, смещаясь к границе области z=1. По сути, автомодельное
решение представляет собой волну, движущуюся из центра координат к границе
области, где значение насыщенности равно нулю.
Итак, для времен  начальная задача Коши
имеет неавтомодельное решение, которое описывает нарастающий профиль
насыщенности новой фазы. Как только
насыщенность новой фазы приближается к максимуму, условия применимости
уравнения (26) нарушаются и решение становится автомодельным. начальная задача Коши
имеет неавтомодельное решение, которое описывает нарастающий профиль
насыщенности новой фазы. Как только
насыщенность новой фазы приближается к максимуму, условия применимости
уравнения (26) нарушаются и решение становится автомодельным.
МЕТОД ЧИСЛЕННОГО РЕШЕНИЯ
Как пояснялось выше, уравнения фильтрации
представляют собой уравнения баланса для каждой компоненты, записанные в
дивергентной форме относительно молярных плотностей. В том случае, когда
компоненты несжимаемы, система
уравнений непрерывности при двухфазной двухкомпонентной фильтрации
сводится к уравнению гиперболического типа для насыщенности одной из компонент
и уравнению эллиптического типа для порового давления (задача Баклея –
Леверетта).
В работах [Pergament A.Kh., Koldoba A.V., Poveschenko Yu.A., Simous N.A. 2000; Radvogim Yu.B. 2001] показано, что
в общем случае уравнения фильтрации могут быть представлены в виде системы
уравнений адвекции для концентраций компонент и уравнения параболического типа
для порового давления. Тогда, система уравнений фильтрации может быть
представлена в двух видах: в виде системы уравнений баланса относительно
молярных плотностей или в виде системы уравнений адвекции для молярных
концентраций и уравнения параболического типа для порового давления. Таким
образом, основываясь на идеях С.К. Годунова, можно построить метод предиктор –
корректор для уравнений фильтрации. На этапе предиктора разрешается с помощью
явной схемы уравнение переноса и на основе неявной схемы уравнение для порового
давления. На этапе корректор, по известному поровому давлению определяются
молярные плотности компонент, а затем осуществляется дивергентное замыкание
системы посредством удовлетворения условий термодинамического равновесия.
В
случае двухкомпонентной двухфазной смеси можно представить систему уравнений
баланса (1) и (2) в виде:
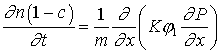 (31) (31)
 (32) (32)
Данные уравнения записаны в универсальной форме одно- и
двухфазного состояния смеси и используются в дальнейшем для построения
разностной схемы типа предиктор-корректор. Перепишем их следующим образом:
 (33) (33)
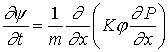 (34) (34)
Здесь  , , 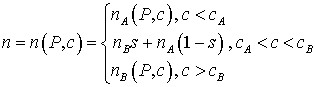 , ,

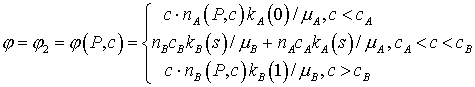
 , , 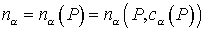
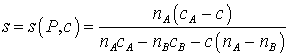
Индексы  соответствуют жидкой
и газообразной фазам; P – поровое
давление; K – общая проницаемость; с, s – молярная концентрация и
насыщенность легкой компоненты (газа); n
– общая молярная плотность смеси; соответствуют жидкой
и газообразной фазам; P – поровое
давление; K – общая проницаемость; с, s – молярная концентрация и
насыщенность легкой компоненты (газа); n
– общая молярная плотность смеси; 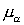 - вязкость; ka – относительная
проницаемость фазы a. - вязкость; ka – относительная
проницаемость фазы a.
Система (31)-(34) описывает различные состояния: однофазное
(с<сA, жидкое состояние
или с>сB, газообразное
состояние) и двухфазное состояние (сA<с<сB).
Причем s определяется только двухфазным состоянием.
Последнее выражение есть следствие соотношений, вытекающих из условий
термодинамического равновесия:
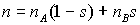 , ,  . .
Здесь 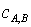 - есть функции
порового давления, определяемые из условий равенства химических потенциалов.
Коэффициенты уравнений соотносятся с коэффициентами модели черной нефти [Aziz
K., Settary A., 1979] следующим образом: - есть функции
порового давления, определяемые из условий равенства химических потенциалов.
Коэффициенты уравнений соотносятся с коэффициентами модели черной нефти [Aziz
K., Settary A., 1979] следующим образом:
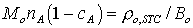 , , 
 , , 
Здесь
 - молекулярные массы
компонентов; RS(P), RV(P)
– растворимость газа и газообразование нефти. Для упрощения используем
модельные уравнения состояния [А.В. Колдоба, Е.В. Колдоба, 1999]: - молекулярные массы
компонентов; RS(P), RV(P)
– растворимость газа и газообразование нефти. Для упрощения используем
модельные уравнения состояния [А.В. Колдоба, Е.В. Колдоба, 1999]:
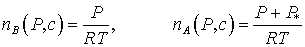 , ,
 , ,
с параметрами:

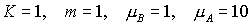
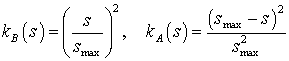 . .
Мы пытаемся определить такую
функцию q, что поток 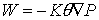 будет непрерывен на ударных
волнах конечной интенсивности. Рассмотрим скорость D ударной волны для
одномерной задачи. Обратим внимание на [f] скачок функции f на фронте волны. Мы
ищем функцию q(P,c), чтобы
удовлетворить условия Гюгонио на фронте ударной волны: будет непрерывен на ударных
волнах конечной интенсивности. Рассмотрим скорость D ударной волны для
одномерной задачи. Обратим внимание на [f] скачок функции f на фронте волны. Мы
ищем функцию q(P,c), чтобы
удовлетворить условия Гюгонио на фронте ударной волны:
 . .
В двухфазной области ее можно получить из
условия непрерывности:
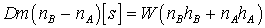 , ,
 , где , где  . .
Таким образом: 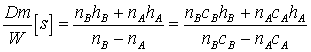 и и  или или 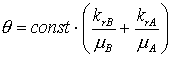 . Отчасти это соответствует значению скорости ударной волны в
двухфазной области: . Отчасти это соответствует значению скорости ударной волны в
двухфазной области:  . .
Это
соотношение может быть применимо для однофазной зоны:
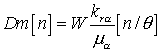 , ,  . .
Итак  , а из этого следует, что , а из этого следует, что 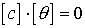 . .
Итак,
полный поток  , где , где 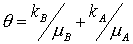 - непрерывен на
разрывах. Используя функцию: - непрерывен на
разрывах. Используя функцию: 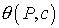 упомянутую ниже,
получаем почти гиперболическое уравнение для концентрации газа с
и почти параболическое уравнение для порового давления P: упомянутую ниже,
получаем почти гиперболическое уравнение для концентрации газа с
и почти параболическое уравнение для порового давления P:
 , , 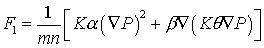 (35) (35)
 , , 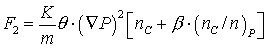 (36) (36)
Здесь 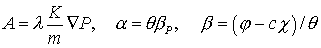
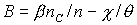 , , 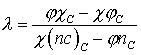 , ,
 , , 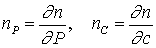 . .
Ряд
некоторых полезных свойств решений может быть получен в результате линейного
анализа уравнений (35), (36). Например, в линейном случае:
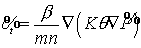 , , 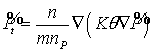 , ,
где  , , 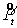 - есть приращения. Откуда
следует, что: - есть приращения. Откуда
следует, что: 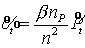 , ,  . Заметим, что np > 0. В однофазной зоне b=0. Это означает, что концентрация
газа увеличивается: . Заметим, что np > 0. В однофазной зоне b=0. Это означает, что концентрация
газа увеличивается: 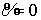 в этом регионе. Обычно
полагают, что внутри двухфазной области фактор b может иметь различные знаки
(главным образом в случае остаточной насыщенности), а знак в этом регионе. Обычно
полагают, что внутри двухфазной области фактор b может иметь различные знаки
(главным образом в случае остаточной насыщенности), а знак 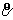 есть равный или
противоположный знаку есть равный или
противоположный знаку  зависящий от позиции
точки. Ниже приведено описание разностной схемы. зависящий от позиции
точки. Ниже приведено описание разностной схемы.
Корректор
– есть явная дивергентная схема определения молярной
плотности.
Для представленной выше схемы расчета, аппроксимирующей уравнения баланса (33),
(34) молярной массы, запишем:
 (37) (37)
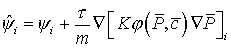 (38) (38)
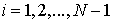 ; ;  - определяется
уравнением - определяется
уравнением 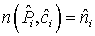 . Функции n=n(P,с), . Функции n=n(P,с),  - значения сеточных
функций во временном слое; - значения сеточных
функций во временном слое; 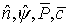 - значения на
временном слое, когда - значения на
временном слое, когда 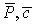 - принимают значения
для времени tj+0.5=tj+tj/2.
Значения - принимают значения
для времени tj+0.5=tj+tj/2.
Значения 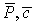 определяются
предиктором. определяются
предиктором.
Предиктор использует неявную
разностную схему для нахождения упомянутых значений. Схема аппроксимаций
уравнений (35), (36) имеет форму:
 (39) (39)
 (40) (40)
Здесь: 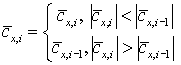
 , ,  , , 
Временной шаг определяется
критерием Куранта, соответствующим скорости переноса концентрации c и вычисляемым на временном
слое:
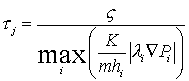 , где , где  - параметр счета. - параметр счета.
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
С
помощью вышеизложенных методов численно была решена следующая одномерная
краевая задача для уравнений переноса:

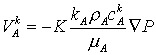 , , 
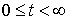 , , 
с граничными условиями:  , , 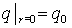 , где , где  – заданный поток на
скважине и начальным условием: – заданный поток на
скважине и начальным условием: 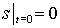 . .
Напомним, что Vik и 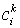 - поток фильтрации и
молярная концентрация k-го компонента в i-й
фазе двухфазной смеси; s – объемная
насыщенность пор фазой B. Остальные величины:
t, P, m, K – размерные время, давление, а также пористость и проницаемость
среды; m, k, r – динамическая
вязкость, относительная фазовая проницаемость и весовая плотность компонента
смеси. - поток фильтрации и
молярная концентрация k-го компонента в i-й
фазе двухфазной смеси; s – объемная
насыщенность пор фазой B. Остальные величины:
t, P, m, K – размерные время, давление, а также пористость и проницаемость
среды; m, k, r – динамическая
вязкость, относительная фазовая проницаемость и весовая плотность компонента
смеси.
В
результате было получено следующее решение для рассмотренной выше краевой
задаче: в течение начального промежутка времени формируется профиль газовой
насыщенности s, а при достижении smax решение приобретает
характер бегущей волны.
На
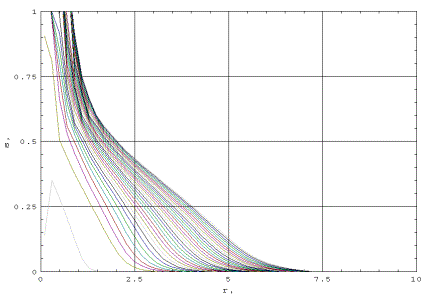
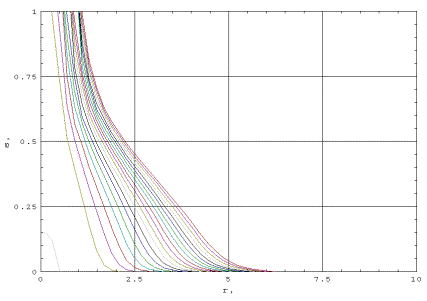
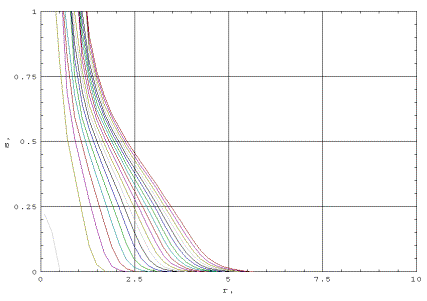
фиг. 3-8 представлена серия графиков исследуемой
краевой задачи фильтрации в переменных r и s построенных для процесса фильтрации с характерным временем t=6000 при заданных значениях потока q=2, 3, 4, 5, 6, 7 и
значения насыщенности smax=1. Используя результаты численного счета, проведем
детальный анализ полученного решения. Как видно из графиков представленных фиг.
3-8, на начальном этапе происходит
формирование профиля насыщенности газовой фазы в течение времени t<10. Времени
достижения максимальной насыщенности зависит от величины потока. Эта
зависимость отражена в приведенной ниже таблице:
|
q
|
2
|
3
|
4
|
5
|
6
|
7
|
|
t
|
10
|
0.9
|
0.34
|
0.13
|
0.091
|
0.0037
|
В начальный момент насыщенность новой фазы
равна нулю либо имеет порядок e1/b, что соответствует
минимальной остаточной насыщенности smin. Далее происходит
нарастание насыщенности в нуле и соответственно ее профиль смещается к границе
области r=10. Это нарастание происходит до момента времени , где , где 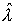 - безразмерное значение интенсивности фазового
перехода. При этом для малой интенсивности фазового перехода - безразмерное значение интенсивности фазового
перехода. При этом для малой интенсивности фазового перехода  характерное время
нарастания может быть достаточно большим. Как только значение насыщенности
становится равным smax, характер поведения
решения принципиально меняется. Это означает, что существует пограничный
временной слой, в течение которого формируется профиль насыщенности газовой
фазы. характерное время
нарастания может быть достаточно большим. Как только значение насыщенности
становится равным smax, характер поведения
решения принципиально меняется. Это означает, что существует пограничный
временной слой, в течение которого формируется профиль насыщенности газовой
фазы.
Когда значение насыщенности максимально, то решение
приобретает характер бегущей волны. Как видно из графиков на фиг. 3-8, для
времен t>10, 0.9, 0.34, 0.13, 0.091, 0.0037 решение
представляет собой бегущую волну, направленную к границе области r=10. Для времен  профиль насыщенности
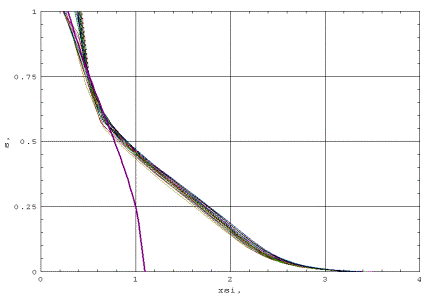
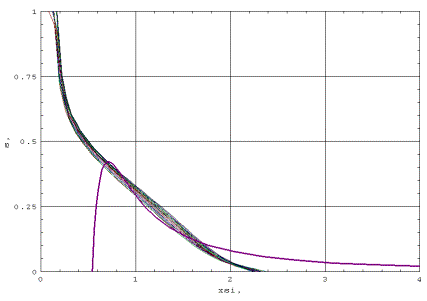
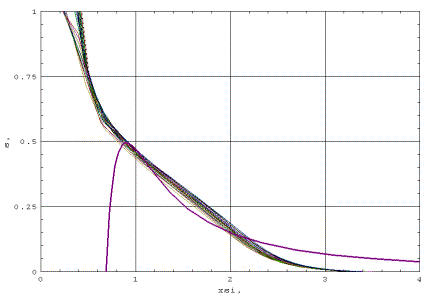
остается постоянным, смещаясь к границе области r=10. На графиках 9-14 профиль
бегущей волны представлен в автомодельных переменных профиль насыщенности
остается постоянным, смещаясь к границе области r=10. На графиках 9-14 профиль
бегущей волны представлен в автомодельных переменных 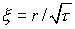 . Из результатов расчета следует, что с хорошей точностью
решение является автомодельным. Как видно из построения, функция s имеет излом при переходе от значения s=1 к значению s<1, так как имеет
слева и справа различные производные: производная слева равна нулю, а справа
отрицательна. . Из результатов расчета следует, что с хорошей точностью
решение является автомодельным. Как видно из построения, функция s имеет излом при переходе от значения s=1 к значению s<1, так как имеет
слева и справа различные производные: производная слева равна нулю, а справа
отрицательна.
Итак, для времен  , что соответствует согласно результатам численной схемы
счета временам t=10, 0.9, 0.34, 0.13, 0.091, 0.0037 соответственно,
краевая задача имеет неавтомодельное решение, которое описывает нарастающий
профиль насыщенности новой фазы. Как
только насыщенность новой фазы достигает smax, условия, при которых было получено уравнение
насыщенности , что соответствует согласно результатам численной схемы
счета временам t=10, 0.9, 0.34, 0.13, 0.091, 0.0037 соответственно,
краевая задача имеет неавтомодельное решение, которое описывает нарастающий
профиль насыщенности новой фазы. Как
только насыщенность новой фазы достигает smax, условия, при которых было получено уравнение
насыщенности  , нарушаются и решение принимает иной характер. Размер
временного слоя, где нарушается условие малой подвижности газовой фазы, есть , нарушаются и решение принимает иной характер. Размер
временного слоя, где нарушается условие малой подвижности газовой фазы, есть 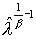 . Для времен . Для времен 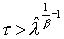 , что соответствует , что соответствует 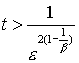 , решение, достигшее smax, ведет себя как бегущая волна. На фиг. 9-14
представлены графики решения исследуемой
краевой задачи фильтрации в автомодельных переменных для различных значений
потоков q. Из построения видно, как образовано автомодельное
решение. По результатам численного счета характерное время формирования профиля
насыщенности новой фазы равно, соответственно t=10, 0.9, 0.34, 0.13,
0.091, 0.0037 и, как следует из графиков представленных на фиг. 9-14, профиль
устанавливается тем дольше, чем меньше значение q, т.е. меньше
значение e. , решение, достигшее smax, ведет себя как бегущая волна. На фиг. 9-14
представлены графики решения исследуемой
краевой задачи фильтрации в автомодельных переменных для различных значений
потоков q. Из построения видно, как образовано автомодельное
решение. По результатам численного счета характерное время формирования профиля
насыщенности новой фазы равно, соответственно t=10, 0.9, 0.34, 0.13,
0.091, 0.0037 и, как следует из графиков представленных на фиг. 9-14, профиль
устанавливается тем дольше, чем меньше значение q, т.е. меньше
значение e.
Сформировавшееся
автомодельное решение может быть описано приближенно уравнением 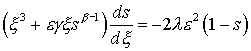 , рассмотренным выше. Уравнение подобного типа имеет особую
точку x=0, в которой
теряется дополнительное условие и является бисингулярно возмущенным, так как
содержит малый параметр e в выражении при производной. Точка x=0 является точкой ветвления этого уравнения. В
окрестности этой точки решение ведет себя как , рассмотренным выше. Уравнение подобного типа имеет особую
точку x=0, в которой
теряется дополнительное условие и является бисингулярно возмущенным, так как
содержит малый параметр e в выражении при производной. Точка x=0 является точкой ветвления этого уравнения. В
окрестности этой точки решение ведет себя как 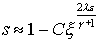 , т.е. s=1 при x=0 для любого C. Однако, как показано в
настоящей работе, только для решения , т.е. s=1 при x=0 для любого C. Однако, как показано в
настоящей работе, только для решения 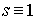 (т.е. C=0) в окрестности x=0 искомая функция s®0 на бесконечности. (т.е. C=0) в окрестности x=0 искомая функция s®0 на бесконечности.
Таким образом, условие на
бесконечности позволяет выбрать одно из решений в точке ветвления.
Так как уравнение 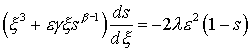 является бисингулярно
возмущенным, то вблизи точки x=0 должен находиться
пограничный слой. Сравнение результатов численного счета краевой задачи
фильтрации с результатами автомодельной задачи для smax=1 и заданных
значений потока q=2, 3, 4, 5, 6, 7 (e=1/5, 1/3, 2/5,
1/2, 2/3, 7/10) показало, что данный пограничный слой совпадает с зоной, где является бисингулярно
возмущенным, то вблизи точки x=0 должен находиться
пограничный слой. Сравнение результатов численного счета краевой задачи
фильтрации с результатами автомодельной задачи для smax=1 и заданных
значений потока q=2, 3, 4, 5, 6, 7 (e=1/5, 1/3, 2/5,
1/2, 2/3, 7/10) показало, что данный пограничный слой совпадает с зоной, где 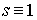 в
автомодельном решении. Численные расчеты показывают, что пограничный слой представляет собой область порядка e, т.е. если поток q и, следовательно, e увеличиваются, то также
увеличивается и пограничный слой, где в
автомодельном решении. Численные расчеты показывают, что пограничный слой представляет собой область порядка e, т.е. если поток q и, следовательно, e увеличиваются, то также
увеличивается и пограничный слой, где  . .
Как показано в работе А.М.
Ильина [Ильин А.М., 1989], для нелинейного уравнения играет роль не только изменение
масштаба независимой переменной x, но и изменение масштаба
неизвестной функции s. Эта промежуточная область характеризуется
дробно-степенным логарифмическим слоем. С одной стороны, решение автомодельной
задачи  в пограничном
слое. С другой стороны, для
автомодельного решения задачи фильтрации существует внешнее разложение по степеням в пограничном
слое. С другой стороны, для
автомодельного решения задачи фильтрации существует внешнее разложение по степеням
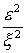 . .
В работах А.Б. Васильевой [Васильева А.Б., Бутузов В.Ф., 1973] и
C.А. Ломова [Ломов С.А., 1968] показано, что данный
пограничный слой возникает в результате решения краевой задачи для нелинейного
дифференциального уравнения первого порядка с множителем 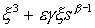 при производной.
Точка x=0 в этом уравнении
является особой точкой, для которой, в частности, дополнительное условие
теряется. В промежуточной области, согласно Ильину А.М., решение ведет себя как
дробная степень логарифмической функции: s»A(elne)1/b, где A константа. При этом размер
промежуточной области является нетривиальной дробно-степенной функцией малого
параметра: D(e)=e1-1/2b. при производной.
Точка x=0 в этом уравнении
является особой точкой, для которой, в частности, дополнительное условие
теряется. В промежуточной области, согласно Ильину А.М., решение ведет себя как
дробная степень логарифмической функции: s»A(elne)1/b, где A константа. При этом размер
промежуточной области является нетривиальной дробно-степенной функцией малого
параметра: D(e)=e1-1/2b.
Для аналитического
автомодельного решения, размер промежуточной области равен 0.3 – 0.765, где это
решение совпадает с аналогичным численным автомодельным решением. По
результатам численного счета начальной задачи, область промежуточного слоя
соответствует 0.05<xsi<0.4 … 0.8<xsi<1.2. Как видно из
графиков на фиг. 9-14, полученное аналитическое автомодельное решение
достаточно точно отражает результаты численного счета начальной задачи.
Полученное решение позволяет
согласовать члены внутреннего разложения в окрестности x=0 с внешним разложением, т.е. где независимая
переменная x=O(1), а решение s разлагается по степеням 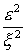 и по величине
эквивалентно и по величине
эквивалентно 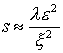 , и таким образом, выбрать с точностью до константы из всего
многообразия решений в точке ветвления одно,
удовлетворяющее условию на бесконечности. Именно это согласование и
позволяет определить, что C=0 для решений стремящихся к нулю на
бесконечности. , и таким образом, выбрать с точностью до константы из всего
многообразия решений в точке ветвления одно,
удовлетворяющее условию на бесконечности. Именно это согласование и
позволяет определить, что C=0 для решений стремящихся к нулю на
бесконечности.
На фиг. 9-20 представлены
две серии графиков исследуемой краевой задачи фильтрации в переменных xsi и s соответственно характерных времен продолжительности процесса t=6000, а также график аналитического решения автомодельного уравнения  во внешней области,
т.е. где независимая переменная x=O(1). Как упоминалось
выше, краевая задача считалась для предельного значения насыщенности smax=1 и заданных
значений потока q=2, 3, 4, 5, 6, 7. Построенные графики
показывают асимптотику поведения решения на границе внешней области, т.е. для во внешней области,
т.е. где независимая переменная x=O(1). Как упоминалось
выше, краевая задача считалась для предельного значения насыщенности smax=1 и заданных
значений потока q=2, 3, 4, 5, 6, 7. Построенные графики
показывают асимптотику поведения решения на границе внешней области, т.е. для  . Решение начальной задачи, полученное по результатам численного
счета, согласуется с аналитическим решением в промежуточной области, т.е. для
значений . Решение начальной задачи, полученное по результатам численного
счета, согласуется с аналитическим решением в промежуточной области, т.е. для
значений  . .
Согласно результатам
численного счета начальной задачи фильтрации, характерное значение r для этой зоны,
равно 2.0 – 2.5 для размера всей области r=10, что
соответствует характерным временам упомянутым выше.
ЛИТЕРАТУРА
1. Вазов
В. Асимптотические разложения решений обыкновенных дифференциальных
уравнений. М.: Мир, 1968. 464 стр.
2. Герольд С.П. Аналитические основы
добычи нефти, газа и воды из скважин. М.-Л.: Нефтеиздат, 1932.
3. Евграфов
М.А. Асимптотические оценки и
целые функции. М.: Наука, 1979.
320 стр.
4. Ильин
А.М. Согласование асимптотических разложений решений краевых задач. М.: Наука, 1989. 336 стр.
5. Васильева
А.Б., Бутузов В.Ф. Асимптотические разложения решений сингулярно возмущенных уравнений. М.: Наука,
1973. 272 стр.
6. Куфарев П.П. Решение задач о
контуре нефтеносности для круга. Доклады АН СССР,
1948, N8, Т.60,
стр.1333-1334.
7. Ломов С.А.
Введение в общую теорию сингулярных возмущений. М.: Наука, 1981. 398
стр.
8. Ломов С.А. Степенной пограничный слой в
задачах с сингулярным возмущением, Изв. АН СССР, сер. Матем. 30, № 4 (1968),
стр. 525-572.
9. Николаевский
В.Н. Геомеханика и флюидодинамика. Москва, Недра, 1996, 447 стр.
10.
Buckley S.E., Leverett M.C. Mechanism of fluid
displacement in sands // Trans. AIME. 1942. Vol.146, p.107-116.
11. Chungshiang P.P.,
Yanosik J.L., Stepenson R.E. A generalized compositional model for
naturally fractured reservoir. SPE Reservoir Engineering, august 1990.
12. Pergament A.Kh.,
Koldoba A.V., Poveschenko Yu.A., Simous N.A. The mathematical modelling of
the multi-phase flow in inhomogeneous media. // Proceedings 7th
Europen Conference on the Mathematics of Oil Recovery. Baveno, Italy, september
2000.
13. Rappoport L.A., Leas
W.I. Properties of linear waterfloods // Trans. AIME. 1953. Vol.198,
p.139-148.
14. Radvogim Yu.B.
The characteristic properties of the two-component filtration equatiens.
Moscow, Preprint, Keldysh Inst. Appl. Math., Rus. Acad. of Sciences, 2001, N
37, p.14 (in Russian).
|
![]() , где
, где ![]() - безразмерное значение интенсивности фазового
перехода. При этом для малой интенсивности фазового перехода
- безразмерное значение интенсивности фазового
перехода. При этом для малой интенсивности фазового перехода ![]() характерное время
нарастания может быть достаточно большим. Как только значение насыщенности
становится равным smax, характер поведения
решения принципиально меняется. Это означает, что существует пограничный
временной слой, в течение которого формируется профиль насыщенности газовой
фазы.
характерное время
нарастания может быть достаточно большим. Как только значение насыщенности
становится равным smax, характер поведения
решения принципиально меняется. Это означает, что существует пограничный
временной слой, в течение которого формируется профиль насыщенности газовой
фазы.![]() профиль насыщенности
остается постоянным, смещаясь к границе области r=10. На графиках 9-14 профиль
бегущей волны представлен в автомодельных переменных
профиль насыщенности
остается постоянным, смещаясь к границе области r=10. На графиках 9-14 профиль
бегущей волны представлен в автомодельных переменных ![]() . Из результатов расчета следует, что с хорошей точностью
решение является автомодельным. Как видно из построения, функция s имеет излом при переходе от значения s=1 к значению s<1, так как имеет
слева и справа различные производные: производная слева равна нулю, а справа
отрицательна.
. Из результатов расчета следует, что с хорошей точностью
решение является автомодельным. Как видно из построения, функция s имеет излом при переходе от значения s=1 к значению s<1, так как имеет
слева и справа различные производные: производная слева равна нулю, а справа
отрицательна. ![]() , что соответствует согласно результатам численной схемы
счета временам t=10, 0.9, 0.34, 0.13, 0.091, 0.0037 соответственно,
краевая задача имеет неавтомодельное решение, которое описывает нарастающий
профиль насыщенности новой фазы. Как
только насыщенность новой фазы достигает smax, условия, при которых было получено уравнение
насыщенности
, что соответствует согласно результатам численной схемы
счета временам t=10, 0.9, 0.34, 0.13, 0.091, 0.0037 соответственно,
краевая задача имеет неавтомодельное решение, которое описывает нарастающий
профиль насыщенности новой фазы. Как
только насыщенность новой фазы достигает smax, условия, при которых было получено уравнение
насыщенности  , нарушаются и решение принимает иной характер. Размер
временного слоя, где нарушается условие малой подвижности газовой фазы, есть
, нарушаются и решение принимает иной характер. Размер
временного слоя, где нарушается условие малой подвижности газовой фазы, есть ![]() . Для времен
. Для времен ![]() , что соответствует
, что соответствует 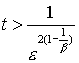 , решение, достигшее smax, ведет себя как бегущая волна. На фиг. 9-14
представлены графики решения исследуемой
краевой задачи фильтрации в автомодельных переменных для различных значений
потоков q. Из построения видно, как образовано автомодельное
решение. По результатам численного счета характерное время формирования профиля
насыщенности новой фазы равно, соответственно t=10, 0.9, 0.34, 0.13,
0.091, 0.0037 и, как следует из графиков представленных на фиг. 9-14, профиль
устанавливается тем дольше, чем меньше значение q, т.е. меньше
значение e.
, решение, достигшее smax, ведет себя как бегущая волна. На фиг. 9-14
представлены графики решения исследуемой
краевой задачи фильтрации в автомодельных переменных для различных значений
потоков q. Из построения видно, как образовано автомодельное
решение. По результатам численного счета характерное время формирования профиля
насыщенности новой фазы равно, соответственно t=10, 0.9, 0.34, 0.13,
0.091, 0.0037 и, как следует из графиков представленных на фиг. 9-14, профиль
устанавливается тем дольше, чем меньше значение q, т.е. меньше
значение e. 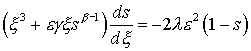 , рассмотренным выше. Уравнение подобного типа имеет особую
точку x=0, в которой
теряется дополнительное условие и является бисингулярно возмущенным, так как
содержит малый параметр e в выражении при производной. Точка x=0 является точкой ветвления этого уравнения. В
окрестности этой точки решение ведет себя как
, рассмотренным выше. Уравнение подобного типа имеет особую
точку x=0, в которой
теряется дополнительное условие и является бисингулярно возмущенным, так как
содержит малый параметр e в выражении при производной. Точка x=0 является точкой ветвления этого уравнения. В
окрестности этой точки решение ведет себя как ![]() , т.е. s=1 при x=0 для любого C. Однако, как показано в
настоящей работе, только для решения
, т.е. s=1 при x=0 для любого C. Однако, как показано в
настоящей работе, только для решения ![]() (т.е. C=0) в окрестности x=0 искомая функция s®0 на бесконечности.
(т.е. C=0) в окрестности x=0 искомая функция s®0 на бесконечности.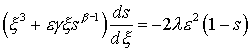 является бисингулярно
возмущенным, то вблизи точки x=0 должен находиться
пограничный слой. Сравнение результатов численного счета краевой задачи
фильтрации с результатами автомодельной задачи для smax=1 и заданных
значений потока q=2, 3, 4, 5, 6, 7 (e=1/5, 1/3, 2/5,
1/2, 2/3, 7/10) показало, что данный пограничный слой совпадает с зоной, где
является бисингулярно
возмущенным, то вблизи точки x=0 должен находиться
пограничный слой. Сравнение результатов численного счета краевой задачи
фильтрации с результатами автомодельной задачи для smax=1 и заданных
значений потока q=2, 3, 4, 5, 6, 7 (e=1/5, 1/3, 2/5,
1/2, 2/3, 7/10) показало, что данный пограничный слой совпадает с зоной, где ![]() в
автомодельном решении. Численные расчеты показывают, что пограничный слой представляет собой область порядка e, т.е. если поток q и, следовательно, e увеличиваются, то также
увеличивается и пограничный слой, где
в
автомодельном решении. Численные расчеты показывают, что пограничный слой представляет собой область порядка e, т.е. если поток q и, следовательно, e увеличиваются, то также
увеличивается и пограничный слой, где ![]() .
.![]() в пограничном
слое. С другой стороны, для
автомодельного решения задачи фильтрации существует внешнее разложение по степеням
в пограничном
слое. С другой стороны, для
автомодельного решения задачи фильтрации существует внешнее разложение по степеням
![]() .
.![]() при производной.
Точка x=0 в этом уравнении
является особой точкой, для которой, в частности, дополнительное условие
теряется. В промежуточной области, согласно Ильину А.М., решение ведет себя как
дробная степень логарифмической функции: s»A(elne)1/b, где A константа. При этом размер
промежуточной области является нетривиальной дробно-степенной функцией малого
параметра: D(e)=e1-1/2b.
при производной.
Точка x=0 в этом уравнении
является особой точкой, для которой, в частности, дополнительное условие
теряется. В промежуточной области, согласно Ильину А.М., решение ведет себя как
дробная степень логарифмической функции: s»A(elne)1/b, где A константа. При этом размер
промежуточной области является нетривиальной дробно-степенной функцией малого
параметра: D(e)=e1-1/2b.![]() и по величине
эквивалентно
и по величине
эквивалентно 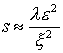 , и таким образом, выбрать с точностью до константы из всего
многообразия решений в точке ветвления одно,
удовлетворяющее условию на бесконечности. Именно это согласование и
позволяет определить, что C=0 для решений стремящихся к нулю на
бесконечности.
, и таким образом, выбрать с точностью до константы из всего
многообразия решений в точке ветвления одно,
удовлетворяющее условию на бесконечности. Именно это согласование и
позволяет определить, что C=0 для решений стремящихся к нулю на
бесконечности. во внешней области,
т.е. где независимая переменная x=O(1). Как упоминалось
выше, краевая задача считалась для предельного значения насыщенности smax=1 и заданных
значений потока q=2, 3, 4, 5, 6, 7. Построенные графики
показывают асимптотику поведения решения на границе внешней области, т.е. для
во внешней области,
т.е. где независимая переменная x=O(1). Как упоминалось
выше, краевая задача считалась для предельного значения насыщенности smax=1 и заданных
значений потока q=2, 3, 4, 5, 6, 7. Построенные графики
показывают асимптотику поведения решения на границе внешней области, т.е. для ![]() . Решение начальной задачи, полученное по результатам численного
счета, согласуется с аналитическим решением в промежуточной области, т.е. для
значений
. Решение начальной задачи, полученное по результатам численного
счета, согласуется с аналитическим решением в промежуточной области, т.е. для
значений ![]() .
.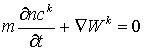 ,
,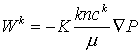 ,
, ,
,
 .
.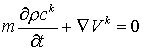 ,
,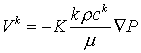
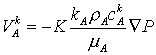 ,
,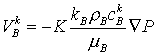
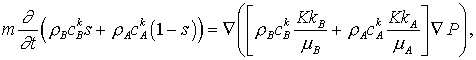

 , где L –
характерный линейный размер области, а индекс “o” ассоциирован с начальным
состоянием системы:
, где L –
характерный линейный размер области, а индекс “o” ассоциирован с начальным
состоянием системы:
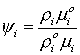 ,
,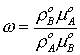 ,
,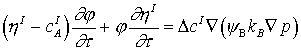 +
+
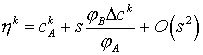 . С учетом
. С учетом 
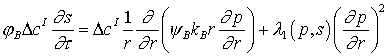

 ,
, 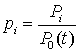

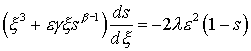
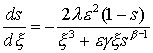 . Рассмотрим
. Рассмотрим  . Имеем:
. Имеем:  .
.
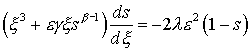
 . Разложение при
. Разложение при 
 ,
,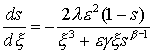 . Выполнив несложные преобразования, получим:
. Выполнив несложные преобразования, получим: .
.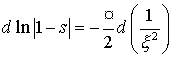 , т.е.
, т.е.  .
.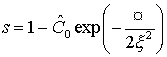 , где
, где 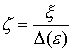
 ,
,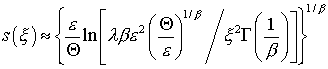




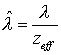 - среднее значение источника. Выписав характеристическое
уравнение, находим уравнения характеристик:
- среднее значение источника. Выписав характеристическое
уравнение, находим уравнения характеристик: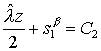
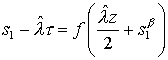

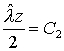 . Тогда
. Тогда 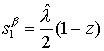
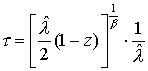 .
.
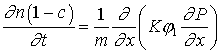


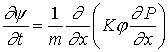
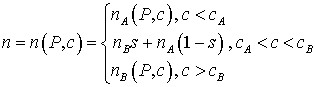 ,
, 
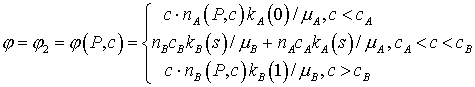
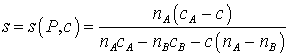
 ,
,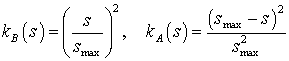 .
. 
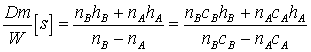
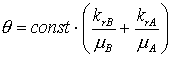

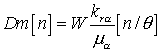
 .
.
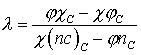 ,
,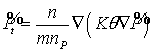 ,
,

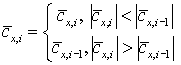
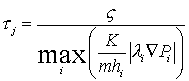 , где
, где 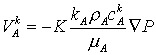 ,
,