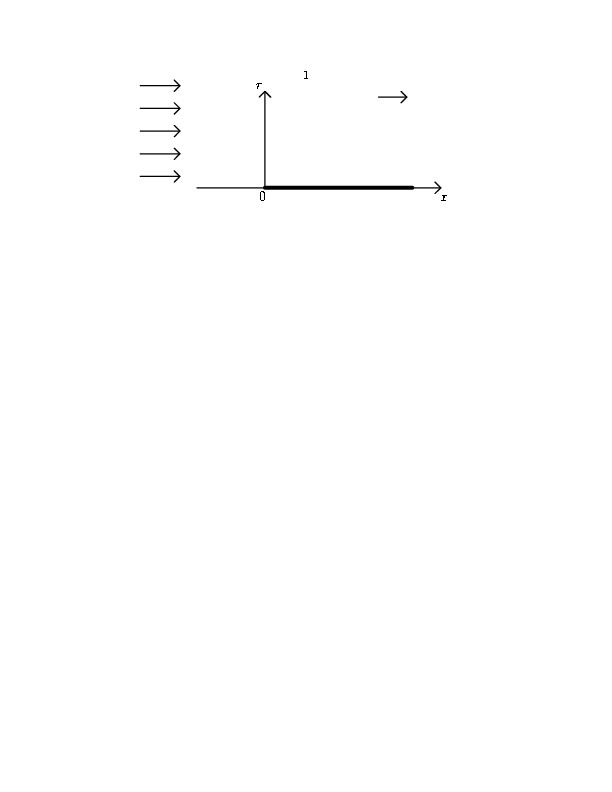
Методы исследования погранслоя на игле
|
|
(1) |
|
(2) |
Используя методы
пространственной степенной геометрии, изложенные в § 1 первой главы,
отбирается укороченная система уравнений, описывающая поток вблизи иглы при x
→
+
∞
.
После введения автомодельных переменных
|
(3) |
укороченная система переходит
в систему двух обыкновенных дифференциальных уравнений, которая сводится к
одному обыкновенному дифференциальному уравнению для h(x) третьего порядка. Асимптотический анализ его решений
методами плоской степенной геометрии, которые изложены в § 2 первой главы,
показал, что это уравнение не имеет решений, удовлетворяющих граничным условиям
прилипания на игле. В § 4 второй главы доказывается, что полученная
укороченная система, соответствующая погранслою вблизи иглы при x
→+∞
,
не имеет также неавтомодельных решений, удовлетворяющих граничному условию (2).
Для этого делается замена переменных
|
т.е. в качестве независимых
переменных берутся x и x.
Полученная система сводится к одному дифференциальному уравнению в частных
производных для h(x,x). При x
→+∞
первым приближением этого уравнения является
уравнение, которое в точности совпадает с обыкновенным дифференциальным
уравнением, полученным в автомодельных координатах. Несмотря на то, что h
зависит в этом случае еще и от x, решения получившегося уравнения все
равно не удовлетворяют граничным условиям прилипания на игле.
В §§ 5 и 6 второй главы
рассматривается возможность существования двуслойного решения исходной системы,
удовлетворяющего граничным условиям (1) и (2). Для этого методами степенной
геометрии из исходной системы была выделена укороченная система, описывающая
поток жидкости в слое, который непосредственно примыкает к слою вблизи иглы.
После введения автомодельных координат
|
(4) |
эта укороченная система
переходит в систему двух обыкновенных дифференциальных уравнений, которая
сводится к одному уравнению для g(h) второго порядка. Асимптотический анализ его решений методами плоской
степенной геометрии показал, что это уравнение имеет решения, которые при h
→
0 имеют асимптотики g=const, g=const h, т.е. в исходных координатах
|
(5) |
Эти асимптотики являются
двумя вариантами граничных условий на внешней границе внутреннего слоя. Вариант
y = const r2
эквивалентен граничному условию (1) и, следовательно, в этом случае применимы
все рассуждения, леммы и теоремы, доказанные для однослойного решения. Для
варианта y = const x2
методами пространственной степенной геометрии выделяется укороченная система,
описывающая погранслой вблизи иглы. И оказывается, что эта укороченная система
в точности совпадает с укороченной системой, описывающей внешний слой. Ее
решения (5) не удовлетворяют граничному условию прилипания на игле (2).
Далее во второй главе
рассматривается возможность существования двуслойного неавтомодельного решения.
Для этого, аналогично случаю однослойного решения, в укороченной системе,
соответствующей внешнему слою, делалась замена переменных x=x, h = r2/x2, g(x,h)=y/x2,
p(x,h)=p.
При x
→
+
∞
первым приближением полученной системы является
система, которая в точности совпадает с системой обыкновенных дифференциальных
уравнений, полученной на внешнем слое после введения автомодельных координат
(4), т.е. при h
→
0
имеются два вида асимптотик решения h=c0(lnx) и
h=c1(lnx)h, где c0(lnx), c1(lnx)
- многочлены от lnx. В исходных координатах эти асимптотики имеют вид
|
(6) |
т.е. опять получили два
варианта граничных условий на внешней границе внутреннего слоя. С точки зрения
пространственной степенной геометрии, при выделении укороченных систем,
описывающих поток во внутреннем слое, варианты граничных условий (6)
эквивалентны вариантам граничных условий (5). Следовательно, в случае y = c0(lnx)r2
укороченная система, описывающая поток во внутреннем слое будет совпадать с
системой для однослойного решения, неавтомодельные решения которой
рассматриваются в § 4 второй главы и которая не имеет решений,
удовлетворяющих граничному условию (2). Для случая y = c1(lnx)x2
укороченная система, описывающая внутренний слой будет такая же, что и для
внешнего слоя. Ее неавтомодельные решения при h
→
0 суть (6) и при x
→+∞
они не удовлетворяют граничному условию прилипания на игле (2).
Основными результатами второй
главы являются теоремы, в которых доказывается, что для задачи осесимметричного
обтекания полубесконечной иглы вязкой несжимаемой жидкостью при x
→+∞
не существует решений, удовлетворяющих всем граничным условиям (1), (2).
В третьей главе
рассматривается задача с большим количеством зависимых переменных. Это задача
осесимметричного обтекания полубесконечной иглы вязкой сжимаемой теплопроводной
жидкостью. Такой поток описывается системой трех дифференциальных уравнений в
частных производных для функции тока y, плотности r и
энтальпии h (аналог температуры) с двумя независимыми переменными: x
(вдоль оси симметрии) и r (расстояние от оси x). Игла задается,
как и во второй главе, как x
≥
0, r=0. Граничные условия задаются в
бесконечности
|
(7) |
и на игле (2). Методами
пространственной степенной геометрии выделяется укороченная система,
описывающая поток в пограничном слое вблизи иглы при x
→
+
∞
.
Оказывается, что для ее автомодельных решений rh=const.
Поэтому, после введения автомодельных координат
|
(8) |
укороченная система сводится
к системе двух обыкновенных дифференциальных уравнений для G(x) и H(x). У этой системы выделяется инвариантное многообразие G
′
H=1, на
котором система сводится к одному обыкновенному дифференциальному уравнению второго
порядка для H(x).
Асимптотический анализ его
решений методами плоской степенной геометрии показал, что это уравнение имеет
решения, которые удовлетворяют граничным условиям в бесконечности и на игле и
при x
→
0 имеют асимптотики
|
(9) |
|
(10) |
где постоянная n
∈
[0,1] - показатель степени в степенном законе связи m/m0=(T/T0)n между
динамическим коэффициентом вязкости m и абсолютной температурой T. Решения (9), (10) были найдены
теоретически.
В § 6 третьей главы
описан численный метод, с помощью которого для n=0,1/4,1/2,3/4,1 были
найдены зависимости между постоянными в асимптотиках (9), (10), при которых
решения, имеющие такие асимптотики, при x
→
+
∞
имеют асимптотику
|
которая удовлетворяет
граничным условиям в бесконечности. Результаты вычислений даны в таблицах 3-6.
В § 7 описано
возвращение к исходной задаче и формулируется основной результат третьей главы,
который заключается в том, что задача осесимметричного обтекания
полубесконечной иглы вязкой сжимаемой теплопроводной жидкостью в пограничном
слое при x
→
+
∞
имеет семейства решений, которые вблизи иглы имеют
асимптотики (9), (10).
Результаты, полученные во
второй и третьей главах являются новыми. Основной материал работы аннонсирован
в [8, 15, 16, 21, 22, 32-36].
Нумерация параграфов, лемм,
теорем, следствий, замечаний и формул в каждой главе своя. Первое число в
номере формулы это номер параграфа. Нумерация таблиц и рисунков сквозная по
всей работе.
Работа выполнена при
финансовой поддержке Российского фонда фундаментальных исследований, проект N
02-01-01067.
|
Глава I |
|
ЭЛЕМЕНТЫ СТЕПЕННОЙ ГЕОМЕТРИИ |
В этой главе кратко излагаются некоторые понятия и результаты степенной
геометрии, которые используются в главах II и III. При этом пространственная
степенная геометрия позволяет выделить и упростить укороченную систему
уравнений, решения которой дают сильные асимптотики для решений исходной
системы. Плоская степенная геометрия позволяет получать не только асимптотики
решений, но и асимптотические разложения решений. В ряде случаев эти разложения
сходятся и дают сами решения.
|
§ 1. Пространственная степенная геометрия |
Здесь кратко объясняются некоторые понятия степенной геометрии [5], которые
используются в § 2 главы II и в § 1 главы III.
Обозначим X
′
=(x1,...,xl) -
вектор независимых переменных и через X"=(xl+1,...,xl+m)
- вектор зависимых переменных. Положим n=l+m и объединим
все переменные в один вектор X=(X
′
,X")=(x1,...,xn)
∈
Rn. Дифференциальным
мономом a(X) называется произведение обычного монома c XR[(
def) || ( = )] c x1r1...xnrn,
где c=const
∈
R и R=(r1,...,rn)
∈
Rn, и
конечного числа частных производных вида
|
где k=|k1|+...+|kl|[( def) || ( = )] ||K
′
||, K
′
=(k1,...,kl).
Каждому дифференциальному моному a(X) ставится в соответствие его
векторный показатель степени Q(a)
∈
Rn по следующим правилам: Q(cXR)=R;
Q(
∂
||K
′
|| xj/
∂
X
′
K
′
)=(-K
′
,Ej), где j > l и Ej
обозначает j-ый единичный вектор; при умножении мономов их векторные
показатели степени складываются: Q(a1a2)=Q(a1)+Q(a2),
где a1 и a2 - дифференциальные мономы.
Конечная сумма
дифференциальных мономов
| (1.1) |
называется дифференциальной
суммой. В Rn ей ставится в соответствие множество векторных
показателей степени ее мономов S(f)={Q(ak)}
- носитель суммы (1.1). Выпуклая оболочка G(f) носителя S(f) называется многогранником
суммы (1.1). Ее граница
∂
G(f)
состоит из граней Gj(d),
где d=dim(Gj(d))
- размерность и j - номер грани.
Пусть R*n обозначает пространство, двойственное к пространству Rn так,
что определено скалярное произведение
б
P,Q
с
[( def) || ( = )] p1q1+...+pnqn
для P=(p1,...,pn)
∈
R*n и Q=(q1,...,qn)
∈
Rn.
На семействе кривых
|
(1.2) |
где bi -
произвольные постоянные из R,
дифференциальный моном ведет себя как constt
б
P,Q
с
, где Q=Q(a), P=(p1,..,pn)
∈
R*n. Поэтому на этом семействе кривых ведущими членами
суммы f(X) являются те, для которых скалярное произведение
б
P,Q
с
является наибольшим среди точек носителя суммы f(x),
т.е.
б
P,Q
с
= max по Q
∈
S(f). Для выделения этих точек
максимумов рассмотрим выпуклую оболочку G(f), т.е. многогранник суммы (1.1). Каждому вектору P
≠
0, P
∈
R*n
соответствует опорная грань Gj(d), на которой
| (1.3) |
Вектор P это вектор
внешней нормали к грани Gj(d), т.е. от нее он направлен наружу многогранника G(f). Множество Uj(d)
всех векторов P с фиксированной опорной гранью Gj(d) называется нормальным конусом грани Gj(d) и описывается системой равенств и неравенств (1.3),
т.е. множество Uj(d) описывается формулой
|
Каждой грани Gj(d) соответствует укороченная сумма
|
Согласно [5, гл. VI] каждое
укорочение [^(f)]j(d)(X)
является первым приближением суммы f(X), когда вектор ln|X|=(ln|x1|,...,ln|xn|) стремится к бесконечности вблизи нормального конуса Uj(d).
В частности, движение t
→∞
по кривой семейства (1.2) соответствует стремлению вектора ln|X|=(ln|x1|,...,ln|xn|) к бесконечности вдоль луча lP при l
→
+
∞
,
т.е. все отличные от нуля компоненты вектора ln|X|
стремятся к бесконечности.
Расширенным нормальным
конусом грани Gj(d) называется объединение нормального конуса Uj(d)
и нормальных конусов граней, входящих в грань Gj(d). Обозначим его
∨
Uj(d).
Смысл этого понятия заключается в том, что укорочение [^(f)]j(d)(X),
соответствующее грани Gj(d),
содержит все слагаемые, которые являются ведущими, когда вектор ln|X|
→∞
вблизи расширенного нормального конуса
∨Uj(d).
Рассмотрим систему
дифференциальных уравнений
|
(1.4) |
где fi(X)
- дифференциальные суммы. Каждой из них соответствует ее носитель S(fi),
многогранник G(fi),
набор граней Giji(di) и набор укороченных уравнений [^(f)]iji(di)(X)=0.
Пусть вектору P
≠
0
соответствуют опорные грани Giji(di), i=1,...,m. Тогда ему соответствует укороченная
система уравнений
|
(1.5) |
Согласно [5, гл. III,
§ 1] при t
→∞
порядок функции j(t) это
|
если предел существует.
Функции j(t) и y(t) сильно асимптотически эквивалентны, если
|
где e > 0 и t
→∞
.
Вектор-функции F(X) = (j1(X),
..., jn(X)) и Y(X) = (y1(X), ..., yn(X))
сильно асимптотически эквивалентны на семействе кривых (1.2), если
|
(1.6) |
где e > 0 и t
→∞
.
Теорема 1 [5, гл. VI, § 1, теорема 1.1]. Пусть система
уравнений (1.4) имеет решение
|
(1.7) |
которое определено на семействе (1.2), т.е. на этом семействе все jj(X
′
(t)) имеют определенные порядки pj когда xi=bitpi, i=1,...,l,
тогда укороченная система (1.5), соответствующая вектору P=(p1,...,pn),
имеет решение
|
(1.8) |
которое на семействе (1.2) сильно асимптотически эквивалентно решению
(1.7).
Замечание 1. Используя теорему 3.3 [7] можно оценить величину e в формуле (1.6), т.е. оценить точность асимптотики,
даваемой формулой (1.8). Если в качестве t взять одну из независимых переменных xk, которая
стремится к бесконечности, 0 < k
≤
l, то у вектора P координата pk=1.
Тогда
|
где
|
а Giji(di) - грани, соответствующие укороченным уравнениям
системы (1.5), вектор P из теоремы 1, i=1,...,m.
Следовательно, выделяя
укороченные системы и решая их, можно получить асимптотики решений исходной
системы. Носители уравнений укороченной системы расположены на опорных
плоскостях с общим нормальным вектором P, т.е. укороченные системы
являются квазиоднородными и имеют автомодельные решения [6]. В автомодельных
переменных каждая укороченная система сводится к системе с меньшим количеством
независимых переменных (см. ниже теорему 3).
Нормальным конусом укороченной
системы (1.5) называется множество
|
где D=(d1,...,dm),
J=(j1,...,jm), т.е. это пересечение
нормальных конусов всех укороченных уравнений, входящих в укороченную систему. Расширенным
нормальным конусом укороченной системы (1.5) называется пересечение
расширенных нормальных конусов всех укороченных уравнений, входящих в
укороченную систему
|
где D=(d1,...,dm),
J=(j1,...,jm).
Пусть кроме системы уравнений
(1.4) в задаче имеются граничные условия вида
| (1.9) |
Эти уравнения можно
рассматривать как дополнительные к системе (1.4). Им соответствуют векторные
показатели степени и все остальные элементы степенной геометрии. Перед нами
стоит задача выделить такую укороченную систему, чтобы ее решение удовлетворяло
граничным условиям (1.9). К уравнениям (1.9) можно применить технику выделения
укорочения. Но они сами являются квазиоднородными, поэтому единственные
содержательные укорочения совпадают с самими уравнениями. Это возможно только
при определенных значениях вектора P, которые гарантируют, что для
каждого из уравнений (1.9) укорочение совпадает с самим уравнением. Используя
эти условия на вектор P можно понизить размерность пространства
показателей степеней Q и решать задачу нахождения укорочений в этом
пространстве меньшей размерности.
Вектор P=(p1,...,pn)=(P
′
,P") должен удовлетворять условиям
| (1.10) |
Систему уравнений (1.10)
можно разрешить и выразить явно pl+1, ..., pl+m
′
через P
′
=(p1, ..., pl),
т.е.
| (1.11) |
Согласно этим условиям можно
спроектировать носители уравнений системы (1.4) на пространство меньшей
размерности. Тогда в пространствах R*n и Rn
векторов P и Q мы получаем проекции P
→
[(P)\tilde] и Q
→
[(Q)\tilde] по следующему правилу
| (1.12) |
где векторы
|
| (1.13) |
|
Теорема 2. Граничным условиям (1.9) соответствуют
проекции в пространствах Rn: Q
→
[(Q)\tilde] и R*n: P
→
[(P)\tilde] по правилам (1.12), (1.13).
Доказательство. Непосредственной проверкой убеждаемся, что из (1.13)
и (1.11) следует (1.12).
Получившейся таким образом
проекции с точками [(Q)\tilde]
∈
Rn-m
′
соответствуют нормальные конуса в пространстве R*n-m
′
.
Кроме граничных условий вида
(1.9) обычно еще бывают дополнительные граничные условия в виде равенства нулю
функций и производных на некоторых подмножествах пространства X
′
. Этим условиям в пространстве R*n или в его проекции R*n-m
′
соответствуют некоторые множества векторов P
или [(P)\tilde]. Нас интересуют те укороченные системы, расширенный
нормальный конус которых включает эти множества. Стремлению xi
→
0 соответствует pi
≤
0; стремлению xi
→
∞
соответствует pi
≥
0. И это надо использовать при описании
дополнительных граничных условий.
Поскольку нас интересуют
асимптотики решения при xj
→
∞
(или xj
→
0),
то этому в пространстве R*n
соответствует pj
≥
0 (или pj
≤
0), j=1,...,l. Исходя из этих условий,
находим укороченные системы вида (1.5), расширенные нормальные конуса которых
содержат указанные выше множества (соответствующие дополнительным граничным
условиям) и обладают свойствами положительности или отрицательности координат,
в зависимости от стремления координаты xi к бесконечности или
нулю. Каждой из этих укороченных систем соответствует свой вектор P,
нормальный к носителям укороченных уравнений и носителям граничных условий
(1.9).
Теорема 3 [6, § 10]. Пусть имеется укороченная система
(1.5) и граничные условия вида (1.9) с вектором P=(P
′
,P")=(p1,...,pn),
нормальным к носителям всех этих уравнений, т.е. выполнено условие (1.11). Пусть B1
′
,...,Bl-1
′
- базис в линейном подпространстве векторов Q
′
, удовлетворяющих уравнению
б
P
′
,Q
′
с
= 0. Тогда система уравнений (1.5), (1.9) имеет автомодельные координаты xi,yj:
|
|
где
б
P
′
,Tj
′
с
= pj, в которых она сводится к системе m
уравнений относительно m зависимых переменных yl+1,...,yn
с независимыми переменными x1,...,xl-1.
При l=2 это система обыкновенных дифференциальных уравнений, при l=1 -
алгебраических.
Этот метод позволяет выбирать
укороченные системы (1.5) и находить их автомодельные решения, которые
удовлетворяют заданным граничным условиям и дают асимптотики решений исходной
системы (1.4).
|
§ 2. Плоская степенная геометрия |
2.1. Постановка задачи о нахождении степенных асимптотик решений [20
§ 1, 17]. Пусть задано обыкновенное дифференциальное уравнение
|
(2.1) |
где f(X) -
дифференциальная сумма, X=(x,y), x - независимая
переменная, зависимая переменная y входит в f(X) в целых
степенях. Положим
| (2.2) |
Пусть x стремится к
нулю или к бесконечности и решение уравнения (2.1) имеет вид
|
(2.3) |
где коэффициент cr=const
∈
R, cr
≠
0, показатели степени r,e
∈
R и ew < 0. Тогда выражение
|
(2.4) |
является степенной
асимптотикой решения (2.3).
Задача 1. При x
→
0 и при x
→∞
для решений y=j(x) уравнения (2.1) найти все степенные
асимптотики (2.4).
Напомним некоторые
определения § 1 применительно к плоской степенной геометрии. Каждому
дифференциальному моному a(X) ставится в соответствие его
(векторный) показатель степени Q(a)=(q1,q2)
∈
R2 по
следующим правилам. Для монома: Q(cxr1yr2)=(r1, r2);
для производной: Q(dly/dxl)=(-l,1); при
умножении дифференциальных мономов их показатели степени складываются как
векторы Q(a1a2)=Q(a1)+Q(a2).
Множество S(f) показателей степеней Q(ai)
всех дифференциальных мономов ai(X), входящих в
дифференциальную сумму f(X), называется носителем суммы.
Очевидно, S(f)
∈
R2. Через fQ(X) обозначим сумму
тех мономов ai(X) из f(X), у которых Q(ai)=Q.
Тогда дифференциальную сумму можно записать в виде
| (2.5) |
Выпуклая оболочка G(f) носителя S(f) называется многоугольником
суммы f(X). Граница
∂G(f) многоугольника G(f) состоит из вершин Gj(0) и ребер Gj(1). Их называют (обобщенными) гранями Gj(d), где верхний индекс указывает размерность грани, а
нижний - ее номер. Каждой грани Gj(d) соответствует укороченная сумма
| (2.6) |
Пусть плоскость R*2 сопряжена плоскости R2 так, что
для P=(p1,p2)
∈
R*2 и Q=(q1,q2)
∈
R2
определено скалярное произведение
| (2.7) |
Каждой грани Gj(d) в R*2
соответствует также свой нормальный конус
|
Для ребра Gj(1) нормальный конус Uj(d)
это тот луч прямой, ортогональной ребру Gj(1) и проходящей через начало координат P=0,
который направлен от ребра Gj(1) наружу многоугольника G(f). Для вершины Gj(0) нормальный конус Uj(0)
это открытый сектор (угол) на плоскости R*2 с вершиной в нуле P=0 и ограниченный лучами,
являющимися нормальными конусами ребер, примыкающих к вершине Gj(0).
Итак, каждой грани Gj(d) носителя S(f) уравнения (2.1) соответствуют:
нормальный конус Uj(d) в R*2 и укороченное уравнение
|
(2.8) |
Носитель степенной
асимптотики (2.4) состоит из двух точек E2[( def) || ( = )] (0,1) и (r,0).
Их выпуклая оболочка является ребром, которое обозначим g1(1). Нормальным к нему является вектор (1,r). Нормальным
конусом u решения вида (2.3) является луч lw(1,r), где w определено по (2.2) и l
> 0.
Теорема 4 [5, гл. VI, теорема 1.1]. Если
уравнение (2.1) имеет решение вида (2.3), для которого u=lw(1,r)
⊂
Uj(d), то укорочение (2.4) решения (2.3) является решением
укороченного уравнения (2.8), соответствующего грани Gj(d).
Это частный случай теоремы 1
для n=2 и степенной асимптотики.
Поэтому для нахождения всех
укороченных решений (2.4) уравнения (2.1) надо вычислить: носитель S(f),
многоугольник G(f),
все его грани Gj(d)
и их нормальные конусы Uj(d). Затем
для каждого укороченного уравнения (2.8) надо найти все его решения (2.4), у
которых один из векторов
±
(1, r)
лежит в нормальном конусе Uj(d).
Если d=0, то это означает, что один из векторов
±
(1,r)=wR лежит в Uj(d).
Если d=1, то это свойство всегда выполнено. При этом определяется также
значение w.
2.2. Решение укороченного
уравнения. Здесь рассмотрим по
отдельности два случая: вершины Gj(0) и ребра Gj(1).
Вершине Gj(0)={Q} соответствует укороченное уравнение (2.8)
с точечным носителем Q и с d=0. Положим g(X)[(
def) || ( = )] X-Q[^(f)]j(0)(X),
тогда решение (2.4) уравнения (2.8) удовлетворяет уравнению g(X)=0.
Подставляя y=cxr в g(X), получаем, что g(x,cxr)
не зависит от x и c и является многочленом от r, т.е. g(x,cxr)
≡
c(r), где c(r) - характеристический многочлен дифференциальной суммы
[^(f)]j(0)(X). Следовательно, для
решения (2.4) уравнения (2.8) показатель r является корнем
характеристического уравнения
|
(2.9) |
а коэффициент cr
- произвольный. Из корней ri уравнения (2.9) надо отобрать
только те, для которых один из векторов w(1,r), где w =
±
1, лежит в нормальном конусе Uj(0)
вершины Gj(0).
Соответствующие выражения (2.4) с произвольной константой cr
являются кандидатами на роль укороченных решений уравнения (2.1). При этом
согласно (2.2), если w = -1, то x
→
0, а если w = 1, то x
→∞
.
Ребру Gj(1) соответствует укороченное уравнение (2.8) с d=1,
нормальный конус Uj(1) которого является
лучом {lNj, l > 0}, где Nj - внешний нормальный вектор к ребру Gj(1). Нормальный конус u укороченного решения (2.4)
пересекается с Uj(1) только если вектор w(1,r)
∈
Uj(1). Этим
однозначно определяются показатель степени r укороченного решения (2.4)
и значение w =
±
1 в (2.2). Для определения коэффициента cr
надо выражение (2.4) подставить в укороченное уравнение (2.8). После сокращения
на некоторую степень x получаем алгебраическое определяющее уравнение
для коэффициента cr
|
(2.10) |
Каждому его корню cr=c(i)r
≠
0 соответствует свое
выражение (2.4), которое является кандидатом на роль укороченного решения
уравнения (2.1).
Итак, каждое укороченное
уравнение (2.8) имеет несколько подходящих решений (2.4) с u
⊂
Uj(d).
Объединим их в непрерывные по w, r,
cr и параметрам уравнения (2.1) семейства, которые обозначим Fj(d)k, где k=1, 2,....
Если нас интересуют не все
решения (2.3) уравнения (2.1), а только те, у которых нормальный конус u
лежит в некотором заданном конусе K, то K называется конусом задачи.
2.3. Критические числа
укороченного решения. Если найдено
укороченное решение (2.4), то замена
|
(2.11) |
приводит уравнение (2.1) к
виду
|
(2.12) |
где [(f)\tilde](x,z)
- дифференциальная сумма, все точки Q=(q1,q2)
ее носителя S([(f)\tilde]) имеют целую неотрицательную координату
q2. При этом L(x) -
линейный дифференциальный оператор и носитель S(Lz) состоит
из одной точки (v,1), являющейся вершиной [(G)\tilde]1(0) многоугольника G([(f)\tilde]), у всех точек Q=(q1,q2)
носителя S(h) координата q2
≥
0 и нет точки Q=(v,1), нормальный конус
вершины [(G)\tilde]1(0)
содержит вектор P=(p1,p2) с p1w > 0. Для уравнения (2.12) конус задачи можно
записать в виде
|
(2.13) |
т.е. ищем только те решения z=csxs+o(xs-r)
уравнения (2.12), у которых s
∈
K.
Напомним, что
дифференциальная сумма f(x,y) имеет первую вариацию
(или производную Фреше) df(x,y)/dy, которая
обладает следующими свойствами:
|
|
Теорема 5 [9]. Пусть (2.4) - решение укороченного уравнения
(2.8) с u
∈
U(d)j. Тогда в уравнении (2.12) оператор
|
(2.14) |
т.е. равен первой
вариации, вычисленной на решении (2.4). При этом S(Lz)=(v,1), где v=
б
Q1,(1,r)
с
-
r с Q1
∈
Gj(d).
Пусть n(k) - характеристический многочлен
дифференциальной суммы L(x)z, т.е.
|
(2.15) |
Если n(k)\not
≡
0, то корни k1,...,ks
многочлена n(k) называются собственными
значениями укороченного решения (2.4). Те из вещественных собственных чисел
ki, которые лежат в конусе задачи (2.13), называются критическими
числами.
2.4. Постановка задачи о
степенно-логарифмических разложениях решений [20 § 3, 18]. Если для уравнения (2.12) с n(k)\not
≡
0 искать решения в виде степенного ряда
| (2.16) |
где cs=const
∈
R, то согласно [9] такое разложение решений существует
только при определенных условиях. При этом основное условие - это отсутствие
критических значений. Если же не накладывать этих условий, то получаются
разложения вида (2.16), где ck суть многочлены от lnx.
Задача 2. Для решений уравнения (2.12) найти разложения
| (2.17) |
где bs суть
многочлены от lnx и показатели s лежат в конусе задачи (2.13).
2.5. Носитель разложения
решения. Рассмотрим уравнение (2.12)
в невырожденном случае, когда L
¬ ≡
0 и n(k)
¬
≡
0. Тогда члену L(x)z соответствует только одна вершина (v,1)
многоугольника G([(f)\tilde]).
Параллельно сдвинем носитель S([(f)\tilde]) на вектор -(v,1). Тогда вершина (v,1) сдвинется в
начало координат. Пусть S
′
+ -
множество конечных сумм векторов Q
∈
S
′
[( def) || ( = )] S([(f)\tilde])-(v,1) и пусть
| (2.18) |
Пусть æ - число
критических значений ki укороченного решения (2.4).
Рассмотрим по отдельности случаи с æ = 0 и æ = 1.
Случай æ = 0.
Теорема 6 [14]. В случае æ = 0 имеется разложение
(2.16) решения уравнения (2.12), в котором все показатели s лежат в
множестве K и все коэффициенты cs определяются однозначно.
Лемма 1. Пусть G(0)j - такая вершина
многоугольника G(f)
уравнения (2.1), что укороченное
уравнение [^(f)](0)j(X)=0 имеет решение (2.4), вектор
w(1, r)
∈
U(0)j и все точки
сдвинутого носителя S(f)-G(0)j представляются в
виде lR1+mR2, где целые l,m
≥
0, R1 и R2 - некоторые вектора.
Тогда для множества (2.18) уравнения
(2.12) справедливо включение
|
где r1=
б
(1, r), R1
с
, r2=
б
(1, r), R2
с
.
Точечное множество Z
плоскости R2 называется решеткой, если для любых двух
векторов Q, Q
′
∈
Z их сумма Q+Q
′
и разность Q-Q
′
принадлежат Z. Векторы B1 и B2
образуют базис решетки Z, если любая точка Q решетки Z
представляется в виде Q=n1B1+n2B2,
где n1 и n2
∈
Z, т.е. целые
числа. Пусть S - некоторое множество в R2 и точка Q
∈
S. Множество точек
S
′
[( def) || ( = )] S-Q будем
называть сдвинутым множеством S. Для укороченного решения (2.4)
носитель s состоит из двух точек Q1=(0, 1) и Q2=(r, 0).
Поэтому сдвинутый носитель s
′
состоит из точек 0 и Q2-Q1=(r, -1).
Замечание 2. Если сдвинутые носители S
′
(f) уравнения (2.1) и s
′
укороченного решения (2.4) лежат в некоторой решетке Z,
то множество
| (2.19) |
Случай æ = 1. Пусть k1 - единственное критическое
значение. Обозначим через S
′
+(k1)
множество конечных сумм векторов Q
∈
S
′
[( def) || ( = )] S([(f)\tilde])-(v,1) и вектора (k1,-1), и положим
| (2.20) |
Теорема 7 [14]. Если в случае æ = 1 единственное
критическое значение k1 не лежит в множестве K, то имеется
разложение (2.16) решения уравнения (2.12), где показатели s
лежат в множестве K(k1), при этом коэффициент ck1
произволен, а остальные коэффициенты cs определяются однозначно.
Лемма 2. Если множество
(2.18) имеет вид
|
то множество (2.20) имеет вид
|
Замечание 3. Если множество S
′
=S([(f)\tilde])-(v,1) и точка (k1,-1) лежат в некоторой решетке Z(k1),
то
| (2.21) |
Теорема 8 [14]. Множества (2.18) и (2.20) не
имеют точек накопления на прямой R, если множество S([(f)\tilde]) не имеет точек накопления на
плоскости R2.
Теорема 9. Если в случае æ = 1 единственное критическое
значение k1
∈
K, то уравнение (2.12) имеет формальное
решение вида (2.17)
| (2.22) |
где bs -
постоянные, если ws
< wk1, bs
суть многочлены от lnx, если ws
≥
wk1, и bk1
является линейным многочленом от lnx с произвольным свободным членом.
Максимум порядков l
всех производных dly/dxl, входящих в
дифференциальный моном a(X), называется его порядком
дифференцирования и обозначается p(a). Порядком дифференцирования p(f) суммы
(1.1) называется наибольший из порядков дифференцирования p(ai) ее мономов ai(X).
Теорема 10 [9]. Пусть в ситуациях теорем 6, 7 в
сумме (2.12) p(Lz)=p([(f)\tilde]), тогда разложение (2.16) абсолютно
сходится для достаточно малых |x|
≠
0, если x
→
0, и |x|-1
≠
0, если x
→
∞
(т.е. для |x|-w
≠
0).
2.6. Постановка задачи о
нестепенных асимптотиках решений [20
§ 5, 19]. Пусть x
→
0 или x
→∞
.
Две функции j(x) и y(x) называются слабо (асимптотически)
эквивалентными, если
|
При этом функция j(x) является слабой асимптотикой функции
y(x) и наоборот. Обозначим
k-кратные экспоненту и логарифм через exp(k)x и
ln(k)x соответственно, т.е.
|
Задача 3. Для решений уравнения (2.1), где f(x,y)
- дифференциальная сумма, найти все (слабые) асимптотики вида
|
(2.23) |
где c=const
∈
R, c
≠
0; r,si,ti=const
∈
R.
В п. 2.2 изложен метод
вычисления всех степенных асимптотик, т.е. асимптотик вида (2.4). Поэтому здесь
сосредоточимся на вычислении всех нестепенных асимптотик решений, т.е.
не имеющих вида (2.4).
Пусть y=j(x) - решение уравнения (2.1), и функция j(x) имеет порядок r. Тогда нормальным
конусом u этого решения является луч
|
Понятие конус задачи
применимо и к решениям с так определенным нормальным конусом u.
Две функции j(x) и y(x) сильно (асимптотически) эквивалентны,
если
|
для некоторого e < 0, где
|
При этом функция j(x) является сильной асимптотикой
функции y(x) и наоборот. Это
частный случай сильной асимптотической эквивалентности, введенной в § 1
этой главы.
Теорема 11 [5, гл. VI, теорема 1.1]. Если решение y=j(x) уравнения (2.1) имеет нормальный конус u,
то укороченное уравнение (2.8), для которого u
⊂
Uj(d), имеет сильно
асимптотически эквивалентное решение y=y(x).
Это теорема 1 для n=2.
Таким образом, задача
сводится к нахождению всех укороченных уравнений и их нормальных конусов и к
конечному числу следующих задач.
Задача 4. Для укороченного уравнения (2.8) найти все (слабые)
асимптотики его решений y=y(x) с w(1,r)
∈
Uj(d).
Уравнению (2.1) соответствует
многоугольник G(f),
а укороченному уравнению (2.8) - его ребро или вершина Gj(d). Ниже рассмотрим по отдельности 3 способа редукции
задачи 4: в зависимости от наклона ребра.
2.7. Случай вертикального
ребра Gj(1). Если ребро
Gj(1)
вертикально, то его нормальный конус
|
(2.24) |
и у всех точек Q=(q1,q2)
∈
Gj(1) координата q1 одинакова. Положим
|
(2.25) |
тогда носитель S(g)
лежит на координатной оси q1=0. Согласно (2.24) все степенные
решения (2.4) с w(1,r)
∈
Uj(1)
являются постоянными y=y0=const,
где y0 - корень определяющего уравнения
|
(2.26) |
Корень y0
уравнения (2.26) называется кратным, если в нем производная d[(g)\tilde](y)/dy
равна нулю.
Для отыскания нестепенных
решений уравнения (2.8) сделаем логарифмическое преобразование
|
(2.27) |
Согласно теореме 2.4 из [5,
гл. VI] при этом дифференциальная сумма g(x,y)
перейдет в дифференциальную сумму h(x,y)[( def) || ( = )] g(x,y) и уравнение
(2.8) примет вид
|
(2.28) |
Из (2.27) видно, что x
→∞
при x
→
0 и при x
→∞
, т.е. для уравнения (2.28) получаем задачи 1 и 2 с
конусом задачи
|
(2.29) |
Теорема 12. Конечные предельные значения y0
≠
0 непостоянных решений уравнения (2.28) являются
кратными решениями уравнения (2.26).
Пусть ребро Gj(1) соединяет вершины Gj-1(0)=(q1
′
,q2
′
) и Gj(0)=(q1
′
,q2
′′
), где целые q2
′
< q2
′′
. Будем говорить, что уравнение (2.26) имеет бесконечный
корень, если степень многочлена в (2.26) меньше q2
′′
; и имеет нулевой корень, если у многочлена в
(2.26) наименьшая степень по y больше q2
′
.
Теорема 13. Если уравнение (2.26) не имеет бесконечного
(нулевого) корня, то уравнение (2.28) не имеет решений, стремящихся к
бесконечности (нулю).
Заметим, что укорочение
уравнения (2.28) относительно вектора (1,0) является уравнением (2.26), т.е. [(g)\tilde](y)
≡
[^(h)](x,y). Для нахождения решений уравнения (2.28) с
бесконечными и нулевыми предельными значениями y надо для уравнения
(2.28) выделить укороченные уравнения, соответствующие конусу задачи (2.29).
Для нахождения решений уравнения (2.28) с конечными предельными значениями надо
найти все кратные корни уравнения (2.26). Пусть y0 - такой
кратный корень. Тогда параллельным сдвигом y=y0+z
надо поместить его в начало координат. Уравнение (2.28) примет вид
|
(2.30) |
Теперь для уравнения (2.30)
надо выделять его укороченные уравнения с конусом задачи p1
≥
0, p2
≤
0. Это опять задача 1.
2.8. Случай наклонного
ребра Gj(1). Пусть
вектор (1,r) с r
≠
0 является нормальным к ребру Gj(1).
Теорема 14 [5, гл. VI, теорема 2.2]. Степенное
преобразование
|
(2.31) |
приводит уравнение (2.8) к
виду
|
где [(f)\tilde](x,z) -
дифференциальная сумма и ее носитель S([(f)\tilde]) расположен на
вертикали q1=const.
Таким образом, степенным
преобразованием (2.31) случай наклонного ребра сводится к случаю вертикального
ребра. Если в укороченное уравнение (2.8) подставить y=cxr,
то для коэффициента c получается определяющее уравнение
|
(2.32) |
где [([(f)\tilde]()\tilde]c)
- многочлен от коэффициента c. Здесь он играет ту же роль, что и
многочлен [(g)\tilde](y) из уравнения (2.26).
Замечание 4. В частности, если этот многочлен не имеет
бесконечного, нулевого и кратных корней, то уравнение (2.8) не имеет подходящих
нестепенных решений, т.е. преобразование (2.31) и дальнейшее исследование
делать не надо.
2.9. Случай
горизонтального ребра Gj(1). В этом случае у всех точек Q=(q1,q2)
ребра Gj(1)
координата q2 одинакова. Положим
| (2.33) |
и сделаем логарифмическое
преобразование
|
(2.34) |
Согласно теореме 2.4 из [5,
гл. VI] при этом преобразовании дифференциальная сумма g(x,y)
перейдет в дифференциальную сумму h(x,h)[( def) || ( = )] g(x,y) и уравнение
(2.8) примет вид
|
(2.35) |
Теперь для уравнения (2.35)
получаем задачу 1 с конусом задачи
|
|
ЛИТЕРАТУРА |
[1] Л.Г.
Лойцянский. Механика жидкости и газа. М.: Наука, 1978.
[2] М.М.
Васильев. Об осесимметричных течениях вязкого теплопроводного газа. Препринт N
11, М.: ИПМ, 2001. 13 с.
[3] M.M.
Vasiliev. Obtaining the Self-Similar Asymptotics of Solutions to the
Navier-Stokes Equations by Power Geometry // Progress in Analysis. Proceedings
of the 3rd International ISAAC Congress (Eds. H. G. Begehr,
R. P. Gilbert, M. W. Wong), Singapore: World Scientific,
2003, vol. 1, p. 93-101.
[4] M.M.
Vasiliev. Asymptotics of some viscose, heat conducting gas flows // Proceedings
of BAIL 2002 (Eds. S. Wang and N. Fowkes), Perth: University of
Western Australia, 2002, p. 251-256.
[5] А.Д.
Брюно. Степенная геометрия в алгебраических и дифференциальных уравнениях. М.:
Физматлит, 1998.
[6] А.Д.
Брюно. Автомодельные решения и степенная геометрия // Успехи мат. наук, 2000,
т. 55, вып. 1, с. 3-44.
[7] А.Д.
Брюно. Степенные разложения решений системы алгебраических и дифференциальных
уравнений // ДАН, 2001, т. 380, N 3, с. 298-304.
[8] Т.В.
Шадрина. Об осесимметричном обтекании иглы вязкой несжимаемой жидкостью.
Препринт N 36, М.: ИПМ, 2002. 21 с.
[9] А.Д.
Брюно. Степенные разложения решений одного алгебраического или
дифференциального уравнения // ДАН, 2001, т. 380, N 2, с. 155-159.
[10] Л.Г.
Лойцянский. Ламинарный пограничный слой. М.: Физматлит, 1962.
[11] L.
Prandtl. Über Flüssigkeitsbewegung bei sehr kleiner Reibung //
Verhandlungen des III. Internat Math.-Kongr., Heidelberg, 1904. Leipzig:
Teubner 1905. S. 484-491.
[12] H.
Blasius. Grenzschichten in Flüssigkeiten mit kleiner Reibung // Zeit.
für Math. und Phys. 1908. V. 56. P. 1-37.
[13] M.B.
Glauert, M.J. Lighthill. The axisymmetric boundary layer on a long thin
cylinder // Proc. Roy. Soc., ser. A, 1955, 230, no. 1181, p. 188-203.
[14] А.Д.
Брюно. Асимптотики и разложения решений обыкновенного дифференциального
уравнения. Препринт N 9, М.: ИПМ, 2003. 39 с.
[15] А.Д.
Брюно, Т.В. Шадрина. Об осесимметричном обтекании иглы вязкой несжимаемой
жидкостью // ДАН, 2002, т. 387, N 5, c. 589-595.
[16] T.V.
Shadrina. The Axially Symmetric Boundary Layer around a Needle // Proceedings
of BAIL 2002 (Eds. S. Wang and N. Fowkes), Perth: University of
Western Australia, 2002, p. 213-220.
[17] А.Д.
Брюно. Степенные асимптотики решений обыкновенного дифференциального уравнения
// ДАН, 2003, т. 392, N 3, с. 295-300.
[18] А.Д.
Брюно. Степенно-логарифмические разложения решений обыкновенного
дифференциального уравнения // ДАН, 2003, т. 392, N 4, с. 439-444.
[19] А.Д.
Брюно. Нестепенные асимптотики решений обыкновенного дифференциального
уравнения // ДАН, 2003, т. 392, N 5, с. 586-591.
[20] А.Д.
Брюно. Асимптотики и разложения решений обыкновенного дифференциального
уравнения // УМН, 2004, т. 59, N 3, с. 31-80.
[21] А.Д.
Брюно, Т.В. Шадрина. Осесимметричный пограничный слой на игле. Препринт N 64,
М.: ИПМ, 2003. 32 с.
[22] А.Д.
Брюно, Т.В. Шадрина. Осесимметричный пограничный слой на игле // ДАН, 2004,
т. 394, N 3, с. 298-304.
[23] S.
Goldstein. On the two-dimensional steady flow of a viscous fluid behind a solid
body // Proceedings Royal Soc. London A 142 (1933), 545-562.
[24] K.
Stewartson. On asymptotic expansions in the theory of boundary layers // J.
Math. and Phys., 36 (1957), 173-191.
[25] A.I.
Van de Vooren, D. Dijkstra. The Navier-Stokes solution for laminar flow past a
semi-infinite flat plate // J. Engineer. Math., vol. 4, no. 1 (1970), 9-27.
[26] R.I.
MacLachlan. The boundary layer on a finite flat plate // Phys Fluids A, v.3,
no.2 (1991), 341-348.
[27] R.A.
Seban, R. Bond. Skin-friction and heat-transfer characteristics of a laminar
boundary layer on a cylinder in axial incompressible flow // J. Aeronaut. Sci.
18 (1951), 671-675.
[28] H.R.
Kelly. A note on the laminar boundary layer on a circular cylinder in axial
incompressible flow // J. Aeronaut. Sci. 21 (1954), 634.
[29] Lord
Rayleigh. On the motion of solid bodies through viscous liquid // Phil. Mag.
(6) 21, (1911), 697-711.
[30] K.
Pohlhausen. Zur näherungsweisen Integration der Differentialgleichung der
laminaren Grenzschicht // Ebenda [Zs. f. angew. Math. u. Mech. 1 (1921)],
252-268.
[31] K.
Stewartson. The asymptotic boundary layer on a circular cylinder in axial
incompressible flow // Quarterly J. Mech and Appl. Math 13 (1955), 113-122.
[32] Шадрина
Т.В. Пограничный слой при осесимметричном обтекании иглы // Дифференциальные
уравнения, 2002, т. 38, N 6, с.853-854.
[33] Шадрина
Т.В. Об осесимметричном обтекании иглы вязкой несжимаемой жидкостью. // XXVIII
Гагаринские чтения. Тезисы докладов. М: МАТИ, 2002, т.2, с. 98-99.
[34] Bruno
A.D., Shadrina T.V. The axially symmetric boundary layer around a needle //
International Conference on Differential and Functional Differential Equations.
Abstracts. M.: MAI, 2002, p.18-19.
[35] Bruno
A.D., Shadrina T.V. The axially symmetric boundary layer around a needle // International
Conference "Navier-Stokes Equations and Related Topics" (NSEC8).
Abstracts. S.Petersburg: Euler Inst., 2002, p.18-19.
[36] Шадрина
Т.В. Осесимметричный пограничный слой на игле // XIV Всероссийская конференция
"Теоретические основы и конструирование численных алгоритмов для решения
задач математической физики". Тезисы докладов. Дюрсо, с.167-168.
File translated from TEX
by TTH, version
3.40.
On 13 May 2005, 17:04.