Сжимаемый теплопроводный погранслой на игле

( The Compressible Heat Conductive Boundary Layer on a Needle
Preprint, Inst. Appl. Math., the Russian Academy of Science)

E-mails: bruno@keldysh.ru, shadrina@keldysh.ru

 

 

Согласно [1-4], стационарный осесимметричный поток вязкого сжимаемого теплопроводного газа описывается системой трех уравнений

f1    def =      й л -    1 r    ∂y ∂x    ∂ ∂r   ж и  1 rr    ∂y ∂x ц ш  +   1 r    ∂y ∂r    ∂ ∂x   ж и  1 rr    ∂y ∂x ц ш щ ы  - A  ∂ ∂r   (rh)  +

+  й л  2 3 Cn   ∂ ∂r   ж и  hn r    ∂ ∂r   ж и  1 r    ∂y ∂x ц ш ц ш  -   2 3 Cn   ∂ ∂r   ж и  hn r    ∂ ∂x   ж и  1 r    ∂y ∂r ц ш ц ш  -

-    2Cn  r    ∂ ∂r   ж и hn r   ∂ ∂r   ж и  1 rr    ∂y ∂x ц ш ц ш  + Cn   ∂ ∂x   ж и hn   ∂ ∂r   ж и  1 rr    ∂y ∂r ц ш ц ш  +

+    2Cn hn rr3    ∂y ∂x щ ы  -  Cn   ∂ ∂x   ж и hn   ∂ ∂x   ж и  1 rr    ∂y ∂x ц ш ц ш  =0,

(1.1)

f2    def =      й л  1 r    ∂y ∂x    ∂ ∂r   ж и  1 rr    ∂y ∂r ц ш  -   1 r    ∂y ∂r    ∂ ∂x   ж и  1 rr    ∂y ∂r ц ш щ ы  - A  ∂ ∂x (rh)  +

+  й л  2 3 Cn   ∂ ∂x   ж и  hn r    ∂ ∂r   ж и  1 r    ∂y ∂x ц ш ц ш  -   2 3 Cn   ∂ ∂x   ж и  hn r    ∂ ∂x   ж и  1 r    ∂y ∂r ц ш ц ш  -

-    Cn r    ∂ ∂r   ж и hn r   ∂ ∂x   ж и  1 rr    ∂y ∂x ц ш ц ш  + 2Cn   ∂ ∂x   ж и hn   ∂ ∂x ж и  1 rr    ∂y ∂r ц ш ц ш щ ы  +

+    Cn r    ∂ ∂r   ж и hn r   ∂ ∂r   ж и  1 rr    ∂y ∂r ц ш ц ш  =0,

(1.2)

f3    def =      й л  1 r    ∂y ∂x    ∂h ∂r    -   1 r    ∂y ∂r    ∂h ∂x   -   A rr    ∂y ∂x    ∂(rh) ∂r  +   A rr    ∂y ∂r    ∂(rh) ∂x щ ы  +

+  й л 2Cn hn ж и  ∂ ∂r   ж и  1 rr    ∂y ∂x ц ш ц ш 2    + 2Cnhn ж и  1 r2r    ∂y ∂x ц ш 2    + 2Cnhn ж и  ∂ ∂x   ж и  1 rr    ∂y ∂r ц ш ц ш 2   щ ы  +

+  й л Cnhn ж и  ∂ ∂x   ж и  1 rr    ∂y ∂x ц ш ц ш 2    - Cnhn   ∂ ∂x   ж и  1 rr    ∂y ∂x ц ш    ∂ ∂r   ж и  1 rr    ∂y ∂r ц ш  -

-    2 3 Cnhn ж и  1 r    ∂ ∂r   ж и  1 r    ∂y ∂x ц ш ц ш 2    +   4Cnhn 3r    ∂ ∂r   ж и  1 r    ∂y ∂x ц ш    ∂ ∂x   ж и  1 rr    ∂y ∂r ц ш  -

-    2 3 Cnhn ж и  ∂ ∂x   ж и  1 rr    ∂y ∂r ц ш ц ш 2   щ ы  + Cnhn ж и  ∂ ∂r   ж и  1 rr    ∂y ∂r ц ш ц ш 2    +

+    Cn sr    ∂ ∂r   ж и r hn   ∂h ∂r ц ш  +   Cn s    ∂ ∂x   ж и hn   ∂h ∂x ц ш  =0,

(1.3)

где координата x направлена по оси симметрии, r - расстояние от оси x (это независимые переменные), зависимые переменные: y - функция тока, r - плотность, h - энтальпия, и константы A, C, s > 0, n ∈ [0,1]. Здесь s - число Прандтля, давление p=Arh (согласно уравнению Клапейрона) и динамический коэффициент вязкости m = Cⁿhⁿ, где n ∈ [0,1] . При этом r ≥ 0, h > 0 и

Cn > 0,  hn > 0.

(1.4)

В обозначениях § 1 главы I здесь

x1=x,  x2=r,  x3 = y,  x4 = r,  x5=h.

(1.5)

Граничные условия задаются в бесконечности и на игле (ср. формулы (2.2), (2.3) гл. II):

y = y0r2,  r = r0,  h=h0 при x = -∞,  y0,r0,h0=const,

(1.6)

∂y/∂x = ∂y/∂r = ∂2y/∂x∂r = ∂2y/∂r2=0 при x ≥ 0,   r=0.

(1.7)

Условие (1.7) выводится в § 2 гл. II.

Лемма 1. Для задачи (1.1)-(1.3), (1.6)-(1.7) имеют место граничные условия

y = y0r2,  r = r0,  h=h0,  при r=+∞.

(1.8)

Доказательство. Заметим, что функции

y = y0 r2,  r = r0,  h=h0;  y0, r0, h0=const

(1.9)

аннулируют каждый из членов в уравнениях (1.1) - (1.3). Следовательно, функции (1.9) являются решением любой укороченной системы для системы (1.1) - (1.3). Поэтому при x < 0 и r→∞ выражения (1.9) являются граничными условиями, которые продолжают граничные условия (1.6). Более того, они продолжаются и для x > 0, r→∞. Доказательство окончено.

Поэтому в дальнейшем ищем решение граничной задачи (1.1) - (1.3), (1.7), (1.8).

Лемма 2. Для системы (1.1)-(1.3) укороченная система, соответствующая пограничному слою на игле при x→ +∞ и граничным условиям (1.8), единственна. Она имеет нормальный вектор P=(2,1,2,0,0) и есть

^ f   (0) 12     def =      -A ∂(rh)/∂r =0,

(1.10)

^ f   (2) 22       def =      й л  1 r    ∂y ∂x    ∂ ∂r   ж и  1 rr    ∂y ∂r ц ш  -   1 r    ∂y ∂r    ∂ ∂x   ж и  1 rr    ∂y ∂r ц ш щ ы  - A  ∂ ∂x (rh)  +

+    Cn r    ∂ ∂r   ж и hn r   ∂ ∂r   ж и  1 rr    ∂y ∂r ц ш ц ш  =0,

(1.11)

^ f   (2) 32       def =      й л  1 r    ∂y ∂x    ∂h ∂r  -   1 r    ∂y ∂r    ∂h ∂x  -   A rr    ∂y ∂x    ∂(rh) ∂r  +   A rr    ∂y ∂r    ∂(rh) ∂x щ ы  +

+  Cnhn  ж и  ∂ ∂r   ж и  1 rr    ∂y ∂r ц ш ц ш 2    +   Cn sr  ∂ ∂r   ж и r hn   ∂h ∂r ц ш  =0,

(1.12)

а автомодельные координаты x, G, P, H для задачи (1.7), (1.8), (1.10)-(1.12) суть

x = r2/x,  y = xG(x),  r = P(x),  h=H(x).

(1.13)

Доказательство. Носители уравнений (1.1)-(1.3) представлены в таблице 2. Первый столбец содержит номер i уравнения f_i=0, второй столбец содержит номер k точки Q_k носителя, третий столбец содержит векторы (или точки) Q_k. В уравнениях (1.1)-(1.3) в квадратные скобки объединены члены с одним векторным показателем степени.

 

 

Согласно (1.8) при r→+∞ имеются три граничных условия вида (1.9) главы I

f4    def =     y-y0 r2=0,

(1.14)

f5    def =     r-r0=0,

(1.15)

f6    def =     h- h0=0.

(1.16)

Каждому из них соответствует носитель, состоящий из двух точек, а именно: S(f₄) состоит из точек Q₁₅=(0,  0,  1,  0,  0) и Q₁₆=(0,  2,  0,  0,  0); S(f₅) из точек Q₁₇=(0,  0,  0,  1,  0) и Q₁₈=(0,  0,  0,  0,  0) и S(f₆) из точек Q₁₉=(0,  0,  0,  0,  1) и Q₂₀=(0,  0,  0,  0,  0). Согласно теореме 2 главы I, вектор P должен удовлетворять условиям (1.10) главы I. А именно: бQ₁₅,Pс = бQ₁₆,Pс, т.е. p₃=2p₂; бQ₁₇,Pс = бQ₁₈,Pс, т.е. p₄=0; бQ₁₉,Pс = бQ₂₀,Pс, т.е. p₅=0. Итак, на вектор P=(p₁,p₂,p₃,p₄,p₅) получены три условия

p3=2p2,  p4=p5=0.

(1.17)

В обозначениях (1.10) и (1.11) главы I здесь m′=l=2 и R′₃=(0,2), R′₄=R′₅=0. По теореме 2 главы I, согласно этим условиям (1.17) вектора Q_k можно спроецировать на двумерную плоскость [Q\tilde]=([q\tilde]₁,[q\tilde]₂) по формулам (1.13) главы I. Эта проекция заключается в том, что [q\tilde]₁=q₁, [q\tilde]₂=q₂+2q₃, а значениями q₄ и q₅ мы пренебрегаем. Четвертый столбец таблицы 2 содержит проекции [Q\tilde]_k = (q₁,q₂+2q₃) векторов Q_k. Проекции [S\tilde] (f₁) - [S\tilde] (f₃) носителей уравнений (1.1)-(1.3), их выпуклые оболочки [(G)\tilde]₁-[(G)\tilde]₃ и их нормальные конуса представлены на рис. 8.

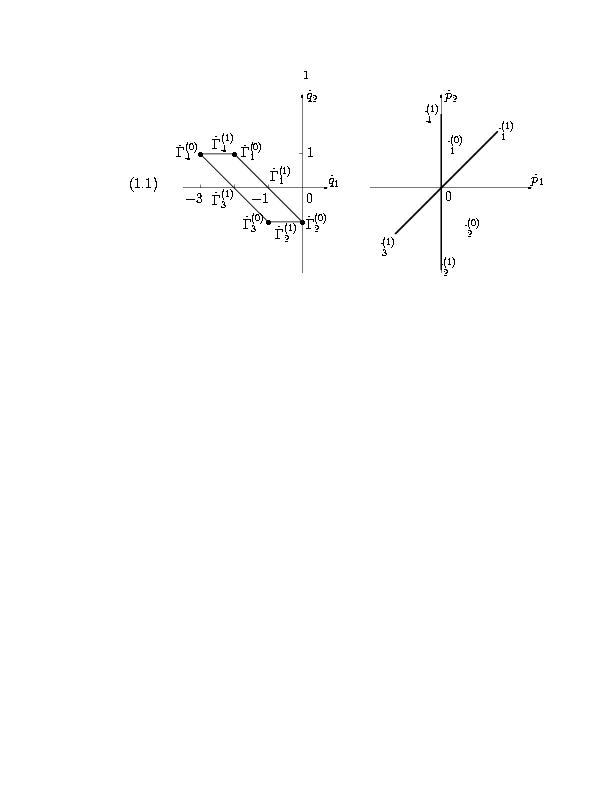
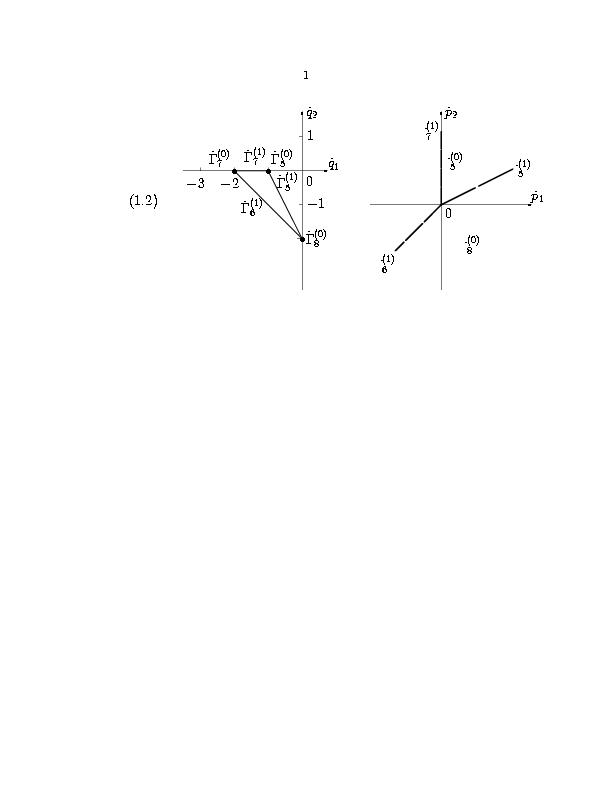
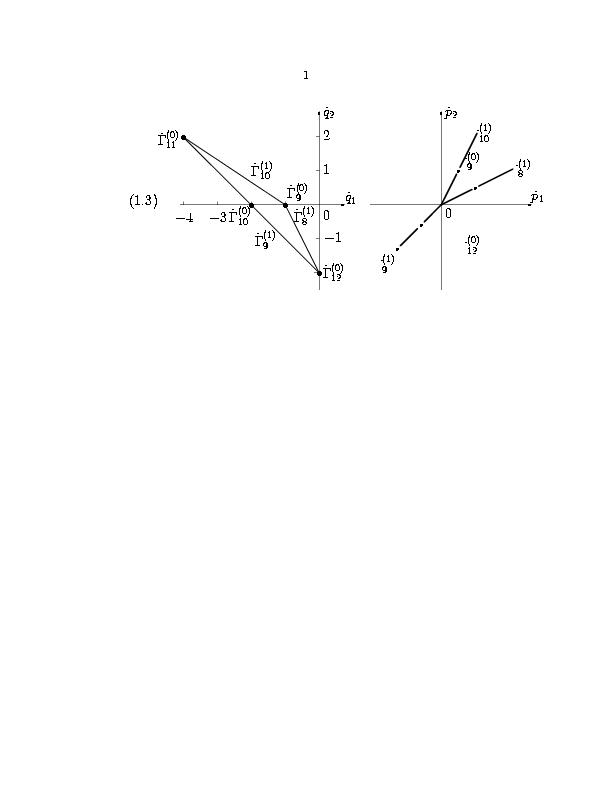
Рис. 8. Проекции носителей уравнений системы (1.1)-(1.3) (а) и нормальные конуса проекций (б).

Игла описывается как x ≥ 0, r=0. Вблизи иглы, при x→+∞ и r→ 0, имеем p₁ > 0, p₂ < 0. Следовательно, игле соответствует IV квадрант плоскости (p₁,p₂). Граничные условия (1.8) при x→+∞ и r→+∞ означают, что p₁,p₂ > 0, т.е. им соответствуют точки из I квадранта плоскости (p₁,p₂). Нас интересуют такие грани проекций [(G)\tilde]_i, i=1,2,3, расширенный нормальный конус которых содержит как IV квадрант, так и точки из I квадранта плоскости (p₁,p₂). Совместим рисунки 8б нормальных конусов проекций на один рисунок 9. Из него видно, что IV квадрант и точки из I квадранта содержаться только в расширенном нормальном конусе системы ^∨U_J^D=^∨U₅⁽¹⁾∩^∨U₈⁽¹⁾. Направляющий вектор нормальных конусов [U\tilde]₅⁽¹⁾=[U\tilde]₈⁽¹⁾ это вектор [P\tilde]=(2,1). По вектору [P\tilde]=(p₁,p₂) восстанавливаем вектор P=(p₁, p₂,p₃,p₄,p₅) согласно условиям (1.17) и получаем в исходных координатах (p₁, p₂,p₃,p₄,p₅) вектор P=(2,1,2,0,0).

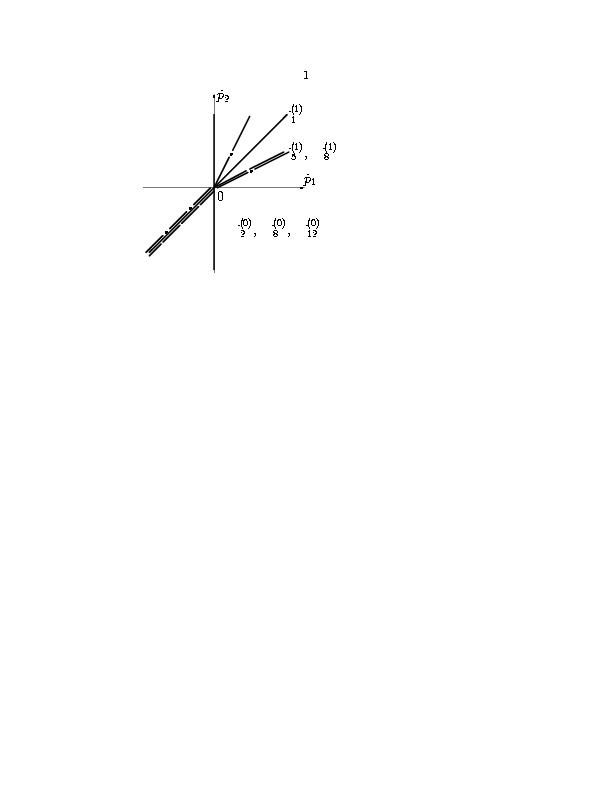
Рис. 9. Совмещенные нормальные конуса проекций носителей уравнений системы (1.1)-(1.3).

Полученным нормальным конусам соответствуют вершины и ребра проекций: [Q\tilde]₂; [Q\tilde]₅=[Q\tilde]₆, [Q\tilde]₈, [(G)\tilde]₅⁽¹⁾; [Q\tilde]₉, [Q\tilde]₁₂=[Q\tilde]₁₃, [(G)\tilde]₈⁽¹⁾. В исходных координатах (q₁,q₂,q₃,q₄,q₅) им соответствуют точки Q₂, Q₅, Q₆, Q₈, Q₉, Q₁₂, Q₁₃ носителей уравнений (1.1)-(1.3). Этим точкам соответствует укороченная система (1.10)-(1.12).

Пятый столбец таблицы 2 содержит значения скалярных произведений D_k=б[P\tilde],[Q\tilde]_kс = бP, Q_kс для P=(2,1,2,0,0), в шестом столбце (T) знак "+" отмечает максимальные значения б[P\tilde],[(Q_k)\tilde]с для данного i (соответствующие члены суммы f_i включены в укорочение [^f]_i2^(d_i⁾).

В обозначениях § 1 главы I имеем l=2 и полученный вектор P=(P′,P"), т.е. P′=(2,1). Кроме того, вектор B₁′=(-1,2) составляет базис в пространстве векторов Q′=(q₁,q₂), удовлетворяющих условию бP′,Q′с = 0. Тогда, согласно теореме 3 главы I, T₃′=(1,0), T₄′=T₅′=0 и согласно (1.5) автомодельные координаты x, G, P, H имеют вид

x = r2/x,  x3    def =     y = xG(x),  x4    def =     r = P(x),  x5    def =     h=H(x),

что соответствует (1.13). Лемма 2 доказана.

§ 2. Система ОДУ

Из (1.10) и (1.13) видно, что P(x)H(x)=const =C₀[(   def) || ( = )]  r₀ h₀ ≠ 0. Поэтому

P(x)=C0/H(x).

(2.1)

После замены (1.13), (2.1) в уравнениях (1.11) и (1.12), получаем систему ОДУ

F2    def =     G(G′H )′+2Cn[ Hn(G′H)′x]′=0, F3    def =     2GH′+16CnC0-2xHn((G′H)′)2+4Cns-1(xHnH′)′=0,

(2.2)

где ′[(   def) || ( = )]  d/dx, с граничными условиями

G=y0x,  H=h0 при x→ +∞,

(2.3)

G=dG/dx = 0 при x = 0.

(2.4)

Теперь заметим, что уравнение

(G′H)′=0

(2.5)

или

G′H=c1=const,

(2.6)

где c₁ - произвольная постоянная, выделяет инвариантное многообразие полной системы (2.2). На нем первое уравнение системы выполнено тождественно, а второе, после сокращения на 2, принимает вид:

GH′+2Cns-1(xHnH′)′=0.

(2.7)

Итак, получили систему двух уравнений (2.6) и (2.7). Нас интересуют ее решения с граничными условиями (2.3), (2.4). Чтобы нормировать константы сделаем линейную замену координат

x =  Cnh0n sy0    ~ x   ,  G=  Cnh0n s    ~ G   ,  H=h0 ~ H   .

(2.8)

Тогда, опуская тильды у переменных, получаем систему уравнений

G′H= ~ c   1  =const,

(2.9)

GH′+2(xHnH′)′=0

(2.10)

с граничными условиями (2.4) и

G=x,  H=1 при x→+∞.

(2.11)

Из граничного условия (2.11) следует, что в уравнении (2.9) [c\tilde]₁=1 и оно имеет вид

G′H=1.

(2.12)

Итак, получили систему (2.12), (2.10) с граничными условиями (2.11) и (2.4). Сложим уравнения (2.12) и (2.10) и сумму проинтегрируем, получим

GH+2xHnH′=x+2c2,

(2.13)

где c₂ - произвольная постоянная. Сведем теперь систему уравнений (2.12), (2.13) к одному уравнению для H, исключив G. Из (2.13) получаем

G=-2xHn-1H′+(x+2c2)H-1.

Отсюда

G′=-  2(xHnH′)′ H +  2(xHnH′)H′ H2 +  1 H -  (x+2c2)H′ H2 .

(2.14)

Согласно (2.12) G′=1/H. Поэтому в последнем уравнении члены G′ и 1/H взаимно уничтожаются. Умножая уравнение (2.14) на -H², получаем уравнение

D    def =     2(xHnH′)′H-2xHnH′2+(x+2c2)H′=0

(2.15)

с граничными условиями

H→+∞ при x→+0,

(2.16)

H=1 при x→+∞.

(2.17)

Кроме того, согласно § 1 из физического смысла энтальпии имеем h > 0; следовательно, нас интересуют только те решения H(x) уравнения (2.15), у которых согласно (1.13) и (1.4)

H(x) > 0 и Hn > 0 для x ∈ (0,∞).

(2.18)

Итак, получена

Лемма 3. В автомодельных координатах (1.13) задача (1.7), (1.8), (1.10)-(1.12) после замены (2.1) сводится к задаче (2.2)-(2.4). Частные решения этой задачи после нормирования (2.8) являются решениями задачи (2.10), (2.11), (2.12). После исключения G согласно (2.12), последняя задача сводится к уравнению (2.15) с граничными условиями (2.16), (2.17) и со свойством (2.18).

Заметим, что уравнение (2.15) всегда имеет постоянные решения

H=const    def =     H0.

(2.19)

Лемма 4. В любой точке x = x⁰=const, H=H⁰=const с x⁰ ∈ (0,∞), H⁰ ≠ 0 непостоянное решение H(x) уравнения (2.15) монотонно.

Доказательство. Перепишем уравнение (2.15) в виде

H"=  2(1-n)H′2 H -  H′ x -  (x+2c2)H′ 2xHn+1 .

(2.20)

Согласно теореме Коши в любой точке x = x⁰=const, H=H⁰=const, H′=H′⁰=const с x⁰ ∈ (0,∞), H⁰ ≠ 0 решение H(x) уравнения (2.15) аналитично. Следовательно, оно имеет в этой точке экстремум, только если H′⁰=0. Но согласно (2.20) тогда в этой точке H"=0. Дифференцируя уравнение (2.20), получаем, что в этой точке и все дальнейшие производные H^(k) равны нулю. Аналитическая функция H(x), у которой в некоторой точке все производные равны нулю, является постоянной. Доказательство окончено.

§ 3. Решения уравнения (2.15) вблизи нуля

Теорема 1. У уравнения (2.15) с фиксированными n ∈ [0,1] и c₂ ≠ 0 все решения, удовлетворяющие условию (2.16), образуют два двупараметрических семейства:

семейство G₁⁽⁰⁾, существующее при n=0, с разложениями

H=c4xl+ е s  asxs, где l < 0, s О K={s=l-ll+m(1-l); целые l,m ≥ 0,  l+m > 0};

(3.1)

и семейство F₁⁽¹⁾G₄⁽⁰⁾ с нестепенными асимптотиками

H ~ ~ c   (lnx)1/n+ е bs(lnx)s,  s О K(k2), при n О (0,1),

(3.2)

K(k2) = {s=1/n-l/n-m,  целые l,m ≥ 0,  l+m > 0},

H ~ ~ c   lnx+ ∞ е l=0  bl(ln|lnx|)(lnx)-l,   при n=1;

(3.3)

а также одно однопараметрическое семейство F₁⁽¹⁾G₄⁽¹⁾ с нестепенными асимптотиками

H ~ [ (n+1)(c2lnx+c3)]1/(n+1),

(3.4)

которое существует при n ∈ [0,1] и c₂ < 0 и является границей предыдущих двупараметрических семейств.

При c₂=0 в (3.1) множество K ={s=l+m(1-l), целые m > 0}, а асимптотики (3.2) и (3.3) имеют вид H ~ (c₄lnx+c₅)^1/n при n ∈ (0,1].

Здесь [c\tilde], c₃, c₄, c₅ и l < 0 - произвольные постоянные, постоянные a_s и b_s - однозначно определены, кроме произвольного b_-1+1/n; а b_l суть многочлены от ln|lnx| с постоянными коэффициентами; все они однозначно определены, кроме многочлена b₀, который имеет произвольный свободный член. Разложения в (3.1) и (3.2) сходятся для малых |x|.

Доказательство разобьем на два случая: c₂ ≠ 0 и c₂=0. Но сначала заметим, что поскольку x→ 0 и H→∞, то конус задачи есть

p1 ≤ 0,  p2 ≥ 0.

(3.5)

Случай c₂ ≠ 0. В этом случае носитель уравнения (2.15) состоит из трех точек Q₁=(-1,2+n), Q₂=(0,1) и Q₃=(-1,1). Носитель S(D), многоугольник G(D) и его грани G_j^(d) для уравнения (2.15) показаны на рис. 10а, а их нормальные конусы U_j^(d) - на рис. 10б, где заштрихован конус задачи (3.5). Согласно рис. 10б с ним пересекаются только нормальные конуса U₁⁽⁰⁾ и U₁⁽¹⁾. Рассмотрим соответствующие им грани и укороченные уравнения, учитывая, что согласно п. 2.2 главы I, w = -1.

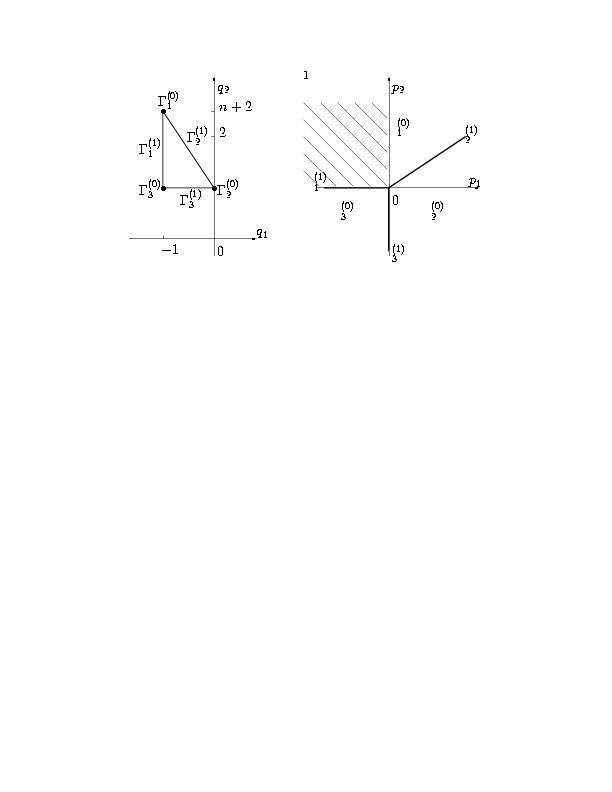
Рис. 10. Носитель S(D), многоугольник G(D) и его грани G_j^(d) для уравнения (2.15) при c₂ ≠ 0 (а) и их нормальные конуса (б); заштрихован конус задачи (3.5).

Вершине G₁⁽⁰⁾ соответствует укороченное уравнение

^ D   (0) 1       def =     2(xHnH′)′H-2xHnH′2 = =2Hn[(n-1)xH′2+xHH"+HH′]=0.

(3.6)

Приравняв нулю квадратные скобки из уравнения (3.6) и разделив их затем на xHH′, получаем уравнение

(n-1)  Hў H  +   H" Hў  +   1 x  =0.

Интегрируя его по x, получаем уравнение

(n-1)lnH+lnH′+lnx = c0,

где c₀ - произвольная постоянная. Это уравнение эквивалентно уравнению

Hn-1H′=c1/x,

где c₁ ≠ 0 - произвольная постоянная. Интегрируя это последнее уравнение, получаем

1 n Hn=c1lnx+c3 при n ≠ 0,

lnH=c1lnx+c3 при n=0,

где c₃ - произвольная постоянная. Эти выражения эквивалентны формулам

H=(c4lnx+c5)1/n при n ≠ 0,

(3.7)

H=c4xl при n=0,

(3.8)

где c₄, c₅ и l - произвольные постоянные.

Для решений (3.7) при x→ 0 порядок r=0 и, согласно п. 2.2 главы I, им соответствует вектор P=w(1,r)=-(1,0), который не лежит в нормальном конусе U₁⁽⁰⁾. Следовательно, при n ≠ 0 вершине G₁⁽⁰⁾ не соответствует никакое подходящее решение (3.7).

Для решений (3.8) при x→ 0 порядок r=l. Вектор P=w(1,r)=(-1,-l) ∈ U₁⁽⁰⁾, если l < 0, что в дальнейшем предполагается. Следовательно, при n=0 выражение (3.8) с l < 0 дает степенные асимптотики решений уравнения (2.15). По п. 2.3 главы I найдем степенные разложения этих решений вида

H=c4xl+ е s  bsxs,  s > l,  s О K.

(3.9)

Первая вариация уравнения (3.6) при n=0 есть

d ^ D   (0) 1  dH =  - 4xHў  d dx  + 2xH" + 2xH  d2 dx2  + 2Hў + 2H  d dx .

По теореме 5 главы I, на кривой (3.8) она дает оператор

L(x) = 2c4xl-1 й л  - 2lx  d dx  + l(l-1) + x2  d2 dx2  + l + x  d dx щ ы  ¬ є 0.

Тогда характеристический многочлен дифференциальной суммы L(x)x^k есть

n(k)=2c4[-2lk+l(l-1)+k(k-1)+l+k] = 2c4(k-l)2.

Он имеет один двукратный корень k₁=l = r, который не является критическим числом, ибо не удовлетворяет неравенству k₁ > r.

Для вычисления множества K воспользуемся леммой 1 главы I. Здесь

M1=(0,-1),  M2=(1,-1).

(3.10)

Поэтому

r1    def =     бM1,(1,r)с = -l,  r2    def =     бM2,(1,r)с = 1-l.

Следовательно,

K={s=l-ll+m(1-l); целые l,m ≥ 0,  l+m > 0}.

(3.11)

В разложениях (3.9), (3.11) все коэффициенты b_s постоянны и однозначно определены; согласно теореме 10 главы I они сходятся для достаточно малых |x| ≠ 0. Их семейство обозначим G₁⁽⁰⁾. Итак, получено разложение (3.1).

Ребру G₁⁽¹⁾ соответствует укороченное уравнение

^ D   (1) 1       def =     2(xHnH′)′H-2xHnH′2+2c2H′=0.

(3.12)

Это уравнение имеет инвариантное многообразие

xHnH′=c2.

(3.13)

На нем HⁿH′=c₂/x. Интегрируя по x это уравнение, получаем

Hn+1/(n+1)=c2lnx+c3,

где c₃ - произвольная постоянная. Итак,

H=[ (n+1)(c2lnx+c3)]1/(n+1).

(3.14)

Для вещественности решений (3.14) надо, чтобы c₂ < 0, ибо lnx < 0 при x→ 0. Таким образом, получено разложение (3.4).

Найдем нестепенные асимптотики решений уравнения (3.12). Ребро G₁⁽¹⁾, как видно из рис. 10, является вертикальным, следовательно, согласно п. 2.7 главы I, делаем логарифмическое преобразование

t=lnx

(3.15)

и производную по t будем обозначать точкой: [ \dot]  [(   def) || ( = )]  d/dt. Тогда H′=[H\dot]/x, и уравнение (3.12) принимает вид

W    def =     2 Ч [Hn Ч H   ]   H-2Hn Ч H   2   +2c2 Ч H   =0.

(3.16)

Его носитель S(W) состоит из двух точек Q₄=(-2,2+n) и Q₅=(-1,1). Многоугольник G(W) является отрезком, их соединяющим. Его нормальный вектор N₄=(1,1/(n+1)). Его грани G_j^(d) показаны на рис. 11а, а их нормальные конуса - на рис. 11б.

Рис. 11. Грани G_j^(d) многоугольника уравнения (3.16) при c₂ ≠ 0 (а) и их нормальные конуса (б).

Обозначим G_j⁽⁰⁾=Q_j. Здесь t→-∞ т.е. w = 1, и конус задачи есть p₁ ≥ 0, p₂ ≥ 0 (заштрихован на рис. 11б). С ним пересекаются все три нормальных конуса U_j^(d). Рассмотрим решения, соответствующие граням G_j^(d).

Вершине G₄⁽⁰⁾ соответствует укороченное уравнение

^ W   (0) 4     def =     2 Ч [Hn Ч H   ]   H-2Hn Ч H   2   = 2[(n-1)Hn Ч H   2   +Hn+1 ЧЧ H   ]=0.

(3.17)

На самом деле, это уравнение (3.6) с независимой переменной t=lnx. Его характеристический многочлен есть

2r(nr+r-1)-2r2=2r(nr-1).

Он имеет два корня r=0 и r=1/n. Соответствующие векторы w(1,r) суть P₁=(1,0) и P₂=(1,1/n). Вектор P₁ не лежит в нормальном конусе U₄⁽⁰⁾, а вектор P₂ лежит в U₄⁽⁰⁾, ибо 1/n > 1/(n+1). Следовательно, при n ≠ 0 укороченное уравнение (3.17) имеет степенные решения

H= ~ c   t1/n,

(3.18)

где [c\tilde] ≠ 0 - произвольная постоянная. Найдем их критические числа. Согласно п. 2.3 главы I первая вариация

d ^ W   (0) 4  dH = 2 й л (n-1)nHn-1 Ч H   2    + 2(n-1)Hn Ч H    d dt   +

+  (n+1)Hn ЧЧ H    + Hn+1  d2 dt2 щ ы .

(3.19)

На кривой (3.18) она дает оператор

L(t) = 2 ~ c   n+1   t(1-n)/n й л  n-1 n  +   n+1 n ж и  1 n  - 1 ц ш  + 2  n-1 n t  d dt  + t2  d2  dt2 щ ы .

Характеристический многочлен дифференциальной суммы L(t)t^k есть

n(k)=2 ~ c   n+1   й л k(k-1) +   2(n-1) n k +   1-n  n2 щ ы .

Он имеет два корня k₁=1/n и k₂=(1-n)/n=k₁-1. Здесь конус задачи k < r=1/n. Поскольку корень k₁=r, то он не является критическим числом, но k₂=r-1 < r, поэтому k₂ - критическое число. Согласно леммам 1 и 2 главы I здесь множества

K={s=-l/n, целые l ≥ 0}, K(k2)={s=1/n-l/n-m, целые l,m ≥ 0,  l+m > 0}.

Если n ∈ (0,1), то k₂=1/n-1 ¬ ∈ K и уравнение (3.16) имеет семейство G₄⁽⁰⁾ степенных разложений решений

H= ~ c   t1/n+ е bsts,  s О K(k2),

(3.20)

где b_s - постоянные коэффициенты, [c\tilde] и b_k2- произвольны, а остальные коэффициенты b_s однозначно определены. Согласно теореме 10 главы I разложение (3.20) сходится для достаточно больших |t|. Если положить b_k2=0, то разложение (3.20) имеет вид

H= ~ c   t1/n+ ∞ е l=0  bl t-l/n,

(3.21)

где [c\tilde] - произвольная постоянная, а постоянные b_l однозначно определены. Так,

b0=  nc2 ~ c   n   (n-1) ,  b1=  n(n-1)b02 2(2-n) ~ c   =  n3c22 2(2-n)(n-1) ~ c   2n+1   .

(3.22)

Согласно (3.14) разложение (3.20) дает двупараметрическое семейство F₁⁽¹⁾G₄⁽⁰⁾ нестепенных асимптотик решений уравнения (2.15)

H ~ ~ c   (lnx)1/n+ е bs(lnx)s,  s О K(k2).

Итак, получено разложение (3.2).

Если n=1, то k₂=0 ∈ K и, согласно п. 2.5 главы I, уравнение (3.16) имеет семейство степенно-логарифмических разложений вида (3.21), где коэффициенты b_l являются многочленами от ln|t|, коэффициент b₀ содержит произвольную постоянную, а остальные коэффициенты b_l однозначно определены. Это семейство также обозначим G₄⁽⁰⁾. Ему также соответствует двупараметрическое семейство F₁⁽¹⁾G₄⁽⁰⁾ нестепенных асимптотических решений уравнения (2.15). Итак, получено разложение (3.3).

Кроме того, можно проинтегрировать уравнение (3.17) явно. Ибо уравнение (3.17) получается из уравнения (3.6) после замены (3.15), а решения уравнения (3.6) суть (3.7) и (3.8).

Вершине G₅⁽⁰⁾ соответствует укороченное уравнение [^(W)]₅⁽⁰⁾[(   def) || ( = )]   2c₂[H\dot]=0. Все его решения суть H=const, т.е. r=0. Вектор P=w(1,r)=(1,0) ∈ U₅⁽⁰⁾ (см. рис. 11б). Соответствующие степенные укороченные решения (2.19) нам не подходят, ибо для них граничное условие (3.4) не выполнено. Поэтому решения, соответствующие вершине G₅⁽⁰⁾ не подходят.

Ребру G₄⁽¹⁾ соответствует все уравнение (3.16). Поскольку нормальным к ребру G₄⁽¹⁾ является вектор N₄=(1,1/(n+1)), то ищем решения уравнения (3.16) в виде

H= ~ c   0  t1/(n+1).

(3.23)

Для [c\tilde]₀ получаем определяющее уравнение

~ c   n+2 0   1 n+1 ж и  n n+1  +   1 n+1  - 1 ц ш  -  ~ c   n+2 0   1 (n+1)2  + c2 ~ c   0   1 n+1  =0.

(3.24)

Из него получаем, что [c\tilde]₀ⁿ⁺¹=(n+1)c₂, т.е.

~ c   0  =[(n+1)c2]1/(n+1).

(3.25)

Следовательно,

H=[(n+1)c2lnx]1/(n+1).

(3.26)

При x→ 0 имеем lnx < 0, поэтому эти решения со свойством (2.18) имеются только при c₂ < 0 и отсутствуют при c₂ ≥ 0.

Найдем теперь критические числа укороченного решения (3.23). Согласно (3.16) и (3.19) первая вариация есть

dW dH = 2 й л (n-1)nHn-1 Ч H   2    + 2(n-1)Hn Ч H    d dt   +

+  (n+1)Hn ЧЧ H    + Hn+1  d2 dt2  + c2  d  dt щ ы .

На кривой (3.23) она дает оператор

L(t)=2 м н о ~ c   n+1 0    й л  (n-1)n (n+1)2   t-1 +   2(n-1) n+1    d dt   +

+    (n+1) (n+1)   ж и    1 n+1  - 1 ц ш   t-1 + t  d2  dt2 щ ы  + c2  d dt ь э ю .

Согласно (3.25) характеристический многочлен дифференциальной суммы L(t)t^k есть

n(k)=2c2 м н о (n+1) й л  (n-1)n (n+1)2 -  (n+1)n (n+1)2 +  2(n-1) n+1 k+k(k-1) щ ы +k ь э ю =

= 2c2(n+1) м н о -  2n (n+1)2 +  n-2 n+1 k+k2 ь э ю .

Его корни суть k₁=2/(n+1) и k₂=-n/(n+1). Здесь конус задачи s < r=1/(n+1). Корень k₁ > r не является критическим числом. Корень k₂ < r является критическим числом.

Выражение (3.23), (3.25) является точным решением уравнения (3.16). Согласно лемме 1 главы I множество K пустое; следовательно, k₂ ¬ ∈ K. По лемме 2 главы I

K(k2)={ r+l(k2-r)} = { r+l(-n/(n+1)-1/(n+1))} = {r-l},

где целое l > 0. Следовательно, имеется однопараметрическое семейство G₄⁽¹⁾ степенных разложений

H= ~ c   0  t1/(n+1) й л 1+ ∞ е l=1  blt-l  щ ы ,

(3.27)

где коэффициенты b_l постоянны, причем b₁, соответствующее критическому числу k₂, является произвольной постоянной, а остальные b_l однозначно определены. Согласно теореме 10 главы I разложение сходится для достаточно больших |t|.

С другой стороны, уравнение (3.12) на инвариантном многообразии (3.13) имеет однопараметрическое (по c₃) семейство решений (3.14). Сравнение его с семейством (3.25), (3.27) показывает, что они совпадают. Таким образом, получено семейство F₁⁽¹⁾G₄⁽¹⁾ с асимптотиками (3.4).

Согласно замечанию 4 главы I, поскольку определяющее уравнение (3.24) не имеет кратного, нулевого и бесконечного корня, то решения уравнения (3.16) не имеют нестепенных асимптотик.

Кроме того, можно понизить порядок уравнения (3.16). Для этого сделаем в уравнении (3.16) замену [H\dot]=p, [H\ddot]=p′p, где p′=dp/dH. Тогда, его решения суть

p=c2H-n+c0H1-n,

где c₀ - произвольная постоянная. Так как p=[H\dot], то получаем

Ч H   =c2H-n + c0H1-n.

(3.28)

Полученное уравнение (3.28) имеет порядок ниже, чем исходное уравнение (3.16). При некоторых значениях n и c₀ это уравнение можно проинтегрировать в конечном виде.

При n=0 оно есть [H\dot]=c₂+c₀H, т.е. H=[c₃x^c₀-c₂]/c₀, где c₃ - произвольная постоянная.

При n=1 уравнение (3.28) принимает вид [H\dot]=c₂H^-1+c₀, т.е. c₀H-c₂ln|c₀H+c₂|=c₀²t+c₄, где c₄ - произвольная постоянная.

При c₀=0 уравнение (3.28) принимает вид [H\dot]=c₂H^-n, т.е. H=[c₂(n+1)lnx+c₄]^1/(n+1), где c₄ - произвольная постоянная. Это формула (3.4).

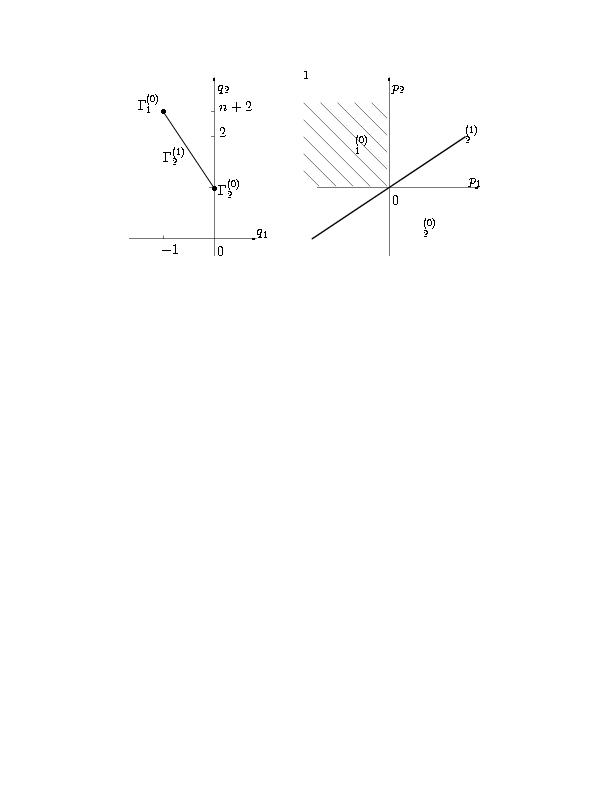
Рис. 12. Носитель и многоугольник уравнения (2.15) при c₂=0 (а) и нормальные конуса его граней (б).

Случай c₂=0. В этом случае носитель S(D) уравнения (2.15) состоит из двух точек Q₁=(-1,n+2) и Q₂=(0,1), многоугольник G(D) является отрезком. На рис. 12а показаны носитель и многоугольник уравнения (2.15) при c₂=0, а на рис. 12б - нормальные конуса его граней и заштрихован конус задачи (3.5). С ним пересекается только нормальный конус U₁⁽⁰⁾. Рассмотрим соответствующую вершину и укороченное уравнение.

Вершине G₁⁽⁰⁾ соответствует укороченное уравнение (3.6). Все его решения найдены выше при рассмотрении случая c₂ ≠ 0 и описываются формулами (3.7), (3.8). Для решений (3.7) вектор P₁=w(1,0)=(-1,0) лежит в нормальном конусе U₁⁽⁰⁾. Поэтому выражения (3.7) являются нестепенными асимптотиками решений уравнения (3.19) при x→ 0. Кроме того, при c₄=0, выражения (3.7) дают также степенные асимптотики решений вблизи x = 0, H=H₀=const.

Для решений (3.8) вектор P₂=w(1,l)=(-1,-l) ∈ U₁⁽⁰⁾, если l < 1. Нахождение степенных разложений вида (3.9) справедливо до формулы (3.10), использовавшейся для вычисления множества K. В данном случае векторы M₁=M₂=(1,-1). Поэтому r₁=r₂=1-l. Следовательно,

K={s=l+m(1-l),    целые m > 0}.

(3.29)

При l ≥ 0 разложение (3.1) с множеством (3.29) не удовлетворяет граничному условию (2.16), т.е. остаются лишь значения l < 0.

Таким образом, решения образуют двупараметрическое семейство, которое при n=0 представляется разложениями (3.9), (3.29) с c₄ ≠ 0, l < 0, а при n ≠ 0 представлено асимптотиками вида (3.7) с c₄ ≠ 0.

Теорема 1 доказана.

Лемма 5. При c₂ ≥ 0 уравнение (2.15) имеет однопараметрическое семейство решений (2.19), а при c₂ < 0 оно имеет двупараметрическое семейство решений, которые при x→ 0 стремятся к постоянным H₀ ≠ 0. Это семейство обозначим F₁⁽¹⁾1.

Доказательство. Укороченное уравнение (3.12) имеет также постоянные решения (2.19), которые при H₀ ≠ 0 можно рассматривать как степенную асимптотику. Найдем решения уравнения (2.15) вблизи решения (2.19) при x→ 0. Согласно п. 2.2 главы I, r=0 и c_r - произвольная постоянная. Первая вариация уравнения (3.12) есть

d ^ D   (1) 1  dH   = 2n(n-1)xHn-1Hў2 + 4(n-1)xHnHў  d dx  + 2xH" + 2(n+1)H"+

+ 2xHn+1  d2 dx2  + 2(n+1)HnHў + 2Hn+1  d dx  +  2c2  d dx .

На решении (2.19) с H₀ ≠ 0, по теореме 5 главы I, она дает оператор

L(x) = 2xH0n+1  d2 dx2 +2H0n+1  d dx +2c2  d dx .

Характеристический многочлен дифференциальной суммы L(x)x^k есть

n(k)=2H0n+1k(k+c2/H0n+1).

Он имеет два корня k₁=0 и k₂=-c₂/H₀ⁿ⁺¹. Собственное значение k₁=r=0 не является критическим числом. Поскольку конус задачи K={s > r=0}, то корень k₂ является критическим числом только при -c₂/H₀ⁿ⁺¹ > 0. Поскольку H₀ и H₀ⁿ⁺¹ > 0, то это означает, что c₂ < 0.

Если нет критических чисел (т.е. c₂ ≥ 0), то из точки x = 0, H=H₀ ≠ 0 выходит единственное решение уравнения (2.15) вида

H=H0+ ∞ е k=1  ckxk,

(3.30)

где все c_k однозначно определены. По лемме 4 из этой точки выходит решение H=H₀[(   def) || ( = )]  const. Следовательно, в формуле (3.30) все c_k=0.

Если есть одно критическое число k₂ (т.е. c₂ < 0), то имеются два подслучая: целого и нецелого k₂. Если критическое число k₂ - не целое, т.е. k₂ ¬ ∈ K ={k=l, целые l > 0}, то из точки x = 0, H=H₀ ≠ 0 выходит однопараметрическое семейство решений уравнения (2.15) с разложением

H=H0+ е s  csxs,  s О K(k2),

где согласно лемме 2 главы I K(k₂)={l+mk₂,   целые l,m ≥ 0,  l+m > 0} и постоянные c_s однозначно определены, кроме s=k₂, для которого c_s произвольно.

Если критическое число k₂ - целое, тогда k₂ ∈ K. Следовательно, из точки x = 0, H=H₀ ≠ 0 выходит однопараметрическое семейство решений уравнения (2.15) с разложением

H=H0+ е s  gsxs,  s О K,

где коэффициенты g_s при s < k₂ - постоянные, которые однозначно определены; g_s при s ≥ k₂ - многочлены от lnx, коэффициент g_k2 содержит произвольную постоянную, а остальные g_s однозначно определены. Лемма 5 доказана.

§ 4. Решения уравнения (2.15) вблизи бесконечности

Теорема 2. При фиксированных n и c₂ и при x→∞ уравнение (2.15) имеет однопараметрическое семейство M решений с H→ 1. Их асимптотики даются формулами

Hў ~ c10xse-x/2,  H-1 ~ c10 у х xse-x/2dx,

(4.1)

где s=-c₂-1 и c₁₀ - произвольная постоянная. Для интеграла в (4.1) справедливо асимптотическое разложение

H-1 ~ -2c10e-x/2 й л xs+ ∞ е l=1  2ls(s-1)...(s-l+1)xs-l щ ы .

(4.2)

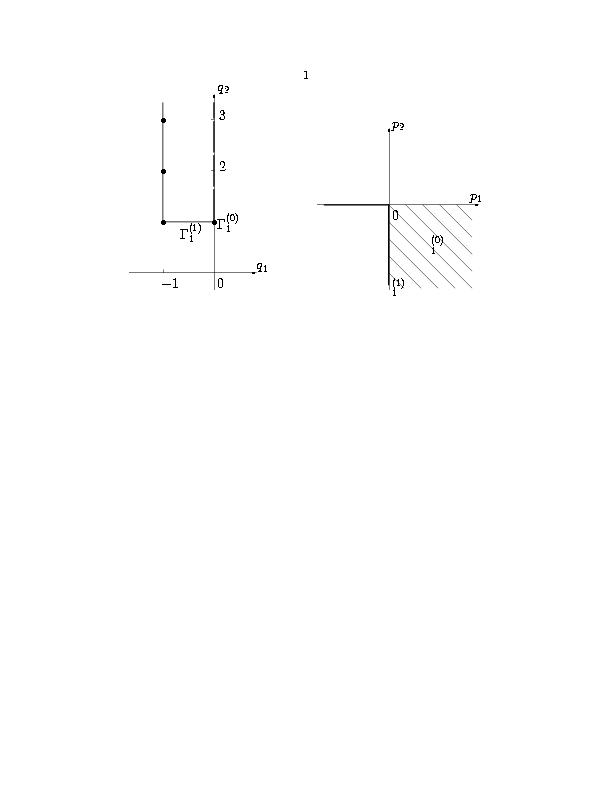
Рис. 13. Носитель и многоугольник уравнения (4.3) (а), нормальные конуса и конус задачи (б).

Доказательство. Заметим, что H=1 является решением уравнения (2.15). В уравнении (2.15) положим H=1+y и рассмотрим уравнение

S(x,y)    def =     D(x,1+y)    def =

def =     2[x(1+y)ny′]′(1+y)-2x(1+y)ny′2+(x+2c2)y′=0.

(4.3)

Оно имеет тривиальное решение y=0. Многоугольник G(S) и нормальные конуса показаны на рисунке 13. Нас интересуют решения при x→∞, y→ 0. Следовательно, конус задачи K={p₁ ≥ 0, p₂ ≤ 0}. Многоугольник G(S) имеет горизонтальное ребро G₁⁽¹⁾ и вершину G₁⁽⁰⁾ с q₂=1 (рис. 13). Вертикальное же ребро с q₁=0 несобственное, т.е. ему не соответствуют свои укороченное уравнение и нормальный конус. С конусом задачи пересекаются нормальные конуса U₁⁽⁰⁾ и U₁⁽¹⁾. Рассмотрим укороченные уравнения, соответствующие вершине G₁⁽⁰⁾ и ребру G₁⁽¹⁾.

Вершине G₁⁽⁰⁾ соответствует укороченное уравнение xy′=0. Все его решения суть y=c₀=const. Поскольку нас интересуют решения y→ 0 при x→∞, то это решение нам не подходит.

Ребру G₁⁽¹⁾ соответствует укороченное уравнение

^ S   (1) 1  (x,y)    def =     2[xy′]′+(x+2c2)y′=0,

т.е.

^ S   (1) 1  (x,y)    def =     2xy"+[x+2(c2+1)]y′=0.

(4.4)

У него разлагаются переменные и его решения имеют вид (4.1).

Согласно п. 2.9 главы I формулы (4.1) с y→ 0 при x→∞ дают асимптотиками решений уравнения (4.3). Для них справедливо асимптотическое разложение (4.2). Действительно, вычисляя интеграл в (4.1) по частям, получаем

у х xse-x/2dx = -2e-x/2xs+2s у х xs-1e-x/2dx.

Полученный интеграл опять вычисляем по частям, получаем первый член суммы в (4.2) и интеграл

у х xse-x/2dx = -2e-x/2[ xs+2sxs-1]+4s(s-1) у х xs-2e-x/2dx.

Продолжая вычислять интегралы по частям, получаем асимптотическое разложение (4.2). Лемма доказана.

При целых неотрицательных s, т.е. для

c2=-1,  -2,  ...,  -n,  ...

(4.5)

сумма в квадратных скобках в (4.2) является конечной, т.е. это многочлен степени s.

При фиксированном n на плоскости c₂, c₁₀ семейству M соответствуют все точки, кроме прямой c₁₀=0.

§ 5. Решения уравнения (2.15) вблизи точки x⁰ > 0

Лемма 6. Решения уравнения (2.15) не уходят в бесконечность и не приходят из бесконечности при любом конечном x > 0.

Доказательство. Сделаем в уравнении (2.15) подстановку

x = x0+ ~ x   ,

(5.1)

где x⁰=const > 0. Тогда уравнение (2.15) примет вид

f( ~ x   ,H)    def =     D(x0+ ~ x   ,H) = 2 й л (x0+ ~ x   )HnHў щ ы ўH-2(x0+ ~ x   )HnHў2+

+(x0+ ~ x   +2c2)Hў = 2(n-1)(x0+ ~ x   )HnHў2+2(x0+ ~ x   )Hn+1H"+

+2Hn+1Hў+(x0+ ~ x   +2c2)Hў=0.

(5.2)

Если x⁰+2c₂ ≠ 0, то его носитель состоит из точек Q₁, Q₂, Q₃ и точки Q₆=(-2,2+n), многоугольник является параллелограммом (рис. 14). Нас интересуют решения уравнения (5.2), у которых [(x)\tilde]→ 0 и H→∞, т.е. конус задачи есть p₁ ≤ 0, p₂ ≥ 0. С ним пересекаются только два нормальных конуса U₆⁽⁰⁾ и U₆⁽¹⁾ (рис. 14б). Рассмотрим соответствующие грани и укороченные уравнения.

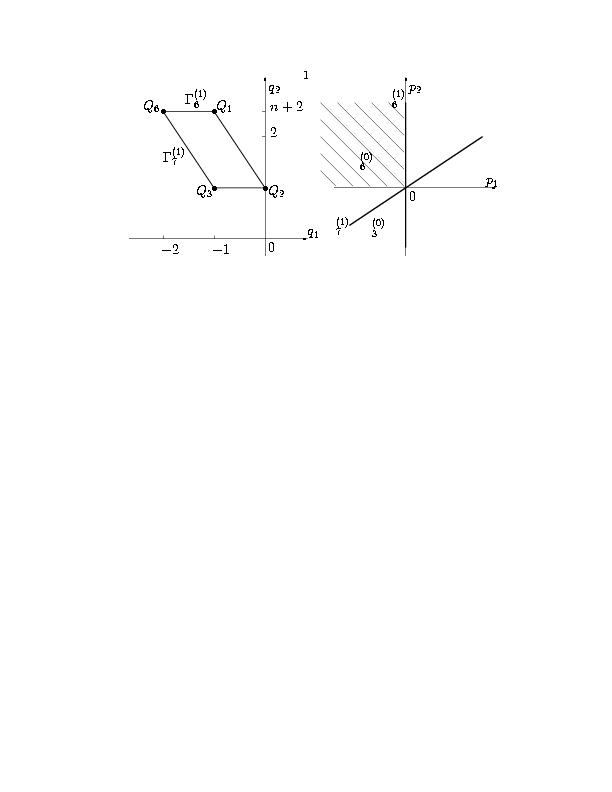
Рис. 14. Носитель и многоугольник уравнения (5.2) (а), нормальные конуса его граней и конус задачи (б).

Вершине G₆⁽⁰⁾ соответствует укороченное уравнение

^ f   (0) 6       def =     2(n-1)x0HnH′2+2x0Hn+1H"=0.

(5.3)

Все его решения имеют вид

1 n Hn=c30 ~ x   +c31, при n ≠ 0,

lnH=c30 ~ x   +c31, при n=0,

(5.4)

где c₃₀ и c₃₁ - произвольные постоянные. При [(x)\tilde]→ 0 эти решения не уходят в бесконечность.

Ребру G₆⁽¹⁾ соответствует укороченное уравнение (3.6). Все его решения имеют вид (3.7) и (3.8). При [(x)\tilde]→ 0 они стремятся к конечным значениям H=(c₄lnx⁰+c₅)^1/n и H=c₄(x⁰)^l, т.е. не уходят в бесконечность.

Если x⁰+2c₂=0, то укороченные уравнения, соответствующие граням G₁⁽⁰⁾, G₆⁽⁰⁾ и G₆⁽¹⁾ не меняются. Лемма 6 доказана.

§ 6. Решения уравнения (2.15), удовлетворяющие
обоим граничным условиям

Здесь изучаются те решения уравнения (2.15), которые удовлетворяют условиям (2.16), (2.17) и обладают свойством (2.18). Для этого рассматриваются отдельно два случая: c₂ ≥ 0 и c₂ < 0.

Случай c₂ ≥ 0.

Лемма 7. При фиксированных c₂ ≥ 0 и n ∈ [0,1] уравнение (2.15) имеет однопараметрическое семейство решений со свойствами (2.16), (2.17), (2.18), и с асимптотиками при x→0

H ~ constxl,  l < 0 при n=0, H ~ const|lnx|1/n при n ≠ 0.

(6.1)

Доказательство. У уравнения (2.15) согласно лемме 4 имеется однопараметрическое (по c₁₀) семейство решений с асимптотикой (4.1). При c₁₀ < 0 эти решения отличны от постоянных и убывают при x→∞. Согласно лемме 4 они монотонно убывают при x > 0 к значению H=1. Согласно лемме 6 эти решения не приходят из бесконечности при любом x > 0. Согласно лемме 5 ни одно из этих решений не стремится к конечному значению при x→ 0. Следовательно, согласно теореме 1, при x→ 0 все эти решения уходят в бесконечность с асимптотиками (6.1). Доказательство леммы окончено.

Введем семейства

M0=M∩(G1(0)∪F1(1)G4(0)∪F1(0)); M1=M∩F1(1)G4(1).

(6.2)

Согласно теоремам 1 и 2 к ним относятся все те решения (2.16), (2.18) уравнения (2.15), которые уходят в +∞ при x→ 0. При этом семейство M₁ имеется только при c₂ < 0 и является границей семейства M₀. Теорема 2 означает, что при c₂ ≥ 0 семейству M₀ соответствует четверть { c₂ ≥ 0, c₁₀ < 0} плоскости c₂, c₁₀.

Случай c₂ < 0. При c₂ < 0 решения с асимптотикой (4.1) и с c₁₀ < 0 при уменьшении x от бесконечности также монотонно возрастают и не уходят в бесконечность при конечных x согласно леммам 4 и 7. Но теперь согласно лемме 5 они могут иметь конечный предел при x→ 0. Для анализа решений уравнения (2.15) при c₂ < 0 использовались две схемы численного счета.

Схема 1. Уравнение (2.15) записывается в виде

2 Ч [Hn Ч H   ]   H-2Hn Ч H   2   +(et+2c2) Ч H   =0,

(6.3)

где t=lnx. При больших отрицательных значениях t₀ задаются начальные значения H₀ и [H\dot]₀ и решение считается методом Рунге-Кутта до больших положительных значений t_N.

Схема 2. Для большого x = x₀ вблизи бесконечности берем начальные значения H=1+y, H′=y′ согласно формулам (4.1) (4.2). При этом бесконечная сумма в формуле (4.2) заменяется ее начальным отрезком, а значения постоянной c₁₀ < 0 берутся из некоторой сетки в R. Методом Рунге-Кутта просчитывается решение уравнения (2.15) до малого x_N > 0.

 

 

 

Для значений

n=0,  1/4,  1/2,  3/4,  1

(6.4)

и фиксированных значений c₂ < 0 сначала вычислялись решения семейства M₁. Для схемы 1 брались начальные данные по формуле (3.4) и постоянная c₃ менялась так, чтобы при t→+∞ решение вышло на H=1. Для этого решения, по первой формуле (4.1) находилось значение постоянной c₁₀. Затем для контроля по второй схеме просчитывалось решение с этими значениями постоянных c₂ и c₁₀ и получались соответствующие начальные данные первой схемы. Результаты этих вычислений по сетке c₂=-1(-1)-10 представлены в табл. 3 и 4 и на рис. 8.1 из [21] показаны графики функций c₃=æ₃(c₂) и c₁₀=æ₁₀(c₂) для значений (6.4). Оказалось, что на семействе M₁ при убывании c₂ значения постоянной c₃ монотонно возрастают, а значения постоянной c₁₀ имеют минимум. В табл. 5 приведены значения c₂, c₃, c₁₀ в точках минимума c₁₀ на семействе M₁. На рис. 8.2 из [21] показаны графики решений H(x) и G(x) системы (2.12), (2.10) для n=0 и n=1 при значениях c₂, c₃ и c₁₀, соответствующих минимуму c₁₀, т.е. из табл. 5. Поскольку семейство M₁ является границей семейства M₀, то при значениях постоянной c₁₀ меньших, чем ее значения на семействе M₁, решение принадлежит семейству M₀ и при x→ 0 имеет асимптотику (3.7), (3.8). С асимптотикой (3.7) все ясно, но для асимптотики (3.8) интересно знать значения показателя l. При n=0 для разных значений c₂ и c₁₀ < 0, соответствующих семейству M₀, вычислялись решения по второй схеме и при x→ 0 вычислялся предел отношения lnH/lnx = l. Результаты представлены в табл. 6. На рис. 8.3 в [21] показаны графики решения H(x) для n=0 и 1, c₂=0 и 10, c₁₀=-1.

 

 

 

Итак, при фиксированных n ∈ [0,1] на семействе M₁ зависимости c₃ в (3.4) и c₁₀ в (4.1) от c₂ < 0 даются кривыми

c3=æ3(c2,n) и c10=æ10(c2,n).

(6.5)

Таким образом, получена

Лемма 8. При фиксированных n ∈ [0,1] к семейству M₀ относятся все те решения семейства M, у которых

c10 < æ10(c2).

Объединением лемм 7 и 8 получается

Теорема 3. При фиксированных n ∈ [0,1] к семейству M₀ относятся все те решения семейства M, у которых

c10 < м н о æ10(c2),   если c2 < 0; 0,   если c2 _ 0.

При x→ 0 они имеют асимптотики (6.1).

§ 7. Возвращение к исходной задаче (1.1)-(1.3), (1.6)-(1.7)

Если для решений H(x) уравнения (2.15) сделать преобразования, обратные к тем которые указаны в лемме 3, то получим решения укороченной системы (1.10)-(1.12). При этом семействам M₀ и M₁ решений задачи (2.15)-(2.17) будут соответствовать семейства [(M)\tilde]₀ и [(M)\tilde]₁ автомодельных решений задачи (1.7), (1.8), (1.10)-(1.12). А именно, сначала получаем G(x) в задаче (2.4), (2.10)-(2.12) и при x→ 0 имеем G ~ x/H, т.е.

G ~ constx1-l,l < 0, при n=0, G ~ constx/|lnx|1/n, при n ≠ 0.

(7.1)

Затем, после преобразования, обратного к (2.8), получаем решения G(x) и H(x) задачи (2.2)-(2.4). При x→ 0 они имеют асимптотики (7.1) и

H ~ constxl,l < 0, при n=0, H ~ const(lnx)1/n, при n ≠ 0.

(7.2)

Из (2.1) получаем P(x) с асимптотикой при x→ 0

P ~ constx-l,l < 0, при n=0, P ~ const/|lnx|1/n, при n ≠ 0.

При переходе от автомодельных координат (1.13) к исходным, получаем решения y, r, h задачи (1.7), (1.8), (1.10)-(1.12). В погранслое при x→ 0 они имеют асимптотики

y ~ const  xx1-l,  r ~ const  x-l,  h ~ const  xl,  l < 0,  n=0; y ~ const  r2/|lnx|1/n,  r ~ const  /|lnx|1/n,                                                                                  h ~ const  |lnx|1/n,  n ∈ (0,1];

(7.3)

Таким образом, получили решения и их асимптотики для семейства [(M)\tilde]₀. Аналогично получаются решения для семейства [(M)\tilde]₁, которые при x→ 0 имеют асимптотики

y ~ const  r2/|lnx|1/(n+1),  r ~ const  /|lnx|1/(n+1),                                                                                          h ~ const|lnx|1/(n+1),  n ∈ [0,1].

(7.4)

По теореме 1 главы I решения семейств [(M)\tilde]₀ и [(M)\tilde]₁ являются асимптотиками решений задачи (1.1)-(1.3), (1.6)-(1.7) при x→+∞ и r²/x < ∞, если таковые существуют. Итак, получен Основной результат:

Теорема 4. В пограничном слое r²/x < ∞ при x→+∞ задача (1.1)-(1.3), (1.6)-(1.7) имеет семейства решений [([(M)\tilde]₀)\tilde] и [([(M)\tilde]₁)\tilde], которые вблизи иглы при x = r²/x→ 0 имеют асимптотики [([(M)\tilde]₀)\tilde]: (7.3), [([(M)\tilde]₁)\tilde]: (7.4) При фиксированных параметрах задачи (1.1)-(1.3), (1.6)-(1.7) семейство [([(M)\tilde]₀)\tilde] - двупараметрическое, а [([(M)\tilde]₁)\tilde] - однопараметрическое и служит границей семейства [([(M)\tilde]₀)\tilde].

В погранслое x ∈ (0,∞) для решений семейств [([(M)\tilde]₀)\tilde] и [([(M)\tilde]₁)\tilde] исходной задачи (1.1)-(1.3), (1.6)-(1.7) асимптотиками являются семейства [(M)\tilde]₀ и [(M)\tilde]₁ автомодельных решений укороченной системы (1.10)-(1.12). При этом точность асимптотик можно оценить по замечанию 1 главы I.

Теорема 5. Точность асимптотик по x→+∞ из семейств [(M)\tilde]₀ и [(M)\tilde]₁ в погранслое x ∈ (0,∞) оценивается по формулам

y- ~ y   = ~ y    O(x-e),  r- ~ r   = ~ r    O(x-e),  h- ~ h   = ~ h    O(x-e),

(7.5)

где 0 < e < 1, [(y)\tilde], [(r)\tilde], [h\tilde] - асимптотики из семейств [(M)\tilde]₀ и [(M)\tilde]₁, а y, r, h - решения из семейств [([(M)\tilde]₀)\tilde] и [([(M)\tilde]₁)\tilde].

Доказательство. По лемме 2 нормальный вектор укороченной системы (1.10)-(1.12) есть P=(2,1,2,0,0). Для применения замечания 1 главы I нужно, чтобы p₁=1. Следовательно, надо использовать вектор P^*=P/2=(1,1/2,1,0,0). Тогда в замечании 1 главы I

a1=бP*,Q2с = -1/2,  b1=бP*,Q1с = бP*,Q3с = -3/2, a2=бP*,Q5с = бP*,Q6с = бP*,Q8с = -1,  b2=бP*,Q7с = -2, a3=бP*,Q9с = бP*,Q12с = бP*,Q13с = -1,   b3=бP*,Q10с = бP*,Q14с = -2.

Следовательно, в формуле (1.6) главы I

0 < e < e0= min 1 ≤ i ≤ 3  |ai-bi|=1,

т.е. получили оценку (7.5). Теорема доказана.

1. Л.Г. Лойцянский. Механика жидкости и газа. М.: Наука, 1978.

2. М.М. Васильев. Об осесимметричных течениях вязкого теплопроводного газа. Препринт N 11, М.: ИПМ, 2001. 13 с.

3. M.M. Vasiliev. Obtaining the Self-Similar Asymptotics of Solutions to the Navier-Stokes Equations by Power Geometry // Progress in Analysis. Proceedings of the 3rd International ISAAC Congress (Eds. H. G. Begehr, R. P. Gilbert, M. W. Wong), Singapore: World Scientific, 2003, vol. 1, p. 93-101.

4. M.M. Vasiliev. Asymptotics of some viscose, heat conducting gas flows // Proceedings of BAIL 2002 (Eds. S. Wang and N. Fowkes), Perth: University of Western Australia, 2002, p. 251-256.

5. А.Д. Брюно. Степенная геометрия в алгебраических и дифференциальных уравнениях. М.: Физматлит, 1998.

6. А.Д. Брюно. Автомодельные решения и степенная геометрия // Успехи мат. наук, 2000, т. 55, вып. 1, с. 3-44.

7. А.Д. Брюно. Степенные разложения решений системы алгебраических и дифференциальных уравнений // ДАН, 2001, т. 380, N 3, с. 298-304.

8. Т.В. Шадрина. Об осесимметричном обтекании иглы вязкой несжимаемой жидкостью. Препринт N 36, М.: ИПМ, 2002. 21 с.

9. А.Д. Брюно. Степенные разложения решений одного алгебраического или дифференциального уравнения // ДАН, 2001, т. 380, N 2, с. 155-159.

10. Л.Г. Лойцянский. Ламинарный пограничный слой. М.: Физматлит, 1962.

11. L. Prandtl. Über Flüssigkeitsbewegung bei sehr kleiner Reibung // Verhandlungen des III. Internat Math.-Kongr., Heidelberg, 1904. Leipzig: Teubner 1905. S. 484-491.

12. H. Blasius. Grenzschichten in Flüssigkeiten mit kleiner Reibung // Zeit. für Math. und Phys. 1908. V. 56. P. 1-37.

13. M.B. Glauert, M.J. Lighthill. The axisymmetric boundary layer on a long thin cylinder // Proc. Roy. Soc., ser. A, 1955, 230, no. 1181, p. 188-203.

14. А.Д. Брюно. Асимптотики и разложения решений обыкновенного дифференциального уравнения. Препринт N 9, М.: ИПМ, 2003. 39 с.

15. А.Д. Брюно, Т.В. Шадрина. Об осесимметричном обтекании иглы вязкой несжимаемой жидкостью // ДАН, 2002, т. 387, N 5, c. 589-595.

16. T.V. Shadrina. The Axially Symmetric Boundary Layer around a Needle // Proceedings of BAIL 2002 (Eds. S. Wang and N. Fowkes), Perth: University of Western Australia, 2002, p. 213-220.

17. А.Д. Брюно. Степенные асимптотики решений обыкновенного дифференциального уравнения // ДАН, 2003, т. 392, N 3, с. 295-300.

18. А.Д. Брюно. Степенно-логарифмические разложения решений обыкновенного дифференциального уравнения // ДАН, 2003, т. 392, N 4, с. 439-444.

19. А.Д. Брюно. Нестепенные асимптотики решений обыкновенного дифференциального уравнения // ДАН, 2003, т. 392, N 5, с. 586-591.

20. А.Д. Брюно. Асимптотики и разложения решений обыкновенного дифференциального уравнения // УМН, 2004, т. 59, N 3, с. 31-80.

21. А.Д. Брюно, Т.В. Шадрина. Осесимметричный пограничный слой на игле. Препринт N 64, М.: ИПМ, 2003. 32 с.

22. А.Д. Брюно, Т.В. Шадрина. Осесимметричный пограничный слой на игле // ДАН, 2004, т. 394, N 3, с. 298-304.

23. S. Goldstein. On the two-dimensional steady flow of a viscous fluid behind a solid body // Proceedings Royal Soc. London A 142 (1933), 545-562.

24. K. Stewartson. On asymptotic expansions in the theory of boundary layers // J. Math. and Phys., 36 (1957), 173-191.

25. A.I. Van de Vooren, D. Dijkstra. The Navier-Stokes solution for laminar flow past a semi-infinite flat plate // J. Engineer. Math., vol. 4, no. 1 (1970), 9-27.

26. R.I. MacLachlan. The boundary layer on a finite flat plate // Phys Fluids A, v.3, no.2 (1991), 341-348.

27. R.A. Seban, R. Bond. Skin-friction and heat-transfer characteristics of a laminar boundary layer on a cylinder in axial incompressible flow // J. Aeronaut. Sci. 18 (1951), 671-675.

28. H.R. Kelly. A note on the laminar boundary layer on a circular cylinder in axial incompressible flow // J. Aeronaut. Sci. 21 (1954), 634.

29. Lord Rayleigh. On the motion of solid bodies through viscous liquid // Phil. Mag. (6) 21, (1911), 697-711.

30. K. Pohlhausen. Zur näherungsweisen Integration der Differentialgleichung der laminaren Grenzschicht // Ebenda [Zs. f. angew. Math. u. Mech. 1 (1921)], 252-268.

31. K. Stewartson. The asymptotic boundary layer on a circular cylinder in axial incompressible flow // Quarterly J. Mech and Appl. Math 13 (1955), 113-122.

32. Шадрина Т.В. Пограничный слой при осесимметричном обтекании иглы // Дифференциальные уравнения, 2002, т. 38, N 6, с.853-854.

33. Шадрина Т.В. Об осесимметричном обтекании иглы вязкой несжимаемой жидкостью. // XXVIII Гагаринские чтения. Тезисы докладов. М: МАТИ, 2002, т.2, с. 98-99.

34. Bruno A.D., Shadrina T.V. The axially symmetric boundary layer around a needle // International Conference on Differential and Functional Differential Equations. Abstracts. M.: MAI, 2002, p.18-19.

35. Bruno A.D., Shadrina T.V. The axially symmetric boundary layer around a needle // International Conference "Navier-Stokes Equations and Related Topics" (NSEC8). Abstracts. S.Petersburg: Euler Inst., 2002, p.18-19.

36. Шадрина Т.В. Осесимметричный пограничный слой на игле // XIV Всероссийская конференция "Теоретические основы и конструирование численных алгоритмов для решения задач математической физики". Тезисы докладов. Дюрсо, с.167-168.

File translated from T_EX by T_TH, version 3.40.
On 24 Oct 2005, 15:22.