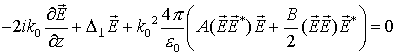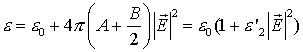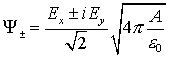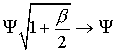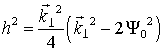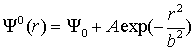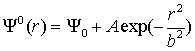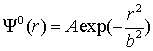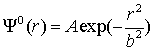Математическое моделирование процессов филаментации в средах с кубической нелинейностью
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
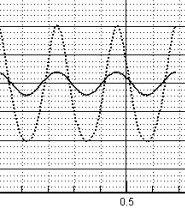
Рис. 2.3.a.
|
Рис. 2.3.б.
|
Рис. 2.3.в. т.е. возмущения
начинают развиваться, увеличивая разброс
амплитуд на фронте волны |
|
|
|
|
|
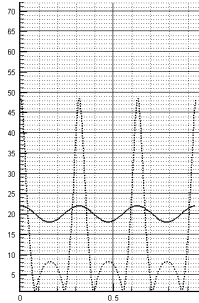
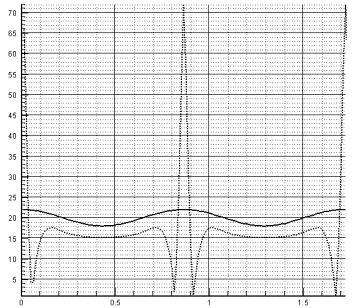
Рис. 2.3.г. Минимальное время
развития неустойчивости t=0.016 |
Рис. 2.3.д. т.е. возмущения
развиваются не так быстро t=0.021 > t=0.016 (ср. рис. 2.3.г) |
|
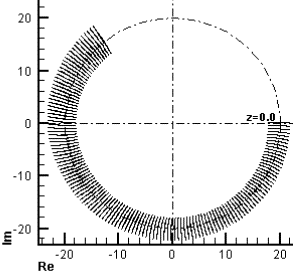
Описанная выше картина развития периодических
возмущений в целом сохраняется и при рассмотрении в двумерном случае начального
возмущений вида:
![]() , т.е. Ψ0=20,
, т.е. Ψ0=20, ![]() .
.

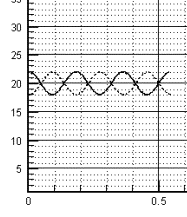
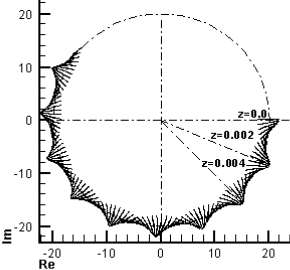
Рис. 2.4.а, ![]() , т.е. устойчивость.
, т.е. устойчивость.
z=0 – черный, z=0.002 – серый.
Периодическое движение
графика по z с периодом z=0.004
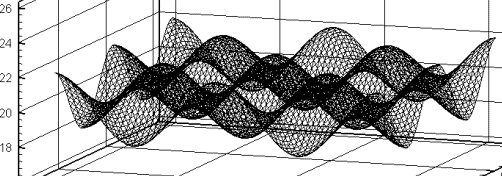
Рис. 2.4.б. ![]() , т.е. граничный случай.
, т.е. граничный случай.
При увеличении z график почти не меняется
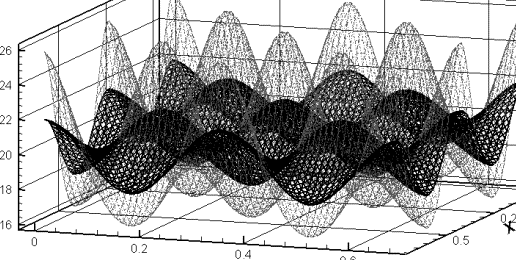
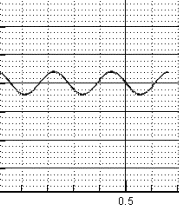
Рис. 2.4.в. ![]() , т.е. неустойчивость.
, т.е. неустойчивость.
z=0 – черный, z=0.01 – серый.
Далее по z нарастание
неустойчивости продолжается
Из приведенных
результатов видно, что неустойчивыми, а значит изменяющими сигнал, являются
шумы с более низкими частотами. Уменьшить их влияние можно, увеличив их
частоту, например, задавая на входе в нелинейную среду сигнал и регулярный
высокочастотный шум.
Картина становиться
более ясной, если полученные на каждом шаге по z значения Ψ изображать на комплексной плоскости (ReΨ, ImΨ). Тогда значения
рассматриваемого квадрата на плоскости (x,y) в сечении z=0 перейдет в
горизонтально расположенный отрезок на плоскости (ReΨ, ImΨ), длина которого равна ![]() . Далее на рисунках 2.5.а-в приведены графики,
соответствующие предыдущим результатам 2.4.а-в.
. Далее на рисунках 2.5.а-в приведены графики,
соответствующие предыдущим результатам 2.4.а-в.
|
|
|
|
Рис. 2.5.а. т.е. устойчивость |
Рис. 2.5.б. т.е. граница устойчивости |
В случае устойчивости ![]() (рис. 2.5.а) этот отрезок при
увеличении z, сохраняя свою длину, будет
вращаться против часовой стрелки вокруг (0,0), одновременно с этим вращаясь
вокруг собственного центра против часовой стрелки.
(рис. 2.5.а) этот отрезок при
увеличении z, сохраняя свою длину, будет
вращаться против часовой стрелки вокруг (0,0), одновременно с этим вращаясь
вокруг собственного центра против часовой стрелки.
·
Повороту вокруг собственного центра на угол 2π соответствует один период колебаний величины ![]() в плоскости (x,y). Частота
колебаний определяется величиной
в плоскости (x,y). Частота
колебаний определяется величиной 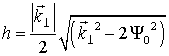 .
.![]() При
При ![]() и z=0.004 значение
угла равно
и z=0.004 значение
угла равно 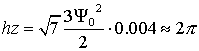 .
.
·
Поворот вокруг (0,0) против часовой стрелки соответствует
сделанному предположению ![]() , т.е. угол
, т.е. угол ![]() . Величина
. Величина ![]() при z=0.004 принимает значение
при z=0.004 принимает значение ![]() , что соответствует периоду колебаний на рис. 2.5.а. При
, что соответствует периоду колебаний на рис. 2.5.а. При ![]() (рис.3.б) поворот
вокруг собственной оси отсутствует, h=0.
(рис.3.б) поворот
вокруг собственной оси отсутствует, h=0.
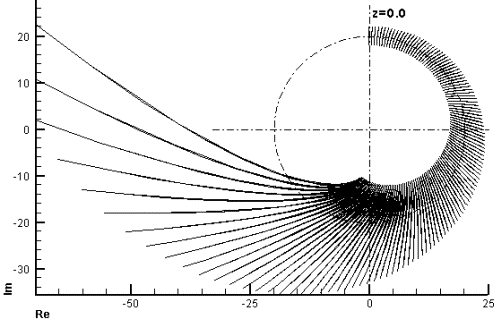
Рис. 2.5.в. Чисто мнимые
начальные условия.
![]() , т.е. неустойчивость
, т.е. неустойчивость
В области неустойчивости
сохраняется поворот вокруг (0,0), но при этом изменяется длина, а потом и
кривизна «отрезка». Если задать чисто мнимые начальные условия, то картина на
комплексной плоскости (ReΨ, ImΨ) будет отличаться
только поворотом на угол ![]() вокруг центра
(0,0) от картины, получаемой при чисто вещественных начальных условиях (рис.
2.5.в). При этом
вокруг центра
(0,0) от картины, получаемой при чисто вещественных начальных условиях (рис.
2.5.в). При этом ![]() .
.
Таким образом, в
устойчивом режиме при сохранении характера решения (гармонические колебания)
сдвиг по фазе между действительной и мнимой частью функции Y(x,y,z) меняется от 0 до 2p в течение одного
периода колебаний по z. Колебания в
плоскости (x,y) становятся ангармоническими, понятие сдвига по
фазе между ReΨ и ImΨ теряет смысл, т.к. эта
величина различна в разных точках плоскости (x,y).
2.2.
Описание
численных методов. Сравнение результатов
Были рассмотрены
различные модели исследуемого процесса и методы их решения.
1. Квазиодномерная задача (цилиндрически
симметричный случай) решалась в эйлеровых и лагранжевых координатах. При
введении лагранжевых координат использовалась гидродинамическая аналогия,
предложенная в [6]. Далее приведен вывод соответствующих уравнений и ход
решения задачи.
Комплекснозначная функция Ψ представляется в виде ![]() . Далее, переписав исходное уравнение, выделим мнимую и
действительную части и в этих двух уравнениях перейдем к переменным t=z, v=
. Далее, переписав исходное уравнение, выделим мнимую и
действительную части и в этих двух уравнениях перейдем к переменным t=z, v=![]() (для этого от одного из уравнений необходимо взять
частную производную
(для этого от одного из уравнений необходимо взять
частную производную ![]() ). Получим уравнения гидродинамики с дифференциальной
связью давления p с плотностью ρ:
). Получим уравнения гидродинамики с дифференциальной
связью давления p с плотностью ρ:
![]() ;
;
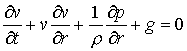 ;
;
где
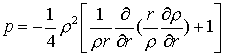 ;
; 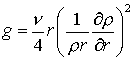 .
.
Введем энергетическую координату 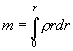 , тогда уравнения перепишутся в виде:
, тогда уравнения перепишутся в виде:
![]() ;
; 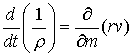 ;
; ![]() ;
;
где
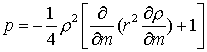 ;
; 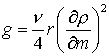 .
.
Краевые условия для исходного уравнения переходят в
v (0,t)=0,
v(I1,t)=0;
![]() при
при ![]() ,
, ![]() ,
,
а начальные данные – в
v(m,0)=v0(m), ![]() ,
,
где 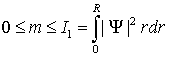 .
.
Аппроксимировав систему
полученных дифференциальных уравнений, исключим из разностной задачи значение ![]() на верхнем слое
(для этого выразим значение
на верхнем слое
(для этого выразим значение ![]() из разностного
уравнения движения и результат подставим уравнение неразрывности). Получим
из разностного
уравнения движения и результат подставим уравнение неразрывности). Получим
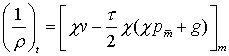 ;
; 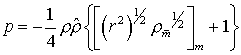 .
.
На основе этих уравнений
построим итерационный процесс, где ![]() и
и ![]() . В результате получим систему трехточечных уравнений для
поправок, которая реазрешается методом матричной прогонки.
. В результате получим систему трехточечных уравнений для
поправок, которая реазрешается методом матричной прогонки.
Лагранжев формализм
применительно к данной нелинейной задаче позволяет довольно близко подойти к
фокусу, сохраняя при этом интеграл мощности (здесь он соответствует полной
массе, а его сохранение изначально заложено в формализм).
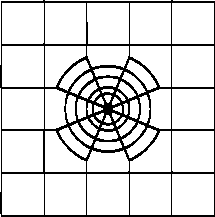
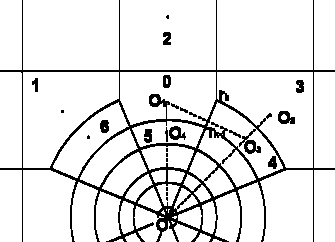
 2. Двумерная
задача решалась на прямоугольной и полярной сетках, а также на нерегулярной
сетке, совмещающей в себе оба вида сеток (рис. 2.6), о которой см. ниже. В
качестве численного метода брался метод Ньютона, шаг по z выбирался
таким, чтобы схемная вязкость была маленькой, а именно изменение интеграла
мощности I1 не превосходило бы 0.1%. Граничные условия в
центре возмущения – равенство нулю потока; на границе области – равенство нулю
самой функции Ψ или потока
через границу.
2. Двумерная
задача решалась на прямоугольной и полярной сетках, а также на нерегулярной
сетке, совмещающей в себе оба вида сеток (рис. 2.6), о которой см. ниже. В
качестве численного метода брался метод Ньютона, шаг по z выбирался
таким, чтобы схемная вязкость была маленькой, а именно изменение интеграла
мощности I1 не превосходило бы 0.1%. Граничные условия в
центре возмущения – равенство нулю потока; на границе области – равенство нулю
самой функции Ψ или потока
через границу.
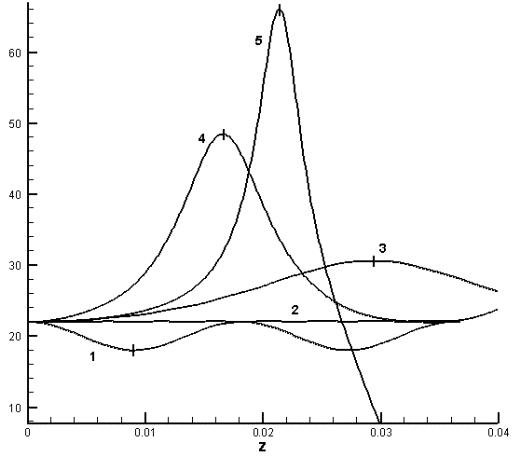
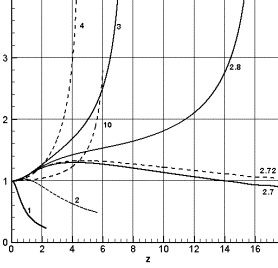
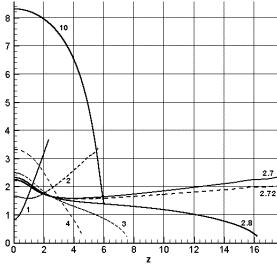
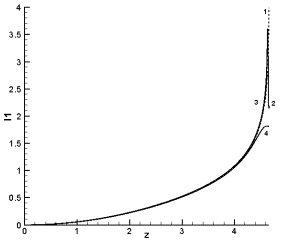
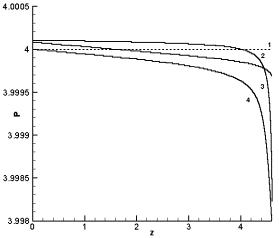
В качестве сравнения численных результатов на
различных сетках приведем зависимости величины интеграла I1(z) и инкремента ![]() на оси возмущения
с параметрами A=1, b=4 (рис. 2.7.а-б). Цифрами на графике изображены
следующие численные решения:
на оси возмущения
с параметрами A=1, b=4 (рис. 2.7.а-б). Цифрами на графике изображены
следующие численные решения:
1. Квазиодномерная
задача (цилиндрический случай). Использовался лагранжев формализм. Отрезок
[0,4] изменения массовой координаты равномерно разбивался на 100 ячеек. Шаг по
времени уменьшался обратно пропорционально возрастанию модуля интенсивности на
оси луча.
2. Квазиодномерная
задача (цилиндрический случай). Решение в эйлеровых координатах. При решении
этой и последующих описанных задач ширина области бралась в ![]() раза больше
характерного размера изменения амплитуды входного луча. Отрезок [0,18]
изменения координаты r равномерно разбивался на 400 ячеек. Шаг по
времени уменьшался обратно пропорционально квадрату модуля интенсивности на оси
луча.
раза больше
характерного размера изменения амплитуды входного луча. Отрезок [0,18]
изменения координаты r равномерно разбивался на 400 ячеек. Шаг по
времени уменьшался обратно пропорционально квадрату модуля интенсивности на оси
луча.
3. Двумерная
задача. Сетка полярных координат (r,φ) разбивалась на 16
секторов по φ и на 400
параллелей по r. Шаг по времени уменьшался обратно
пропорционально возрастанию модуля интенсивности на оси луча. В случае, если
шаг по времени будет аналогичен случаю 2, кривые 2 и 3 на рис.2.7.б будут
совпадать.
4. Двумерная
задача. Ортогональная сетка (rx, ry) разбивалась на ![]() квадратов. Шаг по
времени уменьшался обратно пропорционально возрастанию модуля интенсивности на
оси луча.
квадратов. Шаг по
времени уменьшался обратно пропорционально возрастанию модуля интенсивности на
оси луча.
|
Рис. 2.7.а. Сравнение
инкремента |
Рис. 2.7.б. Сравнение
мощности |
Особое внимание при
исследовании НУШ уделяется описанию поведения решения в окрестности коллапса.
Поэтому необходимо разработать метод, эффективный на нелинейной стадии развития
неустойчивости. Выбор ортогональной сетки с описанными включениями нерегулярной
сетки при решении задачи продиктован целью расчета развития возмущения при
задании начального шума. Каждое «шумовое» возмущение будет задаваться отдельно.
В последующем исследование эволюции случайных возмущений будет осуществляться с
помощью параллельных алгоритмов, основанных на использовании нерегулярной
сетке. Необходимость решения такой численной задачи указана в [5]: «При
постановке численных расчетов возникает следующая трудность. Поперечные размеры
пучка значительно превышают размеры возникающих в сечении пучка
неоднородностей. Трехмерная задача распространения света с учетом дифракции,
нелинейных эффектов и нестационарности усиления является весьма громоздкой».
При использовании нерегулярной сетки были использованы алгоритмы метода конечных объемов, основанные на вычислении операторов
![]() ,
, ![]() ,
,
с применением интегрального тождества
![]() .
.
Тогда для произвольной ячейки (обозначим ее
индексом 0, как центральную среди рассматриваемых соседних ячеек, обозначаемых k(0)):
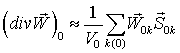 ,
,
 где
где 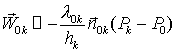 – поток из
рассматриваемой центральной ячейки в соседнюю k-ую ячейку,
– поток из
рассматриваемой центральной ячейки в соседнюю k-ую ячейку, ![]() – среднее
значение
– среднее
значение ![]() на границе 0k,
на границе 0k, ![]() – вектор нормали
к этой границе,
– вектор нормали
к этой границе, ![]() – вектор,
направленный по нормали к границе рассматриваемых ячеек и по величине равный
длине этой границы.
– вектор,
направленный по нормали к границе рассматриваемых ячеек и по величине равный
длине этой границы.
![]() Рассмотрим в
качестве примера верхнюю шестиугольную ячейку рассматриваемого разбиения на
нерегулярной сетке. Для нее из вышеприведенных формул следует:
Рассмотрим в
качестве примера верхнюю шестиугольную ячейку рассматриваемого разбиения на
нерегулярной сетке. Для нее из вышеприведенных формул следует:
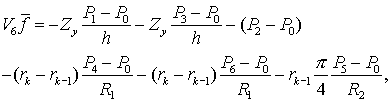
где
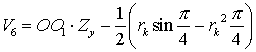 – объем ячейки,
– объем ячейки,
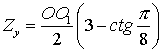 ,
, ![]() ,
, ![]() ,
, ![]() .
.
2.3.
Применение анализа неустойчивости
Беспалова–Таланова к одиночному возмущению
Помимо гармонического возмущения была также
рассмотрена эволюция одиночного возмущения. Возмущение было представлено
гауссовским пучком, т.е. начальное условие в задаче имело следующий вид:
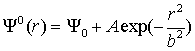 .
.
В результате
численно подтвердился тот факт, что при возрастании начальной ширины возмущения
до определенного момента инкремент неустойчивости растет. При этом решение до
определенного момента времени (t=z) представляет собой уединенный максимум: процессы
последующего распада максимума не рассматриваются. Первоначальная полуширина
пучка есть b. Если b
мало, то это означает, что пучок обладает широким спектром и если доля
низкочастотных составляющих (которые, согласно теории Беспалова–Таланова,
экспоненциально возрастают), мала, то такой пучок на линейной стадии неустойчивости
не будет возрастать. Для таких начальных условий сначала произойдет уширение
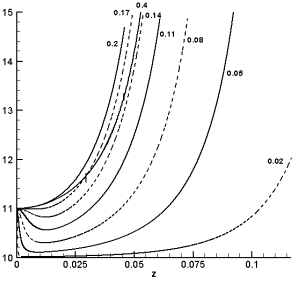
пучка, сопровождающееся падением амплитуды. Действительно (рис. 2.9.б),
полуширина пучков с b=0.05, 0.08, 0.11
первоначально растет. Одновременно для тех же b падает амплитуда поля (рис. 2.9.а).
|
|
|
|
Рис. 2.9.а. Изменение
по z амплитуды
поля |
Рис. 2.9.б. Изменение
по z полуширины
пучка l(z)
А=1 и различных
значениях b |
Для исследования
уединенного максимума напишем преобразование Фурье для функции ![]() :
:
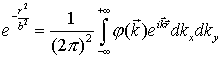 , где
, где 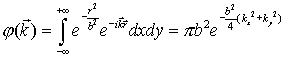 .
.
Т.е.
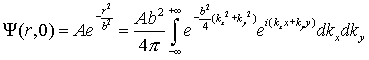
есть разложение первоначального
возмущения в суперпозицию рассмотренных волн. Чем меньше значение b, тем шире спектр
сигнала и тем меньшая доля его приходится на область малых k (здесь ![]() ), т.е. для малых b сигнал будет расти медленнее, чем для больших. Но в целом
такое начальное возмущение неустойчиво, т.к. всегда существуют k, удовлетворяющие условию Беспалова–Таланова.
), т.е. для малых b сигнал будет расти медленнее, чем для больших. Но в целом
такое начальное возмущение неустойчиво, т.к. всегда существуют k, удовлетворяющие условию Беспалова–Таланова.
Если начальная
ширина пучка достаточно велика, то в силу того, что доля низкочастотных
растущих компонент велика, амплитуда такого пучка возрастает, а его полуширина
падает. Для гауссовых пучков спектральное распределение также гауссово, при
этом большая часть спектра сосредоточена в области ![]() . Для того, чтобы эта часть
спектра удовлетворяла условиям Беспалова–Таланова, требуется
. Для того, чтобы эта часть
спектра удовлетворяла условиям Беспалова–Таланова, требуется ![]() , т.е.
, т.е. 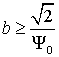 . В данном случае b>0.14, т.к.
. В данном случае b>0.14, т.к. ![]() . Расчеты показывают, что вплоть до
. Расчеты показывают, что вплоть до ![]() амплитуда сначала падает.
Одновременно с падением амплитуды растет полуширина пучка. В дальнейшем на
нелинейной стадии такие пучки будут себя вести так же, как более широкие, но с
большим запозданием по z.
амплитуда сначала падает.
Одновременно с падением амплитуды растет полуширина пучка. В дальнейшем на
нелинейной стадии такие пучки будут себя вести так же, как более широкие, но с
большим запозданием по z.
По мере развития
неустойчивости подавляются те части спектра, где ![]() и происходит уширение пучка, т.е. сужение спектра к малым k (рис. 2.9.а-б для
и происходит уширение пучка, т.е. сужение спектра к малым k (рис. 2.9.а-б для ![]() ). Т.е. высокочастотные
составляющие при уширении пучка, удовлетворяющие условию устойчивости,
затухают, тем самым увеличивая преобладание низкочастотных (неустойчивых)
составляющих (это происходит из-за сохранения первого интеграла – суммарной
мощности пучка).
). Т.е. высокочастотные
составляющие при уширении пучка, удовлетворяющие условию устойчивости,
затухают, тем самым увеличивая преобладание низкочастотных (неустойчивых)
составляющих (это происходит из-за сохранения первого интеграла – суммарной
мощности пучка).
Однако значение
имеет соотношение спектра не только с границей неустойчивости, но и с областью
максимального инкремента. При дальнейшем увеличении b спектр продолжит сужаться, тем самым все большая часть k будет меньше ![]() , что соответствует более
медленному развитию неустойчивости (рис. 2.9.а-б для b=0.2 и b=0.4). В этом случае
устойчивые составляющие отсутствуют, вследствие чего уширения пучка не
происходит. Данный анализ справедлив лишь на начальной, «линейной» стадии
развития неустойчивости.
, что соответствует более
медленному развитию неустойчивости (рис. 2.9.а-б для b=0.2 и b=0.4). В этом случае
устойчивые составляющие отсутствуют, вследствие чего уширения пучка не
происходит. Данный анализ справедлив лишь на начальной, «линейной» стадии
развития неустойчивости.
Аналогичным образом
можно описать эволюцию пучка при отсутствии фона. При этом аналогом
собственного фона для гауссовского возмущения будет являться величина
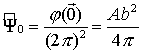 .
.
Исходя из этого, можно применить рассмотренную
теорию к возмущению без общего фона. Для неустойчивости возмущения необходимо
выполнение неравенства 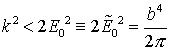 для большинства
составляющих. Если спектр первоначального возмущения есть гауссовское
распределение, т.е.
для большинства
составляющих. Если спектр первоначального возмущения есть гауссовское
распределение, т.е. ![]() , то это соответствует тому, что неустойчивыми являются
большая часть гармоник. В результате имеем пару неравенств, которые заведомо
выполнены если
, то это соответствует тому, что неустойчивыми являются
большая часть гармоник. В результате имеем пару неравенств, которые заведомо
выполнены если 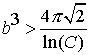 , т.е.
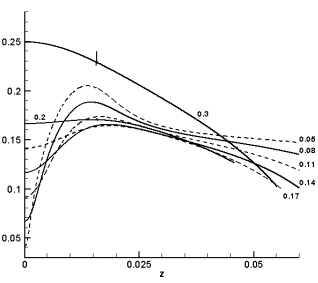
, т.е. ![]() , что и представлено результатами вычислений (рис. 2.10.a-б).
, что и представлено результатами вычислений (рис. 2.10.a-б).
|
|
|
|
Рис. 2.10.а. Изменение амплитуды на оси ограниченного
пучка (t=z)
при А=1 и различных значениях b. |
Рис. 2.10.б. Изменение полуширины l(t) (t=z) пучка при А=1 и различных значениях b. |
Полученный результат
согласуется также с общей теорией, развитой Таунсом [1], где утверждается, что
необходимым условием для неустойчивости возмущения является превышение
мощностью пучка определенного значения, так называемой критической мощности
самофокусировки ![]() , которая достигается в рассмотренном примере при b=2.72.
, которая достигается в рассмотренном примере при b=2.72.
3. Два возмущения. Сближение и взаимное влияние.
Вышесказанное
относится к начальной стадии развития процесса филаментации. Известно [9], что
в дальнейшем возможен распад филамент, но это происходит в областях большой
длины активного элемента. При этом предполагается, что один из возможных
механизмов распада – это развитие новых филамент из кольцевых структур,
окружающих первоначальный максимум. Промоделируем процесс эволюции филамент,
рассмотрев взаимодействие двух максимумов друг с другом.
Рассмотрим два
возмущения на ненулевом фоне Y0=10. L – расстояние
между центрами возмущений (L=1, L=0.6).
Случай 1 –
разные амплитуды (А1=1, А2=1.3.) при одинаковой
ширине (b=0.3). Рассматриваются значения z=0 и z=0.57.
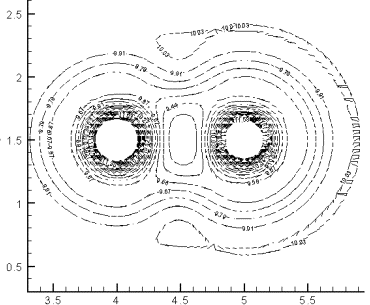
1.1. L=1 (рис.3.1-б)
Взаимное влияние почти
не наблюдается. При рассмотрении уединенного максимума установлено наличие
кольцевых структур (рис. 3.2), которые представляют собой волны на фоне,
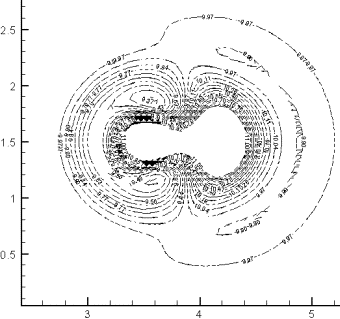
затухающие по мере удаления от возмущения. На представленном рисунке уровень
фона равен 10. Кольцевая структура здесь представлена углублением (т.е. фон
развития возмущения понижен) и небольшим возвышением над уровнем 10 примерно на
0.03. Для двух максимумов также наблюдаются подобные структуры (рис. 3.3). В
рассмотренном случае заметно отличие только в области, расположенной ниже
уровня Ψ0=10, углубление
заметно больше в области между возмущениями, чем на соответствующем одном
возмущении с параметрами A=1, b=0.3 (рис. 3.1-а) или A=1.3, b=0.3 (рис.
3.1-г).
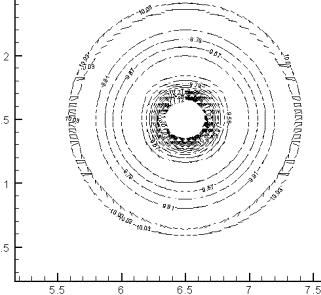
1.2. L=0.6 (рис. 3.1-в)
Взаимное влияние
существенно. Амплитуды обоих возмущений существенно уменьшились по сравнению с
амплитудой таких же возмущений на том же срезе, рассмотренных независимо (рис.
3.1-а,г). По сравнению с предыдущим (L=1) случаем углубление кольцевой структуры несколько изменилось. Теперь
вместо одного минимума, как в предыдущем случае, их стало два, они существенно
глубже (рис. 3.4), но между самими возмущениями величина Y не упала.
Именно это явилось причиной более медленного развития амплитуд обоих
взаимодействующих возмущений.
а
|
б
|
в |
г
Рис. 3.1. Взаимное
влияние двух возмущений
с одинаковой шириной b=0.3 друг на
друга.
а – одно возмущение A=1;
б – два возмущения A=1 и A=1.3 на
расстоянии L=1;
в – два возмущения A=1 и A=1.3 на
расстоянии L=0.6;
г – одно возмущение A=1.3
|
|
Рис. 3.2. Вид сверху.
Возмущение A=1, b=0.3. Соответствует рис. 3.1-а |
|
|
Рис. 3.3. Вид сверху. Два возмущения A=1, b=0.3 и A=1.3, b=0.3 на расстоянии L=1.
Соответствует рис. 3.1-б |
|
|
Рис. 3.4. Вид сверху. Два возмущения A=1, b=0.3 и A=1.3, b=0.3 на расстоянии L=1. Соответствует рис. 3.1-в |
Случай 2 –
разные ширины (b1=0.3, b2=0.5) при
одинаковой амплитуде (A=1). Рассматриваются значения z=0 и z=0.54.
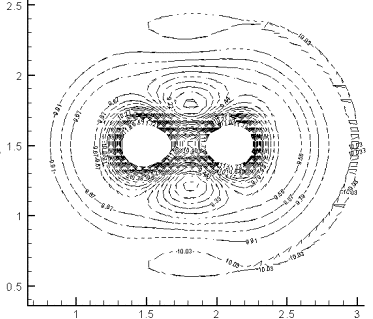
2.1. L=1 (рис. 3.5-б)
Взаимное влияние почти
не наблюдается. Заметно отличие только в углублении кольцевой структуры в
области между возмущениями - она немного глубже, чем на соответствующем одном
возмущении с параметрами A=1, b=0.3 (рис. 3.5-а, 3.6). Приводится данное
сравнение, т.к. у одного возмущения с параметрами A=1, b=0.5 (рис. 3.5-г) кольцевая структура на данном срезе z ещё незаметна.
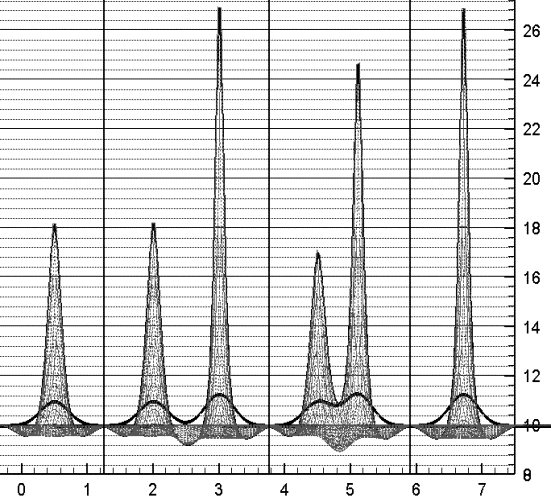
а
|
б
|
в |
г
Рис. 3.5. Взаимное
влияние двух возмущений
с одинаковой амплитудой A=1 друг на
друга.
а – одно возмущение b=0.3;
б – два возмущения b=0.3 и b=0.5 на
расстоянии L=1;
в – два возмущения b=0.3 и b=0.5 на расстоянии L=0.6;
г – одно
возмущение b=0.5.
2.2. L=0.6 (рис. 3.5-в)
Взаимное влияние
существенно. Амплитуда более тонкого (b=0.3) возмущения
существенно увеличилась по сравнению с амплитудой одного такого возмущения на
том же срезе. Этот факт можно объяснить тем, что при таком сближении возмущений
поднимается «фон» для более тонкого (b=0.3) за счет возмущения с большей шириной – это
можно увидеть при сравнении начальных условий для обоих рассмотренных случаев
на рис. 3.5-б,в. Опять, при сближении углубление кольцевой структуры между
возмущениями стало ещё более существенным по сравнению с предыдущим (L=1) случаем
(рис. 3.5-в, 3.7).
|
|
Рис. 3.6. Вид сверху. Два возмущения A=1, b=0.3 и A=1, b=0.5 на расстоянии L=1. Соответствует рис.
3.5-б |
|
|
Рис. 3.7. Вид сверху. Два возмущения A=1, b=0.3 и A=1, b=0.5 на расстоянии L=0.6. Соответствует рис.
3.5-в |
Ни в одном из описанных
случаев не было выявлено существенных изменений в смещении центров возмущений.
В поисках возможных изменений центров возмущений и интуитивно понятных
взаимопоглощений было также рассмотрено влияние возмущений друг на друга без
наличия фона.
Случай 3 – аналогично рассмотренному выше случаю, возьмем сначала возмущения с
одинаковой шириной (b=1) и разными амплитудами (A1=3, A2=4).
3.1. L=1 (рис. 3.8-б)
Взаимное влияние почти
не наблюдается.
3.1. L=0.6 (рис.
3.8-в)
Взаимное влияние
существенно. Амплитуды обоих возмущений существенно увеличились по сравнению с амплитудой
таких же возмущений на том же срезе, рассмотренных отдельно. Ввиду взаимного
увеличения фона при наложении возмущений друг на друга наблюдается более
быстрый рост Ψ.
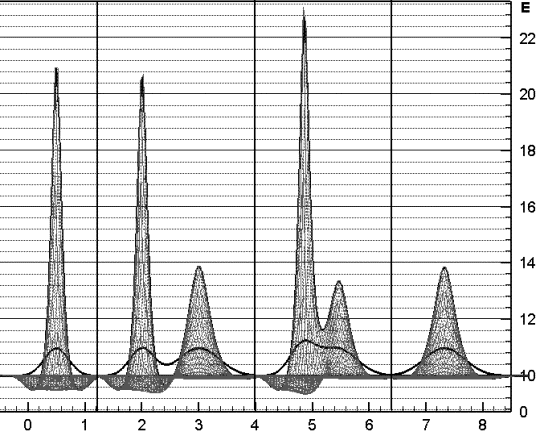
а
|
б
|
в |
г
Рис. 3.8. Взаимное
влияние двух возмущений
с одинаковой шириной b=1 друг на
друга.
а – одно возмущение A=3;
б – два возмущения A=3 и A=4 на расстоянии
L=2;
в – два возмущения A=3 и A=4 на расстоянии
L=1.7;
г – одно возмущение A=4
Случай 4 – при рассмотрении
возмущений с одинаковой амплитудой (A=3) и разными ширинами (b=1, b=0.8) имеет
место значительное сближение центров и поглощение более широким возмущением (b=1) более узкого
(b=0.8). Равномерные срезы по z центрального
профиля таких возмущений представлены на рис. 3.9. При отсутствии фона не
наблюдается образование кольцевых структур.
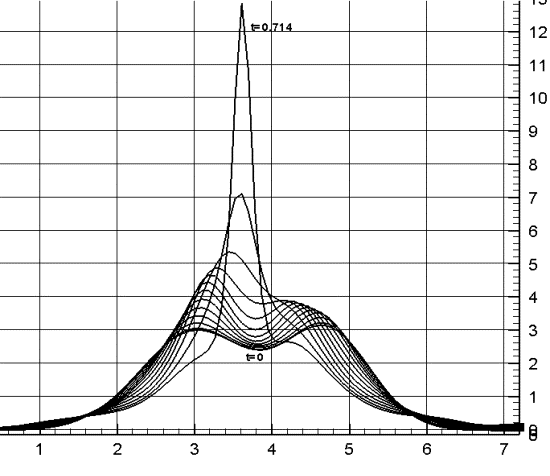
Рис. 3.9.
Развитие двух возмущений
с параметрами A=3 b=1 и A=3 b=0.8.
Графики представляют собой границу
продольного сечения в
разные моменты времени,
распределенные равномерно
Заключение
Целью настоящей работы
была разработка эффективных алгоритмов для расчета явлений филаментации,
способных позволить в будущем произвести математическое моделирование процесса
филаментации в активных элементах реальных лазерных систем. Основные требования
к алгоритму – это правильная передача инкремента и обеспечение
консервативности, т.е. сохранение энергии. Конструирование алгоритма с такими
свойствами для процессов, в которых наблюдается неустойчивость, является одной
из самых сложных задач вычислительного анализа. При использовании
гидродинамической аналогии неявная консервативная схема на достаточно подробной
сетке в лагранжевых переменных обеспечивает строгое сохранение энергии. При
использовании эйлеровых координат в одномерных моделях, а также в том случае,
если при расчете используются комбинированные сетки, необходимо использовать
схемы с весами. В результате точность сохранения полной энергии составляет доли
процента. При использовании на прямоугольной сетке консервативных схем с весами
закон сохранения полной энергии соблюдается также с высокой точностью. Однако
оценка величины инкремента (рис. 2.7.a) показывает, что для схемы на прямоугольной сетке эта величина несколько
меньше, чем для других методов расчета. Поэтому в тех случаях, когда необходимо
исследование развитой стадии неустойчивости в двумерных задачах целесообразно
использовать разностные схемы на комбинированных сетках.
Результаты моделирования
различных режимов филаментации показали, что начальная стадия неустойчивости с
большой степенью точности описывается моделью Беспалова–Таланова. Что касается
развитой стадии, то получены режимы с образованием колец (рис. 3.2).
Рассмотрены также процессы взаимодействия филамент, описывающие нелинейную
стадию процессов неустойчивости. Показано, что сближение филамент на фоне
плоской волны может по-разному влиять на развитие каждой из них в зависимости
от их параметров. Например, филаменты с разными амплитудами при одинаковой
ширине будут расти медленнее при сближении. В то же время сближение пучков на
нулевом фоне способствует их более быстрому росту, что может быть объяснено
теорией Беспалова–Таланова, если рассматривать взаимодействующие пучки, как
новое начальное состояние.
Литература
[1]. R.Y.Chiao, E.Garmire, С.H.Townes «Self-trapping of optical
beams» Phys. Rev. Lett., V.13, №15, p.479, 1964
[2].
В.И.Беспалов, В.И.Таланов «О нитевидной структуре пучков света в нелинейных
жидкостях» Письма в ЖЭТФ. Т.3, с.471-476, 1966
[3]. Н.Б.Баранова,
Н.Е.Быковский, Б.Я.Зельдович, Ю.В.Сенатский «Дифракция и самофокусировка
излучения в усилителе мощных световых импульсах» Квантовая электроника, Т.1,
№11, с.2435-2449, 1974
[4].
Л.М.Дегтярев, В.В.Крылов «Метод численного решения задач динамики волновых
полей с особенностями» Журнал вычислительной математики и математической
физики, Т.17, ноябрь-декабрь 1977
[5]. Л.А.Большев,
Л.М.Дегтярев, А.М.Дыхне и др. «Численное исследование мелкомасштабной
самофокусировки импульсов света в усилителях на неодимовом стекле» Препринт ИПМ
РАН им. М.В.Келдыша №109, 1979
[6].
Л.М.Дегтярев, В.В.Крылов «Гидродинамическое описание самофокусировки пучков
света в кубической среде» Сборник научных трудов под редакцией А.А.Самарского
«Изучение гидродинамической неустойчивости численными методами», Москва, 1980
[7]. А.Н.Тихонов, В.Я.Арсенин, В.И.Павлов, А.Х.Пергамент «Исследование
расходимости излучения в мощных лазерных усилителях на активных элементах
прямоугольно сечения» Препринт ИПМ РАН им. М.В.Келдыша №41, Москва, 1981
[8]. С.Н.Власов, В.И.Таланов «Самофокусировка волн» ИПФ
РАН, Нижний Новгород, 1997
[9]. G.Fibich,
B.Ilan «Vectorial and
random effects in self-focusing and in multiple filamentation» Phisica D, V.157, p.113-147, 2001