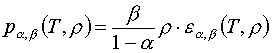Содержание

                                                                                                                стр.

Введение …………………………………………………………..        3

§ 1. Постановка задачи и билинейная интерполяция……………       4

§ 2. Выбор аппроксимирующих функций……………………….        7

§ 3. Вычисление коэффициентов аппроксимации

       для «квадратичного» базиса…………………………………        11

§ 4. Вычисление коэффициентов аппроксимации

       для  «логарифмического» базиса……………………………..      14

§ 5. Применение полученных формул для уравнений

       состояния в газодинамических расчетах……………………        17

§ 6. Об энтропии настоящей и не существующей………………        24

Заключение …………………………………………………………       27

Литература …………………………………………………………       28

Введение

     Знакомясь с монографией [1], в которой рассмотрены различные математические вопросы, возникающие при численном решении гиперболических систем уравнений в частных производных, в частности, применительно к задачам газовой динамики, автор на стр.180 обнаружил краткое изложение содержания части статьи [2]. В ней построен алгоритм решения задачи о распаде разрыва с произвольным уравнением состояния, заданным в виде двумерных таблиц, с билинейной интерполяцией внутри табличной ячейки. Табличные данные задаются в виде двумерных массивов значений давления p и внутренней энергии e как функций температуры Т и плотности r. Однако, как известно, в этом случае второе начало термодинамики накладывает на функции ,  определенное ограничение (см., напр., [3], стр.139).

          Легко проверить, что построенная билинейная аппроксимация этому условию не удовлетворяет. На первый взгляд, казалось бы, что в  таком случае предлагаемый автором [2] достаточно эффективный алгоритм следует рассматривать как приближенное решение задачи о распаде разрыва (в специфической ситуации – табличных уравнений состояния) и только (а на большее автор и не может претендовать, поскольку  уравнение состояния передается приближенно).

          Однако ситуация не столь проста. Невыполнение упомянутого выше условия означает, что, исходя из второго начала термодинамики, для билинейных уравнений состояния не может быть определена энтропия и ее использование является неправомерным. Между тем энтропия играет фундаментальную роль в конструируемом алгоритме расчета распада разрыва и вообще при расчете газодинамических задач.

          Это еще усугубляется тем обстоятельством, что, как указано в [2] на стр.783, «такой сравнительно простой вид уравнения состояния внутри табличной ячейки удается использовать для повышения эффективности алгоритма в случае не слишком подробных таблиц».

Поэтому вызывают беспокойство такие формулировки в [2]: «приведены несколько изэнтроп алюминия в плоскости плотность-температура, полученных по табличному уравнению состояния» (стр.783); «завышение энтропии в энтропийном следе вблизи границ раздела сред, где и образуется струя, может привести к ошибочному выводу о наличии в реальной струе кипящей жидкости» (стр.783); «решение существует, если точка не принадлежит области фазового перехода между жидкостью и газом. Поэтому было решено заменить в этой области ударную адиабату изэнтропой» (стр.791).

          А на стр.793 читаем вообще следующее: «Волнообразный характер профиля температуры в центральной части течения объясняется не ошибками численного метода, а использованием табличного уравнения состояния с билинейной интерполяцией, для которого изэнтропы в плоскости термодинамических переменных имеют волнообразный характер».

          В связи с конструированием уравнений состояния для проведения расчетов нестационарных течений теплопроводного газа в трех-температурном приближении автором в работе [4] уже рассматривалась ситуация с обеспечением выполнения термодинамического тождества.

          Необходимость использования табличных уравнений для расчета таких задач является настоятельной необходимостью. Один из возможных путей ее реализации, устраняющей принципиальный (как нам представляется) недостаток [2], состоит в конструировании нужных уравнений состояния на основе частных решений, удовлетворяющих термодинамическому тождеству. Этот путь оказался, к сожалению, громоздким, но вполне реализуемым. Его изложение и составляет содержание настоящей работы.

§ 1. Постановка задачи и билинейная интерполяция.

1.1. Как и в [2], рассмотрим случай, когда уравнение состояния предполагается заданным в виде:

(1.1)                    ,         .

          В [2] на стр.788 оба уравнения предполагаются однозначно разрешимыми относительно Т, а второе – еще и относительно r. При практической реализации алгоритма расчета распада разрыва, который является основным структурным элементом известной схемы С.К.Годунова и описан в [5], с использованием локальной аппроксимации уравнения состояния общего вида с помощью двучленного уравнения состояния необходимо определять температуру Т из уравнения  при заданных r и p или из уравнения  при заданных r и e. Будем иметь это в виду.

          Рассмотрим случай задания (1.1) в табличной форме. Пусть заданы таблицы  и , где i=1,…,i^* ; j=1,…,j^*. Они являются монотонно возрастающими массивами:  , . Таблицы  и  являются двумерными массивами значений давления p и удельной внутренней энергии e. По своему физическому смыслу таблица монотонно возрастает по обоим индексам, т.е. , , а таблица  монотонно возрастает по первому индексу: .

          Область ,  называется табличной ячейкой с индексами i,j.

1.2. В случае билинейной аппроксимации внутри каждой ячейки уравнения (1.1) имеют вид:

(1.2)                 

Обозначения m_k для постоянных коэффициентов в этих формулах и их нумерация (которая может показаться странной) выбраны, исходя из интересов последующего изложения [см. формулы (2.9)]. Ввиду нелинейного характера будущих формул нам пришлось отказаться от сдвига переменных,  упрощавшего расчетные формулы в случае билинейной интерполяции, приведенные в [2].

          Коэффициенты m_k для функции  определяются так:

(1.3)             ,                  

                     ,         

Коэффициенты m₆, m₃, m₇, m₄  для функции p(T,r) определяются аналогичными формулами заменой e на р:

  (1.4)       ,        

                ,         

1.3. Согласно второму началу термодинамики величина

(1.5)                     ,         ,

является полным дифференциалом функции S=S(V,T), называемой энтропией единицы массы газа. Отсюда следует, что функции (1.1) не являются независимыми, так как условие интегрируемости налагает на них ограничение:

                                .

В терминах переменной r вместо V оно преобразуется к виду:

(1.6)                             

Подставляя в это соотношение формулы (1.2) для билинейных функций, получаем:

(1.7)                            

Очевидно, что (1.7) выполнимо только в случае

(1.8)                        m₅= m₆= m₇= m₈=0.

          Поэтому, как уже отмечалось во введении, в случае (1.2) энтропия S не может быть определена формулой (1.5) со всеми вытекающими последствиями (исключение составляет только случай (1.8)).

1.4. Как известно из курса математического анализа (см., напр., [6], стр.440), с помощью интегрирующего множителя  можно получить полный дифференциал:

(1.9)             .

Множитель j должен удовлетворять уравнению:

(1.10)        

          После упрощения (1.10) - уравнение в частных производных первого порядка. Но за ненадобностью не будем на этом останавливаться.

          Тогда de+pdV=0 будет изолинией для потенциала F, т.е. «изо-фи-линией», а не «изэнтропой», которой не существует при использовании уравнений состояния (1.2).

          Можно было бы надеяться, что отличие этой «изо-фи-линии» от изэнтропы, отвечающей «настоящему» табулированному уравнению состояния, невелико в случае использования таблиц с мелким шагом. В такой ситуации «настоящее» уравнение состояния достаточно часто контролирует ситуацию, хотя и не исключена возможность систематического накопления погрешности. А уж в случае «не слишком подробных таблиц» погрешность может оказаться недопустимо большой для описания достаточно тонких физических эффектов. Это обстоятельство и отмечено во введении.

          Позже, в §6, мы вернемся к обсуждению этого вопроса.

§ 2. Выбор аппроксимирующих функций.

2.1. В силу линейности условия (1.5) относительно e и р одним из возможных путей обеспечения его выполнения является конструирование функций ,  как линейных комбинаций частных решений ,  уравнения (1.6). В рассматриваемой ситуации конструируемое решение должно содержать 8 параметров для получения заданных значений двух функций в четырех углах табличной ячейки:

(2.1)      ,      .

Используемые в (2.1) частные решения будем называть базисными. Непосредственной проверкой можно убедиться, что на роль таких решений могут претендовать функции степенного вида:

(2.2)       ,        ,

где  - постоянные параметры (не обязательно целые числа). Естественно, что они удовлетворяют термодинамическому тождеству (1.5). Можно проверить, что энтропия такого решения определяется формулой (с точностью до const):

(2.3)                             .

Она потребуется нам в §6.

          Специальный интерес представляют вырожденные частные случаи b=0 и a=1. Первый (b=0) дает частные решения:

                      ,                ,

где  - произвольная функция Т. Среди них – степенные решения:

(2.4)                ,           .

Второй случай (a=1) дает частные решения:

                       ,               ,

где   - произвольная функция r. Среди них – степенные решения:

(2.5)              ,                 .

2.2. Использование в суммах (2.1) решений (2.4)-(2.5) позволяет уменьшить количество слагаемых в них. Если бы можно было использовать по 4 базисных решения вида (2.4)-(2.5), получилась бы независимая аппроксимация типа (1.2). Однако это принципиально невозможно (напр., функция e оказалась бы зависящей только от Т).

          Если использовать по 3 базисных          решения вида (2.4) и (2.5), то в дополнение к их 6 свободным параметрам пришлось бы  подключить еще 2 независимых частных решения со своими коэффициентами. Как будет видно из дальнейшего изложения, для определения этих двух коэффициентов возникает переопределенная система из 4 линейных уравнений. Поэтому такой вариант отвергается.

          «Сбалансированный» вариант аппроксимации возникает, если в (2.1) используются по 2 базисных решения вида (2.4)-(2.5), располагающие 4 свободными параметрами m_k (k=1,…,4). К ним должны подключаться еще 4 независимых частных решения со своими коэффициентами m_k (k=5,…,8).

          С точки зрения практической реализации, имея в виду необхо-димость вычислять Т при заданных (r,р) или (r,e), в первую очередь интерес представляют решения с целыми степенями Т не выше 2.

          Несколько примеров таких решений представлено в таблице 1. В ее последнем столбце представлена и энтропия.

          Заметим, что из (2.2) следует:

(2.6)                       

Следовательно, формально каждое из частных решений (2.2) можно рассматривать как газ с показателем адиабаты . Поэтому, наряду с a и b, в таблице 1 представлена также величина g-1. Для удобства дальнейших ссылок строки таблицы 1 занумерованы, и этот порядковый номер приведен в первом столбце. Под номерами 1-6 представлены по 3 решения типов (2.4) и (2.5), под номерами 7-12 – по 3 частных решения с a=0 и a=2. Отметим, что в некоторых решениях изменены оба знака по сравнению с (2.2).

2.3. Степенные решения (2.2), конечно же, не исчерпывают множество частных решений уравнения (1.6). Задав произвольно одну из функций  или , можно интегрированием (см., напр., [6], стр.440) получить ее «пару». Ограничимся 4 примерами таких пар, не охватываемых множеством (2.2):

(2.7)       ,                               ,  

              ,                   ,  

Они занесены в таблицу 1 под номерами 13,14,2 и 5 соответственно и помечены значком *.

Два первых из этих решений вместе с номерами 7 и 8 из таблицы 1 вскрывают причину невыполнения условия (1.6) для билинейной аппроксимации. Все они имеют формулу для энтропии, отличную от (2.3). Энтропия  для них определяется так (с точностью до const):

(2.8)                                    

                         .

Таблица 1 простейших частных решений.

2.4. Поставим цель: исправить формулы (1.2) так, чтобы обеспечить выполнение условия (1.6). Тогда придем к следующему результату. Такими являются функции

(2.9)     

             ,

содержащие 8 свободных параметров. Обращаем внимание, что это достигается за счет параметров m_k (k=5,6,7,8), присутствующих в обеих формулах. (Это и стало причиной введения странной нумерации m_k в формулах (1.2) билинейной интерполяции).

          В качестве базисных функции (2.9) используют 4 частных решения типа (2.4)-(2.5):

(2.10)         ,         ,         ,        

                  ,        ,         ,       

и четыре частных решения вида:

(2.11)      ,      ,       ,     

               ,    ,        ,        

Для краткости условимся называть такой вариант аппроксимации «логарифмическим».

          Поскольку окажется, что такой «сбалансированный» вариант порождает невырожденную систему для определения коэффициентов, его можно будет рассматривать как пример аппроксимации (2.1). Позже (в §4) этот вопрос будет исследован.

2.5. Перейдем к рассмотрению других возможных вариантов.

          Целесообразность использования в качестве базисных частных решений (2.10) настолько очевидна, что их участие не вызывает сомнений.

          Привлечем в качестве четырех других базисных функций частные решения (2.2). Наиболее  естественно казалось бы выбрать в таблице 1 номера 8,9,10,11, т.е. функции

(2.12)    ,      ,       ,     

             ,    ,     ,   

Всем им отвечают положительные значения g-1. Требование g>1 является обычным для газовой динамики. Однако имеется еще одно соображение. Уравнение состояния в виде двучлена, которое широко используется в газовой динамике (в частности, при реализации метода С.К.Годунова [5]),

(2.13)                      

содержит константу .  Возможность ее включения имеется: использовать в качестве базисного частное решение под номером 7: , . Отметим и его присутствие в «логарифмическом» базисе (2.11). Какое из частных решений (2.12) им заменить? По этому поводу напомним постановку задачи: таблица {p_ij} монотонно возрастает по обоим индексам, а таблица {e_ij} – по первому индексу. Естественно и для аппроксимации использовать аналогичные функции. Оказывается, что в (2.12) такими (говоря точнее, неубывающими) являются три решения, а e⁽⁶⁾, р⁽⁶⁾ – нет. Его и заменим.

          Таким образом, в качестве базисных функций в интересах решения газодинамических задач выбираем следующие:

(2.14)    ,      ,      ,       

             ,    ,       ,    

Сравнивая такой базис с «логарифмическим» (2.11), обнаруживаем, что у них общие частные решения  и, а также все решения (2.10).

          Для краткости условимся называть такой вариант базиса «квадратичным» (по степени Т). Для наглядности в таблице 1 базисные решения отмечены значками в столбце Б: значок «о» присвоен общим для обоих базисов, «л» – дополнительным решениям «логарифмического» базиса, «к» – дополнительным решениям «квадратичного» базиса.

          Любопытно отметить, что автор начинал эту работу с получения формул (2.9) как способа «улучшить» билинейную аппроксимацию. Они были получены сначала методом подбора по принципу: «Что бы еще приписать такое, чтобы уравнение (1.6) удовлетворялось?» Получены – и «не понравились», прежде всего, из-за присутствия  в формуле для давления р. Причина будет ясна – см. ниже, в §5, формулу (5.9). И только после тщательного отбора «квадратичного» базиса формулы (2.9) и набор функций (2.10)-(2.11) приобрели законный статус «логарифмического» базиса, который, как увидим в §4, не кажется хуже «квадратичного», с точки зрения вычисления коэффициентов .

§ 3. Вычисление коэффициентов аппроксимации

для «квадратичного» базиса.

3.1. Чтобы иметь возможность изменять четверку базисных решений , k=5,6,7,8, временно не будем их конкретизировать. Выбор (2.10) менять не будем. Тогда формулы (2.1) можно записать так:

(3.1)                       ,    

                             .

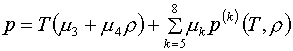Требования, чтобы эти функции в четырех углах табличной ячейки , , ,  принимали заданные значения , , ,  соответственно, записываются в следующем виде: во всех уравнениях слева суммирование по индексу k производится от k=5 до k=8,

                                                    у(1)

                                           у(2)

                                       у(3)

(3.2)                                      у(4)

                                              у(5)

                                     у(6)

                             у(7)

                                     у(8)

Это система 8 линейных уравнений для восьми неизвестных . Целью нашего исследования является не только вопрос о ее однозначной разрешимости, но и получение расчетных формул для решения.

3.2. Прежде всего исключаем из (3.2) неизвестные m₁, m₂ . Для этого из четвертого уравнения вычитаем первое, а из третьего – второе. Получаем два уравнения: слева – суммирование по k от k=5 до k=8,

(3.3)                                                                

                            .

Чуть сложнее исключаются неизвестные m₃ и m₄. Разделим пятое уравнение на T_i, шестое – на T_i+1 и затем возьмем их разность. Аналогично, разделим седьмое уравнение на T_i+1, восьмое – на T_i и возьмем их разность. В результате будут получены еще два уравнения: слева – суммирование по индексу k  от k=5 до k=8,

(3.4)                                                                

Судьбой неизвестных m₁, m₂, m₃, m₄ займемся позже.

Уравнения (3.3) и (3.4) для неизвестных m₅, m₆, m₇, m₈ запишем в виде:

(3.5) 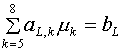                            (L =1,…,4).

Коэффициенты определены формулами (k=5,…,8):

(3.6)       ,                        

              ,                   

              ,         

              ,    

3.3. А вот теперь обратимся к конкретному выбору базисных функций «квадратичного» базиса (2.14).

Введем обозначения

(3.7)                  ,               

Индексы у величин ,  опущены без ущерба для изложения, но это не предполагает постоянства шагов табличной сетки.

 Тогда система (3.5) приобретает такой вид:

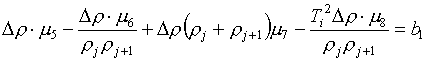
(3.8)                               

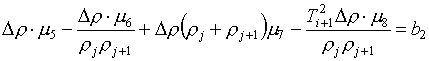
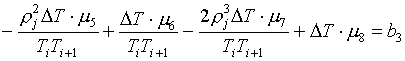
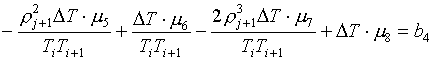
Вычитая из ее первого уравнения второе, получаем:

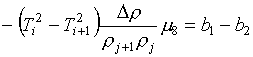
Следовательно, сразу определяется значение m₈ :

(3.9)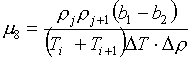                  

Второе, третье и четвертое уравнения (3.8) упростим, разделив соответственно на Dr и дважды на . С учетом уже известного m₈ получим систему уравнений для неизвестных m₅, m₆, m₇:

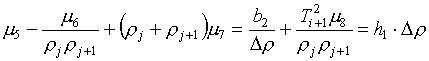
(3.10)         

Здесь введены обозначения h₁×Dr, h₂×Dr, h₃×Dr для  правых частей.

          В качестве следующего шага выразим из второго и третьего уравнений m₅ и m₆ через m₇:

(3.11)     

Подставляя их в первое из уравнений (3.10), получаем уравнение для m₇:

(3.12)  

Из него определяется параметр m₇:

(3.13)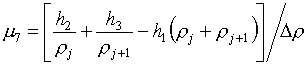            

Далее вычисление m₅ и m₆  производится по формулам (3.11). Работа с системой (3.8) завершена: коэффициенты m_k (k=5,…,8) вычислены.

3.4. А вот теперь обратимся к определению значений m₁, m₂, m₃, m₄. Первые два из уравнений (3.2) после подстановки в них конкретных значений базисных  функций (2.14) могут быть записаны в виде:

(3.14)             

Здесь обозначения ,  введены для уже известных правых частей, а величина а определяется формулой:

(3.15)           .

Решая систему (3.14), получаем:

(3.16)            ,            .

          Для вычисления оставшихся неизвестных m₃ и m₄ воспользуемся, например, пятым и восьмым из уравнений (3.2). После подстановки конкретных значений базисных функций (2.14) они принимают вид:

Отсюда получаем уравнения для m₃ и m₄:

(3.17)           

Обозначения ,  введены для их известных правых частей. Решая систему (3.17), получаем:

(3.18)          ,            .

Отметим, что в соответствии с формулами Крамера (см., напр., [6], стр.149) все m_k  являются линейными комбинациями значений функций в углах табличной ячейки. С вычислительной точки зрения полученные формулы полезно преобразовать, но мы делать это сейчас не будем.

          Таким образом, для «квадратичного» варианта базисных функций (2.10) и (2.14) доказана однозначная разрешимость системы линейных уравнений для коэффициентов m_k, но и получены формулы для них.

§ 4. Вычисление коэффициентов аппроксимации

для «логарифмического» базиса.

4.1. Обратимся теперь к исследованию «логарифмического» варианта выбора базисных функций (2.10) и (2.11). Он отличается от «квадратичного» только функциями  и . Поэтому его исследование может быть проведено по той же схеме, что и описанное для «квадратичного» базиса. В системе (3.8) изменяются коэффициенты при параметрах m₇ и m₈. С учетом (3.7) и того, что

               ,            ,

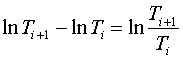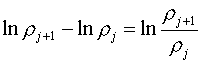она может быть записана в виде:

(4.1)                    

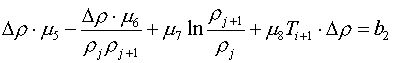
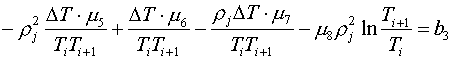
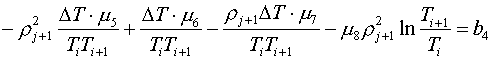
Вычитая из первого уравнения второе, получаем:

Следовательно, вместо (3.9) значение m₈ определяется формулой:

(4.2)                                        .

Далее, система уравнений (3.10) заменяется на следующую:

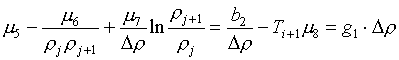
(4.3)      

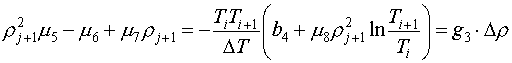
В ней введены обозначения g₁×Dr, g₂×Dr, g₃×Dr для известных правых частей. Как и в §3, выразим из второго и третьего уравнений m₅ и m₆ через m₇:

(4.4)                  

Подставляя их в первое из уравнений (4.3), получаем уравнение для m₇:

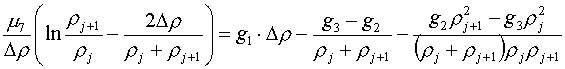
Из него определяется коэффициент m₇:

(4.5)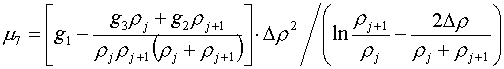        

Далее вычисление m₅ и m₆ производится по формулам (4.4). Работа с системой (4.3) завершена: получены коэффициенты m₅ , m₆ , m₇ , m₈.

          Поскольку базисные функции  для k=1,2,3,4 в случае «логарифмического» базиса те же, что и в случае «квадратичного», вид формул (3.14)-(3.18) для вычисления m₁ , m₂ , m₃ , m₄ остается тем же, но изменяются слагаемые с m₇ и m₈ из-за других базисных функций.

4.2.  Мы молчаливо обошли вопрос о том, не может ли обратиться в нуль знаменатель в формуле (4.5). Обозначив , запишем его в виде:

                         .

Функция j(х) и ее три первых производных таковы:

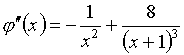
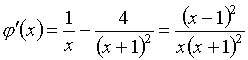
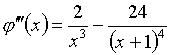
Для х=1 будем иметь j(1)=j¢(1)=j²(1)=0 и только j¢²(1)=0.5. Следовательно, знаменатель в формуле (4.5) является монотонно возрастающей функцией х и в нуль не обращается ни при каких значениях . Присутствие в числителе (4.5) сомножителя  придает формуле (4.5) для параметра m₇ примерно такой же характер, как и (3.13) в случае «квадратичного» базиса.

          Таким образом, для «логарифмического» базиса достигнут такой же результат, как для «квадратичного». Отличия от «квадратичного» варианта состоят в следующем:

     1^о заменена формула (3.9) для m₈ на формулу (4.2);

     2^о формула (3.13) для m₇ заменяется на (4.5);

     3^о при  счете m₅ и m₆ формулы (3.11) с назначением величин h₁, h₂, h₃ согласно формулам (3.10) заменяются на формулы (4.4) с назначением величин g₁, g₂, g₃ согласно формулам (4.3);

     4^о вносятся изменения в слагаемые с m₇ и m₈ в формулах (3.14)-(3.18):

     5^о при расчете функций ,  по формулам (2.1) функции с номерами k=7,8 вместо формул (2.14) используют (2.11).

Заметим, что рассмотренные два примера «логарифмического» и «квадратичного» базиса, конечно, не исчерпывают всех возможностей конструирования аппроксимационных формул (2.1).

§ 5. Применение полученных формул для уравнений состояния

в газодинамических расчетах.

          Кто-то из великих математиков сказал: «Прежде чем решать задачу, подумайте, что вы будете делать с ее результатами». Исходя из этого, обсудим теперь, что нам дают полученные аналитические формулы с точки зрения решения газодинамических задач.

5.1. Пару функций ,  можно считать неявной формой задания функции , посредством которой происходит замыкание системы дифференциальных уравнений газовой динамики.

          Специфика разностной схемы С.К.Годунова для расчета газодинамических задач состоит в том, что уравнение состояния привлекается в такой момент расчета, когда плотность r можно считать известной. Поэтому необходимая для практической реализации алгоритма температура Т должна определяться из уравнений:

(5.1)                      или        ,

где  или  - заданные значения.

          Рассмотрим сначала «квадратичный» вариант базисных функций, определяемых формулами (2.10) и (2.14). Тогда вычисление температуры Т сводится к решению уравнения

(5.2)                

или

(5.3)           .

Вырожденный случай m₈=0 рассмотрим позже. Если m₈¹0, то уравнения – квадратные. Следовательно, расчет Т может быть осуществлен без затруднений, если уравнение будет иметь вещественные корни. Располагая значениями обоих корней, выбор нужного из них можно сделать без труда. Он должен лежать между T_i и T_i+1, так как вне этого отрезка построенное уравнение состояния не имеет силы.

          Очевидно, что вопрос о существовании нужного корня такого уравнения может решаться только непосредственно в момент конкретного расчета. Здравый смысл позволяет лишь надеяться, что разумные принципы, заложенные в идею аппроксимации, приведут к положительному результату. По крайней мере, если исключить ситуации, когда причиной «неприятностей» является несовершенство табличных данных (или их прямые ошибки).

          Что же делать в случае неудачи, т.е. если квадратное уравнение не имеет решения или оба его корня  лежат вне отрезка [T_i,T_i+1]?

5.2. При использовании билинейной аппроксимации (1.2) расчетные формулы были линейными как по Т, так и по r. Обсудим вопрос, не упущена ли нами возможность обойтись линейными функциями по Т.

          Достижение такой цели могло бы быть реализовано посредством замены в (2.14) базисного решения , содержащего Т², частным решением типа (2.2), для которого степень a=1 или a=0. Обратимся к таблице 1 частных решений уравнения (1.6).

          Попробуем заменить  на частное решение с номером 6, т.е. полагаем . Поскольку при этом , система (3.2) для определения коэффициентов m_k может быть переписана в следующем виде.

          Первые четыре уравнения сохраняют прежний вид, но в левой части остается суммирование по k от 5 до 7, поскольку . Следующие четыре уравнения могут быть записаны в виде: слева оставляем суммирование по индексу k от k=5 до  k=7,

(5.4)                 

Проделав описанную ранее в §3 процедуру исключения, получаем 4 уравнения для трех неизвестных m₅ , m₆ , m₇. Очевидно, что такая задача является некорректной.

          Точно также обстоит дело при замене  на любое частное решение с a=0.

Таким образом, вопрос о невозможности корректной аппроксимации, линейной по Т, исчерпан. Если считать в (2.9) сомножитель , как принято говорить, слабой нелинейностью, то «почти линейной» будет аппроксимация с «логарифмическим» базисом.

5.3. Вернемся к поставленному вопросу о ситуации, когда квадратное уравнение (5.2) или (5.3) не дает нужного решения. Альтернативой может служить замена базисных функций ,  на частное решение (2.2), отвечающее a=3, b=-1:

(5.5)             ,        

Нетрудно убедиться, что в таком случае описанная в §3 процедура вычисления коэффициентов аппроксимации полностью сохраняется. Необходимо лишь заменить формулу (3.8) для вычисления m₈ :

(5.6)                                                             

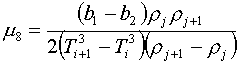
и внести изменения в слагаемые, которые его используют.

Естественно, за этим следует пересчет всех коэффициентов m_k по тем же формулам, но с новыми результатами.

          Вместо квадратного уравнения (5.2) или (5.3) необходимо будет решать кубическое:

(5.7)              

или

(5.8)               .

          Как известно, кубическое уравнение всегда имеет хотя бы один вещественный корень (см., напр., [6], стр.138-139). Вопрос о пригодности такого корня (также как и отбор нужного в случае, если корней три), конечно же, остается.

          По-видимому, целесообразна реализация в качестве альтернативного и такого варианта базисных функций. Назовем его условно «кубическим».

5.4. Еще один альтернативный вариант преодоления возможных трудностей связан с «логарифмическим» базисом, использующим функции (2.10) и (2.11). В нем формула для энергии e является линейной по Т. Формула же для давления такова, что для вычисления температуры Т придется решать трансцендентное уравнение:

(5.9)       

Для уравнения такого вида

(5.10)                       

будем иметь:           ,           

Знакоопределенность второй производной позволяет использовать ньютоновский итерационный процесс. Предварительно можно выяснить, существует ли корень, с помощью «невязок» уравнения на концах отрезка и, возможно, экстремальной точки внутри отрезка. Главный вопрос опять же в том, существует ли приемлемый результат.

          Можно было бы рассуждать о привлечении в качестве альтернативных и других базисов, но мы ограничимся этим.

5.5. Обратимся теперь к рассмотрению «вырожденного» случая m₈=0. Он имеет место, если b₁-b₂=0. Заметим, что так будет для всех описанных базисов – и «квадратичного», и «логарифмического», и «кубического». Поскольку, согласно формулам (3.6),

(5.11)  

требование монотонности таблицы по первому индексу возможности b₁-b₂=0 не исключает. Заметим попутно, что в общем случае коэффициент m₈ может оказаться как положительным, так и отрицательным.

В случае m₈=0 уравнения (5.2)-(5.3), (5.7)-(5.9) вырождаются в линейные, если только одновременно коэффициент  при Т не обращается в нуль. Исследуем такую возможность.

          Для «квадратичного» базиса из формул (3.17) легко получить, что

(5.12)             

          Получить формулу для правой части F_* через табличные данные можно, но очень громоздко. Очевидно, что из системы (3.2), в силу уже упоминавшихся формул Крамера, следует, что F_* представляет линейную комбинацию значений функций в угловых точках табличной ячейки. Может ли оказаться, что F_*=0? Исключить такую возможность без привлечения точных формул для F_* мы не можем. Во всяком случае, следует допустить существование таких «патовых» табличных данных (удовлетворяющих требованиям монотонности таблиц  и ), что для них получится именно такой результат: F_*=0.

Что тогда делать? Замена «квадратичного» базиса «кубическим» или «степенным» ничего не дает. Они различаются только базисными функциями e⁽⁸⁾, р⁽⁸⁾, роль которых сведется к получению m₈=0. После этого остальные m_k останутся без изменения.

          Обратимся к «логарифмическому» базису. Он отличается от «квадратичного» еще и функциями e⁽⁷⁾, р⁽⁷⁾. Поэтому для  возникнет формула, аналогичная (5.12), но совсем с другими коэффициентами. Представляется невероятным, чтобы те же значения правых частей системы (3.2) дали «патовый» результат F_*=0 и для новой линейной комбинации. Так что можно надеяться, что для «логарифмического» базиса окажется . Из соответствующего линейного уравнения получаем искомое значение Т.

          На этом наши заботы не кончаются. Нужно, чтобы этот корень был заключен между T_i и T_i+1. Исследовать и гарантировать такой результат возможным не представляется. Критерием истины станет конкретная практика, как уже было описано выше.

          Очевидно, что ситуация при определении Т по заданным значениям плотности r_* и энергии e_* будет аналогичной.

5.6. В дополнение к описанным возможным затруднениям при определении из уравнений состояния температуры Т  должны быть рассмотрены и другие. В первую очередь они могут возникать в задаче о распаде разрыва, которая является одним из основных элементов расчетной схемы при использовании метода С.К.Годунова. Как уже неоднократно описывалось в литературе (см., напр., [1], стр.177), в случае сложного уравнения состояния для ее решения привлекается локальная аппроксимация двучленным уравнением состояния (2.13). Локальные эффективные параметры  для уравнения состояния в виде  определяются формулами, предложенными А.В.Забродиным:

(5.13)       ,            ,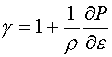        

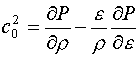Пару функций ,  можно считать неявной формой задания такой функции . Нужные для (5.13) производные могут быть вычислены по формулам (см., напр., [4], стр.51):

(5.14)                    ,        .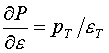

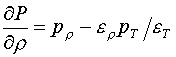Для предложенной конструкции уравнений состояния (2.1) с выбором «квадратичного» базиса (2.10) и (2.14) будем иметь:

(5.15)                  

Для «логарифмического» базиса формулы аналогичны, отличаясь только слагаемыми с m₇ и m₈. Для корректности формул в алгоритмах расчета распада разрыва предполагаются выполненными ограничения на параметры, вычисленные по формулам (5.13)-(5.15):

(5.16)                 ,            ,           .

Если они не выполнены, то возникает тот же вопрос: что делать? Гипотетически предполагается преодолевать трудности с помощью альтернативных вариантов, которые уже обсуждались.

5.7. Кроме того, заслуживает серьезного внимания еще одна возможность. В интерполяционные формулы (2.1) можно включить в качестве дополнительного слагаемого любые заданные функции e⁽⁰⁾, р⁽⁰⁾, удовлетворяющие уравнению (1.6). Для краткости назовем их опорными. Тогда решается задача об аппроксимации не функций , , а их «возмущений»:

(5.17)   ,   .

Такой прием практически не изменяет описанный алгоритм. Нужно лишь вычислить значения опорных функций в 4 углах табличной ячейки и заменить в алгоритме вычисления коэффициентов аппроксимации m_k и в уравнениях для вычисления температуры Т заданные табличные значения на их «возмущения». Это создает новую ситуацию, например, при решении квадратных уравнений. Еще существенней вклад опорных функций в формулы (5.15), дополненные производными опорных функций. А именно р_Т, e_Т, р_r, e_r определяют «судьбу» ограничений (5.16).

Большое преимущество такого приема в том, что он позволяет подключить в качестве опорных любые представляющие интерес функции, не вошедшие в используемый базис. Это можно трактовать как режим альтернативного поиска и пытаться его автоматизировать.

Функции e⁽⁰⁾, р⁽⁰⁾ в определенном смысле могут нести основную физическую нагрузку (являясь, например, асимптотическими режимами для исследуемого газодинамического процесса). В качестве таких функций, например, могут рассматриваться уравнения состояния «газа с учетом излучения»:

(5.18)              ,         

При В=0 реализуется идеальный газ с показателем адиабаты g. При А=0, В=s, где s выражается через скорость света и постоянную Стефана-Больцмана, реализуется «фотонный» (безмассовый) газ с показателем адиабаты g=4/3.

          Более общий пример такого рода, связанный с моделированием неполностью ионизованной среды (плазмы) рассматривался автором в [4] (внешние различия вызваны только обозначениями):

(5.19)                            ,

Это могут быть также заданные комбинации нескольких частных решений степенного типа (2.2). Как уже отмечалось, параметры a,b могут быть произвольными вещественными числами.

          Заметим, что уравнение состояния (5.19) или его частный случай (5.18), реализуемый при a=4, b=-1, можно было бы включить и в описанную выше процедуру аппроксимации. Для этого достаточно назначить в качестве базисных функций вместо прежних

                           ,          

с конкретными значениями a и b. Первое слагаемое в (5.18) и (5.19) уже охвачено базисом (2.10). Возникающий базис условно назовем «степенным». Аналогично описанному ранее для «кубического» базиса, при этом должна быть заменена формула для коэффициента m₈, изменены слагаемые, которые его используют, и пересчитаны по прежним формулам остальные коэффициенты m_k.

Для вычисления температуры Т по заданным  придется решать трансцендентное уравнение вида:

                                   .

Для него      ,          .

Знакоопределенность второй производной позволяет использовать итерационный метод Ньютона. Он рассматривался в [4]. Была обоснована также корректность использования для уравнения состояния (5.19) процедуры локальной аппроксимации двучленным уравнением состояния. Доказано, что значения эффективных параметров, назначенные по формулам (5.13), удовлетворяют ограничениям (5.16).

5.8. Вернемся к вопросу о практической реализации разностных методов с использованием полученных формул для уравнений состояния.      Если трудности, связанные с выполнением (5.16), удалось преодолеть, то задача о распаде разрыва успешно решается с помощью итерационных процессов, описанных в литературе (см., напр., [1]). Обратим также внимание на работу [7], в которой предложен итерационный алгоритм, позволяющий в ходе расчета распада разрыва добиться сколь угодно точного выполнения заданных сложных уравнений состояния. Этот алгоритм основан на введении в аппроксимирующее уравнение состояния двучленного вида специального параметра. За счет его подбора в ходе итерационного процесса и достигается выполнение точного уравнения состояния. В работе [8] автором предложена некоторая модификация способа введения такого параметра и более подробно изложен алгоритм, реализующий итерационный процесс.

§ 6. Об энтропии настоящей и не существующей.

6.1. Как уже отмечалось в §2, частные решения уравнения (1.6), естественно, удовлетворяют термодинамическому тождеству (1.5). Поэтому для них определена энтропия S. Для решений степенного вида (2.2) она определяется формулой (2.3) и представлена в таблице 1. Для решений (2.7), используемых в «логарифмическом» варианте базисных функций, энтропия определена формулами (2.8).

          Аддитивный характер аппроксимационных формул (2.1) для уравнений состояния позволяет определить энтропию и для них:

(6.1)                                   .

Полагаем целесообразным привести соответствующие формулы для  «квадратичного» (S_кв) и «логарифмического» (S_лог) базисов:

(6.2)              

(6.3)                             

Формулы неожиданно оказались достаточно компактными благодаря тому, что базисные функции с номерами 1,5,6,7 имеют энтропию S=0. «Квадратичный» и «логарифмический» базисы имеют шесть общих первых функций. Поэтому формулы (6.2) и (6.3) отличаются только последним слагаемым, отвечающим базисным функциям с коэффициентом m₈.  Наличие формул для энтропии позволяет точно формулировать соотношения, которые должны быть выполнены на изэнтропах. Возможно, при конструировании численных методов для задачи о распаде разрыва целесообразно ставить вопрос об использовании таких соотношений. Впрочем, пока в этом нет острой необходимости в силу упомянутых в конце §5 возможностей рассчитывать (при желании) точные распады разрыва даже в случае сложных уравнений состояния.

6.2. Полученная формула для энтропии (6.3) позволяет более конкретно обсудить затронутый в конце §1 вопрос о том, что для билинейной аппроксимации (1.2) энтропии не существует.

          В самом деле, выпишем для (1.2) формулу:

(6.4)                        

Для «улучшенной» билинейной аппроксимации (2.9), достигающейся с помощью «логарифмического» базиса, аналогичная формула будет иметь вид:

(6.5)      

          Существенное их различие налицо. Кроме того, нужно еще принимать во внимание, что в формулах (1.2) и (2.9), а, следовательно, и в (6.4)-(6.5), давление р и коэффициенты, обозначенные одинаковыми буквами m_k, определяются совершенно разными формулами. Поэтому ситуация, что в случае билинейной интерполяции энтропия не может быть определена, является весьма серьезной. Называть «изэнтропой» линию  в случае (1.2) бессмысленно.

6.3. Существенная роль термодинамического тождества (1.5), отражающего второе начало термодинамики, отмечалась еще в [9].                 В монографии [5], стр. 104-105, описаны дополнительные требования, предъявляемые к уравнениям состояния, в виде неравенств:

(6.6)                    ,             .

Кроме того, функция  должна удовлетворять дополнительным ограничениям, предложенным Бете и Вейлем:

(6.7)                    ,             .

          Уже обеспечение термодинамического тождества (1.5) оказалось достаточно трудной и громоздкой задачей. В §5 гипотетически обсуждались возможные затруднения в газодинамических расчетах, которые могут возникнуть при использовании аппроксимаций уравнений состояния функциями, обеспечивающими выполнение термодинамического тождества. Автор счел нужным обратить на это внимание именно потому, что вопрос об обеспечении требований (6.6)-(6.7) пока остался без обсуждения.

6.4. Позволим себе сделать замечание, навеянное монографией [10], из которой приведем следующую цитату (стр.62):

«Из термодинамики известно, что для задания всех зависимостей между термодинамическими величинами достаточно задать одну функцию от двух аргументов – какой-либо термодинамический потенциал. Выберем в качестве такой функции внутреннюю энергию e. В качестве аргументов при этом придется взять удельный объем  и энтропию S. Таким образом, мы предполагаем зависимость . Однако не всегда реальные уравнения состояния задаются интерполяционными формулами именно такого вида. Оказывается, класс допустимых формул существенно расширяется, если зависимость  задается при помощи параметрического представления. Параметры подбираются наиболее удобным способом для каждого уравнения состояния» (конец цитаты).

          Таким образом, если бы мы располагали одной двумерной таблицей , то этого было бы достаточно для полного задания уравнения состояния.      ,  у нас есть. Полагаем

                    ,                   ,

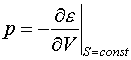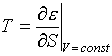и нет никаких проблем с обеспечением термодинамического тождества.

          Что касается аппроксимации одной двумерной таблицы , то для аппроксимации в табличной ячейке достаточно 4 свободных параметров. Естественно, что для этого билинейная аппроксимация – как раз то, что нужно:

                              .

И формулы для коэффициентов – а₁, а₂, а₃, а₄ – простейшие, аналогичные в (1.3) m₁, m₂, m₅, m₈ , соответственно, только использующие S вместо Т.

          Проблема в том, где же такую таблицу  взять? Мы работаем в ситуации, когда уравнение состояния задается двумя таблицами для представления (1.1). Это явно избыточная информация с точки зрения термодинамики.

          Настоящее исследование представляет один из путей, учитывающий скрытые внутренние связи при работе с этой избыточной информацией. «Нелепое» равенство (1.7), которое (за указанным (1.8) исключением) невозможно выполнить, - следствие того, что билинейная аппроксимация (1.2) такого рода скрытые внутренние связи двух таблиц игнорирует.

          Автор считает логичным отметить, что следует осторожно относиться и к самим таблицам, задающим уравнения состояния в рассматриваемой табличной форме. Не исключено, что они могут содержать скрытые погрешности (внутренние противоречия). Анализ  таблиц с точки зрения пригодности для газодинамических расчетов целесообразно проводить независимо и до решения самих задач.

          Уже после того, как настоящая работа была подготовлена к печати, С.К.Годунов обратил внимание автора на следующее. Кроме E(V,S), существуют и другие формы термодинамических потенциалов (см., напр., [11], стр. 60-67). Если в качестве независимых переменных выбираются Т и r (что равносильно ), то в роли термодинамического потенциала будет выступать функция F=e-TS, называемая свободной энергией. Одна таблица для функции F(T,r) полностью задает уравнение состояния.

          Описанную в настоящей работе согласованную аппроксимацию функций e(T,r) и  p(T, r), заданных таблично, можно считать одним из путей реализации такой возможности, если в табличной ячейке воспользоваться возникающей аппроксимацией для термодинамического потенциала F. Поэтому автор счел возможным сохранить подготовленный текст работы.

Заключение

          Табличную форму задания уравнений состояния можно считать самой универсальной. Для практического использования в газодинамических расчетах целесообразно оперировать с ее аналитическими представлениями. Рассматривался случай задания давления и внутренней энергии от температуры и плотности.

Как оказалось, независимая билинейная аппроксимация их таблиц не удовлетворяет основному термодинамическому тождеству. В настоящей работе автору удалось разработать алгоритмы, которые, в принципе, могут устранить этот недостаток. Аппроксимирующие функции для давления и внутренней энергии конструируются как линейная комбинация 8 частных решений, удовлетворяющих термодинамическому тождеству.

Рассмотрены также вопросы, связанные с применением полученных аналитических формул для уравнений состояния при численном решении газодинамических задач. Ввиду их громоздкости изучались гипотетически трудности, которые могут препятствовать их использованию, и возможные пути преодоления таких трудностей. Конечно, они прежде всего зависят от конкретных табличных данных.

При решении практических задач уравнения состояния приходится использовать в широком диапазоне изменения параметров. Поэтому с вычислительной точки зрения, полученные расчетные формулы необходимо преобразовать.

В заключение автор считает необходимым подчеркнуть, что вопрос о работоспособности предложенного алгоритма (с учетом его возможного усовершенствования) остался открытым, и это должно стать предметом специальных исследований. В случае неблагоприятного результата вопрос о конструировании приемлемого решения, термодинамически согласованного, остается актуальным.

          Автор выражает благодарность М.С.Гавреевой за помощь в оформлении работы.

Литература

1.     Куликовский А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения гиперболических систем уравнений.// М.: ФИЗМАТЛИТ, 2001, 608 С.

2.     Чарахчьян А.А. Об алгоритмах расчета распада разрыва для схем С.К.Годунова.// Ж. вычисл. матем. и матем. физики, 2000, 40, №5, С.782-796.

3.     Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных уравнений и их приложения к газовой динамики.// М.:, «Наука», Главная редакция физ.-мат. лит., 1968, 592 С.

4.     Прокопов Г.П. О задании уравнений состояния при моделировании неполностью ионизованной плазмы.// Вопросы атомной науки и техники. Сер.: Матем. моделир. физ. процессов, 2000, вып.3, С.45-63.

5.     Численное решение многомерных задач газовой динамики. Под общей ред.  С.К.Годунова// М., «Наука», 1976, 400 С.

6.     Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся ВТУЗов.// М., Главиздат, Гос. изд-во техн.-теор. лит., 1953, 608 С.

7.     Кобзева Т.А., Моисеев Н.Я. Метод неопределенных коэффициентов для решения задачи о распаде произвольного разрыва.// Вопросы атомной науки и техники. Сер.: Мат. моделир. физ. процессов, 2003, вып. 1, С.3-9.

8.     Прокопов Г.П. Задача о распаде разрыва в трехтемпературной газовой динамике.//М., Препринт ИПМ им.М.В.Келдыша РАН, 2004, №66, 28 С.

9.     Курант Р., Фридрихс К.О. Сверхзвуковое течение и ударные волны.// Изд-во иностр. литературы, М., 1950, 426 С.

10.    Алалыкин Г.Б., Годунов С.К., Киреева И.Л., Плинер Л.А. Решение одномерных задач газовой динамики в подвижных сетках.// М., «Наука», Гл. ред. физ.-мат. лит., 1970, 112 С.

11.    Зоммерфельд А. Термодинамика и статистическая физика.// М., Изд-во иностр. литер., 1955, 480 С.
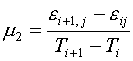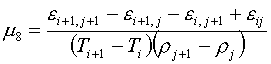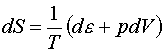
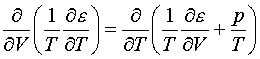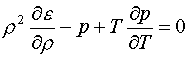
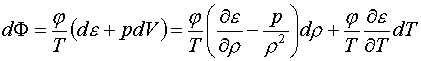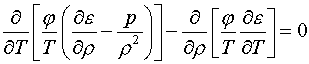
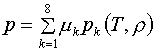