ДИНАМИКА ГРАВИТАЦИОННОЙ СИСТЕМЫ СПУТНИК-СТАБИЛИЗАТОР
НА КРУГОВОЙ И ЭЛЛИПТИЧЕСКОЙ ОРБИТАХ
В. А. Сарычев1, А. М. Сеабра2,
Л. Ф. Сантуш3
1Институт прикладной математики им. М. В. Келдыша РАН, г. Москва
2Высшая техническая школа г. Визеу, Португалия
3Университет г. Ковильян, Португалия
Исследована динамика спутника с пассивной гравитационной системой ориентации в плоскости круговой и эллиптической орбит. Вначале рассмотрены малые колебания системы спутник-стабилизатор в плоскости круговой орбиты в окрестности наиболее простого положения равновесия. Получены необходимые и достаточные условия асимптотической устойчивости положения равновесия, аналитически определены параметры, обеспечивающие максимальную скорость затухания собственных колебаний системы спутник-стабилизатор. Исследованы также эксцентриситетные колебания системы в плоскости эллиптической орбиты. Определены параметры, соответствующие минимальной величине амплитуды эксцентриситетных колебаний спутника.
1. Рассмотрим движение системы,
состоящей из тела 1 (спутник) с центром масс ![]() и связанной с ним системы координат
и связанной с ним системы координат ![]() и тела 2 (стабилизатор) с центром масс
и тела 2 (стабилизатор) с центром масс ![]() и связанной с ним системы координат
и связанной с ним системы координат ![]() , в плоскости
эллиптической орбиты. Здесь
, в плоскости
эллиптической орбиты. Здесь ![]() - главные центральные оси инерции тел (i=1,2). Оба тела соединены шарниром в точке
- главные центральные оси инерции тел (i=1,2). Оба тела соединены шарниром в точке ![]() . В шарнире
введено линейное трение.
. В шарнире
введено линейное трение.
Движение спутника и стабилизатора будем рассматривать в орбитальной системе
координат ![]() , где
, где ![]() - центр масс системы тел, движущейся по
эллиптической орбите с эксцентриситетом
- центр масс системы тел, движущейся по
эллиптической орбите с эксцентриситетом ![]() , ось
, ось ![]() направлена
вдоль радиус-вектора орбиты, ось OX лежит в плоскости орбиты и перпендикулярна
направлена
вдоль радиус-вектора орбиты, ось OX лежит в плоскости орбиты и перпендикулярна ![]() , ось
, ось ![]() перпендикулярна плоскости орбиты. Для
написания уравнений движения тел системы введем углы
перпендикулярна плоскости орбиты. Для
написания уравнений движения тел системы введем углы ![]() ,
, ![]() между осями
между осями ![]() и OX и
и OX и ![]() и
OX соответственно; эти углы определяют ориентацию обоих тел в плоскости
и
OX соответственно; эти углы определяют ориентацию обоих тел в плоскости ![]() .
.
Рассмотрим простейшую схему системы, когда положения центров масс ![]() и
и ![]() обоих тел, центра масс
обоих тел, центра масс ![]() системы и шарнира
системы и шарнира ![]() совпадают. Тогда выражения для кинетической
энергии, силовой функции и диссипативной функции могут быть записаны в
следующем виде [1]:
совпадают. Тогда выражения для кинетической
энергии, силовой функции и диссипативной функции могут быть записаны в
следующем виде [1]:
![]() (1)
(1)
![]()
(2)
![]() (3)
(3)
В приведенных
выражениях величины ![]() и
и ![]() суть главные
центральные моменты инерции тел системы,
суть главные
центральные моменты инерции тел системы, ![]() - гравитационный параметр планеты,
- гравитационный параметр планеты, ![]() - угловая скорость движения центра масс
системы по орбите,
- угловая скорость движения центра масс
системы по орбите, ![]() - модуль радиус-вектора орбиты,
- модуль радиус-вектора орбиты, ![]() - постоянный коэффициент демпфирования.
Штрихом обозначено дифференцирование по времени
- постоянный коэффициент демпфирования.
Штрихом обозначено дифференцирование по времени ![]() .
.
Нелинейные уравнения движения системы двух связанных тел проще всего
записать в форме уравнений Лагранжа второго рода
![]()
(4)
![]()
Переменные коэффициенты ![]() и
и ![]() определяются из решения задачи двух тел и
имеют вид
определяются из решения задачи двух тел и
имеют вид
![]() ,
, ![]() =
=![]() 2η3, η=1+e cos θ, (5)
2η3, η=1+e cos θ, (5)
где θ – истинная
аномалия, ![]() – постоянная величина. После перехода к новой
независимой переменной
– постоянная величина. После перехода к новой
независимой переменной ![]() и введения
безразмерных параметров
и введения
безразмерных параметров
![]() (6)
(6)
система (4) может быть представлена в виде
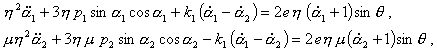 (7)
(7)
где точкой обозначено дифференцирование по ![]() .
.
2. На круговой орбите ![]() и система (7)
несколько упрощается:
и система (7)
несколько упрощается:
![]()
(8)
![]()
Система (8) обладает положениями равновесия ![]() , удовлетворяющими уравнениям
, удовлетворяющими уравнениям
![]() . (9)
. (9)
В статье будет исследовано поведение системы в окрестности простейшего
положения равновесия, когда
![]() ,
, ![]() . (10)
. (10)
Получим линеаризованную в
окрестности решения (10) систему уравнений движения
![]()
и соответствующее этой системе характеристическое уравнение
![]()
(11)
В линеаризованной системе величины x и y представляют собой малые отклонения от
положений равновесия (10). Используя критерий Льенара и Шипара, приходим к
необходимым и достаточным условиям асимптотической устойчивости решения (10)
![]() (12)
(12)
3. При определении
параметров, обеспечивающих минимальную длительность переходного процесса
системы, используем понятие степени устойчивости [2], представляющей собой
расстояние самого правого корня характеристического уравнения от мнимой оси.
Максимальная степень устойчивости соответствует минимальной длительности
переходного процесса системы. Используя результаты работ [2-6], можно
заключить, что величина степени устойчивости ![]() достигает максимума,
когда корни характеристического уравнения (11)
достигает максимума,
когда корни характеристического уравнения (11) ![]() -
-![]() . Случай четырех равных действительных корней возможен, если
система уравнений
. Случай четырех равных действительных корней возможен, если
система уравнений
![]() (13)
(13)
имеет решение.
Из второго и третьего
уравнений системы (13) получаем
![]() . (14)
. (14)
Подставляя выражения (14) в последнее уравнение (13), приходим к
квадратному уравнению
![]() (15)
(15)
с корнями ![]() ,
, ![]() . Для первого
корня из (14) получаем
. Для первого
корня из (14) получаем
![]() (16)
(16)
Принимая во внимание (12) и условия физической реализуемости ![]() и
и ![]() для обоих тел системы, приходим к неравенству
для обоих тел системы, приходим к неравенству
![]() . (17)
. (17)
Для второго корня ![]() квадратного уравнения (15)
квадратного уравнения (15)
![]()
а величина степени
устойчивости δ и в этом случае
удовлетворяет неравенству (17).
Таким образом, из неравенства (17)
следует, что максимальное значение степени устойчивости
![]() (18)
(18)
Задача оптимизации
переходного процесса исследуемой системы имеет следующие два решения:
Решение 1.
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Решение 2.
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Можно показать, что
решения 1 и 2 переходят одно в другое, если тело 1 (спутник) переходит в тело 2
(стабилизатор) и тело 2 (стабилизатор) – в тело 1 (спутник).
4. Вернемся теперь к неоднородной
системе уравнений (7), которая определяет колебания системы
спутник-стабилизатор на эллиптической орбите. При e≠0 система (7) не имеет стационарных решений. Представляет
интерес исследовать вынужденное решение системы (7), обусловленное
неравномерностью движения центра масс системы спутник-стабилизатор по орбите.
Очень часто это вынужденное решение называют эксцентриситетными колебаниями.
Будем искать вынужденное решение системы (7) методом малого параметра в виде
рядов по степени e
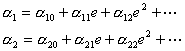 (19)
(19)
Полагая эксцентриситет орбиты малым, ограничимся определением лишь
первых членов разложения
![]() (20)
(20)
где, в соответствии с (10), ![]() ,
, ![]() . Подставляя
(20) в (7), получаем систему
. Подставляя
(20) в (7), получаем систему
![]() (21)
(21)
вынужденное решение которой определяет
эксцентриситетные колебания спутника и стабилизатора. Подставив общие формулы
для вынужденного решения системы (21)
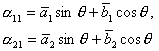 (22)
(22)
и приравняв нулю коэффициенты при ![]() и
и ![]() , получим
линейную систему
, получим
линейную систему
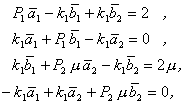 (23)
(23)
для определения параметров ![]() . В системе (23)
введены обозначения
. В системе (23)
введены обозначения ![]() ,
, ![]() . Из уравнений
(23) получаем
. Из уравнений
(23) получаем
![]()
![]() (24)
(24)
![]()
![]()
и выражения для амплитуд эксцентриситетных колебаний спутника ![]() и стабилизатора
и стабилизатора ![]()
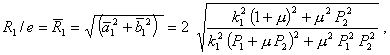
(25)
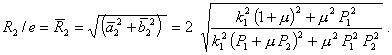
Параметры ![]() и
и ![]() должны удовлетворять
условиям
должны удовлетворять
условиям
![]() <
<![]() ,
, ![]() <
<![]() ,
, ![]() . (26)
. (26)
С практической точки
зрения наибольший интерес представляет минимизация амплитуды эксцентриситетных
колебаний спутника ![]() , а точнее величины
, а точнее величины ![]() , зависящей от параметров системы
, зависящей от параметров системы ![]() ,
, ![]() ,
, ![]()
![]() . Рассмотрим
частные производные функции
. Рассмотрим
частные производные функции ![]() по переменным
по переменным ![]() и
и ![]() при фиксированных
значениях
при фиксированных
значениях ![]() и
и ![]() . Тогда
необходимые условия экстремума функции
. Тогда
необходимые условия экстремума функции ![]() внутри области
внутри области
![]() (27)
(27)
примут вид
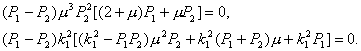 (28)
(28)
Следует отметить, что экстремум функции ![]() может реализоваться не
только при выполнении условий (28), но и на границе области (27) определения
функции
может реализоваться не
только при выполнении условий (28), но и на границе области (27) определения
функции ![]() .
.
Опуская анализ всех
решений системы (28) и поведения функции ![]() на границе ее области
определения, приведем лишь наиболее общие случаи минимума амплитуды
эксцентриситетных колебаний спутника.
на границе ее области
определения, приведем лишь наиболее общие случаи минимума амплитуды
эксцентриситетных колебаний спутника.
1) ![]() Тогда
Тогда ![]() и минимум функции
и минимум функции ![]() =1 достигается при
=1 достигается при
![]() и любых значениях
и любых значениях ![]() и
и ![]() .
.
2) ![]() =0. В этом случае система спутник-стабилизатор сводится к
одному твердому телу (спутник),
=0. В этом случае система спутник-стабилизатор сводится к
одному твердому телу (спутник), ![]() , минимум
, минимум ![]() =1 достигается при
=1 достигается при ![]()
3) ![]() =0. Система уравнений (7) разделяется на два независимых
уравнения, минимум
=0. Система уравнений (7) разделяется на два независимых
уравнения, минимум ![]() =1 достигается при
=1 достигается при ![]() и любых значениях
и любых значениях ![]() .
.
Все другие, не приведенные здесь, решения или сводятся к этим трем
случаям, или не являются точками минимума, или существуют при физически
нереальных параметрах исследуемой системы.
Таким образом, минимум
амплитуды эксцентриситетных колебаний спутника ![]() достигается на границе
области асимптотической устойчивости или на границе физической реализуемости
параметров системы.
достигается на границе
области асимптотической устойчивости или на границе физической реализуемости
параметров системы.
5. Исследована динамика
простейшей гравитационной системы спутник-стабилизатор, когда положения
шарнира, соединяющего оба тела, и их центров масс совпадают, а упругие силы в
шарнире отсутствуют. В связи с этими упрощающими предположениями система
уравнений движения (7) представляет собой частный случай соответствующих
уравнений движения работы [1], записанных с использованием других безразмерных
параметров. Аналогичная ситуация возникает при исследовании необходимых и
достаточных условий асимптотической устойчивости (12). При определении
оптимальных по быстродействию параметров системы результат (18) ![]() отличается от
результата работ [1, 4-6], где для схемы системы с моментом упругих сил в
шарнире
отличается от
результата работ [1, 4-6], где для схемы системы с моментом упругих сил в
шарнире ![]() Задача минимизации
амплитуды эксцентриситетных колебаний спутника была, по-видимому, впервые
рассмотрена в [1]. Используя геометрический подход, удалось получить некоторые
общие оценки для амплитуды
Задача минимизации
амплитуды эксцентриситетных колебаний спутника была, по-видимому, впервые
рассмотрена в [1]. Используя геометрический подход, удалось получить некоторые
общие оценки для амплитуды ![]() . В настоящей статье для более простой схемы системы
спутник-стабилизатор параметры, обеспечивающие минимум амплитуды эксцентриситетных
колебаний спутника
. В настоящей статье для более простой схемы системы
спутник-стабилизатор параметры, обеспечивающие минимум амплитуды эксцентриситетных
колебаний спутника ![]() , определены аналитически. Следует также отметить работу [7],
в которой показана возможность компенсации эксцентриситетных колебаний спутника (
, определены аналитически. Следует также отметить работу [7],
в которой показана возможность компенсации эксцентриситетных колебаний спутника (![]() ) при некотором усложнении выражения для момента
упругих сил в подвесе P.
) при некотором усложнении выражения для момента
упругих сил в подвесе P.
Работа поддержана
Проектом Stabisat Португальского
фонда науки и техники.
СПИСОК ЛИТЕРАТУРЫ
1. Сарычев
В.А. Исследование динамики
системы гравитационной стабилизации // Искусственные спутники Земли. М.: Изд.
АН СССР, 1963. №16. С.10-33.
2. Цыпкин
Я.З., Бромберг П.В. О
степени устойчивости линейных систем // Изв. АН СССР. Отделение технич. наук.
1945. №12. С.1163-1168.
3.
Borelli
R.L., Leliakov I.P. An optimization technique for the transient
response of passively stable satellites // J. of Optimization Theory and
Applications. 1972. V.10. №6. P.344-361.
4. Сарычев
В.А., Сазонов В.В. Оптимальные параметры пассивных систем ориентации
спутников // Космич. исслед. 1976. Т.14. №2. С.198-208.
5. Сарычев
В.А., Мирер С.А. Оптимальные параметры гравитационной системы
спутник-стабилизатор // Космич. исслед. 1976. Т.14. №2. С.209-219.
6. Sarychev V.A., Mirer S.A., Sazonov V.V. Plane
oscillations of a gravitational system satellite-stabilizer with maximal speed
of response // Acta Astronautica. 1976. V.3. №9-10. P.651-669.
7.
Пеньков В.И. Компенсация эксцентриситетных колебаний
спутника с гравитационной системой стабилизации // Космич. исслед. 1977. Т.15. №3. С.376-383.
DYNAMICS
OF GRAVITATIONAL SYSTEM SATELLITE-STABILIZER
ON
CIRCULAR AND ELLIPTIC ORBITS
V. A.
Sarychev1, A. M. Seabra2, and L. F. Santos3
1Keldysh Institute of Applied Mathematics,
Miusskaya
pl. 4,
2Escola Superior de Tecnologia de Viseu,
Viseu,
3Universidade da Beira Interior,
Covilhã,
Abstract–This paper studies
the dynamics of a satellite with passive gravitational attitude control system
in the plane of circular and elliptic orbits. At first it discusses small
oscillations of the satellite-stabilizer system in the plane of a circular
orbit in a vicinity of the more simple equilibrium position. The necessary and
sufficient conditions for asymptotic stability of that equilibrium are obtained
and the values of the parameters, where the maximal speed of response of the
system is achieved, are analytically determined. The paper also studies the
eccentricity oscillations in elliptic orbit. The forced solution of the system
is determined and the minimal value for magnitude of the eccentricity
oscillations amplitude of the satellite is determined.