СОДЕРЖАНИЕ
Введение 3
§ 1. Метод решения
уравнений вида  . 7 . 7
§ 2. Метод решения
бигармонического уравнения. 10
§ 3. Дискретизация
задачи для уравнений вида  . 13 . 13
§ 4. Дискретизация
задачи для бигармонического уравнения. 17
§ 5. Результаты тестовых расчетов. 19
Заключение 28
Литература 28
Введение
Необходимость решения
эллиптических уравнений в неограниченной области возникает в различных задачах
математической физики. Как правило, в подобных задачах источники сосредоточены
на некотором ограниченном множестве S, так что находить решение во всем
пространстве нет необходимости. Это позволяет заменить исходную задачу задачей
в некоторой ограниченной области, на границе которой поставлены искусственные
граничные условия (ИГУ). Проблеме построения таких условий посвящено большое
количество работ, подробный обзор которых приведен в [1]. В идеальном случае
ИГУ должны быть выбраны так, чтобы решение задачи в ограниченной расчетной
области совпадало в этой области с решением исходной задачи. Однако точные ИГУ
являются, как правило, нелокальными и требуют значительных вычислительных
затрат при реализации. Поэтому на практике их обычно приходится заменять
приближенными локальными условиями.
В качестве примера
рассмотрим уравнение Пуассона на плоскости:
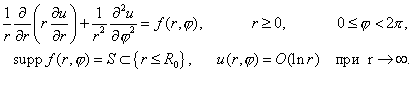
Разложим функцию 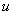 в ряд по гармоникам
при в ряд по гармоникам
при  : :
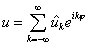 , , 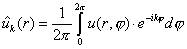 .
(0.1) .
(0.1)
Для каждой из 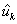 имеем: имеем:
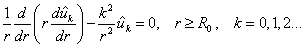
Каждое из этих уравнений имеет два линейно независимых
решения:
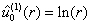 и и 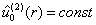 при при 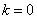 , ,
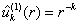 и и 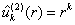 при при 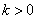 . .
Из них только  удовлетворяют условиям
на бесконечности, поэтому следует потребовать выполнения следующего
соотношения: удовлетворяют условиям
на бесконечности, поэтому следует потребовать выполнения следующего
соотношения:
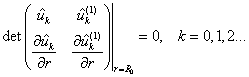
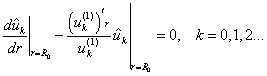
Для самой функции 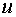 граничное условие
имеет вид: граничное условие
имеет вид:
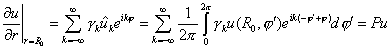 ,
(0.2) ,
(0.2)
где 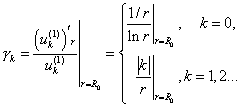
Это условие является, очевидно,
нелокальным. Ограничив количество слагаемых в разложении
(0.1),(0.2)
, на его основе можно получить
приближенные локальные условия. Они более удобны для реализации, однако точными
уже не являются. В частности, удерживая единственное слагаемое (k = 0), имеем граничное условие 3
рода:
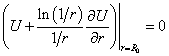 .
(0.3) .
(0.3)
Здесь 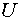 - решение задачи
описанного вида в ограниченной области с условием (0.3) на ее границе. - решение задачи
описанного вида в ограниченной области с условием (0.3) на ее границе.
Его погрешность можно
оценить величиной 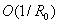 , которая зависит от размера вспомогательной области. На
практике размер области, необходимый для получения приемлемых результатов,
может оказаться достаточно большим. Кроме того, в некоторых случаях (когда в
разложении точного решения отсутствует член при k = 0) это условие будет
неработоспособным при любом значении , которая зависит от размера вспомогательной области. На
практике размер области, необходимый для получения приемлемых результатов,
может оказаться достаточно большим. Кроме того, в некоторых случаях (когда в
разложении точного решения отсутствует член при k = 0) это условие будет
неработоспособным при любом значении 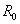 . .
Удерживая дополнительные
слагаемые в разложении 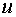 , можно получить локальные условия более высокого порядка.
Однако их точность также будет зависеть от размера области. , можно получить локальные условия более высокого порядка.
Однако их точность также будет зависеть от размера области.
Одним из эффективных
подходов к решению задач в неограниченных областях является использование
граничных условий на основе метода разностных потенциалов [2]. Пусть решение
исходной задачи вне некоторой ограниченной области 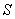 удовлетворяет
уравнению удовлетворяет
уравнению 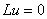 , где , где  - линейный оператор.
Внутри области - линейный оператор.
Внутри области 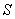 может действовать
более сложный оператор. Тогда для значений функции на сеточной границе
записываются нелокальные условия вида может действовать
более сложный оператор. Тогда для значений функции на сеточной границе
записываются нелокальные условия вида
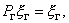
где действие оператора 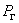 определяется через
решение некоторой вспомогательной задачи. Это также задача в неограниченной
области, но с более простым оператором определяется через
решение некоторой вспомогательной задачи. Это также задача в неограниченной
области, но с более простым оператором  . .
В случае линейного
оператора с постоянными коэффициентами можно воспользоваться интегральным
представлением точного решения. Известно [3], что решение линейного
эллиптического уравнения может быть записано в виде свертки с соответствующей
функцией Грина. Для линейных уравнений с коэффициентами, постоянными во всем
пространстве или вне достаточно простой области, эта функция часто известна.
Наиболее очевидный способ использования интегрального представления для
определения граничных данных и решения задачи в ограниченной области состоит в
следующем: необходимо вычислить значения функции 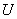 на границе некоторой
вспомогательной области D, а затем решить в этой области первую краевую задачу.
Погрешность получаемого таким образом решения будет определяться только
точностью квадратурной формулы, используемой для вычисления интеграла, и
точностью метода, применяемого для решения краевой задачи. на границе некоторой
вспомогательной области D, а затем решить в этой области первую краевую задачу.
Погрешность получаемого таким образом решения будет определяться только
точностью квадратурной формулы, используемой для вычисления интеграла, и
точностью метода, применяемого для решения краевой задачи.
Оценим по порядку
величины расчетные затраты на получение решения.
В двумерном случае на
прямое вычисление решения во всей пространственной области, представляющей
интерес, потребуется 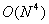 действий (вычисление
двойного интеграла во всех точках сетки). Здесь действий (вычисление
двойного интеграла во всех точках сетки). Здесь 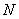 - число точек по одной
координате. - число точек по одной
координате.
Вычисление решения на
границе вспомогательной области требует 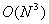 операций (вычисление
двойного интеграла во всех точках границы). Столько же действий необходимо
выполнить для нахождения решения в ограниченной области, например, методом
сопряженных градиентов [4, с. 349], [5, с. 83]. При фиксированной относительной
точности решения системы линейных алгебраических уравнений число итераций
метода пропорционально операций (вычисление
двойного интеграла во всех точках границы). Столько же действий необходимо
выполнить для нахождения решения в ограниченной области, например, методом
сопряженных градиентов [4, с. 349], [5, с. 83]. При фиксированной относительной
точности решения системы линейных алгебраических уравнений число итераций
метода пропорционально 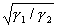 , где , где 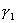 и и 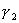 - постоянные
энергетической эквивалентности оператора задачи (в простых ситуациях это
границы спектра). Значение этого квадратного корня можно грубо оценить
величиной - постоянные
энергетической эквивалентности оператора задачи (в простых ситуациях это
границы спектра). Значение этого квадратного корня можно грубо оценить
величиной 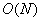 [4, с. 348]. При этом
на выполнение одной итерации требуется [4, с. 348]. При этом
на выполнение одной итерации требуется 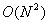 операций. Отсюда и
получаем указанное выше число действий. операций. Отсюда и
получаем указанное выше число действий.
Рассмотрим трехмерный
случай.
В трехмерном случае на
прямое вычисление решения во всей пространственной области, представляющей
интерес, потребуется 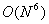 действий (вычисление
тройного интеграла во всех точках сетки). действий (вычисление
тройного интеграла во всех точках сетки).
Вычисление решения на
границе вспомогательной области в этом случае требует  операций (вычисление
тройного интеграла во всех точках границы). Для нахождения же решения в
ограниченной области методом сопряженных градиентов требуется выполнить операций (вычисление
тройного интеграла во всех точках границы). Для нахождения же решения в
ограниченной области методом сопряженных градиентов требуется выполнить 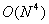 действий. При этом
число итераций метода также есть действий. При этом
число итераций метода также есть 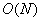 , а на выполнение одной итерации требуется выполнить , а на выполнение одной итерации требуется выполнить 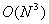 операций. В результате
имеем указанное выше число. операций. В результате
имеем указанное выше число.
Таким образом, прямое
вычисление решения во всей области с помощью интегрального представления
заведомо неприемлемо в обоих рассмотренных вариантах. Дополнительное вычисление
решения на границе также оказывается дорогим в трехмерном случае.
Целью данной работы
является построение численного алгоритма решения задач в неограниченных
областях, который требовал бы количества действий, не превышающего числа
действий на прямое решение задачи в ограниченной области как в двумерном, так и
в трехмерном случаях.
В данной работе предложен
метод решения эллиптических уравнений с постоянными коэффициентами, позволяющий
найти решение в двумерном случае за 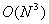 операций, а в
трехмерном – за операций, а в
трехмерном – за 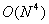 операций. При этом
погрешность численного решения для гладких источников не зависит от размера
вспомогательной области и не превышает операций. При этом
погрешность численного решения для гладких источников не зависит от размера
вспомогательной области и не превышает 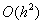 , где , где 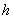 - шаг сетки по каждому
из направлений. Такой результат достигнут за счет использования формул Грина,
позволяющих избежать вычисления двойных интегралов. - шаг сетки по каждому
из направлений. Такой результат достигнут за счет использования формул Грина,
позволяющих избежать вычисления двойных интегралов.
Авторы
приносят свою благодарность И.Л. Софронову и А.В. Колдобе за интерес к работе и
полезные обсуждения.
Необходимо
также указать, что на возможность использования вспомогательных задач для
нахождения решений в неограниченных областях авторов натолкнуло сообщение Л.М.
Дегтярева, услышанное от него в первой половине 1990 – х годов.
Работа
выполнена при частичной финансовой поддержке Российского фонда фундаментальных
исследований (проект РФФИ № 03 - 01 - 00461).
§
1. Метод решения
уравнений вида 
Необходимо решить следующее уравнение
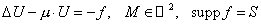 , ,
дополненное на бесконечности одним из
следующих условий [3]:
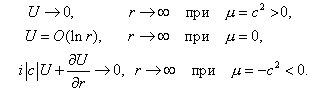
Будем рассматривать только действительную
часть получаемого решения.
Тогда
фундаментальное решение задачи имеет вид [3]:
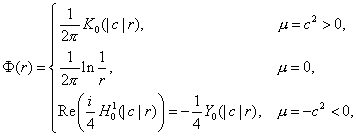
где 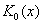 - функция Макдональда
нулевого порядка, а - функция Макдональда
нулевого порядка, а  - функция Неймана
нулевого порядка. - функция Неймана
нулевого порядка.
Решение задачи можно
записать следующим образом:
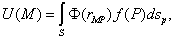
где 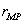 - расстояние между точками - расстояние между точками 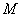 и и 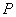 . Индекс . Индекс 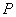 при элементе площади
означает, что при интегрировании соответствующая область пробегается точкой при элементе площади
означает, что при интегрировании соответствующая область пробегается точкой 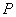 . .
Рассмотрим
вспомогательную область 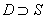 с кусочно-гладкой
границей с кусочно-гладкой
границей 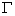 и будем искать решение
внутри этой области в виде суммы двух функций и будем искать решение
внутри этой области в виде суммы двух функций
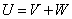 , ,
где 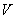 есть решение краевой
задачи есть решение краевой
задачи
 (1.1)
(1.1)
а  - некоторая
неизвестная функция такая, что - некоторая
неизвестная функция такая, что
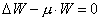 в в 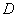 . .
Задача
(1.1)
имеет единственное решение при 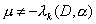 , где , где 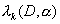 - собственные значения
соответствующего оператора – решения задачи Штурма - Лиувилля: - собственные значения
соответствующего оператора – решения задачи Штурма - Лиувилля:
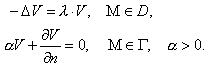
Далее всегда будем предполагать,
что 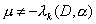 . Так как при . Так как при  все все 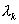 положительны [3], то
для положительны [3], то
для 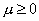 это условие
выполняется автоматически. Если же окажется, что это условие
выполняется автоматически. Если же окажется, что 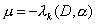 , то значения , то значения 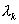 можно изменить,
сместив границу области можно изменить,
сместив границу области 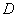 или выбрав другое
значение коэффициента или выбрав другое
значение коэффициента 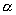 . .
Для функции 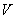 запишем третью
интегральную формулу Грина [3]: запишем третью
интегральную формулу Грина [3]:
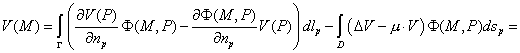

где
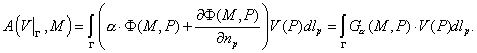
Тогда
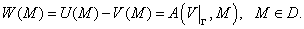
Для нахождения функции 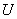 необходимо найти
значения интеграла необходимо найти
значения интеграла 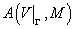 в точках области в точках области 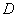 . Непосредственное вычисление этого интеграла во всей области
требует значительных вычислительных затрат. Однако можно поступить следующим
образом: выбрать некоторую область . Непосредственное вычисление этого интеграла во всей области
требует значительных вычислительных затрат. Однако можно поступить следующим
образом: выбрать некоторую область 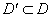 (см. рис. 1), вычислить значения этого интеграла на ее
границе (см. рис. 1), вычислить значения этого интеграла на ее
границе 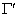 и решить следующую
краевую задачу: и решить следующую
краевую задачу:
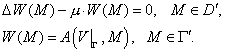 (1.2)
(1.2)
Здесь также
предполагается, что условия единственности выполнены.
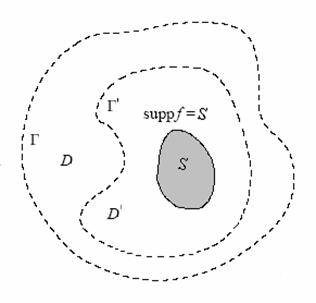
Рис. 1.
Таким образом, для
решения исходной задачи необходимо:
1) Найти решение
вспомогательной задачи
(1.1)
2) Вычислить значения 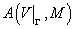 в точках на границе
области в точках на границе
области 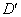 . .
3) Решить краевую задачу
для функции  в области в области 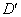 с построенными
граничными условиями. с построенными
граничными условиями.
После этого остается
вычислить решение:
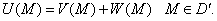
§
2. Метод решения бигармонического
уравнения: 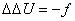
Требуется решить задачу:
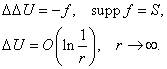
Данное
уравнение имеет четвертый порядок, но путем введения новой переменной его можно
записать в виде системы двух уравнений второго порядка типа уравнений Пуассона.
Поэтому для его решения можно применить метод для уравнений второго порядка,
изложенный в § 1.
Фундаментальное
решение данного уравнения имеет вид [3]:
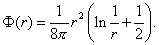
Решение задачи можно записать
следующим образом:
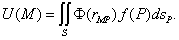
Можно
получить соотношение, аналогичное формуле Грина:
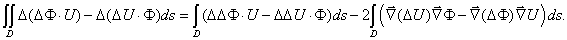
Преобразуем интегралы по
области в контурные интегралы:
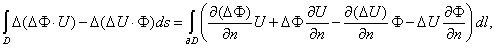

Учитывая, что
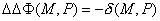 , ,
имеем:
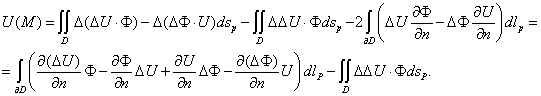 (2.1)
(2.1)
Выберем
вспомогательную область 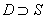 с кусочно - гладкой границей Г и будем искать решение в виде суммы
двух функций с кусочно - гладкой границей Г и будем искать решение в виде суммы
двух функций 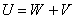 .
Здесь W –
некоторая неизвестная функция, удовлетворяющая в области D уравнению .
Здесь W –
некоторая неизвестная функция, удовлетворяющая в области D уравнению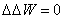 ,
а V - решение
краевой задачи ,
а V - решение
краевой задачи
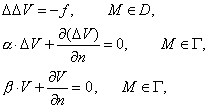 (2.2)
(2.2)
где α и b -
произвольные положительные числа, 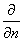 - производная по направлению внешней нормали. - производная по направлению внешней нормали.
Для
функции V запишем
формулу
(2.1)
и преобразуем ее с учетом граничных
условий:
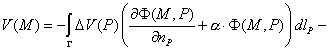
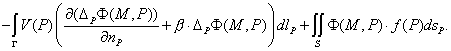
Последнее слагаемое представляет
собой в точности решение задачи в неограниченной области, т.е. функцию U.
Введем
следующие обозначения:
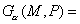 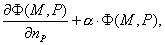
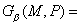 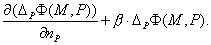
Фундаментальное решение задачи 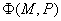 известно, так что эти функции всегда можно
вычислить с достаточной точностью. известно, так что эти функции всегда можно
вычислить с достаточной точностью.
Тогда
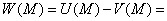
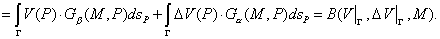
Значения этого интеграла можно вычислить
непосредственно в каждой точке области D, а можно найти их, решив некоторую краевую задачу для
функции W. Для этого
необходимо поставить дополнительные граничные условия на 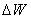 . .
Так как 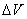 удовлетворяет в
области удовлетворяет в
области 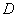 уравнению Пуассона уравнению Пуассона
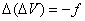 , ,
то для нее можно записать формулу Грина. При этом
функцию Грина 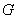 следует выбирать так,
чтобы для нее выполнялось условие следует выбирать так,
чтобы для нее выполнялось условие
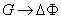 при при 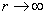 . .
В данном случае
 . .
Учитывая, что
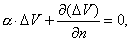
имеем:
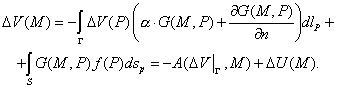
Отсюда
 . .
Таким образом, для W возникает следующая задача:
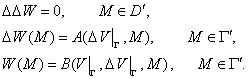 (2.3)
(2.3)
Для решения исходной задачи необходимо:
1) Найти решение вспомогательной задачи
(2.2)
2) Вычислить значения интегралов 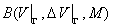 и и 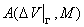 на границе области на границе области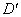 . .
3) Решить краевую задачу для функции W с построенными граничными условиями.
После этого остается вычислить решение:
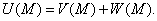
§ 3.
Дискретизация задачи для уравнений вида 
Рассмотрим полярную систему координат с центром в
некоторой точке. В этой системе уравнение
(1.1)
принимает вид:
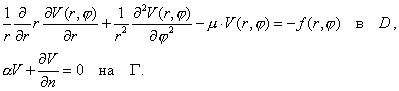
В качестве
вспомогательной области выберем круг 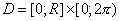 и введем на нем
равномерную сетку по и введем на нем
равномерную сетку по 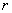 и и 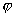 : :
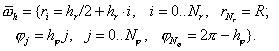
Предполагается, что при измельчении
сетки шаги по 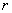 и по и по 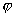 имеют одинаковый
порядок малости, т.е. имеют одинаковый
порядок малости, т.е. 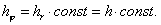
Для построения разностной схемы проинтегрируем уравнение
(1.1)
по элементарной ячейке:
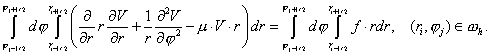
Заменив первые
производные центральными разностями, с точностью до слагаемых порядка  получим: получим:
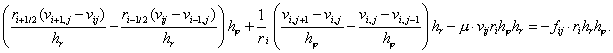
Заметим, что при 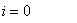 выполнены равенства выполнены равенства 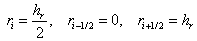 (см. рис. 2) и
справедливо уравнение (см. рис. 2) и
справедливо уравнение
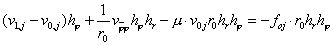 . .
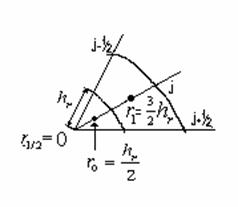
Рис. 2.
Для аппроксимации
уравнения (1.1) в окрестности границы проинтегрируем его по ячейке от  до до 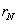 с учетом граничных
условий: с учетом граничных
условий:
 . .
В итоге получим схему следующего
вида:
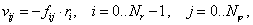
где
 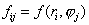
Для компактности записи
здесь и далее используются соотношения
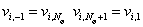 , ,
учитывающие периодичность по 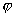 . .
Эти же уравнения можно
записать в виде
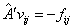 , , 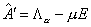 , ,
где 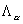 - разностная
аппроксимация оператора Лапласа с граничными условиями 3-го рода. - разностная
аппроксимация оператора Лапласа с граничными условиями 3-го рода.
Погрешность аппроксимации
этой схемы [4, 6] на четырежды непрерывно дифференцируемых решениях равна 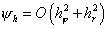 . .
Если 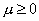 и и  , то при любых значениях , то при любых значениях 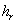 и и  для схемы выполнен
принцип максимума [6] и в соответствии с ним для схемы выполнен
принцип максимума [6] и в соответствии с ним
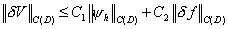 . .
где 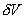 - ошибка численного решения, - ошибка численного решения,
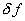 - ошибка задания
правой части. - ошибка задания
правой части.
Считая, что функция 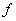 задана точно, имеем задана точно, имеем
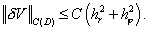
Если же 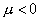 , то знакоопределенность матрицы , то знакоопределенность матрицы 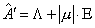 имеет место при имеет место при 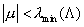 и и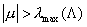 . В этом случае схема устойчива [6] и верна оценка . В этом случае схема устойчива [6] и верна оценка
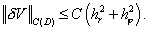
Теперь обратимся к
решению задачи
(1.2)
. Введем область 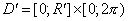 , , 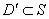 . Если граница этой области . Если граница этой области 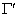 не является линией
сетки, сместим ее так, чтобы между не является линией
сетки, сместим ее так, чтобы между 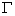 и и 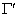 укладывалось целое
число шагов, т.е. укладывалось целое
число шагов, т.е. 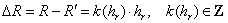 (рис. 3). Тогда на (рис. 3). Тогда на 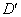 можно пользоваться
сеткой можно пользоваться
сеткой 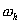 . .
При расчете граничных
данных для задачи
(1.2)
необходимо вычислять интегралы вида
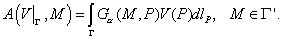
Для их вычисления можно использовать,
например, квадратурную формулу трапеций:
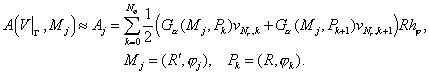
Функция 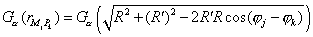 зависит только от
разности зависит только от
разности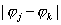 , поэтому ее значения достаточно вычислить в , поэтому ее значения достаточно вычислить в 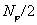 точках. точках.
Оценим погрешность
квадратурной формулы, обозначив для краткости 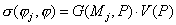 : :
Рис. 3.
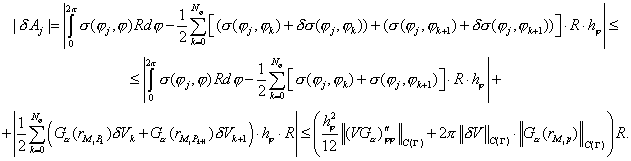
Функция 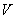 является решением 3-й
краевой задачи, поэтому является решением 3-й
краевой задачи, поэтому 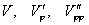 ограничены на контуре ограничены на контуре 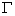 . .
При 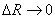 функция функция 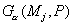 неограниченно
возрастает в точках неограниченно
возрастает в точках  , но при любом фиксированном значении , но при любом фиксированном значении 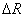 она ограничена и имеет
ограниченные производные нужного порядка. она ограничена и имеет
ограниченные производные нужного порядка.
Кроме того,
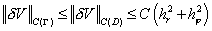 . .
Поэтому
верна оценка
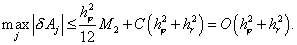
Для решения задачи
(1.2)
будем использовать ту же схему, что и для задачи
(1.1)
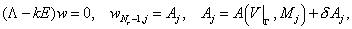
где 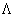 - разностный оператор
Лапласа с граничными условиями 1-го рода, аналогичный описанному в начале § 3. - разностный оператор
Лапласа с граничными условиями 1-го рода, аналогичный описанному в начале § 3.
Т.к. для схемы выполнен
принцип максимума, то
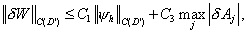
и решение может быть вычислено с
точностью  . .
Для решения полученной
системы разностных уравнений будем использовать метод сопряженных градиентов
[4].
Оценим число
арифметических действий, необходимых для реализации данного алгоритма в
двумерном случае. Как уже указывалось во Введении, для решения задачи методом
сопряженных градиентов необходимо 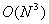 операций. На
вычисление граничных данных по интегральным формулам затрачивается операций. На
вычисление граничных данных по интегральным формулам затрачивается 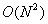 действий. В целом же
для реализации алгоритма необходимо выполнить действий. В целом же
для реализации алгоритма необходимо выполнить 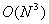 арифметических
действий, как и на решение задачи в ограниченной области. Отметим, что сам
расчет граничных данных в описываемом алгоритме требует меньшего числа действий,
чем расчет граничных данных по интегральному представлению решения. Правда, это
компенсируется необходимостью решать дополнительную задачу. арифметических
действий, как и на решение задачи в ограниченной области. Отметим, что сам
расчет граничных данных в описываемом алгоритме требует меньшего числа действий,
чем расчет граничных данных по интегральному представлению решения. Правда, это
компенсируется необходимостью решать дополнительную задачу.
Описанный метод можно распространить
и на пространственные (трехмерные) задачи. Для решения задачи в ограниченной
области методом сопряженных градиентов необходимо 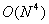 операций. При
использовании описанного метода возникает необходимость вычисления двойных
интегралов в точках некоторой поверхности, что требует того же количества
действий. В результате чего итоговая оценка числа операций принимает вид операций. При
использовании описанного метода возникает необходимость вычисления двойных
интегралов в точках некоторой поверхности, что требует того же количества
действий. В результате чего итоговая оценка числа операций принимает вид 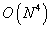 . .
§ 4. Дискретизация задачи для бигармонического
уравнения
Рассмотрим задачу
(2.2)
. Она эквивалентна (считаем решения
достаточно гладкими) следующей системе
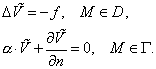
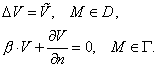
Преобразовав
(2.3)
аналогичным образом, имеем:
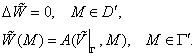
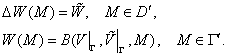
Для решения полученных
краевых задач будем использовать разностную схему, описанную в предыдущем
параграфе. При этом имеют место следующие оценки:
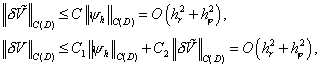
где 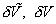 - ошибки численного решения. - ошибки численного решения.
Величины 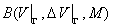 и и 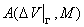 представляют собой суммы
однотипных интегралов вида представляют собой суммы
однотипных интегралов вида  где функция где функция 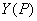 - решение некоторой
3-й краевой задачи, а - решение некоторой
3-й краевой задачи, а 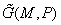 - линейная комбинация
функций - линейная комбинация
функций 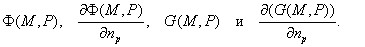
Вычисление таких интегралов описано в § 3.
Для нахождения функций 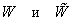 можно использовать уже
известную схему. можно использовать уже
известную схему.
Для нее выполнен принцип
максимума, поэтому имеют место оценки
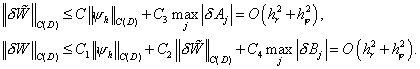
Таким образом, решения 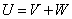 и и 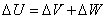 будут вычислены с
точностью будут вычислены с
точностью 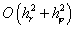 . Оценка числа операций остается такой же, как и в предыдущем
случае. . Оценка числа операций остается такой же, как и в предыдущем
случае.
§ 5. Результаты
тестовых расчетов
Описанный выше алгоритм
реализован в виде программы на языке C++. Для тестирования программы и
проверки работоспособности метода была решена серия задач, имеющих простое
аналитическое решение.
При вычислениях в
качестве вспомогательных областей 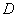 и и 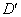 использовались круги
радиусов использовались круги
радиусов 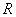 и и  соответственно.
Возникающие в задаче разностные уравнения для соответственно.
Возникающие в задаче разностные уравнения для 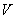 и и  решались методом
сопряженных градиентов [4]. Во всех случаях использовался следующий критерий
прекращения итераций: решались методом
сопряженных градиентов [4]. Во всех случаях использовался следующий критерий
прекращения итераций:
 , , 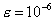 . .
Значения специальных
функций в нужных точках вычислялись стандартными средствами пакета Matlab 7.0 [7]. Затем эти значения
записывались в файл и считывались программой.
Результаты численного
решения тестовых задач приведены в виде таблиц.
Во всех таблицах далее
использованы следующие обозначения:
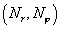 - число точек сетки по - число точек сетки по
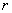 и и 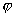 , ,
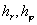 - значения
соответствующих шагов, - значения
соответствующих шагов,
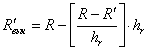 - значение радиуса, использованное при вычислениях (см. рис.
3), - значение радиуса, использованное при вычислениях (см. рис.
3),
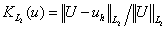 , , 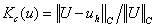 - отношения норм погрешности и точного
решения, - отношения норм погрешности и точного
решения,
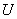 - точное решение, - точное решение, 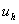 - приближенное
решение, - приближенное
решение,
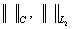 - разностные аналоги соответствующих норм функций, - разностные аналоги соответствующих норм функций,
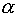 -
коэффициент в граничных условиях 3-го рода для вспомогательной задачи. -
коэффициент в граничных условиях 3-го рода для вспомогательной задачи.
Тестовая задача 1 :
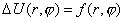 , ,

Точное решение имеет вид:
где
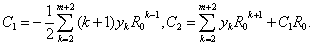
Таблица 1.
Результаты решения задачи 1 при 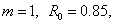 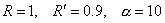
|
(Nr,Nφ)
|
hr
|
hφ
|
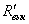
|
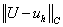
|
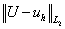
|
|
(10,50)
|
0.105263
|
0.125664
|
0.894737
|
0.00864689
|
0.0080306
|
|
(20,100)
|
0.051282
|
0.062832
|
0.897436
|
0.0013749
|
0.00109687
|
|
(50,250)
|
0.020202
|
0.025133
|
0.89899
|
0.00032447
|
0.00030831
|
|
(100,500)
|
0.010050
|
0.012566
|
0.899497
|
6.08897e-005
|
4.25809e-005
|
Из этой таблицы видно,
что погрешность действительно убывает пропорционально 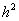 как в равномерной, так
и в интегральной нормах. как в равномерной, так
и в интегральной нормах.
Также представляет
интерес поведение погрешности при уменьшении размеров вспомогательной области.
Из построения метода следует, что его погрешность не должна сильно зависеть от
размеров области.
В таблицах 2 - 4
приведены результаты расчетов при различном выборе вспомогательных областей.
Таблица 2.
Результаты решения задачи 1 при
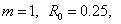 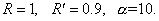
|
(Nr,Nφ)
|
hr
|
hφ
|
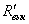
|
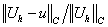
|

|
|
(10,50)
|
0.105263
|
0.125664
|
0.894737
|
0.147042
|
0.212887
|
|
(20,100)
|
0.051282
|
0.062832
|
0.897436
|
0.0206864
|
0.0183026
|
|
(50,250)
|
0.020202
|
0.025133
|
0.89899
|
0.00227075
|
0.00229832
|
|
(100,500)
|
0.010050
|
0.012566
|
0.899497
|
0.000788506
|
0.000658062
|
Таблица 3.
Результаты решения задачи 1 при
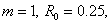 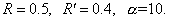
|
(Nr,Nφ)
|
hr
|
hφ
|
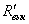
|
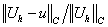
|

|
|
(10,100)
|
0.0526316
|
0.062832
|
0.394737
|
0.0383266
|
0.0383266
|
|
(25,250)
|
0.0204082
|
0.025133
|
0.397959
|
0.00272425
|
0.00165604
|
|
(50,500)
|
0.0101
|
0.012566
|
0.39899
|
0.000664831
|
0.000412263
|
Таблица 4.
Результаты решения задачи 1 при
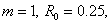 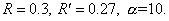
|
(Nr,Nφ)
|
hr
|
hφ
|
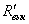
|
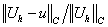
|

|
|
(17,250)
|
0.0181818
|
0.025133
|
0.263636
|
0.00223799
|
0.0017188
|
|
(34,500)
|
0.0089552
|
0.012566
|
0.273134
|
0.000655564
|
0.000615554
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сравнивая значения
погрешностей при одинаковом числе точек сетки по 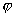 (например, значения в
3-й строке таблицы 2 и 2-й строке таблицы 3), можно убедится в том, что
погрешность метода практически не зависит от размеров вспомогательной области. (например, значения в
3-й строке таблицы 2 и 2-й строке таблицы 3), можно убедится в том, что
погрешность метода практически не зависит от размеров вспомогательной области.
При построении
вспомогательной задачи для функции 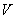 имеется некоторая
свобода в выборе коэффициента имеется некоторая
свобода в выборе коэффициента 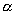 в граничных условиях
3-го рода. Ясно, что решение не должно зависеть от этого параметра, однако его
значение влияет на собственные числа матрицы в граничных условиях
3-го рода. Ясно, что решение не должно зависеть от этого параметра, однако его
значение влияет на собственные числа матрицы 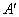 вспомогательной
задачи. При этом с увеличением вспомогательной
задачи. При этом с увеличением 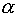 обусловленность
матрицы улучшается. обусловленность
матрицы улучшается.
Это должно приводить к
уменьшению числа итераций, необходимых для решения задачи методом сопряженных
градиентов. Соответствующие результаты приведены в таблице 5: 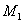 и и 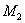 - количество итераций,
затраченных на нахождение функций - количество итераций,
затраченных на нахождение функций 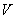 и и  (соответственно)
методом сопряженных градиентов. (соответственно)
методом сопряженных градиентов.
Таблица 5.
Результаты решения задачи 1 при
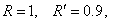 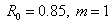 и различных и различных 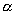 , , 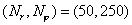 , , 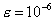 . .
|
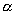
|
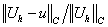
|

|
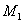
|
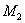
|
|
0.01
|
0.000326599
|
0.00031488
|
5994
|
263
|
|
0.1
|
0.000327565
|
0.000315732
|
5839
|
263
|
|
1
|
0.000324052
|
0.000308127
|
4275
|
0*
|
|
10
|
0.00032524
|
0.000307632
|
2056
|
261
|
|
100
|
0.000322977
|
0.000305613
|
2371
|
292
|
|
1000
|
0.000323876
|
0.000307187
|
705
|
289
|
|
104
|
0.000326066
|
0.000309486
|
690
|
319
|
*при 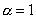 решение 3-й краевой
задачи для V совпадает с точным решение 3-й краевой
задачи для V совпадает с точным
решением исходной задачи в неограниченной
области
Из
таблицы видно, что 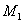 действительно убывает
с увеличением действительно убывает
с увеличением 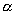 . В данной задаче за счет выбора . В данной задаче за счет выбора 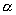 необходимое число итераций удалось снизить
почти на порядок. необходимое число итераций удалось снизить
почти на порядок.
Для сравнения построенных
граничных условий с локальными условиями (0.3), описанными во введении, вида
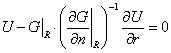
была проведена серия расчетов при 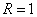 и различном числе
точек сетки. и различном числе
точек сетки.
В этом случае 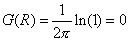 , так что имеют место условия 1-го рода , так что имеют место условия 1-го рода
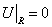 . .
На приведенных ниже
графиках показана зависимость относительной погрешности от числа точек при
использовании граничных условий 3-го рода (пунктирная линия) и при расчете по
построенному алгоритму (сплошная линия). Последняя соответствует данным таблицы
4.
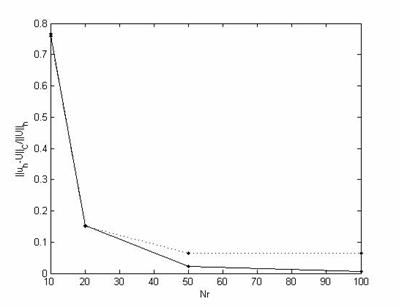
Рис. 4. Зависимость относительной
погрешности от числа точек (в равномерной норме 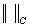 ). ).

Рис. 5. Зависимость относительной
погрешности от числа точек (в интегральной норме  ). ).
Видно, что решение задачи с граничными
условиями первого рода содержит систематическую ошибку, которая не уменьшается
с ростом числа точек.
Тестовая задача 2:
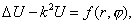
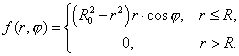
Точное
решение:
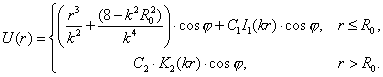
где

Результаты решения этой
задачи при 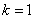 и различном числе точек сетки приведены в
таблице 6. и различном числе точек сетки приведены в
таблице 6.
Таблица 6.
Результаты решения задачи 2 при
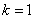 , ,  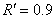 , , 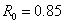 
|
(Nr,Nφ)
|
hr
|
hφ
|
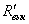
|
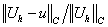
|

|
|
(10,50)
|
0.105263
|
0.125664
|
0.894737
|
0.0143531
|
0.0136375
|
|
(20,100)
|
0.051282
|
0.062832
|
0.897436
|
0.00315890
|
0.00197086
|
|
(50,250)
|
0.020202
|
0.025133
|
0.89899
|
0.000533993
|
0.000509884
|
|
(100,500)
|
0.010050
|
0.012566
|
0.899497
|
0.000120951
|
7.00274e-005
|
Из этой таблицы видно,
что погрешность решения убывает с квадратичной скоростью как в интегральной,
так и в равномерной норме.
В таблицах 7 - 9
приведены результаты расчетов при различном выборе вспомогательных областей.
Таблица 7.
Результаты решения задачи 2 при
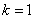 , , 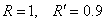 , , 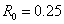 , ,
|
(Nr,Nφ)
|
hr
|
hφ
|
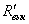
|
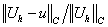
|

|
|
(10,50)
|
0.105263
|
0.125664
|
0.894737
|
0.154048
|
0.169800
|
|
(20,100)
|
0.051282
|
0.062832
|
0.897436
|
0.0363932
|
0.0366361
|
|
(50,250)
|
0.020202
|
0.025133
|
0.89899
|
0.00461905
|
0.00442613
|
|
(100,500)
|
0.010050
|
0.012566
|
0.899497
|
0.00136373
|
0.001336582
|
Таблица 8.
Результаты решения задачи 2 при
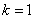 , ,  , , 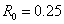 , ,
|
(Nr,Nφ)
|
hr
|
hφ
|
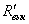
|
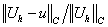
|

|
|
(10,100)
|
0.0526316
|
0.062832
|
0.394737
|
0.0256204
|
0.0211052
|
|
(25,250)
|
0.0204082
|
0.025133
|
0.397959
|
0.00321061
|
0.0020671
|
|
(50,500)
|
0.0101
|
0.012566
|
0.39899
|
0.00084187
|
0.000606913
|
Таблица 9. Результаты
решения задачи 2 при
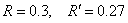 , , 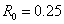 , ,
|
(Nr,Nφ)
|
hr
|
hφ
|
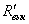
|
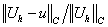
|

|
|
(17,250)
|
0.0181818
|
0.025133
|
0.263636
|
0.00294396
|
0.00244587
|
|
(34,500)
|
0.0089552
|
0.012566
|
0.273134
|
0.000860839
|
0.000758193
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из этих таблиц видно, что
при сгущении сетки погрешность убывает пропорционально 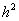 и практически не
зависит от размеров вспомогательной области. и практически не
зависит от размеров вспомогательной области.
В следующих двух таблицах
(табл. 10 и 11) приведены результаты решения этой же задачи со значениями
коэффициента 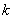 , отличными от единицы. Из них видно, что и при таких
значениях коэффициента метод имеет квадратичный порядок точности. , отличными от единицы. Из них видно, что и при таких
значениях коэффициента метод имеет квадратичный порядок точности.
Таблица 10.
Результаты решения задачи 2
при 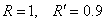 , ,  , , 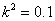
|
(Nr,Nφ)
|
hr
|
hφ
|
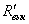
|
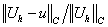
|

|
|
(10,50)
|
0.105263
|
0.125664
|
0.894737
|
0.0144415
|
0.0136045
|
|
(20,100)
|
0.051282
|
0.062832
|
0.897436
|
0.00332
|
0.00213348
|
|
(50,250)
|
0.020202
|
0.025133
|
0.89899
|
0.00054033
|
0.000510689
|
|
(100,500)
|
0.010050
|
0.012566
|
0.899497
|
0.000127227
|
7.69336e-005
|
Таблица 11.
Результаты решения задачи 2
при 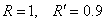 , , , , 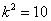
|
(Nr,Nφ)
|
hr
|
hφ
|
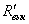
|
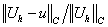
|

|
|
(10,50)
|
0.105263
|
0.125664
|
0.894737
|
0.0127693
|
0.0125663
|
|
(20,100)
|
0.051282
|
0.062832
|
0.897436
|
0.00349497
|
0.00211311
|
|
(50,250)
|
0.020202
|
0.025133
|
0.89899
|
0.000469108
|
0.000458505
|
|
(100,500)
|
0.010050
|
0.012566
|
0.899497
|
0.000133479
|
7.3982e-005
|
Тестовая задача 3:
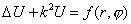 , ,
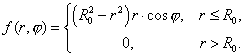
Точное решение:
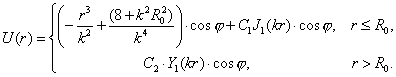
где
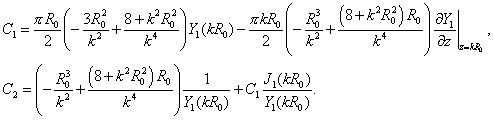
Результаты
решения этой задачи приведены в таблице 12.
Таблица 12. Результаты решения задачи 5
при 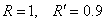 , ,  , , 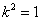
|
(Nr,Nφ)
|
hr
|
hφ
|
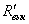
|
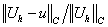
|

|
|
(10,50)
|
0.105263
|
0.125664
|
0.894737
|
0.0142418
|
0.0133602
|
|
(20,100)
|
0.051282
|
0.062832
|
0.897436
|
0.00326799
|
0.00217309
|
|
(50,250)
|
0.020202
|
0.025133
|
0.89899
|
0.000536064
|
0.000504426
|
|
(100,500)
|
0.010050
|
0.012566
|
0.899497
|
0.000127264
|
8.07959e-005
|
При данном значении
коэффициента 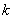 решение
вспомогательных задач существует и единственно, так что проблем с применением
описанного метода не возникло. Результаты расчетов (табл. 12) показали, что в
этом случае метод работает и его погрешность убывает пропорционально решение
вспомогательных задач существует и единственно, так что проблем с применением
описанного метода не возникло. Результаты расчетов (табл. 12) показали, что в
этом случае метод работает и его погрешность убывает пропорционально 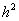 . .
Тестовая задача 4:
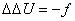 , ,
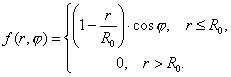
Точное решение:
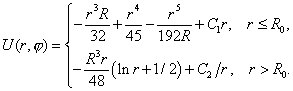
где
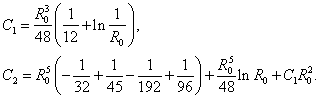
Результаты решения этой задачи приведены в таблице 13.
Таблица 13.
Результаты решения задачи 4 при
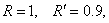 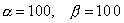
|
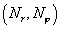
|
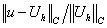
|
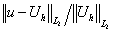
|
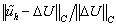
|

|
|
(10,50)
|
0.00764829
|
0.00692964
|
0.0574866
|
0.0505767
|
|
(20,100)
|
0.00150599
|
0.00104931
|
0.0102951
|
0.00707112
|
|
(50,250)
|
0.000284844
|
0.00026261
|
0.00211738
|
0.00190325
|
|
(100,500)
|
5.81778e-005
|
3.909e-005
|
0.000400304
|
0.000265356
|
Из этой таблицы видно, что погрешность как
самой функции, так и ее лапласиана убывает со сгущением сетки пропорционально 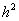 . .
Заключение
В работе построен метод решения
линейных эллиптических уравнений, заданных в неограниченной области. Метод
применен для решения уравнений второго порядка с постоянными коэффициентами
(уравнений Лапласа, Гельмгольца, уравнения с поглощением) и бигармонического
уравнения. Получены оценки погрешности, показывающие, что метод имеет второй
порядок точности. Эти оценки подтверждаются результатами проведенных тестовых
расчетов.
Количество
операций, необходимое для реализации метода, оценивается величиной 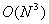 в двумерном случае, а
в трехмерном - в двумерном случае, а
в трехмерном - 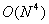 действий. Это по
порядку величины не превышает количества операций, затрачиваемого на решение
краевой задачи в ограниченной области. действий. Это по
порядку величины не превышает количества операций, затрачиваемого на решение
краевой задачи в ограниченной области.
К
недостаткам метода можно отнести тот факт, что для его реализации необходимо
знать явный вид функции 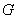 - фундаментального
решения. Это ограничивает применимость метода в случае уравнений с переменными
коэффициентами. - фундаментального
решения. Это ограничивает применимость метода в случае уравнений с переменными
коэффициентами.
Литература
1. S.V. Tsynkov. Numerical solution
of problems on unbounded domains. A review // Appl. Math. – 1998. – V. 27. – P.
465 - 532.
2.
В.С. Рябенький. Метод разностных потенциалов и его приложения. М., Физматлит.
2002. 496 с.
3.
А.Н. Тихонов, А.А. Самарский. Уравнения математической физики. - М.: Наука.
Физматлит. 1972. 736 с.
4. А.А. Самарский, Е.C. Николаев. Методы решения сеточных
уравнений. -М.: Наука. 1978. 592 с.
5. В.П. Ильин. Методы неполной факторизации для
решения алгебраических систем. М., Наука, Физматлит. 1995. 288 с.
6. А.А. Самарский. Теория разностных схем. - М.:
Наука. Физматлит. 1989. 616 с.
7. К. Чен, П. Джиблин, А. Ирвинг. MATLAB в математических исследованиях.
М., Мир. 2001. 346
с.
|
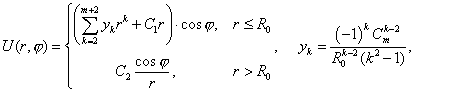
![]()
![]()
![]()
![]() как в равномерной, так
и в интегральной нормах.
как в равномерной, так
и в интегральной нормах.![]()
![]()
![]()
![]()
![]()
![]()
![]() (например, значения в
3-й строке таблицы 2 и 2-й строке таблицы 3), можно убедится в том, что
погрешность метода практически не зависит от размеров вспомогательной области.
(например, значения в
3-й строке таблицы 2 и 2-й строке таблицы 3), можно убедится в том, что
погрешность метода практически не зависит от размеров вспомогательной области. ![]() имеется некоторая
свобода в выборе коэффициента
имеется некоторая
свобода в выборе коэффициента ![]() в граничных условиях
3-го рода. Ясно, что решение не должно зависеть от этого параметра, однако его
значение влияет на собственные числа матрицы
в граничных условиях
3-го рода. Ясно, что решение не должно зависеть от этого параметра, однако его
значение влияет на собственные числа матрицы ![]() вспомогательной
задачи. При этом с увеличением
вспомогательной
задачи. При этом с увеличением ![]() обусловленность
матрицы улучшается.
обусловленность
матрицы улучшается.![]() и
и ![]() - количество итераций,
затраченных на нахождение функций
- количество итераций,
затраченных на нахождение функций ![]() и
и ![]() (соответственно)
методом сопряженных градиентов.
(соответственно)
методом сопряженных градиентов.![]()
![]() и различных
и различных ![]() ,
, ![]() ,
, ![]() .
.![]() решение 3-й краевой
задачи для V совпадает с точным
решение 3-й краевой
задачи для V совпадает с точным![]() действительно убывает
с увеличением
действительно убывает
с увеличением ![]() . В данной задаче за счет выбора
. В данной задаче за счет выбора ![]() необходимое число итераций удалось снизить
почти на порядок.
необходимое число итераций удалось снизить
почти на порядок.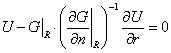
![]() и различном числе
точек сетки.
и различном числе
точек сетки.![]() , так что имеют место условия 1-го рода
, так что имеют место условия 1-го рода ![]() .
.
![]() ).
).
![]() ).
).![]()
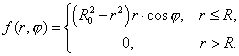
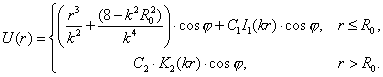

![]() и различном числе точек сетки приведены в
таблице 6.
и различном числе точек сетки приведены в
таблице 6.![]() ,
, ![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]() ,
, ![]() ,
,![]()
![]() ,
, ![]() ,
, ![]() ,
,![]()
![]() ,
, ![]() ,
,![]()
![]() и практически не
зависит от размеров вспомогательной области.
и практически не
зависит от размеров вспомогательной области. ![]() , отличными от единицы. Из них видно, что и при таких
значениях коэффициента метод имеет квадратичный порядок точности.
, отличными от единицы. Из них видно, что и при таких
значениях коэффициента метод имеет квадратичный порядок точности.![]() ,
, ![]() ,
, ![]()
![]() ,
,![]() ,
, ![]()
![]() ,
,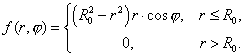
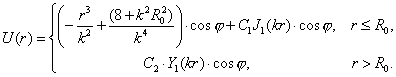
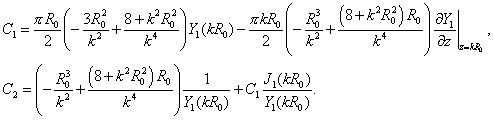
![]() ,
, ![]() ,
, ![]()
![]() решение
вспомогательных задач существует и единственно, так что проблем с применением
описанного метода не возникло. Результаты расчетов (табл. 12) показали, что в
этом случае метод работает и его погрешность убывает пропорционально
решение
вспомогательных задач существует и единственно, так что проблем с применением
описанного метода не возникло. Результаты расчетов (табл. 12) показали, что в
этом случае метод работает и его погрешность убывает пропорционально ![]() .
.![]() ,
,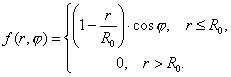
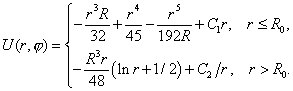
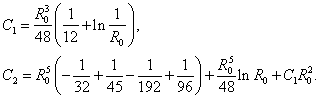
![]()
![]()
![]() .
.![]() в двумерном случае, а
в трехмерном -
в двумерном случае, а
в трехмерном - ![]() действий. Это по
порядку величины не превышает количества операций, затрачиваемого на решение
краевой задачи в ограниченной области.
действий. Это по
порядку величины не превышает количества операций, затрачиваемого на решение
краевой задачи в ограниченной области.![]() - фундаментального
решения. Это ограничивает применимость метода в случае уравнений с переменными
коэффициентами.
- фундаментального
решения. Это ограничивает применимость метода в случае уравнений с переменными
коэффициентами.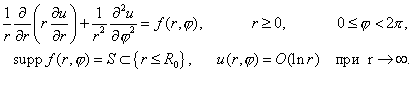
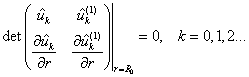
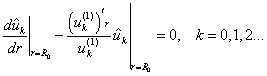
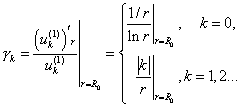
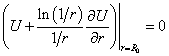 .
.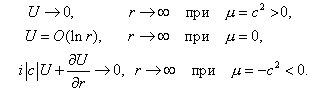
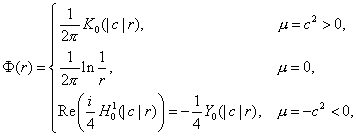

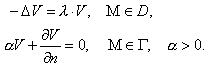
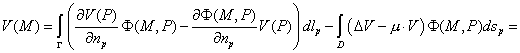

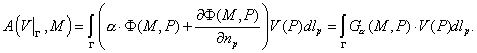
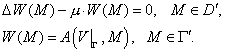

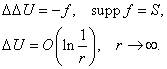
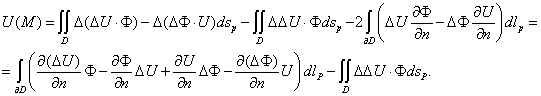
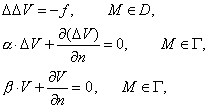
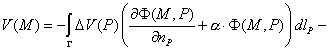
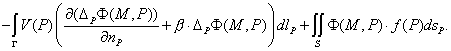
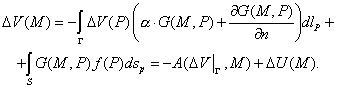
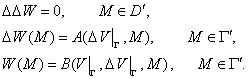
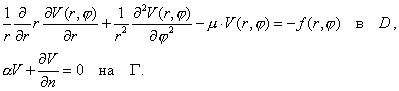
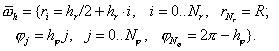
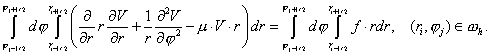
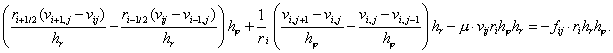

 .
.
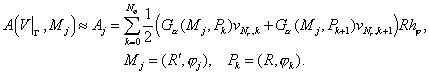

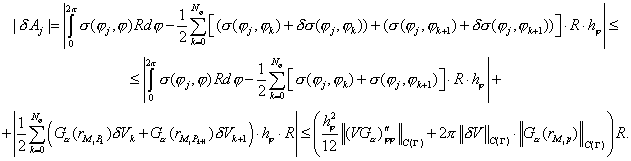
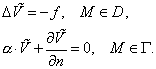
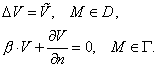
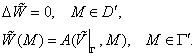
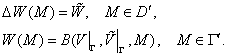
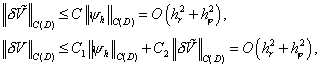
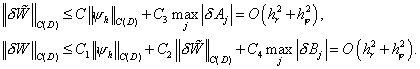
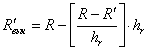 - значение радиуса, использованное при вычислениях (см. рис.
3),
- значение радиуса, использованное при вычислениях (см. рис.
3), 