Аннотация
Работа посвящена тестированию разрывного метода Галеркина для численного решения квазилинейного
уравнения переноса, а также его сравнению с другими известными схемами. Сравнение проводилось
между различными вариантами разрывного метода Галеркина, а также со схемами, рассмотренными
в [2]. Приведенная информация об ошибках численного решения позволяет сравнить качество
различных схем. Сравнительный анализ ошибок численного решения показал, что рассмотренный
метод дает более высокую точность в широком диапазоне изменения чисел Куранта, а также
меньшее “размазывание” разрывов решений.
Abstract
The paper is dedicated to the testing of discontinuous Galerkin method for numerical solution
of quasi - linear advection equation, as well as its comparison with other well - known schemes.
The comparison was carried out between different variants of the discontinuous Galerkin method
and schemes considered in [2]. The presented information about the errors of numerical
solutions allows to compare the quality of the schemes. Analysis of the errors has shown
that the studied method gives higher accuracy in the broad range of Courant numbers,
as well as smaller "spreading" of shock solutions.
Содержание
Введение ………………………………………………………… 3
§ 1. Постановка задачи …………………………………………. 3
§ 2. Разрывный метод Галеркина
(RKDG – Runge-Kutta discontinuous Galerkin method)
……….. 6
§ 3. Организация вычислительного эксперимента …………… 11
§ 4. Результаты численного исследования ……………………. 12
§ 5. Сравнение
схем ……………………………………….. 27
Заключение …………………………………………………….... 34
Литература ………………………………………………………. 35
Введение
В данной работе проведено тестирование разрывного метода Галеркина [1]
для численного решения квазилинейного уравнения переноса, а также выполнен
сравнительный анализ различных вариантов этого метода и методов, использованных
в [2]. Целью данной работы является продолжение исследований, проведенных в
[2, 3, 4, 5].
Решения получены для финитных начальных условий и различных чисел Куранта
на пространственно-временном прямоугольнике достаточно больших размеров. Для
определения ошибок численных решений использованы конечномерные аналоги норм
пространств C, L1, L2. В работе
представлены графики с точными и численными решениями для некоторых моментов
времени, а также таблицы ошибок для конечного момента времени и для всего
временного промежутка. Такой способ представления результатов позволяет
качественно и количественно оценивать характеристики схем.
Работа выполнена при частичной поддержке Российского фонда фундаментальных
исследований (проект № 03-01-00461).
§ 1. Постановка задачи
Будем рассматривать задачу Коши для квазилинейного уравнения
переноса
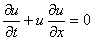 , , 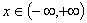 , , 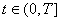 (1.1) (1.1)
с финитными
начальными условиями u(x,0)= u0(x) вида:
1. 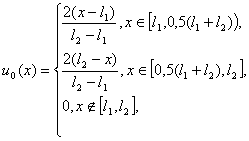 “треугольник”, “треугольник”,
2. 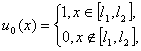 “прямоугольник”, “прямоугольник”,
3. 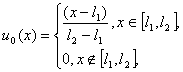 “левый
треугольник”, “левый
треугольник”,
4.  “правый треугольник”, “правый треугольник”,
5. 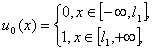 “ступенька
вверх”, “ступенька
вверх”,
6. 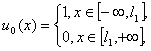 “ступенька
вниз”. “ступенька
вниз”.
Приведем точные решения
задачи (1.1) для указанных выше начальных условий:
1.
“треугольник”:
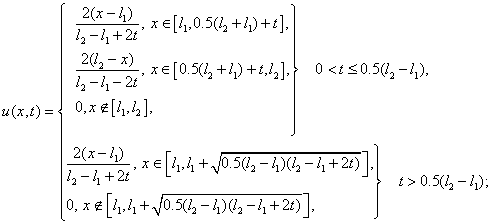
2.
“прямоугольник”:
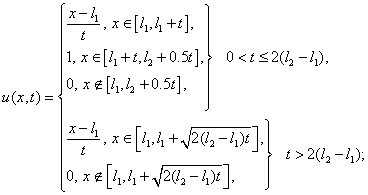
3.
“левый
треугольник”:
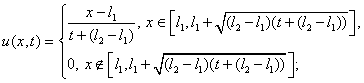
4.
“правый
треугольник”:
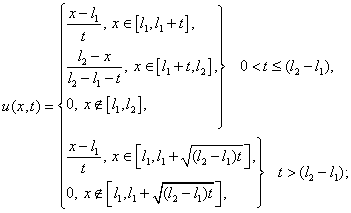
5.
“ступенька
вверх”:
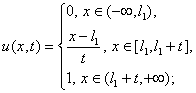
6.
“ступенька
вниз”:
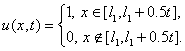
Сравнение численного решения с точным будем проводить с использованием
конечномерных аналогов норм в пространствах C, L1, L2 на W=(-¥,+¥)´[0,T]:
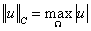 , , 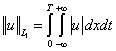 , , 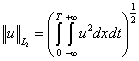 ; ;
и на R=(-¥,+¥)
при t=ti :
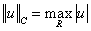 , , 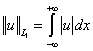 , , 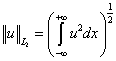 . .
§
2. Разрывный метод Галеркина
(RKDG – Runge-Kutta discontinuous Galerkin
method)
Рассмотрим применение RKDG
- метода на примере поставленной задачи (1.1), записав ее в дивергентном виде:
 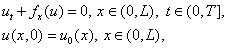 (2.1) (2.1)
где 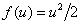 . .
На 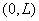 введем равномерную
сетку с узлами введем равномерную
сетку с узлами 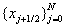 , обозначим , обозначим 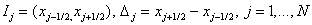 . .
Умножим уравнения (2.1) на произвольную гладкую функцию 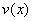 и проинтегрируем это
произведение по и проинтегрируем это
произведение по 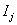 . После интегрирования по частям получим: . После интегрирования по частям получим:
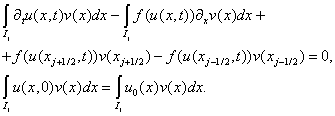 (2.2) (2.2)
Для каждого момента времени 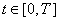 будем искать
приближенное решение будем искать
приближенное решение 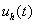 как элемент
конечномерного пространства как элемент
конечномерного пространства
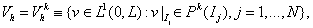
где 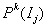 – пространство
полиномов степени не выше – пространство
полиномов степени не выше 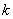 на на 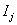 . .
Заменим гладкую функцию 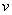 произвольной пробной
функцией, принадлежащей пространству произвольной пробной
функцией, принадлежащей пространству  , а точное решение , а точное решение 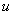 – приближенным
решением – приближенным
решением 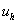 . Функция . Функция 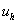 разрывна в точках разрывна в точках 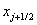 , поэтому необходимо заменить поток , поэтому необходимо заменить поток 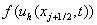 численным
потоком численным
потоком  , зависящим от предельных значений функции , зависящим от предельных значений функции 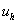 слева и справа от
точки слева и справа от
точки 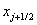 , т.е. , т.е.
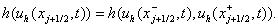
Тогда уравнения
(2.2) принимают следующий вид:
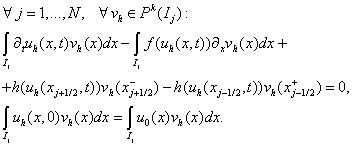 (2.3) (2.3)
Численный поток  должен быть монотонным
и согласованным с физическим потоком должен быть монотонным
и согласованным с физическим потоком 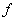 , т.е.: , т.е.:
1. 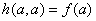 , ,
2. 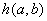 – неубывающая
функция по – неубывающая
функция по 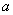 , ,
3. 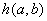 –
невозрастающая функция по –
невозрастающая функция по 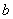 . .
Численные потоки могут быть выбраны различными
способами, широко распространенными являются следующие [6]:
1. поток Годунова:
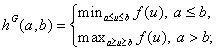
2. поток Энгквиста-Ошера:
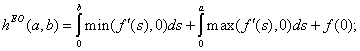
3. поток Лакса-Фридрихса:

4. «локальный»
поток Лакса-Фридрихса:
 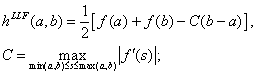
5. поток Роу:
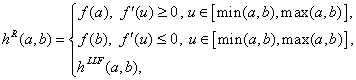
На следующем этапе необходимо выбрать на каждом интервале 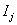 систему базисных
функций. Для этого удобно использовать ортогональную систему функций, например,
полиномы Лежандра. Использование ортогональных базисных функций позволяет
получить диагональную матрицу масс и, следовательно, явную схему. систему базисных
функций. Для этого удобно использовать ортогональную систему функций, например,
полиномы Лежандра. Использование ортогональных базисных функций позволяет
получить диагональную матрицу масс и, следовательно, явную схему.
Пусть 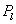 - полином Лежандра
степени - полином Лежандра
степени 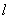 . .
Для 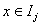 приближенное решение приближенное решение 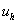 будем искать в виде: будем искать в виде:
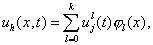
где  . .
Учитывая равенства
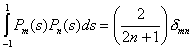 , , 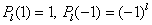 , ,
получаем
следующую форму уравнений (2.3):
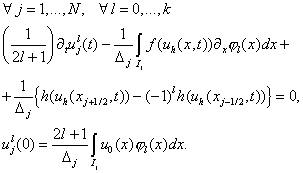 (2.4) (2.4)
Таким образом, задача нахождения приближенного решения 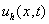 сводится к задаче
решения системы обыкновенных дифференциальных уравнений относительно сводится к задаче
решения системы обыкновенных дифференциальных уравнений относительно 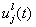 . Запишем систему (2.4) в виде: . Запишем систему (2.4) в виде:
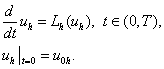
Пусть 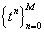 – разбиение отрезка – разбиение отрезка 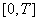 , , 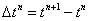 . Для решения системы дифференциальных уравнений используется
явный метод Рунге-Кутты порядка . Для решения системы дифференциальных уравнений используется
явный метод Рунге-Кутты порядка 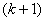 , который записывается следующим образом: , который записывается следующим образом:
1.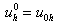 ; ;
2. 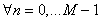 ; ;
1) 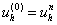 ; ;
2) 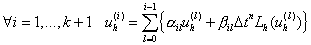 ; ;
3) 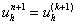 . .
Коэффициенты 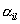 должны выбираться
таким образом, чтобы выполнялись условия: должны выбираться
таким образом, чтобы выполнялись условия:
 . .
Для обеспечения монотонности получаемой схемы необходимо на каждом
промежуточном этапе метода Рунге-Кутты применять специальные монотонизаторы
(лимитеры).
Обозначим через 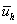 среднее значение
приближенного решения на интервале среднее значение
приближенного решения на интервале 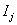 . «Идеальным» [1] является лимитер . «Идеальным» [1] является лимитер 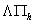 , удовлетворяющий следующим требованиям. , удовлетворяющий следующим требованиям.
1. Лимитер не может изменять «массу», содержащуюся в каждом интервале,
т.е. если 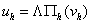 , то , то 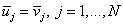 . .
2. Если 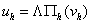 , , 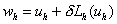 , то для достаточно малого параметра , то для достаточно малого параметра 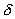 должно выполняться
неравенство: должно выполняться
неравенство: 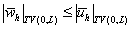 , где , где 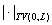 – полная вариация
функции на интервале (0,L). – полная вариация
функции на интервале (0,L).
3. Лимитер не должен снижать точность метода.
Однако невозможно построить такой «идеальный» лимитер, т.к. при попытке
обеспечить свойство TVDM
(total
variation diminishing in the means)
теряется точность в локальных экстремумах решения. Избежать этого можно с помощью TVBM (total variation bounded in the means) лимитеров. При этом условие TVBM является более слабым,
чем TVDM.
TVDM свойство RKDG метода означает
выполнение неравенства
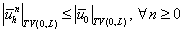 , ,
а TVBM свойство – выполнение
неравенства
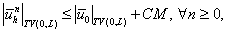
где 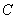 зависит только от зависит только от 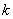 . .
Приведем примеры TVDM
лимитеров.
Определим функцию
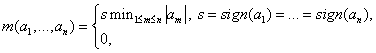
1. MUSCL лимитер (monotonic upstream-centered scheme
for conservation laws).
В случае кусочно-линейной аппроксимации решения, т.е.

имеем

2. «Менее строгий» лимитер  . .
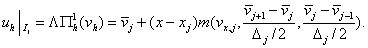
Отметим, что 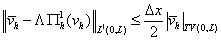 . .
3. Лимитер 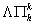 . .
В случае кусочно-полиномиальной аппроксимации решения, т.е.
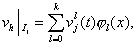
лимитер
вычисляется следующим образом.
Обозначим 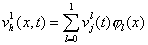 . .
Для 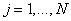
·
Вычисляем
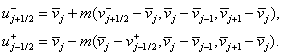
·
Если 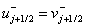 и и 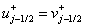 , то полагаем , то полагаем 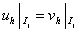 . .
·
Если нет, то полагаем 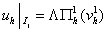 . .
4. Лимитер 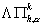 . .
Модифицированный
лимитер 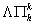 , в котором , в котором
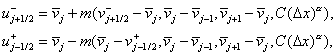
где 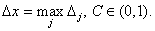
Данный лимитер применяется только в теоретических исследованиях.
Если вместо функции 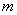 использовать функцию использовать функцию 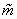 : :
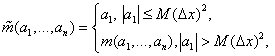
где 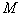 – заданная константа,
то получим TVBM
лимитеры. – заданная константа,
то получим TVBM
лимитеры.
Справедлив следующий результат [1].
Теорема. Пусть в RKDG методе используется TVDM или TVBM лимитер. Пусть все
коэффициенты 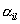 неотрицательны и
удовлетворяют следующему условию: неотрицательны и
удовлетворяют следующему условию:
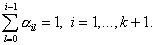
Тогда существует подпоследовательность 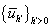 последовательности последовательности 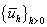 , порожденной RKDG
методом, которая сходится в , порожденной RKDG
методом, которая сходится в 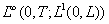 к обобщенному решению
задачи (2.1). к обобщенному решению
задачи (2.1).
Если к тому же используется TVBM лимитер 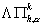 , то обобщенное решение является энтропийным решением, и вся
последовательность сходится. , то обобщенное решение является энтропийным решением, и вся
последовательность сходится.
Наконец, если используемый лимитер 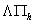 удовлетворяет условию удовлетворяет условию
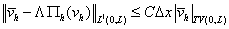 , ,
то результаты справедливы
не только для последовательности средних значений 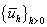 , но и для последовательности функций , но и для последовательности функций 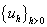 . .
§ 3. Организация вычислительного эксперимента
Аналогично работе [2] численное решение поставленной задачи (1.1) получено
для всех указанных форм начальных профилей при следующих значениях параметров: L=520, l1=0, l2=20, T=1000. Шаги по 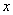 и и 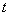 выбирались постоянными: выбирались постоянными:
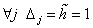 , , 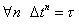 . .
Число Куранта g (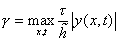 ) ограничено сверху величиной gm, которая
принимала значения: 0.1, 0.25, 0.5, 0.9. Таким образом, временной шаг t
принимал те же значения, что и число Куранта. Для определения точности полученного
при этом решения вычислялись относительные ошибки с использованием норм ) ограничено сверху величиной gm, которая
принимала значения: 0.1, 0.25, 0.5, 0.9. Таким образом, временной шаг t
принимал те же значения, что и число Куранта. Для определения точности полученного
при этом решения вычислялись относительные ошибки с использованием норм
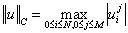 , , 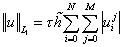 , , 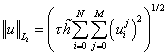
интегрально по временному
промежутку 0 £
t £
T, а также
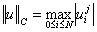 , , 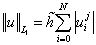 , , 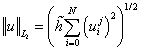
локально для
момента времени tj.
В данной работе тестировался RKDG метод для
кусочно-линейной и кусочно-квадратичной аппроксимаций (т.е. для 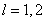 ). ).
Для проведения численного эксперимента создана программа для персонального
компьютера, реализующая алгоритмы поиска решения по указанным разностным
схемам. На экран монитора выводится графическое изображение точного и
численного решений для каждого временного слоя, а также относительные ошибки
вычислений для нескольких промежуточных и конечного моментов времени. Такое
представление результатов позволяет визуально и численно оценить качество
полученного решения и тем самым сравнить используемые схемы.
§ 4. Результаты численного исследования
Полученные в численном эксперименте результаты представлены следующим
образом. Для каждой схемы, используемой для получения численного решения,
приведены таблицы интегральных и локальных по времени ошибок для различных
чисел Куранта. В каждой таблице указаны относительные ошибки вычислений для
всех начальных условий и используемых норм, соответствующее число Куранта
приведено в левом верхнем углу таблицы.
С целью иллюстрации всех
особенностей поведения решения для каждого из начальных профилей представлены
графики решения для нескольких промежуточных моментов времени. При этом каждый
рисунок содержит графики точного решения и численного решения для числа Куранта
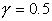 . .
1. Кусочно-линейная
аппроксимация
а) с использованием TVDM лимитера  . .
Таблицы
ошибок (локально при t = T)
|
γ
= 0.1
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6310
|
0.4022
|
0.6216
|
0.6305
|
0.0003
|
0.2252
|
|
L1
|
0.0044
|
0.0043
|
0.0046
|
0.0075
|
0.0006
|
0.0005
|
|
L2
|
0.0423
|
0.0315
|
0.0487
|
0.0551
|
0.0005
|
0.0086
|
|
γ
= 0.25
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6311
|
0.4105
|
0.6214
|
0.6329
|
0.0004
|
0.2331
|
|
L1
|
0.0044
|
0.0044
|
0.0046
|
0.0075
|
0.0006
|
0.0005
|
|
L2
|
0.0423
|
0.0321
|
0.0487
|
0.0553
|
0.0005
|
0.0089
|
|
γ
= 0.5
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6315
|
0.4351
|
0.6209
|
0.6438
|
0.0004
|
0.2657
|
|
L1
|
0.0044
|
0.0047
|
0.0047
|
0.0077
|
0.0007
|
0.0006
|
|
L2
|
0.0423
|
0.0338
|
0.0487
|
0.0563
|
0.0006
|
0.0099
|
|
γ
= 0.9
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6326
|
0.5311
|
0.6191
|
0.6998
|
0.0013
|
0.4211
|
|
L1
|
0.0044
|
0.0058
|
0.0047
|
0.0090
|
0.0010
|
0.0009
|
|
L2
|
0.0424
|
0.0409
|
0.0487
|
0.0616
|
0.0009
|
0.0145
|
Таблицы
ошибок (интегрально по t)
|
γ
= 0.1
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6257
|
0.8200
|
0.7412
|
0.7039
|
0.3967
|
0.8200
|
|
L1
|
0.0081
|
0.0086
|
0.0080
|
0.0129
|
0.0005
|
0.0012
|
|
L2
|
0.0668
|
0.0598
|
0.0674
|
0.0737
|
0.0012
|
0.0192
|
|
γ
= 0.25
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.5998
|
0.7750
|
0.7816
|
0.6755
|
0.3750
|
0.7750
|
|
L1
|
0.0081
|
0.0088
|
0.0080
|
0.0130
|
0.0005
|
0.0012
|
|
L2
|
0.0669
|
0.0604
|
0.0675
|
0.0737
|
0.0012
|
0.0196
|
|
γ
= 0.5
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.5485
|
0.6116
|
0.6136
|
0.6221
|
0.4000
|
0.6000
|
|
L1
|
0.0082
|
0.0093
|
0.0080
|
0.0133
|
0.0006
|
0.0013
|
|
L2
|
0.0674
|
0.0616
|
0.0679
|
0.0742
|
0.0014
|
0.0197
|
|
γ
= 0.9
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.5718
|
0.7301
|
0.5317
|
0.5809
|
0.4098
|
0.7417
|
|
L1
|
0.0087
|
0.0113
|
0.0083
|
0.0160
|
0.0009
|
0.0017
|
|
L2
|
0.0696
|
0.0683
|
0.0694
|
0.0824
|
0.0021
|
0.0228
|
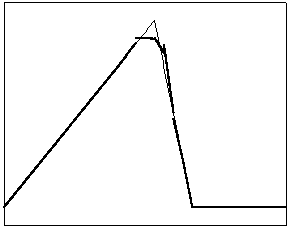 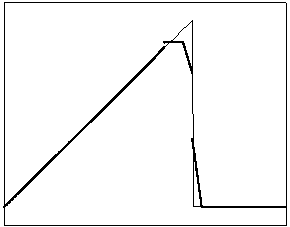
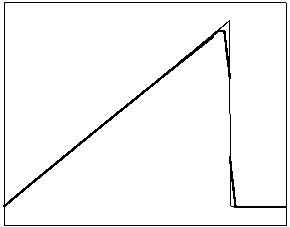
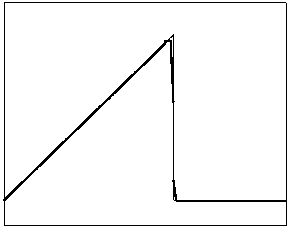
t=6
t=10
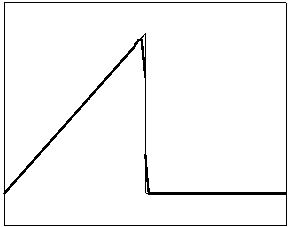 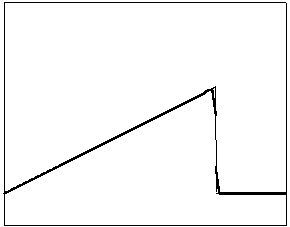
t=70
t=170
Рис. 4.1.1 Численное решение для “треугольника” (g = 0.5)
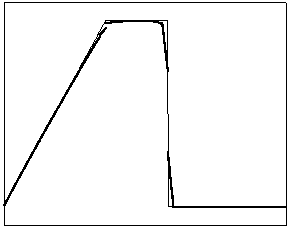 
t=18
t=40
t=90
t=160
Рис. 4.1.2 Численное решение для “прямоугольника” (g = 0.5)
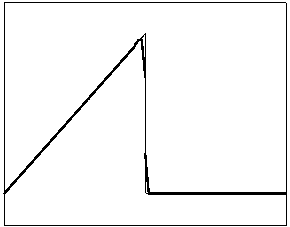 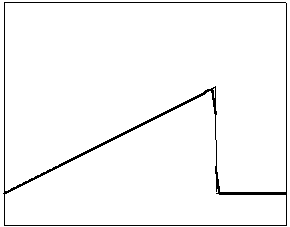
t=60
t=160
Рис. 4.1.3 Численное решение для “левого треугольника” (g = 0.5)
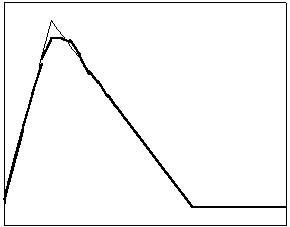 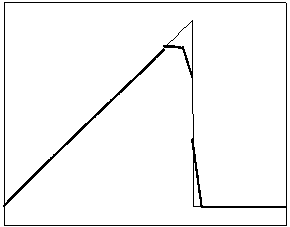
t=5 t=20
Рис. 4.1.4 Численное решение для “правого треугольника” (g = 0.5)
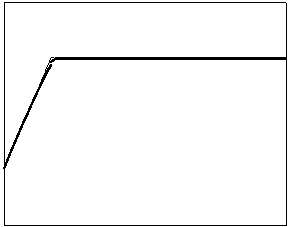 
t=10 t=40
Рис. 4.1.5 Численное решение для “ступеньки вверх” (g = 0.5)
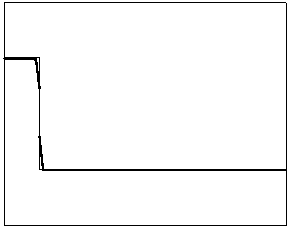 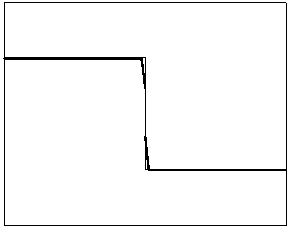
t=20
t=80
Рис. 4.1.6 Численное решение для “ступеньки вниз” (g = 0.5)
б) с использованием MUSCL лимитера.
Таблицы
ошибок (локально при t = T)
|
γ
= 0.1
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6819
|
0.5061
|
0.6496
|
0.7505
|
0.0008
|
0.2553
|
|
L1
|
0.0072
|
0.0077
|
0.0072
|
0.0125
|
0.0012
|
0.0007
|
|
L2
|
0.0487
|
0.0465
|
0.0547
|
0.0727
|
0.0011
|
0.0113
|
|
γ
= 0.25
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6813
|
0.5075
|
0.6496
|
0.7510
|
0.0008
|
0.2598
|
|
L1
|
0.0072
|
0.0077
|
0.0072
|
0.0125
|
0.0012
|
0.0007
|
|
L2
|
0.0487
|
0.0466
|
0.0547
|
0.0728
|
0.0011
|
0.0114
|
|
γ
= 0.5
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6805
|
0.5123
|
0.6493
|
0.7531
|
0.0008
|
0.2769
|
|
L1
|
0.0072
|
0.0078
|
0.0072
|
0.0126
|
0.0013
|
0.0008
|
|
L2
|
0.0487
|
0.0471
|
0.0547
|
0.0730
|
0.0011
|
0.0120
|
|
γ
= 0.9
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6796
|
0.5339
|
0.6485
|
0.7623
|
0.0008
|
0.3197
|
|
L1
|
0.0072
|
0.0081
|
0.0072
|
0.0129
|
0.0013
|
0.0009
|
|
L2
|
0.0487
|
0.0490
|
0.0547
|
0.0740
|
0.0011
|
0.0132
|
Таблицы
ошибок (интегрально по t)
|
γ
= 0.1
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6389
|
0.8602
|
0.7992
|
0.7508
|
0.5042
|
0.8602
|
|
L1
|
0.0131
|
0.0145
|
0.0121
|
0.0216
|
0.0011
|
0.0017
|
|
L2
|
0.0803
|
0.0784
|
0.0805
|
0.0991
|
0.0027
|
0.0234
|
|
γ
= 0.25
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6244
|
0.8254
|
0.8306
|
0.7367
|
0.5028
|
0.8254
|
|
L1
|
0.0131
|
0.0145
|
0.0121
|
0.0216
|
0.0011
|
0.0018
|
|
L2
|
0.0803
|
0.0783
|
0.0806
|
0.0989
|
0.0027
|
0.0234
|
|
γ
= 0.5
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6058
|
0.7321
|
0.6892
|
0.7062
|
0.5027
|
0.6781
|
|
L1
|
0.0131
|
0.0147
|
0.0121
|
0.0217
|
0.0011
|
0.0018
|
|
L2
|
0.0806
|
0.0786
|
0.0808
|
0.0987
|
0.0026
|
0.0235
|
|
γ
= 0.9
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6088
|
0.7204
|
0.5852
|
0.6429
|
0.4208
|
0.7526
|
|
L1
|
0.0132
|
0.0153
|
0.0123
|
0.0223
|
0.0011
|
0.0021
|
|
L2
|
0.0817
|
0.0801
|
0.0817
|
0.0994
|
0.0024
|
0.0250
|
2. Кусочно-квадратичная
аппроксимация
а) с использованием TVDM - лимитера 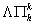 . .
Таблицы
ошибок (локально при t = T)
|
γ = 0.1
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.5651
|
0.3603
|
0.5633
|
0.7421
|
0.0006
|
0.2750
|
|
L1
|
0.0042
|
0.0038
|
0.0055
|
0.0071
|
0.0008
|
0.0004
|
|
L2
|
0.0380
|
0.0282
|
0.0510
|
0.0565
|
0.0007
|
0.0083
|
|
γ
= 0.25
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6027
|
0.3807
|
0.5659
|
0.7167
|
0.0004
|
0.2475
|
|
L1
|
0.0048
|
0.0042
|
0.0054
|
0.0071
|
0.0006
|
0.0005
|
|
L2
|
0.0439
|
0.0327
|
0.0509
|
0.0551
|
0.0005
|
0.0095
|
|
γ
= 0.5
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.5144
|
0.3644
|
0.5736
|
0.5290
|
0.0022
|
0.2380
|
|
L1
|
0.0045
|
0.0040
|
0.0053
|
0.0057
|
0.0007
|
0.0005
|
|
L2
|
0.0392
|
0.0317
|
0.0503
|
0.0479
|
0.0007
|
0.0091
|
|
γ
= 0.9
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6139
|
0.4062
|
0.5792
|
0.6974
|
0.0039
|
0.2943
|
|
L1
|
0.0047
|
0.0045
|
0.0052
|
0.0075
|
0.0021
|
0.0005
|
|
L2
|
0.0436
|
0.0336
|
0.0501
|
0.0549
|
0.0023
|
0.0095
|
Таблицы
ошибок (интегрально по t)
|
γ
= 0.1
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6606
|
0.8201
|
0.7429
|
0.7347
|
0.3661
|
0.9000
|
|
L1
|
0.0089
|
0.0099
|
0.0086
|
0.0145
|
0.0008
|
0.0013
|
|
L2
|
0.0683
|
0.0663
|
0.0683
|
0.0856
|
0.0020
|
0.0193
|
|
γ
= 0.25
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6324
|
0.7750
|
0.7849
|
0.7641
|
0.3750
|
0.7750
|
|
L1
|
0.0089
|
0.0090
|
0.0087
|
0.0144
|
0.0006
|
0.0012
|
|
L2
|
0.0675
|
0.0625
|
0.0680
|
0.0838
|
0.0016
|
0.0190
|
|
γ
= 0.5
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6048
|
0.7505
|
0.6186
|
0.7026
|
0.4396
|
0.6823
|
|
L1
|
0.0088
|
0.0091
|
0.0086
|
0.0122
|
0.0011
|
0.0012
|
|
L2
|
0.0674
|
0.0641
|
0.0678
|
0.0756
|
0.0028
|
0.0188
|
|
γ
= 0.9
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.5698
|
0.8466
|
0.6882
|
0.6605
|
0.3670
|
0.8028
|
|
L1
|
0.0091
|
0.0129
|
0.0086
|
0.0158
|
0.0020
|
0.0012
|
|
L2
|
0.0685
|
0.0821
|
0.0686
|
0.0904
|
0.0043
|
0.0196
|
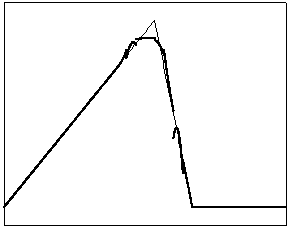 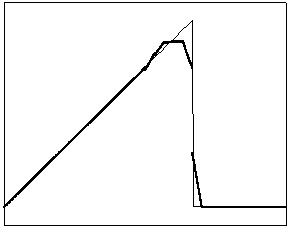
t=6 t=10
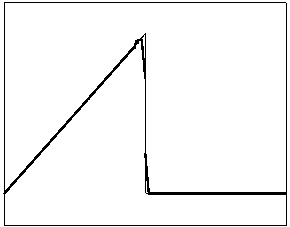 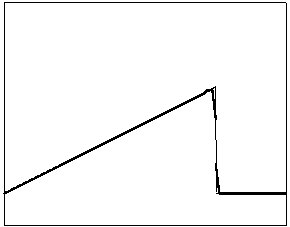
t=70 t=170
Рис. 4.2.1 Численное решение
для “треугольника” (g = 0.5)
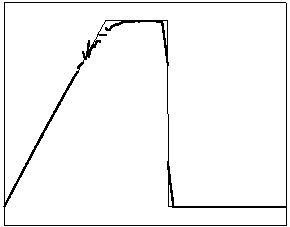 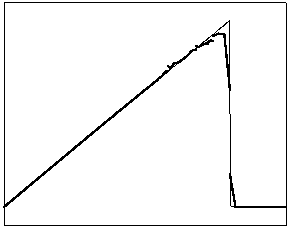
t=18 t=40
 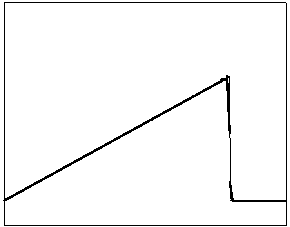
t=90 t=160
Рис.
4.2.2 Численное решение для
“прямоугольника” (g = 0.5)
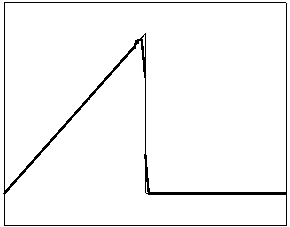 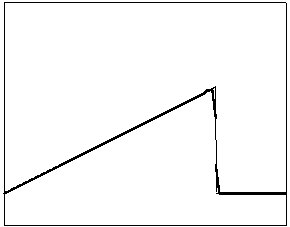
t=60 t=160
Рис. 4.2.3 Численное решение для “левого треугольника” (g = 0.5)
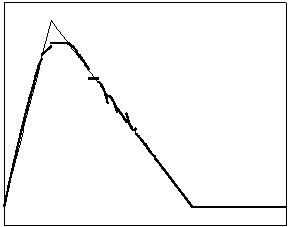 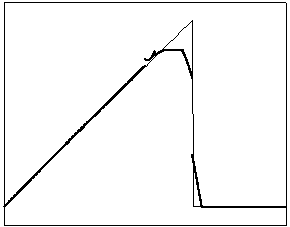
t=5 t=20
Рис. 4.2.4 Численное решение для “правого треугольника” (g = 0.5)
 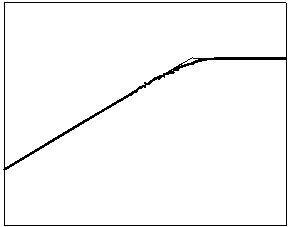
t=10 t=40
Рис. 4.2.5 Численное решение для “ступеньки вверх” (g = 0.5)
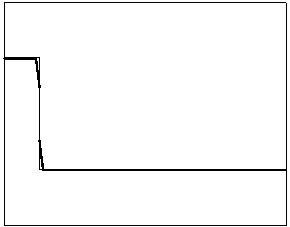 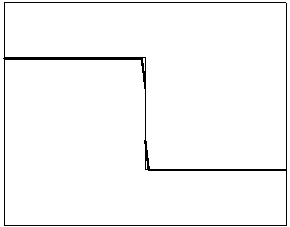 t=20 t=80 t=20 t=80
Рис.
4.2.6 Численное решение для “ступеньки
вниз” (g
= 0.5)
Из приведенных рисунков видно, что
использование кусочно-квадратичной аппроксимации в сочетании с рассматриваемыми
типами лимитеров не всегда обеспечивает монотонность получаемого численного
решения. Это явление характерно для разрывных квадратичных галеркинских
аппроксимаций, т.к. данный метод уменьшает полные вариации только средних
значений приближенного решения.
б) с использованием TVBM - лимитера 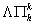 ( (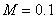 ). ).
Таблицы
ошибок (локально при t = T)
|
γ = 0.1
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.4284
|
0.7666
|
0.4808
|
0.7183
|
0.0003
|
0.2700
|
|
L1
|
0.0030
|
0.0035
|
0.0027
|
0.0044
|
0.0004
|
0.0005
|
|
L2
|
0.0302
|
0.0394
|
0.0297
|
0.0428
|
0.0004
|
0.0085
|
|
γ
= 0.25
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.4392
|
0.7799
|
0.4497
|
0.7290
|
0.0004
|
0.8063
|
|
L1
|
0.0030
|
0.0037
|
0.0023
|
0.0045
|
0.0006
|
0.0185
|
|
L2
|
0.0304
|
0.0409
|
0.0288
|
0.0435
|
0.0006
|
0.0321
|
|
γ
= 0.5
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.4367
|
0.8047
|
0.4446
|
0.7699
|
0.0047
|
0.9641
|
|
L1
|
0.0030
|
0.0041
|
0.0023
|
0.0052
|
0.0010
|
0.0298
|
|
L2
|
0.0304
|
0.0429
|
0.0289
|
0.0463
|
0.0009
|
0.0459
|
|
γ
= 0.9
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.4720
|
0.5533
|
0.4454
|
0.5557
|
0.2425
|
1.0092
|
|
L1
|
0.0031
|
0.0035
|
0.0023
|
0.0055
|
0.0366
|
0.0386
|
|
L2
|
0.0312
|
0.0299
|
0.0289
|
0.0361
|
0.0633
|
0.0593
|
Таблицы
ошибок (интегрально по t)
|
γ
= 0.1
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6444
|
0.8231
|
0.6539
|
0.6321
|
0.4248
|
0.8385
|
|
L1
|
0.0061
|
0.0083
|
0.0061
|
0.0092
|
0.0004
|
0.0012
|
|
L2
|
0.0582
|
0.0589
|
0.0589
|
0.0629
|
0.0011
|
0.0182
|
|
γ
= 0.25
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6248
|
0.7767
|
0.7777
|
0.6869
|
0.4566
|
0.9840
|
|
L1
|
0.0061
|
0.0084
|
0.0061
|
0.0098
|
0.0077
|
0.0166
|
|
L2
|
0.0584
|
0.0586
|
0.0591
|
0.0653
|
0.0180
|
0.0337
|
|
γ
= 0.5
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6132
|
0.8880
|
0.6104
|
0.7620
|
0.3284
|
1.1099
|
|
L1
|
0.0067
|
0.0122
|
0.0062
|
0.0144
|
0.0208
|
0.0299
|
|
L2
|
0.0612
|
0.0824
|
0.0592
|
0.0911
|
0.0342
|
0.0487
|
|
γ
= 0.9
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6538
|
0.8739
|
0.7773
|
0.7818
|
0.3670
|
1.2158
|
|
L1
|
0.0107
|
0.0206
|
0.0082
|
0.0231
|
0.0339
|
0.0387
|
|
L2
|
0.0834
|
0.1149
|
0.0701
|
0.1309
|
0.0478
|
0.0595
|
в) с использованием TVBM - лимитера 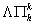 ( (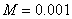 ). ).
Таблицы
ошибок (локально при t = T)
|
γ = 0.1
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.5729
|
0.3628
|
0.6205
|
0.7307
|
0.0005
|
0.2735
|
|
L1
|
0.0043
|
0.0039
|
0.0046
|
0.0073
|
0.0007
|
0.0004
|
|
L2
|
0.0382
|
0.0284
|
0.0487
|
0.0562
|
0.0006
|
0.0082
|
|
γ
= 0.25
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.5386
|
0.4138
|
0.5423
|
0.7331
|
0.0004
|
0.2268
|
|
L1
|
0.0046
|
0.0044
|
0.0056
|
0.0073
|
0.0006
|
0.0007
|
|
L2
|
0.0393
|
0.0343
|
0.0494
|
0.0563
|
0.0005
|
0.0087
|
|
γ
= 0.5
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6300
|
0.3614
|
0.5443
|
0.7212
|
0.0060
|
0.2360
|
|
L1
|
0.0049
|
0.0039
|
0.0056
|
0.0070
|
0.0007
|
0.0008
|
|
L2
|
0.0437
|
0.0301
|
0.0492
|
0.0552
|
0.0008
|
0.0090
|
|
γ
= 0.9
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.5761
|
0.4125
|
0.5628
|
0.7686
|
0.0080
|
0.2015
|
|
L1
|
0.0044
|
0.0044
|
0.0052
|
0.0078
|
0.0030
|
0.0008
|
|
L2
|
0.0387
|
0.0328
|
0.0485
|
0.0588
|
0.0038
|
0.0076
|
Таблицы
ошибок (интегрально по t)
|
γ
= 0.1
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6636
|
0.8201
|
0.7429
|
0.7293
|
0.3646
|
0.8427
|
|
L1
|
0.0091
|
0.0099
|
0.0088
|
0.0146
|
0.0007
|
0.0013
|
|
L2
|
0.0683
|
0.0668
|
0.0681
|
0.0857
|
0.0017
|
0.0193
|
|
γ
= 0.25
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6385
|
0.7750
|
0.7849
|
0.7376
|
0.3750
|
0.7750
|
|
L1
|
0.0089
|
0.0091
|
0.0088
|
0.0146
|
0.0007
|
0.0014
|
|
L2
|
0.0670
|
0.0627
|
0.0677
|
0.0848
|
0.0016
|
0.0189
|
|
γ
= 0.5
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.6104
|
0.7473
|
0.6186
|
0.7035
|
0.4396
|
0.6823
|
|
L1
|
0.0088
|
0.0092
|
0.0086
|
0.0124
|
0.0015
|
0.0015
|
|
L2
|
0.0669
|
0.0644
|
0.0674
|
0.0758
|
0.0030
|
0.0189
|
|
γ
= 0.9
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.5560
|
0.8120
|
0.6882
|
0.6982
|
0.3670
|
0.8485
|
|
L1
|
0.0091
|
0.0136
|
0.0086
|
0.0161
|
0.0025
|
0.0016
|
|
L2
|
0.0680
|
0.0840
|
0.0682
|
0.0910
|
0.0045
|
0.0197
|
3. Кусочно-квадратичная
аппроксимация (по средним значениям)
с
использованием TVDM
- лимитера 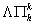 . .
Таблицы
ошибок (локально при t = T)
|
γ = 0.1
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.2000
|
0.1785
|
0.2549
|
0.3350
|
0.0006
|
0.1227
|
|
L1
|
0.0040
|
0.0037
|
0.0049
|
0.0071
|
0.0008
|
0.0005
|
|
L2
|
0.0312
|
0.0231
|
0.0387
|
0.0491
|
0.0007
|
0.0077
|
|
γ
= 0.25
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.2220
|
0.2001
|
0.2533
|
0.3466
|
0.0004
|
0.1379
|
|
L1
|
0.0046
|
0.0041
|
0.0048
|
0.0074
|
0.0006
|
0.0006
|
|
L2
|
0.0352
|
0.0274
|
0.0384
|
0.0510
|
0.0005
|
0.0087
|
|
γ
= 0.5
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.2182
|
0.1898
|
0.2474
|
0.3954
|
0.0014
|
0.1320
|
|
L1
|
0.0046
|
0.0039
|
0.0047
|
0.0072
|
0.0007
|
0.0005
|
|
L2
|
0.0346
|
0.0266
|
0.0374
|
0.0578
|
0.0006
|
0.0083
|
|
γ
= 0.9
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.2168
|
0.2118
|
0.2436
|
0.3276
|
0.0036
|
0.1418
|
|
L1
|
0.0045
|
0.0043
|
0.0046
|
0.0075
|
0.0021
|
0.0005
|
|
L2
|
0.0343
|
0.0278
|
0.0367
|
0.0483
|
0.0023
|
0.0088
|
Таблицы
ошибок (интегрально по t)
|
γ
= 0.1
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.5030
|
0.5660
|
0.5029
|
0.6065
|
0.2197
|
0.5827
|
|
L1
|
0.0099
|
0.0105
|
0.0096
|
0.0152
|
0.0008
|
0.0015
|
|
L2
|
0.0726
|
0.0675
|
0.0729
|
0.0846
|
0.0020
|
0.0207
|
|
γ
= 0.25
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.4660
|
0.5330
|
0.4661
|
0.5779
|
0.2411
|
0.5391
|
|
L1
|
0.0098
|
0.0097
|
0.0097
|
0.0150
|
0.0006
|
0.0015
|
|
L2
|
0.0719
|
0.0644
|
0.0726
|
0.0828
|
0.0016
|
0.0207
|
|
γ
= 0.5
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.4689
|
0.5588
|
0.4839
|
0.5228
|
0.2155
|
0.5000
|
|
L1
|
0.0097
|
0.0098
|
0.0095
|
0.0130
|
0.0011
|
0.0014
|
|
L2
|
0.0717
|
0.0655
|
0.0723
|
0.0756
|
0.0027
|
0.0209
|
|
γ
= 0.9
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
0.4107
|
0.6296
|
0.4533
|
0.5287
|
0.1882
|
0.5275
|
|
L1
|
0.0098
|
0.0134
|
0.0095
|
0.0162
|
0.0020
|
0.0014
|
|
L2
|
0.0716
|
0.0802
|
0.0728
|
0.0859
|
0.0042
|
0.0199
|
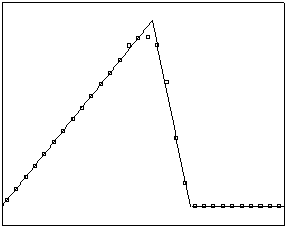 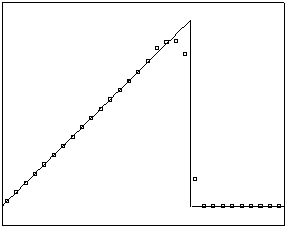
t=6
t=10
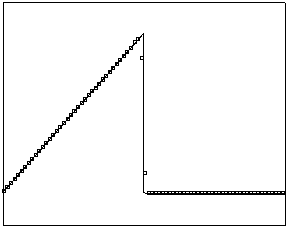 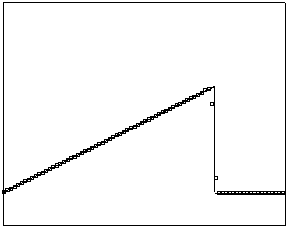
t=70
t=170
Рис. 4.3.1 Численное решение
для “треугольника” (g = 0.5)
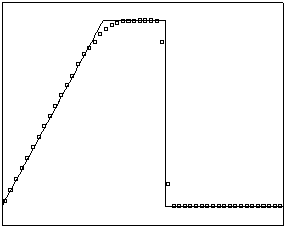 
t=18
t=40
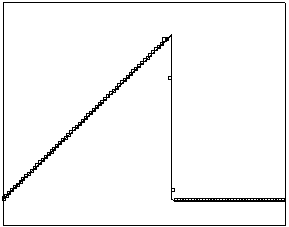 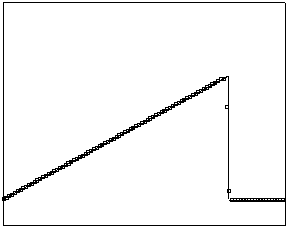
t=90 t=160
Рис.
4.3.2 Численное решение для
“прямоугольника” (g = 0.5)
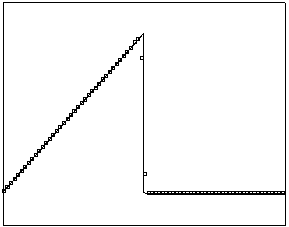 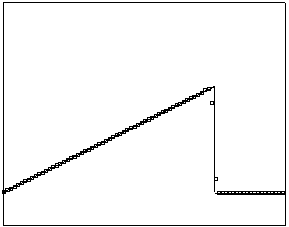
t=60 t=160
Рис. 4.3.3 Численное решение для “левого треугольника” (g = 0.5)
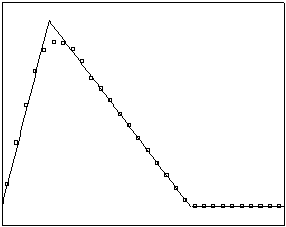 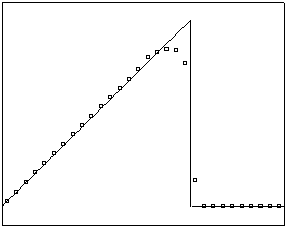
t=5 t=20
Рис. 4.3.4 Численное решение для “правого треугольника” (g = 0.5)
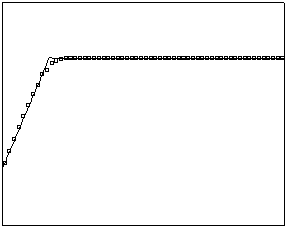 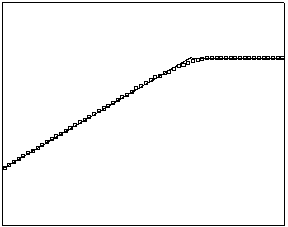
t=10 t=40
Рис. 4.3.5 Численное решение для “ступеньки вверх” (g = 0.5)
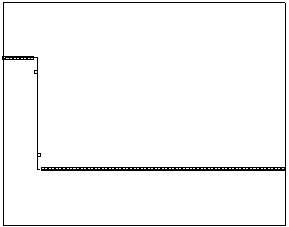 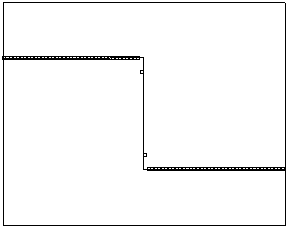
t=20
t=80
Рис. 4.3.6 Численное решение для “ступеньки вниз” (g = 0.5)
§ 5. Сравнение схем
На основе полученных численных результатов сравнены рассмотренные выше и
в [2] схемы. Ниже приведены таблицы сравнения, содержащие названия тех схем,
которые при данном числе Куранта дали наименьшую относительную ошибку в
соответствующей норме. Если в ячейке таблицы указаны несколько схем, то ошибки
вычислений, полученные для данных схем, либо совпадают, либо очень
незначительно отличаются друг от друга.
Обозначения:
·
Г_1а – разрывный метод Галеркина с
кусочно-линейной аппроксимацией и лимитером  (т.е. (т.е. 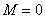 ) ; ) ;
·
Г_1б – кусочно-линейная аппроксимация и MUSCL лимитер;
·
Г_2а – кусочно-квадратичная аппроксимация и
лимитер 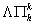 (т.е. (т.е. 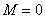 ); );
·
Г_2б –
кусочно-квадратичная аппроксимация и TVBM-лимитер с 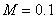 ; ;
·
Г_2в –
кусочно-квадратичная аппроксимация и TVBM-лимитер с 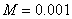 ; ;
·
Г_3 –
кусочно-квадратичная аппроксимация по средним значениям, лимитер 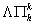 ; ;
·
Г – один
из вариантов метода Галеркина;
·
ЯЛ – явная схема с левой разностью;
·
НЛ – неявная схема с левой разностью;
·
ЛВ – схема Лакса-Вендрофа;
·
ПП – метод прыжкового переноса;
·
Б – схема К.И. Бабенко.
1. Сравнение различных вариантов разрывного метода Галеркина.
1) Сравнение
схем по локальным (при t = T)
ошибкам.
|
γ
= 0.1
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
Г_3
|
Г_3
|
Г_3
|
Г_3
|
Г_1а, Г_2б
|
Г_3
|
|
L1
|
Г_3
|
Г_2б, Г_3
|
Г_2б
|
Г_2б
|
Г_2б
|
Г_1а, Г_2а, Г_2в, Г_3
|
|
L2
|
Г_3
|
Г_3
|
Г_2б
|
Г_3
|
Г_1а, Г_2б
|
Г_3
|
При g
= 0.1 в норме С для тестов №№ 1,
2, 3, 4, 6 наименьшие ошибки дает вариант метода Г_3, для теста № 5 – варианты
Г_1а, Г_2б. В норме L1 вариант Г_3 является наиболее эффективным
для тестов № 1, 2, 6, вариант Г_2б – для тестов №№ 2, 3, 4, 5, варианты Г_1а,
Г_2а – для теста № 6. В норме L2 наилучшим
для тестов №№ 1, 2, 4, 6 является вариант Г_3, для теста № 3 – Г_2б, для теста
№ 5 – варианты Г_1а и Г_2б.
|
γ
= 0.25
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
Г_3
|
Г_3
|
Г_3
|
Г_3
|
Г_1а, Г_2а,
Г_2б, Г_2в,
Г_3
|
Г_3
|
|
L1
|
Г_2б
|
Г_2б, Г_3
|
Г_2б
|
Г_2б
|
Г_1а, Г_2а,
Г_2б, Г_2в,
Г_3
|
Г_1а, Г_2а,
Г_3
|
|
L2
|
Г_2б
|
Г_3
|
Г_2б
|
Г_2б
|
Г_1а, Г_2а,
Г_2б, Г_2в,
Г_3
|
Г_2в,
Г_3
|
При g
= 0.25 в норме С лучшим является
вариант Г_3 для условий №№ 1, 2, 3, 4, 6. В норме L1 вариант Г_2б является наилучшим для
начальных условий №№ 1, 2, 3, 4, для условия № 6 варианты Г_1а, Г_2а, Г_3 дают
близкие ошибки. В норме L2 для тестов №№ 1, 3, 4 лучшим оказывается
вариант Г_2б, для теста № 2 – вариант Г_3, для теста № 6 – варианты Г_2в и Г_3.
Для условия № 5 во всех нормах одинаковые ошибки дают все модификации метода,
кроме Г_1б.
|
γ
= 0.5
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
Г_3
|
Г_3
|
Г_3
|
Г_3
|
Г_1а
|
Г_3
|
|
L1
|
Г_2б
|
Г_2а, Г_2б,
Г_2в, Г_3
|
Г_2б
|
Г_2б
|
Г_1а, Г_2а,
Г_2в, Г_3
|
Г_1а, Г_2а,
Г_3
|
|
L2
|
Г_3
|
Г_3
|
Г_2б
|
Г_2б
|
Г_1а, Г_2а,
Г_3
|
Г_3
|
При g
= 0.5 в норме С лучшие результаты
показывает модификация Г_3 для всех тестов, кроме № 5, для которого лучшим
оказался вариант Г_1а. В норме L1 для
теста № 1 лучшими является вариант Г_2б, для теста № 2 – все варианты с
квадратичной аппроксимацией, для тестов № 3, 4 – вариант Г_2б, для теста № 5 –
Г_1а, Г_2а, Г_2в, Г_3, для теста № 6 – Г_1а, Г_2а, Г_3. В норме L2 вариант Г_3 показывает лучшие результаты
для начальных условий №№ 1, 2, 6, вариант Г_2б – для условий 3, 4, для условия
№ 5 аналогичные ошибки дают варианты Г_1а, Г_2а, Г_3.
|
γ
= 0.9
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
Г_3
|
Г_3
|
Г_3
|
Г_3
|
Г_1а
|
Г_3
|
|
L1
|
Г_2б
|
Г_2б
|
Г_2б
|
Г_2б
|
Г_1а
|
Г_2а, Г_3
|
|
L2
|
Г_2б
|
Г_3
|
Г_2б
|
Г_2б
|
Г_1а
|
Г_2в
|
При g
= 0.9 вариант Г_3 оказывается более эффективным в норме С для начальных условий №№ 1, 2, 3, 4,
6. В норме L1 наилучшим образом работает вариант
Г_2б для условий №№ 1, 2, 3, 4, варианты Г_2а, Г_3 для условия № 6. В
норме L2
вариант Г_2б оказывается лучшим для тестов №№ 1, 3, 4, вариант Г_3 –
для тестов №№ 2, 6, вариант Г_2в – для теста № 6. Для теста № 5 во всех нормах
наименьшие ошибки дает модификация Г_1а.
2) Сравнение
схем по интегральным (по времени) ошибкам.
|
γ
= 0.1
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
Г_3
|
Г_3
|
Г_3
|
Г_3
|
Г_3
|
Г_3
|
|
L1
|
Г_2б
|
Г_2б
|
Г_2б
|
Г_2б
|
Г_1а, Г_2б
|
Г_1а, Г_2а,
Г_2б, Г_2в, Г_3
|
|
L2
|
Г_2б
|
Г_2б
|
Г_2б
|
Г_2б
|
Г_1а, Г_2б
|
Г_2б
|
При g
= 0.1 в норме С для всех
начальных профилей лучшие результаты показывает вариант Г_3. В норме L1 для тестов №№ 1, 2, 3, 4 лучшим оказывается
вариант Г_2б, для теста № 5 – варианты Г_1а, Г_2б, для теста № 6 – все варианты,
кроме Г_1б. В норме L2 для тестов
№№ 1, 2, 3, 6 лучшим является вариант Г_2б, для теста № 5 – варианты Г_1а,
Г_2б.
|
γ
= 0.25
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
Г_3
|
Г_3
|
Г_3
|
Г_3
|
Г_3
|
Г_3
|
|
L1
|
Г_2б
|
Г_2б
|
Г_2б
|
Г_2б
|
Г_1а, Г_2а,
Г_3
|
Г_1а, Г_2а,
Г_3
|
|
L2
|
Г_2б
|
Г_2б
|
Г_2б
|
Г_2б
|
Г_1а
|
Г_2а, Г_2в
|
При g
= 0.25 в норме С модификация
метода Галеркина Г_3 оказывается более эффективной для всех тестов. В норме L1 для тестов
№№ 1, 2, 3, 4 лучшим является вариант
Г_2б, для тестов №№ 5, 6 – варианты Г_1а, Г_2а, Г_3. В норме L2 вариант
Г_2б дает лучшие результаты для тестов №№ 1, 2, 3, 4, вариант Г_1а – для теста
№ 5, варианты Г_2а, Г_2в – для теста № 6.
|
γ
= 0.5
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
Г_3
|
Г_3
|
Г_3
|
Г_3
|
Г_3
|
Г_3
|
|
L1
|
Г_2б
|
Г_2а, Г_2в
|
Г_2б
|
Г_2а
|
Г_1а
|
Г_1а, Г_2а
|
|
L2
|
Г_2б
|
Г_1а
|
Г_2б
|
Г_1а
|
Г_1а
|
Г_2а, Г_2в
|
При g
= 0.5 в норме С лучшие результаты
показывает вариант Г_3. В норме L1 для условий №№ 1, 3 наименьшие
ошибки дает вариант Г_2б, для условия № 2 – варианты Г_2а, Г_2в, для условия №
4 – Г_2а, для условия № 5 – Г_1а, для условия № 6 – варианты Г_2а, Г_2в. В
норме L2 для
тестов №№ 1, 3 наиболее эффективным оказывается вариант Г_2б, для тестов №№ 2,
4, 5 – вариант Г_1а, для теста № 6 – варианты Г_2а, Г_2в
|
γ
= 0.9
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
Г_3
|
Г_3
|
Г_3
|
Г_3
|
Г_3
|
Г_3
|
|
L1
|
Г_1а
|
Г_1а
|
Г_1а, Г_2б
|
Г_2а
|
Г_1а
|
Г_2а
|
|
L2
|
Г_2в
|
Г_1а
|
Г_2в
|
Г_1а
|
Г_1а
|
Г_2а, Г_2в
|
При g
= 0.9 в норме С вариант Г_3
является лучшим для всех начальных условий. В норме L1
для условий № 1, 2, 5 лучшие результаты дает вариант Г_1а, для
условия №3 – варианты Г_1а, Г_ 2б, для условий № 4, 6 – вариант Г_2а. В норме L2 минимальную
ошибку для условий №№ 2, 4, 5 дает вариант Г_1а, для условий №№ 1, 3 – вариант
Г_2в, для условия № 6 – варианты Г_2а, Г_2в.
2. Сравнение разрывного метода Галеркина со схемами из [2].
1) Сравнение
схем по локальным (при t = T)
ошибкам.
|
γ
= 0.1
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
Г
|
Г
|
Г
|
Г
|
Г
|
Б
|
|
L1
|
Г
|
Г
|
Г
|
Г
|
Г
|
Б, Г
|
|
L2
|
Г
|
Г
|
Г
|
Г, ЯЛ
|
Г
|
Г
|
При g
= 0.1 в норме C лучшие результаты показал
разрывный метод Галеркина для начальных условий №№ 1, 2, 3, 4, 5, для условия №
6 – схема К.И.Бабенко. В нормах L1 и L2 для всех тестов лучшим оказался метод Галеркина,
а также схема К.И.Бабенко для теста № 6 и явная схема с левой разностью для
теста № 4.
|
γ
= 0.25
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
Г
|
Г
|
Г
|
Г, НЛ
|
Г
|
Б
|
|
L1
|
Г
|
Г
|
Г
|
Г
|
Г
|
Б, Г
|
|
L2
|
Г
|
Г
|
Г
|
Г, НЛ
|
Г
|
Б, Г
|
При g
= 0.25 в норме C для начального условия № 6 лучшие
результаты получены с использованием схемы К.И.Бабенко. Для остальных тестов во всех нормах наиболее
эффективным оказался рассмотренный метод Галеркина. Для условия № 4 похожие
результаты в нормах С и L1 дала неявная схема с левой разностью, для
условия № 6 в нормах L1, L2 – схема К.И.Бабенко.
|
γ
= 0.5
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
Г
|
Г
|
Г
|
Г, ЯЛ
|
Г
|
Б
|
|
L1
|
Г
|
Г
|
Г
|
Г
|
Г
|
Б, Г
|
|
L2
|
Г
|
Г
|
Г
|
Г, ЯЛ
|
Г
|
Б, Г
|
При g
= 0.5 разрывный метод Галеркина дал наименьшие ошибки для всех начальных
условий во всех нормах, кроме условия № 6 в норме С, где лучше оказалась схема К.И.Бабенко.
Для теста № 4 аналогичные результаты в нормах С, L2 дала явная схема с левой разностью, для
теста № 6 в нормах L1, L2 – схема К.И.Бабенко.
|
γ
= 0.9
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
Б
|
Г
|
Г
|
Г
|
Г
|
Б
|
|
L1
|
Б, Г
|
Г
|
Г
|
Г
|
Б, Г
|
Г
|
|
L2
|
Б, Г
|
Г
|
Г
|
Г, ЯЛ
|
Г
|
Б, Г
|
При g
= 0.9 в норме С для начальных
профилей №№ 1, 6 лучшие результаты показала схема К.И.Бабенко, а для условий №№
2, 3, 4, 5 – разрывный метод Галеркина. В норме L1 для условий №№ 1, 5 лучшими были схема К.И.Бабенко и метод Галеркина,
для условий №№ 2, 3, 4, 6 – метод Галеркина. В норме L2 для тестов №№ 1, 6 наименьшие ошибки дали
схема К.И.Бабенко и метод Галеркина, для теста № 4 – метод Галеркина и явная
схема с левой разностью.
2) Сравнение
схем по интегральным (по времени) ошибкам.
|
γ
= 0.1
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
Б, Г, ЯЛ
|
Г, ЯЛ
|
Г, НЛ
|
Б
|
Г
|
Г
|
|
L1
|
Г
|
Г
|
Г
|
Г
|
Г
|
Г, ПП
|
|
L2
|
Б, Г
|
Г
|
Г
|
Г
|
Г
|
Г
|
При g
= 0.1 в норме С для начального
условия № 1 лучшие результаты дали схема К.И.Бабенко, метод Галеркина и явная
схема с левой разностью, для условия № 2 – метод Галеркина и явная схема с левой
разностью, для условия № 3 – неявная схема с левой разностью и метод Галеркина,
для условия № 4 – схема К.И.Бабенко, для условий №№ 5, 6 – метод Галеркина. В
норме L1 лучшим оказался метод Галеркина, а также
метод прыжкового переноса для теста № 6. В норме L2 наименьшие ошибки дал метод Галеркина, а для условия № 1 также схема
К.И.Бабенко.
|
γ
= 0.25
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
ЯЛ
|
ЛВ
|
Г
|
Б, Г
|
Г
|
Б, ЛВ
|
|
L1
|
Г
|
Г
|
Г, ПП
|
Г
|
Г
|
Г, ПП
|
|
L2
|
Б, Г
|
Г
|
Г
|
Г
|
Г
|
Г
|
При g
= 0.25 в норме С для теста № 1
лучшей оказалась явная схема с левой разностью, схема Лакса-Вендрофа для тестов
№ 2 и № 6, схема К.И.Бабенко для условий №№ 4, 6 , разрывный метод Галеркина
для условий №№ 3, 4, 5. В норме L1 лучшие
результаты показал метод Галеркина, а также метод прыжкового переноса для
начальных условий №№ 3, 6. В норме L2
наиболее эффективным оказался разрывный метод Галеркина и схема К.И.Бабенко для
условия № 1.
|
γ
= 0.5
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
Г, ЯЛ
|
Г, ЛВ
|
Г
|
Б
|
Г, НЛ
|
ЛВ
|
|
L1
|
Г
|
Г
|
Г
|
Г
|
Г
|
Г
|
|
L2
|
Б, Г
|
Г
|
Г
|
Г
|
Г
|
Г
|
При g
= 0.5 в норме С для начального
условия № 4 лучшей является схема К.И.Бабенко, для условий №№ 2, 6 – схема
Лакса-Вендрофа, явная схема с левой разностью для условия № 1, метод Галеркина
для условий №№ 1, 2, 3, 5. В норме L1
наименьшие ошибки дал метод Галеркина для всех начальных профилей. В норме L2 лучшим оказался метод Галеркина, а также
схема К.И.Бабенко для начального условия № 1.
|
γ
= 0.9
|
треугольник
|
прямоуголь-ник
|
левый
треугольник
|
правый
треугольник
|
ступенька
вверх
|
ступенька
вниз
|
|
C
|
Б
|
Г, НЛ
|
Г
|
Б
|
Г, НЛ
|
НЛ
|
|
L1
|
Г
|
Г
|
Г
|
Г
|
Г
|
Г
|
|
L2
|
Б, Г
|
Г
|
Г
|
Г
|
Г
|
Г
|
При g = 0.9 метод Галеркина
оказался наиболее эффективным в норме L1 для всех
тестов. В норме С схема К.И.Бабенко
является лучшей для условий №№ 1, 4, неявная схема с левой разностью – для
условий №№ 2, 5, 6, разрывный метод Галеркина – для условий №№ 2, 3, 5. В норме
L2 лучшие результаты показал метод Галеркина, а
также схема К.И.Бабенко для начального условия №1.
Заключение
Рассмотренный в данной работе RKDG метод в большинстве случаев обеспечивает более высокое
качество решения квазилинейного уравнения переноса по сравнению с другими
известными методами [2]. Размазывание разрывов происходит на 2-3 шага.
Проведенное исследование показывает, что наиболее оптимальным монотонизатором
является TVDM лимитер  . .
Следует отметить, что аппроксимация решения кусочно-линейными функциями
оказывается в целом более эффективной, чем кусочно-квадратичная аппроксимация,
т.к. она обеспечивает монотонность получаемой схемы.
Литература.
1. Bernardo Cockburn. An introduction
to the discontinuous Galerkin method for convection-dominated problems. SIAM
J. Sci. Comput. Vol. 16, pp. 173-261
2.
Александрикова Т. А., Галанин М. П. Нелинейная
монотонизация схемы К. И. Бабенко для численного решения квазилинейного
уравнения переноса. // Препринт ИПМ им. М. В. Келдыша РАН, 2003 г., № 62, 35 с.
3.
Галанин М. П., Еленина Т. Г. Сравнительный анализ
разностных схем для линейного уравнения переноса. // Препринт ИПМ им. М. В. Келдыша РАН, 1998 г., № 52, 33 с.
4.
Галанин М. П., Еленина Т. Г. Нелинейная монотонизация
разностных схем для линейного уравнения переноса. // Препринт ИПМ им. М. В.
Келдыша РАН, 1999 г.,
№ 44, 33 с.
5.
Галанин М. П., Еленина Т. Г. Нелинейная монотонизация
схемы К. И. Бабенко (“квадрат”) для
уравнения переноса. // Препринт ИПМ им. М. В. Келдыша РАН, 2002 г., № 4, 26 с.
6.
Куликовский А. Г., Погорелов Н. В., Семенов А. Ю. Математические вопросы
численного решения гиперболических систем уравнений. – М.: Физматлит, 2001г.,
608 с.
|