Ари Штернфельд и космонавтика
( Ary Sternfeld and cosmonautics
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Cодержание

1.           А.А. ШТЕРНФЕЛЬД И ЕГО ВКЛАД В КОСМОНАВТИКУ……..….……...4

2.           А.А. ШТЕРНФЕЛЬД И «ВВЕДЕНИЕ В КОСМОНАВТИКУ»……...………8

3.           РАБОТЫ А.А. ШТЕРНФЕЛЬДА ПО ИССЛЕДОВАНИЮ                               ТРАЕКТОРИЙ  КА.……………………………….………..11

4.           СВЯЗЬ РЕЗУЛЬТАТОВ А.А. ШТЕРНФЕЛЬДА С

СОВРЕМЕННОЙ КОСМОНАВТИКОЙ………..…………………………...13

А) ТЕОРИЯ КОСМИЧЕСКИХ МАНЕВРОВ………...……...………………13

Б) ПЕРЕЛЕТ  КА  НА ГЕОСТАЦИОНАРНУЮ ОРБИТУ И

ВОЗВРАЩЕНИЕ С  ГСО  К ЗЕМЛЕ...……………………..………...…..17

В) ЛУННЫЕ ПЕРЕЛЕТЫ………...………………………..…………………19

Г) ПОЛЕТ К СОЛНЦУ ВНЕ ПЛОСКОСТИ ЭКЛИПТИКИ.….……...…….25

5.    ЗАКЛЮЧЕНИЕ….……………………………………………………………..27

6.    ЛИТЕРАТУРА……………...……………………………………………...…..28

CONTENTS

1. А.А. STERNFELD AND HIS CONTRIBUTION TO COSMONAUTICS……….4

2. А.А. STERNFELD AND «INTRODUCTION TO COSMONAUTICS»…………8

3. A.A. STERNFELD’S STUDIES IN SPACE TRAJECTORIES…………...…….11

4. CONNECTION OF STERNFELD’S RESULTS WITH MODERN COSMONAUTICS………………………………………………………………13

     А) THEORY OF SPACECRAFT MANEUVERS…….………………………...13

     B) SPACECRAFT FLIGHT TO GEOSTATIONARY ORBIT AND

ITS RETURN FROM GSO TO EARTH…………………..……………...….17

C) LUNAR FLIGHTS…….…….……………….……………………………….19

D) FLIGHT TO SUN OUTSIDE ECLIPTIC’S PLANE………..…………….....25

5. CONCLUSIONS..………………………………………………………………...27

6.     references..…………………………………………………...……………..28

1.     А.А. ШТЕРНФЕЛЬД И ЕГО ВКЛАД В КОСМОНАВТИКУ

Ари Абрамович Штернфельд (1905-1980) прошел яркий жизненный и творческий путь. Расцвет его творческой деятельности приходится на 20-50-е годы нашего века, на период резкого подъема интереса ученых и инженеров к проблемам космического полета и начала космонавтики. В это время мечта Человечества о полете в космос встала на прочную научную и инженерную основу теоретических и экспериментальных исследований в результате пионерских работ К. Э. Циолковского, Р. Эсно-Пельтри, Р. Годдарда, Г. Оберта, В. Гомана, Ю. В. Кондратюка, Ф. А. Цандера, С. П. Королева, В. П. Глушко, М. К. Тихонравова и ряда других ученых, пионеров ракетно-космической науки и техники. Большой вклад в становление и развитие космонавтики внес и А. А. Штернфельд, посвятивший всю свою творческую жизнь проблемам освоения космического пространства. Его работы и идеи выдержали самое трудное испытание - испытание временем и не потеряли своей значимости до сих пор.

А. Штернфельд писал [Введение в космонавтику, 1974, с. 10], что он начал серьезно заниматься космонавтикой с 20-летнего возраста, но уже в школьные годы у него зарождались идеи - некоторые из них он позже разрабатывал и включил в свое «Введение в космонавтику». В космонавтике он нашел свое призвание, она поглотила всю его жизнь. После окончания в 1927 г. Института электротехники и прикладной механики Нансийского университета Франции А. Штернфельд поступил в докторантуру Сорбонны, избрав темой диссертации исследование проблем космонавтики. Он изучал труды Циолковского, Оберта, Гомана, Эсно-Пельтри и проводил оригинальные исследования по теории космонавтики. Однако избранный им путь был тернист. Его французские руководители в докторантуре не одобрили выбранную им проблему. Но А. Штернфельд продолжил свою работу. Он вступил в переписку с К.Э. Циолковским.

В 1930 г. в Парижской газете «Юманите» А. Штернфельд опубликовал научно-популярную статью по космонавтике, где он, поместив портрет К.Э. Циолковского, сообщал о его пионерских работах по ракетным полетам на другие планеты  и пророчески написал: «Только социалистическое общество откроет путь к освоению космического пространства». На Рис. 1 приведен фрагмент этой статьи. С тех давних пор научную популяризацию идей космонавтики А. Штернфельд блестяще продолжал всю свою жизнь, это, несомненно, - его большой вклад в мировую космонавтику.

В 1932 г. по приглашению Наркомтяжпрома СССР А. Штернфельд ездил в СССР для оформления проекта недавно изобретенного им робота-андроида, первоначально задуманного им для дистанционного выполнения опасных работ. На Рис. 2 приведена схема робота. Впоследствии стало ясно, что эта идея может быть использована в будущем и для космических операций. Данный проект продемонстрировал, с одной стороны, умение А. Штернфельда решать не только теоретические задачи, но и инженерные. А с другой стороны, он показал широту кругозора ученого. Затем А. Штернфельд выполнил еще несколько работ в данном направлении [Штернфельд, 1939, 1940, 1946].

После этого А. Штернфельд вернулся в Лодзь, где в 1933 г. закончил рукопись книги «Введение в космонавтику» и в декабре 1933 г. доложил свою работу в Астрономической обсерватории Варшавского университета [Штернфельд, 1981, с. 135]. Хотя в его докладе не было обнаружено научных ошибок, ее приняли довольно холодно, так как его идеи казались слишком фантастическими [Штернфельд, 1974, с. 11].

В начале 1934 г. две оригинальные научные работы А. Штернфельда были представлены (Ж. Перреном и Э. Эсклангоном) Французской академии наук.

В первой работе автор предложил интересную идею и прибор для автономной навигации «Метод определения траектории тела, движущегося в межпланетном пространстве, наблюдателем, связанным с подвижной системой» [Sternfeld, 1934a]. Расстояние до Солнца здесь предлагается определять по измерению температуры бортовым термометром.

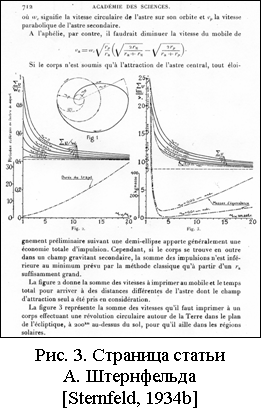Во второй работе «О траекториях, позволяющих приблизиться к центральному притягивающему телу, исходя из определенной кеплеровской орбиты» [Sternfeld, 1934b; Первые работы] автор рассмотрел задачу подлета к небесному телу. Он впервые показал, что при определенных условиях подлет КА к светилу энергетически выгоднее осуществить не по дуге полуэллипса, а по биэллиптической траектории с первоначальным удалением от центра притяжения (эти две возможные схемы полета указаны на приведенной на Рис. 3 странице этой статьи). Этот результат стал главным научным достижением А. Штернфельда. Благодаря нему несомненен и важен научный вклад А. Штернфельда в мировую космонавтику.

В мае 1934 г. в Париже, Сорбонне А. Штернфельд повторил свой доклад по книге «Введениие в космонавтику» - в присутствии Р. Эсно-Пельтри, А. Луи-Гирша и др. [Штернфельд, 1981, с. 135—136]. Этот доклад был тепло встречен учеными. Положительные отзывы о его работе дали Р. Эсно-Пельтри, Г. Оберт, Ж. Перрен, П. Ланжевен, В. Гоман [Штернфельд, 1974, с. 11]. Рукопись была удостоена в 1934 г. Международной поощрительной премии по астронавтике Комитета астронавтики Французского астрономического общества. В письме А. Луи-Гирша к автору было выражено пожелание, чтобы А. Штернфельд нашел издателя для публикации его труда [Луи-Гирш, 1934].

Однако это пожелание было осуществлено позднее - в Советском Союзе. У А. Штернфельда тогда «была глубокая уверенность, что первым к освоению космического пространства приступит Советский Союз» [Штернфельд A.А., 1974, с. 11]. Поэтому в 1935 г. он переехал в Советский Союз и принял советское гражданство. Он стал сотрудником Реактивного научно-исследовательского института (РНИИ), работал вместе с С. П. Королевым, В. П. Глушко, М. К. Тихонравовым, Ю. А. Победоносцевым, Г. Э. Лангемаком и некоторыми другими ныне хорошо известными учеными. В 1937 г. его книга «Введение в космонавтику», дополненная новыми данными, была издана в нашей стране [Штернфельд, 1937] (на Рис. 4 приведена ее обложка) и получила положительные отзывы специалистов, занимавшихся исследованием межпланетных полетов [Тихонравов М.К., 1938; Штернфельд, 1974, с. 11-12].

Эта книга «Введение в космонавтику» сыграла большую роль в распространении в нашей стране знаний об освоении космического пространства и поэтому, несомненно, стала важным вкладом А. Штернфельда в космонавтику. Отметим также то немаловажное обстоятельство, что важные термины «Космонавтика», «первая космическая скорость» были здесь впервые введены автором и вошли с тех пор в лексикон Космонавтики.

После этого А. Штернфельд продолжал свои исследования. В 1938—1946 гг. он подал заявки на изобретения и получил несколько авторских свидетельств [Штернфельд, 1939, 1940, 1946], развивших его давнюю идею андроида. В 1940-е и последующие годы своей жизни А. А. Штернфельд, хотя и не принимал непосредственного участия в разработке конкретных ракетно-космических систем, однако активно продолжал исследования в области теории космического полета. В 1945 г. он опубликовал в «Докладах Академии наук СССР» работу о пересечении атмосферы космической ракетой [Штернфельд, 1945]. Помимо «Введения в космонавтику», Штернфельд опубликовал еще несколько книг, статей [Штернфельд, 1949, 1955, 1956, 1957, 1958, 1974 и др.]. В 1956 г., незадолго до запуска Советским Союзом первого в мире спутника и начала космической эры, он выпустил интересную книгу «Искусственные спутники Земли» и в 1958 г. - ее второе издание «Искусственные спутники», где развил свою давнюю идею «обходной» траектории с задачи подлета к центральному телу (например, Солнцу) на задачу межорбитального перелета. В 1974 г. вышло второе издание его «Введения в космонавтику». Труды А. А. Штернфельда издавались более 80 раз на нескольких десятках языков во многих странах мира. Его научная деятельность получила признание как у нас в стране, так и за рубежом. В СССР ему присвоена ученая степень доктора технических наук honoris causa, звание заслуженного деятеля науки и техники РСФСР. Университет в Нанси и Национальный политехнический институт Лотарингии присвоили ему степень доктора физико-математических наук honoris causa. В 1963 г. он был удостоен второй международной премии – премии Галабера по астронавтике.

2. А.А. ШТЕРНФЕЛЬД И «ВВЕДЕНИЕ В КОСМОНАВТИКУ»

Монография А. А. Штернфельда «Введение в космонавтику» стала наиболее важной вехой в его творческом наследии. На основе этой книги можно сделать краткий анализ творчества Штернфельда [Ивашкин, Энеев, 1985]. Что характерно для этой работы? Во-первых, широта охвата проблем, связанных с исследованием межпланетных полетов. Книга явилась своеобразной энциклопедией ракетно-космической техники своего времени — времени становления теории и техники ракетного полета. Во-вторых, следует отметить достаточно глубокую проработку большинства рассматриваемых вопросов, стремление связывать решение теоретических вопросов с практическими задачами космонавтики. Хотя не все гипотезы и суждения автора подтвердились последующим развитием ракетной и космической техники, ряд его исследований выдержал испытание временем. В-третьих, в работах Штернфельда есть ряд оригинальных, ярких идей, особенно в области исследования траекторий космических полетов. Найденные биэллиптические траектории полета к центральному телу стали классическими и вошли в сокровищницу космонавтики.

Кратко изложим содержание книги. В первой части автор излагает свои представления о научном значении космических исследований. Он подчеркивает их важность для изучения атмосферы Земли и характеристик других планет Солнечной системы, а также условий жизни на них, для проведения астрофизических опытов. Далее излагаются сведения о законах движения небесных тел, о Солнечной системе, о свойствах земной атмосферы, о физиологических явлениях, которые должны испытывать космонавты при полете космического аппарата. Автор проводит анализ различных принципов космического полета, неосуществимых или бесперспективных с его точки зрения. Отметим, что и во втором издании книги к бесперспективным он относит использование солнечного давления, но зато замечание о бесперспективности электрических ракет во втором издании опущено.

Во второй части книги развивается теория ракет. Автор дает обзор истории ракет — как теории, так и экспериментальных работ. Далее излагается теория ракеты (причем во второе издание добавлен раздел об электрическом ракетном двигателе), описываются физико-химические процессы, происходящие в двигателе ракеты. Специальная глава посвящена анализу областей применения ракет, способов их испытания. Отдельно описывается космическая ракета: ее двигатель, способы управления ракетой, как при активном, так и пассивном полете, измерительные и регулирующие приборы. И хотя в настоящее время определение параметров движения космического аппарата производится не так, как предполагал А. А. Штернфельд, тем не менее, сама постановка им указанных вопросов заслуживает уважения. Далее автор описывает условия жизни в космическом аппарате и возможные принципы построения систем жизнеобеспечения.

Третья часть монографии («Пути космического корабля») посвящена анализу вопросов механики полета ракеты. Автор рассматривает орбиты космических аппаратов в рамках задачи двух тел, вопросы, связанные с созданием искусственного спутника Земли, в частности геостационарного, изучает вопросы полета к Луне, к другим планетам Солнечной системы. При этом он использует близкую к Земле орбиту спутника как промежуточную для полета к конечной цели. При анализе полетов к планетам автор изучает и вопросы возвращения космических аппаратов на Землю, вводит для этого биэллиптические траектории с предварительным прохождением космическим аппаратом апоцентра («афелической точки»), рассматривает траектории, обеспечивающие возвращение к Земле через целое и дробное число лет. По-видимому, в связи с этим автор пришел к пионерской идее биэллиптической траектории полета к центральному телу, которую он развивает здесь. Подробнее рассмотрим ее ниже, в п. 3.

Далее Штернфельд вслед за К.Э. Циолковским рассматривает наклонный и вертикальный взлет ракеты в поле тяготения, взлет в атмосфере с поверхности Земли, спуск на Землю. Даны примеры определения траекторий ракет с помощью численных расчетов, выполнен анализ составных ракет, рассматривается гипотетическая возможность уменьшения энергетических затрат при разгоне ракеты, проходящей через так называемый «вертикальный туннель». Это раскрывает одну интересную особенность механики полета ракеты, состоящую в том, что чем больше скорость космического аппарата, тем больше меняется его энергия при сообщении импульса скорости. Приведено и несколько других примеров характерных особенностей механики полета ракеты, названных автором «парадоксами ракеты». К этой теме «парадоксов» космонавтики автор затем обращался часто [Штернфельд, 1991].

В заключительной главе автор рассматривает такой экзотический для того времени вопрос, как применение теории относительности для анализа межзвездных полетов, для повышения точности траекторных расчетов. В приложении обсуждаются вопросы обитаемости других планет и, вообще, Вселенной, вопросы о связи мифологии разных народов и идеи межпланетных путешествий.

Из приведенного краткого обзора «Введения в космонавтику» видна несомненная важность творческого наследия Штернфельда для космонавтики. Недаром «Введение в космонавтику» на заре космонавтики, в 1950-х годах, было настольной книгой для ряда специалистов по космическим исследованиям [Белецкий, c. 264].

3.     РАБОТЫ А.А. ШТЕРНФЕЛЬДА ПО ИССЛЕДОВАНИЮ ТРАЕКТОРИЙ КА

Исследование траекторий движения КА образует центральное место в творчестве А. Штернфельда. Многие из его работ в этом направлении вошли в 3 часть «Введения в космонавтику», как уже описано выше. Главным здесь является исследование биэллиптических перелетов. До этого на основании пионерских работ немецкого ученого В. Гомана (1880-1943) [Hohmann, 1925] и советского ученого Ф.A. Цандера (1887-1933) [Цандер, 1924, 1961, 1964, 1967] предполагалось, что для классической задачи перелета между круговыми компланарными орбитами в центральном ньютоновском гравитационном поле оптимальным является всегда двухимпульсный перелет по касательному полуэллипсу (Рис. 5).

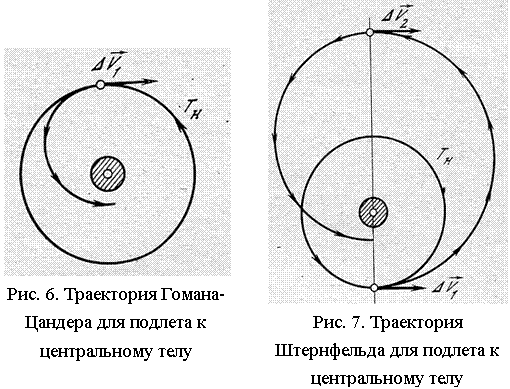
Интереснейшее исследование было выполнено А. А. Штернфельдом при анализе задачи близкого подлета к центральному светилу [Sternfeld, 1934b; Штернфельд, 1937, 1974; Первые работы]. Он впервые показал, что прямой подлет к светилу по одному полуэллипсу, касательному к начальной орбите (Рис. 6), может быть энергетически невыгоднее полета по так называемой «обходной», биэллиптической траектории с начальным удалением от центрального светила, последующим сообщением тормозного импульса скорости в апоцентре переходной орбиты и дальнейшим подлетом к светилу (Рис. 7).

Автор применил эту схему для задачи полета от Земли к Солнцу с учетом и без учета земного притяжения и для подлета к Юпитеру с его спутника Каллисто [Штернфельд, 1974, с. 133]. Интересно, что сравнительный анализ двух схем полета произведен автором также по полезному весу с учетом возрастания некоторых затрат при увеличении времени полета. Уже в статье 1934 года [Sternfeld, 1934b; Первые работы А.А. Штернфельда, с. 199-200] автор отметил также, что еще бóльший интерес могут представлять обходные полеты, образованные орбитами, сопрягаемыми под малыми углами. О подтверждении этого будет сказано ниже, в п. 4а. Позднее [Штернфельд, 1956, 1958] «обходная» идея была развита автором для задачи запуска космического аппарата с Земли на орбиту спутника, для перехода с одной круговой орбиты на другую (Рис. 8). Интересно, что автор пророчески отметил возможность использования данной обходной схемы для полета на Луну [Штернфельд, 1958, с. 103], об этом будет сказано ниже, в п. 4в. Подводя итог краткому обзору развития А. Штернфельдом этой идеи, хотелось бы отметить, что в 1930-х годах в РНИИ была реальная возможность, объединив результаты Ф.А. Цандера по гравитационным маневрам и межпланетным полетам с результатами А.А. Штернфельда по «обходной» схеме полета, разработать ряд космических проектов на уровне сегодняшнего дня. Это, например, полет к Солнцу с гравитационным маневром у Юпитера, полет на геостационарную орбиту с гравитационным маневром у Луны, о которых будет сказано ниже.

Из других работ А. Штернфельда по траекториям отметим исследование межпланетных экспедиций Земля-планета (Марс, Венера)-Земля, планета-Земля-планета. Анализируя упрощенную модель полета, автор выявил возможность скачкообразного сокращения времени экспедиции при некотором критическом увеличении скорости отлета от минимальной. Большое внимание уделено А. Штернфельдом анализу траекторий полета мирных ракет на Земле для доставки пассажиров, почты, грузов между пунктами на Земле. Статьи по этим задачам, а также по полету к Солнцу намечено опубликовать в специальном сборнике, посвященном 100-летию со дня рождения ученого [Штернфельд, 2005а; 2005б; 2005в].

4.     СВЯЗЬ РЕЗУЛЬТАТОВ А.А. ШТЕРНФЕЛЬДА

С СОВРЕМЕННОЙ КОСМОНАВТИКОЙ

А) ТЕОРИЯ КОСМИЧЕСКИХ МАНЕВРОВ

Рассмотрим кратко развитие идей Штернфельда, связанных с биэллиптическим переходом между орбитами. Это развитие теории оптимальных многоимпульсных маневров осуществлялось в нескольких направлениях. Укажем некоторые из них. Результаты В. Гомана, Ф.А. Цандера и А. А. Штернфельда о двух- и трехимпульсных переходах между круговыми компланарными орбитами были развиты на более общие случаи. В частности, многоимпульсные, биэллиптические переходы вошли органично не только в перелеты между эллиптическими орбитами, но и в перелеты между эллиптическими и гиперболическими орбитами, а также между гиперболическими орбитами. Рассмотрим, для примера, перелеты между компланарными эллиптическими орбитами со свободной взаимной ориентацией, с ограниченным расстоянием (r_min£r(t)£r_max) и свободным временем перехода. Было показано [Hoelker, and Silber, 1959; Ting, 1960; Marec, 1965, 1979; Marchal, 1965; Гурман, 1966; Ивашкин, 1966, 1975; и др.], что оптимальными для данной задачи могут быть только двух- или трехимпульсные переходы – обобщения классических решений В. Гомана, Ф.А. Цандера и А. А. Штернфельда.

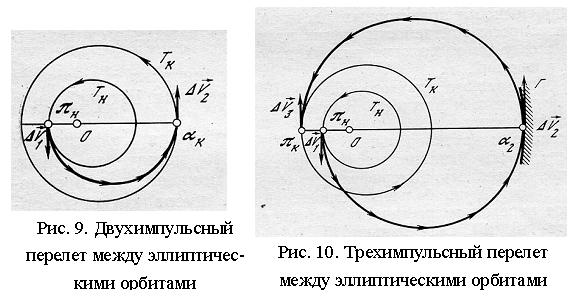
В двухимпульсной схеме (с числом импульсов скорости N=2) перелет осуществляется между перицентром одной орбиты и более удаленным апоцентром другой орбиты (Рис. 9). В трехимпульсной схеме (N=3) первый импульс в перицентре начальной орбиты p_н увеличивает скорость космического аппарата, после чего КА удаляется от центра притяжения. В апоцентре a₂ первой переходной орбиты, на максимально допустимом расстоянии от центра притяжения r=r_a2=r_max, сообщается вдоль или противоположно скорости второй промежуточный импульс так, чтобы полученная вторая переходная орбита касалась конечной орбиты в ее перицентре p_к, где и сообщается последний третий тормозной импульс (Рис. 10). Все импульсы этого перехода апсидальны.

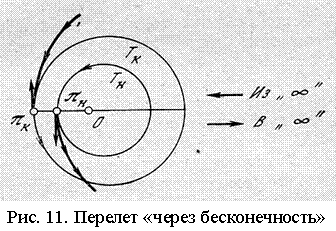
Если нет и ограничения на наибольшее расстояние от планеты, то оптимальным (по сумме величин импульсов) среди трехимпульсных переходов может быть лишь его предельный случай, соответствующий полету «через бесконечность» по параболическим орбитам, так называемый бипараболический переход (Рис. 11).

Конечно, этого бы не случилось, если бы учитывалось возрастание некоторых затрат при увеличении времени перехода, как это делал А. А. Штернфельд во «Введении в космонавтику».

Указанные оптимальные траектории будут реализовывать оптимум и при ограниченной тяге путем большого числа предельно малых включений в соответствующих апсидальных точках орбит через оборот пассивного движения.

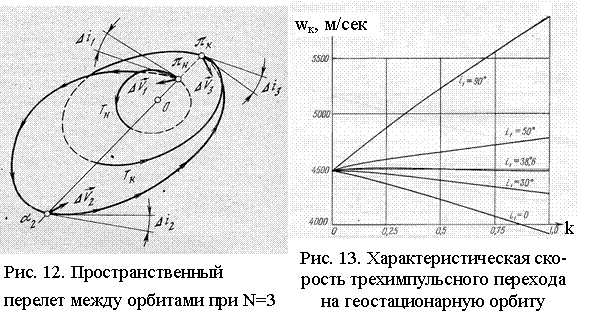
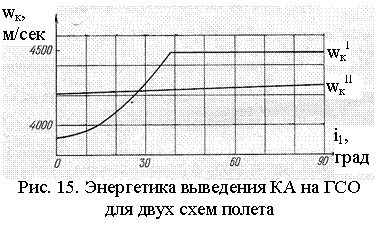
Плоские решения, в частности, решение А. А. Штернфельда, были обобщены [Райдер, 1961; Гобец, Долл, 1969; Ивашкин, Тупицын, 1970, 1971; Ивашкин, 1975; и др.] на случай перехода между некомпланарными орбитами со свободной ориентацией. В этом случае в переходе N=3 каждый импульс сообщается опять в тех же апсидах, но под некоторым углом к плоскости орбит (Рис. 12). Область оптимальности трехимпульсных переходов N=3 здесь больше, чем в плоском случае. Так, для перелета с близкой к Земле круговой орбиты радиуса r=6630 км на геостационарную орбиту радиуса R=42164 км (при соотношении радиусов этих орбит R/r»6,6) решение N=2 уступает переходу N=3 при начальном наклонении к экватору Земли свыше ~ 39°, что выполняется при запуске КА с космодрома Байконур. На Рис. 13 дана сумма величин трех импульсов скорости как функция параметра k=R/r_a2 (0£k£1, k=1 при N=2). Ниже, в п. 4б, будет рассмотрено развитие этого результата.

Не рассматривая других случаев маневров, косвенно связанных с переходом Штернфельда, отметим еще одно его обобщение. Было исследовано [Ивашкин, Скороходов, 1980], как меняется этот переход, если верхнее ограничение на расстояние r£r_max заменяется ограничением на время перехода t_к£t_max. В последнем случае оптимальная траектория определяется численно, с помощью результатов теории оптимального импульсного маневра. Эта оптимальная траектория геометрически заметно отличается от апсидальной траектории Штернфельда (Рис. 14). Точки приложения импульсов смещаются от апсид, все импульсы теперь сообщаются под некоторыми углами к векторам скорости. Но оказалось, что энергетически обе траектории близки друг к другу. Если время перелета одно и то же, то характеристическая скорость оптимальной при ограниченном времени траектории меньше, чем на траектории Штернфельда, но не более чем на 1% при отношении радиусов круговых орбит, не превосходящем 100. Следовательно, апсидальная трехимпульсная траектория, впервые предложенная Штернфельдом, хорошо моделирует в ряде случаев и оптимальный переход при ограничении на время перелета.

Таким образом, идея трехимпульсных перелетов Штернфельда оказалась плодотворной и органически вошла в современную механику космического полета. Теперь рассмотрим три проекта, в которых прослеживается эта идея «обходного» полета КА к цели. Первым будет проект выведения КА на геостационарную орбиту (ГСО).

Б) ПЕРЕЛЕТ  КА  НА ГЕОСТАЦИОНАРНУЮ ОРБИТУ И

ВОЗВРАЩЕНИЕ С  ГСО  К ЗЕМЛЕ

Обычным является выведение КА на геостационарную орбиту (ГСО) по двухимпульсной схеме, N=2. Однако, как показано выше, при большом наклонении i₁ начальной орбиты (i₁>39°) трехимпульсная схема N=3 имеет мéньшую сумму величин импульсов w_к. При i₁=50° имеем w_к »4780 м/с для N=2, и w_к »4485-4530 м/с для N=3 при r_a2>400 тыс. км. При r_a2»400 тыс. км промежуточный импульс скорости еще велик, его величина DV₂»300 м/с.

Возникает идея - заменить действие этого импульса скорости гравитационным маневром у Луны [Ивашкин, Тупицын, 1970, 1971; Ивашкин, 1975]. Тогда затраты скорости на выведение еще уменьшатся и составят ~4250 м/с. На Рис. 15 кривая w_к^I дает сумму величин импульсов для выведения без учета влияния Луны, а w_к^II – с учетом гравитационного маневра у Луны [Ивашкин, Тупицын, 1971; Ивашкин, 1975].

На Рис. 16 приведена одна такая типичная траектория выведения КА на ГСО с близким пролетом у Луны.

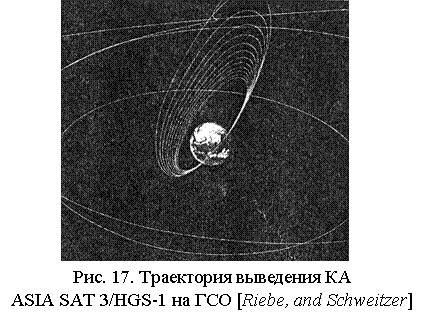
В 1997-1998 гг. был выведен КА (ASIASAT 3/HGS-1) на ГСО по данной схеме полета. На Рис. 17 приведена траектория полета этого КА. Его запуск был осуществлен с космодрома Байконур. Из-за неполадки с 4 ступенью ракеты «Протон» обычная 2-импульсная схема не смогла быть реализована, и только использование более экономичной схемы полета с гравитационным маневром у Луны позволило вывести КА на ГСО. Этот полет был назван «наиболее впечатляющим» космическим событием 1998 г. [Riebe, and Schweitzer].

Таким образом, при выведении КА на ГСО с космодрома с достаточно большой широтой оптимальным становится применение не прямой схемы полета, а «обходной» схемы, с гравитационным маневром у Луны.

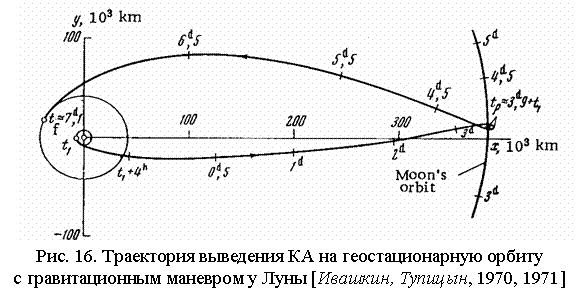
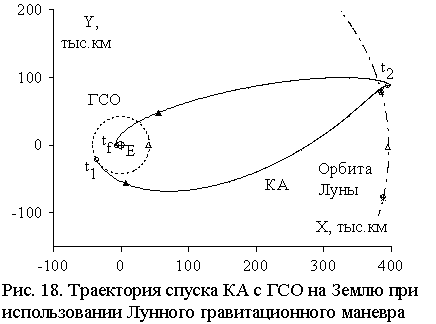
Кроме того, для задачи спуска КА с ГСО на Землю также выгоднее использовать не «прямую» схему с уменьшением скорости КА (на ~ 1490 м/c), а «обходную» схему с разгоном (на ~ 1100 м/c), подлетом к Луне, выполнением гравитационного маневра и последующим полетом к Земле. На Рис. 18 приведена в проекции на плоскость геоэкватора траектория такого спуска на Землю E с отлетом с ГСО 29.XII.2000 и временем полета ~ 9,4 сут.

В) ЛУННЫЕ ПЕРЕЛЕТЫ

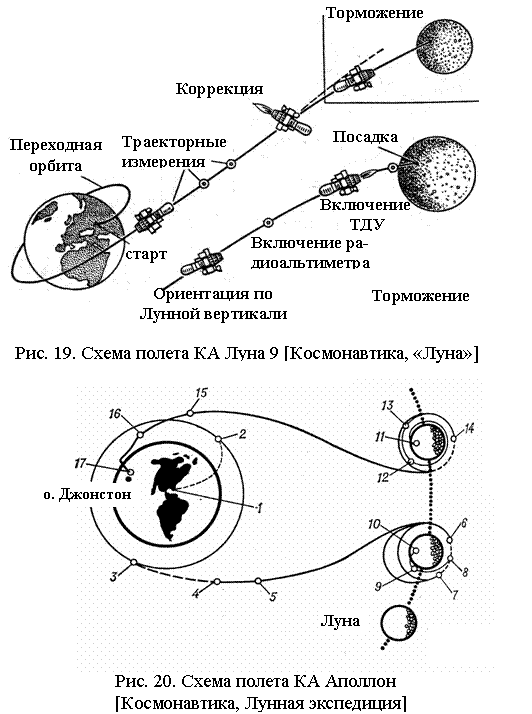
ПРЯМЫЕ ПЕРЕЛЕТЫ ЗЕМЛЯ-ЛУНА И ЛУНА-ЗЕМЛЯ. Исследование перелетов между Землей и Луной имеет большое значение, как для Небесной механики, так и для Космонавтики. Для практически всех полетов, начиная с 1959 г., использовались «прямые» траектории [В.А. Егоров, 1957, 1965; В.А. Егоров, Л.И. Гусев, 1980; и др.]. На Рис.19, 20 для примера приведены схемы полета КА СССР «Луна-9» для первой мягкой посадки на Луну и КА США «Аполлон» для первой пилотируемой экспедиции на Луну [Космонавтика].

         Обычные Лунные траектории прямого типа с химическими двигателями имеют довольно небольшое (несколько суток) время перелета между Землей и Луной. Подлет к Луне и отлет от нее происходят по гиперболическим селеноцентрическим орбитам (со скоростью на «бесконечности» V_¥»1 км/с). Это приводит к большому расходу топлива для торможения и разгона КА у Луны при использовании данных траекторий. Поэтому важен поиск новых слабо-энергетических Лунных перелетов: a) с другими схемами полета; б) перелетов Земля-Луна с пассивным захватом и перелетов Луна-Земля с пассивным освобождением у Луны; в) с другими двигателями.

Электрореактивные двигатели малой тяги (вместо химических) были использованы в проекте Европейского космического агенства для полета к Луне КА SMART-1, который начал реализовываться в 2003 г. Рассмотрим первые два варианта.

БИЭЛЛИПТИЧЕСКАЯ СХЕМА ПЕРЕЛЕТА. При импульсном перелете в центральном поле, как отмечено выше, есть два основных типа перехода: двухимпульсный переход Гомана-Цандера (Рис. 5, 9) и трехимпульсный биэллиптический переход Штернфельда (Рис. 8, 10). Первая схема ведет к прямым Лунным перелетам в системе Земля-Луна-точка. Вторая схема дает биэллиптические Лунные перелеты в системе Земля-Луна-точка. Если в ней максимальное расстояние отлета от Земли r_a достаточно велико (> 4 млн. км), то эта вторая схема становится энергетически лучше первой. Но в данном случае должно быть учтено влияние Солнца.

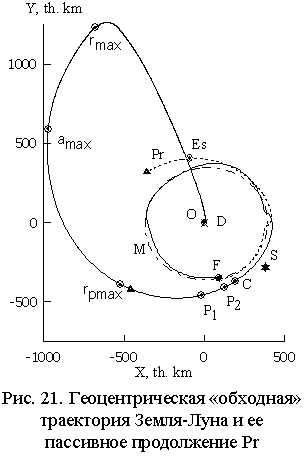“ОБХОДНЫЕ” ПЕРЕЛЕТЫ ЗЕМЛЯ-ЛУНА. Рассмотрев биэллиптическую схему полета Земля-Луна в гравитационом поле системы Земля-Луна-Солнце-точка, можно получить новый, «обходной» тип траекторий Земля-Луна, см. Рис. 21, 22 [Belbruno, and Miller, 1993; Hiroshi Yamakawa, et al., 1993; Uesugi, 1993; Biesroek, and Janin, 2000; Bello Mora, et al., 2000; Koon, et al., 2001; Ивашкин, 2001, 2002; и др.].

На рис. 21 точка D – начало полета, F – его конец (через ~140 сут. полета), М – Луна, S – Солнце при r=r_max»1,5×10⁶ км, пунктир Pr – пассивное продолжение движения за конечную точку F, штрих-пунктир – орбита Луны, P₁: V_¥= 0.4 км/с; P₂: V_¥ =0.2 км/с; C, Es: V_¥ = 0, в точке C – захват, в точке Es на Pr - освобождение. Указаны также точки достижения максимальных значений: расстояния до Земли r_max, большой полуоси a_max, перигейного расстояния r_pmax. Видим, что внешне эти перелеты похожи на биэллиптический перелет Штернфельда. Однако динамически они отличны от перелетов Штернфельда:

- подъем перигея здесь производится Солнечным притяжением, а не импульсом скорости, двигателем;

- приближение к Луне происходит по эллиптической орбите из-за притяжения Земли (есть захват Луной – в точке С).

Отсюда следует заметное уменьшение скорости торможения у Луны.

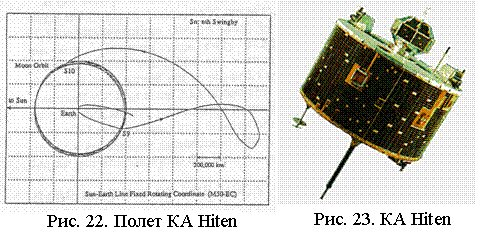
Эта схема полета к Луне была реализована при полете Японского КА Hiten (Рис. 22, 23). Он был запущен в январе 1990 г. Это был небольшой КА, массой 197 кг (143 кг – КА + 42 кг – топливо + 12 кг - дополнительный суб-спутник Hagoromо). КА имел высокоточное управление, бортовой компьютер, оптическую систему для навигации и управления. Были выполнены десять гравитационных маневров у Луны, аэроторможение, выведен небольшой суб-спутник на орбиту  ИСЛ (март 1990 г.), была реализована новая траектория полета к Луне -  «обходного» типа, с апогеем ~ 1 500 тыс. км (1991 г.). Затем для исследования количества микрочастиц был выполнен полет в окрестности треугольных точек либрации L₄ и L₅. В 1992 г. основной КА Hiten был выведен на орбиту спутника Луны (11300 ´ 51100 km). В конце полета, апреле 1993 г., было произведено соударение КА Hiten с Луной.

Разрабатываемый сейчас в Японии КА Lunar-A имеет время полета до Луны ~ полгода [Mizutani, 2004]; по-видимому, он использует такую же «обходную» схему полета.

“ОБХОДНЫЕ” ПЕРЕЛЕТЫ ЛУНА- ЗЕМЛЯ. Затем были построены также «обходные» перелеты Луна-Земля, полученные в рамках системы Земля-Луна-Солнце-точка [Hiroshi Yamakawa, 1993; Ивашкин, 2004; Ivashkin, 2004a, 2004b]. Они используют сначала полет от Луны и орбиты Луны за сферу притяжения Земли и только затем – к Земле.

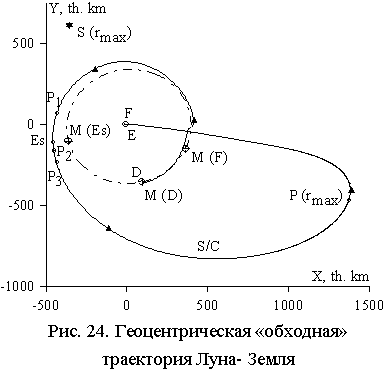На Рис. 24 представле-на одна типичная траектория Луна-Земля [Ивашкин, 2004]. Здесь и на Рис. 25: D - отлет от Луны (11.05. 2001), в точке P₁ селеноцентрическая большая полуось a_s=79 тыс. км, Es – точка освобождения (время Dt»20,6 сут, скорость V_¥ =0), P₂: Dt»21,1 сут, V_¥ =0,15 км/с; P₃: Dt»21,9 сут,V_¥ =0,25 км/с; r_max » 1.47·10⁶ км, F-конечная точка (H_p=50 км, время полета Dt = 113 сут), M - Луна, E – Земля, S - Солнце. Внешне эти траектории похожи на биэллиптические траектории Штернфельда. Однако динамически они также отличны от них, как и для перелетов Земля-Луна:

- Отлет от Луны происходит по эллиптической орбите с пассивным освобождением от Лунного притяжения из-за гравитации Земли (в точке Es на Рис. 24, 25);

- Снижение перигея происходит пассивно, из-за гравитации Солнца, а не с помощью импульса скорости.

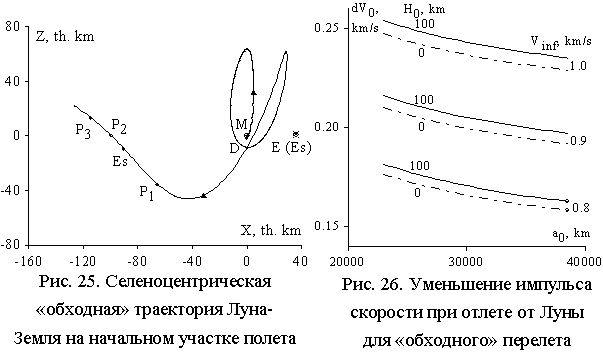
На Рис. 25 приведено селеноцентрическое движение КА на начальном участке полета. В точке D КА отлетает с периселения начальной эллиптической орбиты высотой 100 км. На дуге D P₁ Es - эллиптическое селеноцентрическое движение. Es – точка освобождения; здесь достигается нулевая селеноцентрическая энергия, точка Е (Es) дает направление на Землю в этот момент. Поэтому освобождение происходит вблизи залунной коллинеарной точки либрации L₂. На дуге Es P₂ P₃ - гиперболическое движение. Затем КА отлетает от Лунной орбиты и Земли.

На Рис. 26 приведено уменьшение импульса скорости dV₀ при отлете от Луны для «обходного» перелета Луна-Земля по сравнению с прямым перелетом - в зависимости от большой полуоси орбиты отлета к Земле a₀ и скорости на «бесконечности» прямого полета V_¥. Здесь кривые H₀=100 км соответствуют отлету КА с периселения орбиты ИСЛ с данной высотой. Линии H₀=0 представляют старт КА с поверхности Луны. Величина V_inf есть скорость на “бесконечности” V_¥ для прямого полета: V_¥ = 0,8 км/с соответствует ~ плоскому оптимальному полету с апогея Луны, V_¥ = 0,9 км/с - оптимальному полету с перигея Луны, V_¥ = 1,0 км/с – пространственному и более быстрому полету. Для перелета на Рис. 24, 25 a₀~38000 км. При a₀=24-38 тыс. км и V_¥ = 0,8-1 км/с выигрыш в скорости отлета dV₀ »160-250 м/с для H₀=0-100 км.

Таким образом, численный и теоретический анализ задачи движения КА между Землей и Луной доказывает существование «обходных» траекторий, которые

- для полета Земля-Луна имеют пассивный (без учета коррекции) перелет на некоторую орбиту спутника Луны, т.е. обеспечивают гравитационный захват;

- для полета Луна-Земля имеют пассивный полет к Земле с некоторой орбиты спутника Луны, т.е. обеспечивают гравитационное освобождение от Лунного притяжения. Эти траектории имеют мéньший расход топлива; однако они имеют бóльшее время полета, и для их реализации требуется более точная система управления, чем для обычных, прямых перелетов. Видим, что оправдалось замечание А. Штернфельда [Штернфельд, 1958, с. 103] о возможном применении биэллиптической схемы для полета на Луну.

Г) ПОЛЕТ К СОЛНЦУ ВНЕ ПЛОСКОСТИ ЭКЛИПТИКИ

В качестве последнего примера КА со схемой полета, напоминающей «обходную» схему, рассмотрим полет международного (США и Европа) КА Ulysses, главной целью которого является исследование солнечных внеэклиптических полярных районов. Кроме того, проводятся исследования межпланетной среды и около-юпитерианского пространства. Для обеспечения выхода траектории из плоскости эклиптики, поворота плоскости гелиоцентрической орбиты на большой угол использован прием, аналогичный тому, который был выше рассмотрен для перехода на геостационарную орбиту. КА сначала выводится на орбиту отлета от Земли, КА удаляется от Земли на большое расстояние, к орбите Юпитера и там меняется его наклонение. Только, в отличие от решения Штернфельда, это изменение орбиты делается не двигателем и импульсом скорости, а с помощью гравитационного маневра у Юпитера. Запуск КА был осуществлен в октябре 1990 г.

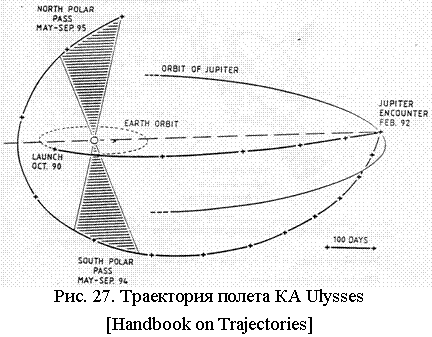
На Рис. 27 приведена траектория полета КА к Юпитеру и движение КА на первом витке полета после маневра у Юпитера в феврале 1992 г. Наклонение полученной орбиты - ~80°, перигелий – 1,35 а.е., афелий – 5,4 а.е. [NSSDS Master Catalog: Ulysses].

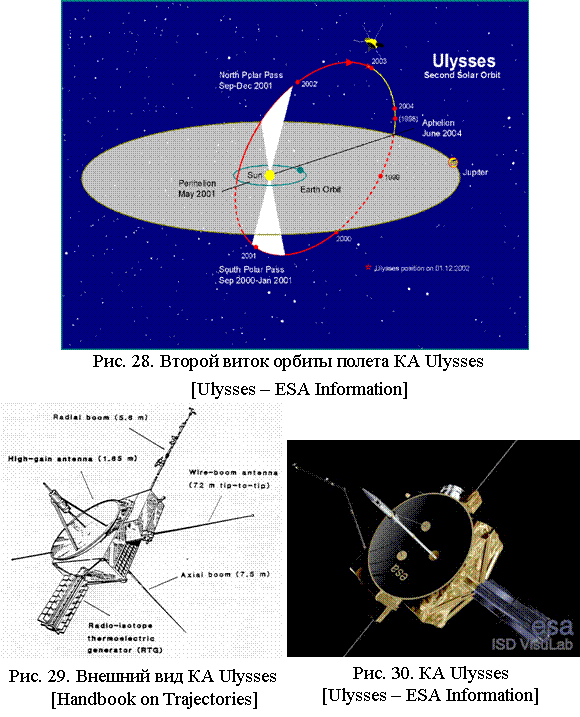
В середине 1994 г. КА пролетел над южным полюсом Солнца, в середине 1995 г. – над северным полюсом, что позволило провести исследования физических характеристик околосолнечного пространства вне эклиптики. После оборота по орбите, в 1998 г. КА опять пролетел афелий вблизи Юпитера. Период орбиты КА составляет ~ 6,2 года. С таким периодом повторяются сближения КА с Юпитером и Солнцем. На рис. 28 приведен второй виток орбиты КА. КА опять пролетел в 2000 г. и в 2001 г. над Южным полюсом и Cеверным, соответственно, в феврале-марте 2004 г. - вблизи Юпитера, на расстоянии ~120 млн км. Сейчас продолжаются исследования при полете КА Ulysses на третьем витке орбиты.

На Рис. 29, 30 приведены внешний вид и художественное изображение КА.

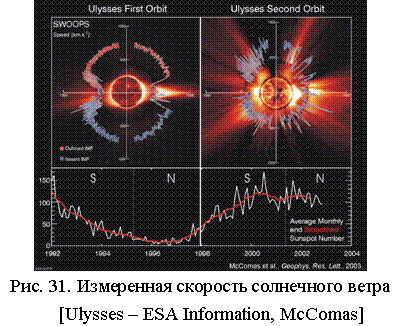
На Рис. 31 приведена измеренная аппаратурой КА Ulysses на двух витках орбитального движения вокруг Солнца скорость солнечного ветра.

Следует отметить также, что обсуждаемый в научной литературе проект «Солнечный зонд» для полета на близкое расстояние к Солнцу предусматривает аналогичную схему полета: сначала полет к Юпитеру, гравитационный маневр у Юпитера, чтобы получить гелиоцентрическую орбиту с малым расстоянием от Солнца в перигелии. Это близко к идеям А. Штернфельда для полета к Солнцу [Штернфельд, 2005а].

5.     ЗАКЛЮЧЕНИЕ

         Выполненный анализ творческого наследия А. Штернфельда позволяет сделать вывод, что, во-первых, своей научной и научно-популяризаторской деятельностью А. Штернфельд внес заметный вклад в становление космонавтики и, во-вторых, его идеи непрямых, биэллиптических перелетов органично вошли как в теорию, так и в практику современной космонавтики.

            В заключение автор хотел бы выразить искреннюю признательность Политехническому музею за предложение подготовить данную статью, М.А. Штернфельд и А.Ф. Цандер за содействие материалами семейных архивов, а также Dr. M. Bello Mora, Dr. Yoshikawa Makoto, Dr. Toshio Fukushima и Dr. Hitoshi Mizutani за любезное предоставление материалов по КА Ulysses, Hiten и Lunar-A.

6.     ЛИТЕРАТУРА

1.      Белецкий В.В. (2004) Шесть дюжин. - Москва-Ижевск: Институт компьютерных исследований. 688 с.

2.      Гобец Ф.У., Долл Дж.Р. (1969) Обзор импульсных траекторий. - Ракетная техника и космонавтика. Т. 7, N 5. С. 3-46.

3.      Гурман В.И. (1966) Об оптимальных переходах между компланарными эллиптическими орбитами в центральном поле. - Космические исследования. Т. IV, вып. 1. С. 26.

4.      Егоров В.А. (1957) О некоторых задачах динамики полета к Луне. - Успехи физических наук, т. 63, вып. 1а, с. 73-117.

5.      Егоров В.А. (1965) Пространственная задача достижения Луны. - М.: Наука. 224 с.

6.      Егоров В.А., Гусев Л.И. (1980) Динамика перелетов между Землей и Луной. - М.: Наука. 544 с.

7.      Ивашкин В.В. (1966) Оптимальный переход между эллиптическими орбитами, лежащими в заданном кольце. - Космические исследования. Т. IV, вып. 6. С. 795-804.

8.      Ивашкин В.В. (1975) Оптимизация космических маневров при ограничениях на расстояния до планет. М.: Наука. 392 с.

9.      Ивашкин В.В. (2001) Об оптимальных траекториях полета КА к Луне в системе Земля-Луна-Солнце. - Препринт, Институт прикладной математики им. Келдыша РАН, 2001, N 85. 32 с.

10. Ивашкин В.В. (2002) О траекториях полета точки к Луне с временным захватом ее Луной. // Доклады Академии наук, 2002, том 387, N 2, с. 196-199.

11. Ивашкин В.В. (2004) О траекториях полета точки от Луны к Земле с гравитационным освобождением от лунного притяжения. // Доклады Академии Наук. Том 398, N 3, с. 340-342.

12. Ивашкин В.В., Скороходов А.П. (1980) Сравнительный анализ трехимпульсных траекторий, оптимальных при ограничениях на время перехода и на наибольшее расстояние от планеты. - Космические исследования. Т. XVIII, вып. 1. С. 11-21.

13. Ивашкин В.В., Тупицын Н.Н. (1970) Об использовании гравитационного поля Луны для выведения космического аппарата на стационарную орбиту спутника Земли. - Препринт, Институт прикладной математики АН СССР. Москва, 1970 г. 31 с.

14. Ивашкин В.В., Тупицын Н.Н. (1971) Об использовании гравитационного поля Луны для выведения космического аппарата на стационарную орбиту спутника Земли. - Космические исследования. Т. IX, вып. 2. С. 163-172.

15. Ивашкин В.В., Энеев Т.М. (1985) О работах А.А. Штернфельда по космонавтике. - Исследования по истории и теории развития авиационной и ракетно-космической науки и техники. Выпуск 4. М.: Наука. С. 215-224.

16. Космонавтика (1985) Энциклопедия. Гл. ред. В.П. Глушко. М.: Советская энциклопедия. 528 с.

17. Луи-Гирш А. (1934) Письмо А.А. Штернфельду, 11 июля 1934. Личный архив семьи А.А. Штернфельда.

18. Охоцимский Д.Е., Сихарулидзе Ю.Г. (1990) Основы механики космического полета. М.: Наука. 448 с.

19. Первые работы А.А. Штернфельда по космонавтике, представленные в 1934 г. во Французскую Академию наук (1988) - Исследования по истории и теории развития авиационной и ракетно-космической науки и техники. Выпуск 6. М.: Наука. С. 194-200.

20. Пионеры ракетной техники: Кибальчич. Циолковский. Цандер. Кондратюк. (1964) Избранные труды. М.: Наука. 673 с.

21. Пионеры ракетной техники: Гансвинд. Годдард. Эсно-Пельтри. Оберт. Гоман. (1977) Избранные труды. М.: Наука. 633 с.

22. Прищепа В.И., Дронова Г.П. (1987) Ари Штернфельд - пионер космонавтики. М.: Наука. 192 c.

23. Райдер Л. (1961) Необходимая характеристическая скорость для перелета между некомпланарными круговыми орбитами с помощью импульсов тяги. - Ракетная техника. N 3. С. 78.

24. Тихонравов М.К. (1938) Критика и библиография: Штернфельд А.Я. Введение в космонавтику // Вестник инженеров и техников. N 7. Июль 1938. С. 443-445.

25. Цандер Ф.А. (1924) Полеты к другим планетам - Техника и жизнь, Москва, N 13, с. 15-16.

26. Цандер Ф.А. (1961) Проблема полета при помощи реактивных аппаратов. Межпланетные полеты. Сборник статей. Второе издание. М.: ГНТИ. 461 с.

27. Цандер Ф.А. (1964) Перелеты на другие планеты: (Теория межпланетных путешествий).- В кн.: Пионеры ракетной техники: Кибальчич. Циолковский. Цандер. Кондратюк. Избранные труды, М.: Наука, 1964, с. 277-359.

28. Цандер Ф.А. (1967) Из научного наследия. М.: Наука, 1967. 100 с.

29. Циолковский К.Э. Исследование мировых пространств реактивными приборами.- Научное обозрение, 1903, № 5, с. 45-75. В кн.: Пионеры ракетной техники. М.: Наука, 1964, с. 23-53.

30. Штернфельд А.А. (1937) Введение в космонавтику. М.- Л.: ОНТИ. 318 с.

31. Штернфельд А.А. (1939) Авторское свидетельство 55105 (СССР). Винтовой пресс. Опубл. 30.06.1939. Заявлено 03.09.1938.

32. Штернфельд А.А. (1940) Авторское свидетельство 57746 (СССР). Устройство для записи движений органов человека. Опубл. 31.08.1940. Заявлено 03.09.1938.

33. Штернфельд А.А. (1945) О расходе топлива при пересечении атмосферы ракетой с постоянным ускорением. // Доклады АН СССР, т. 49, № 9. C. 653-656.

34. Штернфельд А.А. (1946) Авторское свидетельство 67162 (СССР). Андроид. Опубл. 30.09.1946. Заявлено 03.09.1938.

35. Штернфельд А.А. (1949) Полет в мировое пространство. М.-Л.: ГИТТЛ. 140 c.

36. Штернфельд А.А. (1955) Межпланетные полеты. М..: ГИТТЛ. 2-е изд.: М., Гостехиздат, 1956. 48 c.

37. Штернфельд А.А. (1956) Искусственные спутники Земли. М.: ГИТТЛ. 180 c.

38. Штернфельд А.А. (1957) От искусственных спутников к межпланетным полетам. М.: Гостехиздат. 126 c. 2-е изд.: М., Физматтиз, 1959. 204 c.

39. Штернфельд А.А. (1958) Искусственные спутники. 2-е изд., перераб. и доп.: М.: Гостехиздат, 1958. 296 c.

40. Штернфельд А.А. (1974) Введение в космонавтику. 2-е изд. М.: Наука, 1974. 240 с.

41. Штернфельд А.А. (1981) История моей первой книги. - Вопросы истории естествознания и техники, № 3. C. 134-139.

42. Штернфельд А.А. (1991) Парадоксы космонавтики. М.: Наука, 160 с.

43. Штернфельд А.А. (2005а) К Солнцу:Полеты к Солнцу с предварительным удалением. - Москва, Политехнический музей. Архив А.А. Штернфельда.

44. Штернфельд А.А. (2005б) О скачкообразном сокращении длительности меж-планетных экспедиций туда и обратно при постепенном увеличении скоростей отлета. - Москва, Политехнический музей. Архив А.А. Штернфельда.

45. Штернфельд А.А. (2005в) Расчет траектории сверхдальней баллистической ракеты. - Москва, Политехнический музей. Архив А.А. Штернфельда.

46. Belbruno E.A. and Miller J.K. (1993) Sun-Perturbed Earth-to-Moon Transfers with Ballistiс Capture; - Journal of Guidance, Control and Dynamics. Vol. 16. № 4. Pp. 770 - 775.

47. Bello Mora M., F. Graziani, P. Tiofilatto, et al. (2000) A Systematic Analysis On Week Stability Boundary Transfers To The Moon. - The 51^st International Astronautical Congress, Rio de Janeiro, Brazil, October 2000. Paper IAF-00-A.6.03. 12 p.

48. Biesbroek R., Janin G. (2000) Ways to the Moon? ESA Bulletin. Vol. 103. Pp. 92 - 99.

49. Edelbaum T.N. (1967) How many impulses? - Astronautics and Aeronautics, 1967, vol. 5. N 11. Pp. 64-69.

50. Handbook on Trajectories, Mission Design, and Operations - third Edition, Volume 1 - Current Missions. Prepared by Working Group 3 of the Inter-Agency Consultative Group for Space Science (IACG). November 1991. Section 12 - Ulysses. Pp. I-12-1-5.

51. Hiroshi Yamakawa, Jun'ichiro Kawaguchi, Nobuaki Ishii, Hiroki Matsuo (1993) On the Earth-Moon Transfer Trajectory with Gravitational Capture: Presented at AAS/AIAA Astrodynamics Specialist Conference, Victoria, USA. Paper AAS 93-633, 20 p.

52. Hiten - ISAS Information: http://www.isas.jaxa.jp/e/enterp/missions/complate/hiten.shtml

53. Hoelker R.F., Silber R. (1959) The Bi-elliptic Transfer between Circular Coplanar Orbits, Army Ballistic Missile Agency, Alabama, DA-TM-2-59, January 1959.

54. Hohmann W. (1925) Die Erreichbarkeit der Himmelskorper. München, 1925. В книге <Пионеры ракетной техники: Гансвинд. Годдард. Эсно-Пельтри. Оберт. Гоман. (1977) Избранные труды. М.: Наука. Вальтер Гоман. С. 526-607.

55. Ivashkin V. V. (2003) On the Earth-to-Moon Trajectories with Temporary Capture of a Particle by the Moon: Presented at the 54th International Astronautical Congress, held in Bremen, Germany, September 29 - October 3, 2003. Paper IAC-03-A.P.01, 9 p.

56. Ivashkin V.V. (2004a) On the Moon-to-Earth Trajectories with Gravitational Escape from the Moon Attraction. // 18^th International Symposium on Space Flight Dynamics, 11-15 October 2004, Munich, Germany. European Space Agency, Proceedings, SP-548, December 2004, Paper P0111, pp. 149-153;
a) http://www.issfd.dlr.de/papers/ P0111.pdf 
b) http://www.keldysh.ru/ papers/2004/source/article/ISSFD_IvashkinVV-4.pdf

57. Ivashkin V.V. (2004b) Low Energy Trajectories for the Moon-to-Earth Space Flight: Presented at the International Conference on Exploration and Utilization of the Moon - 2004 (ICEUM-6), November 22-26, 2004. Udaipur, India. Paper, 15 p. http://www.keldysh.ru/papers/2004/art02/ILC6-Ivashkin-KIAM.html .

58. Koon W.S., Lo M.W., Marsden J.E., et al. (2001) Low Energy Transfer to the Moon; Celestial Mechanics and Dynamical Astronomy (Kluwer Academic Publishers, Netherlands) Vol. 81, pp. 63-73.

59. Marchal C. (1965) Transfers optimaux entre orbites elliptiques: Commun. presentee au XVI Congr. Intern. d'Astronaut. Athens.

60. Marec J. P. (1965) Transfers orbitaux economiques. - Rech. aerosp., N 105, pp. 11-21.

61. Marec J.P. (1979) Optimal space trajectories. Elsevier Scientific Publishing Company. Amsterdam-Oxford-New York. 329 p.

62. Miller J.K., Belbruno E.A. (1991) A Method for the Constructing of a Lunar Transfer Trajectory Using Ballistic Capture. Presented at the AAS/AIAA Spaceflight Mechanics Meeting, Houston. Paper AAS 91-100, pp. 97-109.

63. Mizutani H., Fujimura A., Tanaka S., Shiraishi H., and Nakjima T. (2004) Lunar-A Mission: Outline and Current Status // Presented at the International Conference on Exploration and Utilization of the Moon (ICEUM-6), November 22-26, 2004. Udaipur, India. Paper, 14 p.

64. NSSDC Master Catalog: - Hiten; AsiaSat 3/HGS-1; Ulysses:

http://nssdc.gsfc.nasa.gov/planetary/lunar/lunartimeline.html ;

http://nssdc.gsfc.nasa.gov/database/MasterCatalog?sc=1990-007A ; http://nssdc.gsfc.nasa.gov/database/MasterCatalog?sc=1997-086A ; http://nssdc.gsfc.nasa.gov/database/MasterCatalog?sc=1990-090B

65. Riebe T., and Schweitzer M. (1998) Space operations and support. - AEROSPACE AMERICA/Dec. 1998, p. 83.

66. Sternfeld A. (1934a) Méthode de détermination de la trajectoire d'un corps en mouvement dans 1'espace interplanétaire par un observateiur lié au système mobile. - Comptes rendus de l'Académie des Sciences (Paris), 1934, vol. 198, pp. 333-334.

67.  Sternfeld A. (1934b) Sur les trajectoires permettant d'approcher d'un corps attractifs central à partir d'une orbite Keplérienne donnée. - Comptes rendus de l'Académie des Sciences (Paris), vol. 198, pp. 711- 713.

68. Ting Lu (1960) Optimum orbital transfers by several impulses. - Acta Astronautica. Vol. 6, N 5. Pp. 256-265.

69. Uesugi, Kuninori (1993) Space Odyssey of an Angel - Summary of the Hiten's Three Years Mission: Presented at AAS/GSFC International Symposium on Space Flight Dynamics, AAS Paper 93-292. 20 p.

70. Ulysses - ESA Information:

a) http://sci.esa.int/science-e-media/img/43/first_orbit_rev99.gif ;

b) http://sci.esa.int/science-e-media/img/43/second_orbit_rev2003.gif ;

c) http://sci.esa.int/science-e-media/img/43/second_orbit_1520_rev2003.gif

d) http://sci.esa.int/science-e-media/img/0f/migration-14351_-2.jpg

e) http://sci.esa.int/science-e-media/img/0f/McComas_GRL_2003.jpg.