1.   Введение

Исследование многоагентных систем – multi-agent systems (MAS) играет все большую роль из-за возможности моделирования сложных систем, т.е. систем, составленных из многих объектов, взаимодействующих между собой и с внешней средой. Они используются в тех областях, где классические мат. модели недоступны, поскольку динамика системы далека от равновесия, или системы открыты (объекты могут создаваться и уничтожаться в процессе моделирования), или необходимо проводить исследование явлений на стадии становления, или объекты моделирования существенно неоднородны, или просто потому, что они более точно соответствуют интуитивному пониманию.

Моделирования многоагентных систем применяется к исследованиям в области экосистем и окружающей среды в целом, психологии, производства и логистики, виртуальной реальности, социально-экономических систем.

Важнейшая особенность этого метода – то, что каждый объект состоит из множества распределенных агентов, действующих параллельно без глобального контроля, ответственного за их поведение. Более того, действия каждого агента зависят от состояний некоторого ограниченного числа других агентов, и результирующее состояние системы определяется конкуренцией и координацией среди агентов, подчиненных структурным ограничениям. Сложность системы, таким образом, увеличивается в большей степени от взаимодействия среди агентов, чем от увеличения сложности самих агентов, более того локальная сеть взаимосвязей, соединяющая отдельные агенты друг с другом, постоянно перекомбинируется и пересматривается.

Одно из применений этого метода – моделирование экономических систем взаимодействующих агентов (Agent-based Computational Economics, ACE) [1-3]. Для него характерен синтетический подход – сначала в модель вводятся свойства отдельных агентов и принципы их взаимодействия между собой и с окружающей средой, а затем в результате моделирования определяются закономерности эволюции формирующейся экономической системы.

Отметим кратко особенности моделей ACE [1]:

-         агенты взаимодействуют на базе собственных знаний и правил поведения;

-         допускается широкий спектр взаимодействий между агентами, таких как конкурентная борьба и формирование кооперативных ассоциаций;

-         рассматривается естественный эволюционный процесс популяции агентов, в котором они могут рождаться и погибать в результате своей деятельности и постоянно меняющихся взаимодействий в популяции;

-         вмешательство экспериментатора (проводящего моделирование) в естественный процесс эволюции экономической системы не допускается.

Подчеркнем, что в моделях АСЕ могут быть учтены психологические, социальные особенности поведения агентов, таким образом эти модели характеризуют социально-экономические закономерности развития общественных систем.

В данной работе рассматриваются два взаимосвязанных класса моделей взаимодействия агентов в информационном сообществе. В первом рассмотрение ведется на уровне популяции малых высокотехнологичных фирм в рамках технопарка. При этом рассматриваются две взаимосвязанных модели, по-разному трактующие знания фирм, и имеющие различную область применимости. В работе проводится сравнительное исследование моделей.

Во второй части работы исследуется взаимодействие между странами. Здесь также рассматриваются две модели, характеризующие различные варианты взаимодействия.

Основная идея всех предложенных моделей – учесть знания (в широком смысле этого слова) экономических систем в информационной среде и их влияние на динамику развития популяции.

2.   Модели эволюции популяции фирм

2.1.                    Общая характеристика моделей

Объект исследования – популяция малых высокотехнологичных фирм в структуре инновационно-производственного комплекса (ИПК), оказывающего информационную и финансовую поддержку. Университет, тесно связанный с ИПК, обеспечивает приток квалифицированных кадров и научную помощь.

Фирмы стремятся удовлетворить свои потребности (в знаниях, деньгах, развитии и т.д.). В результате взаимодействия возникает конкуренция или кооперация. Моделирование позволяет определить поведение всей популяции, варианты совместного существования фирм, границы перехода от конкуренции к симбиозу, от разорения к процветанию.

Цель моделирования – исследовать закономерности эволюции популяции фирм, выработать рекомендации по действиям ИПК для выживания зарождающихся и процветания существующих фирм.

Основные предположения модели состоят в следующем:

-         изучается эволюция популяции малых высокотехнологичных (high-tech) фирм, рассматриваемых как искусственные организмы (агенты);

-         агенты имеют две основные потребности: знания и деньги (более точные их определения см. ниже), которые они стремятся удовлетворить;

-         агенты взаимодействуют друг с другом и с внешней средой, в которой есть источники знаний и денег;

-         если деньги агента становятся ниже определенного уровня, он умирает;

-         агенты в процессе своей деятельности создают продукты, полезные для сообщества, в котором они существуют.

Считаем, что популяция фирм характеризуется следующими переменными: I_i, M_i – знания и деньги i–той фирмы соответственно. Время считаем дискретным (в непрерывном случае вместо приращений следует рассматривать производные по времени).

2.2.                    Динамика жизни фирм

2.2.1. Первая модель

Динамику жизни фирм характеризуем следующими соотношениями:

D I_i = k₁ I_i M_i + k₂ S _k I_k  – k₃ I_i                                 (1)

D M_i  = k₅ I_i M_i – k₆ S _k M_k  – k₇ M_i                                   (2)

Здесь и далее k_i – константы (их нумерация выбрана для удобства работы со всеми моделями), D I_i ,D M_i – прирост знаний и денег фирмы за такт времени.

Первые слагаемые справа в (1) и (2) – прирост знаний и денег в результате собственной работы фирмы (монотонно увеличивается с ростом как знаний, так и денег). Второе слагаемое в (1) – прирост знаний в результате информационного обмена между фирмами, третье – старение информации.

Второе слагаемое справа в (2) соответствует конкуренции между фирмами, третье – налоги, амортизация и получение прибыли собственниками фирмы.

Если деньги фирмы оказываются ниже определенного порога (например, его можно положить равным нулю), она погибает.

2.2.2. Вторая модель

В первой модели не вполне четко введено понятие знаний: очевидно, само по себе наличие знаний и даже технологий не гарантирует успеха. Зачастую определяющую роль играют эффективность их внедрения и эффективность управления, которые в России пока оставляют желать лучшего.

Поэтому во второй модели будем использовать термин «знания» условно – дабы подчеркнуть логическую связь с первой. Будем называть «знаниями» весь комплекс технологических, интеллектуальных, управленческих и иных знаний, навыков, ресурсов, позволяющих эффективно использовать активы фирмы.

Из (3) и (4) видно, что «деньги» и «знания» близки к таким понятиям как собственный капитал (=активы–обязательства) и маржинальная рентабельность (=1–(переменные издержки)/выручка). Т.к. наша основная задача – учесть взаимодействие в информационной среде, не будем чрезмерно детализировать основные понятия модели, а сохраним некоторую свободу в их применении.

Все это не повод отказа от первой модели – она весьма проста как идейно, так и при моделировании, и имеет значительную область применимости. Кроме того, интуитивное понимание знаний в ней позволяет получать интересные выводы, которые в дальнейшем могут стать основой для других моделей.

Динамику жизни фирм характеризуем следующими соотношениями:

D I_i = k₁ I_i M_i + k₂ S _k I_k  – k₃ I_i – k₄ I_i² M_i,                         (3)

D M_i  = k₅ I_i M_i – k₆ S _k M_k  – k₇ M_i – k₈ I_i M_i² ,                            (4)

Отличие от первой модели – введение четвертых слагаемых в каждое из уравнений. Их смысл – естественное ограничение роста знаний и денег выше некоторого предела, например, в связи с усложнением управления и структуры фирмы. Выбор слагаемых обусловлен как требованиями простоты системы, так и тем, что при таком выборе получается вполне естественный фазовый портрет.

2.3.                    Динамика знаний и денег одной фирмы

2.3.1.  Первая модель

Максимально упростим задачу и рассмотрим в непрерывном времени одну фирму, не взаимодействующую с другими:

dI/dt = k₁ I M – k₃ I,                                              (5)

dM/dt = k₅ I M – k₇ M.                                          (6)

Начнем анализ с построения фазового портрета системы (5), (6). Особые точки определяются условиями dI/dt = 0 и dM/dt = 0, т.е.

k₁ I M  – k₃ I = 0,                                                   (7)

k₅ I M –  k₇ M  = 0.                                                 (8)

Отметим, что (7) и (8) – уравнения изоклин, определяющих смену знака производных dI/dt , dM/dt . Система (7), (8) имеет два решения:

тривиальное –      M₀ = I₀ = 0                               (9)

нетривиальное – M₀ = k₃ / k₁ I₀ = k₇ / k₅.             (10)

Нетрудно показать, что решение (9) устойчиво (оба характеристических числа линеаризованной в окрестности этого решения системы отрицательны), а решение (10) неустойчиво (характеристические числа разных знаков).

Качественную картину поведения динамической системы (5), (6) можно получить, используя изоклины (7), (8). Они разбивают фазовую плоскость на 4 области. Направления векторного поля в них схематично показаны на рис.1.

Важно оценить, насколько изменится качественная картина поведения, если изменить систему (5), (6). Рассмотрим более сложный вариант модели:

dI /dt = k₁ I M – k₃ I,                                                       (11)

dM/dt = k₅ I M ² (A²+M ²)^-1– k₇ M_.                                              (12)

Особые точки: M₀ = I₀ = 0 и M₀ = k₃ / k₁, I₀ = k₁ k₇ [A²+ (k₃ / k₁)²] / k₃ k₅. Качественную картину поведения см. на рис. 1.

Не очень приятное место моделей (5), (6) и (11), (12) – уход переменных в бесконечность в области выживания IV (рис.1). Посмотрим, нельзя ли устранить это, вводя квадратичные расходы в уравнение (6):

dI/dt = k₁ I M – k₃ I,                                                        (13)

dM/dt = k₅ I M –k₇ M –k₈ M ²                                          (14)

Качественную картину поведения см. на рис. 1.

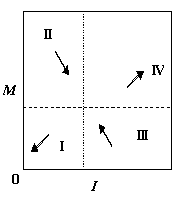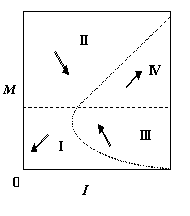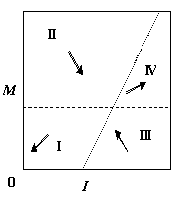
Рис. 1. Направления векторного поля в фазовой плоскости. Слева направо: для систем (5), (6); (11), (12) и (13), (14).

Видно, что фирма погибнет, если ее переменные находятся в области I, где dI/dt < 0 и dM/dt < 0, и будет развиваться, если они находятся в области IV, где dI/dt > 0 и dM/dt > 0.

Итак, в данной модели есть определенный порог для выживания фирм. Если знания и деньги ниже порога, фирма вымирает, если выше – появляются условия для дальнейшего развития и инновационной деятельности.

Качественное подобие систем и наличие порога выживания рассмотренных систем позволяет рассматривать систему (5), (6) как более простой случай.

2.3.2. Вторая модель

Для не взаимодействующей с другими фирмы уравнения модели имеют вид:

dI/dt = k₁ I M – k₃ I – k₄ I² M,                                          (15)

dM/dt = k₅ I M – k₇ M – k₈ I M².                                               (16)

Отметим характерные соотношения между коэффициентами, полученные при численном эксперименте для первой модели. Коэффициенты k₁ и k₅, k₃ и k₇, k₄ и k₈ соответственно одного порядка, а k₁ > k₃ >> k₄  и k₅ > k₇ >> k₈.

Именно такой выбор представляется наиболее естественным: в модели характерные значения знаний и денег порядка единицы. Первые неравенства в каждом случае характеризуют превышение скорости роста над устареванием, амортизацией и т.п. Вторые говорят о том, что роль “сдерживающих” последних слагаемых становится значимой только при больших размерах фирм.

Особые точки системы (15), (16) найдем из системы dI/dt = 0 и dM/dt = 0, т.е.

k₁ I M – k₃ I – k₄ I² M   = 0,                                             (17)

k₅ I M – k₇ M – k₈ I M² = 0.                                             (18)

В отличие от аналогичной системы (7), (8), система (17), (18) имеет три решения. Одно из них – тривиальное решение (9): M₀ = I₀ = 0.

Найдем остальные, решив систему (17), (18). Поделим на I ¹ 0 и M ¹ 0:

k₁ M – k₃ = k₄ I M,                                                           (19)

k₅ I  – k₇  = k₈ I M.                                                           (20)

Приравняв правые части получившихся уравнений с соответствующими коэффициентами и выразив I через M и наоборот, получим уравнения для M и I:

k₁k₈ M² + (k₄k₇ – k₁k₅ – k₃k₈) M + k₃k₅ = 0,                       (21)

k₅k₄ I²    + (k₈k₃ – k₁k₅ – k₄k₇) I  + k₇k₁ = 0,                        (22)

Каждое из квадратных уравнений (21), (22) имеет по два вещественных положительных корня, лежащих по разные стороны от единицы.

Большему корню для M соответствует больший корень для I и наоборот.

Например, для случая k₁=k₅=n k₃= n k₇ = n² k₄ = n² k₈ (n>1) больший и меньший корни каждого из уравнений (21) и (22) ~ n² и 1/n соответственно.

Тривиальное решение устойчиво (характеристические числа отрицательны).

Для нетривиальных решений линеаризованная система имеет вид:

dΔI/dt = (k₁M – k₃ – 2 k₄ I M) ΔI + (k₁ I – k₄ I² ) ΔM,       (23)

dΔM/dt = (k₅ M – k₈ M²) ΔI +( k₅ I – k₇ – 2 k₈ I M) ΔM.   (24)

После упрощений, с учетом (17) и (18), получаем:

dΔI/dt = (– k₄ I M ) ΔI + (k₃ I / M ) ΔM,                           (25)

dΔM/dt = ( k₇ M / I ) ΔI +( – k₈ I M) ΔM.                         (26)

Характеристическое уравнение линеаризованной системы имеет вид:

λ² + (k₄ + k₈) I M λ + k₄k₈ (I M)² – k₃k₇ =0.                         (27)

Его дискриминант всегда положителен и оно имеет два вещественных корня. Учитывая характерные значения коэффициентов и переменных, получаем, что положение равновесия с меньшими M и I неустойчиво (корни разных знаков), а с большими – устойчиво (оба корня отрицательны).

Качественный фазовый портрет представлен на рис. 2.

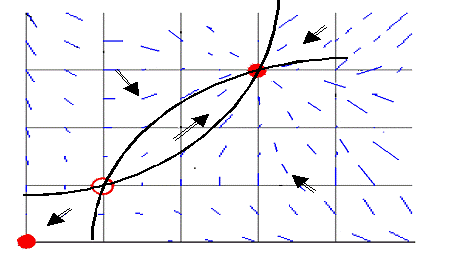
Рис. 2. Окружность – неустойчивое, сплошные круги – устойчивые равновесия.

Итак, введение в модель дополнительных нелинейных слагаемых качественно меняет ее поведение:

·          Полученная система имеет два аттрактора – (0,0) и положение равновесия с большими M и I. Тем самым устранен один из главных недостатков системы (5), (6) – уход переменных успешной фирмы в бесконечность.

·          Появилось устойчивое нетривиальное положение равновесия, параметры которого легко вычислить по коэффициентам системы (15), (16). Оно соответствует характерным размерам благополучной фирмы.

Вместе с тем, сохранился один из важнейших результатов для первой модели – наличие порога по знаниям и деньгам.

2.4.                    Динамика развития популяции фирм

2.4.1.  Первая модель

Рассмотрим модель в непрерывном времени:

dI_i /dt = k₁ I_i M_i + k₂ S_j I_j   – k₃ I_i,                                                (28)

dM_i/dt = k₅ I_i M_i – k₆ S_j M_j  – k₇ M_i , i, j=1..N, но j ¹ i.      (29)

После введения новых переменных (I_i^*= k₅ I_i  M_i^*= k₁M_i) и переобозначения

(k₂^* = k₂/k₅     k₃^* = k₃/k₅  k₆^* = k₆/k₁    k₇^* = k₇/k₁) получаем:

dI_i /dt = I_i M_i  + k₂ S_j I_j  – (k₃ + k₂) I_i,                                (30)

dM_i /dt = I_i M_i – k₆ S_j M_j  – (k₇ - k₆) M_i , i, j = 1..N.  (31)

Найдем положения равновесия системы (30), (31):

Лемма: Если k₂ k₆ ¹0 и в точке равновесия системы (30), (31) "i  I_i M_i ¹ 0 и $ такие k и l, что (I_k ,M_k) ¹ (I_l ,M_l), то I_k ¹ I_l  и M_k ¹ M_l , причем

k₂ k₆ ( S_j I_j )( S_j M_j )= – I_k M_k I_l M_l .                                          (32)

Доказательство: Рассмотрим A= I_k M_k I_l M_l (M_k - M_l). Из (30), (31) имеем:

A= I_k M_k I_l M_l (M_k - M_l) = M_k M_l (I_l* M_k I_k - I_k * M_l I_l) = M_k M_l (I_l* ((k₃ + k₂) I_k - k₂ S_j I_j) - - I_k *((k₃  + k₂) I_l - k₂ S_j I_j))= k₂ M_k M_l ( S_j I_j ) (I_k -I_l)= k₂  ( S_j I_j ) (M_l * M_k I_k  - M_k * M_l I_l)=

= k₂  ( S_j I_j ) (M_l * ((k₇  - k₆) M_k + k₆  S_j M_j)  - M_k *((k₇  - k₆) M_l + k₆  S_j M_j))=

= k₂ k₆ ( S_j I_j )( S_j M_j ) (M_l - M_k) = A= I_k M_k I_l M_l (M_k - M_l).  (33)

Т.о. (I_k = I_l) ó (M_k = M_l), значит I_k ¹ I_l  и M_k ¹ M_l, поскольку (I_k ,M_k) ¹ (I_l ,M_l) и все I_i M_i ¹ 0. Сокращая в (33) обе части на (M_l - M_k) ¹ 0, получим (32).

Следствие 1: в области допустимых значений параметров может находиться только положение равновесия, в котором параметры всех фирм одинаковы.

Следствие 2: в положении равновесия системы (30), (31) при условии

k₂k₆ ¹0, k₇ ¹ k_6, Nk₆/(k₇ - k₆) ¹1 существует не более 2 различных видов пар (I_k ,M_k).

Следствие 3: лемма 1 и формула (32), верны и при снятии условия I_i M_i ¹ 0.

Следствие 4: если в условиях следствия 2 ($ k: I_kM_k=0), то (" i  I_i  = M_i = 0).

Т.о. в условиях следствия 2 нет положений равновесия отличных от:

·        Тривиальное (все переменные равны нулю):

Рассматривая линеаризованную систему

dI_i /dt = k₂  S_j I_j  – (k₃  + k₂) I_i,                                           (34)

dM_i /dt = – k₆  S_j M_j  – (k₇ - k₆) M_i ,                                   (35)

получаем собственные значения

-(k₃ + k₂)                и        -(k₇ - k₆)                 кратности (N-1)

((N-1)k₂ - k₃)          и        (-(N-1)k₆ - k₇)        кратности 1

Данное положение равновесия устойчиво только при выполнении условий

k₄ > (N-1) k₂, k₇ > k₆                                           (36)

·        «Симметричное» – переменные всех фирм совпадают. Задается формулами

M = k₃ - (N-1) k₂                                                             (37)

I   = k₇ + (N-1) k₆                                                             (38)

Заметим, что (36) – необходимое и достаточное условие положительности всех переменных в «симметричном» положении равновесия.

Аналогично случаю одной фирмы получаем, что оно неустойчиво.

·        «Несимметричное»: (для некоторых коэффициентов) два вида наборов
(I_k ,M_k), причем как минимум для одного из них I_kM_k<0.

Итак, в рассматриваемой системе нет положений равновесия отличных от:

-          тривиальное (все переменные равны нулю);

-         «симметричное» (переменные всех фирм совпадают);

-         «несимметричное» (вне области допустимых значений параметров).

В отличие от случая одной фирмы, тривиальное положение равновесия не всегда устойчиво.

2.4.2. Вторая модель

Для N фирм качественная картина поведения отличается от таковой в первой модели. Рассмотрим «симметричные» нетривиальные положения равновесия.

Система для их нахождения аналогична (17), (18) и имеет вид:

k₁ I M – (k₃ – (N –1)* k₂) I – k₄ I² M= 0,                         (39)

k₅ I M – (k₇ + (N –1)* k₆)M – k₈ I M²=0.                         (40)

Нетрудно видеть, что если

(k₃ – (N –1)* k₂)>0[1],                                                       (41)

можно сделать замену

k₃^*= k₃ – (N –1)* k₂,                                                        (42)

k₇^*= k₇ + (N –1)* k₆.                                                       (43)

Для получившейся системы существует устойчивое «благополучное» положение равновесия, в котором переменные всех фирм больше единицы.

Изменения в коэффициентах в уравнениях (21) и (22) таковы, что равновесное значение I будет больше, чем равновесное значение для одной независимой фирмы, а значение M будет меньше. Этот результат неудивителен и характеризует положительное влияние взаимодействия между фирмами, в том числе конкуренции, заставляющей работать эффективнее.

Данное положение равновесия не единственно. Как и в случае одной фирмы существует еще одно (неустойчивое) нетривиальное положение равновесия, в котором переменные всех фирм одинаковы и меньше одного. Это пример негативного воздействия конкуренции – рынок оказался пересыщен. Со стороны руководства ИПК необходим постоянный мониторинг и вмешательство, если банкротство будет грозить не только наименее жизнеспособным. В данном случае ограничение свободы рынка неизбежно.

То же касается случая, если популяция попала в область притяжения тривиального аттрактора. В этом случае руководство технопарка должно или прямым вмешательством поддержать часть фирм, или закрыть часть из них для спасения остальных (либо вообще уничтожить данный рынок).

Итак, для N фирм качественная картина поведения отличается от таковой в первой модели:

Существует устойчивое положение равновесия, в котором переменные фирм равны и больше единицы (при этом знания больше, а деньги меньше, чем для независимой фирмы). Это пример удачного конкурентного взаимодействия. В области притяжения этого аттрактора внешнее вмешательство излишне.

Как и в случае одной фирмы существует еще одно (неустойчивое) нетривиальное положение равновесия, в котором переменные всех фирм одинаковы и меньше единицы. Это пример негативного воздействия конкуренции – рынок оказался пересыщен и, как правило, нуждается во вмешательстве извне. В противном случае есть опасность гибели популяции.

Характерный размер знаний и денег в этом положении равновесия является показателем существующих экономических барьеров для входа на рынок.

2.5.        Случай двух фирм

Интересные результаты были получены для случая двух фирм. По первой модели приводятся результаты численного моделирования, выполненного аспирантом МИЭТ М.А. Ляшко. По второй модели был рассмотрен важный частный случай.

2.5.1.  Первая модель

Моделирование проводилось для системы уравнений

D I_i  = k₁ I_i M_i  + k₂  I_j   – k₃ I_i,                                           (44)

D M_i = k₅ I_i M_i – k₆  M_j  – k₇ M_i ,  i, j = 1,2, но j ¹ i.           (45)

Взаимодействие пары одинаковых фирм

Фазовый портрет аналогичен таковому для случая одной фирмы: точка отталкивания, два аттрактора и разделяющая их сепаратриса. В результате серии экспериментов показано, что увеличение k₂ приводит к смещению сепаратрисы вниз и влево, т.е. увеличение информационного обмена может перевести пару фирм из состояния разорения в состояние процветания.

Пример расчета представлен на рис. 3. Значения коэффициентов k₃,k₇ = k₁,k₅=0.01, k₂,k₆=0.001. Число шагов итерации N~1000. Большие круги – аттракторы, маленькие – начальные координаты фирмы, окружность – точка отталкивания. Жирные линии – траектории движения фирм с различными начальными переменными.

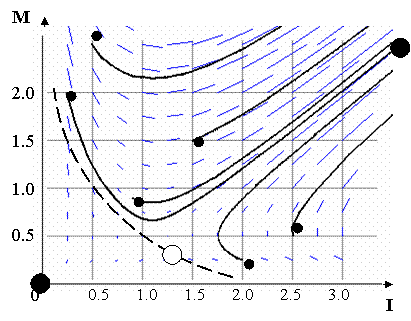
Рис. 3. Приращения знаний и денег пары фирм.

Взаимодействие двух сбалансированных фирм

Рассмотрим поведение двух фирм с различными начальными переменными: I₁~1.5, M₁~0.5, I₂~0.5, M₂~1.5. Параметры k_i те же, что и в условиях эксперимента рис. 3. Результаты эксперимента приведены на рис. 4.

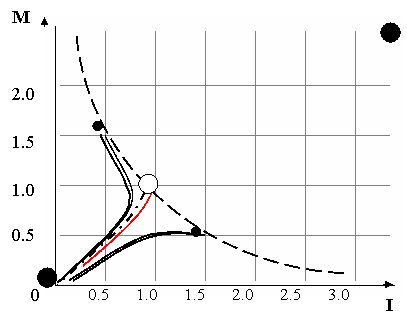
Рис. 4. Поведение двух сбалансированных фирм

Штрихпунктирной линией изображено изменение средних знаний и денег системы двух фирм. Остальные обозначения как на рис. 3.

Увеличение k₂ до 0.005 изменяет положение особой точки и сепаратрисы, и обе фирмы могут попасть в область притяжения аттрактора (∞,∞) и процветать.

Соотношение между k₂ и k₆ может привести к обострению конкуренции между фирмами, когда одна разоряется, а другая процветает. Для этого k₂ должно лежать между его значениями в предыдущих экспериментах (0.0025).

Результаты эксперимента приведены на рис. 5.

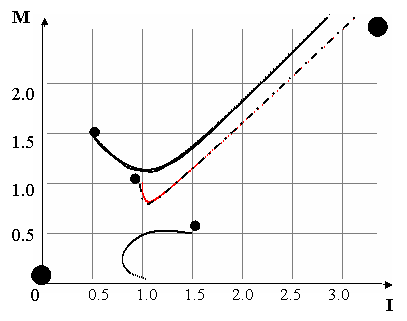
Рис. 5. Конкуренция между двумя сбалансированными фирмами.

Итак, фазовый портрет для пары одинаковых фирм аналогичен таковому для случая одной фирмы: одна точка отталкивания, два аттрактора и разделяющая их сепаратриса. Увеличение информационного обмена способно перевести пару фирм из состояния разорения в состояние процветания.

Соотношение между коэффициентами k₂ и k₆ может привести к обострению конкуренции между фирмами, когда одна разоряется, а другая процветает.

2.5.2.  Вторая модель

Рассмотрим следующий частный случай:

k₁=k₅, k₂= k₆, k₃= k₇, k₄ = k₈.                                           (46)

Найдем особые точки, в которых фирмы различны, решив систему:

k₁ I₁ M₁ + k₂ I₂  – k₃ I₁ – k₄ I₁² M₁=0,                                (47)

k₁ I₁ M₁ – k₂ M₂  – k₃ M₁ – k₄ I₁ M₁² =0,                            (48)

k₁ I₂ M₂ + k₂ I₁  – k₃ I₂ – k₄ I₂² M₂=0,                                (49)

k₁ I₂ M₂ – k₂ M₁  – k₃ M₂ – k₄ I₂ M₂² =0 ,                            (50)

Вычитая из (47), умноженного на M₁ (48), умноженное на I₁, получим:

k₁ I_l M_l (M₁ – I_l) = – (I_l M₂ + I₂ M_l) = k₁ I₂ M₂ (M₂ – I₂)         (51)

Из условия положительности переменных и коэффициентов следует M_i – I_i <0

Складывая (47) и (50) и вычитая (48) и (49), с учетом (51) получим:

(k₃– k₂) (M₂ – M₁) = (k₃+ k₂) (I₂ – I₁),                              (52)

Рассмотрим случай сильного взаимодействия между фирмами – k₃= k₂.

При этом очевидно I₂ = I₁= I.

После всех сокращений система (47)-(50) примет вид:

k₁   – k₄ I =0,                                                                  (53)

k₁ I M₁ – k₂ (M₂  + M₁)– k₄ I M₁² =0,                                (54)

k₁   – k₄ I =0,                                                                  (55)

k₁ I M₂ – k₂ (M₂  + M₁) – k₄ I M₂² =0,                                (56)

Из (52) получаем I = M₂  + M₁                                   (57)

После чего из (54), (55) и (57) получаем

I = k₁ / k₄,                                                                        (58)

k₄ M²  – k₁M + k₂ = 0,                                                      (59)

Корнями последнего уравнения являются деньги обеих фирм. Как было отмечено выше, один из них заметно больше второго.

Линеаризованная система в окрестности этого положения равновесия имеет вид (после упрощений с учетом (53)-(59))

dΔI₁/dt = (– k₁ M₁ – k₂) ΔI₁ + k₂ ΔI₂,                                (60)

dΔM₁/dt =  k₂ ΔI₁+( k₁ M₂ – k₁ M₁ – k₂) ΔM₁ – k₂ ΔM₂,     (61)

dΔI₂/dt =  k₂ ΔI₁ + (– k₁ M₂ – k₂) ΔI₂,                               (62)

dΔM₂/dt = – k₂ ΔM₁ +  k₂ ΔI₂ + ( k₁ M₁ – k₁ M₂ – k₂) ΔM₂.          (63)

Матрица системы содержит нулевую подматрицу второго порядка, не содержащую диагональных элементов (элементы 12,14,32,34), следовательно, характеристическое уравнение легко раскладывается на множители. Имеем:

(λ^*+ k₁ M₂ – k₁ M₁) (λ^*+ k₁ M₁ – k₁ M₂) – k₂² =0, или      (64)

(λ^*+ k₁ M₂) (λ^*+ k₁ M₁) – k₂² =0,                                     (65)

где λ^*= λ+ k₂.                                                                (66)

Из (64) получаем

(λ+ k₂)² = (k₁ M₂ – k₁ M₁)²+ k₂².                                  (67)

Т.о. больший корень положителен и это положение равновесия неустойчиво.

Экономический смысл получившегося положения равновесия достаточно прозрачен – одна из фирм фактически «выжила» такую же по «знаниям» фирму с рынка. Этот случай требует вмешательства руководства технопарка для обеспечения конкуренции и перевода системы в состояние «благополучного» устойчивого равновесия.

3.            Взаимодействие государств в информационной среде

Изложенная выше модель может быть естественным образом перенесена на случай эволюции популяции государств в информационной среде. Например, исходя из уравнений (44), (45) или их аналогов для второй модели, мы можем исследовать следующую задачу. Пусть есть два государства: Россия и США. Что делать России? Стремиться изолироваться от Америки (уменьшать k₂ и k₆ до нуля и развиваться независимо от США) или увеличивать информационный обмен (увеличивать k₂), с тем, чтобы развиваться кооперативно со США?

3.1.        Первая модель

В данной серии экспериментов, также проведенных М.А. Ляшко, было исследовано поведение двух обособленных стран (названных условно "Россия" и "Америка"). Можно считать, что их научные потенциалы одного порядка: I₁ = I₂, а экономика России существенно слабее американской: M₁ < M₂.

Для моделирования были взяты следующие значения переменных и параметров: для первой страны (Россия) I~1.0, M~0.75, для второй (Америка) – I~1.0, M~1.25; k₁= k₄ = k₅ = k₇ =0,01; k₂ = 0,005; k₆ = 0,001. Этот случай сравнивался со случаем отдельного существования каждой из стран (k₂ = k₆ =0).

Результаты показаны на графиках.

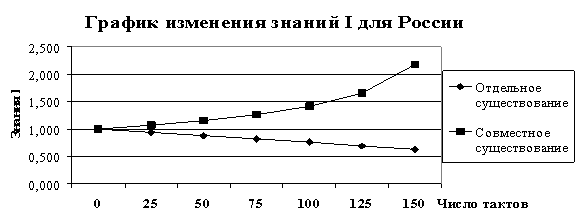
Рис. 6. Знания России при самостоятельном и совместном существовании

Линейное уменьшение знаний слабого государства при самостоятельном существовании приводит, в конечном счете, к его разорению. При кооперации информационный обмен позволяет более слабому государству выживать.

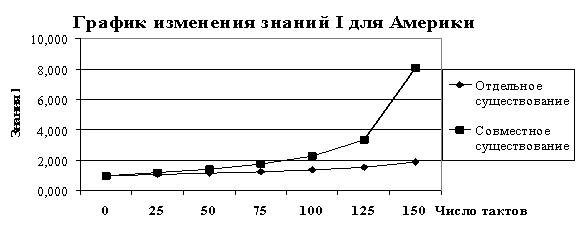
Рис. 7. Знания Америки при самостоятельном и совместном существовании

Сильное государство способно на самостоятельное существование и развитие. Однако линейный рост его знаний при самостоятельном существовании сменяется практически экспоненциальным при кооперации.

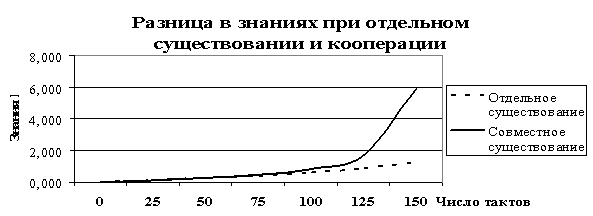
Рис. 8. Разница в знаниях между государствами.

Сильное государство не просто увеличивает скорость своего развития, начинает возрастать разрыв между сильным и слабым государством.

Аналогичная ситуация происходит и по второй переменной – по деньгам.

Итак, в рассмотренной модели совместное существование выгодно и для России, и для Америки. На графиках отчетливо видно увеличение и знаний и денег при совместном существовании двух государств:

-         совместное существование и информационный обмен позволяют слабому государству перейти от разорения к выживанию и дальнейшему развитию;

-         сильное государство в результате кооперации и информационного обмена увеличивает скорость своего развития и увеличивает отрыв от слабого государства и по знаниям, и по деньгам.

3.2.        Вторая модель

В данной модели сама постановка эксперимента должна быть несколько иной, поскольку «знания» получили новую трактовку: речь идет не только и не столько о научных достижениях и технологиях, сколько об умении их эффективно использовать. Очевидно сейчас уровень «технологичности» (будем так называть «знания» в рамках модели взаимодействия государств) отличается достаточно сильно и также не в пользу России.

При моделировании важно различить ситуации, описанные в п.п. 3.1 и 2.5.2. В первом случае совместное существование оказывалось выгодным для обоих агентов, во втором – более сильный агент подавлял менее сильного даже несмотря на одинаковый уровень «технологичности».

По-видимому, следует рассмотреть данную модель при различных возможных уровнях открытости. Неприемлемость крайних вариантов для слабого агента следует из п. 2.5.2 (случай полной открытости и максимально сильного взаимодействия ведет к подавлению более сильным) и п.3.1. (банкротство в случае изолированного существования). Исследование степени разумной открытости может рассматриваться как продолжение данной работы.

4.        Заключение

§        Разработаны два варианта моделей эволюции многоагентной экономической системы в информационном сообществе. Модели рассматриваются в применении к двум системам – популяции малых высокотехнологичных фирм в структуре технопарка и популяции государств в информационном сообществе.

§        Проведен сравнительный анализ моделей и показано, что

-         первая модель является более грубой и может рассматриваться как частный случай второй при малых значениях переменных

-         введение в модель дополнительных нелинейных слагаемы качественно меняет ее поведение.

Первая система не имела устойчивых особых точек за исключением нулевого положения равновесия. Во второй модели есть два аттрактора – (0,0) и положение равновесия с большими M и I. Таким образом устранен один из главных недостатков первой модели – уход переменных в бесконечность при успешной деятельности фирмы.

Кроме того, появилось устойчивое нетривиальное положение равновесия, параметры которого легко вычислить по коэффициентам системы. Оно соответствует характерным оптимальным размерам благополучной фирмы.

Вместе с тем, сохранился один из важнейших результатов для первой модели – наличие порога по знаниям и деньгам. Если знания и деньги ниже порога, фирма вымирает, если выше – появляются условия для дальнейшего развития и инновационной деятельности.

Существует устойчивое положение равновесия, в котором переменные фирм равны достаточно велики (при этом знания больше, а деньги меньше, чем для независимой фирмы). Это пример удачного конкурентного взаимодействия. В области притяжения этого аттрактора внешнее вмешательство излишне.

Характерный размер знаний и денег в этом положении равновесия является показателем необходимости слияний и поглощений или разделений компаний.

Существует еще одно неустойчивое положение равновесия, отличное от тривиального, в котором переменные параметры всех фирм одинаковы и малы. В данном случае воздействие конкуренции является негативным – рынок оказался пересыщен и нуждается во вмешательстве извне. В противном случае есть опасность гибели популяции.

Характерный размер знаний и денег в этом положении равновесия является показателем существующих экономических барьеров для входа на рынок.

Получены интересные результаты, касающиеся взаимодействия между государствами. Для первой модели рассмотрен пример взаимодействия двух одинаковых по знаниям, но отличающихся по деньгам агентов и показано, что в ряде ситуаций информационный обмен позволяет обоим государствам развиваться более быстро по сравнению с отдельным существованием.

При естественном наборе параметров для слабого государства вопрос кооперации с сильным означает выживет государство или нет, а сильное государство способно выжить самостоятельно. Однако информационный обмен позволяет сильному государству ускорить темп своего развития и увеличивать отрыв от слабого и по знаниям, и по деньгам.

Вместе с тем, во второй модели при рассмотрении частного слуучая сильного взаимодействия было получено, что более сильный агент может подавлять более слабого. Исследование степени разумной открытости рассматривается как естественное продолжение данной работы.

5.        Литература

1.      Leigh Tesfatsion, "Agent-Based Computational Economics: A Brief Guide to the Literature", prepared for the Reader's Guide to the Social Sciences, Fitzroy-Dearborn, London, UK, 1998 www.econ.iastate.edu/tesfatsi/surveys.htm

2.      LeBaron, B. "Agent Based Computational Finance: Suggested Readings and Early Research" Working Paper, Brandeis University, 1999, to appear in the Journal of Economic Dynamics and Control www.econ.iastate.edu/tesfatsi/surveys.htm

3.      Tesfatsion, L "How Economists Can Get Alife" in W. Brian Arthur, Steven Durlauf, and David Lane (eds.), The Economy as an Evolving Complex System, II, Santa Fe Institute Studies in the Sciences of Complexity, Volume XXVII, Addison-Wesley, 1997. pp. 533—564.

4.      А.К. Гуц, В.В. Коробицын, А.А. Лаптев, Л.А. Паутова, Ю.В. Фролова “Социальные системы. Формализация и компьютерное моделирование”. Омск, 2000, стр. 21-27, 40-43.

5.     Редько В.Г., Тухвебер С. М. “Модель эволюции популяции малых фирм в условиях технопарка”, Математика, компьютер, образование. Тезисы VIII Конференции, Пущино, 2001, с. 385, Москва: “Прогресс-Традиция”.

6.     Ляшко М.А., Редько В.Г., Тухвебер С.М. Модель эволюции взаимодействующих агентов в популяции высокотехнологичных фирм // Рефлексивные процессы и управление. Тезисы III Международного симпозиума 8-10 октября 2001 г., Москва / Под редакцией А.В. Брушлинского и В.Е. Лепского - М.: Изд-во "Институт психологии РАН", 2001. - 242 с. С. 154-156

7.     Ляшко М.А., Тухвебер С.М., Редько В.Г. "Модель эволюции популяции высокотехнологичных фирм". Электронный журнал "Исследовано в России", 08, стр. 109-110, 2002 г. zhurnal.ape.relarn.ru/articles/2002/008.pdf

8.     Тухвебер С.М. “Модель эволюции многоагентных экономических систем в информационном сообществе” – выпускная квалификационная работа на степень магистра, Москва, 2003 г.