Аннотация
В работе рассмотрены несколько математических моделей влияния возрастного состава экологической
популяции на ее развитие. Моделирование проводится путем численного решения динамической
системы дифференциальных уравнений (обыкновенных и в частных производных), относящейся к классу
Вольтерровских систем и матриц Лесли.
Abstract
The review of models of age structure influence on ecological population dynamics is presented.
We consider a number of dynamical systems of ordinary and PDE differential equations based on
classic Volterra model and Leslie matrixes approach.
§1. Базовая модель
В последнее время для решения практических задач все шире применяется
моделирование динамики развития экосистем на основе дифференциальных и
интегро-дифференциальных уравнений. Данный подход широко используется для
моделирования разнообразных биологических сообществ и, в частности, лесных
массивов [1-3]. Наибольшую сложность при этом представляют два момента:
·
правильный выбор уравнений, особенно входящих в них
параметров, описывающих величину влияния тех или иных параметров на состояние данного
участка экосистемы;
·
адекватное моделирование возрастных эффектов, а также
пространственного распределения неоднородных экосистем.
В данной
работе мы рассматриваем различные возрастные эффекты в лесных биоценозах на
основе численного моделирования обыкновенных дифференциальных, и
дифференциально-разностных уравнений, а также дифференциальных уравнений в
частных производных. Прежде всего, представим упрощённую модель развития
двувидового леса, описывающую эволюцию популяции как единого целого, не учитывающую
ни пространственного распределения, ни возрастных эффектов. На этом этапе, по
сути, выражающем глобально-экологические требования, необходимо адекватно
определить характер основных взаимодействий.
Будем
характеризовать популяцию вектором
плотности биомассы 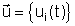 , i=л (лиственные породы), х(хвойные). Ограничимся
двухуровневой системой трофических взаимодействий типа «ресурс - потребитель»
[2,3]: почва - конкурирующий между собой двувидовой лес. Состояние почвы
характеризуем третьей переменной - обобщённым показателем плодородия Р(t).
Динамическая система, использованная нами для описания данной сосредоточенной
модели, выглядит следующим образом [5]: , i=л (лиственные породы), х(хвойные). Ограничимся
двухуровневой системой трофических взаимодействий типа «ресурс - потребитель»
[2,3]: почва - конкурирующий между собой двувидовой лес. Состояние почвы
характеризуем третьей переменной - обобщённым показателем плодородия Р(t).
Динамическая система, использованная нами для описания данной сосредоточенной
модели, выглядит следующим образом [5]:
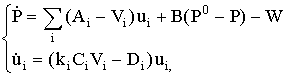 i = {х, л} (1) i = {х, л} (1)
·
P – обобщённый показатель плодородия – плотность ресурса
(кг/м2);
·
uл – плотность биомассы лиственных пород (кг/м2);
·
uх – плотность биомассы хвойных пород (кг/м2);
·
Аi – коэффициент восстановления почвы за счёт
опада i-ой породы (1/год);
·
В – коэффициент самовосстановления почвы (1/год);
·
Р0 – асимптотическое значение плодородия в отсутствие
леса (кг/м2);
·
Vi – скорость потребления ресурса (трофическая
функция) (1/год);
·
сi – поправочный множитель, описывающий
конкуренцию;
·
ki – коэффициент роста i–ой породы;
·
Di – коэффициент естественной смертности
деревьев (1/год);
·
W – влияние внешних факторов, чаще пагубное, поэтому с
отрицательным знаком,
(кг/(год×м2))
·
t0 – среднее время взросления молодого леса
(год)
Данная
система, как нетрудно видеть, является обобщением классической модели Вольтерра
[4]. Коэффициенты являются комбинацией экспериментально установленной константы
(определяющей развитие популяции в нормальных условиях) и некоторой поправочной
функции. Явный вид коэффициентов обсуждался нами в работе [6], и там же приводились
типичные графики решения системы (1).
Одно из
решений, соответствующее развитию леса в нормальных условиях (при достаточном
увлажении), представлено на рис. 1. Оно описывает в хорошо известное
явление смены лиственного леса хвойным на протяжении развития популяции.
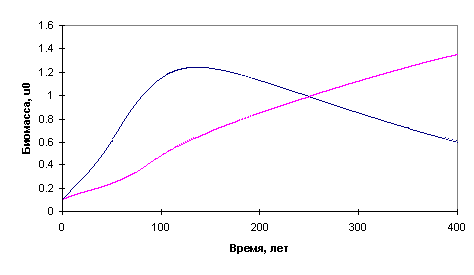
Рис.1. Типичное решение системы (1).
Надо сразу
заметить, что сосредоточенная модель (1) допускает лишь самый грубый учет
возрастных эффектов, т.к. в уравнения входят суммарные плотности биомассы (без
деления на возрастные группы). Например, в расчетах, приведенных на
рис. 1, мы (посредством
соответствующей поправочной функции) учитывали [6], что коэффициент
естественной смертности Di существенно зависит от среднего возраста
популяции.
Сделав эти
предварительные замечания, можно переходить к основной теме данной работы –
различным моделям лесных популяций с неоднородным возрастным составом.
§2. Матричная модель Лесли
Матричное исчисление для описания развития сложных многовидовых популяций
(применительно к сосредоточенным моделям) было предложено Лесли [7] в середине
века. До сих пор упомянутые экологические модели опирались на методы
дифференциального исчисления. Это уже само по себе является некоторым
приближением. При переходе к практическим расчётам, например, по данным
демографических таблиц, приходится иметь дело с дискретными величинами.
Например, в демографии человека, как правило, используются пятилетние временные
интервалы. Кроме того, развитие многих популяций (в том числе, лесов) имеет
ярко выраженный сезонный характер. Поэтому для правильного описания популяции и
для практических расчётов скорее применимы не методы дифференциального и
интегрального исчисления, а методы дискретной математики (матричные и т.п.).
Лесли предложил для описания сложной
многовозрастной популяции использовать так называемую переходную матрицу
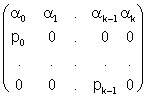 , (2) , (2)
которая при
умножении на вектор-столбец численностей особей разных возрастных классов (от
нулевого – новорожденных особей, до k-го – самых cтарых особей) даёт
численность особей в возрастных группах через определённую единицу времени
(чаще всего, год). Таким образом, в переходной матрице Лесли pi –
это выживаемость (т.е. вероятность того, что особь i-го класса перейдёт на
следующий год в (i+1)-й), ai – средняя плодовитость сособей i-й возрастной группы.
Таким образом, матрица перехода представляет собой
квадратную матрицу размером (k+1)´(k+1), а вектор-столбец численностей возрастных групп –
матрицу (k+1)´1. Если
элементы матрицы постоянны, т.е. не меняются со временем, то из их
неотрицательности следует, что максимальное по модулю собственное число матрицы
действительно и положительно. Если максимальное собственное число меньше
единицы, то популяция обречена на вымирание, если больше – происходит неограниченный
рост популяции. У примитивных матриц Лесли максимальное собственное число равно
единице. Это означает, что популяция будет со временем стремиться к некоторому
устойчивому возрастному распределению, задаваемому собственным вектором,
соответствующим максимальному собственному числу, а скорость роста популяции
будет определяться этим собственным числом.
При популяционно-динамическом описании необходимо прежде всего учитывать
различие в способности особей к размножению
[2]. С этой целью обычно выделяют три группы: прегенеративных (молодых,
ещё не способных к размножению), генеративных (способных к размножению, но не
обязательно размножающихся в данный момент) и постгенеративных (старческих, уже
утерявших способность к размножению). В зависимости от особенностей жизненного
цикла конкретного вида и при наличии надёжных диагностических признаков каждая
из этих больших групп разбивается на более мелкие возрастные категории.
Необходимо отметить, что деление популяции на возрастные группы оправдано с
практической точки зрения в тех случаях, когда организмы данного вида обладают
признаками, позволяющими определить точно возраст особи. Применительно к нашим
моделям, в случае лесной популяции, возраст отдельного дерева может быть точно
определён с помощью годичных колец.
Рассмотрим теперь приложение матриц
Лесли к модели, введенной в §1. Напомним, что эта базовая модель описывала лесной
массив без учета возраста. Устойчивость
растений к засухе, заболачиванию, затенению, загрязнению, низовым пожарам,
заболеваниям и другим факторам в значительной мере зависит от возраста.
Далее мы опускаем
индекс вида, так как выкладки от
него не зависят. Индекс вида появится только в окончательном результате. Надо
учесть также, что если интервалы возрастных групп гораздо больше шага по времени, то надо учитывать распределение по возрастам в
пределах самой группы. Число возрастных
групп может быть небольшим, например, 4
группы на каждый типичный интервал возраста: молодой лес, лес репродукционного
возраста и лес перестойный (не дает
семян). То-есть всего 12 групп. Однако до начала расчета это распределение неизвестно. Вполне возможен
вариант, когда на каждом шаге по времени производится уточнение распределения
внутри группы, например, путем интерполяции по значениям групповых переменных на шаг по времени. Затем проводится
уточнение групповых констант. Мы
выбираем более простой путь: делается
предположение о распределении по возрастам априори, а затем находятся
групповые константы. На самом деле эти
«константы» могут зависеть от групповых
переменных. Это дает гарантию
корректировки групповых констант в
соответствии со значениями групповых
переменных.
Чтобы определить коэффициенты
перехода из группы в группу, прибегнем к дискретной схеме (рис.2). Пусть
возрастная группа включает р лет
и мы рассматриваем установившийся режим, когда на вход группы поступает одно и
то же значение биомассы 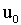 . .
        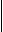 

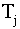 1 2
3 4
1 2
3 4
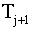
Рис.2. Схема, поясняющая модель Лесли
Тогда на каждый год по возрасту мы будем иметь такие плотности биомасс:
1 год=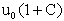 , 2 год= , 2 год=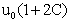 , 3 год= , 3 год=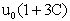 , ... р год= , ... р год=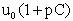
Здесь С коэффициент, показывающий, насколько увеличивается исходная плотность биомассы за год. Эта величина
обычно составляет 0.1-0.18 и
зависит от группы, плотности биомассы, плодородия и др. Однако в пределах группы она меняется мало. Если брать группы
по порядку 10 лет, то
принятый нами линейный закон прироста в группе вполне оправдан.
Доля биомассы от массы группы, которая за каждый год приходит в другую
группу, можно определить
отношением:
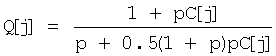 (3) (3)
Это следует из того, что полный объем биомассы в группе есть сумма всех
объемов по годам: 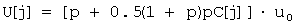 . Учитывая эти замечания, можно получить [5], что . Учитывая эти замечания, можно получить [5], что
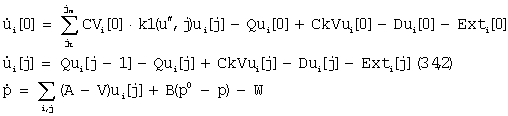 (4) (4)
Как мы видим, эволюция функций ui[j] описывается уравнениями,
схожими с системой (1), но вместо коэффициентов Ci0 и Di0
вводятся массивы прироста и умирания Ci0[j] и Di0[j] соответственно.
Учёт возраста, очевидно, должен быть произведён и с учетом различного отношения молодых и старых
деревьев к засухе, заболоченности и т.д. Для этого применяются соответствующие
поправочные функции, по аналогии с базовой моделью (1). При этом, разумеется,
они так же, как и неизвестные функции, становятся векторными, т.к. представляют
возрастные особенности по отношению к засухе, заболачиванию, затенению,
загрязнению и другим факторам. Например, они учитывают, что наиболее сильно страдают
от недостатка воды молодые деревья., а зрелые деревья устойчивее и относительно
заболачиваемости, так как обладают более глубокой корневой системой. Для записи
системы уравнений модели (4) мы используем
такой прием сокращения: в произведении функций одинаковой структуры
будем указывать индексы лишь правого
сомножителя: запись 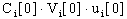 эквивалентна эквивалентна 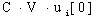 . .
Общее число дифференциальных
уравнений: 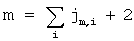 . Здесь . Здесь 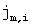  максимальное число
групп максимальное число
групп 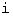 -го вида, еще два
уравнения для продуктивности почвы и толщины увлажненного слоя). Размер
возрастной группы р лет. -го вида, еще два
уравнения для продуктивности почвы и толщины увлажненного слоя). Размер
возрастной группы р лет.
Приведём теперь некоторые результаты моделирования, опирающиеся на систему
уравнений (4) с учётом возрастного состава лесной популяции. Ширина каждой
возрастной группы составляла 10 лет. На рис. 3 развитие леса в обобщенной модели: при нормальном увлажнении (устойчивая смена смешанного леса на хвойный, как и в базисной
модели на рис. 1). Однако здесь есть колебания плотности биомассы, связанные
с колебаниями среднего возраста (рис.4.). В целом можно признать, что модель с
учётом возраста на основе матриц Лесли более реалистична и сохраняет те же
основные свойства, что и базисная модель
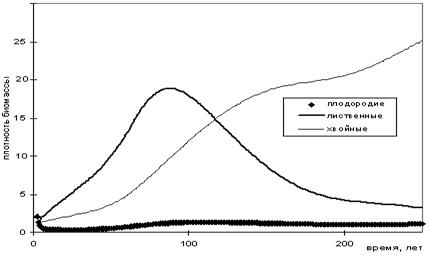
Рис.3..Устойчиво развивающаяся популяция деревьев
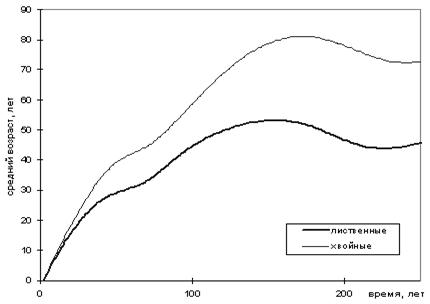
Рис.4. Колебания среднего возраста деревьев
§3. Модель моновозрастной посадки
Рассмотрим теперь еще одну модель, описывающую эволюцию
массива саженцев одного возраста, учитывая
ежегодное размножение семенами, порог возраста для начала размножения, а
также внутривидовую конкуренцию и
«экологические» вырубки (определяются
только состоянием массива), сохраняющие автономность.
Мы используем следующую
дискретную систему координат. По
оси ординат будем откладывать
номер поколения. По оси абсцисс будем откладывать время. Если для простоты записи считать возраст
саженцев нулевым, то на координатной плоскости будет в начальный момент всего одна точка. Новые поколения будут появляться с учетом порога для размножения, а,
появившись, они начинают
перемещаться вдоль оси времени,
«синхронно старея».
Тогда можно записать для каждого поколения свое
эволюционное уравнение баланса:
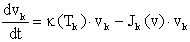 , (5) , (5)
где 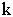 номер
поколения, номер
поколения, 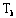 возраст поколения
к на данный момент времени t, возраст поколения
к на данный момент времени t,
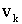 плотность биомассы
к-го поколения, плотность биомассы
к-го поколения, 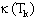 есть разность
коэффициентов естественного прироста и естественной смертности, есть разность
коэффициентов естественного прироста и естественной смертности, 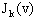 некоторая функция,
зависящая от всего вектора плотности поколений некоторая функция,
зависящая от всего вектора плотности поколений 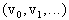 (длина вектора зависит
от того времени, на котором мы будем рассматривать
нашу систему, т.е. не постоянна). (длина вектора зависит
от того времени, на котором мы будем рассматривать
нашу систему, т.е. не постоянна).
Эта функция может
выражать внутривидовую конкуренцию:
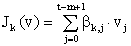 , (6) , (6)
где m репродукционный возраст, t-m+1
дает полное число поколений на
момент времени t, 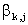 коэффициенты
конкурентного взаимодействия поколений
k и j
, т.е. это квадратичные члены конкуренции. коэффициенты
конкурентного взаимодействия поколений
k и j
, т.е. это квадратичные члены конкуренции.
Будем решать
уравнение для поколения к на интервале времени в один год, считая при этом к(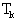 ) и ) и 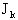 некоторыми известными
функциями от номера поколения. Тогда можно написать: некоторыми известными
функциями от номера поколения. Тогда можно написать:
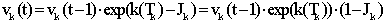 (7) (7)
В этой записи мы
учли, что величина 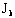 невелика по
сравнению с невелика по
сравнению с 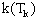 и поэтому можно разложить и поэтому можно разложить 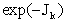 в ряд,
ограничившись первым членом
разложения. Если теперь ввести
обозначения для второго сомножителя в
последнем произведении: в ряд,
ограничившись первым членом
разложения. Если теперь ввести
обозначения для второго сомножителя в
последнем произведении:
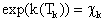 , (8) , (8)
то можно получить счетную схему для перехода со слоя времени
t-1 на слой t , если к ней добавить недостающее значение вновь
созданного поколения на слое t :
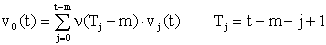 (9) (9)
Мы видим, что значения поколения только что народившегося
на данном временном слое t получается из
значений поколений также на слое t. В случае учета конкуренции интеграл
приходится вычислять, используя данные с предыдущего временного слоя.
Если подходить к
системе уравнений для поколений как к динамической системе, то можно
обосновать устойчивость и аппроксимацию
схемы и тем самым обосновать сходимость схемы [8].
Поскольку
предложенная система
уравнений (без конкуренции и
выборки) линейная, то она будет вести
себя как логистическая модель без вольтерровского члена конкуренции. Это значит, что она либо
неустойчива, либо имеет всего одно устойчивое состояние равновесия нуль. Между тем проведенные расчеты (рис. 5)
для некоторого варианта лесного массива показывают, что расходимость очень медленная. Только к 320 году происходит заметное увеличение
общей плотности посадки. Схема
правильно отражает и начальный период, когда установление профиля возрастного
распределения еще не произошло.
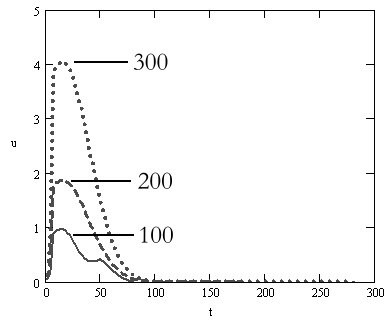
Рис.5.Эволюция возрастного спектра моновозрастной посадки
(для 100, 200 и 300-летних популяций)
Численное решение той же задачи, но с конкуренцией,
приводит к результатам, когда
установление стационарного профиля наступает для 120 года существования посадки. Что же касается абсолютных значений биомасс, то они
устанавливаются позже (около 200 года).
Отсюда можно сделать заключение, что моновозрастные
посадки не дают естественного
распределения лесного массива по
возрастам. За обозримое время мы имеем дело с
переходным периодом, что наблюдается на практике.
Гораздо эффективнее с точки зрения времени выхода на стационарный профиль и стационарное значение биомасс
оказываются «экологические» вырубки. На рис. 6 приведены данные расчетов по
той же схеме, но вместо конкуренции
введена вырубка. Вырубка
проводятся до тех пор, пока общая биомасса
не снизилась до некоторого критического значения. Возраст вырубаемых
деревьев 40-45 лет, вырубается 5 %. Естественный профиль и асимптотические
значения биомасс устанавливаются
значительно быстрее, чем при конкуренции.
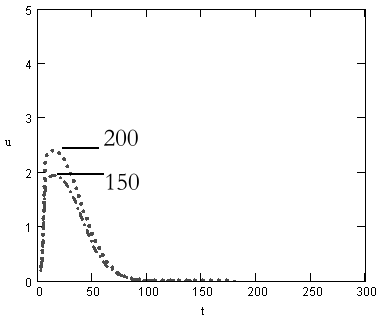
Рис.6. Эволюция возрастного спектра моновозрастной посадки
(для 150 и 200-летних популяций): модель с
вырубкой
§4. Непрерывная диффузионная модель
Ниже мы рассмотрим непрерывную модель возраста,
позволяющую описать эффект репродукционного порога. В качестве биологической переменной здесь будет функция двух переменных:
времени t и возраста
Т. В таком случае u(t,T) dT
есть количество биомассы,
заключенной в интервале возрастной переменной
(Т, Т+dT).
Подсчитаем баланс
для возрастной группы в интервале Т,Т+dT
за время 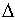 t : t :
·
u(t, T)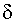 T столько биомассы
входит за время T столько биомассы
входит за время 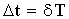 (где та же величина воспринимается как
возрастной интервал) с левого конца, (где та же величина воспринимается как
возрастной интервал) с левого конца,
·
u(t,T+dT)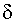 T такое количество
биомассы покидает группу за время T такое количество
биомассы покидает группу за время 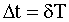 с правого края группы, с правого края группы,
·
u(t,T) 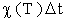 изменение биомассы за
счет процессов естественной смертности, прироста и процессов внутривидовой борьбы: изменение биомассы за
счет процессов естественной смертности, прироста и процессов внутривидовой борьбы:
   Левая граница Правая граница Левая граница Правая граница

Рис.7. К построению временной сетки
В последнем случае
в 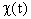 входит интеграл по
биомассам всех возрастов. входит интеграл по
биомассам всех возрастов.
Учтем, что
биомасса группы dT равна u(t,T)dT :
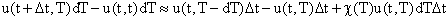
Переходя к пределу и сокращая на произведение
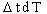 ,найдем полный вид
уравнения : ,найдем полный вид
уравнения :
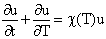 (10) (10)
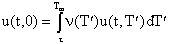 граничное условие
(11) граничное условие
(11)
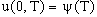 где где 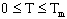 , , 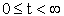 начальное условие начальное условие
В граничном условии на левом конце возрастного интервала
- интеграл вычисляется по всему репродукционному периоду. Функция 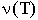 дает производительность взрослой биомассы по семенам. дает производительность взрослой биомассы по семенам.
Здесь 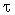 репродукционный
возраст, репродукционный
возраст,  правая граница репродукционного возраста. правая граница репродукционного возраста.
Для решения
проблем, связанных с устойчивостью, мы
сведем это уравнение к уравнениям с запаздывающим аргументом, для которых этот
вопрос хорошо разработан. Для этого рассмотрим замену искомой функции (рис. 8):
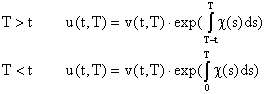 (12) (12)
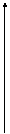 t
t
t>T
T>t

0 T
Рис.8. К построению временной сетки
Подставляя обе замены в
исходное уравнение, получим для
v(t,T) однородное уравнение с решениями, которые можно записать через две пока неизвестные функции:
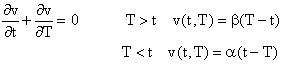 (13) (13)
В справедливости этих формул можно убедиться
непосредственной проверкой. Остается
найти введенные функции.
Начальное и граничное
условия дают:
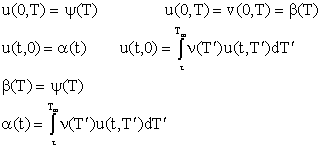 (14) (14)
Из этих уравнений мы уже можем получить u(t,T) для
t<T (нижняя часть плоскости
t,T):
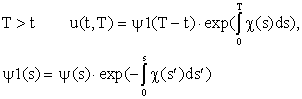 (15) (15)
Для нахождения решений
при T<t нам придется решать уравнения, которые можно
последовательно выписать для разных значений времени t:
 (16) (16)
Эти выражения
можно получили после замены под интегралом u(t,T`) на
введенные нами функции . Если теперь
учесть, что значения 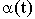 в первой строчке
есть не что иное , как известное начальное условие, заданное на интервале
репродукционного периода, то, после дифференцирования, мы получим
дифференциальное уравнения с запаздывающим аргументом, правда только, если зависимость q(s) от
аргумента отсутствует или имеет специальный вид - exp(s): в первой строчке
есть не что иное , как известное начальное условие, заданное на интервале
репродукционного периода, то, после дифференцирования, мы получим
дифференциальное уравнения с запаздывающим аргументом, правда только, если зависимость q(s) от
аргумента отсутствует или имеет специальный вид - exp(s):
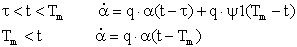 (17) (17)
Эти уравнения должны быть
дополнены начальным условием,
заданным на интервале времени 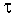 . После этого
уравнения могут быть последовательно
решены. . После этого
уравнения могут быть последовательно
решены.
Мы не будем решать эти уравнения, так как ниже для такого типа уравнений в более общем виде проводим численное решение. Полезность проведенных выкладок состоит в том, что они дают подсказку , как можно
решать проблему устойчивости для таких
уравнений.
Из теории уравнений с
запаздывающим аргументом строится
характеристическое уравнение.
Однако оно, в отличие от разобранных ранее характеристических уравнений,
представляет собой трансцендентное уравнение, имеющее бесконечно много корней. В [9]
подробна разобрана теория,
связанная с решением
характеристических уравнений
такого вида. Из этой теории следует, что для линейных случаев можно сформулировать теорему, аналогичную
теореме для линейных уравнений без
запаздывающих аргументов.
В [10] приведена
соответствующая формулировка для почти линейных уравнений обычного типа. Для нашего случая, как это
следует из [9], мы ее можем повторить
дословно: если действительные корни характеристического уравнения отрицательны, а
все комплексные имеют отрицательные действительные части, то уравнения
асимптотически устойчивы по Ляпунову.
В противном случае, либо
устойчивости нет (корни или их действительные части положительны), либо она
не асимптотическая ( есть равенство
нулю действительной части корней).
В нашем случае для нахождения характеристического уравнения нет надобности переходить к
дифференциальным уравнениям, тем более что это сужает область практически интересных случаев. Разобранная нами возможность такого сведения
дает нам право опереться на мощные результаты, полученные для
уравнений с запаздывающим
аргументом. Только и всего. Это относится и к теоремам о корнях трансцендентного характеристического уравнения и о возможности
разложить решение в ряд по экспонентам. Что же касается получения самого
уравнения, то будем пользоваться другим приемом. Будем считать, что решение исходного уравнения
можно представить в виде суперпозиции решений
следующим образом: 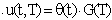 . .
Подставляя это выражение в исходное уравнения, найдем:
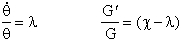 (18) (18)
Такой прием широко применяется в математической физике
для линейных задач.
Чтобы найти характеристическое уравнение для 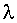 , мы должны подставить
принятое нами представление решения в граничное условие. После сокращение
обеих частей равенств на функцию,
содержащую время, мы получим
характеристическое уравнение: , мы должны подставить
принятое нами представление решения в граничное условие. После сокращение
обеих частей равенств на функцию,
содержащую время, мы получим
характеристическое уравнение:
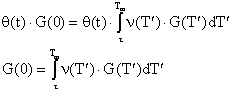 (19) (19)
Последнее равенство и есть характеристическое
уравнение. Интересно, что оно может быть
получено в замкнутом виде для весьма произвольных функций 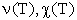 , так как линейное
уравнение для G(T) первого порядка и решается
в квадратурах. Правда простого экспоненциального полинома
можно и не получить. Однако свойство корней в значительной мере
сохраняется. На этом мы не будем
останавливаться, так как сложные случаи
исследуем численно. , так как линейное
уравнение для G(T) первого порядка и решается
в квадратурах. Правда простого экспоненциального полинома
можно и не получить. Однако свойство корней в значительной мере
сохраняется. На этом мы не будем
останавливаться, так как сложные случаи
исследуем численно.
В простейшем случае, когда функции
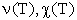 не зависят от Т,
выражение для характеристического уравнения выглядит особо просто: не зависят от Т,
выражение для характеристического уравнения выглядит особо просто:
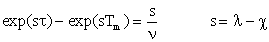 (20) (20)
Такие уравнения называют экспоненциальными полиномами.
Расположение корней s такого
полинома хорошо изучено.
Если оказалось, что единственный
действительный корень - отрицательный, то
все комплексные корни имеют отрицательные действительные части. В этом
случае устойчивость системы будет определяться еще и значением 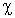 . .
Если 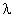 оказалось
положительны, то система устойчива.
Следовательно , в случае постоянных величин оказалось
положительны, то система устойчива.
Следовательно , в случае постоянных величин
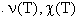 проверять надо
только действительный корень. проверять надо
только действительный корень.
Итак, уравнение в
качестве устойчивого решения имеет нулевое, а
в качестве неустойчивого экспоненциально возрастающее.
В дискретном
варианте добавление конкурентной борьбы приводило к стабилизации лесного массива. Если до включения конкурентной борьбы лес
убывал со временем, то конкурентная
борьба только усилит этот процесс. Зато при
неустойчивом состоянии включение
конкурентной борьбы приводит к
нетривиальной стабилизации.
Заметим, что даже
в случае учета только конкурентных отношений исследование устойчивости теоретически невозможно (впрочем и для обычных нелинейных систем ситуация
аналогична). Это показывает, что
ценность аналитического подхода для практики невелика. Мы провели его для того, чтобы убедиться
в таком факте: необычное краевое условие по возрасту не дает каких-либо
новых математических явлений.
Для решения (10) мы используем неявные схемы бегущего
счета [11] (рис. 9).
 t t
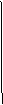    
    n+1 n+1
 n n
 T
T
m
m+1
Рис.9. Шаблон схемы бегущего счета
Построим разностную схему с одинаковым по времени и возрасту шагом, выбирая нулевую
точку по возрасту с предыдущего шага:
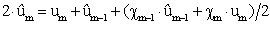 (21) (21)
Для
расписывания интеграла в граничном условии по возрасту используется
формула Симпсона. Правую часть уравнений
берем в средней точке .
Все зависимости от
возраста и времени мы задаем в
виде кусочно - гладких функций (в ниже
приведенных расчетах это отрезки
прямых). Использованные зависимости никак не влияют на исследовательские
программы и могут быть изменены.
Программы организованы
так, чтобы можно было просчитать определенное число шагов по времени и выдать
результат на график. Так удается проследить
процесс установления профиля.
На рис. 10
показаны результаты расчетов возрастного спектра по линейной модели. Приведены начальное распределение по
возрастам U0 и три распределения в последовательные моменты времени. Мы можем
наблюдать за процессом установления, когда нет конкуренции (лес молодой). Видно, что идет нарастание плотности
биомассы, сопровождающееся переносом профиля возрастного спектра вправо.
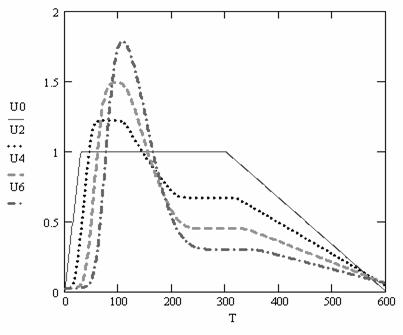
Рис.10. Эволюция возрастного спектра моновозрастной популяции
При расчетах с
конкуренцией мы вводим интеграл
конкуренции в общий коэффициент 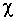 . Он вычисляется на предыдущем шаге. Надо сказать, что такая
организация счета достаточно
естественна для эволюции лесного
массива: сначала происходят изменения, а затем
они дают эффект в виде конкуренции. . Он вычисляется на предыдущем шаге. Надо сказать, что такая
организация счета достаточно
естественна для эволюции лесного
массива: сначала происходят изменения, а затем
они дают эффект в виде конкуренции.
Видно, что в случае
конкуренции мы выходим на
стационарный режим: молодой лес превращается в зрелый (рис. 11).
Рис.11. Эволюция возрастного спектра
моновозрастной популяции (с конкуренцией)
Заключение
В данной работе мы привели три модели эволюции леса с
учетом возраста, которые построили на основе различных методов. Первая (§2) – это дискретная модель на основе матриц Лесли, учитывающая
распределение популяции по конечным возрастным группам. Две другие модели –
непрерывные, причем первая из них (§3) относится к обыкновенным
дифференциальным уравнениям, а последняя (§4) -
к дифференциальным уравнениям в частных производных.
Список литературы
[1] Свирежев Ю.М., Логофет Д.О. Устойчивость биологических сообществ. М.,
Наука, 1978.
[2] Фёдоров В.Д., Гильманов Т.Г.
Экология. М., Изд. МГУ, 1980.
[3] Уильямсон М. Анализ биологических популяций. М.: Мир, 1975.
[4] Вольтерра В. Математическая теория борьбы за существование. М.: Наука,
1976.
[5] В.И.Кузнецов «Математическая модель эволюции леса», диссертация на
соискание ученой степени кандидата физ-мат наук, М, 1998
[6] Козлов Н.И., Кузнецов В.И., Кирьянов Д.В., Кирьянова Е.Н. Динамические
модели развития среднеширотного леса. Препринт ИПМ РАН М., 2005.
[7] Leslie P.H. On the use of matrices in
certain population mathematics. Biometrica, v.33(1945), N3, p.183
[8] Годунов С.К., Рябенький В.С. Разностные схемы.
«Наука», М. 1973.
[9] Беллман Р.,Кук К.Л.
Дифференциально-разностные уравнения. «Мир»,М.,1967.
[10] Годунов С.К. Обыкновенные дифференциальные уравнения
с постоянными коэффициентами. Том 1.
Изд. НГУ, 1994.
[11] Калиткин Н.Н. Численные методы. «Мир», М., 1978.
|