Аннотация
Рассматривается плоский тонкий упругий стержень, свободная форма которого представляет собой
периодическую кривую. Показывается, что при постоянной нагрузке, в пределе, с ростом частоты
функции, описывающей свободную форму стержня, до бесконечности, его равновесная форма стремится
к равновесной форме тонкого прямолинейного стержня. В соответствии с аналогией Кирхгофа задача
интерпретируется как движение математического маятника, к которому приложена быстро меняющаяся
периодическая возмущающая сила. Решение рассматриваемой задачи проводится в рамках обоснования
применимости моделирования пространственных форм кольцевых молекул ДНК тонким прямолинейным
упругим стержнем.
Abstract
The flat thin elastic rod with free form represented by a periodic curve is considered.
It is shown, that in a limit, with constant forces and moments enclosed and indefinitely
growth of frequency of a function that describes the free form, the equilibrium form of a rod
aspires to the one of a thin rectilinear rod. According to Kirhgoff analogy this task
can be interpreted as a movement of a mathematical pendulum with a quickly varying periodic
revolting force enclosed. The solution of a considered task is carried out within the
framework of substantiating the applicability of modeling the spatial forms of ring
DNA molecules by a thin rectilinear elastic rod.
Содержание
Введение. 3
1. Уравнения равновесия тонкого упругого стержня в
плоском случае. 4
2. Интегральная форма уравнений равновесия. 10
3. Слабая сходимость в ограниченном смысле. 11
4. Равновесные формы плоского стержня с быстроменяющимися
периодическими характеристиками. 15
5. Математический маятник с быстро меняющимися
периодическими воздействиями. 19
Литература. 20
При функционировании живой клетки одним из основных ее
объектов является молекула ДНК. Ее биохимические свойства во многом определяются
той формой, которую молекула может принимать под действием различных внешних
факторов. Исследование ее возможных форм является важной задачей молекулярной
биологии [1]. ДНК представляет собой
длинное нитевидное образование, или, точнее, двухнитевую структуру, в форме
двойной спирали. Иногда концы этой спирали замыкаются, и нить ДНК склеивается в
кольцо.
При математическом анализе возможных пространственных
форм ДНК наиболее распространенной является модель, в которой нить ДНК
представляются однородным тонким упругим стержнем, изгибающимся под действием
внешних сил [2]. В большинстве работ принято считать, что упругий стержень в
свободном состоянии является прямолинейным. Стержень считается однородным (его
упругие характеристики не изменяются вдоль длины), и изгибные жесткости
одинаковы во всех направлениях. В то же время
реальная молекула ДНК больше напоминает нить, которая в свободном
состоянии принимает форму винтовой линии, ее упругие характеристики (в первом приближении)
меняются периодически, с частотой, соответствующей длине витка спирали. Однако,
исследование подобной модели намного сложнее, поэтому использование упрощенной
модели более предпочтительно.
Следует сразу отметить, что по сравнению с длиной
молекулы (до нескольких сантиметров) шаг
витка (3 – 4 А) и толщина ДНК (20 А) незначительны. Именно поэтому использование
упрощенной прямолинейной модели считается допустимым. В данной работе
рассматривается вопрос о ее применимости. Проблема ставится следующим образом.
Допустим, у нас есть тонкий упругий стержень общего вида, характеристики
которого очень быстро периодически меняются вдоль его оси. Рассмотрим тонкий
прямолинейный стержень с осредненными характеристиками. Будут ли его
равновесные формы близки к равновесным формам исходного упругого стержня?
В терминах пространственных структур ДНК постановка
такова. Мы берем в качестве модели ДНК спиралевидный стержень с малой толщиной
спирали. При этом стержень находится под действием каких-то сил и моментов. Устремляем
толщину спирали к нулю, но сохраняем при этом геометрическую форму спирали и
действующие нагрузки, и пытаемся показать, что форма такого спиралевидного
стержня будет стремиться к форме прямолинейного стержня при тех же нагрузках.
То, что в пределе форма одной модели стремится к форме другой, будет означать,
что использование прямолинейного стержня при изучении пространственных форм ДНК
является корректным.
В данной работе указанная проблема рассматривается в простейшей,
плоской постановке, когда ДНК принимает только плоские формы. В этом случае структура молекулы описывается как равновесная
форма плоского тонкого упругого стержня, к концам которого приложена нагрузка.
Геометрия стержня в свободном (ненапряженном) состоянии периодически
повторяется. Наша цель – показать, что с ростом частоты повторения геометрии
свободного стержня до бесконечности равновесные формы, которые он принимает,
стремятся к равновесным формам тонкого прямолинейного стержня при некоторой
нагрузке.
Опишем более
подробно содержание работы.
В
первом разделе для полноты изложения приводится краткий вывод известных уравнений
равновесия тонкого упругого стержня в плоской постановке. Формулируется краевая
задача и вариационный принцип.
Во
втором разделе уравнения равновесия тонких упругих стержней выписываются в интегральной
форме. Это используется при выводе основного утверждения.
В третьем разделе вводится определение,
формулируются основные свойства слабой сходимости в ограниченном смысле, и
сходимости на гладких и непрерывных функциях. Это является некоторым
расширением обычной слабой сходимости функций в 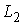 . Введенное понятие также используется при выводе основного
утверждения. . Введенное понятие также используется при выводе основного
утверждения.
В четвертом разделе
доказывается основной результат работы. Подводя итог изложенному в этом
разделе, можно утверждать, что использование модели тонкого прямолинейного
стержня для плоского случая корректно, поскольку форма криволинейного стержня
под нагрузкой стремится к форме прямолинейного стержня при устремлении частоты повторения
геометрии свободного стержня к бесконечности.
В пятом разделе
на основе аналогии Кирхгофа полученные результаты интерпретируются в терминах
движения математического маятника, к которому приложено быстро меняющееся
периодическое воздействие. Результат этого раздела можно трактовать следующим
образом. На конечном интервале времени влияние высокочастотного возмущающего
момента на движение математического маятника эквивалентно изменению начальной
скорости. Отметим, что ранее, в
работе [3], рассматривалась задача о движении математического маятника, к
которому приложено случайное воздействие.
В данном разделе для
полноты изложения мы рассмотрим известную задачу об определении равновесной
формы тонкого упругого стержня на плоскости [4].
Аксиомы линейной теории
упругости. Рассмотрим тонкий
упругий стержень длины 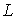 , к концам которого
приложены силы , к концам которого
приложены силы  , , 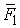 и моменты и моменты 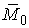 , , 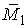 (см. Рис.
1-1). Пусть он находится в равновесии, и его осевая линия принимает форму
некоторой плоской кривой (см. Рис.
1-1). Пусть он находится в равновесии, и его осевая линия принимает форму
некоторой плоской кривой 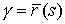 , концы которой
расположены в точках A и B. Здесь , концы которой
расположены в точках A и B. Здесь 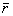 – радиус-вектор точек кривой, а – радиус-вектор точек кривой, а 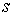 – натуральный параметр на кривой, т.е. длина
дуги кривой, измеряемая от начальной точки A до текущей точки – натуральный параметр на кривой, т.е. длина
дуги кривой, измеряемая от начальной точки A до текущей точки 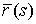 . Обозначим . Обозначим 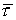 – касательный вектор к
кривой – касательный вектор к
кривой 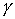 , а , а 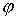 – угол наклона касательной к оси абсцисс. Тогда – угол наклона касательной к оси абсцисс. Тогда
 (1.1) (1.1)
Напомним, что величина 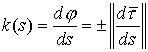 называется кривизной плоской кривой. называется кривизной плоской кривой.

Рис. 1-1 Тонкий упругий стержень на
плоскости.
В каждой точке кривой 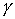 на бесконечно малый
элемент упругого стержня действует крутящий момент на бесконечно малый
элемент упругого стержня действует крутящий момент 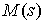 , под действием которого
стержень изгибается. Этот момент направлен ортогонально плоскости, в которой
лежит стержень. В векторных обозначениях , под действием которого
стержень изгибается. Этот момент направлен ортогонально плоскости, в которой
лежит стержень. В векторных обозначениях 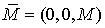 . Силы, приложенные к стержню, лежат в его плоскости. В векторных
обозначениях . Силы, приложенные к стержню, лежат в его плоскости. В векторных
обозначениях 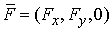 . .
Свободным состоянием тонкого упругого стержня будем называть ту его форму,
которую он приобретает в отсутствие всяких сил и моментов. Форма стержня в
свободном состоянии описывается некими величинами 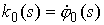 и определяется с
точностью до начальной ориентации и определяется с
точностью до начальной ориентации 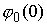 . Если . Если 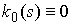 , то стержень называется прямолинейным (его свободное
состояние есть прямая линия). , то стержень называется прямолинейным (его свободное
состояние есть прямая линия).
Будем называть упругой
энергией 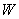 стержня работу, которая была совершена какими-то внешними
силами при переводе стержня из свободного состояния в данное. стержня работу, которая была совершена какими-то внешними
силами при переводе стержня из свободного состояния в данное.
Аксиомами линейной теории
упругости тонкого стержня мы
будем называть следующие соотношения:
– Упругая энергия стержня
“потенциальна” – она зависит только от его формы и не зависит от
последовательности (пути) деформаций, приведших его к данной форме. 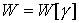
– Упругая энергия
аддитивна (т.е. упругая энергия всего стержня равна сумме упругих энергий его
частей) и для каждой данной формы стержня существует некая неотрицательная
функция 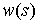 – плотность упругой энергии, такая,
что – плотность упругой энергии, такая,
что 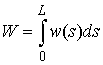
– Для тонкого прямолинейного
упругого стержня выполняются следующие уравнения состояния: существует
положительная функция 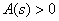 , независимая от формы
стержня, такая, что , независимая от формы
стержня, такая, что
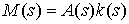 , , 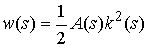 (1.2) (1.2)
Величина 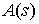 называется
коэффициентом упругости в точке называется
коэффициентом упругости в точке 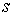 стержня. Тогда полная упругая энергия стержня. Тогда полная упругая энергия 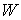 вычисляется следующим образом: вычисляется следующим образом:
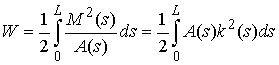 (1.3) (1.3)
Замечание. Эта аксиома получается, если изгибающий момент и плотность энергии
представить в виде функций от кривизны: 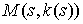 , , 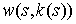 . Заметим, что при
отсутствии изгиба ( . Заметим, что при
отсутствии изгиба (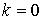 ) момент и плотность
энергии равны нулю. Поскольку ) момент и плотность
энергии равны нулю. Поскольку 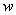 не зависит от направления изгиба, т.е. от
знака кривизны, то равна нулю и не зависит от направления изгиба, т.е. от
знака кривизны, то равна нулю и 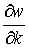 . Разложим момент и
плотность в ряд по кривизне и отбросим высшие члены. Получим . Разложим момент и
плотность в ряд по кривизне и отбросим высшие члены. Получим 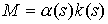 , , 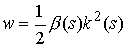 . В силу положительности
энергии имеем . В силу положительности
энергии имеем 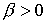 . Теперь осталось заметить,
что . Теперь осталось заметить,
что  . В противном случае
уравнения равновесия стержня не обеспечивали бы экстремальности упругой энергии
стержня в равновесном случае. Иначе говоря, вариационные условия равновесия
(см. ниже) отличались бы от уравнений равновесия, выведенных в рамках
геометрической статики. . В противном случае
уравнения равновесия стержня не обеспечивали бы экстремальности упругой энергии
стержня в равновесном случае. Иначе говоря, вариационные условия равновесия
(см. ниже) отличались бы от уравнений равновесия, выведенных в рамках
геометрической статики.
Для тонкого упругого
стержня общего вида выполняются следующие уравнения состояния:
существует положительная функция 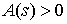 , независимая от формы
стержня, такая, что , независимая от формы
стержня, такая, что
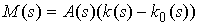 , , 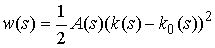
Величина 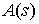 называется
коэффициентом упругости в точке называется
коэффициентом упругости в точке 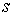 стержня. Тогда полная упругая
энергия W вычисляется следующим образом: стержня. Тогда полная упругая
энергия W вычисляется следующим образом:
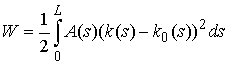
Если 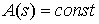 , то стержень называется
однородным. , то стержень называется
однородным.
Поскольку
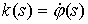 , то уравнения состояния
можно переписать следующим образом (в общем случае) , то уравнения состояния
можно переписать следующим образом (в общем случае)
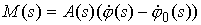 , , 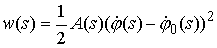
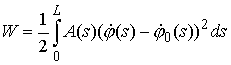
Уравнения равновесия тонкого
упругого стержня в плоском случае. Рассмотрим форму
прямолинейного тонкого упругого стержня под нагрузкой. Перережем стержень в
точке 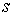 , тогда на левую часть
будут действовать некие силы , тогда на левую часть
будут действовать некие силы  и моменты и моменты 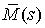 , а на правую часть (в соответствии с третьим законом
Ньютона) , а на правую часть (в соответствии с третьим законом
Ньютона) 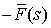 и и 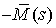 (см. Рис.1-2). Перережем
стержень также в точке (см. Рис.1-2). Перережем
стержень также в точке 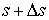 и получим бесконечно
малый упругий элемент стержня между точками и получим бесконечно
малый упругий элемент стержня между точками 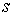 и и 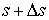 . К его правому концу приложены некоторые силы и моменты . К его правому концу приложены некоторые силы и моменты 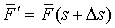 и и  , а к левому концу , а к левому концу 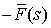 , и , и 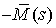 . .
Вектор смещения от
левого конца упругого элемента к его правому концу (с точностью до бесконечно
малых первого порядка) равен 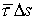 . Условием равновесия упругого элемента является равенство
нулю суммарных сил и моментов, приведенных к одной точке. Приведем все силы и
моменты к правому концу упругого элемента. . Условием равновесия упругого элемента является равенство
нулю суммарных сил и моментов, приведенных к одной точке. Приведем все силы и
моменты к правому концу упругого элемента.
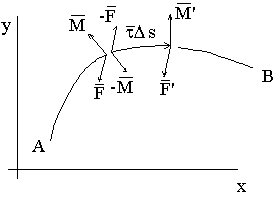
Рис. 1-2. Упругий
стержень перерезан в точках 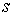 и и 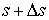
Условие равновесия по силам будет выглядеть так: 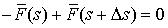 , или (при переходе к пределу при , или (при переходе к пределу при 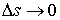 ) )
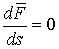 (1.4) (1.4)
При приведении моментов в правом конце упругого
элемента будут действовать моменты 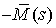 , , 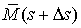 и момент силы,
приложенной к левому концу, т.е. и момент силы,
приложенной к левому концу, т.е.  . Условие равновесия по моментам будет выглядеть так: . Условие равновесия по моментам будет выглядеть так: 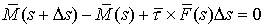 , или (при переходе к пределу при , или (при переходе к пределу при 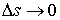 ) )
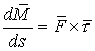 (1.5) (1.5)
Используя соотношения (5.1-5.4) можем получить
отсюда следующие уравнения равновесия:
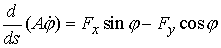 (1.6) (1.6)
где 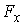 , и , и 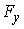 – некоторые константы
(компоненты вектора силы – некоторые константы
(компоненты вектора силы 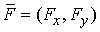 ), A(s) > 0 – величина, характеризующая упругие свойства
стержня (коэффициент упругости), точкой обозначена производная по s. ), A(s) > 0 – величина, характеризующая упругие свойства
стержня (коэффициент упругости), точкой обозначена производная по s.
Для
тонкого упругого стержня общего вида уравнения равновесия получаются аналогично
и выглядят следующим образом:
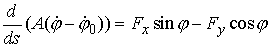 (1.7) (1.7)
Начальные и краевые условия Мы считаем, что упругие свойства стержня описывают (в
линейном приближении) потенциалы межатомного взаимодействия в молекулярной цепи
и не зависят от ее расположения в пространстве. Поэтому функции A(s) и 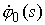 предполагаются заданными
и не зависящими от формы, которую принимает стержень под нагрузкой. В этом
случае уравнение (1.7) зависит только от двух параметров ( предполагаются заданными
и не зависящими от формы, которую принимает стержень под нагрузкой. В этом
случае уравнение (1.7) зависит только от двух параметров (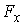 и и 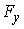 ) и его решение однозначно определяется начальными условиями ) и его решение однозначно определяется начальными условиями 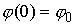 и и 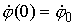 . . 
После
того, как уравнение (1.7) проинтегрировано и найдена функция 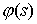 , мы можем найти геометрическую форму стержня. Для этого надо
проинтегрировать уравнение (1.1), которое в координатной записи выглядит так: , мы можем найти геометрическую форму стержня. Для этого надо
проинтегрировать уравнение (1.1), которое в координатной записи выглядит так:
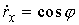 , ,  (1.8) (1.8)
Начальные условия для этого уравнения суть 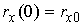 и и  . .
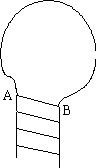
Рис. 1-3. При определении пространственной формы
шпилечной петли упругий стержень гладко исходит из левой нити стебля и гладко
входит в правую нить.
Таким
образом, задав 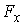 , , 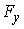 , , 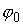 , , 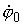 , , 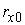 , , 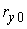 и проинтегрировав (1.7-1.8),
мы получим геометрическую форму тонкого упругого стержня в равновесии. Из (1.2)
имеем и проинтегрировав (1.7-1.8),
мы получим геометрическую форму тонкого упругого стержня в равновесии. Из (1.2)
имеем 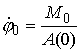 , поэтому можно говорить, что расположение стержня на
плоскости однозначно определяется заданием силы и момента, приложенных к его
начальной точке, а также его начального положения и ориентации. , поэтому можно говорить, что расположение стержня на
плоскости однозначно определяется заданием силы и момента, приложенных к его
начальной точке, а также его начального положения и ориентации.
При
анализе пространственных структур РНК нас, в частности, интересует форма,
которую будет принимать упругая петля, концы которой гладко исходят и входят в
двухнитевую двойную спираль. Это означает, что в качестве условий нам известно
относительное расположение и ориентация концов стержня (т.е. краевые условия).
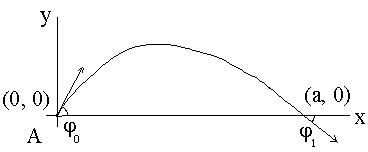
Рис. 5-4. Краевые условия.
Поскольку нас интересует собственно форма стержня,
а не его расположение на плоскости, то можно считать, что  , т.е. что стержень начинается в начале системы координат. Будем
также считать, что система координат повернута таким образом, что правый конец
стержня располагается на оси абсцисс, т.е. , т.е. что стержень начинается в начале системы координат. Будем
также считать, что система координат повернута таким образом, что правый конец
стержня располагается на оси абсцисс, т.е. 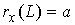 , , 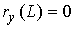 , где , где 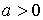 – расстояние между
концами стержня, а – расстояние между
концами стержня, а 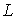 – длина
стержня. – длина
стержня.
Поэтому
основная задача – это определение формы стержня не по начальным, а по краевым
условиям, т.е. по условиям, заданным на концах стержня. Эти условия
формулируются так:
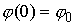 , , 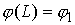 , , 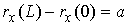 , , 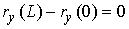
Последние два условия можно заменить на следующие:
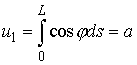 , , 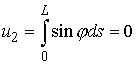 (1.9) (1.9)
Окончательно краевая задача формулируется таким
образом: найти такие значения величин 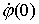 , , 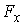 , и , и 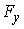 , чтобы траектория системы (1.7), испущенная с начальными
условиями , чтобы траектория системы (1.7), испущенная с начальными
условиями 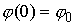 , удовлетворяла краевым условиям , удовлетворяла краевым условиям 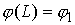 и (1.9). и (1.9).
Вариационные условия равновесия. Исходя из
общефизических соображений, можно сформулировать вариационный принцип для
отбора равновесных форм упругого стержня.
Вариационный принцип. Функция 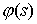 для равновесного
состояния тонкого упругого стержня является экстремалью функционала полной
упругой энергии для равновесного
состояния тонкого упругого стержня является экстремалью функционала полной
упругой энергии
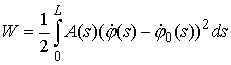
В задаче с фиксированным “временем” и
закрепленными концами: 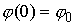 , , 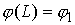 при ограничениях (1.9). при ограничениях (1.9).
Докажем,
что этот принцип эквивалентен условиям равновесия (1.7), выведенным выше. Введем
функционал 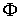 с множителями Лагранжа с множителями Лагранжа
 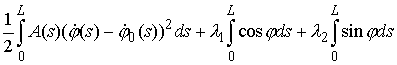
Тогда экстремали исходной вариационной задачи
совпадают с экстремалями функционала 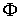 в задаче с
закрепленными концами: в задаче с
закрепленными концами: 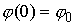 , , 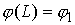 (при некоторых
значениях констант (при некоторых
значениях констант 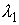 и и 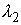 ). Обозначим ). Обозначим 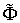 подынтегральную функцию функционала подынтегральную функцию функционала 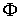 . .
 
Тогда уравнения Эйлера в этой задаче выглядят
следующим образом:
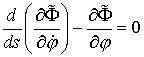 , или , или 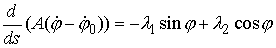
При 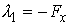 и и  эти уравнения
совпадают с уравнениями (1.7), что и доказывает эквивалентность вариационного
принципа и условий равновесия. эти уравнения
совпадают с уравнениями (1.7), что и доказывает эквивалентность вариационного
принципа и условий равновесия.
2. Интегральная форма уравнений равновесия.
В дальнейшем нам понадобятся уравнения равновесия тонких
упругих стержней в интегральной форме. Для краткости изложения будем считать,
что стержень однородный, и начальная точка стержня находится в начале системы
координат, т.е. что 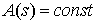 , и , и 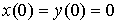 . К концам стержня приложены силы, которые на левом конце
имеют координаты . К концам стержня приложены силы, которые на левом конце
имеют координаты 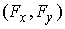 , а также изгибающий момент сил , а также изгибающий момент сил 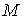 . .
Для однородного прямолинейного стержня мы имеем следующие
уравнения равновесия:
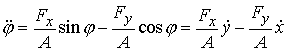 , , 
Проинтегрировав это
выражение, получим:
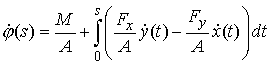 (2.1) (2.1)
Воспользуемся тем, что 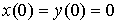 . Получаем . Получаем
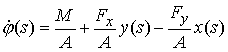 (2.2) (2.2)
После повторного
интегрирования выражение приобретает вид:
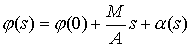 (2.3) (2.3)
где обозначено
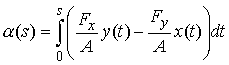 (2.4) (2.4)
Взяв от выражения (2.3) соответственно
cos и sin, получим:
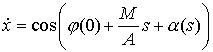 , , 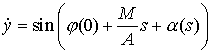 (2.5) (2.5)
Для стержня общего вида имеем
 , , 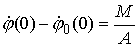
Проинтегрируем это
выражение:
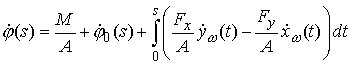 (2.6) (2.6)
Воспользуемся тем, что 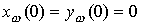 . Получаем . Получаем
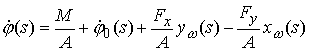 (2.7) (2.7)
Проинтегрировав еще раз,
получим
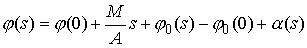
Опять возьмем от этого
выражения синус и косинус, и воспользуемся (2.1):
 (2.8) (2.8)
Рассмотрим пространство 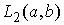 – пространство функций,
суммируемых с квадратом на отрезке – пространство функций,
суммируемых с квадратом на отрезке 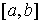 . В обычном определении полагается, что последовательность
функций . В обычном определении полагается, что последовательность
функций 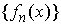 , , 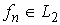 слабо сходится к
функции слабо сходится к
функции 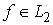 , если для любой функции , если для любой функции 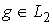 выполняется выполняется
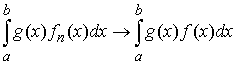 (3.1) (3.1)
Мы
будем пользоваться определением слабой сходимости со следующими ограничениями.
1) Мы будем рассматривать только равномерно ограниченные
почти всюду последовательности 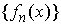 , т.е. , т.е. 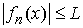 для любого для любого 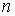 , почти всюду на , почти всюду на 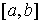 . .
2) Сходимость в (3.1) будем требовать только для функций  и и 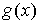 , ограниченных почти всюду на , ограниченных почти всюду на 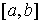 , т.е. , т.е. 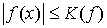 , , 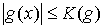 почти всюду на почти всюду на 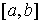 . .
Введем еще два определения. Если (3.1) выполняется только
для функций 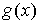 , непрерывных на , непрерывных на 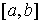 , то такую сходимость будем называть слабой сходимостью на
непрерывных функциях. Если же (3.1) выполняется только для гладких функций , то такую сходимость будем называть слабой сходимостью на
непрерывных функциях. Если же (3.1) выполняется только для гладких функций  , непрерывных на отрезке , непрерывных на отрезке 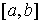 вместе со своей
производной, то такую сходимость будем называть слабой сходимостью на гладких
функциях. вместе со своей
производной, то такую сходимость будем называть слабой сходимостью на гладких
функциях.
Для краткости мы будем пользоваться обычным термином "слабая сходимость"
и использовать обычное обозначение 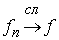 . .
Нам понадобится несколько свойств
слабой сходимости в ограниченном смысле. При их выводе для краткости обозначим 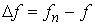 . .
Свойство 3.1. Слабая сходимость на непрерывных функциях эквивалентна
слабой сходимости в ограниченном смысле.
Доказательство. Пусть 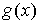 измерима и измерима и 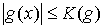 почти всюду. Из
теоремы Лузина [5] следует, что для любого почти всюду. Из
теоремы Лузина [5] следует, что для любого 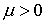 можно найти
непрерывную функцию можно найти
непрерывную функцию  , такую, что , такую, что 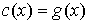 на некотором множестве на некотором множестве
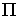 , мера которого не более чем на , мера которого не более чем на 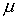 меньше полной меры,
т.е. меньше полной меры,
т.е. 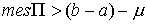 , и, кроме того, , и, кроме того, 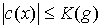 при при  . Тогда выполнено неравенство . Тогда выполнено неравенство
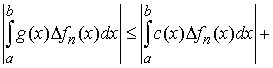 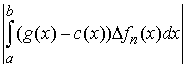
В
правой части этого неравенства первый член стремится к нулю по условию.
Поскольку 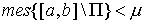 и и 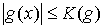 , , 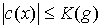 , , 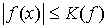 , , 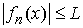 почти всюду, то второй
член оценивается следующим образом: почти всюду, то второй
член оценивается следующим образом:

Для
любого 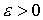 выберем выберем  и найдем и найдем  . Пусть . Пусть 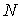 таково, что для всех таково, что для всех 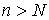 выполнено выполнено 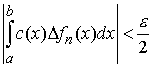 . Тогда для всех . Тогда для всех 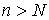 будет будет 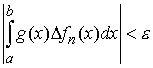 . Сходимость (3.1) доказана. . Сходимость (3.1) доказана.
Свойство 3.2. Слабая сходимость на гладких функциях эквивалентна
слабой сходимости на непрерывных функциях.
Доказательство. Сразу вытекает из того, что гладкие функции всюду плотны
в пространстве непрерывных функций.
Итак, слабая сходимость на гладких функциях эквивалентна
слабой сходимости в ограниченном смысле.
Свойство 3.3. Рассмотрим измеримые
функции, ограниченные почти всюду на 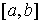 величиной величиной 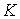 : : 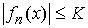 , , 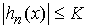 , , 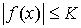 , ,  . Если . Если 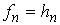 почти всюду на почти всюду на 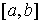 и и 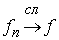 , ,  , то , то 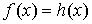 почти всюду на почти всюду на 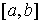 . .
Доказательство. Возьмем 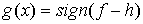 , где , где 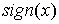 - обычная функция
знака числа - обычная функция
знака числа 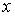 , причем , причем 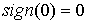 . Тогда из слабой сходимости . Тогда из слабой сходимости
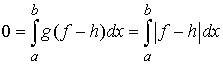
Значит,
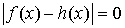 почти всюду, что и
требовалось показать. почти всюду, что и
требовалось показать.
Свойство 3.4. Пусть функции 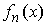  непрерывно дифференцируемы
и удовлетворяют условию Липшица с некоей константой непрерывно дифференцируемы
и удовлетворяют условию Липшица с некоей константой 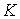 . Если последовательность . Если последовательность 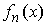 сходится к функции сходится к функции  равномерно на отрезке равномерно на отрезке 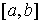 , то предельная функция удовлетворяет условию Липшица с той
же константой (значит, она абсолютно непрерывна) и последовательность производных
слабо (в нашем смысле) сходится к её производной: , то предельная функция удовлетворяет условию Липшица с той
же константой (значит, она абсолютно непрерывна) и последовательность производных
слабо (в нашем смысле) сходится к её производной: 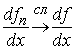 . .
Доказательство.
Переходя к пределу в неравенстве 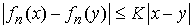 , получаем первую часть утверждения. Пусть , получаем первую часть утверждения. Пусть 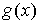 – гладкая функция.
Тогда – гладкая функция.
Тогда  . Отсюда сразу вытекает слабая сходимость на гладких функциях
и, значит, и слабая сходимость в ограниченном смысле. . Отсюда сразу вытекает слабая сходимость на гладких функциях
и, значит, и слабая сходимость в ограниченном смысле.
Заметим, что Свойство 3.4 – это просто
ослабленная переформулировка теоремы Хелли о предельном переходе под знаком
интеграла Лебега-Стилтьеса [5]. И, например, условие равномерной сходимости
можно заменить на поточечную сходимость.
Свойство 3.5. Если последовательность непрерывных функций 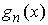 сходится к функции сходится к функции 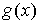 равномерно на отрезке равномерно на отрезке 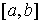 , а последовательность функций , а последовательность функций 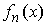 слабо в ограниченном
смысле сходится к функции слабо в ограниченном
смысле сходится к функции  , то последовательность , то последовательность 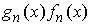 слабо в ограниченном
смысле сходится к функции слабо в ограниченном
смысле сходится к функции 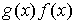 . .
Доказательство.
Сразу вытекает из того, что
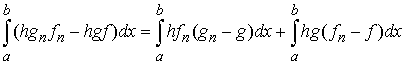
Свойство 3.6. Пусть 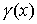 – это – это  периодическая функция с
нулевым средним значением на периоде, тогда на любом фиксированном отрезке периодическая функция с
нулевым средним значением на периоде, тогда на любом фиксированном отрезке 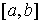 будет будет 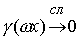 при при 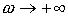 . .
Доказательство. Поскольку среднее по периоду есть нуль, то для любого
отрезка 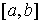 при при 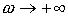 имеем имеем 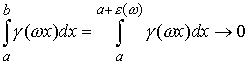 , где , где 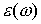 дробная часть от
деления дробная часть от
деления 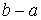 на период: на период: 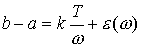 , , 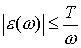 . .
Покажем, что 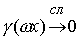 при при 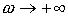 . Допустим, что это не так, тогда существует гладкая функция . Допустим, что это не так, тогда существует гладкая функция 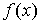 такая, что такая, что
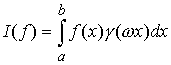
не
сходится к нулю. Гладкую функцию можно с любой точностью приблизить
ступенчатыми. Значит, существует ступенчатая функция 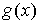 , для которой , для которой 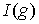 не сходится к нулю. Но
на каждой ступеньке имеем не сходится к нулю. Но
на каждой ступеньке имеем
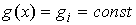 , , 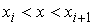
Поэтому
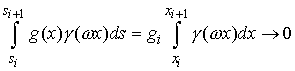 . Пришли к противоречию. . Пришли к противоречию.
Свойство 3.7. Пусть 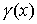 – это – это  периодическая функция,
тогда на любом фиксированном отрезке периодическая функция,
тогда на любом фиксированном отрезке 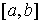 будет будет 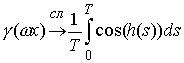 при при 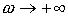 . .
Доказательство. Вытекает из свойства 3.5 для функции
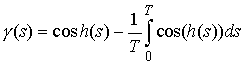
Поскольку
функция 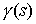 – это – это  периодическая функция с
нулевым средним значением на периоде, то, значит, периодическая функция с
нулевым средним значением на периоде, то, значит, 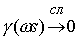 при при 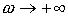 . .
В этом разделе мы рассмотрим
равновесные формы плоского тонкого упругого стержня, к концам которого
приложена нагрузка. Форма стержня в свободном (ненапряженном) состоянии
периодически повторяется. Это означает, что функция 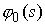 , описывающая ненапряженное состояние стержня, является
периодической с частотой , описывающая ненапряженное состояние стержня, является
периодической с частотой 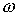 и периодом и периодом 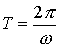 . Будем увеличивать частоту
повторения формы свободного стержня, сохраняя приложенные к концам стержня силы
и моменты и сохраняя начальное значение угла наклона осевой линии стержня. . Будем увеличивать частоту
повторения формы свободного стержня, сохраняя приложенные к концам стержня силы
и моменты и сохраняя начальное значение угла наклона осевой линии стержня.
Возьмем любую 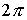 периодическую гладкую
функцию периодическую гладкую
функцию 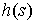 и распространим ее по
периоду на всю числовую ось. Будем считать, что эта функция дает величину угла
наклона осевой линии ненапряженного стержня при единичной частоте и распространим ее по
периоду на всю числовую ось. Будем считать, что эта функция дает величину угла
наклона осевой линии ненапряженного стержня при единичной частоте 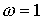 . Параметр . Параметр 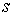 – это натуральный
параметр (длина) вдоль осевой линии стержня. Пусть стержень имеет длину – это натуральный
параметр (длина) вдоль осевой линии стержня. Пусть стержень имеет длину 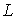 . .
Рассмотрим положение стержня на плоскости  . Пусть ( . Пусть (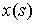 , ,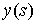 ) – осевая
линия стержня, параметризованная натуральным параметром ) – осевая
линия стержня, параметризованная натуральным параметром 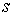 . Она удовлетворяет уравнениям . Она удовлетворяет уравнениям
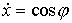 , , 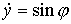 (4.1) (4.1)
Рассмотрим сначала стержень без нагрузки в случае, когда 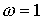 , , 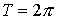 . Его осевую линию обозначим . Его осевую линию обозначим 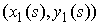 . Угол наклона осевой линии к оси абсцисс будем обозначать . Угол наклона осевой линии к оси абсцисс будем обозначать 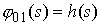 . .
Поместим начало стержня в начало системы координат,
т.е. 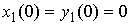 . Развернем систему координат так, чтобы ось . Развернем систему координат так, чтобы ось 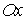 проходила через точку
( проходила через точку
(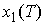 , , 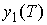 ), тогда ), тогда 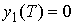 . Это значит, что . Это значит, что
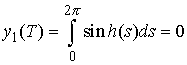 (4.2) (4.2)
Будем считать, что 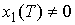 , и ось , и ось 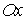 развернута так, что развернута так, что
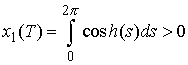 (4.3) (4.3)
Возьмем стержень со свободной формой, которая
описывается функцией 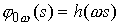 , , 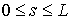 . Он получается из исходного стержня сжатием плоскости . Он получается из исходного стержня сжатием плоскости  в в 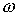 раз. В самом деле,
обозначим осевую линию нового стержня через раз. В самом деле,
обозначим осевую линию нового стержня через  . Тогда . Тогда
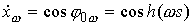 , , 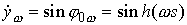
Проведя замену времени 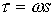 , получим , получим
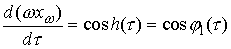 , , 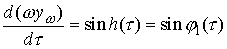
Значит, 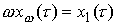 , , 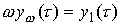 , и , и
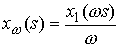 , , 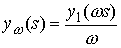
Значит, для стержня в свободном состоянии при 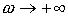 разброс осевой линии
по разброс осевой линии
по 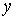 (т.е.
"толщина") уменьшается до нуля, но форма осевой линии сохраняется. (т.е.
"толщина") уменьшается до нуля, но форма осевой линии сохраняется.
Приложим к такому стержню силы и моменты. Он
примет какую-то форму. Будем теперь менять 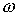 так, чтобы так, чтобы 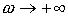 . Форма при этом будет меняться. Покажем, что она будет
стремиться к форме, которую примет прямолинейный стержень под действием тех же
нагрузок. . Форма при этом будет меняться. Покажем, что она будет
стремиться к форме, которую примет прямолинейный стержень под действием тех же
нагрузок.
Рассмотрим последовательность 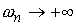 . Ей отвечают последовательности . Ей отвечают последовательности 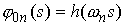 , , 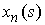 , , 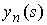 . Все эти функции гладкие . Все эти функции гладкие
Мы считаем, что стержень однородный, т.е. 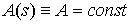 . .
В соответствии с критерием Арцела, если есть некоторое
семейство абсолютно непрерывных функций  , заданных на отрезке , заданных на отрезке 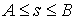 , такое, что эти функции равномерно ограничены и имеют
равномерно ограниченные первые производные, тогда существует такая
подпоследовательность , такое, что эти функции равномерно ограничены и имеют
равномерно ограниченные первые производные, тогда существует такая
подпоследовательность 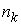 , что , что 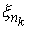 сходится равномерно к некоторой
абсолютно непрерывной функции сходится равномерно к некоторой
абсолютно непрерывной функции 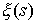 . .
В нашем случае, учитывая (4.1), получаем 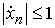 , , 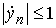 , т.е. производные ограничены, а так как мы рассматриваем
задачу на ограниченном отрезке , т.е. производные ограничены, а так как мы рассматриваем
задачу на ограниченном отрезке 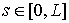 , где L – длина стержня, то и координаты , где L – длина стержня, то и координаты 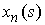 , , 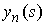 также будут ограничены.
Поэтому в соответствии с критерием Арцела найдется подпоследовательность также будут ограничены.
Поэтому в соответствии с критерием Арцела найдется подпоследовательность 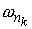 , такая, что , такая, что 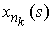 , ,  сходятся равномерно к сходятся равномерно к  , , 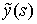 . Для краткости записи мы будем считать, что равномерно
сходятся сами последовательности: . Для краткости записи мы будем считать, что равномерно
сходятся сами последовательности: 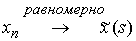 , , 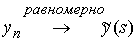 . .
Из свойства 3.4 слабой сходимости (см. п.3) следует, что
для найденной нами выше последовательности 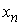 последовательность её
производных последовательность её
производных 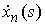 слабо сходится к
производной ее предела: слабо сходится к
производной ее предела: 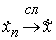 . Аналогичное утверждение верно и для последовательности . Аналогичное утверждение верно и для последовательности 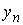 . Это означает, что осевая линия стержня будет сходиться к
некоторой кривой . Это означает, что осевая линия стержня будет сходиться к
некоторой кривой 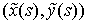 . Мы хотим показать, что эта предельная кривая будет
удовлетворять уравнениям равновесия для однородного прямолинейного стержня под нагрузкой. . Мы хотим показать, что эта предельная кривая будет
удовлетворять уравнениям равновесия для однородного прямолинейного стержня под нагрузкой.
Для однородного прямолинейного стержня в п. 2 мы вывели
интегральные уравнения равновесия:
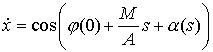 , , 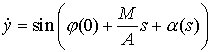 , ,
где 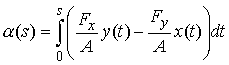 . .
Покажем, что 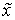 , , 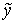 удовлетворяют именно
этим уравнениям для некоторого значения параметра удовлетворяют именно
этим уравнениям для некоторого значения параметра 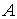 , при заданных , при заданных 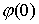 . .
Начиная с этого момента, мы для краткости мы пишем 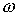 , подразумевая под этим , подразумевая под этим 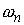 . Для стержней из нашей последовательности мы имеем . Для стержней из нашей последовательности мы имеем
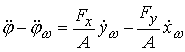 , где , где 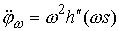 , , 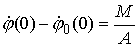
Проинтегрируем также это
выражение:
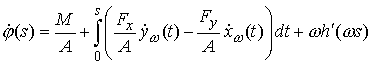
Воспользуемся тем, что 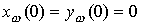 . Получаем . Получаем
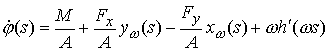
Проинтегрировав еще раз,
получим
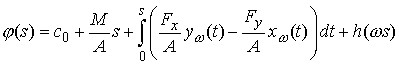
Здесь
использованы обозначения 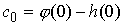 . Опять возьмем от этого выражения синус и косинус и
воспользуемся (2.1). Получим . Опять возьмем от этого выражения синус и косинус и
воспользуемся (2.1). Получим
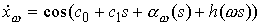 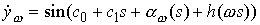 , ,
где 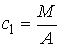 , , 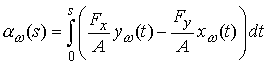 . Нетрудно видеть, что . Нетрудно видеть, что
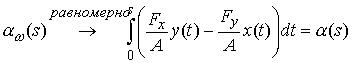 . .
Воспользовавшись
формулами для косинуса и синуса суммы углов, получим:
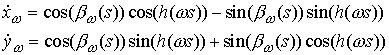 (4.4) (4.4)
Здесь
использовано обозначение 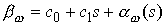 . Теперь заметим, что
функции . Теперь заметим, что
функции 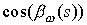 , , 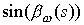 сходятся равномерно к сходятся равномерно к 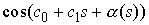 , , 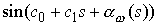 соответственно при соответственно при 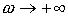 , а функции , а функции 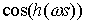 , , 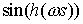 в силу свойства 3.7 сходятся
слабо к в силу свойства 3.7 сходятся
слабо к
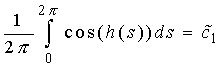 и и 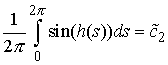
соответственно. В силу
(4.2, 4.3)) имеем 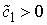 , ,  . .
Итак, в правой части уравнений (4.4) стоят слагаемые,
состоящие каждый из двух сомножителей. Один сомножитель сходится равномерно,
другой — слабо. Их произведение, очевидно, сходится слабо. Следовательно, правые
части уравнений (4.4) сходятся слабо к 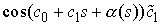 и и 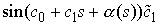 соответственно. Левые же части, как мы уже
показывали, сходятся слабо к соответственно. Левые же части, как мы уже
показывали, сходятся слабо к 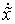 и и 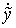 . Таким образом, почти всюду выполнено . Таким образом, почти всюду выполнено
 , , 
Введем новые обозначения:
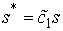 , , 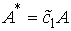 , ,  , тогда , тогда
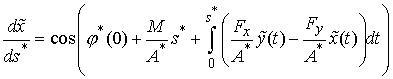
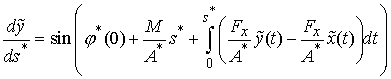
Мы
получили уравнения равновесия для прямолинейного стержня под действием таких же
сил и моментов, но имеющего иную жесткость и новый угол наклона осевой линии в
левом конце. Длина нового стержня также иная:
 . .
Мы рассмотрели случай, когда длина стержня на периоде 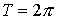 . Здесь . Здесь 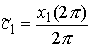 . Если же . Если же 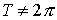 , то мы можем свести этот случай к исходному, сделав замену
координат , то мы можем свести этот случай к исходному, сделав замену
координат 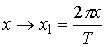 , ,  , ,  . Тогда . Тогда 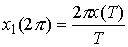 и, значит, и, значит, 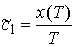 . .
Подводя итог изложенному в этом разделе, можно
утверждать, что использование прямолинейной модели для плоского случая
корректно, поскольку форма периодически криволинейного стержня под нагрузкой
стремится к форме прямолинейного стержня при устремлении частоты повторения
формы к бесконечности. Жесткость же предельного стержня  связана с исходной
жесткостью соотношением связана с исходной
жесткостью соотношением 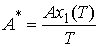 , где , где  – длина исходного
стержня на периоде формы, – длина исходного
стержня на периоде формы, 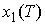 – длина проекции
периода формы на ось Ox. – длина проекции
периода формы на ось Ox.
В качестве примера возьмем стержень, имеющий форму
синусоиды:
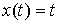 , , 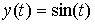 . В этом случае . В этом случае 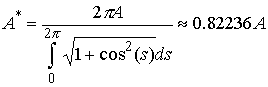 . .
Аналогия Кирхгофа утверждает,
что уравнения равновесия тонкого упругого однородного стержня эквивалентны
уравнениям движения математического маятника. Напомним, что математическим
маятником называется механическая система, состоящая из
материальной точки массы 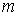 , движущейся в
однородном поле силы тяжести по гладкой окружности радиуса , движущейся в
однородном поле силы тяжести по гладкой окружности радиуса 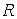 , расположенной в вертикальной плоскости. , расположенной в вертикальной плоскости.
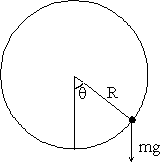
Рис. 5-5. Математический маятник.
Лагранжиан этой системы (т.е. разность кинетической и
потенциальной энергии) имеет следующий вид: 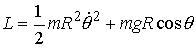 , а уравнения движения: , а уравнения движения: 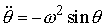 , где , где 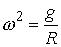 . (5.1) . (5.1)
Рассмотрим
теперь тонкий линейный однородный стержень. Однородность означает постоянство
коэффициента упругости вдоль его длины:  . Уравнения равновесия стержня выглядят следующим образом: . Уравнения равновесия стержня выглядят следующим образом:
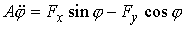
Введя величины  и и 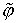 такие,
что такие,
что 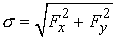 , , 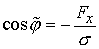 , , 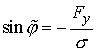 , ,
можно переписать (5.10) следующим образом: 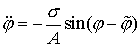 . Подстановка . Подстановка
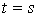 , , 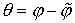 , , 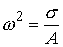 завершает доказательство
аналогии Кирхгофа. завершает доказательство
аналогии Кирхгофа.
В аналогии Кирхгофа время математического маятника
соответствует длине дуги стержня, а изменение угла математического маятника
полностью соответствует изменению угла наклона касательной к осевой линии
упругого стержня.
Возмущающие силы. Приложим к
точке математического маятника некий возмущающий момент  . Тогда уравнения движения приобретут вид . Тогда уравнения движения приобретут вид
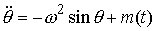 (5.2) (5.2)
Обозначим производящую функцию возмущающего
момента 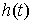 : :
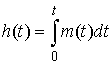 , , 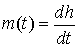 , , 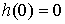 , ,
Это мощность возмущающего момента при единичной
скорости. Будем считать, что это гладкая
 периодическая функция.
Зафиксируем конечное время: периодическая функция.
Зафиксируем конечное время: 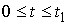 . Проинтегрировав (5.2) по времени, получим . Проинтегрировав (5.2) по времени, получим
 , , 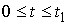
Начнем теперь линейно увеличивать частоту и
амплитуду возмущающего момента, сохраняя его форму. Точнее, рассмотрим
возмущающий момент 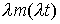 с производящей
функцией с производящей
функцией 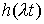 . Решение уравнения
обозначаем . Решение уравнения
обозначаем  . Точно так же, как это мы делали в предыдущем разделе,
фиксируем начальные значения . Точно так же, как это мы делали в предыдущем разделе,
фиксируем начальные значения 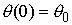 , , 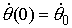 и переходим к пределу
при и переходим к пределу
при 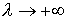 . Тогда . Тогда 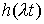 слабо сходится к слабо сходится к 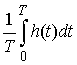 , а , а  равномерно сходится к некоей
функции равномерно сходится к некоей
функции 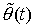 , которая удовлетворяет уравнению , которая удовлетворяет уравнению
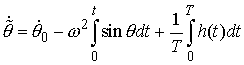
Это решение уравнения математического маятника
(5.1), соответствующее начальным условиям 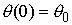 , , 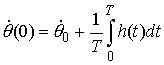 . .
Этот результат можно трактовать следующим образом.
На конечном интервале времени влияние высокочастотного возмущающего момента на
движение математического маятника эквивалентно изменению начальной скорости.
Благодарности. Авторы весьма признательны И.Л. Антонову и Ю. Ф.
Голубеву за полезные обсуждения данной работы.
1.
Льюин Б.
Гены. М., Мир, 1987, с. 544.
2. Benham C.J.
(1983) Geometry and mechanics of DNA superhelicity. Biopolymers, 22, 11, 2477 -
2495.
3. И.Л. Антонов Случайные
колебания. Свойства траекторий. М., МГУ, 1993, с. 176.
4. Попов Е.П. (1948) Нелинейные задачи статики тонких
стержней. Л.М. ОГИЗ, с.170.
5. Натансон И.П. Теория функций вещественной
переменной. М., Наука, 1974 – 480с.
|