Содержание

1 Введение................................................................................................... 4

2 Эксперименты......................................................................................... 5

2.1 Элементарные операции с ДНК......................................................... 5

Комплементарность............................................................................ 6

Удлинение и дополнение цепочки ДНК............................................. 6

Укорочение и разрезание................................................................... 7

Сшивка................................................................................................ 8

Модификация...................................................................................... 8

Полимеразная цепная реакция............................................................ 9

Сплетение.......................................................................................... 10

Секвенирование................................................................................ 11

Гель-электрофорез............................................................................ 11

Синтез............................................................................................... 12

2.2 Эксперимент Эдлмана...................................................................... 12

2.3 Эксперимент Э.Шапиро................................................................... 14

2.4 Эксперимент Э. Винфри.................................................................. 19

3 Модели................................................................................................... 22

Модель параллельной фильтрации (Parallel Filtering Model).................. 22

3.2 Плиточная модель............................................................................ 23

3.3 Операции ДНК в терминах теории формальных языков................ 24

4 Алгоритмы............................................................................................. 25

5  Инструментальные средства.............................................................. 27

5.1 Xgrow................................................................................................ 28

5.2 Namot................................................................................................ 28

6 Заключение. Приглашение к диалогу............................................... 29

Список литературы................................................................................. 31

1 Введение

Вычисления на ДНК – это раздел области молекулярных вычислений, нового междисциплинарного направления исследований на границе молекулярной биологии и компьютерных наук. Основная идея ДНК-вычислений – построение новой парадигмы вычислений, новых моделей, новых алгоритмов на основе знаний о строении и функциях молекулы ДНК и операций, которые выполняются в живых клетках над молекулами ДНК при помощи различных ферментов. Основные надежды, которые возлагаются на область ДНК-вычислений в практическом смысле – это новые методы синтеза веществ и объектов на молекулярном уровне.

Область ДНК-вычислений несет новые идеи для специалистов по нанотехнологиям, идеи, связанные с программируемым синтезом структур на наноуровне, со сборкой методами «снизу вверх» с использованием механизмов самоорганизации и самоформирования на молекулярном уровне [1, 2].

Для специалистов в области компьютерных наук, теории вычислений, парадигма ДНК-вычислений интересна новыми открывающимися возможностями: новыми моделями вычислений, новыми алгоритмами, возможностью решения задач, не решаемых в рамках классической парадигмы вычислений, возможностью исследования процессов массового параллелизма, которые средствами классической парадигмы даются трудно.

Специалистам по молекулярной биологии область ДНК-вычислений может дать новые идеи, которые развивались ранее в компьютерных науках, новые инструментальные средства, новые подходы в моделировании живого вещества на молекулярном уровне.

Опыт междисциплинарного диалога между математиками, специалистами по генетике и молекулярной биологии уже существует. Этот диалог начался с идей А.А.Ляпунова и продолжался долгие годы в Новосибирском университете и Институте цитологии и генетики СО АН СССР. Было выпущено несколько поколений специалистов – математических биологов и развивалась теория молекулярно-генетических систем управления, в основе которой лежит информационно-кибернетический подход к описанию молекулярно-генетических систем и процессов в клетках и организмах [3]. Возможно что сейчас, когда уже созданы необходимые технологические предпосылки, разработанные подходы получат новое развитие.

При этом в контексте ДНК-вычислений могут быть переосмыслены и использованы и существующие математические модели синтеза различных молекулярных структур [4], и огромный накопленный к настоящему времени экспериментальный потенциал.

2 Эксперименты

2.1 Элементарные операции с ДНК

Разберем кратко основные «команды», которые доступны нам при работе с ДНК в лабораторном опыте, и на которые должны опираться и теоретические разработки в области компьютерных наук.

Молекула ДНК (рис. 1) представляет собой двойную ленту, составленную из четырех оснований: А (аденин), Т (тимин), Г (гуанин), Ц (цитозин).

Нуклеотид с тиминовым основанием (рис. 2) состоит из 34 атомов.  Диаметр двойной спирали ДНК – 2нм, расстояние между соседними парами оснований – 0.34 нм. Полный оборот двойная спираль делает через 10 пар. ДНК простейших типов вирусов содержит всего несколько тысяч звеньев, бактерий – несколько миллионов,  а высших организмов – миллиарды: ДНК млекопитающих содержит  пар нуклеотидов, птиц -, пресмыкающихся - , насекомых - , высших растений - , бактерий - , вируса папилломы - .

Рис. 1. Молекула ДНК под электронным микроскопом

Рис. 2. Строение нуклеотида с тиминовым основанием

Комплементарность

Комплементарность оснований заключается в том, что образование водородных связей при соединении одинарных цепочек ДНК  в двойную цепочку возможно только между парами А-Т и Г-Ц (рис. 3). Этот же рисунок иллюстрирует операции ренатурации и денатурации. Ренатурация – это соединение двух одинарных цепочек ДНК за счет связывания комплементарных оснований. Денатурация – разъединение двойной цепочки и получение двух одинарных цепочек. Денатурация и ренатурация происходят при нагревании и охлаждении раствора с ДНК соответственно. Плавление ДНК происходит в диапазоне температур 85-95°C. Некоторые катализаторы позволяют понизить температуру этого процесса.

Рис. 3. Комплементарность, ренатурация, денатурация

Удлинение и дополнение цепочки ДНК

Удлинение цепочки ДНК происходит при воздействии на исходную молекулу ферментов – полимераз (рис. 4). Для работы полимеразы необходимо наличие:

1.     одноцепочечной матрицы, которая определяет цепочку добавляемых нуклеотидов по принципу комплементарности оснований;

2.     праймера – двухцепочечного участка, который присоединен к матрице, и к которому присоединяются свободные нуклеотиды;

3.     свободных нуклеотидов в растворе.

Рис. 4. Действие полимеразы

         Существуют полимеразы, которым не требуются матрицы для удлинения цепочки ДНК. Например, терминальная трансфераза добавляет одинарные цепочки ДНК к обоим концам двухцепочечной молекулы (рис. 5).

Рис. 5. Действие терминальной трансферазы

Укорочение и разрезание

         За укорочение и разрезание молекул ДНК отвечают ферменты – нуклеазы. Различают эндонуклеазы и экзонуклеазы. Экзонуклеазы осуществляют укорочение молекулы ДНК с концов (рис. 6), эндонуклеазы же разрушают внутренние фосфодиэфирные связи в молекуле ДНК (рис. 7). Экзонуклеазы могут укорачивать одноцепочечные молекулы и двухцепочечные, с одного конца или с обоих.

Эндонуклеазы могут быть весьма избирательными в отношении того, что они разрезают, где они разрезают и как они разрезают. Сайт-специфичные эндонуклеазы – рестриктазы – разрезают молекулу ДНК в определенном месте, которое закодировано последовательностью нуклеотидов – сайтом узнавания. Разрез может быть прямым, или несимметричным, как на рис. 7. Разрез может проходить по сайту узнавания, или же вне его.

Рис. 7. Разрезание молекулы ДНК

Сшивка

         Сшивка - операция, обратная операции разрезания, происходит под воздействием ферментов – лигаз (рис. 8). Когда двухцепочечные молекулы ДНК имеют комплементарные одноцепочечные концы (как на рис. 8а), то говорят, что это «липкие концы». Липкие концы соединяются вместе с образованием водородных связей (рис.8б), однако при этом остаются «зазоры», называемые насечками, т.е. отсутствующие фосфодиэфирные связи между соседними нуклеотидами одинарной цепочки (рис.8в). Фосфодиэфирные связи гораздо сильнее водородных, поэтому, в частности, при нагревании сначала разрушаются водородные связи, что приводит к образованию двух одинарных цепочек. Лигазы как раз и служат для того, чтобы закрыть насечки, т.е. способствовать образованию в нужных местах фосфодиэфирных связей (рис.8г).

Рис. 8 Сшивка молекулы ДНК

Модификация

         Потребность в модификации может возникнуть, например, для того, чтобы исключить молекулу из какой-либо операции. В живой клетке рестриктазы играют роль защитников от агрессии – например, в клетке бактерии, рестриктазы разрушают ДНК вируса-агрессора. Чтобы собственная ДНК не подверглась разрезанию, она модифицируется. Существует несколько типов модифицирующих ферментов – метилазы, фосфатазы и т.д.  Метилаза имеет тот же сайт узнавания, что и соответствующая рестриктаза. При нахождении нужной молекулы, метилаза модифицирует участок с сайтом так, что рестриктаза уже не сможет идентифицировать эту молекулу (рис. 9).

Рис. 9. Модификация

Полимеразная цепная реакция  

Иногда необходимо увеличить количество определенных фрагментов ДНК. Это делается при помощи метода полимеразной цепной реакции. Этот метод позволяет получить миллионы копий желаемой молекулы, даже если начать всего лишь с одного ее экземпляра. Метод применяется для двойных цепочек длиной от 100 до ~ 35000 звеньев (рис. 10).

Рис. 10. Полимеразная цепная реакция

         Каждая итерация метода требует трех стадий: денатурации, праймирования и удлинения (рис. 11). На каждой итерации количество молекул (теоретически) увеличивается в 2 раза.

Денатурация (рис. 11а) происходит при нагревании, поэтому полимеразы, находящиеся в растворе, должны быть устойчивыми к воздействию температуры. Такие полимеразы выделены из бактерий, живущих в горячих источниках.

Праймирование (рис. 11б) заключается в том, что к концам обеих одноцепочечных молекул, полученных в результате денатурации, присоединяются праймеры – заранее синтезированные короткие одноцепочечные молекулы. Праймирование необходимо для корректной работы полимераз.

На третьем этапе итерации (рис.11в) происходит дополнение праймированных одноцепочечных молекул до двухцепочечных под действием полимераз.

В результате всей итерации из одной молекулы мы получили две ее копии.

Рис.11. Итерация полимеразной цепной реакции

Сплетение

Операция сплетения (рис. 12) представляет собой последовательное разрезание двух молекул ДНК и сшивания полученных одноцепочечных молекул между собой.

Рис. 12. Сплетение

Секвенирование

         Секвенирование – это определение последовательности нуклеотидов в ДНК. Для секвенирования цепочек различной длины применяют различные методы. При помощи метода праймер-опосредованной прогулки удается на одном шаге секвенировать последовательность в 250-350 нуклеотидов. Отдельные шаги этого метода были автоматизированы, что позволило с легкостью секвенировать последовательности длиной в десятки тысяч пар нуклеотидов [5]. Естественно, после открытия рестриктаз стало возможным секвенировать длинные последовательности по частям. Как известно, не так давно был закончен проект «Геном человека» - секвенирование всего генома человека [6].

Гель-электрофорез

         Гель-электрофорез используется для разделения молекул ДНК по длине. Молекулы ДНК имеют отрицательный заряд, поэтому, если их поместить в гель и приложить постоянное электрическое поле, то они будут двигаться по направлению к аноду, причем молекулы меньшей длины будут двигаться быстрее. Когда первые, самые короткие молекулы достигают анода, процесс останавливают. Для маркировки молекул используют либо методы окрашивания, либо радиоактивные маркеры. Часто используют калибровочные молекулы (молекулы известной длины). Пример снимка, полученного в результате гель-электрофореза представлен на рис. 13 (снимок взят из работы  18). Молекулы двигались слева направо. После остановки видно, что молекулы одинаковой длины двигаются единым фронтом, образуя в геле дискретные полосы. По первой дорожке пущены калибровочные молекулы.

Рис. 13. Результаты гель-электрофореза

Для молекул различных диапазонов длины применяют разновидности метода. Некоторые из них позволяют разделить по длине молекулы, состоящие из миллионов пар оснований, и, напротив, применение полиакриламидных гелей позволяет работать с фрагментами ДНК, состоящими из порядка шести оснований, различающихся одним нуклеотидом.                   

Синтез

         Современные приборы автоматического химического синтеза позволяют быстро создавать одноцепочные последовательности длиной ≤ 50 звеньев. Более длинные цепочки (≥ 300) не удается синтезировать теми же методами, что и короткие. Дело в том, что синтез ДНК происходит последовательно, нуклеотид за нуклеотидом, при этом, естественно, на каждом шаге происходят потери: не все введенные в реакционную среду нуклеотиды присоединяются к нужным цепочкам.  Доля успешно присоединившихся нуклеотидов на одной итерации цикла синтеза называется эффективностью цикла. Как правило, реальная эффективность составляет 95%, хотя иногда удается достичь и 99% эффективности. Следовательно, при средней эффективности 95% в результате синтеза последовательности длиной 100 звеньев выход составит 0,6%, что нельзя считать удовлетворительным. Поэтому при синтезе длинных цепочек сначала синтезируют их короткие составляющие, а затем из них при помощи операций сшивания получают длинную цепочку. Таким образом получают последовательности длиной более 1000 звеньев [5].

2.2 Эксперимент Эдлмана

В 1994 г. Л.Эдлман продемонстрировал решение задачи о доказательстве существования гамильтонова пути в графе при помощи ДНК-вычислителя [7]. Задача формулируется следующим образом: существует ли в данном направленном графе G, в котором выделена начальная и конечная вершины, гамильтонов путь, т.е. путь, который проходит через каждую вершину в точности один раз (рис. 14) ?  Для решения задачи был применен следующий алгоритм:

·        Вход. Ориентированный граф G с n вершинами, среди которых выделены

2 вершины – v_in и v_out.

·        Шаг 1. Породить большое количество случайных путей в G.

·        Шаг 2. Отбросить все пути, которые не начинаются с v_in или не заканчиваются на v_out.

·        Шаг 3. Отбросить все пути, которые не содержат точно n вершин.

·        Шаг 4. Для каждой из n вершин v отбросить пути, которые не содержат v.

·        Выход. Да, если есть хоть один путь, нет – в противном случае.

Рис. 14. Граф в опыте Эдлмана

Каждая вершина графа кодируется последовательностью 20 нуклеотидов (рис. 15a). На рисунке даны коды вершин v₀ и v₁.

Ребра кодируются так, как показано на рис. 15б: берется вторая половина цепочки для начальной вершины, и первая половина цепочки для конечной вершины, эти цепочки соединяются в одну, затем берется комплементарная к полученной цепочке последовательность нуклеотидов, которой и кодируется соответствующее ребро графа. На рис. 15б показано общее правило кодирования ребер,  дан оператор комплементарности, затем показан процесс кодирования ребра u₀₁: взята вторая половина цепочки для вершины v₀ – v₀^’’, первая половина цепочки для вершины v₁ – v₁^’, эти цепочки последовательно соединены в одну, и к получившейся цепочке применен оператор комплементарности.

Ключевой момент опыта Эдлмана иллюстрирует рис. 15в. Пусть элементарный объем реакционной среды содержит три молекулы – кодирующие соответственно два различных ребра u_i,j, u_j,k и общую для них вершину v_j. Тогда произойдет соединение этих молекул в одну длинную цепочку u_i,k, кодирующую путь из вершины i в вершину k. Полученная цепочка будет способна соединяться с другой подходящей цепочкой, кодирующей вершину, или другой фрагмент пути на графе.

                  

U01=h(V0''V1')

(в)

(б)

(a)

V

0

=

ТАТЦГГАТЦГГТАТАТЦЦГА

V

1

= ГЦТАТТЦГАГЦТТАААГЦТА

V

1

’

V

1

’’

V

0

’’

=

ГТАТАТЦЦГА

V

1

’

=

ГЦТАТТЦГАГ

U01=h(ГТАТАТЦЦГАГЦТАТТЦГАГ)= =        ЦАТАТАГГЦТЦГАТААГЦТЦ

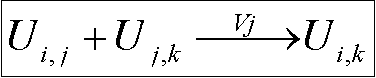
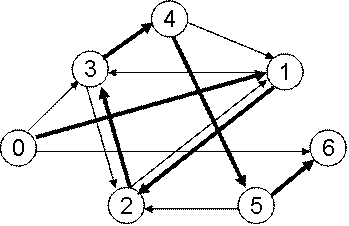
Рис. 15. Кодирование ребер и вершин и взаимодействие ребер и вершин в опыте Эдлмана

В ходе опыта сначала синтезируются цепочки, которые кодируют ребра и вершины графа, затем они в необходимом количестве запускаются в реакционную среду. Через некоторое время в среде образуются молекулы, которые соответствуют всем возможным путям на графе. Далее вопрос только в том, чтобы отыскать среди всех возможных путей гамильтонов путь, что и делается при помощи трех шагов фильтрации, описанных в алгоритме. Опыт Эдлмана занял 7 дней, больше всего времени заняла процедура фильтрации на шаге 4.

2.3 Эксперимент Э.Шапиро

Опыт, осуществленный в 2001 г. группой Э. Шапиро [8], принципиально отличается от опыта Эдлмана тем, что и «исходные данные», и «программа» описываются молекулами ДНК, в то время как в опыте Эдлмана «программа» - это, по существу, последовательность реакций, задаваемых человеком.

В опыте Э. Шапиро был реализован конечный автомат, т.е. система, состоящая из множества состояний, алфавита (множества символов, которые могут поступать на вход), начального состояния, множества заключительных состояний и функции переходов. Данный автомат изображен на рис. 16. Автомат может находиться в двух состояниях – S0 и S1. Алфавит автомата состоит из двух символов – a и b. На вход автомату подается последовательность символов a и b. Автомат отвечает на вопрос – четное или нечетное количество символов а содержится во входной последовательности. Автомат может отвечать на 765 подобных «вопросов». Программирование автомата заключается в задании функции переходов, которой соответствует набор стрелок на рис. 16. И переходам, и состояниям, и входной последовательности в опыте Шапиро отвечают молекулы ДНК.

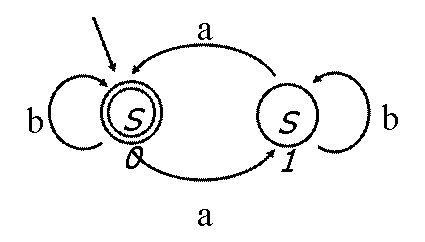
Рис. 16 Конечный автомат в опыте Э. Шапиро

«Программа» для этого автомата (правила переходов) записывается следующим образом:

S0, a → S1

S0, b → S0

S1, a → S0

S1, b → S1

Если по окончании обработки входной последовательности автомат находится в состоянии S0 – это означает, что во входной последовательности было четное количество символов а, если же он находится в состоянии S1 – количество символов а было нечетным. Вычисления происходят по перечисленным правилам, причем воспринимать их следует «буквальным образом», т.е. как замену строки S0a на строку S1 для первого правила. Тогда процесс вычислений будет проходить, например, так:

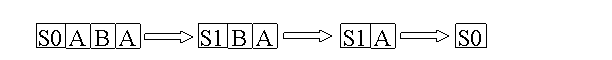
Рис. 17. Пример работы конечного автомата

         Так же просто работает и автомат на ДНК. Символы алфавита – а и b - кодируются молекулами ДНК (рис. 18а). Далее кодируются «полные» состояния автоматов, т.е. состояние автомата + символ на входе. Таких «полных» состояний получается 4: S0,A; S0,B; S1,A; S1,B;, их ДНК-коды также показаны на рис. 18б.

В нашем случае «программа» автомата содержит 4 перехода. Их коды показаны на рис. 18в. Забегая вперед, отметим, что каждый шаг работы автомата выполняется за два «молекулярных шага»: к закодированной входной последовательности присоединяется нужный переход, образовавшиеся насечки закрываются посредством действия лигазы, затем необходимо отделить от полученной цепочки ненужную часть так, чтобы конец оставшейся цепочки кодировал следующее «полное» состояние автомата: следующий входной символ и собственно состояние. Это и происходит при помощи рестриктазы. Для того, чтобы рестриктаза работала корректно, необходимо так закодировать переходы, чтобы они содержали в себе сайты узнавания – точку отсчета для рестриктазы. Для перехода S0,A→ S1 сайт узнавания показан на рис. 18в.

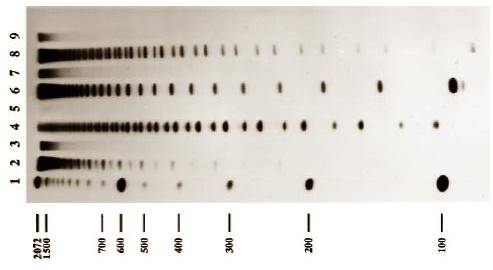
В конце входной цепочки располагается символ-терминатор (рис. 18г). По окончании работы автомата получается одна из молекул- S0,Т, или S1,Т (рис. 18г), к которым присоединяется одна из молекул – индикаторов конечного состояния, различных по длине, что позволяет выяснить конечное состояние при помощи гель-электрофореза.

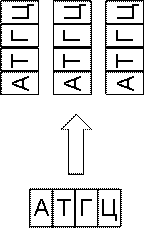
Непосредственно опыт Э.Шапиро на примере простой входной последовательности показан на рис. 19 и 20.  Опыт начинается с синтеза молекул, соответствующих символам алфавита, переходам, полным состояниям, символу-терминатору и молекулам – индикаторам конечного состояния. Далее все эти молекулы в необходимом количестве помещаются в реакционную среду, в которую дополнительно помещаются и необходимые рестриктазы и лигазы.

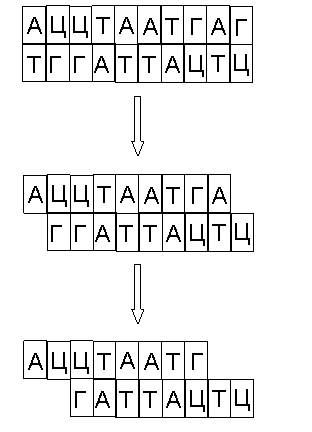
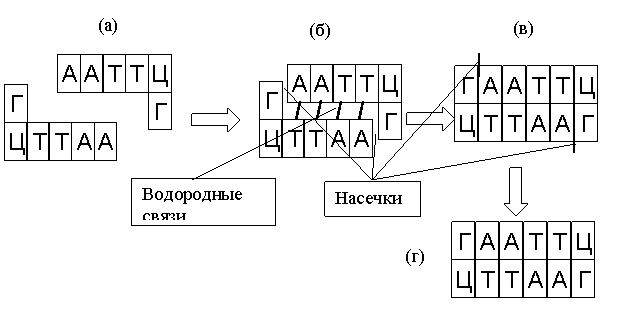
Пусть на вход автомата подается последовательность ABA и он работает по уже описанным правилам. Начальное состояние автомата – S0. Исходная цепочка ДНК состоит из фрагментов S0, A, B, A и выглядит так, как на рис. 19а. Очевидно, что, в силу принципа комплементарности, из четырех возможных вариантов, к молекуле, кодирующей входящую последовательность и начальное состояние может присоединиться только переход S0,A→S1 (рис. 19б). Молекулы соединяются липкими концами, далее при помощи лигазы закрываются насечки, т.е. образуются более прочные фосфодиэфирные связи между соседними нуклеотидами на местах стыков в одинарных цепочках. В результате получается молекула, показанная на рис. 19в, которая содержит сайт узнавания для рестриктазы. Рестриктаза, определив сайт узнавания, разрезает молекулу строго в местах, отмеченных на рис. 19в, т.е. отступая на 9 нуклеотидов в верхней цепочке и на 13 в нижней от границы сайта узнавания. Говорить о верхней и нижней цепочке можно потому, что молекула, в силу особенностей на уровне химических связей, имеет направление. После разрезания молекула становится такой, как на рис. 19г. Отметим, что конец молекулы кодирует теперь не просто следующий входной символ – В, а «полное» состояние, т.е. S1,B.

Далее, к полученной молекуле может присоединиться только переход S1,B→S1 и никакой другой. Затем происходит сшивка и разрезание (рис. 19д) таким же образом, как и на предыдущем шаге. Обратим внимание на то, что переход S1,B→S1 содержит тот же сайт узнавания, что и переход S0,A→S1, да и любой другой переход,  что позволяет обойтись в опыте рестриктазой одного типа.

В результате последней итерации получилась молекула, показанная на рис. 19е, которая кодирует «полное» состояние S1,A, т.е. автомат находится в состоянии S1 и на входе символ A. Следующая итерация аналогична двум предыдущим – прилипание перехода S1,A→S0, сшивка и разрезание (рис. 20е). Для того, чтобы не загромождать рисунок, символ-терминатор был опущен, поэтому можно представить, что полученная в ходе третьей итерации молекула 20з заканчивается символом-терминатором. Полученная молекула соответствует состоянию S0,Т. Теперь к ней может присоединиться только  молекула-индикатор, с липким концом АГЦГ, имеющая определенную длину. Под действием лигазы происходит сшивка. Затем при помощи калибровочных молекул и гель-электрофореза мы можем выяснить, что в ходе вычислений получен результат – автомат обработал входную последовательность полностью, до символа-терминатора и находится в состоянии S0, а, значит, входная последовательность содержала четное количество символов А.

В опыте одновременно работали 10¹² автоматов с одинаковым «программным обеспечением». Входные данные, в принципе, для автоматов могут быть различными. «Вычислительная мощность» составляла 10⁹ переходов в секунду с вероятностью больше, чем 99,8%.

Рис. 18. Кодирование символов алфавита и переходов последовательностями нуклеотидов

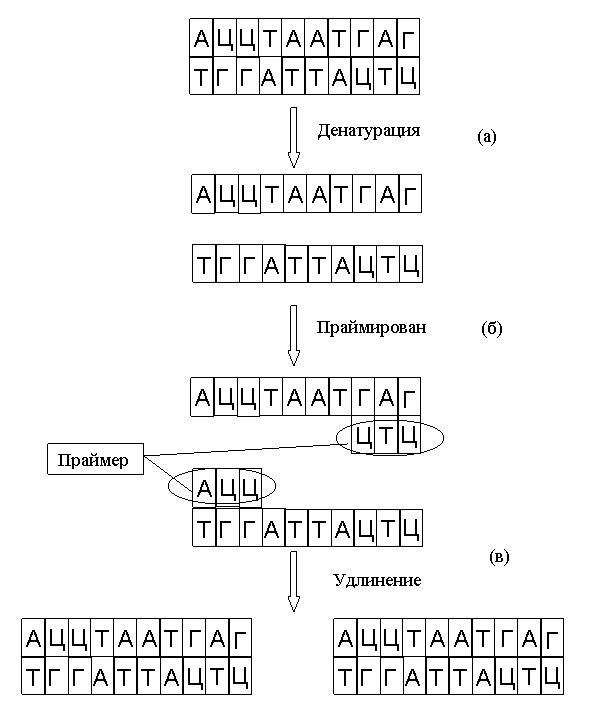
Рис. 19. Схема опыта Э.Шапиро

Рис. 20. Схема опыта Э.Шапиро. Продолжение

В статье [9] проанализированы вычислительные возможности класса автоматов, предложенных группой Э. Шапиро. Показано, что эти автоматы могут вычислять произвольные булевы функции.

На вопрос о том, смогут ли ДНК-вычислители конкурировать в будущем с существующими процессорами, Э. Шапиро отвечает, что такой вопрос даже не ставится. Как и многие другие исследователи, Э. Шапиро полагает, что основное назначение ДНК вычислителей – это тонкий химический синтез, сборка нужных молекул и конструкций. В самом деле, как мы видим, собственно вычисление – обработка входной последовательности, занимает очень малое время. Значительное время тратится на то, чтобы понять, какой собственно результат получен.

2.4 Эксперимент Э. Винфри

В лаборатории молекулярных вычислений в Калифорнийском технологическом институте под руководством Э. Винфри (E.Winfree) успешно разрабатываются методы синтеза различных поверхностей при помощи ДНК. В этих экспериментах переосмысливается само понятие вычисления. Оказывается, можно использовать двумерные плитки различной формы, которые могут взаимодействовать по локальным правилам (соединяться друг с другом), для того, чтобы получить в результате взаимодействия множества плиток желаемую глобальную структуру. При этом под вычислением понимается процесс создания такой структуры.

Разберем простейший пример вычисления, который приводится в работах сотрудников лаборатории Э. Винфри. Пусть необходимо реализовать простейший алгоритм  – счетчик. Для этого нам понадобятся рабочие элементы четырех типов (рис. 21), и элементы, задающие граничные условия – трех типов (рис. 22).

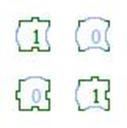
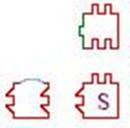
Рис. 21.                                                                 Рис. 22.

Правило создания структуры чрезвычайно простое: во главу угла ставится плитка S, две оставшиеся граничные плитки выкладываются в направлении вверх и влево, затем, справа налево ряд за рядом укладываются рабочие плитки. При этом укладывать плитку можно лишь в том случае, если уже уложены ее соседи снизу и справа. Результат показан на рис. 23 и соответствует счетчику.

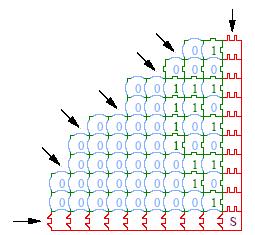
Рис. 23. Плиточный счетчик

Еще в 60-х годах доказано, что при помощи «плиточных вычислений»  можно реализовать машину Тьюринга. Однако обратное утверждение неверно – проблема замощения плоскости плитками различной формы не разрешима в парадигме машины Тьюринга.

В работах Э. Винфри отработана методика перехода от двумерных плиток к молекулам ДНК. Например, в [10] описывается эксперимент синтеза известной фрактальной структуры – ковра Серпинского. В опыте используются всего 4 плитки, которые соответствуют правилам таблицы истинности для оператора XOR (рис. 24).

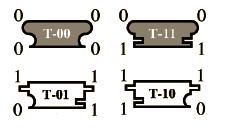
Рис. 24. Плитки для создания ковра Серпинского

Начальный слой укладывается из плиток типа Т-00. Затем плитки укладываются по направлению снизу вверх (рис.25).

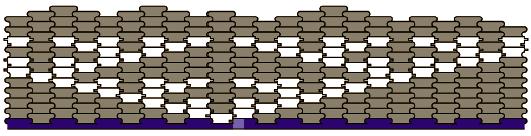
Рис. 25. Ковер Серпинского из плиток

Далее, каждой плитке ставится в соответствие молекула ДНК. В реальном опыте используются несколько иные плитки, чем показанные на рис. 24. Схема опыта Винфри на порядок сложнее рассмотренных опытов Эдлмана и Шапиро, поэтому ограничимся только демонстрацией кодировки рабочих плиток (рис. 26, 27).

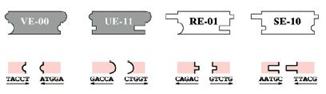
Рис. 26. Набор плиток в опыте по получению ковра Серпинского

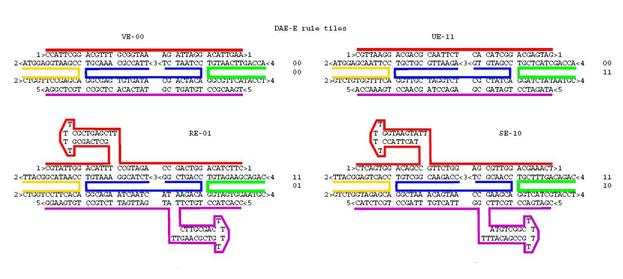
Рис. 27. Соответствие двумерных плиток молекулам ДНК

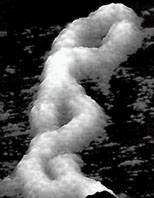
         В результате опыта под атомно-силовым микроскопом можно видеть следующую структуру (рис. 28). На рисунке видно, что в результате опыта получаются достаточно большие (порядка десятков слоев) структуры, в которых количество ошибок не слишком велико (ошибки отмечены крестиками).

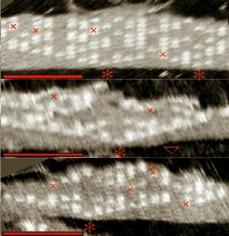
Рис. 28. Синтез ковра Серпинского при помощи ДНК

         Методика, разработанная в лаборатории Э.Винфри позволяет синтезировать и трехмерные объекты – например, микротрубочки [11].  

3 Модели

         После проведения пионерских опытов возникает потребность в общих моделях молекулярных вычислений, которые бы позволяли проектировать новые эксперименты и обобщать существующие.

Модель параллельной фильтрации (Parallel Filtering Model)

Происхождение данной модели уходит корнями в эксперимент Элдмана. Описание модели приводится по [12]. В модели основной упор делается на фильтрацию потому, что множество всевозможных решений задачи получается уже на первом шаге за счет того, что взаимодействующие молекулы ДНК спроектированы нужным образом. А основная часть алгоритма – это извлечение нужного результата из множества всевозможных результатов.

Пробирка – это мультимножество слов (конечных строк) над алфавитом {А, Ц, Г, Т}.  Мультимножество – это, по сути, объединение множеств, каждое из которых содержит элементы только одного типа, или же о мультимножестве можно думать как о множестве, которое определяется множеством неповторяющихся элементов, каждому из которых приписано натуральное число, означающее количество элементов данного типа в мультимножестве. Следующие основные операции были первоначально определены для пробирок, т.е. мультимножеств одинарных цепочек ДНК. Однако их подходящие модификации будут применяться и к двойным цепочкам.

Слить. Образовать объединение (в смысле мультимножеств) двух данных пробирок N₁ и N₂.

Размножить. Изготовить две копии данной пробирки N.

Обнаружить. Возвратить значение истина, если данная пробирка N содержит по крайней мере одну цепочку ДНК, в противном случае возвратить значение ложь.

Разделить (или Извлечь). По данным пробирке N и слову w над алфавитом {А,Ц,Г,Т} изготовить две пробирки +(N,w) и –(N,w) такие, что +(N,w) состоит из всех цепочек в N, содержащих w в качестве (последовательной) подстроки, а – (N,w) состоит из всех цепочек в N, которые не содержат w в качестве подстроки.

Разделить по длине. По данным пробирке N и целому числу n, изготовить пробирку (N, ≤ n), состоящую из всех цепочек из N длины не больше n.

Разделить по префиксу (суффиксу). По данным пробирке N и слову w, изготовить пробирку B(N,w) (соответственно E(N,w)), состоящую из всех цепочек в N, начало (соответственно конец) которых совпадает со словом w.

В приведенных терминах стадия фильтрации в опыте Эдлмана может быть описана следующей программой, которая начинает свою работу после того, как произошло сшивание всех нужных молекул и в пробирке N образовалось множество всех возможных путей в графе G. (Каждый из олигонуклеотидов s_i, 0 ≤ i ≤ 6, имеет длину 20).

(1) ввести (N)

(2) N ← B (N,s₀) // выделить все цепочки, которые начинаются с вершины S0

(3) N ← E (N,s₆) // выделить все цепочки, которые заканчиваются на S6

(4) N ←  (N, ≤ 140) //выделить все цепочки длиной не больше 140

(5) для i от 1 до 5 выполнить N ← + (N,s_i) // для каждой из вершин от s1 до s5 выделить //только те цепочки, которые содержат данную вершину

(6) обнаружить (N) //true если осталась хоть одна цепочка, false – в противном случае.

3.2 Плиточная модель

Существует задача об отыскании набора геометрических фигур на плоскости (плиток), которыми Евклидова плоскость может быть покрыта только непериодическим образом.  В 1961 г. было показано, что невозможно создать алгоритм, который определяет, можно ли покрыть плоскость при помощи заданного набора плиток, или нет. Позже был предъявлен набор из 20426 плиток, которыми можно покрыть плоскость только непериодически. В дальнейшем количество плиток было сокращено сначала до 104, а затем и до 6, и, наконец, до двух (рис. 29) [20].

Интересен следующий факт: Р. Пенроуз получил свой набор из 2-х плиток путем различных манипуляций разрезания и склеивания над набором Робинсона из 6 плиток.

В свете мысли о задаче покрытия и мысли об экспериментах Э.Винфри, в которых исходным материалом служат наборы плиток, которые затем преобразуются в молекулы ДНК, рождается идея о разработке парадигмы ДНК-вычислений именно в «плиточных терминах». При этом ДНК-вычислитель будет представлять собой клеточный автомат из клеток произвольной формы, а локальные правила взаимодействия клеток будут определяться их формой. С одной стороны, такой автомат будет дискретным, т.к. будет состоять из отдельных взаимодействующих плиток, и к нему будет применимо понятие шага. А с другой стороны, локальные правила задаются за счет непрерывной формы границы взаимодействующих плиток. Данный подход сразу же обеспечивает возможность описания параллельных процессов, которые изначально присущи ДНК-вычислителю. При всей фантастичности данного подхода, нельзя не признать, что он несет значительный эвристический потенциал.

Рис. 29. Плитки Пенроуза, которыми плоскость может быть заполнена только непериодическим образом

Теоретическим базисом «плиточной» модели могут быть, с одной стороны, все работы, относящиеся к проблеме покрытия (Ванга, Бергера, Робинсона, Пенроуза), с другой стороны – работы Э. Винфри, направленные на получение нужных структур на практике, а с третьей – работы по теории клеточных автоматов с «квадратными клетками».

3.3 Операции ДНК в терминах теории формальных языков

         Монография [12] практически полностью, за исключением первых глав вводного характера, посвящена разработке теории ДНК-операций с позиций теории формальных языков. Молекулы ДНК представляются как двойные строки над алфавитом {А,Т, Г, Ц}, ферментативные манипуляции над молекулами ДНК представляются как операции над этими строками. Используя мощь теории формальных языков, авторам монографии удалось формализовать операции с ДНК. Разработанный теоретический базис вполне может быть использован для проектирования и разработки инструментальных средств: специального байт-кода, который имитирует работу ДНК-компьютера, интерпретатора этого байт-кода, языков высокого уровня, компиляторов в байт-код и т.д. Среди недостатков данного подхода следует отметить то, что с его помощью не удается моделировать важнейший аспект ДНК-вычислений – массовый параллелизм ДНК-вычислителя. Кроме того, теория формальных языков – это тот базис, на котором во многом стоит классическая парадигма вычислений.  

4 Алгоритмы

С. Смейл, составляя список математических проблем 21 столетия [13], утверждает, что, если в 20 в. важную роль в математике сыграло изучение множеств решений уравнений, то в 21в. не меньшую роль может сыграть изучение процесса нахождения решений, т.е. изучение алгоритмов.

Одна из проблем, вошедших в список из 18 проблем С.Смейла, это знаменитая проблема P ≠ NP. В теории сложности алгоритмов задача относятся к классу P, если существует алгоритм, который решает ее за время не более O(n^k), где k – некоторая константа, не зависящая от n – длины входной последовательности данных. Класс задач NP определяется как множество задач, для которых существует проверяющий алгоритм, работающий за полиномиальное время. Т.е., если предъявлено решение NP-полной задачи, то проверить, правильное оно или нет, можно за полиномиальное время. Вся проблема в том, что для NP полных задач существует очень большое количество вариантов, которые нужно перебрать, а алгоритмов, которые бы решили задачу не путем перебора, а за полиномиальное время, отыскать не удается.

На практике в программировании считается, что, если удается доказать принадлежность задачи к классу NP–полных, то не нужно пытаться искать эффективного алгоритма ее решения, нужно считать эту задачу практически неразрешимой и пытаться построить приближенный алгоритм [14].

С.Смейл сформулировал проблему P ≠ NP на языке, понятном математическому сообществу следующим образом [13].

Рассмотрим теорему Гильберта о нулях над множеством комплексных чисел. Пусть f₁,….f_k – комплексные полиномы от n переменных. Требуется решить, имеют ли они общий нуль . Теорема о нулях утверждает, что общего нуля нет тогда и только тогда, когда существуют комплексные полиномы g₁,…,g_k от n переменных, удовлетворяющие полиномиальному тождеству

                                                            (1)

Эффективная теорема о нулях, доказанная Браунуэллом (1987) и другими, утверждает,  что в приведенной выше формулировке можно допустить, что степени g_i удовлетворяют неравенствам

                                     (2)

         С таким ограничением степеней задача разрешимости становится задачей линейной алгебры. При заданных коэффициентах f_i можно проверить, имеет ли (1) решение относительно коэффициентов g_i. Таким образом, мы получаем некоторый алгоритм решения теоремы о нулях. Количество необходимых для решения арифметических шагов возрастает по экспоненте при увеличении количества коэффициентов f_i (входных данных).

         Гипотеза (над C). Не существует алгоритма решения теоремы о нулях, в котором количество арифметических шагов возрастает полиномиально по времени.

В настоящее время известно множество NP-полных задач, связанных с самыми разными областями математики и информатики: логикой, теорией графов, компьютерными сетями, множествами и разбиениями, расписаниями, математическим программированием, алгеброй и теорией чисел, играми и головоломками, оптимизацией программ [14].

К NP-полным задачам относятся задачи: задача о гамильтоновом цикле, задача о выполнимости для схем, задача о выполнимости для пропозициональных формул, задача о выполнимости 3-CNF-формул, задача о клике, задача о вершинном покрытии, задача о суммах подмножеств, задача коммивояжера и другие задачи [14]. На данный момент известны сотни NP-полных задач.

Наиболее удивительный факт заключается в том, что для NP-полных задач не найдены алгоритмы, решающие их за полиномиальное время, однако, не доказано, что таких алгоритмов не существует. Уверенность специалистов в отсутствии полиномиальных алгоритмов для NP-полных задач основывается на том, что, если бы удалось найти такой алгоритм хотя бы для одной NP-полной задачи, то это означало бы существование полиномиальных алгоритмов для всех NP-полных задач. А поскольку на поиск таких алгоритмов для различных NP-полных задач были затрачены огромные усилия, которые не увенчались успехом, то считается, что их и не существует.

         В теоретических моделях молекулярных вычислений, например в модели параллельной фильтрации (parallel filtering model) NP-полные задачи решаются за полиномиальное время. На практике, в лаборатории, подобные вычисления  для реальных, представляющих практический интерес входных данных, полном объеме осуществить пока невозможно, и не ясно, станет ли возможно в дальнейшем, но примеры алгоритмов для NP-полных задач в моделях для молекулярных вычислений и понимание того, что в живых клетках происходят очень сложные процессы обработки информации, обеспечивают мотивацию для дальнейшей разработки парадигмы молекулярных вычислений.

         Основная идея решения NP-полных задач при помощи ДНК-вычислителей состоит в том, что, используя массовый параллелизм молекул ДНК, весь набор решений можно получить на одном шаге алгоритма (как в опыте Эдлмана), а затем уже выделять нужное решение при помощи фильтрующих шагов. С одной стороны, к данному подходу можно отнестись скептически:  последовательный перебор вариантов заменяется «синтезом» всех вариантов, т.е. от полного перебора мы никуда не уходим, т.е. задача решается методом грубой силы. С другой стороны, при использовании массового параллелизма ДНК мы можем себе это позволить. Проведем небольшую оценку для задачи поиска гамильтонова цикла на графе. Гамильтонов цикл в неориентированном графе G -  это простой цикл, который проходит через все вершины графа. Оценим время решения этой задачи методом полного перебора всех перестановок вершин. Имеется граф G = (V,E). Если мы используем представление графа при помощи матрицы инцидентности, то число вершин m в графе будет , где - длина представления графа. Имеется m! различных перестановок вершин графа, т.е. время работы переборного алгоритма составит . Пусть мы имеем 10000 вершин, тогда время работы алгоритма будет , т.е., если принять длительность одной операции равной 10^-11с (современный суперкомпьютер HP SuperDome), то время счета составит порядка 2⁶⁴с., т.е. 4.5·ּ10¹⁹ лет. Теперь возьмем ДНК бактерии, длиной 2·10⁶ нуклеотидов, и будем рассматривать ее всего лишь как запись числа в четверичной системе счисления с повышенной надежностью. Подобный подход позволяет кодировать (4^2000000 ≈ 10^1204120) вершин. Естественно, для того, чтобы алгоритм на ДНК работал, необходимо кодировать вершины совершенно определенным образом, и их код должен отличаться не в «одном знаке», однако, совершенно ясно, что при любом кодировании поражающий воображение порядок этой величины значительно уменьшить не удастся.  Таким образом, не решая NP-полную задачу теоретически (для сколь угодно большого размера задачи), ДНК-вычислитель решает ее практически, т.е. для всех размеров задач, которые могут представлять для нас интерес.

         Согласно обзору [15], на данный момент в парадигме молекулярных вычислений решены следующие задачи (многие из них относятся к классу NP-полных):

В той же работе описаны алгоритмы решения 7 NP-полных задач в модели параллельной фильтрации.

5  Инструментальные средства

Помимо разработки новых алгоритмов и новых принципов вычислений, область молекулярных вычислений интересна для специалистов по компьютерным наукам как источник задач создания инструментальных средств для работы с последовательностями ДНК, молекулами, замощениями.

5.1 Xgrow

         Симулятор Xgrow разработан в лаборатории молекулярных вычислений Калифорнийского технологического института Э.Винфри. Он использует в своей работе модели aTAM (abstract Tile Assembly Model) и kTAM (kinetic Tile Assembly Model), описанные в работах [16] и [17] соответственно. Попросту говоря, симулятор Xgrow    позволяет имитировать процесс синтеза различных структур, получая на входе набор плиток, а также позволяет оценить возможные ошибки при создании структуры.  Например, на рис. 30 представлен процесс моделирования синтеза структуры «ковер Серпинского».

5.2 Namot

         Система Namot была разработана в 1994-1995 годах в Лос-Аламосской лаборатории США. Namot расшифровывается как Nucleic Acid MOdeling Tool. Она представляет собой графическое средство работы с молекулярными структурами. С ее помощью можно составлять структуры из атомов, задавать связи в трехмерном пространстве, строить последовательности молекулярных операций. Внешний вид программы с собранной молекулярной структурой показан на рис. 31.

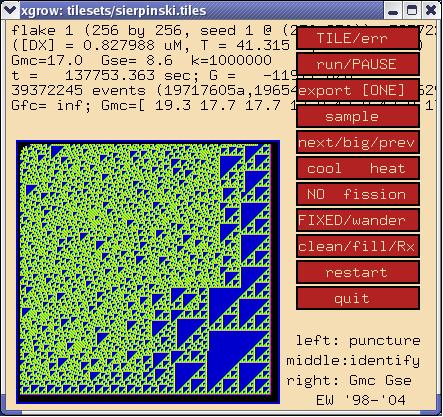
Рис. 30. Симулятор Xgrow в работе

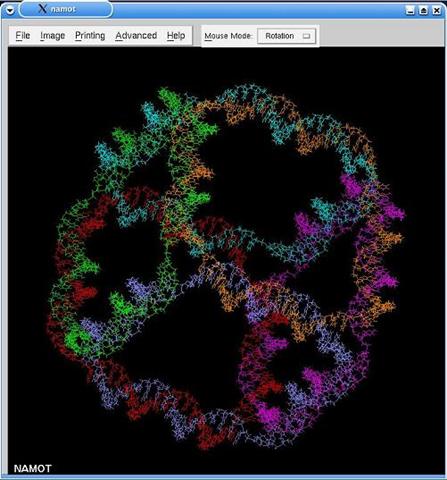
Рис. 31. Namot в действии

6 Заключение. Приглашение к диалогу

… в те невообразимые времена, когда еще не существовала молекулярная кулинария и обыкновенную котлету приходилось изготавливать посредством сложнейших и не очень аппетитных процедур…

А. и Б. Стругацкие. Волны гасят ветер.

В рамках первых двух парадигм синергетики – парадигме диссипативных структур и парадигме динамического хаоса - исследователи изучали процессы самоорганизации в различных системах, в частности, структуры, возникающие в диссипативных системах. При этом, по-видимому,  даже не ставился вопрос о том, какие условия, какие законы должны присутствовать в системе для того, чтобы получилась структура нужного вида. Сейчас мы подходим к тому, чтобы воспользоваться законами «самоорганизации» природы для сборки собственных конструкций и материалов. Под самоорганизацией здесь можно понимать сборку методом «снизу вверх»: мы задаем цель, структуру, которую необходимо получить, программу сборки и условия работы системы, затем получаем результат. Мы не контролируем каждый шаг. Ключевым моментом такой самоорганизации представляется следующий принцип: локальные взаимодействия определяют глобальную структуру.

Отдельный вопрос – это вопрос: почему локальные взаимодействия могут определять глобальную структуру, как это происходит в общем случае? Простейший пример реализации этого принципа – счетчик на рис. 23. Другими словами, это вопрос о механизмах усиления.

Один из больших вопросов, требующих разработки – это алгоритмы решения обратных задач, или алгоритмы построения алгоритмов по известной конечной структуре. На данный момент мы умеем строить лишь такие структуры, в основе которых лежит какая-то простейшая операция, например, сдвиг вправо, инкремент, операция XOR. Девизом этого направления должен быть, конечно же, следующий: больше структур хороших и разных, а еще лучше, больше универсальных алгоритмов.

Представим себе, что задача проектирования и синтеза практически любых структур на молекулярном уровне при помощи ДНК-вычислителя решена. Какими теоретическими методами и инструментальными средствами мы должны для этого обладать?

Должна быть создана общая теория «плиточных» автоматов, разработаны эффективные методы перехода от «плиточного» описания к молекулярному, разработаны лабораторные методы синтеза, комплексы, которые осуществляют программируемый синтез, разработана библиотека алгоритмов синтеза различных структур, разработаны методы проектирования алгоритмов сборки на основе существующих алгоритмов, разработаны методы решения обратных задач: задач синтеза алгоритмов по известной конечной структуре.  При наличии такого арсенала недалеко и до молекулярной кулинарии!

Если опуститься на почву реальности сегодняшнего дня, то, вероятно, ДНК-вычислители в первую очередь будут использоваться в криптоанализе и для синтеза определенных типов лекарств.

С точки зрения компьютерных наук и математического моделирования, дальнейшее развитие парадигмы ДНК-вычислений, по-видимому, обещает нам новые методы построения и анализа моделей: вместо того, чтобы упрощать, строить иерархии упрощенных моделей, мы, по-видимому, сможем учитывать в моделях большое количество вариантов и параметров, а параметрами порядка станут какие-то биологические параметры модели.

Дальнейшее развитие области ДНК-вычислений требует значительных междисциплинарных усилий. С одной стороны, специалисты по теории вычислений и математическому моделированию представляют себе ситуацию на уровне молекул чрезвычайно упрощенно. С другой стороны, возможно как раз в силу недооценки сложности ситуации они располагают арсеналом идей, которые могут быть применены для молекулярной сборки, а также методами построения моделей процессов, происходящих на молекулярном уровне. Участие же в исследованиях по ДНК-вычислениям, с одной стороны, специалистов по молекулярной биологии, которые смогут ответить на вопросы принципиальной осуществимости тех или иных идей сборки, и специалистов - нанотехнологов, которые понимают, какие структуры и объекты нужно синтезировать, и какие структуры могут быть синтезированы при текущем уровне развитии технологий, является решающим.

Опыт междисциплинарного диалога в других областях говорит о том, что этот процесс чрезвычайно плодотворен и часто приводит к результатам, которые не могли предсказать участники в начале исследований. Мы уверены в том, что область ДНК-вычислений  состоится.

Список литературы

1.     Нанотехнология в ближайшем десятилетии. Прогноз направления исследований. /Под ред. М.К. Роко, Р.С. Уильямса и П. Аливисатоса. Пер. с англ. – М.: Мир, 2002 – 292с.

2.     Малинецкий Г.Г., Митин Н.А., Науменко С.А. Нанобиология и синергетика. Проблемы и идеи. Препринт ИПМ им. М.В. Келдыша РАН № 29 за 2005г.

3.     Ратнер В.А. Генетика, молекулярная кибернетика: Личности и проблемы. - Новосибирск: Наука, 2002. - 272с.

4.     Козлов Н.Н., Кугушев Е.И., Сабитов Д.И., Энеев Т.М. Компьютерный анализ процессов структурообразования нуклеиновых кислот. Препринт ИПМ им. М.В. Келдыша РАН № 42, 2002г.

5.      Глик Б., Пастернак Дж. Молекулярная биотехнология. Принципы и применение. Пер. с англ. - М.: Мир, 2002. - 589с.

6.     Франк-Каменецкий М.Д.Век ДНК. М.:КДУ, 2004. - 240с.

7.     Adleman L.M., Computing with DNA, Scientific American, August 1998, p. 34-41.

8.     Shapiro E. Programmable and autonomus computing machine made of biomolecules//Letters to nature, vol 414,  22 november 2001.

9.     Soloveichik D, Winfree E. The computational Power of Benenson Automata. // Preprint submitted to arXiv.org, 21 December 2004.

10. Rothemund P., Papadakis N, Winfree E. Algorighmic Self-Assembly of DNA Sierpinski Triangles. // Plos Biology, December 2004, Volume 2, Issue 12.

11. Rothemund P., Ekani-Nkodo A., Papadakis N.,Kumar A.,Fygenson D.K.,Winfree E. Design and Characterization of Programmable DNA Nanotubes. //J. AM. CHEM. SOC. 2004, 126, 16344-16352.

12. Паун Г., Розенберг Г., Саломаа А. ДНК-компьютер. Новая парадигма вычислений. – М.: Мир, 2004. – 528с.

13. Смейл С. Математические проблемы следующего столетия. // Симо К., Смейл С., Шенсине А. и др. Современные проблемы хаоса и нелинейности. – Ижевск: Институт компьютерных исследований, 2002, 304 стр.

14. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ / Пер. с англ. под ред. А.Шеня. – М.: МЦНМО: БИНОМ. Лаборатория знаний, 2004. – 2-е изд., стереотип. – 960 с.

15. Istvan Katsanyi. Molecular Computing Solutions of some Classical Problems.

16. Winfree, E. Simulations of Computing by Self-Assembly. Presented at DNA Based Computers IV; published as Caltech CS Tech Report 1998.22, (25 pages).

17. Winfree, E., Bekbolatov R. Proofreading tile sets: error correction for algorithmic self-assembly. // DNA 9.

18. Winfree E.,Liu F.,Wenzler L.A.,Seeman N.C. Design and Self-assembly of two-dimensional DNA crystals. //Nature, vol. 394, 6 august 1998.

19. Албертс Б., Брей Д., Льюис Дж., Рэфф М., Робертс К., Уотсон Дж. Молекулярная биология клетки. М.: Мир, 1993, т.1.

20. Пенроуз Р. Новый ум короля: О компьютерах, мышлении и законах физики: Пер. с англ. /Общ.ред. В.О.Малышенко. – М.: Едиториал УРСС, 2003. – 384с.