Модель тонкого деформируемого пневматика
|
|
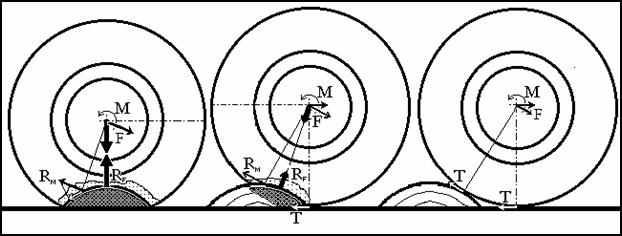
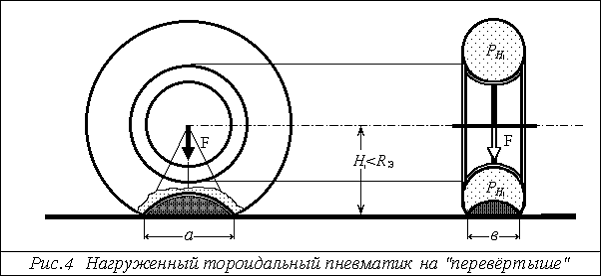
Действительно, любая часть поверхности камня в форме сегмента тора является поверхностью тора, а её зеркальное отражение совпадает (если мысленно убрать камень в текущей позиции колеса) с вытесненной камнем частью тора (т.е. – той его поверхностью, которая соприкасается в текущей позиции с поверхностью камня). Поэтому в каждый момент наезда колеса на камень-перевёртыш существует плоскость основания текущего сегмента тора, нормаль к которой определяет направление силы реакции, отражающей давление пневматика и препятствующей наезду колеса на камень (см. рис.5).
Для определения площади опорной проекции камня-перевертыша проинтегрируем
по y уравнение
сечения тора в основании сегмента в плоскости Y-Z (см. Приложение) в виде:
z(y,H):
z=![]() .
.
Интегрирование следует выполнить в пределах
±ymax=±![]() = ±a.
= ±a.
Используя симметрию отрезков сечения
z(y)Î ±[0, zmax=![]() =b], имеем: Sосн=4
=b], имеем: Sосн=4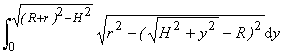
В качестве оценки величины искомой площади основания сегмента, по-видимому, можно использовать площадь аппроксимирующего её эллипса с полуосями a=ymax и b= zmax: Sосн» Sэ=pab.
Тогда - для заданных размеров колеса R и r, начального давления P0(T0), показателя политропы газа n и температуры газа T - имеем значение поддерживающей силы F пневматика (с безмоментной оболочкой), стоящего на изометричном для тора камне с его объемом: Vсег(R,r,H)
(*)
F =
![]()

Величина этой силы определяется по формуле (*), с переменным значением параметра H, который меняется от величины R до величины R-h, где h – высота камня (или – сегмента тора в момент, когда сила реакции вертикальна).
Более сложный случай: колесо стоит на плоскости или на уклоне
Общие соображения
Знание давления внутри оболочки пневматика позволяет построить модель сил взаимодействия колеса с опорной плоскостью - F(P,S). Представляют интерес два основных расчётных случая: колесо, стоящее на опорном рельефе, и колесо, катящееся по опорному рельефу, когда на его оси приложены тянущая сила и/или крутящий момент. Как было сказано главным условием механического равновесия является равенство силе`F и моменту`M на оси колеса соответствующих интегралов по площади контакта с опорной поверхностью, от нормальных и касательных сил в точках контакта.
 В
таком же приближении модели высокого давления в пневматике рассмотрим предварительно
случай колеса, стоящего на плоскости. В этой простейшей модели
форма оболочки остаётся неизменной везде кроме небольшой опорной площадки
колеса, площадь которой по предположению равна площади основания "срезанного"
в опоре сегмента тора. Требуемое в этой модели сокращение площади поверхности
тора реализуется в виде морщин и/или образования складки.
В
таком же приближении модели высокого давления в пневматике рассмотрим предварительно
случай колеса, стоящего на плоскости. В этой простейшей модели
форма оболочки остаётся неизменной везде кроме небольшой опорной площадки
колеса, площадь которой по предположению равна площади основания "срезанного"
в опоре сегмента тора. Требуемое в этой модели сокращение площади поверхности
тора реализуется в виде морщин и/или образования складки.

 Параметры
нагружения оболочки в этом случае определяются соотношением, аналогичным (*)
для стояния на камне перевёртыше, с той разницей, что вытесняемый объём пневматика
в этой модели равен не удвоенному, а единичному объёму Vсег(R,r,H) "срезанного" сегмента
тора:
Параметры
нагружения оболочки в этом случае определяются соотношением, аналогичным (*)
для стояния на камне перевёртыше, с той разницей, что вытесняемый объём пневматика
в этой модели равен не удвоенному, а единичному объёму Vсег(R,r,H) "срезанного" сегмента
тора:
(**)
F =
![]()

Эта модель, при всей её умозрительности, интересна тем, что позволяет получить оценку сверху для высоты H оси колеса, нагруженного силой F и катящегося по плоскому опорному рельефу.
Реальная высота оси колеса по необходимости должна быть несколько меньше. Действительно, запас площади оболочки позволяет расширить площадь опоры в пределах условий нерастяжимости элементов оболочки, понизив, тем самым, и высоту оси, и давление, требуемое для поддержания силы F, а значит - и значение потенциальной энергии колеса. Это приводит к изменениям формы оболочки в районе её контакта с опорной поверхностью – разным при разных предположениях о характере взаимодействия с внешней средой. Простейшим взаимодействием является нагружение оболочки колеса, стоящего на плоскости вертикальной силой при невысоком давлении внутри оболочки. Рассмотрим этот случай подробнее.
Модель взаимодействия оболочки колеса с плоскостью
 В
предположении безмоментной оболочки тора и колесе нулевой ширины меридиональные
сечения оболочки, взаимодействующие с опорной плоскостью, должны состоять из
трёх частей: опорной прямой и двух симметричных дуг окружностей, равномерно
"распираемых" внутренним давлением по нормалям к элементам сечения.
В
предположении безмоментной оболочки тора и колесе нулевой ширины меридиональные
сечения оболочки, взаимодействующие с опорной плоскостью, должны состоять из
трёх частей: опорной прямой и двух симметричных дуг окружностей, равномерно
"распираемых" внутренним давлением по нормалям к элементам сечения.
Для определённости рассмотрим, прежде всего, одну из симметричных половин центрального меридионального сечения в состоянии опоры. Пусть длина половины опорной линии равна b, тогда длина дуги окружности равна pr-b. Радиус дуги окружности и высота меридионального сечения h связаны для двух крайних случаев соотношениями, вытекающими из геометрических обстоятельств сопряжения двух частей меридионального сечения - опорной прямой и дуги окружности (рис.8):
Если дуга окружности гладко сопрягается с опорной прямой, то:
![]() ;
;
Если дуга окружности минимального радиуса сопрягается с опорной прямой под некоторым углом, то: 4(rp-b)2-(pb)2=(ph)2.
 Из
этих случаев следует выбрать тот, в котором изменение высоты h (а следовательно и
работа, производимая силой F)
меньше.
Из
этих случаев следует выбрать тот, в котором изменение высоты h (а следовательно и
работа, производимая силой F)
меньше.
![]() Из сравнения положения центров дуг на левой и правой половинах рис.8 видно, что во
втором случае высота h
больше. Это означает, что безмоментная оболочка под действием сил давления в
центральном меридиональном сечении не будет иметь гладкое сопряжение с плоской
опорной поверхностью.
Из сравнения положения центров дуг на левой и правой половинах рис.8 видно, что во
втором случае высота h
больше. Это означает, что безмоментная оболочка под действием сил давления в
центральном меридиональном сечении не будет иметь гладкое сопряжение с плоской
опорной поверхностью.
В этом случае высота сечения и радиус дуги равны: h=![]() , rд=r-b/
p
.
, rд=r-b/
p
.
При этом высота оси колеса будет равна H= R-r+h.
Параметры соседних сечений вычисляются по параметрам b и y
из условия, что при смещении вдоль границы диска оболочки на угол y
высота hм
в плоскости соответствующего сечения от диска до опорной плоскости увеличится
до значения hм=H/cosy -(R-r).
Тогда новое значение bм
определяется из условия bм+prдм=pr (т.е. rдм=r-bм/p), где bм находится из решения
квадратного уравнения
bм2(p2-4)+8pr bм-p2
(4r2-
hм2)=0.
bм=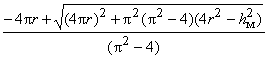 = bм(b,y).
= bм(b,y).
 Проверка
этого выражения на крайних случаях даёт: при нулевой нагрузке на ось колеса (F=0),- h=2r, и b=0; а при максимальной нагрузке F, такой, что h=0,- поперечник площади
опоры центрального меридиана b=
Проверка
этого выражения на крайних случаях даёт: при нулевой нагрузке на ось колеса (F=0),- h=2r, и b=0; а при максимальной нагрузке F, такой, что h=0,- поперечник площади
опоры центрального меридиана b=![]() .
.
Последний случай особенно интересен, он объясняет, почему не может быть b=pr при h=0. Действительно, когда предельная нагрузка F на ось колеса прижимает его к опоре, то полученная зависимость H(b) определяет избыток длины меридионального сечения, сохраняющего под действием давления форму дуги окружности (рис. 8).
Из условий последовательного по углу y увеличения расстояния hм меридиональных сечений от диска колеса до опорной плоскости находятся параметры деформации меридиональных сечений, пока bм не превратится в нуль. Это произойдёт при hм=2 rдм, и rдм=r, когда долгота y=arccos(H/(R+r).
При этом, форма меридиана оболочки в таком крайнем сечении, когда b=0; в соответствии с приведенными выше соображениями должна стать окружностью меридиана ненагруженного тора радиуса r.
Но какую форму будут
иметь соседние меридианы оболочки? Ответ зависит от модели поведения
экваториальной дуги свободного тора при её прижатии к опорной плоскости. Если
принята модель возникновения складок в площадке опоры, то оставшаяся часть
оболочки сохраняет форму тора (см. рис.7). Но если предположить сохранение длины
экватора в продольном размере опорной площадки (это требует нарушения условия
концентричности окружностей внутреннего и внешнего экваторов оболочки), то
форма меридианов оставшейся части оболочки определяется из условий b=0 и hм>2r.
Приведенные соотношения простейшей модели тонкого колеса распространяются
на общий случай колеса, связанного с оболочкой по некоторой дуге
меридионального сечения rм2jД (как это показано на рис.1). Для
этого геометрическое условие bм+prдм=pr следует заменить на bм+(p-jД)rдм=pr, и учесть условия
равновесия каждого меридионального сечения под действием сил давления и силы F на ободе колеса. Эти
условия в совокупности определяют в каждом сечении ширину bM опоры и радиус дуги
окружности свободной части меридиана.
Полученная таким образом модель геометрии безмоментной оболочки однозначно определяет нужные площади и объёмы, а при выбранном давлении P0 – поддерживающую силу F (см., также, Приложение 2).
Колесо, стоящее на уклоне
При стоянии на уклоне под действием равновесного
момента или силы на его оси, порождаемая сила реакции трения на площади опоры
от сил вертикальной нагрузки, уравновешивает горизонтальные и вертикальные
проекции сил, и колесо остаётся неподвижным. Избыток момента или тянущей силы
порождает увеличение сил реакций. Это приводит к движению колеса вверх по
уклону в моделе равновесия сил и моментов в квазистатическом приближении
движения.
 В более ранний момент первого контакта
с уклоном в процессе движения по горизонтальной опорной поверхности под
действием равновесного момента возникает горизонтальная проекция торможения
нормальной силы этого контакта. Для её преодоления требуется увеличение тягового
момента колеса до получения равновесия двуопорных сил давления и сил реакций
трения. По мере наезда на уклон этот момент растёт до равновесного значения,
соответствующего схеме сил, показанных на рисунке 10.
В более ранний момент первого контакта
с уклоном в процессе движения по горизонтальной опорной поверхности под
действием равновесного момента возникает горизонтальная проекция торможения
нормальной силы этого контакта. Для её преодоления требуется увеличение тягового
момента колеса до получения равновесия двуопорных сил давления и сил реакций
трения. По мере наезда на уклон этот момент растёт до равновесного значения,
соответствующего схеме сил, показанных на рисунке 10.
Для
увеличения сил трения при движении по уклону или в других двигательных
ситуациях в конструкцию колеса вставляется цилиндрическая беговая дорожка с
грунтозацепами [8] (рис.11). Модель деформации такого колеса отличается от
модели тора только учётом длин меридианов, площади опоры и объёма, добавляемых
не изгибаемой цилиндрической вставкой.
![]()
О боковом смещении колеса
Рассмотрим геометрию тора при его боковом смещении под действием только горизонтальной силы. Вначале рассмотрим случай, когда контактная площадка, сформированная под действием сил до возникновения бокового усилия, не может оторваться от опорной поверхности. Это, довольно умозрительное предположение, тем не менее, имеет смысл для лучшего понимания процессов боковой устойчивости колеса с одной стороны, а с другой, - ввиду выполнения этого условия, когда на внешней экваториальной поверхности колеса имеется несгибаемая цилиндрическая вставка (см. ниже).
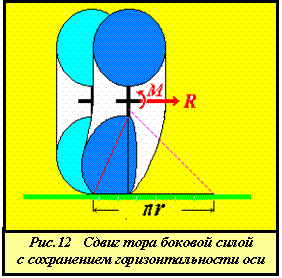 В
этом случае любое боковое смещение оси колеса приводит к "наезду" на
опорную поверхность избытка поверхности оболочки спереди (относительно направления
действия силы) и вытягиванию её поверхности сзади. Это, по необходимости,
вызывает появление опорной площадки даже в случае отсутствия вертикальных сил
(при сцеплении ненагруженного тора с опорной поверхностью в единственной точке
внешнего экватора) и момента пары сил сцепления колеса с грунтом и сил на оси
колеса.
В
этом случае любое боковое смещение оси колеса приводит к "наезду" на
опорную поверхность избытка поверхности оболочки спереди (относительно направления
действия силы) и вытягиванию её поверхности сзади. Это, по необходимости,
вызывает появление опорной площадки даже в случае отсутствия вертикальных сил
(при сцеплении ненагруженного тора с опорной поверхностью в единственной точке
внешнего экватора) и момента пары сил сцепления колеса с грунтом и сил на оси
колеса.
Для компенсации этого момента необходимо прикладывать соответствующий момент на оси колеса. При этом обязательно возникает сокращение объёма полости тора, ограниченного в каждом меридиональном сечении постоянной длинной его периметра, в его конфигурации состоящей из двух хордовых дуг окружностей и прямолинейного участка между ними. Геометрия центрального сечения для простейшего колеса с плоским диском и цилиндрической вставкой нулевой ширины (которая, тем не менее, по предположению, не может оторваться от опоры) показана на рис. 10. Крайние случаи бокового смещения в принятом предположении показаны на рис.11.
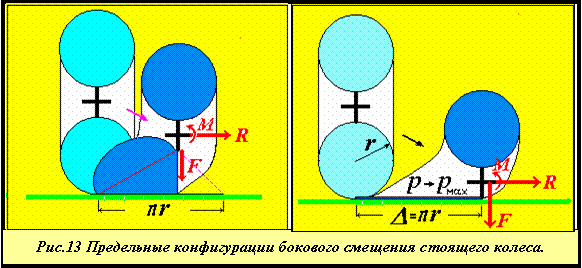
Что показывает анализ этого случая? - Два обстоятельства:
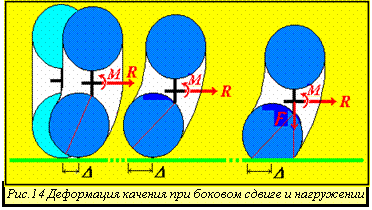 Если
прижимающая сила F мала
и отсутствует "прилипание" оболочки поверхности опоры, то при
отсутствии вертикального нагружения равновесному состоянию с минимальной
потенциальной энергией соответствует конфигурация, показанная на рис. 12 слева и
в центре. В этой конфигурации дуги периметра в каждом меридиональном сечении опираются
на диаметры (а не на хорды, как на рис.10 и 11), что обеспечивает максимальный
объём оболочки и наименьшее увеличение давления.
Если
прижимающая сила F мала
и отсутствует "прилипание" оболочки поверхности опоры, то при
отсутствии вертикального нагружения равновесному состоянию с минимальной
потенциальной энергией соответствует конфигурация, показанная на рис. 12 слева и
в центре. В этой конфигурации дуги периметра в каждом меридиональном сечении опираются
на диаметры (а не на хорды, как на рис.10 и 11), что обеспечивает максимальный
объём оболочки и наименьшее увеличение давления.
Однако, если колесо нагружено вертикальной силой, то в обязательно возникает опорная площадка в соответствии с соображениями рис.8.
В любом случае в рассматриваемой модели колеса под действием боковой силы "сдвиговая" деформация соседних меридианов оболочки колеса заменяется деформацией их относительного "кручения". Допустимость последней и возможное уменьшение объёма полости колеса из-за образования складок зависят от направления волокон ткани оболочки, отвечающих за анизотропные свойства деформационных перемещений соседних дифференциальных элементов её поверхности.
Если же в конструкции колеса присутствует несгибаемая цилиндрическая вставка ("беговая дорожка"), то равновесная конфигурация зависит от величины боковой и вертикальной сил (рис.13). Начиная с некоторого бокового усилия момент от давления на опорную площадку становится меньше момента от действия боковой силы, что приводит к отрыву цилиндрической дорожки от опорной поверхности и превращению сдвиговой деформации соседних меридианов в крутильную. Величина соответствующей "критической боковой силы" зависит от геометрических параметров ненагруженного колеса и от начального давления, - чем больше объём оболочки колеса и чем меньше начальное давление, тем больше боковая критическая сила.
Рис.15 Деформация сдвига у колеса с
цилиндрической беговой дорожкой
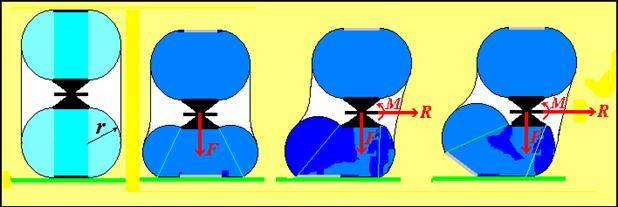
Модель деформаций трёхкамерного пневматика
Для проверки возможности увеличения боковой устойчивости колеса была рассмотрена трёхкамерная конструкция колеса (рис. 16) с продольной перемычкой в основном объёме колеса и конической перемычкой на его внешней стороне. Эти нерастяжимые поверхности создают структуру сил, препятствующих боковым сдвигам колеса под действием осевой силы.
Структура сил и объёмов трёхкамерного колеса
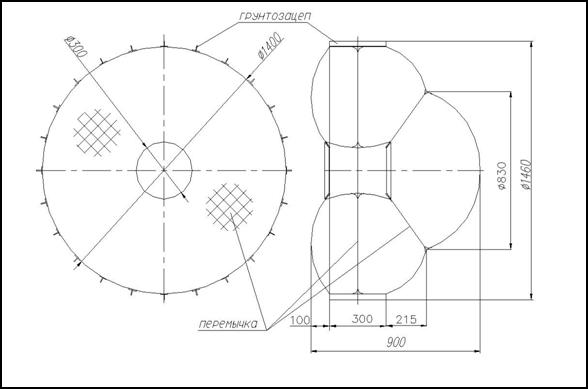
Рис. 16. Схема трёхкамерного колеса с перемычками
Главным элементом, препятствующим боковым сдвигам, при наличии давления в основной камере колеса является разделяющая её нерастяжимая диафрагма, закреплённая по её внешнему и внутреннему периметрам к конструкции ступицы и беговой дорожке колеса. Любая попытка при боковом сдвиге ступицы превратить плоскую поверхность такого диска в коническую поверхность со складками будет встречать противодействие сил давления уменьшению объёма камер и внешнего радиуса колеса.
Заметим, что максимальный объём боковой камеры формируется суммой объёма усечённого конуса и объёма, присоединённого к нему сегмента сферы (см. рис. 16). Отсюда следует, что если в боковой камере давление держать выше давления в основном объёме колеса, то при деформации последнего форма и объём боковой камеры остаются неизменными. Поэтому главной целью расчётов здесь является расчёт деформаций только основного объёма оболочки колеса. При этом элементом, значительно усложняющим расчёты, является упомянутая продольная диафрагма основной камеры колеса, ограничивающая в силу её нерастяжимости величину возможных деформаций оболочки.
Расчётная схема

Исходные формы оболочек
камер пневматика, как и раньше, разбиваются меридианами и параллелями (относительно
оси пневматика) на отдельные клетки (рис. 17). Форма каждого меридионального
сечения имеет вид, показанный на рис.18. В отличие от однокамерного колеса
картина деформация меридионального сечения определяется не только параметром
длины его периметра, но и расположением на этом периметре точки E сопряжения
границ оболочки колеса и его боковой камеры (см. рис. 16 и 18). В расчётах эта
точка принималась неподвижной (в соответствии с изложенным выше утверждением о
неизменности формы боковой камеры колеса). В такой модели геометрии колеса
расчёт формы деформации оболочки хотя и несколько усложняется, но в принципе
остаётся прежним.

Расчёт выполняется так:
Каждое новое меридиональное сечение рассматривается в отношении соседства с сечением, рассчитанным на предыдущем шаге расчёта. Расчёт ведется в двух симметричных направлениях, начиная с центрального опорного сечения, определяемого плоскостью действия осевых сил нагружения и бокового сдвига (плоскостью симметрии деформаций). На каждом шаге расчёта:
1. Строятся точки
меридиональной линии С-D внутреннего обода колеса.
2. Боковое смещение опорной
части сечения (прямые A-B и A-F) устанавливается через
заданное исходное смещение и условие нерастяжимости оболочки и перемычки (см.
ниже п. 5), а боковое смещение всех остальных точек сечения – линейной интерполяцией к нулю до верха колеса.
3. Расстояние до оси колеса
определяется пересечением контура ненагруженного меридиана с опорной
поверхностью (в простейшем случае – с опорной плоскостью).
4. Проверяется длина линии
пересечения плоскости меридиана и плоскости средней перемычки на условие её
нерастяжимости (нарушение этого условия означает конец множества меридианов,
принадлежащих опорной площадке).
5. Из условия нерастяжимости
оболочки проверяется допустимость горизонтального сдвига точек соседних
меридиональных сечений в плоскости симметрии деформаций (все остальные точки
периметров меридианов в предположении сохранения их плоскостей можно не проверять) . Если условие нарушается, то величина сдвига
и расстояние до оси колеса корректируются.
6. Для каждого сечения по
известным отрезкам хорд B-C и E-F строятся точки, принадлежащие
их дугам окружностей в контуре оболочки колеса:
Для этого:
·
В окрестности участка В-С ищется центр окружности, проходящей через
точки «В» и «С», и имеющей ту же длину, что и в исходном контуре меридиана.
Возможно, что часть окружности окажется ниже линии BF. Тогда решается задача
поиска центра дуги, при условии, что часть окружности лежит на прямой BF.
Новая точка «В» увеличивает расстояние А-B.
·
Отрезок С-D
неизменен. Точка «Е» задается.
·
Для линии DE
рассматриваются два варианта – отрезок прямой, если расстояние DE равно
максимально допустимому, или дуга окружности. Центр соответствующей окружности
рассчитывается исходя из длины отрезка и координат точек «Е» и «D». Аналогично
дуге ВС рассчитывается центр дуги EF. Учитывается возможность её
прилегания к линии BF. Таким образом, длина участка BF,
вообще говоря, отличается от исходной.
7. Проверяются на реализуемость
все длины участков ВС, DE, EF.
8. Вычисляются параметры формы
клеток, получаемых от пересечения соседних меридианов и параллелей оболочки.
При этом, взаимные смещения и деформации клеток при нагружении колеса
вычисляются из квадратичных условий нерастяжимости главного диагонального
направления клетки и сохранения длин меридианов и параллелей колеса, но с
учётом возможного образования складок и соответствующего уменьшения площадей и
объёмов.
9. Суммируются площади всех
клеток, получаемых от пересечения меридианов и параллелей оболочки, и связанные
с ними объёмы.
10. В рамах принятой газодинамической модели
вычисляется новое внутреннее давление и его относительное изменение.
11. Для каждой клетки, взаимодействующей
(совпадающей) с опорной поверхностью, вычисляется произведение её площади на
единичный вектор направления нормали лежащей под ней опорной поверхности. Далее
вычисляются векторы соответствующих сил нормальных и касательных реакций опоры
колеса и, если требуется, - параметры деформации
грунта и буксования [?].. Суммирование
полученных сил определяет силы и момент, приведенные к оси колеса.
 Описанная модель реализована в интерактивной
программе, позволяющей выбирать картину деформации колеса и определять
соответствующие условия нагружения. Расчётная модель пневматического колеса
описывается 30-ю параметрами (геометрические размеры, объёмы, давления, число
сечений, параметры деформации и др.). Кроме этого имеется 18 параметров процедур
рисования, движения и изменения масштаба изображения колеса (см. таблицы 1 и
2).
Описанная модель реализована в интерактивной
программе, позволяющей выбирать картину деформации колеса и определять
соответствующие условия нагружения. Расчётная модель пневматического колеса
описывается 30-ю параметрами (геометрические размеры, объёмы, давления, число
сечений, параметры деформации и др.). Кроме этого имеется 18 параметров процедур
рисования, движения и изменения масштаба изображения колеса (см. таблицы 1 и
2).
Таблица 1
|
№ |
ПАРАМЕТРЫ МОДЕЛИ ПНЕВМАТИЧЕСКОГО КОЛЕСА |
Примечания |
|
1.
|
Внешний радиус колеса |
Задаётся |
|
2.
|
Внутренний радиус колеса |
Задаётся |
|
3.
|
Ширина внешнего обода с зацепами |
Задаётся |
|
4.
|
Ширина ступицы |
Задаётся |
|
5.
|
Длина меридиана в левой части тора |
Задаётся |
|
6.
|
Длина участка меридиана в правой части тора |
Задаётся |
|
7.
|
Внешний радиус конуса |
Задаётся |
|
8.
|
Высота усеченного конуса |
Задаётся |
|
9.
|
Радиус прогиба (если есть) на конусе |
Вычисляется |
|
10.
|
Радиус сферы третьей камеры колеса |
Вычисляется |
|
11.
|
Объём 1-й камеры |
Вычисляется |
|
12.
|
Объём 2-й камеры |
Вычисляется |
|
13.
|
Объём 3-й камеры |
Вычисляется |
|
14.
|
Начальное давление |
Выбирается |
|
15.
|
Начальное давление 2-й камеры |
Выбирается |
|
16.
|
Начальное давление 3-й камеры |
Выбирается |
|
17.
|
Высота опоры над нижней точкой ненагруженного колеса |
Выбирается |
|
18.
|
Боковое смещение ступицы колеса |
Выбирается |
|
19.
|
Параметр формы при деформации камер колеса |
Выбирается |
|
20.
|
Дефицит объёма 1-й камеры при наезде на камень |
Выбирается |
|
21.
|
Дефицит объёма 2-й камеры при наезде на камень |
Выбирается |
|
22.
|
Вектор площади опоры в 1-й камере при наезде на камень |
Выбирается |
|
23.
|
Вектор площади опоры во 2-й камере при наезде на камень |
Выбирается |
|
24.
|
Число меридиональных сечений |
Выбирается |
|
25.
|
Число точек в сечении |
Выбирается |
|
26.
|
Расстояние между площадками |
Вычисляется |
|
27.
|
Площадь свободной площадки |
Вычисляется |
|
28.
|
Площадь опорной площадки |
Вычисляется |
|
29.
|
Суммарная площадь опоры 1 камеры |
Вычисляется |
|
30.
|
Суммарная площадь опоры 2 камеры |
Вычисляется |
|
31.
|
Суммарная площадь опоры 3 камеры |
Вычисляется |
|
32.
|
Суммарная сила, отнесённая к начальному давлению 1 камеры |
Вычисляется |
|
33.
|
Суммарная сила, отнесённая к начальному давлению 2 камеры |
Вычисляется |
|
34.
|
Суммарный момент, отнесённый к начальному давлению 1 камеры |
Вычисляется |
|
35.
|
Суммарный момент, отнесённый к начальному давлению 2 камеры |
Вычисляется |
|
36.
|
Вектор равнодействующей сил на ступице колеса |
Вычисляется |
|
37.
|
Вектор суммарного момента на ступице колеса |
Вычисляется |
Таблица 2
|
№ |
ПАРАМЕТРЫ
ПРОЦЕДУРЫ ИЗОБРАЖЕНИЯ КОЛЕСА |
Примечания |
|
1,2 |
"Проволока" или "Заполнение" |
Выбирается |
|
3 |
"Переднее сечение" (Z-координата плоскости обреза) |
Выбирается |
|
4-7 |
Цвета проволоки, заполнения, беговой дорожки , ступицы |
Задаётся |
|
8 |
Цвета опорной площадки снаружи, изнутри |
Задаётся |
|
9 |
Цвет фона |
Задаётся |
|
10-14 |
Направления осей координат экрана (3 вектора) |
Задаётся |
|
15-17 |
Координаты центра проектирования |
Выбирается |
|
18 |
Расстояние до картинной плоскости (масштаб) |
Выбирается |
Примеры
результатов расчетов
Расчёт однокамерного колеса
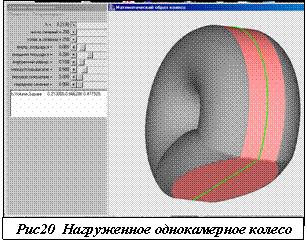
Простейший пример расчёта колеса,
сжатого осевым нагружением, показан на рис.20. В частности, здесь хорошо видно,
какую форму принимает опорная площадка при 40% продавливания от максимально
возможной величины (опора на диск
колеса).
Более интересный пример –
расчёт бокового давления на такое колесо (рис.21). Здесь при виде снизу на ту
же опорную площадку и её среднею линию хорошо видно, что при боковом осевом
нажиме, стоящее под нагрузкой однокамерное колесо очень плохо ему
сопротивляется. Это объясняется тем, что при боковом сдвиге такого колеса, его
объём практически не изменяется в процессе "перекатывания" оболочки
через требуемую опорную площадь.
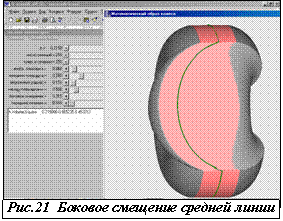
В этом примере исходный объём при нулевом
нагружении этого колеса составлял величину 0,74м3. После
вертикального продавливания он уменьшился до 0,66м3, а при
последующем боковом нажиме этот объём с точностью до третьего знака после
запятой не изменился. Заметим, что сам факт плохой боковой устойчивости слабо
надутого пневматика хорошо известен. Здесь этот феномен получил лишь свое
модельное и численное представления.
На рис.22 показан общий результат расчётов однокамерного
колеса – график зависимости удельной силы вертикальной нагрузки (отнесённой к
начальному давлению) при вертикальной и
боковой деформациях колеса.

Расчёт трёхкамерного колеса
Моделирование однокамерного пневматика показало
целесообразность применения внутренней продольной перегородки в основном объёме
пневматика для увеличения боковой устойчивости колеса. На рис.23 показан общий
результат расчётов параметров деформирования трёхкамерного колеса. Как и выше,
это – график зависимости удельной силы F/P0 (вертикальной нагрузки,
отнесённой к начальному давлению) при вертикальной и боковой деформациях
колеса.
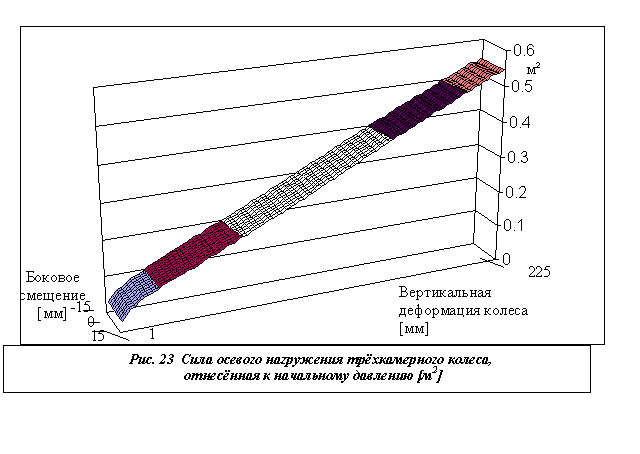
Сравнение этого графика с предыдущим показывает, что трёхкамерное колесо является значительно более жестким в боковом направлении действия сил. Как показывают расчёты, оно позволяет иметь боковой сдвиг на порядок меньший возможного бокового сдвига однокамерного пневматика. Это обстоятельство особенно важно при реализации схемы бортового поворота. Заметим, что ограничения бокового сдвига колеса вызвано не противодействием сил давления, а чисто геометрическими ограничениями (в предположении необходимой прочности) работы нерастяжимой оболочки пневматика.
В то же время, удельные вертикальные податливости обеих конструктивных схем пневматика практически одинаковы (0,6 м2/250мм). При этом, важными особенностями полученных результатов является обнаруженная (вне начального участка сжатия) примерно линейная зависимость деформаций от сил нагружения в вертикальном направлении и независимость этого свойства работы пневматика от начального давления. Это означает, что в геометрическом приближении работы нерастяжимой безмоментной оболочки отношение величины опорной площади к объёму пневматика линейно зависит от клиренса оси колеса.
Заключение
Рассмотренная модель нерастяжимой безмоментной оболочки пневматического колеса обладает рядом качеств, оправдывающих её использование:
Прежде всего, она позволяет понять основные свойства работы материала оболочки пневматика в процессе движения. Анализ свойств нагружения материала показывает, что помимо очевидных требований герметичности от материала оболочки необходимо требовать высокую усталостную и "складко-изгибную" стойкость наряду с высокой прочностью в режимах растяжения и прокалывания.
Отмеченная выше практическая линейность модели деформации такого пневматика облегчает грубую оценку работы машины с такими колёсами.
В модели удобным образом учитываются термодинамические свойства работы газа пневматика с возможностью оценки влияния температурных условий внешней среды и параметров теплообмена с ней.
Важным достоинством геометрической модели пневматика является её достаточно высокий порядок точности. Фактически это – модель главного порядка точности, допускающая уточнение следующих порядков погрешности путем оценки вариаций объёмов и площадей от модели сил упругости в легко определяемых местах наибольшего изгиба и растяжения оболочки.
Наконец, рассмотренная модель позволяет построить удобную расчётную схему, обеспечивающую сравнительно просто, но эффективно с учётом предыдущего замечания вычислять требуемые характеристики работы колеса на требуемом уровне точности.
Использованная литература
1.
Клаузиус Р.
Кинетическая теория газов
В кн. "Основатели
кинетической теории материи". М.:ОНТИ. 1937. сс.39-184
2.
Келдыш М.В. Шимми
переднего колеса трёхколёсного шасси.
Труды ЦАГИ №564.
1945, 33с.
3.
Лурье А.И. Статика тонкостенных упругих оболочек.
М.-Л.: ОГИЗ ГосТехИздат,
1947, 252с.
4.
Норден А.П.
Геометрические работы Гаусса. В кн."Карл Фридрих Гаусс".
М.: АН СССР 1956.
сс.113-144.
5.
Ландау Л.Д.,
Лившиц Е.М. Теория упругости. М.:Наука, 1965, 201с.
6.
Бекер М.Г.
Введение в теорию "местность –машина".
М.:Машинострокение, 1973, 520с.
7.
Авотин Е.В.
Болховитинов И.С. Кемурджиан А.Л. Маленков М.И. Шпак Ф.П.
Динамика планетохода.
М.:Наука, 1979, 440с.
8.
Аминов Ю.А.
Дифференциальная геометрия и топология кривых. М.:Наука. 1987,160с.
9. IUTAMM-IASS Symp.on
Deploable Stutures. 6-8 Sept1998. Kluwep Acad.Publ. 2000,492p.
10. Pacejka H.B. Tire
and vehicle dynamics.
11.
Галанин М.П.,
Савенков Е.Б.,.Темис Ю.М.
Метод конечных суперэлементов Федоренко для задач теории упругости.
М.Препринт ИПМ им. М.В.Келдыша РАН, №38, 2004, 38с.
12.
Якушев В.Л. Нелинейные деформации и
устойчивость тонких оболочек.
М.:Наука. 2004, 275с.
Приложение 1
Основные геометрические параметры
тора
Уравнения тора (оси X и Y принадлежат экваториальной плоскости, ось X на рис.1 направлена из центра тора вниз, ось Y - вправо, ось Z – на зрителя. все углы положительны при их отсчёте против часовой стрелки):
x=( Rц + rм cosj)cosy = y·ctgy ;
y=( Rц + rм cosj)siny = x· tgy;
z= rм sinj,
где j и y "внутренние углы" тора:
j - угол в меридиональных сечениях тора от линии центр тора-экватор;
y - угол в экваториальной плоскости от оси X до меридиана.
В декартовых координатах тор описывается неявной зависимостью:
![]() ,
,
но можно выписать и явные зависимости каждой
координаты от двух других координат: ![]()
![]()
![]()
Отсечём у тора некоторый сегмент на расстоянии H от центра тора. Размеры его основания по оси Y (в экваториальной плоскости) и по оси Z (по нормали к экваториальной плоскости) соответственно равны:

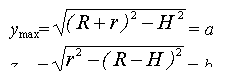
Соответствующие углы ymax и j max равны:
ymax=arctg(![]() ) = arcos(
) = arcos(![]() );
);
j max=arcsin(![]() ) = arcos(
) = arcos(![]() ).
).
Уравнение сечения тора в основании сегмента в плоскости Y-Z следующие:
- в виде z(y,H):
z=![]() ;
;
- в виде y(z,H): y=![]() .
.
или x=H;
y=Htgy=ay ; z= = by .
= by .
Заметим, что уравнение "оскулирующего" по y эллипса
в плоскости основания сегмента тора имеет вид: 
Приложение 2
"Законы сохранения" свойств пневматика с безмоментной оболочкой
I: При заданной силе на оси стоящего
пневматика проекция площади опоры на плоскость, перпендикулярную направлению
действия силы, зависит только от избыточного давления внутри пневматика и не
зависит ни от его конструкции, ни от его формы, ни от его размеров.
И обратно:
II: У стоящего или равномерно катящегося пневматика мгновенная форма опорной площади и коэффициент трения в её пределах однозначно определяют мгновенное направление действий осевой силы и осевого момента с линейной зависимостью их величин от давления в пневматике.
Эти свойства и однозначная связь действующих сил и моментов с давлением внутри пневматика при выбранной площади опоры определяются условиями механического равновесия внешних сил и моментов, действующих на пневматик.
Например, пусть выбрана некоторая форма опорной площади неподвижно стоящего пневматика с неизвестной силой, приложенной к его оси, и пусть отсутствует момент на его оси. Тогда из условий равновесия равнодействующая сил нормальных реакций и трения в пределах опорной площади должна проходить через ось пневматика. Величина нормальных сил реакций и соответствующих сил трения линейно зависят от давления в оболочке. И тогда из этих параметров равновесия однозначно определяется сила, приложенная к оси пневматика, коллинеарная и равная по модулю равнодействующей сил реакций.
Если же равнодействующая сил реакции не проходит через ось пневматика, то осевая сила должна вместе с силой реакции образовывать пару сил, которую, в свою очередь, должен уравновесить приложенный к оси момент.
Если пневматик катится, то внешние силы реакций, приложенные к его опорной площади, должны уравновешиваться моментом и/или силой, приложенными к оси пневматика.
Таким образом, в каждом из механически разных случаев нагружения пневматика (стоящий пневматик, "пассивный" пневматик, катящийся под действием тянущей за ось силы и "активный" пневматик ведущих колёс машины) при отсутствии сил упругости оболочки все силовые параметры однозначно определяются после выбора формы и величины опорной площадки. Это обстоятельство существенно упрощает расчеты и определяет удобный метод моделирования ("от геометрии к силам", а не наоборот).
 Рассмотрим
пневматическое колесо с давлением Р, которое в ненагруженном состоянии
представляет собой тор с центральным радиусом
Рассмотрим
пневматическое колесо с давлением Р, которое в ненагруженном состоянии
представляет собой тор с центральным радиусом 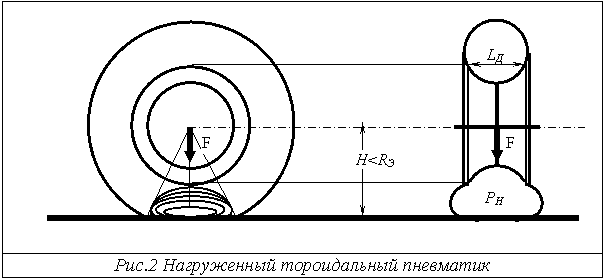 Если
такое колесо поставить на плоскость и нагрузить вертикальной силой
Если
такое колесо поставить на плоскость и нагрузить вертикальной силой 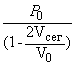
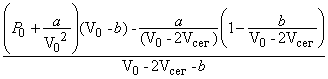 ;
;
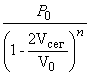 ,
,
 = 2
= 2 .
. .
.