Аннотация
В работе проводится обобщение теорем Пуанкаре-Козлова о предельных по времени свойствах
слабых решений уравнения Лиувилля для газа невзаимодействующих частиц на случай, когда
функции распределения системы принадлежат классу обобщенных функций с точечным носителем
по пространственной координате. Доказано, что при t→∞ функция распределения системы в слабом
смысле стремится к постоянному значению.
Abstract
In this work the generalization of Poincare-Kozlov theorems has been made. These theorems
are concern to the weak convergence of distribution function for t→∞ . The generalization is
that the distribution function may be represented as generalized function of the singular
type, such as delta-function. It is proved, that the weak limit of the solution of Liouville
equation exists and equals to constant.
Введение
Одной из основных задач статистической механики
является обоснование перехода от представления о дискретном характере
распределения материи к описанию ее как сплошной среды. Таким обоснованием
является вывод уравнений гидродинамики из «первых принципов», т.е. из уравнений
микроскопического движения составляющих систему частиц. Исторически существует
два подхода к этой проблеме. Метод Н.Н. Боголюбова [1], когда рассматривается
конечное число частиц N в объеме V, так, что при получении плотностных характеристик
среды (плотности, средней скорости, средней внутренней энергии) делается
предельный переход 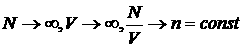 , называемый термодинамическим пределом. В другом подходе (Р.
Балеску [2]) та же физическая система рассматривается как периодическое
продолжение «ящиков», в которых заключено неизменное количество частиц.
Математической трудностью в обоих подходах является корректное обоснование
предельного перехода. , называемый термодинамическим пределом. В другом подходе (Р.
Балеску [2]) та же физическая система рассматривается как периодическое
продолжение «ящиков», в которых заключено неизменное количество частиц.
Математической трудностью в обоих подходах является корректное обоснование
предельного перехода.
Фундаментальной проблемой является также обоснование
существования равновесия у механической системы с большим, но конечным числом
частиц. В математическом плане эта задача сводится к исследованию
асимптотических по времени свойств решения уравнения Лиувилля относительно
функции распределения частиц по каноническим фазовым переменным.
Простейшей моделью статистической механики является
идеальный газ – система из большого числа одинаковых частиц, представляемых
безразмерными точками, свободно (т.е. без столкновения одна с другой)
движущимися в пространстве и, если выбрана модель замкнутого сосуда,
отражающихся по тому или иному закону от его стенок. Более сложной моделью
является газ Больцмана-Гиббса: это совокупность абсолютно упругих шариков,
сталкивающихся между собой и со стенками сосуда. Статистическое равновесие в
системе многих тел означает в классическом понимании [3], что скорости частиц
имеют максвелловское распределение, а плотность постоянна по всему объему (с
точностью до флуктуаций), т.е. равна средней плотности газа. Выравнивание же
плотности означает, что имеет место диффузия, при которой начальные
неоднородные условия необратимо размываются. В то же время уравнения динамики
отдельных частиц и всей системы в целом обратимы по времени. Согласование этих
двух положений именно для случая идеального газа представляет особую важность:
может оказаться, что необратимость является скорее математическим свойством,
чем следствием физических гипотез, таких, например, как гипотеза молекулярного
хаоса в уравнении Больцмана.
Фундаментальные результаты о необратимом поведении
идеального газа содержатся в книге В.В. Козлова [4], который обобщил подход А.
Пуанкаре [5], основанный на представлении идеального газа как
бесстолкновительной сплошной среды. Такое представление основано на аналогии
между уравнением Лиувилля для функции распределения идеального газа по
координатам и скоростям и уравнением неразрывности в механике жидкости.
В [5] на упрощенной одномерной модели идеального газа
было показано, что из-за неравномерности свойства возвращаемости имеет место
необратимая диффузия газа. В [4] это свойство корректно доказывается в
некотором классе распределений частиц по скоростям и координатам, в частности,
распределение должно быть интегрируемой по Лебегу функцией. В настоящей работе
проводится доказательство теорем В.В. Козлова о диффузии для случая
принадлежности распределений другим классам функций. Именно, нашей задачей
является доказательство существования слабого предела решения уравнения
Лиувилля для бесстолкновительной сплошной среды в случае, когда это решение
является сингулярной обобщенной функцией.
Постановка задачи
Введем следующую систему обозначений.
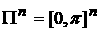 – «сосуд», в котором
находится система; – «сосуд», в котором
находится система;
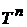 – n-мерный тор, – n-мерный тор, 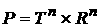 ; ;
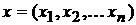 , ,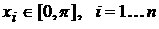 , , 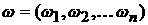 , , 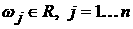 ; ;
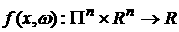 – функция
распределения; рассматривается также распределение – функция
распределения; рассматривается также распределение 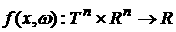 ; кроме того, возможно определение ; кроме того, возможно определение 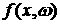 как обобщенной
функции. как обобщенной
функции.
Рассмотрим сплошную среду, удовлетворяющую уравнению
неразрывности, которое также моделирует систему из большого числа
невзаимодействующих частиц в сосуде, представляющем собой параллелепипед 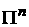 . Будем считать, что частицы среды отражаются от стенок сосуда
абсолютно упруго. Поставим следующие вопросы относительно поведения системы с
течением времени: . Будем считать, что частицы среды отражаются от стенок сосуда
абсолютно упруго. Поставим следующие вопросы относительно поведения системы с
течением времени:
1) Сходится ли и в каком смысле функция распределения
частиц при  ? ?
2) Будет ли среда иметь равномерное распределение по
координатам при 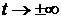 ? ?
Для исследования указанных асимптотических свойств
решений введем оператор эволюции системы 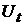 : : 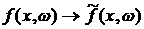 , где , где 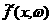 – функция плотности
распределения через промежуток времени t. Поскольку движение частицы происходит в потенциальном
поле, созданном стенками сосуда в форме параллелепипеда, то при – функция плотности
распределения через промежуток времени t. Поскольку движение частицы происходит в потенциальном
поле, созданном стенками сосуда в форме параллелепипеда, то при 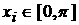 и и 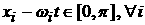 выполняется выполняется 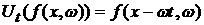 , что демонстрирует свободное движение частицы между
стенками. , что демонстрирует свободное движение частицы между
стенками.
Предположение о зеркальном отражении от стенок сосуда
приводит к тому, что при 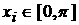 и и 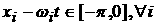 получаем получаем 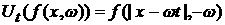 . .
Аналогично при 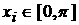 и и 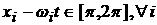 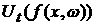 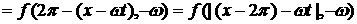 . .
Возможны еще варианты, когда 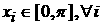 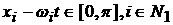 , , 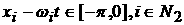 , , 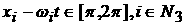 , , 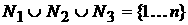 . В этом случае, полагая для простоты что . В этом случае, полагая для простоты что 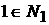 , , 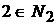 , , 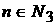 , имеем , имеем
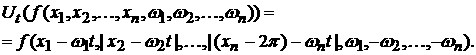
Пользуясь свойством оператора эволюции 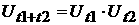 , его действие можно определить для любого t. Удобно
доопределить функцию , его действие можно определить для любого t. Удобно
доопределить функцию 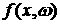 таким образом, чтобы
выполнялось равенство таким образом, чтобы
выполнялось равенство
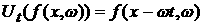 . (1) . (1)
С этой целью доопределим 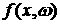 на отрезке [-p, 0]: на отрезке [-p, 0]:
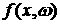 = =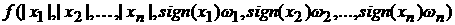 , ,
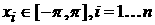 , ,
и
затем периодически продолжим ее по каждой из координат на всю действительную
ось. При этом получится периодическая функция с периодом 2p. Заметим, что результат действия оператора эволюции 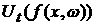 также дает
периодическую функцию с тем же периодом. При движении системы в фазовом
пространстве также дает
периодическую функцию с тем же периодом. При движении системы в фазовом
пространстве 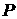 ее динамика задается
уравнениями ее динамика задается
уравнениями
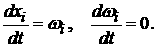 (2) (2)
Для такой системы приведем формулировки теорем,
доказанных В.В. Козловым (см. [4]). Это позволит проследить направления, в
которых будет проведена модификация условий этих теорем.
Первая теорема о диффузии (В. В. Козлов).
Пусть 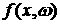 : : 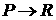 есть интегрируемая по
Лебегу функция, а есть интегрируемая по
Лебегу функция, а 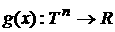 интегрируемая по
Риману функция. Введем функционал интегрируемая по
Риману функция. Введем функционал
K(t)=
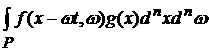 . (3)
. (3)
Тогда
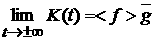 ,
(4) ,
(4)
где
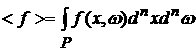 , , 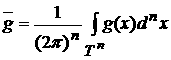 . (5) . (5)
Вторая теорема о диффузии (В. В. Козлов).
Пусть f, g: 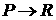 интегрируемые по
Лебегу функции вместе со своими квадратами, т.е. f, g интегрируемые по
Лебегу функции вместе со своими квадратами, т.е. f, g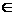 L2(P). Введем функционал L2(P). Введем функционал
K(t)= =
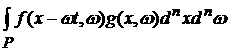 .
.
Тогда
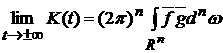 .
(6) .
(6)
В частном случае первой теоремы, когда g(x) является
характеристической функцией некоторого множества G, измеримого в смысле Жордановой меры (последнее
возможно, т.к. в теореме 1 предполагается, что g(x) является
интегрируемой по Риману функцией), функционал K(t) в формуле
(3) может быть представлен в виде
K(t) =
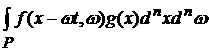 =
=
 .
.
Последний
интеграл представляет собой долю частиц, находящихся в момент времени t в объеме G.
Следовательно, указанная теорема имеет следующую интерпретацию:
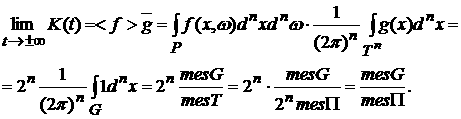 (7) (7)
Таким
образом, доля частиц в объеме G стремится
к некоторой константе при 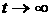 , причем эта константа равна отношению объема множества G к объему всего сосуда. Иначе говоря, частицы со
временем стремятся равномерно заполнить сосуд. , причем эта константа равна отношению объема множества G к объему всего сосуда. Иначе говоря, частицы со
временем стремятся равномерно заполнить сосуд.
В более общей формулировке первой теоремы функцию
распределения следует считать обобщенной функцией, то есть определять ее как
линейный функционал на пробных функциях, например, из пространства L2. В
пространстве обобщенных функций предел f(x,w) при 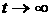 понимается в слабом
смысле, и вторая теорема позволяет найти этот предел. Именно, определим
непрерывный линейный функционал понимается в слабом
смысле, и вторая теорема позволяет найти этот предел. Именно, определим
непрерывный линейный функционал
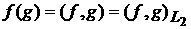 . .
Тогда
вторая теорема о диффузии может быть записана в следующем виде:
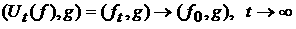 , ,
где
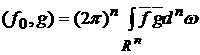 . .
Далее
мы рассмотрим обобщения вышеприведенных теорем о диффузии. Основной вопрос
заключается в следующем: можно ли обобщить первую и вторую теорему на случай, когда f(x, w) не является интегрируемой по Лебегу функцией и
представима в виде: a) f(x, w) = d(w)h(x); б) f(x, w) = d(x)h(w)?
Обобщение первой теоремы о диффузии
Принципиально важным свойством функции плотности
распределения является ее интегрируемость по Лебегу. Отказ от этого свойства в
общем случае приводит к тому, что первая теорема о диффузии не имеет места.
Например, пусть в системе существует конечная доля 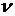 частиц с одинаковой
скоростью частиц с одинаковой
скоростью 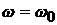 . В этом случае среднее
значение некоторой функции g по распределению . В этом случае среднее
значение некоторой функции g по распределению  определяется как определяется как
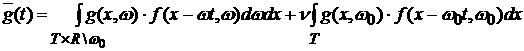 . .
В
этом выражении первое слагаемое при 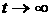 , как уже известно, стремится к константе, а вот второе
слагаемое является в общем случае периодической функцией, и в результате сумма
не будет стремиться к константе. Если же существует конечный набор таких групп
частиц со скоростями , как уже известно, стремится к константе, а вот второе
слагаемое является в общем случае периодической функцией, и в результате сумма
не будет стремиться к константе. Если же существует конечный набор таких групп
частиц со скоростями 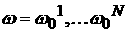 , то получающаяся в результате
сумма периодических функций является почти-периодической функцией, и не имеет
предела при , то получающаяся в результате
сумма периодических функций является почти-периодической функцией, и не имеет
предела при 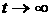 . .
Однако есть важный пример
обобщения первой теоремы о диффузии на случай, когда распределение f(x,w)
представляется в виде линейной комбинации обобщенных функций с точечным
носителем по пространственным координатам с коэффициентами, являющимися
интегрируемыми по Лебегу функциями в пространстве скоростей. В частности, пусть
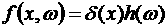 . (8) . (8)
Тогда для функционала (3) имеем
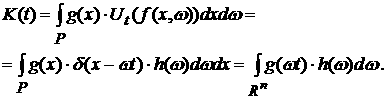
Исследуем
поведение K(t) при t®¥ и покажем, что частицы с течением времени равномерно заполняют сосуд.
Подчеркнем, что функция распределения (8) имеет совершенно другие свойства
относительно пространственных координат, чем в первой теореме о диффузии.
Теорема 1. Пусть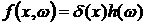 , где h(w) – интегрируемая по Лебегу функция на , где h(w) – интегрируемая по Лебегу функция на 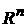 , и пусть g(x) есть интегрируемая по Риману функция на , и пусть g(x) есть интегрируемая по Риману функция на 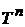 . .
Тогда существует предел
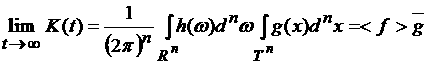 .
(9) .
(9)
Доказательство.
Так как интегрируемую по Лебегу
функцию можно представить как разность двух положительных функций, то
доказательство проводится только для положительных функций h. Сначала докажем для случая, когда
функция g является
тригонометрическим полиномом. Затем получим то же равенство для всех функций g из пространства функций, интегрируемых по Риману на 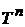 . Доказательство проводим в несколько этапов. . Доказательство проводим в несколько этапов.
1) Пусть g = C = const. Тогда
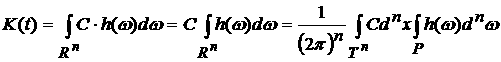 =
=
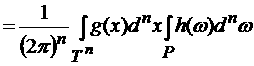 . .
2)
Пусть теперь 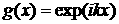 . Тогда . Тогда
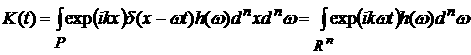 , ,
после
чего по теореме Римана получаем 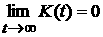 . В силу линейности из пунктов 1) и 2) следует, что равенство
(9) выполнено для всех тригонометрических полиномов. . В силу линейности из пунктов 1) и 2) следует, что равенство
(9) выполнено для всех тригонометрических полиномов.
3)
Из курса анализа известно (теорема Вейля), что если 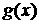 – функция,
интегрируемая по Риману, то для любого e существуют такие тригонометрические полиномы – функция,
интегрируемая по Риману, то для любого e существуют такие тригонометрические полиномы 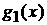 и и 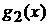 , что , что
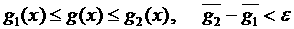 , где , где 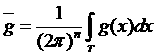 . .
Введем обозначения для функционалов
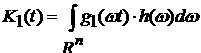 , , 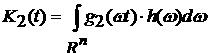 . .
Тогда, так как 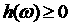 , то , то
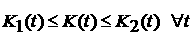 , ,
и, кроме того,
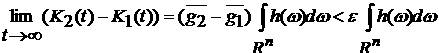 . .
Следовательно,
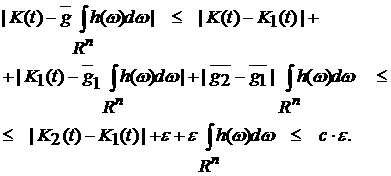
Теорема 1 доказана.
Обобщение второй теоремы о диффузии
Теорема 2. Пусть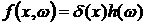 , где h(w) –
ограниченная и интегрируемая по Лебегу функция на , где h(w) –
ограниченная и интегрируемая по Лебегу функция на 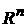 , , 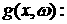 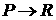 интегрируемая по
Риману функция. Обозначим интегрируемая по
Риману функция. Обозначим
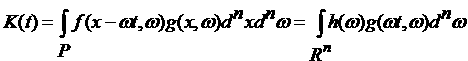 . .
Тогда существует предел
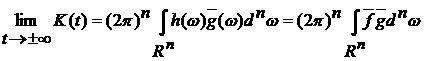 . (10) . (10)
Доказательство.
1)
Поскольку g(x,w) является интегрируемой по Риману, то она ограничена и
измерима, и, следовательно, интеграл
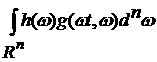
существует.
2)
Так как функция h(w) интегрируема по Лебегу, то ее можно представить в
виде разности двух положительных интегрируемых по Лебегу функций. Как и выше,
нам достаточно доказать утверждение
(10) только для случая h(w)>0.
3)
В силу существования интеграла 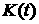 справедливы оценки: справедливы оценки:
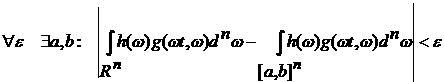
и
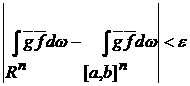 . .
Поэтому,
если мы докажем, что
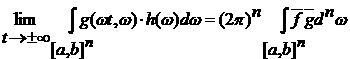 , ,
то
фактически теорема 2 будет доказана. Следовательно, мы свели задачу к случаю
финитных функций g(x, w).
4)
Если g(x,w) = g(w), то
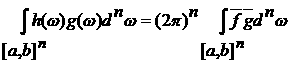
Это
следует из того, что
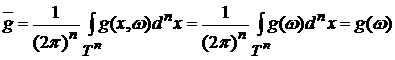 . .
5) Пусть g(x,w)=exp(ikx+imwp/(b-a)). Тогда
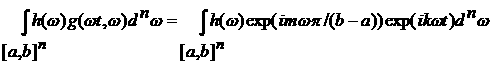
Так
как функция 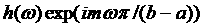 интегрируема по Лебегу, то по теореме Римана
существует равный нулю предел интегрируема по Лебегу, то по теореме Римана
существует равный нулю предел
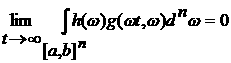 . .
Отсюда
следует, что равенство
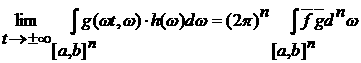
доказано для тригонометрических полиномов.
5) Как и в случае доказательства теоремы 1, воспользуемся
теоремой Вейля о том, что если g – функция, интегрируемая по Риману, то для любого e
существуют такие тригонометрические полиномы g1
и g2, что
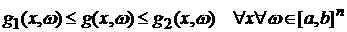 , , 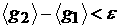 , ,
где
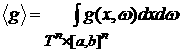 . .
Введем
функционалы
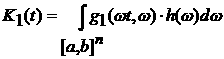 , ,
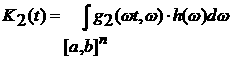 . .
Так
как  , то , то
 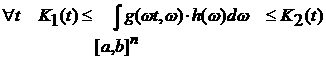
6)
Из пункта 5) доказательства следует, что
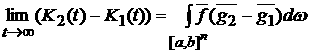 . .
По условию теоремы h(w) ограниченная функция, т.е. h(w)<M. Тогда 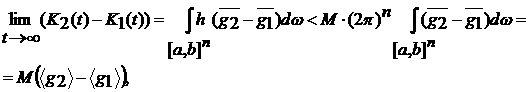
т.е.
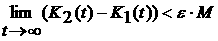 . .
Следовательно,
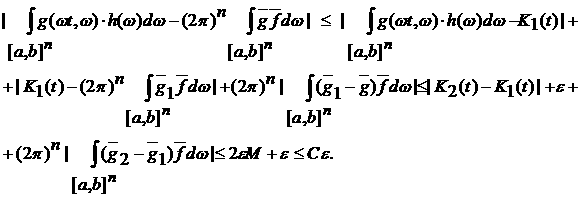
Таким
образом, мы доказали теорему для любой финитной интегрируемой по Риману функции
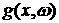 . Отсюда и из пункта 3) следует утверждение теоремы. . Отсюда и из пункта 3) следует утверждение теоремы.
Заключение
Итак, в настоящей работе изучена возможность доказательства
теорем В.В. Козлова о существовании пределов функций распределения для
динамических систем, моделирующих бесстолкновительную сплошную среду при других
условиях на принадлежность функций некоторому классу. Мы рассмотрели случай,
когда функция распределения
представляется в виде f(x,w)=d(x)h(w), где h(w) интегрируемая по Лебегу функция. Это соответствует
тому, что все частицы в начальный момент времени находятся в одной точке. Для
этого случая мы доказали обе теоремы В.В. Козлова с дополнительным условием во
второй теореме, что h(w)
ограниченная функция. Таким образом, при вышеперечисленных условиях справедливы
равенства:
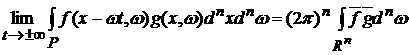 , ,
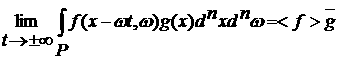 . .
В
силу линейности можно считать, что допустимы также функции вида 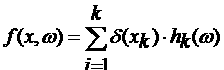 , где , где 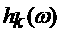 интегрируемые по
Лебегу функции. интегрируемые по
Лебегу функции.
Целью проведенного исследования было
расширение класса функций, для которых были доказаны исходные теоремы о диффузии.
Важной задачей является также расширение класса динамических систем, для
которых функции распределения имеют предел при 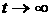 . Эти вопросы будут рассмотрены в дальнейшем. . Эти вопросы будут рассмотрены в дальнейшем.
Работа
выполнена при поддержке гранта РФФИ № 05-01-00642
Литература
1. Боголюбов Н.Н. Проблемы динамической теории в
статистической физике. М.-Л.: ГИТТЛ, 1946.
2. Балеску Р. Равновесная и неравновесная статистическая
механика. М.: Мир, 1978.
3. Больцман Л. Лекции по теории газов. М.:
Гостехиздат, 1956.
4. Козлов В.В. Тепловое равновесие по Гиббсу и
Пуанкаре. Москва-Ижевск: Институт компьютерных исследований, 2002.
5. Пуанкаре А. Замечания о кинетической теории
газов. Избранные труды, т. III. М.: Наука, 1974.
|