Аннотация
В работе предложен новый подход к задаче локализации транзиентов (резких изменений в характере
звука). Для решения этой задачи мы анализируем те параметры непрерывного вейвлет-преобразования
данного звукового сигнала, которые применяются при оценке локального показателя Гёльдера.
Многочисленные эксперименты показали, что в точках транзиента эти параметры испытывают резкий
скачок. Это позволяет в большинстве случаев локализовать транзиенты с большой точностью.
Abstract
A new approach to the problem of localization of transients (sharp changes in a sound
behavior) is presented. Our method uses parameters of the continuous wavelet transform of
the sound signal that are commonly used for estimation of the local Hölder exponent.
Numerous experiments have shown that these parameters exhibit an abrupt jump at the transient
points. This allows, in most cases, to locate the transients with high precision.
1. ВВЕДЕНИЕ
1.1 Традиционные
подходы к задаче локализации транзиентов
Насколько нам известно, не существует общепринятого
строгого определения транзиента в звуковом сигнале. Обычно транзиентом называют
короткий участок резкого изменения характера звука. В данной работе мы, следуя
[1], считаем транзиентами зоны резкого
изменения локального спектра сигнала. В первую очередь нас интересовали музыкальные
сигналы, а в них такие транзиенты часто связаны с звуками ударных инструментов.
Выделение транзиентов в звуковых
сигналах - очень важный этап в решении многих задач анализа и компрессии звука.
В частности, все большее внимание привлекают алгоритмы сжатия и синтеза звука,
кодирующие «гармонические» и транзиентные участки совершенно различным образом.
Такое представление может быть заметно более эффективным, чем использование
разбиения на стандартные блоки, не связанные с содержательной структурой звука.
Однако эта эффективность достигается только при очень точном разделении на
транзиентную и гармоническую составляющие.
В литературе рассматривались различные
методы локализации транзиентов. Значительная часть таких методов основана на
поисках локальных «пиков энергии» сигнала (типичные примеры такого подхода
можно найти в [2] и приведенных там ссылках), где эта энергия определяется как
норма «столбцов» спектрограммы (оконного преобразования Фурье), то есть ограничений
модуля спектрограммы на прямые t=const.
Недостаток этого метода связан с тем, что источником всплеска энергии не всегда
служит транзиент. Для локализации транзиентов с учетом их более тонких
структурных характеристик ряд авторов использовали вейвлетные методы. В [3] в
качестве детектора транзиентов рассматривалась норма разности между соседними
столбцами непрерывного вейвлет-преобразования сигнала. Предполагается, что
узкие пики этой величины соответствуют зонам резкого изменения распределения
энергии по частотным диапазонам, и таким образом могут служить детекторами
транзиента. Однако эта технология подвержена «ложным срабатываниям», борьба с
которыми требует довольно сложного содержательного анализа поведения сигнала в
окрестности каждого пика. В серии работ Бруно Торрезани (Bruno Torresani)
и его соавторов ([4-6]) развивается идея о
том, что транзиентом следует считать кратковременный участок сигнала,
обладающий на этом узком временном интервале «плотным» разложением в базисе
ортогональных вейвлетов. Множество коэффициентов разложения по ортогональным
вейвлетам имеет на ограниченном интервале естественную структуру бинарного
дерева, а «плотность» в данном контексте означает, что существенно ненулевые
коэффициенты заполняют значительную часть его достаточно длинных ветвей.
Идеология работ [4-6] состоит в поиске участков сигнала, демонстрирующих такую
структуру вейвлетных коэффициентов, с применением методов распознавания образов
и машинного обучения. Сложность практического применения этих идей связана с
большим разнообразием структур распределения коэффициентов, удовлетворяющих сформулированному
критерию.
1.2 Наш подход к локализации транзиентов
Наш подход отличается от перечисленных
тем, что мы стремимся выявлять не те или иные предписанные особенности
локальной структуры сигнала в области транзиента, а сам факт резкого усложнения
этой структуры в начале транзиента (и ее упрощения в конце). В качестве
индикатора локальной сложности мы рассматриваем величину, широко применяемую
для оценки локального показателя Гёльдера сигналов. А именно, для каждого
столбца (временного среза t=const)
скейлограммы (scalogram), то есть квадрата модуля
непрерывного вейвлет-преобразования изучаемого сигнала, строится прямая,
наилучшим образом приближающая log-log график
этого столбца (функцию одной масштабной переменной s). Наклон 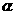 этой прямой при подходящем выборе диапазона изменения s и при
определенных предположениях о природе сигнала равен показателю степенной
асимптотики убывания скейлограммы по s при s стремящемся к нулю, и линейно связан с величиной H показателя
Гёльдера в точке t ([7 - 9]): этой прямой при подходящем выборе диапазона изменения s и при
определенных предположениях о природе сигнала равен показателю степенной
асимптотики убывания скейлограммы по s при s стремящемся к нулю, и линейно связан с величиной H показателя
Гёльдера в точке t ([7 - 9]):
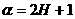 (1) (1)
В частности, это так при условии
статистического самоподобия изучаемого сигнала [7] – в этом случае все точки с
вероятностью 1 сингулярны по Гёльдеру, а показатель Гёльдера может меняться от
точки к точке. Если сигнал имеет только изолированные сингулярности, показатель
Гёльдера измеряется аналогичной величиной, вычисленной вдоль линий максимумов
скейлограммы, идущих из этих изолированных точек.
Как показали наши многочисленные эксперименты,
вблизи начала транзиента наш индикатор испытывает резкий скачок (в сторону
уменьшения). Алгоритм локализации транзиента состоит из двух основных шагов:
·
вычисление
индикатора 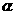 по скейлограмме на той
же временной сетке, на которой задан исходный сигнал по скейлограмме на той
же временной сетке, на которой задан исходный сигнал
·
сглаживание
полученной функции времени 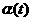 и определение точек, в
которых она совершает резкие скачки и определение точек, в
которых она совершает резкие скачки
Отметим, что музыкальные звуковые
сигналы, с которыми мы экспериментировали, не принадлежат, строго говоря, ни к
одному из двух перечисленных выше типов сигналов, обладающих гёльдеровскими
сингулярностями, которые локализуются и оцениваются по величине с помощью скейлограммы.
Поэтому мы не можем утверждать, что скачки в величине нашего индикатора
транзиентов связаны с изменением локальной регулярности сигнала. Мы считаем,
что эти скачки определяются
одновременным появлением (исчезновением) в сигнале большого количества
локальных гармоник, составляющих транзиент (например, удар барабана), и
возникают за счет резкого изменения локальной геометрии поверхности
скейлограммы. С другой стороны, «форма волны», т.е. график самого сигнала,
также становится менее регулярной в точке начала транзиента, что соответствует падению гладкости, т.е. уменьшению показателя
Гёльдера.
В будущем мы планируем более тщательно
изучить математическую природу нашего
индикатора транзиентов – в частности, его связь с так называемыми
«осциллирующими сингулярностями», которые могут возникать в звуковых сигналах в
точках транзиентов.
Все упомянутые в этом пункте математические понятия
подробно поясняются в разделе 2. В разделе 3 мы приводим и комментируем
результаты экспериментов, в разделе 4 делаем заключительные замечания и
перечисляем некоторые направления дальнейших исследований.
2. НЕПРЕРЫВНОЕ ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЕ И ЛОКАЛИЗАЦИЯ СИНГУЛЯРНОСТЕЙ
В
этом разделе приведены определения вейвлет-преобразования, скейлограммы, а
также формулировки основных теорем о связи асимптотики скейлограммы с
локальными сингулярностями изучаемой функции ([9-10]).
2.1 Вейвлет-преобразование
Определение 1. Пусть 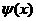 - комплекснозначная
функция. Функция - комплекснозначная
функция. Функция 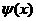 называется вейвлетом,
если ее преобразование Фурье называется вейвлетом,
если ее преобразование Фурье 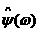 удовлетворяет условию: удовлетворяет условию:
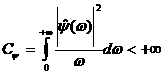 (2) (2)
Вейвлет-преобразование функции 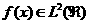 при помощи вейвлета при помощи вейвлета 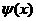 - это функция двух
переменных, определяемая формулой - это функция двух
переменных, определяемая формулой
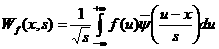 .
(3) .
(3)
Из
(3) ясно, что вейвлет-преобразование представляет собой совокупность сверток данной
функции с всевозможными разномасштабными версиями вейвлета. Переменная s называется
масштабной переменной.
В
фурье-области вейвлет-преобразование при фиксированном значении масштабной переменной
может быть записано так: 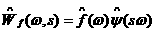 . .
Известно
([10]), что вейвлет преобразование обратимо, и функция 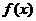 может быть восстановлена по формуле может быть восстановлена по формуле
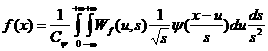 (4) (4)
Наконец,
скейлограммой будем называть функцию 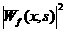 . .
В
качестве вейвлетов обычно используются функции с хорошей локализацией и по переменной
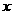 , и по переменной , и по переменной  . Функция . Функция 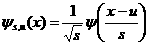 - сдвинутый и
перенормированный вейвлет – локализована в окрестности точки - сдвинутый и
перенормированный вейвлет – локализована в окрестности точки 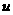 на оси времени и точки на оси времени и точки 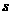 на шкале масштабов
(которая соответствует перенормированной частотной шкале). Существуют ортогональные вейвлеты [9 – 10], для
которых достаточно вычислить (3) при на шкале масштабов
(которая соответствует перенормированной частотной шкале). Существуют ортогональные вейвлеты [9 – 10], для
которых достаточно вычислить (3) при 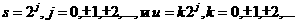 , так как функции , так как функции 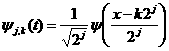 образуют ортогональный
базис в пространстве образуют ортогональный
базис в пространстве 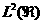 . .
В этом случае аналогом (3) является набор
коэффициентов 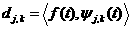 , а вместо (4)
функцию можно восстановить по формуле , а вместо (4)
функцию можно восстановить по формуле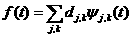 . .
2.2 Показатели Гёльдера и максимумы
модуля вейвлет-преобразования.
Локальную
регулярность функции часто «измеряют» с помощью показателей Гёльдера.
Определение 2: Говорят, что
функция 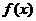 в точке в точке 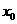 удовлетворяет условию Гёльдера с
показателем удовлетворяет условию Гёльдера с
показателем 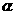 , , 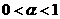 , если существует константа , если существует константа  , такая что для всех
точек , такая что для всех
точек 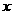 из окрестности точки из окрестности точки 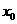 выполняется выполняется
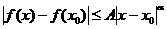 (5) (5)
Для показателей 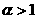 условие имеет
следующий вид: условие имеет
следующий вид: 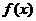 в
точке в
точке 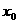 удовлетворяет
условию Гёльдера с показателем удовлетворяет
условию Гёльдера с показателем 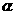 , , 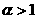 , тогда и только тогда когда существует
константа , тогда и только тогда когда существует
константа  и
полином и
полином 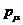 степени степени 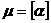 ,
такие что для всех точек ,
такие что для всех точек 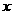 из
окрестности точки из
окрестности точки 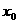 выполняется выполняется
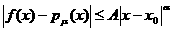 (6) (6)
Функция 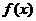 равномерно на равномерно на 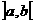 удовлетворяет
условию Гёльдера с показателем удовлетворяет
условию Гёльдера с показателем 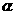 , если существует константа A такая
что указанные условия выполнены для всех , если существует константа A такая
что указанные условия выполнены для всех
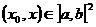 . .
Определение 3: Максимум
модуля вейвлет-преобразования функции f – это точка 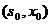 в плоскости в плоскости 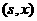 , такая
что выполняется строгое неравенство , такая
что выполняется строгое неравенство 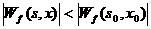 при при 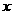 лежащем в правой или
левой полуокрестности точки лежащем в правой или
левой полуокрестности точки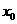 , и при этом , и при этом 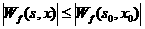 , когда , когда 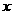 принадлежит полуокрестности с противоположной стороны точки принадлежит полуокрестности с противоположной стороны точки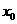 . .
Непрерывную
кривую в плоскости 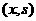 , соединяющую максимумы модуля, называют линией максимумов. , соединяющую максимумы модуля, называют линией максимумов.
Следующая
теорема [10] устанавливает связь между убыванием максимума модуля вейвлет-преобразования и
локальной регулярностью функции (ее показателями Гёльдера):
Теорема
(Джаффар): Пусть вейвлет 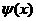 имеет n нулевых моментов
и имеет n непрерывных
быстро убывающих производных. имеет n нулевых моментов
и имеет n непрерывных
быстро убывающих производных.
Пусть 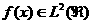 удовлетворяет условию Гёльдера с показателем удовлетворяет условию Гёльдера с показателем 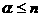 в точке в точке 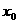 , тогда существует константа , тогда существует константа  такая
что выполняется такая
что выполняется
 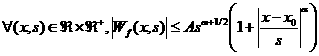 , (7) , (7)
и,
наоборот, если  - нецелое число, и существуют - нецелое число, и существуют  и и 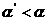 такие что такие что
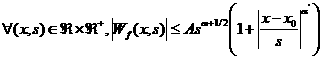 , (8) , (8)
то
тогда 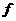 удовлетворяет условию Гёльдера с показателем удовлетворяет условию Гёльдера с показателем 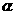 в точке в точке 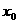 . .
Наклон
log-log графика модуля вейвлет-преобразования вдоль линии
максимумов, выходящей из точки на оси x (s=0), где у
функции имеется изолированная особенность гёльдеровского типа с показателем 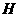 , равен , равен 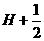 (см. [8-10]). (см. [8-10]).
Аналогичное соотношение связывает
поведение скейлограммы на малых масштабах с локальным показателем Гёльдера
реализации самоподобного случайного процесса ([7, 9-10]).
Определение
4: Стохастический сигнал 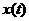 называется локально самоподобным с показателем Гёльдера называется локально самоподобным с показателем Гёльдера 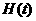 , если , если
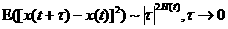 (9) (9)
Здесь Е (.) – среднее по ансамблю
реализаций случайного процесса, 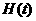 детерминированная функция, задающая динамику показателя
Гёльдера по времени. детерминированная функция, задающая динамику показателя
Гёльдера по времени.
При выполнении (9) скейлограмма
удовлетворяет соотношению:
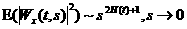 . (10) . (10)
Это
означает, что усредненный по ансамблю реализаций наклон log-log графика скейлограммы при фиксированном t должен
быть близок к величине  . В [7] отмечается, что при работе с единственной
реализацией сигнала (т.е. когда среднее по ансамблю недоступно) . В [7] отмечается, что при работе с единственной
реализацией сигнала (т.е. когда среднее по ансамблю недоступно)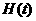 , полученное из соотношения (10), может сильно колебаться
вокруг истинного значения. Нечто подобное мы наблюдали в наших экспериментах с
оценкой локального наклона скейлограммы, описанных в следующем разделе. , полученное из соотношения (10), может сильно колебаться
вокруг истинного значения. Нечто подобное мы наблюдали в наших экспериментах с
оценкой локального наклона скейлограммы, описанных в следующем разделе.
3. ЭКСПЕРИМЕНТЫ И ВЫВОДЫ
В
наших экспериментах был использован широко известный вейвлет Морле (Morlet), заданный в фурье-области формулой 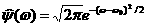 (откуда (откуда 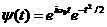 ). В частотной области эта функция имеет вид обычного гауссиана,
локализованного вблизи некоторого значения ). В частотной области эта функция имеет вид обычного гауссиана,
локализованного вблизи некоторого значения 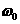 , во временной области это гауссиан, модулированный
комплексной гармоникой с частотой , во временной области это гауссиан, модулированный
комплексной гармоникой с частотой 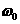 . .
Наш алгоритм строит скейлограмму
изучаемого звукового сигнала при помощи вейвлета Морле, затем в каждой точке по
времени вычисляется наклон log-log графика
скейлограммы при помощи построения прямой наилучшего среднеквадратичного приближения
этого графика.
Эвристические соображения в пользу того, что этот
наклон должен сильно меняться при переходе между гармоническими и транзиентными
участками, таковы. На основании определения транзиентов [4-6] можно ожидать,
что в промежутке транзиентности вейвлет-коэффициенты заметно отличны от нуля
«почти на всем» диапазоне изменения переменной s. Поэтому можно предположить, что прямая, которую мы
строим, будет в промежутке транзиентности иметь меньший наклон к оси абсцисс,
нежели вне этого промежутка.
Эксперименты показали, что как правило так и
происходит: в точке начала отрезка транзиентности оценка показателя Гёльдера
через наклон построенной прямой испытывает резкое падение, а в конечной точке этого отрезка наш индикатор
возвращается к среднему значению, которое он имел до появления транзиента.
Приведем
описание экспериментов над четырьмя музыкальными сигналами.
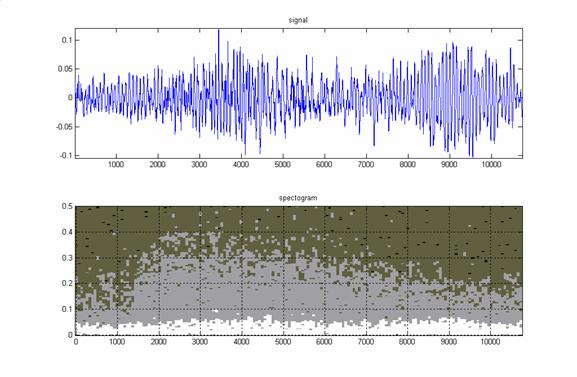
1. В первом сигнале (микрофрагмент «Шутки» из Сюиты №2 B-minor
И. С. Баха) на фоне флейты звучит клавесин.
|
|
|
Рис.1
По
оси абсцисс указаны номера отсчетов сигнала. Примерно в точке 1500 на фоне флейты начинает звучать клавесин.
Этому транзиенту отвечает всплеск интенсивности на спектрограмме.
|
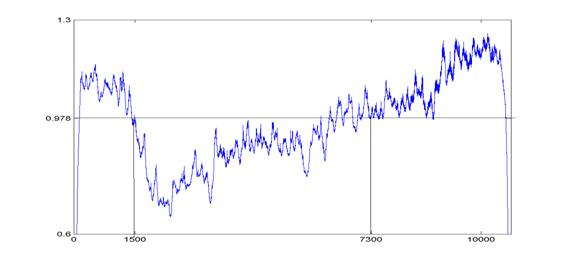
Оценка локального показателя Гёльдера, вычисленная для
этого сигнала из соотношения (10), имеет такую динамику во времени (рис. 2):
|
|
|
Рис.2
В
начале отрезка транзиентности величина функции H(t) резко падает,
к концу этого отрезка она постепенно возвращается к исходному значению.
|
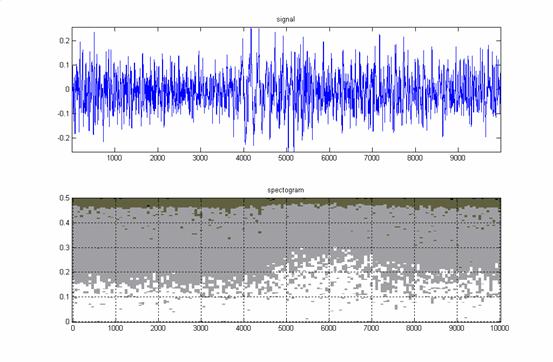
2. Во втором примере (микрофрагмент «Болеро» М. Равеля)
сигнал содержит звук ударного инструмента на фоне духовых и струнных.
|
|
|
Рис.3
Удар
происходит примерно в точке 4500. Этому транзиенту соответствует всплеск на
спектрограмме.
|
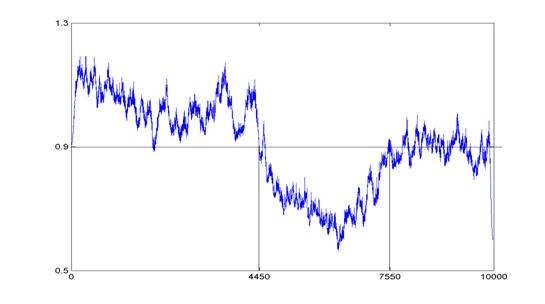
Оценка
функции H(t) показана
на рис. 4
|
|
|
Рис.4
Начало
транзиента локализуется по точке резкого падения величины H(t). Длительность транзиентного участка здесь меньше, чем
в примере 2.
|
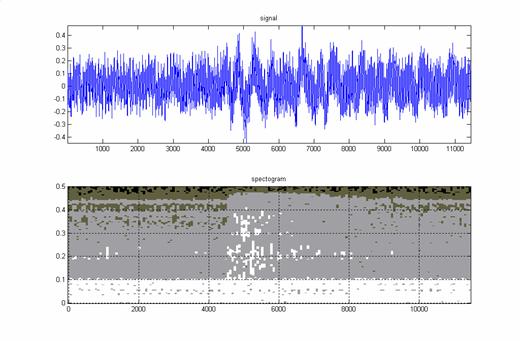
3. В третьем примере (микрофрагмент песни Уитни Хьюстон “I will always love you”) звучат ударные на фоне голоса.
|
|
|
Рис.5
В
данном пример удар барабана в точке 4500 заметен не только на спектрограмме, но и по форме
волны самого сигнала.
|
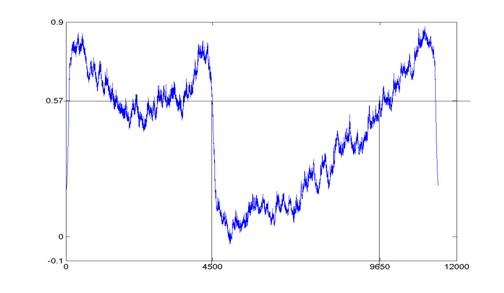
Оценка
динамики показателя H(t) показана
на рис. 6:
|
|
|
Рис.6
Оцененный показатель Гёльдера для этого сигнала
меньше 1 даже вне транзиентного участка. Это может быть связано с
особенностями голосовых сигналов (см. также следующий пример).
|
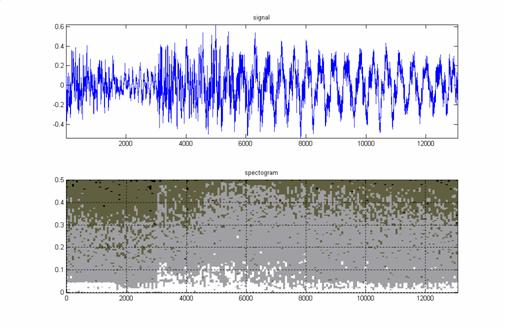
4. Четвертый пример - также ударные на фоне голоса
(микрофрагмент песни The Beatles “Can’t buy me love”). Сигнал
очень зашумлен.
|
|
|
Рис.7
Начало
транзиента (удар) вблизи точки 3000 заметно и на спектрограмме и по форме
волны.
|
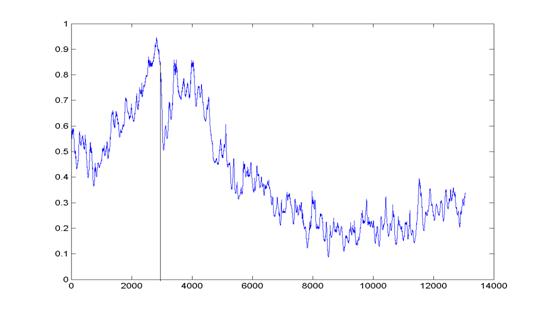
Оценка показателя Гёльдера в данном случае позволяет
локализовать только начало транзиента. Это может быть связано с высоким уровнем
шума.
|
|
|
Рис.8
В
данном примере оценка показателя Гёльдера позволяет локализовать только
начало транзиента.
|
В
заключение этого раздела приведем два примера работы данного алгоритма на сигналах
большей длительности.
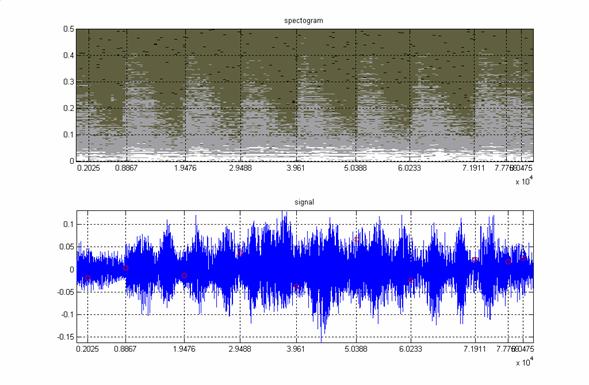
На рисунке 9 показан результат локализации транзиентов
на отрывке «Шутки» из Сюиты №2 B-minor И. С. Баха
(см. пример 1). Длительность отрывка – 1.22 сек. Играют два инструмента – клавесин
(транзиентный сигнал) на фоне флейты (гармонический сигнал). Вертикальные линии
показывают точки транзиентов, найденные по скачкам оценки показателя Гёльдера.
Эти точки очень хорошо согласуются со структурой спектрограммы.
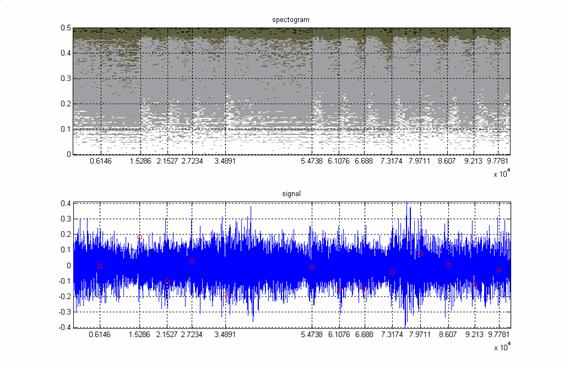
Рисунок 10 представляет аналогичным образом
размеченный двухсекундный (около 90 тыс. отсчетов) отрывок из «Болеро» М.
Равеля (см. пример 2).
|
|
Рис.9
Клавесин на фоне флейты. Обнаруженные
транзиенты показаны вертикальными линиями. Начало транзиента обычно
локализуется более четко, чем конец.
|
|
|
Рис.10
Ударные
на фоне духовых и струнных. Найденные транзиенты показаны вертикальными линиями.
|
4. ЗАКЛЮЧЕНИЕ
Проблема
идентификации транзиентов в настоящее время активно изучается
разработчиками методов сжатия звука нового поколения (например, она играет
важную роль в методе "звукового генома" для компактного представления
звука, разрабатываемом компанией "Sound Genetics, см. www.soundgenetics.com, www.fidelityamplifier.com/Sound_Genome_Theory_page).
В дальнейших исследованиях этой проблемы мы планируем выяснить математическую
природу обнаруженного эффекта для различных моделей транзиентов в звуковых
сигналах. Мы надеемся, что это позволит
создать эффективный алгоритм выделения транзиентной части звукового сигнала –
такой алгоритм был бы весьма полезен во многих задачах распознавания,
сегментации и сжатия звука.
5. ЛИТЕРАТУРА
[1] Xavier Rodet, Florent
Jaillet, Detection and modeling of fast attack transients. Proc. International Computer Music
Conference (ICMC’01), Havana, Sept., 2001.
[2] Scott N. Levine,
Julius O. Smith, A Sines+Transients+Noise
Audio
Representation
for Data Compression and Time/Pitch Scale Modifications. 105th Audio
Engineering Society Convention, San Francisco 1998.
[3] Crawford Tait, William
Findlay, Wavelet Analysis for Onset Detection. Proc. International Computer Music Conference 1996.
[4] S.Molla, B. Torresani, Hidden Markov trees of wavelet coefficients
for transient detection in audiophonic signals. Proc. Conf. Self-Similarity
and Applications, A. Benassi Ed. (2003).
[5] Laurent
Daudet, Transients modeling by pruned wavelet trees. Proc. International Computer Music Conference
(ICMC'01), Havana, Sept., 2001.
[6] L. Daudet, S. Molla, B.
Torresani, Transient detection and
encoding using wavelet coefficient trees. Proc. 18th Symposium GRETSI’01 on Signal and Image Processing,Toulouse,
2001.
[7] P. Goncalves, P. Flandrin,
Scaling exponents estimation from
time-scale energy distributions, IEEE
International Conference on Acoustics, Speech, and Signal Processing
(ICASSP-92), 1992.
[8] Stephane Mallat, Wen Liang
Hwang, Singularity detection and
processing with wavelets. IEEE Trans. Inf. Theory, v. 38, No. 2,
March 1992.
[9] Gregory Wornell, Signal processing with fractals: a
wavelet-based approach. Prentice Hall PTR, 1996.
[10] Stephane Mallat, A wavelet tour of signal processing. AP,
1998.
[11] P. Flandrin, Wavelet
analysis and synthesis of fractional browinian motion. IEEE Trans. Inf. Theory, v. 38, No. 2, March 1992.
|
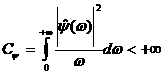
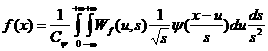
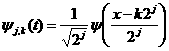
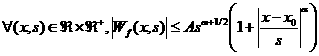 ,
, 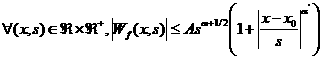 ,
,








