Математическое моделирование электромагнитного ускорения лайнера в различных двумерных
приближениях
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Б
|
|
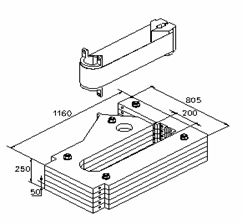
Рис. 1.1. Эскиз основных деталей генератора тока и продольное сечение собранного устройства: А - ускоряемая плоская лента с натяжным устройством и виток индуктора магнитного поля; Б - продольное сечение генератора с присоединенной к нему внешней электрической цепью плоскостью y = const. |
|
В нулевой
момент времени конденсатор в цепи индуктора заряжен до некоторого начального
напряжения. После замыкания цепи по
индуктору (и лайнеру) начинает течь
разрядный ток. Созданное им в канале ускорителя магнитное поле взаимодействует
с протекающим по лайнеру током, ускоряя лайнер в направлении от индуктора. В
некоторый момент времени (возможно, нулевой) замыкается и цепь лайнера. Ток этой цепи протекает по лайнеру и создает внутри полости лайнера
дополнительное магнитное поле. Ускорившись, лайнер сжимает это поле, которое окончательно
и выводится из системы в виде импульса тока в цепи лайнера.
В какой-то
момент времени лайнер достигает призмы, расположенной в торцевой части
ускорителя (см. рис.1.1.А), и происходит удар, в результате чего возникают
дополнительные деформации. Более подробно движение лайнера в контактной зоне
будет рассмотрено в последующих работах авторов.
Требуется
по начальным и граничным данным, физическим характеристикам сред рассчитать скорость
и положение ускоряемого лайнера, напряженности электрического и магнитного
полей, токи и напряжения во внешних электрических цепях.
В качестве
первого шага к решению задачи рассмотрим два двумерных приближения. Сечение
исходной пространственной области плоскостью z = const подробно разобрано в работах
[6], [7]. Для нее построена и
проанализирована модель, которую в дальнейшем будем называть поперечной. В данной работе рассмотрим сечение исходной
пространственной области плоскостью y = const (рис. 1.1.Б). Соответствующую модель
в дальнейшем будем называть
продольной.
При
построении продольной модели используем некоторые предположения. Все величины зависят
только от координат x и z. Это означает
формально бесконечную протяженность системы в
направлении оси y. Однако в модели будем учитывать и некую
"эффективную" длину системы в y - направлении, в значительной степени определяющую процесс
перекачки энергии из внешней
электрической цепи в кинетическую энергию лайнера. Индуктор предполагается
неподвижным. Его форма остается неизменной, материал индуктора является
проводником. Лайнер подвижен, его положение подлежит расчету в зависимости от
протекающих процессов. Считаем, что
материал лайнера представляет собой упругое твердое тело.
Лайнер и
индуктор располагаются в области, ограниченной идеально проводящим кожухом,
находящимся от проводников на достаточно большом расстоянии с тем, чтобы его
влияние было не слишком существенным. Эта область, если не учитывать внешние
электрические цепи, имеет две плоскости симметрии. Поэтому в дальнейшем задача
рассматривается в одной четвертой части исходной области, которая схематично
изображена на рис. 1.2.
Цель данной
работы состоит в построении математической и численной модели для описанного
двумерного приближения. Одной из
поставленных задач является проведение сравнительного анализа продольной
и поперечной моделей.

Рис. 1.2. Характерная схема четверти сечения пространственной области плоскостью у = const, в которой решается продольная задача.
Работа выполнена
при частичной финансовой поддержке РФФИ (проект № 05-02-17737).
2. Математическая модель движения упругого лайнера в электромагнитном поле
2.1. Электродинамическая часть
Электродинамическая
часть модели основана на системе уравнений Максвелла в квазистационарном
приближении (см. [2])
![]()
![]() (2.1)
(2.1)
![]()
Здесь ![]() - электропроводность,
- электропроводность, ![]() и
и ![]() - напряженности
электрического и магнитного полей,
- напряженности
электрического и магнитного полей, ![]() - плотность тока,
- плотность тока, ![]() - вектор скорости
движения лайнера. С учетом двумерного приближения рассматриваемые величины
имеют следующий вид:
- вектор скорости
движения лайнера. С учетом двумерного приближения рассматриваемые величины
имеют следующий вид: ![]() ,
, ![]() ,
, ![]() , то есть векторы скорости, напряженности электрического поля
и плотности тока лежат в плоскости рис.
1.2, а вектор напряженности магнитного поля направлен перпендикулярно плоскости рис. 1.2.
Это означает, что в данной системе имеет место электромагнитное поле TM типа.
, то есть векторы скорости, напряженности электрического поля
и плотности тока лежат в плоскости рис.
1.2, а вектор напряженности магнитного поля направлен перпендикулярно плоскости рис. 1.2.
Это означает, что в данной системе имеет место электромагнитное поле TM типа.
В данной
постановке задачи оказывается, что можно сразу выразить напряженность
магнитного поля в диэлектрике через значение полных токов, которые протекают
через проводники. Суперпозиция магнитного поля, созданного током ![]() , текущим по
индуктору, и поля, созданного током (
, текущим по
индуктору, и поля, созданного током (![]() ), текущим по лайнеру, дает следующий результат:
), текущим по лайнеру, дает следующий результат:
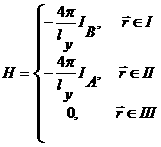 .
(2.2)
.
(2.2)
Для того, чтобы найти ![]() в проводниках, выразим из второго
уравнения (2.1) напряженность магнитного поля и подставим в первое уравнение. В
итоге приходим к выражению:
в проводниках, выразим из второго
уравнения (2.1) напряженность магнитного поля и подставим в первое уравнение. В
итоге приходим к выражению:
![]() .
.
В данной
задаче
![]() ,
, ![]() , поэтому можно перейти к скалярной форме записи:
, поэтому можно перейти к скалярной форме записи:
![]()
![]() .
.
Если выделить
в этом выражении полную производную по времени
![]() ,
,
то уравнение примет окончательный вид:
![]() .
(2.3)
.
(2.3)
На границах проводников имеют место следующие граничные условия:
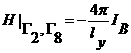 ,
, 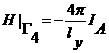 ,
, ![]() ,
,
здесь ![]() - границы лайнера,
- границы лайнера, ![]() - границы индуктора (см. рис. 1.2). Ставится начальное
условие
- границы индуктора (см. рис. 1.2). Ставится начальное
условие ![]() .
.
2.2. Уравнения внешних электрических цепей
Параметры
внешних электрических цепей предполагаются сосредоточенными, так что для
описания цепей можно применять уравнения Кирхгоффа [3]. Они являются следствием
интегрирования первого уравнения (2.1) по плоскости и контуру данных цепей (площадка
ABCD на рис. 2.1) .
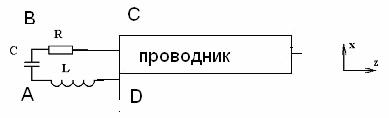
Рис. 2.1. Схема площадки, по которой идет интегрирование уравнения Максвелла
С учетом
формулы Стокса, позволяющей перейти к
контурному интегралу, получаем следующее уравнение:
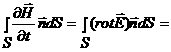
![]()
![]() .
.
На той части границы DC, которая принадлежит проводнику, из
второго уравнения Максвелла следует, что![]() . Следовательно, остается только интеграл по участку
. Следовательно, остается только интеграл по участку ![]() (граница диэлектрика, см. рис.1.2.).
(граница диэлектрика, см. рис.1.2.).
Используя известные соотношения, связывающие интегралы по участкам электрической цепи с индуктивностью в катушке, напряжением в конденсаторе и сопротивлением в цепи (см. [3]), приходим к следующему соотношению:
![]() .
.
Коэффициент 2 появился из учета симметрии области.
Чтобы определить значение ![]() , снова проинтегрируем первое уравнение (2.1), которое можно
записать в виде
, снова проинтегрируем первое уравнение (2.1), которое можно
записать в виде ![]() , но уже по области I. После несложных
преобразований получаем
, но уже по области I. После несложных
преобразований получаем
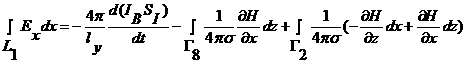 .
.
В итоге уравнения для внешней электрической цепи индуктора имеют следующий вид:
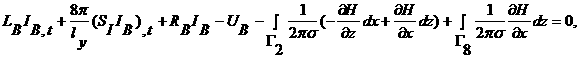 (2.4)
(2.4)
![]()
Аналогичные рассуждения можно провести
для цепи лайнера и получить следующие уравнения (![]() и
и ![]() - площади соответствующих областей):
- площади соответствующих областей):
![]() или
или
 (2.5)
(2.5)
![]() .
.
В уравнениях (2.4)-(2.5) L, R,
C, соответственно, - индуктивность,
сопротивление и емкость в цепи, I и U – сила тока и напряжение на обкладках
конденсатора. Задача замыкается выбранными начальными значениями для токов и
напряжений.
2.3. Математическая модель термоупругого тела
Рассмотрим лайнер как изотропное сжимаемое термоупругое твердое тело. Пусть![]() и
и ![]() – текущая и начальная плотность материала
лайнера,
– текущая и начальная плотность материала
лайнера, ![]() и
и ![]() – эйлеровые и лагранжевые переменные,
– эйлеровые и лагранжевые переменные, ![]() – компоненты вектора перемещения (
– компоненты вектора перемещения (![]() = 1, 2, 3 в общем
случае, в данном – до 2:
= 1, 2, 3 в общем
случае, в данном – до 2: ![]() ,
, ![]() ). В
дальнейшем будем использовать лагранжевые переменные.
). В
дальнейшем будем использовать лагранжевые переменные.
Тензор деформации и два его
первых инварианта имеют вид:
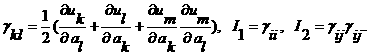
Уравнение движения в форме Лагранжа:
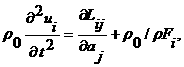 (2.6)
(2.6)
где ![]() - сила Лоренца, действующая на тело,
- сила Лоренца, действующая на тело, ![]() - тензор напряжений Лагранжа. Отметим, что силу можно
представить в следующей форме записи:
- тензор напряжений Лагранжа. Отметим, что силу можно
представить в следующей форме записи:
![]() .
.
Поставим начальные условия ![]() и граничные условия
и граничные условия ![]() на
на ![]() и
и ![]() ,
, ![]() на всей границе
лайнера (
на всей границе
лайнера (![]() - нормаль).
- нормаль).
Введем переменные: ![]() - энтропия на единицу массы,
- энтропия на единицу массы, ![]() - внутренняя энергия на единицу массы, которая
связана с компонентами
- внутренняя энергия на единицу массы, которая
связана с компонентами ![]() следующей формулой:
следующей формулой:
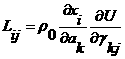 .
.
Так как рассматривается линейно-упругий случай, то в
разложении функции ![]() можно ограничиться
членами до второго порядка включительно:
можно ограничиться
членами до второго порядка включительно:
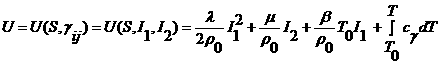 ,
,
при этом энтропия принимается равной следующей функции
 .
.
Здесь λ и
μ – коэффициенты Ламе, β = (3 λ + 2 μ) ![]() ,
, ![]() - коэффициент линейного теплового расширения,
- коэффициент линейного теплового расширения, ![]() – удельная объемная теплоемкость при
постоянной деформации.
– удельная объемная теплоемкость при
постоянной деформации.
Тогда, учитывая, что 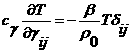 (это выражение можно
вывести, продифференцировав энтропию по
(это выражение можно
вывести, продифференцировав энтропию по ![]() ), приходим к выражению
), приходим к выражению
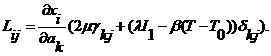
Уравнение энергии представимо в виде:
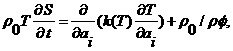 (2.7)
(2.7)
здесь ![]() - коэффициент
теплопроводности,
- коэффициент
теплопроводности, ![]() - мощность
тепловыделения.
- мощность
тепловыделения.
Если подставить в (2.7) формулу для ![]() , то получим уравнение теплопроводности вида
, то получим уравнение теплопроводности вида
 (2.8)
(2.8)
Дополним его начальными условиями ![]() и граничными условиями
и граничными условиями
 .
.
2.4. Энергетические соотношения
Из уравнений Максвелла легко получить равенство:
![]() .
.
Если воспользоваться представлением
![]() ,
,
то придем к следующему уравнению:
![]() .
.
Если использовать известное выражение для якобиана ![]() , то можно получить, что
, то можно получить, что
![]() .
.
Проинтегрируем его по области G – половине исходной, дважды воспользовавшись теоремой Остроградского-Гаусса:
![]() .
.
На торцевых границах лайнера нормальная составляющая скорости равна нулю, поэтому первое слагаемое в правой части тоже обращается в нуль.
Так как ![]() , на границах области
, на границах области ![]() поставлено условие
поставлено условие ![]() , а на границе проводников
, а на границе проводников ![]() , то
, то
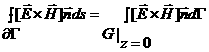
![]()
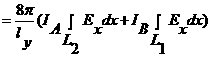 .
.
Коэффициент 2 снова появился из-за учета симметрии области.
Перенесем все слагаемые в левую часть и учтем выражение для силы Лоренца. Окончательная форма баланса электромагнитной энергии:
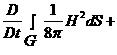
![]()
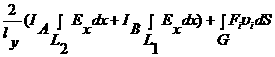 =0.
(2.9)
=0.
(2.9)
Если умножить первое уравнение из системы (2.4) на ![]() , а второе - на
, а второе - на ![]() , провести аналогичную операцию с уравнениями из (2.5), а
потом все сложить, то получим закон
изменения энергии в цепи:
, провести аналогичную операцию с уравнениями из (2.5), а
потом все сложить, то получим закон
изменения энергии в цепи:
![]()
![]() (2.10)
(2.10)
Сложив уравнения (2.9) и (2.10), запишем закон изменения электромагнитной энергии во всей системе, включая внешнюю цепь:
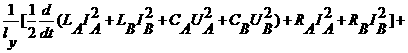
+
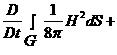
![]()
![]() =0.
(2.11)
=0.
(2.11)
Теперь рассмотрим баланс механической и внутренней энергии. Сначала получим несколько вспомогательных соотношений:
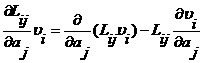 ,
,
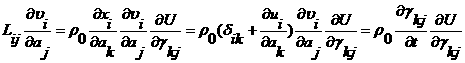 ,
,
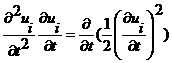 .
.
Теперь умножим каждое из уравнений движения (2.6) на
соответствующую компоненту скорости ![]() и проинтегрируем по
половине исходной области
и проинтегрируем по
половине исходной области ![]() , используя приведенные выше соотношения:
, используя приведенные выше соотношения:
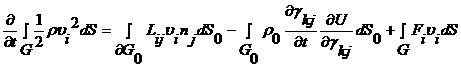 . (2.12)
. (2.12)
На границах лайнера ставится условие ![]() , поэтому первое слагаемое в правой части обращается в нуль.
Для учета теплового баланса проинтегрируем уравнение теплопроводности (2.7) по
той же области:
, поэтому первое слагаемое в правой части обращается в нуль.
Для учета теплового баланса проинтегрируем уравнение теплопроводности (2.7) по
той же области:
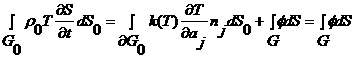 . (2.13)
. (2.13)
Учитывая, что
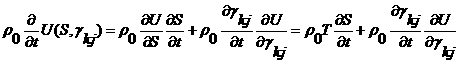 ,
,
сложим (2.12) и (2.13) и перенесем все слагаемые в левую часть:
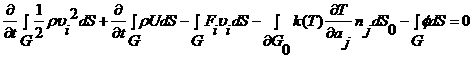 . (2.14)
. (2.14)
Если сложить (2.11) и (2.14), учитывая что ![]() , то получим закон изменения полной энергии системы:
, то получим закон изменения полной энергии системы:
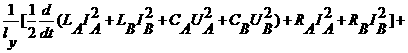
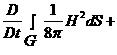
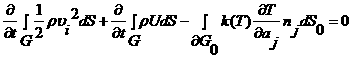 .
(2.15)
.
(2.15)
3. Метод численного решения
Для численного решения применяем метод конечных
элементов (МКЭ). Введем в области
треугольную сетку, причем, так как напряженность магнитного поля в
диэлектрике выражается через токи, то ограничимся 2 сетками для 2 проводников,
независящими друг от друга. Поскольку лайнер движется, то точки соответствующей
сетки двигаются вместе с веществом. Раскладываем искомые величины, используя
следующие базисы: стандартные кусочно-линейные функции ![]() и кусочно-постоянные
функции
и кусочно-постоянные
функции ![]() , определенные на ячейках Дирихле (см. [11]). Напряженность
магнитного поля, температура и обе составляющие скорости заданы в узлах сетки,
а напряженность электрического поля и плотность тока постоянны в пределах
каждого сеточного треугольника.
, определенные на ячейках Дирихле (см. [11]). Напряженность
магнитного поля, температура и обе составляющие скорости заданы в узлах сетки,
а напряженность электрического поля и плотность тока постоянны в пределах
каждого сеточного треугольника.
Решение задачи на каждом временном слое разбиваем на последовательное решение группы электродинамических уравнений, группы уравнений, описывающих движение лайнера, и уравнения теплопроводности.
В каждой группе вводим свой итерационный процесс поиска решения.
3.1. Разностная схема для электрической цепи
Если провести стандартную дискретизацию уравнений
(2.4) и (2.5), используя неявную схему (см. [12]), и представить напряженность
магнитного поля в виде суммы ![]() (см. [11]), то
нетрудно выразить значения токов и
напряжений на текущем временном слое:
(см. [11]), то
нетрудно выразить значения токов и
напряжений на текущем временном слое:
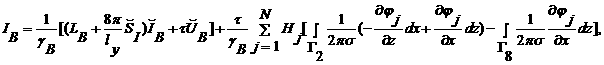
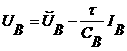 ,
(3.1)
,
(3.1)
где ![]() - шаг по времени,
- шаг по времени, ![]() и
и ![]() - известные значения,
взятые с предыдущего слоя,
- известные значения,
взятые с предыдущего слоя, 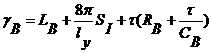 .
.
Аналогично для тока в цепи лайнера имеем:
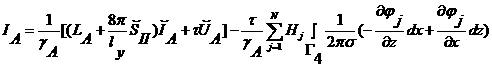 ,
,
 , (3.2)
, (3.2)
где 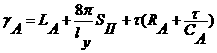 .
.
Ставим начальные
условия: ![]() .
.
3.2. Система конечномерных уравнений для напряженности магнитного поля в проводниках
Рассмотрим сначала область, занимаемую индуктором. В этой области справедливо уравнение (2.3). Если применить к нему метод Галеркина-Петрова (см. [11]), то после несложных преобразований можно прийти к следующей разностной задаче:
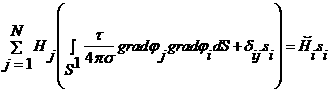 (3.3)
(3.3)
для всех ![]() , соответствующих внутренним узлам, а также
, соответствующих внутренним узлам, а также ![]() и
и ![]() . Здесь
. Здесь ![]() - площадь ячейки Дирихле. Значения искомой
функции в узлах сетки на других границах
задаются равенствами:
- площадь ячейки Дирихле. Значения искомой
функции в узлах сетки на других границах
задаются равенствами:
![]() ,
, 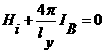 ,
, ![]() .
.
Аналогичную процедуру можно проделать для лайнера. В
итоге получаем, что значения ![]() определяются из
системы уравнений
определяются из
системы уравнений
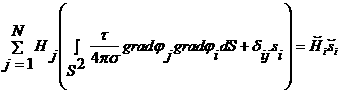 (3.4)
(3.4)
для всех ![]() , соответствующих внутренним узлам, а также
, соответствующих внутренним узлам, а также ![]() и
и ![]() . Здесь
. Здесь ![]() - площадь ячейки Дирихле на старом слое. Значения
- площадь ячейки Дирихле на старом слое. Значения ![]() в оставшихся точках задаются равенствами:
в оставшихся точках задаются равенствами:
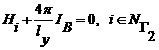 ,
, 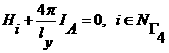 .
.
Итоговая система уравнений будет включать в себя
системы (3.3) и (3.4), уравнения для
узлов, лежащих на границах ![]() ,
, ![]() ,
,![]() ,
,![]() , и выражения для токов:
, и выражения для токов:
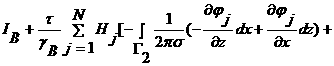
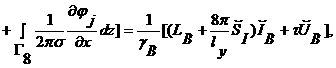
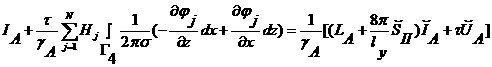 .
.
3.3. Система конечномерных уравнений для уравнения движения
Движение лайнера задается уравнением (2.6), которое можно представить в виде системы
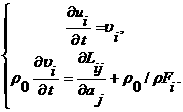 (3.5)
(3.5)
Дискретизацию этой системы проводим в терминах
следующей величины: ![]() . При этом
. При этом ![]() . После нахождения решения происходит переход к искомому
значению
. После нахождения решения происходит переход к искомому
значению ![]() . Ко второму уравнению системы (3.5) применяем метод
Галеркина-Петрова (см. [11]), при этом квадратичные слагаемые, входящие в
выражение для тензора деформации, берем с предыдущей внутренней итерации. Температуру
характеризует параметр
. Ко второму уравнению системы (3.5) применяем метод
Галеркина-Петрова (см. [11]), при этом квадратичные слагаемые, входящие в
выражение для тензора деформации, берем с предыдущей внутренней итерации. Температуру
характеризует параметр ![]() (аппроксимация
температуры в
(аппроксимация
температуры в ![]() -м треугольнике путем усреднения температуры в его вершинах),
считающийся известным на данной внешней итерации.
-м треугольнике путем усреднения температуры в его вершинах),
считающийся известным на данной внешней итерации.
Введение одномерного массива ![]() такого, что
такого, что ![]() (значение
(значение ![]() в
в ![]() узле) и
узле) и ![]() (значение
(значение ![]() в
в ![]() узле), позволяет
записать систему линейных уравнений в виде матричного уравнения
узле), позволяет
записать систему линейных уравнений в виде матричного уравнения ![]() .
.
Правую часть составляют следующие известные слагаемые:
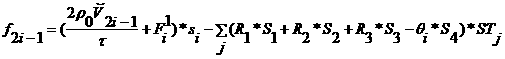 ,
,
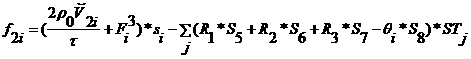 ,
,
где ![]() - значение соответствующей проекции силы Лоренца,
- значение соответствующей проекции силы Лоренца, ![]() - площадь соответствующего треугольника,
- площадь соответствующего треугольника, ![]() - площадь ячейки Дирихле (в эйлеровых координатах).
- площадь ячейки Дирихле (в эйлеровых координатах).
Элементы матрицы системы задаются равенствами
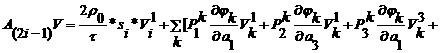
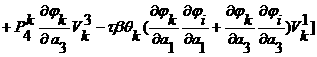 ,
,
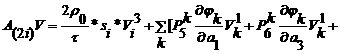
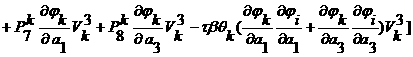 .
.
Суммирование идет по треугольникам, в состав которых
входит ![]() -я вершина и в которых
-я вершина и в которых ![]() отлична от нуля.
Множители
отлична от нуля.
Множители ![]() ,
, ![]() ,
, ![]() - это выражения, содержащие в себе известные слагаемые,
которые можно посчитать для каждого треугольника.
- это выражения, содержащие в себе известные слагаемые,
которые можно посчитать для каждого треугольника.
3.4. Конечномерная аппроксимация уравнения теплопроводности
Уравнение теплопроводности представлено в виде (2.8). После применения метода Галеркина получается
система линейных уравнений. Решая ее методом Якоби, получаем следующую формулу для
температуры в ![]() -ой точке:
-ой точке:
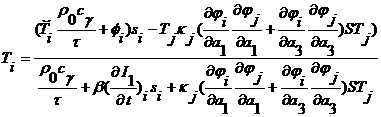 .
.
Суммирование идет по треугольникам с площадью ![]() , в состав которых входят
, в состав которых входят ![]() -я вершина и в которых
-я вершина и в которых ![]() отлична от нуля.
отлична от нуля.
4. Одномерная модель
При проведении численных расчетов выяснилось, что до
определенного момента времени (когда лайнер достигает призмы и начинает
деформироваться) искомые величины не зависят от координаты ![]() . Поэтому построена
одномерная модель, задаваемая уравнениями (2.1)-(2.7), в которых все величины
считаются функциями двух переменных
. Поэтому построена
одномерная модель, задаваемая уравнениями (2.1)-(2.7), в которых все величины
считаются функциями двух переменных ![]() и
и ![]() . При этом граничные условия на
. При этом граничные условия на ![]() ,
, ![]() ,
, ![]() ,
, ![]() выполняются
автоматически, а граничные условия на
выполняются
автоматически, а граничные условия на ![]() ,
, ![]() ,
,![]() и
и ![]() задаются для точек –
концов отрезков, в которых находятся проводники. Вводим соответствующую
одномерную сетку, на которой задаем
стандартные базисные одномерные функции (см. [11]), и получаем разностные
соотношения, аналогичные (3.1)-(3.5). Одномерную сетку можно интерпретировать и
как двумерную, ячейки которой представляют собой прямоугольники, вытянутые
вдоль всей области по оси
задаются для точек –
концов отрезков, в которых находятся проводники. Вводим соответствующую
одномерную сетку, на которой задаем
стандартные базисные одномерные функции (см. [11]), и получаем разностные
соотношения, аналогичные (3.1)-(3.5). Одномерную сетку можно интерпретировать и
как двумерную, ячейки которой представляют собой прямоугольники, вытянутые
вдоль всей области по оси ![]() . Чтобы это учесть, надо домножить площади самих ячеек и
ячеек Дирихле на величину
. Чтобы это учесть, надо домножить площади самих ячеек и
ячеек Дирихле на величину ![]() . Результаты, полученные с помощью одномерной модели, очень
хорошо согласуются с расчетами, проводимыми для двумерного случая, но при этом
скорость счета существенно повышается и время работы программы сокращается в
десятки раз.
. Результаты, полученные с помощью одномерной модели, очень
хорошо согласуются с расчетами, проводимыми для двумерного случая, но при этом
скорость счета существенно повышается и время работы программы сокращается в
десятки раз.
|
FX |
VX |
|
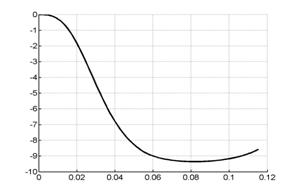
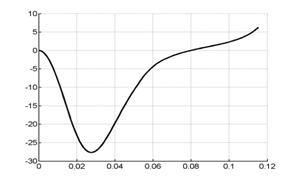
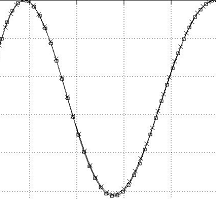
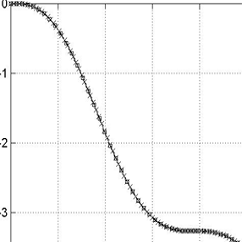
Рис. 4.1. Сравнение графиков сосредоточенной информации для одномерной и двумерной моделей |
|
На рис. 4.1 представлены графики интегральной ускоряющей силы (в направлении х) и скорости центра масс, полученные для одномерной (график с маркером «х») и двумерной модели (график с маркером в виде квадрата).
5. Физические параметры
Приведем в
безразмерном виде некоторые данные о характерных параметрах задачи.
Начальная
температура T = 1.45. Начальная скорость лайнера равна нулю. Далее описаны
размеры конструкции в соответствии с рис. 1.1 – 1.2. Высота индуктора равна
2.0, его полуширина – 1.5. Высота лайнера равна 0.02. Расстояние между лайнером
и индуктором по высоте в начальный момент времени равно 0.02. Начальная высота
нижней кромки лайнера равна 0.96.
Параметры
материала индуктора взяты равными соответствующим величинам стали: плотность
ρ = 1.95, теплоемкость cv = 9.21, теплопроводность κ =
1.998 10-5, электропроводность σ = 52.9 при 00 C.
Параметры
материала лайнера взяты равными соответствующим величинам алюминия: плотность
ρ = 0.63525, теплоемкость cv = 18.037, теплопроводность κ
= 1.035 10-4, электропроводность σ = 40.66 при 00 C.
Для всех
материалов электропроводность взята в виде функции температуры вида σ =
σs / (1 + ασ T) c соответствующими
параметрами из [10].
Параметры
электрической цепи индуктора составили: индуктивность LB = 20.0,
емкость СB = 3 10–5, сопротивление RB = 102.
Частота электромагнитных колебаний в свободной цепи с такими параметрами ώ
= 40.82, коэффициент затухания ά = 2.5 (см. [3]). Начальное напряжение на
обкладках конденсатора в цепи индуктора взято равным 2000.0, начальный ток –
нулевой. Во всех расчетах момент
замыкания цепи лайнера t0 = 0.062.
Параметры
электрической цепи лайнера составили: индуктивность ![]() = 2.5,
емкость
= 2.5,
емкость ![]() = 1000, сопротивление
= 1000, сопротивление ![]() = 10-5.
= 10-5.
Число
точек разностной сетки во всей пространственной области составило 2595, при
этом получено 4742 соответствующих треугольников.
Геометрические
размеры индуктора позволяют задать в нем относительно крупную сетку, но так как
высота лайнера гораздо меньше его ширины, то сетку в данном проводнике
приходилось мельчить, поэтому аналогичные числа для области лайнера – 2452/4502.
При расчете
решения контролировалось соответствие полного протекающего через сечения
(расположенные на левом и на правом краях области) тока полному току в
соответствующей цепи. Токи передавались с относительной точностью не хуже 10–3, как правило.
6. Результаты расчетов
Ниже представлены 3 варианта расчета
задачи, отличающиеся некоторыми параметрами. Процессы,
связанные с деформацией лайнера в результате его соударения о призму, в данных
вариантах не рассматривались. Расчет
проводился до момента достижения лайнером нижней границы области.
6.1. Вариант 1
Длина ускоряемого лайнера по направлению y
– ly = 5.0. Расчет продолжался до
момента времени t = 0.2231,
в который координата центра масс составила
x = 0.0155.
Максимальная величина скорости центра
масс лайнера за время ускорения составила V = -7.148, максимальная температура - T = 1.809, интегральная ускоряющая сила (в направлении x) изменялась от 0 до -9.015, ток в цепи индуктора изменялся
в пределах от -1.672 до 2.196, напряжение на обкладках конденсатора в цепи
индуктора менялось от -1612.1 до 2000.0.
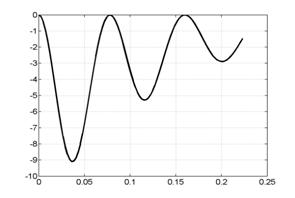
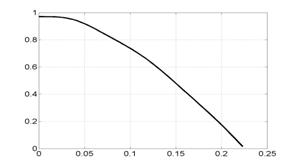
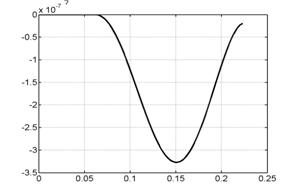
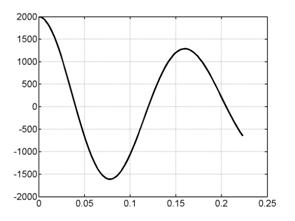
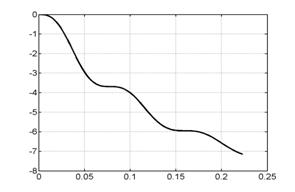
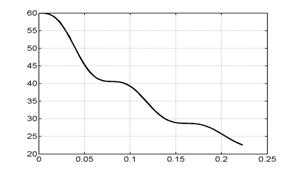
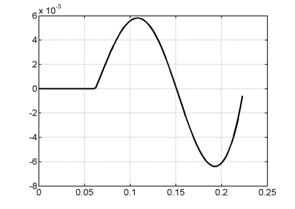
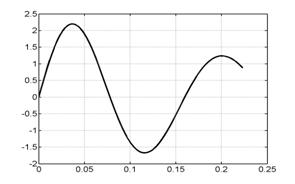
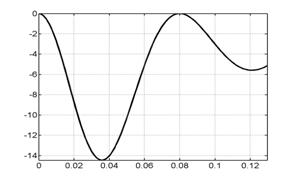
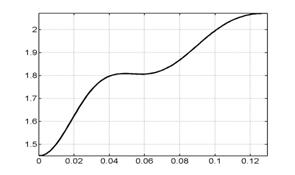
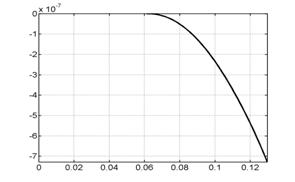
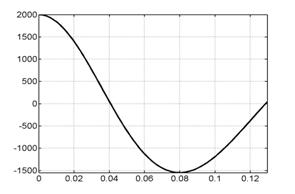
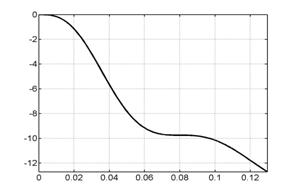
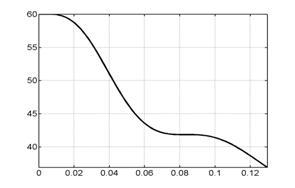
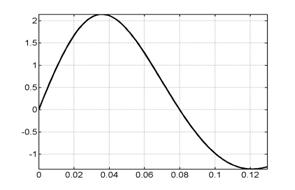
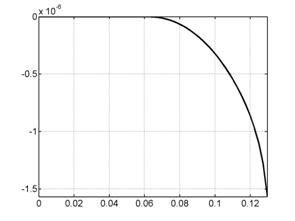
На рис. 6.1 представлены
графики сосредоточенной информации о
расчете, характеризующие процесс в
целом. Это, соответственно (слева направо, сверху вниз), зависимости от времени
интегральной силы, скорости центра масс лайнера, координаты центра масс
лайнера, полной энергии (она состоит из энергии цепи, энергии магнитного поля,
внутренней и кинетической энергии) напряжения и силы тока в цепи лайнера и в
цепи индуктора.
|
FX
X центра масс
UA
UB |
VX
Energy
IA
IB |
|
Рис. 6.1. Графики сосредоточенной информации для варианта 1. |
|
6.2. Вариант 2
Длина ускоряемого лайнера
по направлению y – ly = 3.0. Расчет
продолжался до момента времени t =
0.1297. Максимальная величина скорости центра масс лайнера за время ускорения
составила V = -12.7014, максимальная температура - T = 2.0714, интегральная ускоряющая сила (в направлении x) изменялась от 0 до -14.42, ток в цепи индуктора
изменялся в пределах от -1.334 до 2.145, напряжение на обкладках конденсатора в
цепи индуктора менялось от -1548 до 2000.0.
На рис. 6.2 представлены
графики сосредоточенной информации о расчете, характеризующие процесс в целом. Это,
соответственно (слева направо, сверху вниз), зависимости от времени
интегральной силы, скорости центра масс лайнера, максимальной температуры в
области, полной энергии, напряжения и силы тока в цепи лайнера и в цепи
индуктора.
|
FX
T
UA
UB |
VX
Energy
IA
IB |
|
Рис. 6.2. Графики сосредоточенной информации для варианта 2. |
|
6.3. Вариант 3
Длина ускоряемого лайнера по направлению y – ly = 3.0.
Индуктивность в цепи лайнера уменьшается в 20 раз до значения ![]() = 0.125. Расчет продолжался до момента времени t = 0.1297.
Существенные изменения, по сравнению с вариантом 2, наблюдаются только в
графиках напряжения и силы тока в цепи лайнера, которые приведены на рис. 6.3.
= 0.125. Расчет продолжался до момента времени t = 0.1297.
Существенные изменения, по сравнению с вариантом 2, наблюдаются только в
графиках напряжения и силы тока в цепи лайнера, которые приведены на рис. 6.3.
|
UA |
IA |
|
Рис. 6.3. Графики сосредоточенной информации для варианта 3 |
|
7. Сравнение двумерных моделей
7.1. Поперечная модель движения лайнера

Рис. 7.1. Характерная схема
четверти сечения пространственной области плоскостью
z = const, в
которой решается поперечная задача.
В поперечной модели все величины считаются зависящими только от координат х и у. Она подробно описана в [6-7]. На рис. 7.1 изображена область, в которой решается задача.
В данной модели векторы имеют следующие ненулевые компоненты E = {0, 0, Ez}, H = {Hx, Hy, 0}, v = {vx, vy, 0}, все производные по z в уравнениях модели равны нулю.
После введения векторного потенциала A задача для определения полей внутри области принимает вид:
![]() ,
,
 ,
,
(ck играет роль плотности поверхностных магнитных токов (см. [9]))
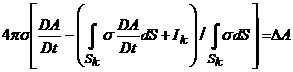 в Sk , k=1,
2 (проводники),
в Sk , k=1,
2 (проводники),
DA = 0 в диэлектрике,
с условиями ![]()
Уравнения
внешней электрической цепи:
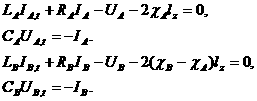
Уравнения
движения и энергии имеют вид, аналогичный (2.6) и (2.8), с учетом разницы в
распределении ненулевых компонентов векторов.
7.2. Сравнение продольной и поперечной моделей
Обе модели задают двумерное приближение трехмерной
задачи. Длины системы в третьем направлении (![]() - для продольной модели и
- для продольной модели и ![]() - для поперечной), как
уже упоминалось выше, в значительной степени определяют процесс перекачки
энергии из внешней электрической цепи в кинетическую энергию лайнера. Поэтому
имеет смысл посмотреть, как характеристики обеих задач зависят от этой длины.
- для поперечной), как
уже упоминалось выше, в значительной степени определяют процесс перекачки
энергии из внешней электрической цепи в кинетическую энергию лайнера. Поэтому
имеет смысл посмотреть, как характеристики обеих задач зависят от этой длины.
|
А |
Б |
|
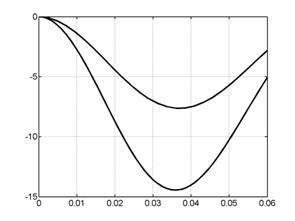
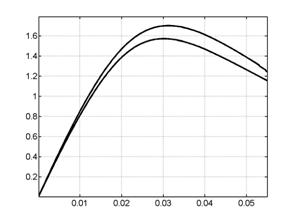
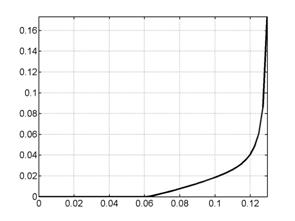
Рис. 7.2. Скорость центра масс: А – поперечная модель,
верхний график соответствует |
|
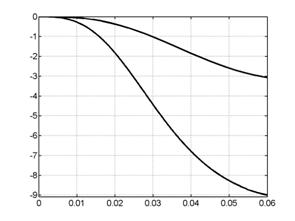
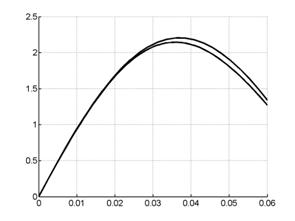
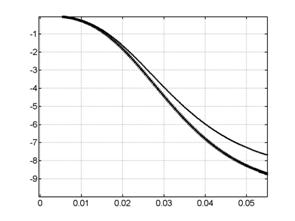
На рис.7.2 - 7.3 видно, что для продольного случая
скорость центра масс обратно пропорциональна ![]() , а интегральная ускоряющая сила -
, а интегральная ускоряющая сила - ![]() , в то время как для поперечной модели столь четких
зависимостей не наблюдается, а интегральная сила и вовсе ведет себя
противоположным образом, увеличиваясь с ростом
, в то время как для поперечной модели столь четких
зависимостей не наблюдается, а интегральная сила и вовсе ведет себя
противоположным образом, увеличиваясь с ростом ![]() .
.
|
А |
Б |
|
Рис. 7.3. Интегральная ускоряющая сила (в направлении х): А
– поперечная модель, верхний график соответствует верхний график соответствует |
|
Более того,
для продольного случая можно аналитически вывести указанные зависимости,
рассмотрев движение центра масс.
По второму закону Ньютона ![]() , где
, где ![]() - внешние силы, а
- внешние силы, а ![]() - ускорение центра масс лайнера. На лайнер действуют только давление внешнего
магнитного поля в областях I и II. В каждой из этих областей магнитное поле постоянно по
пространству, следовательно, магнитное давление равно
- ускорение центра масс лайнера. На лайнер действуют только давление внешнего
магнитного поля в областях I и II. В каждой из этих областей магнитное поле постоянно по
пространству, следовательно, магнитное давление равно ![]() , а сила давления
, а сила давления ![]() , где
, где ![]() - площадь соприкосновения лайнера с одной из областей.
Подставляя значение
- площадь соприкосновения лайнера с одной из областей.
Подставляя значение ![]() , получаем
, получаем
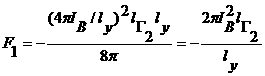 ,
,  ,
(7.1)
,
(7.1)
![]() .
.
Тогда сеточное значение скорости центра масс лайнера
на новом временном слое определяется по формуле: ![]() . (7.2)
. (7.2)
Массу лайнера можно вычислить, зная
его размеры и площадь:
![]() .
.
Из проведенных выше рассуждений становится
ясно, что модели будут достаточно сильно
отличаться, но это вытекает из самой физической постановки задачи, которая
имеет свои особенности для каждого из этих двумерных случаев. Сравним некоторые
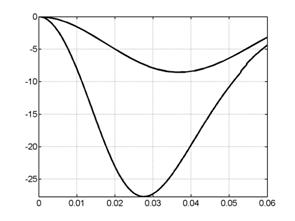
характеристики двух рассматриваемых моделей, варьируя параметры задачи. Если
потребовать равенства масс и считать, что в поперечной задаче ![]() =8, то
получим, что в продольной задаче
=8, то
получим, что в продольной задаче ![]() =5.3333. На рис. 7.4 видно, что рассчитанные величины отличаются
друг от друга более чем в 2 раза.
=5.3333. На рис. 7.4 видно, что рассчитанные величины отличаются
друг от друга более чем в 2 раза.
|
Скорость центра масс |
Интегральная ускоряющая сила |
|
Рис. 7.4. Графики сосредоточенной информации: нижние графики
соответствуют поперечной модели ( |
|
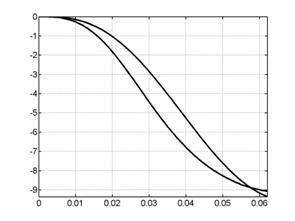
В расчетах исследована возможность так подобрать
параметры задачи в продольном случае, чтобы полученные интегральные
характеристики были близки
соответствующим величинам в поперечной модели. Оказалось, что это
действительно возможно, но приходится менять не только ![]() , но и плотность. На рис. 7.5 показаны графики, для которых в
продольной модели полагалось, что
, но и плотность. На рис. 7.5 показаны графики, для которых в
продольной модели полагалось, что ![]() =2,
=2, ![]() =1.7.
=1.7.
|
Скорость
центра масс |
Интегральная ускоряющая сила |
|
Рис. 7.5. Графики сосредоточенной информации: нижние графики
соответствуют поперечной модели ( |
|
До сих пор рассматривались только величины, характеризующие процессы, протекающие внутри области, но встает вопрос, как между собой соотносятся токи и напряжения во внешней электрической цепи.
|
А |
Б |
|
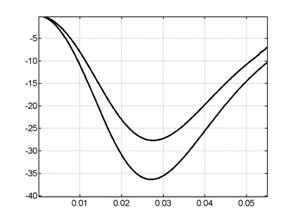
Рис. 7.6. Сила тока в цепи индуктора: А – поперечная модель,
верхний график соответствует |
|
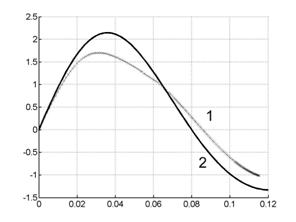
На рис. 7.6 видно, что с увеличением ![]() ток в цепи индуктора в поперечной
модели уменьшается, а с увеличением
ток в цепи индуктора в поперечной
модели уменьшается, а с увеличением ![]() в продольной
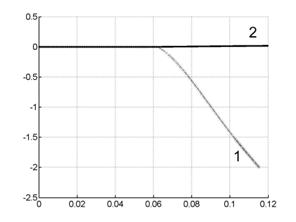
модели – увеличивается. На рис. 7.7 непосредственно сравниваются токи в разных
моделях: график с номером 1 соответствует поперечной модели (
в продольной
модели – увеличивается. На рис. 7.7 непосредственно сравниваются токи в разных
моделях: график с номером 1 соответствует поперечной модели (![]() =8), график с номером 2 соответствует продольной модели (
=8), график с номером 2 соответствует продольной модели (![]() =3).
=3).
|
IB |
IA |
|
Рис. 7.7. Сила тока в цепи индуктора и в цепи лайнера. |
|
8. Анализ полученных результатов
Результаты, показанные на графиках в разделе 7, говорят о том, что две рассматриваемые модели ведут себя по-разному. В частности, рис. 7.7 наглядно демонстрирует, что тот значительный рост силы тока в цепи лайнера после ее замыкания, который характерен для поперечной модели, в продольной модели отсутствует. А между тем этот параметр тесно связан с формированием мощного выходного импульса, который и является целью физического эксперимента (см. [6]-[7]). Этот импульс обусловлен отношением времени разгона проводников к времени их торможения давлением генерируемого магнитного поля. Но если посмотреть на формулы (7.1) –(7.2), то из них становится ясным, что процесс торможения лайнера начнется только тогда, когда сила тока в цепи лайнера будет превосходить силу тока в цепи индуктора. Соответствующие графики на рис. 6.1-6.2 показывают, что при данных параметрах цепей этого не происходит, и лайнер продолжает ускоряться до самого конца расчета. Для поперечного варианта зависимости более сложные, но проведенные в [6]-[7] расчеты показывают, что данная модель действительно описывает конечное торможение лайнера.
|
VX |
FX |
|
Рис. 8.1. Скорость центра масс и интегральная ускоряющая
сила для поперечного варианта ( |
|
Это хорошо видно из графиков на рис. 8.1, на которых изображены данные для варианта, который рассчитывался до момента достижения лайнером нижнего края области.
Для того, чтобы понять причины такого резкого
несоответствия тока в цепи лайнера в продольной и поперечной моделях, нужно
сравнить пространственные области, в которых решались задачи (см. рис.1.2 и
рис. 7.1). Очевидно, что для поперечной модели магнитное поле, распространяясь
по диэлектрику, может обтекать проводники, которые не доходят до границы
области. Таким образом, в подобласти, расположенной под лайнером (аналог
области II), может
возникнуть сильное магнитное поле, которое и приведет к торможению. В то же
время для продольной модели такая ситуация невозможна, так как проводники
доходят до границы области. Единственный путь, с помощью которого магнитное
поле может проникнуть в область II
– непосредственно сквозь лайнер. При этом до замыкания цепи лайнера магнитного
поля в этой зоне вообще нет, что и обуславливает такой медленный рост ![]() .
.
Итак, продольная модель не описывает эффекта обтекания магнитным полем проводников, а значит не может описывать и образование мощного выходного импульса. Но она позволяет оценить другие особенности физического процесса. Как было показано в пункте 4, в данной модели лайнер движется как твердое тело, сохраняя свою начальную форму, что позволяет ввести одномерную модель. В дальнейшем продольная модель будет доработана и сможет описывать движение лайнера в зоне контакта, что представляет собой большой интерес. Таким образом, две указанные модели будут дополнять друг друга, позволяя оценивать общую трехмерную картину процесса.
9. Заключение
В работе представлены математическая и численная модели процесса электромагнитного ускорения пластинчатого лайнера в устройствах обострения мощности. Основными ее характеристиками являются пространственная двумерность, представление лайнера в виде упругого тела и включение токов во внешней цепи в число неизвестных величин, подлежащих определению. На основе представленных вычислительных алгоритмов разработан соответствующий программный комплекс для численного моделирования. Полученные результаты представлены в работе. Проведен их сравнительный анализ с результатами другой двумерной модели, построенной для данной физической задачи.
Основной вывод из просчитанных вариантов и их сравнения с вариантами поперечной задачи состоит в том, что представленная модель не описывает торможение лайнера и образование мощного выходного импульса, но позволяет сделать выводы о характере движения лайнера в продольной плоскости. Лайнер движется как твердое тело. Дальнейшее развитие этой модели также позволит моделировать движение лайнера в контактной зоне торцевых частей ускорителя.
10. Литература
2.
М.П. Галанин,
Ю.П. Попов. Квазистационарные электромагнитные поля в неоднородных средах.
Математическое моделирование. М., Наука. Физматлит. 1995. 320 с.
3.
И.Е. Тамм. Основы
теории электричества. М. Наука. 1989. 504 с.
4.
В.С. Зарубин,
Г.Н. Кувыркин. Математические модели термомеханики. М. Физматлит. 2002. 168 с.
5.
Д. Бленд.
Нелинейная динамическая теория упругости. М. Мир. 1972. 184 с.
6.
М.П. Галанин,
А.П. Лотоцкий, В.Ф. Левашов. Расчет электродинамического ускорения плоских
пластин в лабораторном магнитокумулятивном генераторе. // Препринт ИПМ им. М.В.
Келдыша РАН. 2001. № 3. 30 с.
7.
М.П. Галанин, Е.
В. Грабовский, А. П. Лотоцкий, Т. Г. Суфиев.
Математическое моделирование электромагнитного ускорения проводящей
пластины в компрессоре потока. // Препринт ИПМ им. М.В. Келдыша РАН. 2005. № . 29 с.
8.
М.П. Галанин,
А.П. Лотоцкий. Моделирование разгона и торможения лайнера в устройствах
обострения мощности. // Радиотехника и электроника. 2005, Т. 50, №2, с.256 - 264.
9.
М.П. Галанин,
С.С. Храмцовский. Решение пространственно трехмерных задач электромагнитного
ускорения в системе длинных проводников. // Препринт ИПМ им. М. В. Келдыша РАН.
1998. №29, 20 с.
10. Физические величины. Справочник. Под ред. И.С.
Григорьева, Е.З. Мейлахова. М. Энергоатомиздат, 1991, 1232 с.
11. В.К. Агошков, Г.И. Марчук. Введение в
проекционно-сеточные методы. - М.: Наука. Физматлит, 1981. - 416 с.
12. А.А. Самарский. Теория разностных схем. - М.: Наука,
1983.- 28 с.
13. А.А. Самарский, А.В. Гулин. Численные методы. - М.:
Наука, 1989. - 438 с.
 А
А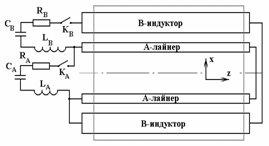


 А
А