Средства визуализации распространения света в задачах проектирования и анализа оптических систем

( Visualization techniques of light propagation in optical design tasks
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Оглавление

1. Введение. 4

2. Критерий и визуализация распространения лучей в оптической системе . 5

2.1. Простой критерий распространения лучей . 8

2.2. Критерий последовательности событий распространения луча. 9

2.3. Составной критерий распространения лучей. 10

2.4. Особенности применения критерия распространения луча для визуализации его траектории и выходных световых характеристик. 11

3. Использование визуального представления распространения света в практических приложениях проектирования оптических систем. 12

3.1. Анализ рассеянного света в оптических системах. 13

3.2. Проектирование сложных зеркальных осветительных систем. 14

3.3. Проектирование осветительных систем жидкокристаллических дисплеев. 15

3.4. Проектирование многоканальных осветительных систем. 16

3.5. Анализ причин непонятного поведения выходного распределения света. 17

3.6. Анализ корректности модели оптической системы.. 18

3.7. Анализ вклада определенных объектов оптической системы в общий уровень выходного сигнала. 19

4. Заключение. 19

Благодарности. 20

Литература. 20

1. Введение

Проектирование современных оптических систем, таких как зеркально-линзовые осветительные системы, осветительные системы жидкокристаллических дисплеев,  многолинзовые объективы, светодиоды и т.п., требует применения физически аккуратных и эффективных моделей распространения света в данных устройствах. Однако использование такого рода моделей распространения света является необходимым, но не достаточным условием эффективного проектирования. Достаточным условием является наглядное представление данных, получаемых в процессе оптического моделирования.

Существующие системы оптического моделирования предоставляют два основных способа визуализации результатов оптического моделирования –  во-первых, это визуализация распределения выходных световых характеристик (освещенность, яркость, интенсивность света) на приемнике излучения и, во-вторых, визуализация световых полей (траекторий лучей, например) в оптической системе [1]. Выходные оптические характеристики – это непосредственный результат оптического моделирования, наблюдаемый на приемнике излучения. Такая форма представления результата удобна, когда нас в первую очередь интересует сам результат моделирования, а не то, каким образом он был получен, например моделирование распределения яркости на поверхности жидкокристаллического дисплея. Однако при проектировании оптических систем часто необходимо понимать, каким образом был получен выходной результат, то есть каким образом свет от источников света попал на приемник излучения. Например, при анализе рассеянного света в линзовом объективе необходимо знать, какая поверхность и какой линзы создает блик на изображении. Кроме того, визуальное представление информации о распространении световых лучей в оптической системе полезно и для разработчика программного обеспечения, как средство отладки и оптимизации алгоритмов [2].

Для физически аккуратного и эффективного моделирования распространения света в оптических системах используются различные лучевые методы. Наиболее эффективным методом лучевого моделирования, позволяющим решать сложные задачи распространения света в светопроводящих оптических системах с элементами поверхностного и объемного рассеивания,  является прямая трассировка лучей методом Монте-Карло. Впервые этот алгоритм был предложен в [3] и затем получил широкое развитие в системах оптического моделирования [4, 5, 6]. Для оптического моделирования наиболее предпочтительной разновидностью метода Монте-Карло  является «русская рулетка» [1, 7]. Этот метод с одной стороны имеет наиболее простой программный интерфейс, а с другой стороны обладает наивысшей производительностью в задачах моделирования высокоэффективных оптических систем. Прямая трассировка лучей методом Монте-Карло моделирует распространение световых лучей от источника света до приемника излучения и тем самым статистически воспроизводит распределение освещенности, интенсивности или яркости на приемнике излучения. Метод Монте-Карло позволяет моделировать все физические эффекты распространения лучей (диффузное рассеивание на поверхностях, зеркальное отражение, преломление, изменение состояния поляризации, двойное лучепреломление и т.п.).

При проектировании оптических систем часто возникает задача определить влияние заданных компонентов оптической системы на выходной результат оптического моделирования, либо на то, каким образом эти компоненты влияют на распространение света. Например, при анализе осветительной системы может возникнуть потребность узнать, какой вклад в выходное распределение освещенности вносит свет, отраженный от определенной поверхности системы, или, например, необходимо определить каким образом формируется блик между двумя поверхностями линзового объектива.

 Использование лучевого метода Монте-Карло для моделирования распространения света в оптических системах очень подходит для анализа влияния отдельных компонентов системы на распространение света. Необходимо селектировать только лучи, которые удовлетворяют некоторому критерию. Этот критерий может быть либо простым, например, выделять все лучи, претерпевшие двойное Френелевское отражение, или более сложным, учитывающим порядок событий, происходящих с лучом, во времени, например, сначала луч должен пройти через определенную поверхность, а затем претерпеть двойное Френелевское отражение. В результате, оптическое моделирование будет использовать набор критериев траекторий лучей, и приемники излучения будут накапливать лучи, удовлетворяющие выбранным критериям, и отображать выходные распределения освещенности, яркости или интенсивности в соответствии с данными критериями. Для световых полей наиболее наглядное представление – это визуализация траекторий лучей. Они накладываются на изображение оптической системы, наглядным образом показывая влияние выбранных критериев на распространение света в оптической системе.

Данная работа вводит понятие критерия распространения лучей в оптической системе как элемента программной системы оптического моделирования, интеграцию критерия в систему визуализации траекторий лучей и расчета выходных световых характеристик оптической системы. Также рассматриваются основные приложения критерия трассировки лучей к задачам анализа и проектирования оптических систем.

2. Критерий и визуализация  распространения лучей

 в оптической системе

Анализ и проектирование оптических систем требуют включения в систему оптического моделирования специальных критериев, которые позволяют селектировать лучи, обладающие определенными свойствами и являющиеся предметом анализа распространения света в оптической системе. Критерий распространения луча – это специальный программный объект, который анализирует историю распространения луча в оптической системе и принимает решение, удовлетворяет ли луч заданным условиям или нет. Если луч удовлетворяет условиям, то он принимается системой оптического моделирования и его траектория может быть визуализирована (наложена) на изображение оптической системы.

Критерий распространения луча тесно взаимосвязан с историей распространения луча в оптической системе. История распространения луча фиксирует все события, которые возникают на пути луча от источника света:

·        источник света, который испускает луч,

·        траектория луча (координаты прямолинейных сегментов траектории луча),

·        цвет луча на сегментах его траектории,

·        Тип преобразования луча на сегментах его траектории (преломление или отражение на поверхностях и тип отражения / преломления (зеркальное, диффузное, и т.п.), рассеивание в объеме, поглощение на поверхности или объеме),

·        объекты, которые пересекает луч (их типы, имена, индексы),

·        приемники излучения, которые пересекает луч.

Для оптимального взаимодействия критерия распространения луча с его историей распространения критерий реализован в виде дерева, листьями которого являются элементарные события, которые могут произойти с лучом во время его трассировки, а узлами этого дерева являются логические операции, определяющие логическую связь между элементарными событиями [8]. Элементарные события аналогичны событиям истории распространения луча в оптической системе, что упрощает применение критерия распространения луча к его истории. Основные события, которые анализирует критерий это:

·        луч выпущен из заданного источника света;

·        трасса луча пересекается с заданной частью геометрии оптической системы, и луч претерпевает заданное оптическое преобразование;

·        трасса луча пересекается с заданным приемником излучения;

·        трасса луча пересекается с поверхностью с заданными оптическими свойствами, и луч претерпевает заданное оптическое преобразование;

·        луч претерпевает заданное оптическое преобразование (зеркальное или диффузное отражение, поглощение и т.д.) на одной из пересекаемых им поверхностей; можно также задать счетчик, позволяющий визуализировать только те лучи, данное преобразование с которыми произошло определенное число раз.

Элементарные события могут быть объединены не только чисто логическими операциями. Допускается временная последовательность элементарных событий, то есть, для того чтобы критерий был выполнен, одно событие или группа событий должно предшествовать другому событию или группе событий. Например, прохождение света через диафрагму оптической системы должно предшествовать зеркальному отражению от линзовой поверхности.

Далее применение различных типов построения критерия распространения луча рассматривается на примере анализа системы подсветки мобильного устройства, показанного на рис. 1 и 2.

Рис. 1. Система подсветки мобильного телефона. Пиктограммами L1-L6 

обозначены источники света.

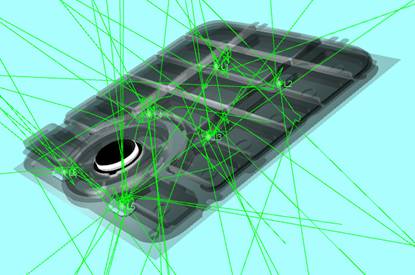
Рис. 2. Визуализация распространения лучей в системе без учета какого-либо критерия.

2.1. Простой критерий распространения лучей

Критерий первого типа, или простой критерий, представляет собой дерево, узлами которого являются логические операции «И», «ИЛИ», «НЕ» и исключающее «ИЛИ». Листьями дерева являются вышеперечисленные элементарные события. Таким образом, простой критерий представляет собой булеву формулу. Критерий отбирает только те лучи, история элементарных событий которых доставляет этой формуле истинное значение. Такие критерии можно использовать, когда нас интересует факт того, что некоторые события произошли или не произошли с визуализируемыми лучами, но не интересует последовательность, в которой эти события произошли.

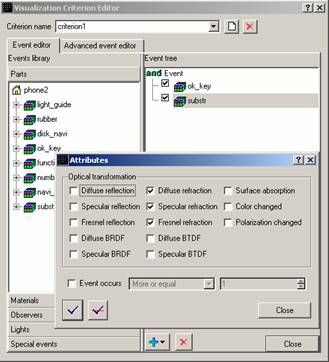
Рис. 3. Пример критерия первого типа.

Например, в рассматриваемой нами системе можно задать критерий, позволяющий визуализировать только те лучи, которые попали на центральную кнопку мобильного телефона и вышли через подложку системы. На рис. 3 показан интерфейс пользователя, позволяющий сформировать заданный критерий.

Рис. 4 демонстрирует результат применения данного критерия на примере визуализации хода лучей в оптической системе.

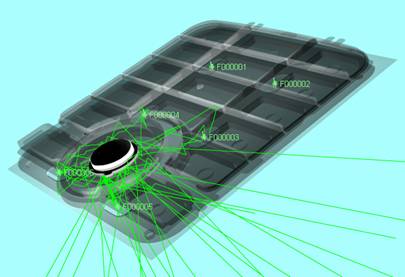
Рис. 4. Визуализация лучей, попавших на центральную кнопку и вышедших через подложку.

2.2. Критерий последовательности событий распространения луча

Критерий второго типа, или критерий с последовательностями во времени, предназначен для случаев, когда есть необходимость визуализировать только те лучи, с которыми заданные события произошли в заданном порядке. Такой критерий представляет собой дерево, корнем которого является операция предшествования. Левым и правым поддеревом корня являются критерии первого типа. Такой критерий считается выполненным для данной трассы луча, если выполняются оба его поддерева и все события из левого поддерева произошли раньше событий из правого поддерева.

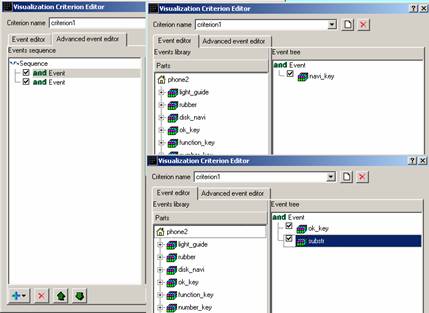
Рис. 5. Пример задания критерия второго типа. Слева показано дерево с операцией предшествования в корне, справа – его поддеревья.

Пример задания критерия второго типа в графическом интерфейсе пользователя представлен на рис. 5. Такой критерий позволяет визуализировать только те лучи, которые прежде, чем попасть на центральную кнопку и выйти через подложку, попали на диск вокруг центральной кнопки.

Результат визуализации лучей, полученных в результате применения данного критерия, представлен на рис. 6.

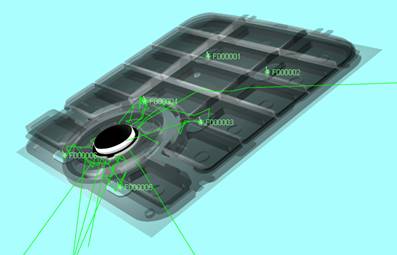
Рис. 6. Пример визуализации лучей с использованием критерия второго типа.

2.3. Составной критерий распространения лучей

Критерий третьего типа является обобщением критерия первого и второго типов. Такой критерий представляет собой булеву формулу, в узлах которой кроме обычных логических операций может быть определенная выше операция предшествования. То есть это булева формула, элементами которой являются не элементарные события, а деревья, объединенные операцией предшествования.

Рис.7. Пример задания критерия третьего типа.

Приведем пример критерия третьего типа: визуализируются лучи, которые прежде, чем попасть на центральную кнопку и выйти через подложку, попали на диск вокруг центральной кнопки ИЛИ сначала отразились от подложки, а потом вышли через верхнюю панель системы подсветки. Графический интерфейс пользователя, формирующий данный критерий, показан на рис. 7.

Результат визуализации лучей, полученных в результате применения составного критерия, представлен на рис.8.

Рис.8. Пример визуализации лучей с использованием критерия третьего типа.

2.4. Особенности применения критерия распространения луча для          визуализации его траектории и выходных световых характеристик

При моделировании сложных оптических систем траектория луча в оптической системе может оказаться слишком большой, а полная история распространения луча будет содержать информацию, избыточную для его визуализации. Кроме того, необходимо помнить, что визуализация хода луча это интерактивный процесс, который не требует высокой скорости трассировки, поскольку количество траекторий, одновременно представленных на экране, не будет превышать нескольких сотен (иначе они сливаются).

Исходя из этих требований, был реализован алгоритм повторной трассировки лучей. Суть метода заключатся в том, что при первичной трассировке лучей сохраняется только состояние датчика псевдослучайных чисел перед трассировкой луча и информация, которая необходима для проверки критерия (а именно – события, произошедшие с лучом). После первичной трассировки порции лучей, не удовлетворяющие критерию, отсеиваются, а лучи, удовлетворяющие критерию, трассируются повторно с сохранением  всей необходимой для визуализации информации (траектория лучей во время вторичной трассировки является такой же, как и во время первичной, благодаря свойству воспроизводимости используемого датчика псевдослучайных чисел). Далее информация о  вторично протрассированных  лучах передается модулю, визуализирующему ход лучей. Кроме визуализации траектории луча возможна дополнительная визуализация его хода в текстовом виде. То есть на каждом сегменте луча отображаются его координаты, направление, цвет, среда распространения, объект, который пересек луч, тип преобразования луча, состояние поляризации.

Приведенные выше примеры демонстрировали применение критерия распространения луча для визуализации траектории его распространения. Кроме того, критерии всех типов могут применяться для получения результатов оптического моделирования в виде пространственных (освещенность или яркость) или угловых (интенсивность) распределений световых характеристик на приемнике излучения. Принимая во внимание, что приемник излучения не обязан находиться в конце траектории луча, и проверка критерия на момент пересечения луча с приемником излучения невозможна, необходим специальный алгоритм – как применить критерий распространения луча к накоплению света на приемниках излучения. В данном случае применение повторной трассировки лучей неэффективно, поскольку такое решение снижает эффективность оптического моделирования в два раза.

Поэтому был разработан и реализован алгоритм временного накопления света на приемнике излучения. Его суть заключается в том, что каждый приемник излучения имеет временную область, которая может быть добавлена к постоянной, только если луч удовлетворяет критерию трассировки луча. Если нет, то эта временная область удаляется и формируется заново новым лучом. На рис. 9 представлено распределение освещенности на приемнике излучения, расположенного в верхней части рассматриваемой оптической системы, которое было получено без учета каких-либо критериев. На рис. 10 представлено распределение освещенности с учетом только тех лучей, которые на своем пути встретили центральную кнопку.

3. Использование визуального представления распространения света в практических приложениях проектирования оптических систем

В большинстве случаев для проектирования сложных оптических систем требуется не только анализ результирующих выходных оптических характеристик, но и анализ того, какие компоненты оптической системы и каким образом определяют эти характеристики. Наиболее подходящим решением в данном случае является визуализация выходных результатов моделирования или хода лучей в оптической системе, удовлетворяющих требуемому критерию. Следующие примеры иллюстрируют преимущества выбранного решения для различных типов оптических систем и задач оптического моделирования.

3.1. Анализ рассеянного света в оптических системах

Как известно, одно из  основных требований к качеству изображения, формируемого линзовыми системами, это отсутствие паразитного освещения. Как правило, паразитное освещение в оптических системах образуется либо в результате переотражения  света между поверхностями линз (блики), либо как результат диффузного рассеивания на деталях крепежа оптических элементов. Возможные источники формирования паразитного освещения показаны на рис. 11.

Для анализа блика на линзе, показанного на рис. 11 (а), использовался специальный критерий прохождения луча в оптической системе. Критерий состоял из трех последовательных событий – отражение луча от задней поверхности четвертой линзы, затем отражение от фронтальной поверхности четвертой линзы и, наконец, попадание на приемник излучения. Для анализа диффузного рассеивания на деталях крепежа, показанного на рис. 11 (б), использовался критерий, состоящий из двух событий – диффузного рассеивания на оправах 3-5 линз и попадания на приемник излучения.

Рис. 11 (а) и 11 (б)  демонстрируют как ход паразитных лучей в объективе, так и выходное распределение паразитной освещенности. Данные примеры показывают простейшие случаи анализа паразитного света. Гибкость и простота формирования критерия траектории луча позволяет производить анализ любых источников паразитного света, как составных (все блики всех порядков), так и индивидуальных (блик заданного порядка между заданными поверхностями).

            Рис. 11. Источники формирования паразитного освещения в линзовой системе:

                           (а) блик на линзе, (б) диффузное рассеивание на элементах крепежа.

3.2. Проектирование сложных зеркальных осветительных систем

Поскольку программы автоматического проектирования зеркальных осветительных систем используют упрощенные модели источников света, геометрия излучающей поверхности сводится к примитивной форме, как то точка, линия, цилиндр, сфера и т.п. Реальная форма поверхности источника света и ее оптические свойства при этом игнорируются. Зачастую источник света, как физическое тело, оказывает существенное влияние на распространение света в оптической системе и его воздействие на выходное распределение должно быть оценено дополнительно. Рис. 12 демонстрирует, каким образом реальный источник света  оказывает влияние на свет, отраженный рефлектором.

Для анализа света, захватываемого источником света, как показано на рис.      12 (б), использовался критерий, состоящий из двух событий – попадание луча на поверхность источника света и попадание на приемник излучения. В качестве приемника излучения использовался гониометрический приемник, который фиксировал выходное направление распространения света безотносительно к его пространственному распределению.

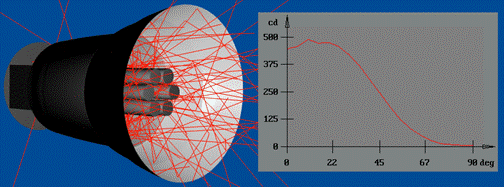
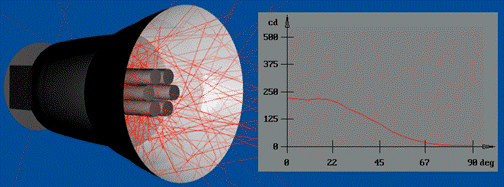
Рис. 12. Влияние источника света на распределение выходного излучения:

 (а) общее выходное распределение, (б) выходное распределение,

 сформированное светом, захваченным источником света.

Сравнительный анализ результатов, представленных на рис. 12 (а) и (б),  позволяет определить, какое влияние форма и оптические свойства поверхностей источника света оказывают на выходное угловое распределение.

3.3. Проектирование осветительных систем жидкокристаллических дисплеев

Системы подсветки жидкокристаллических дисплеев являются сложными оптическими устройствами, в которых уровень и распределение выходной яркости дисплея зависят от множества факторов – формы и распределения микроэлементов на поверхностях светопроводящей пластины, положения и параметров источников света, формы и оптических свойств отражателей, и т.п. При проектировании таких оптических систем необходимо знать, какой вклад в выходное распределение яркости вносит каждый элемент, и подобрать его оптимальные характеристики. На рис. 13 представлен пример проектирования оптической системы подсветки жидкокристаллического дисплея.

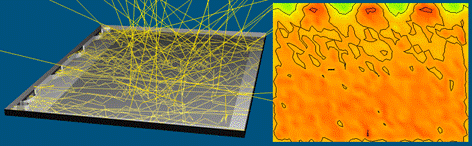
Рис. 13. Влияние нижнего рефлектора жидкокристаллического дисплея

 на эффективность системы подсветки: (а) зеркальные свойства нижнего

рефлектора, (б) диффузные свойства нижнего рефлектора.

В качестве объекта анализа системы подсветки использовались оптические свойства нижнего рефлектора. Был построен специальный критерий, который включал два события – отражение света от нижнего рефлектора и попадание света на выходной экран жидкокристаллического дисплея. На рис. 13 (а) показаны результаты моделирования, полученные при использовании зеркальных свойств рефлектора, а на рис. 13 (б) – диффузных свойств. В дальнейшем информация о влиянии оптических свойств нижнего рефлектора может оказаться полезной при выборе других компонентов оптической системы, например, распределения рассеивающих элементов.

3.4. Проектирование многоканальных осветительных систем

Многоканальные оптические системы характеризуются разделением пучка лучей на несколько независимых пучков, которые затем либо собираются на общем приемнике, либо расходятся на различные приемники. На рис. 14 представлен пример многоканальной осветительной системы контрольного канала измерительного прибора. В данном случае свет от источника света расходится по пяти каналам измерительного прибора, каждый из которых имеет собственный приемник. Использование различных критериев позволяет включать все каналы (рис. 14 (а)) или выбирать один (рис. 14 (б)).

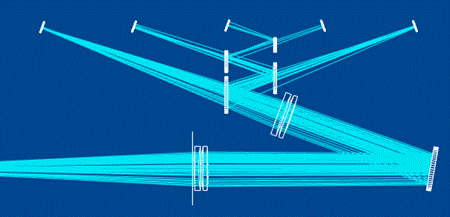
а)

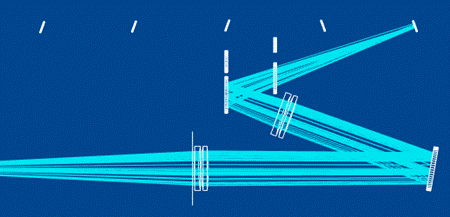
б)

  Рис. 14. Многоканальная оптическая система:

  (а) все каналы включены, (б) включен только один канал.

3.5. Анализ причин непонятного поведения выходного распределения света

В ряде случаев, особенно это касается сложных оптических систем, результат моделирования непонятен с точки зрения принципов функционирования оптического устройства.  На рис. 15 представлена торцевая система подсветки жидкокристаллического дисплея. В результате специфики конструкции данного прибора образуется пик яркости, показанный на рис. 15 (а), который локализован вблизи источника света. Причина возникновения этого пика яркости неясна и задача анализа заключается в нахождении специфики конструкции, вызывающей данный пик яркости. Для определения причин пика яркости использовался специальный критерий, показанный на рис. 15 (а), который фиксировал только те лучи, которые попадают в зону пика.

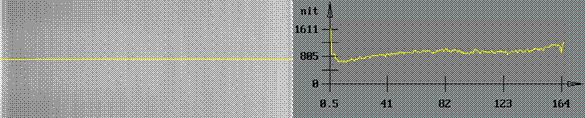
а)

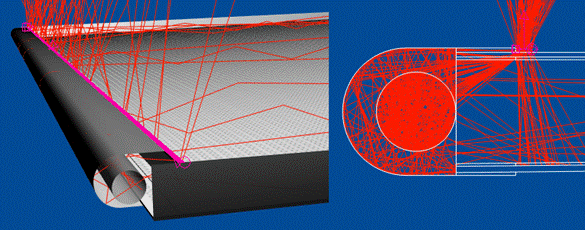
б)

   Рис. 15. Анализ причин пика яркости в системе подсветки жидкокристаллического дисплея:

 (а) общее распределение яркости, (б) анализ света попадающего в зону пика.

Очевидно, что использование средств визуализации хода луча совместно с его критерием позволяет выявить причину возникновения пика яркости, которой оказался оптический контакт светопроводящей пластины и рассеивающей пленки.

3.6. Анализ корректности модели оптической системы

Формирование цифровой модели сложной оптической системы всегда сопряжено с возможностью ошибки. Ошибка может появиться либо в геометрии модели, например, модель замкнутого объекта будет содержать разрывы, либо в задании положения объектов, например, один объект может оказаться внутри другого объекта, и т.п. Такие ошибки достаточно трудны для визуального обнаружения, особенно когда речь идет о сложных оптических системах. Поэтому для детектирования ошибок модели оптической системы удобно использовать критерий, содержащий событие «гибель луча в связи с некорректностью геометрии». Рис. 16 демонстрирует использование критерия для анализа некорректности модели жидкокристаллического дисплея.

Рис. 16. Детектирование некорректности задания геометрической модели

жидкокристаллического дисплея.

Визуализация хода луча совместно с критерием некорректности геометрии показала источник проблемы – незамкнутость заднего торца жидкокристаллического дисплея.

3.7. Анализ вклада определенных объектов оптической системы в общий уровень выходного сигнала

Программный модуль визуализации хода лучей содержит в себе ряд дополнительных возможностей. Наиболее полезной возможностью, связанной с анализом и проектированием оптических систем, является лучевая статистика. Лучевая статистика позволяет оценить, какой процент лучей, трассируемых в оптической системе, удовлетворяет заданному критерию. Такая статистика удобна при анализе эффективности оптической системы и для определения вклада отдельных ее компонентов в общий уровень выходного сигнала.

Лучевая статистика позволяет оценить общую эффективность оптической системы, процент лучей, погибающих в ней из-за некорректности ее цифровой модели, оценить долю паразитного света в оптической системе, определить влияние оптических свойств отельных элементов на уровень выходного сигнала и т.п. Поэтому лучевая статистика совместно с критерием траектории луча является незаменимым инструментом проектирования сложных оптических систем.

4. Заключение

Значимость визуального представления результатов моделирования распространения света в оптической системе не вызывает сомнений. Большинство существующих программных систем оптического моделирования, таких как LightTools, TracePro, ASAP и SPEOS, обладают данными возможностями. Однако ни одна из этих систем не обладает развитыми средствами построения критериев распространения лучей в оптической системе и не позволяет применять различные критерии для разных приемников излучения и визуализации хода лучей. Интеграция разработанного критерия распространения лучей в систему оптического моделирования SPECTER показала его эффективность при проектировании сложных оптических систем, таких как линзовые и зеркально линзовые объективы и осветительные системы, системы подсветки жидкокристаллических дисплеев и др.

Благодарности

Авторы выражают свою признательность А.Д. Жданову и А.С. Потемкину за помощь в написании программы, а также В.Г. Соколову и А.А. Гарбулю за предоставленные примеры.

Литература

[1] Edward A. Kopylov, Kirill A. Dmitriev.  Light propagation visualization as a tool for 3D scene analysis in lighting design // Computers & Graphics, vol.24, no.1, pp.31-39, 2000.

[2] E. Wernert. A unified environment for presenting, developing and analyzing graphics algorithms. / In: Computer Graphics, vol. 31, no. 3, pp. 26-28, August 1997.

[3] R. Cook, T. Porter, L. Carpenter. Distributed ray tracing. / In: Computer Graphics,

SIGGRAPH ’84 Proceedings, pp.137-145, 1984.

[4] А.Г. Волобой, В.А. Галактионов, К.А. Дмитриев, Э.А. Копылов. Двунаправленная трассировка лучей для интегрирования освещенности методом квази- Монте Карло // "Программирование",  № 5, 2004, с. 25-34.

[5] M.Pharr, G.Humphreys Physically Based Rendering. From theory to implementation // Morgan Kaufmann, 2004.

[6] Баяковский Ю.М., Галактионов В.А. О некоторых фундаментальных проблемах компьютерной (машинной) графики // "Информационные технологии и вычислительные системы", № 4, 2004, стр. 3-24.

[7] SPECTER – Computer-Based Optical Modeling and Design System. http://www.integra.jp/eng/products/specter/index.htm

[8]. I. Bratko. Prolog Programming for Artificial Intelligence. / Addison Wesley, London (1990).