Методика расчета параметров маневров встречи КА с орбитальной станцией
|
 |
Рис. 1
Рис. 2
Если все углы приложения импульсов
лежат с одной стороны от направления φz (рис. 2), то брать надо не две
ближайшие, а одну ближайшую и одну самую отдаленную составляющие импульсов
скорости. Этому решению соответствует ломаная АВК на рис. 2. Решению с использованием двух других составляющих
соответствует ломаная АDК, длина которой очевидно больше длины
ломаной АВК. Таким образом,
определены наименее эффективные составляющие, которые лучше брать в качестве
независимых переменных при минимизации функционала W, а в
качестве начальной точки процесса минимизации берутся их нулевые значения.
Используя эту же оценку
эффективности боковых составляющих можно вообще избавиться от минимизации в их
пространстве, оставив две наиболее эффективные составляющие.
Полезным является еще один вывод,
который следует из рассмотренных выше примеров. Для коррекции боковых
отклонений эффективней использовать наборы углов приложения импульсов скорости,
в которых присутствуют углы лежащие по разные стороны от направления φz.
Поскольку в процессе обеспечения
полетов реальных КА приходится решать задачи с различным числом импульсов
скорости и с различными ограничениями, программное обеспечение должно быть
достаточно универсальным.
Для обеспечения этой
универсальности, если возникает необходимость в минимизации в пространстве
составляющих импульсов скорости, применяется следующая схема вычислений
При помощи матрицы J задаем, какие отклонения необходимо корректировать
(от полного вектора отклонений D,
который используется в системе (1), переходим, если требуется, к вектору меньшей
размерности Dk=
JD). В соответствующей шкале ставим
признаки, какие составляющие импульсов скорости, обозначим их DVk, будут использоваться для
решения задачи. Формируется матрица влияния Аk этих составляющих импульсов скорости
на выделенные отклонения. Ограничения (1) принимают вид
АkDVk=Dк
(4)
Ещё в одной шкале указывается, какие
из составляющих импульсов скорости являются независимыми переменными, в
пространстве которых будет проводиться оптимизация, их обозначим DVi, остальные составляющие будут
зависимыми переменными, их обозначим DVd (DVк=DVi+DVd).
На соответствующие части можно
разбить и матрицу Аk, тогда ограничение (4) принимает вид
АiDVi+
АdDVd=
Dк (5)
Из системы (5.5) можно найти DVd
DVd = АDVi +![]() (6)
(6)
где А=-![]() Аi ,
Аi ,
![]() =
=![]() Dк.
Dк.
Таким
образом, перешли к безусловной минимизации W в
пространстве DVi
W=W(DVi).
Необходимые для
минимизации градиентными методами частные производные W по независимым переменным вычисляются по аналогичной
схеме с использованием информации из тех же шкал. Основой служат вычисляемые по
аналитическим формулам производные по всем используемым составляющим импульсов
скорости.
Если требуется сделать нулевыми
только часть отклонений (Dк), то остальные отклонения (Dp=D-Dк) добавляются в минимизируемый
функционал в виде штрафов
 ,
,
здесь G - заданная матрица. Например, можно
требовать точного выхода в окрестность орбитальной станции, а отклонения по
скоростям не обязательно должны быть нулевыми, тогда за счет штрафов их можно
несколько уменьшить. Такая ситуация обычно возникает, когда число используемых
составляющих импульсов скорости меньше числа терминальных ограничений.
Следует отметить, что в качестве
метода минимизации в пространстве составляющих импульсов целесообразно
использовать метод сопряженных градиентов, эффективность которого для данного
класса задач примерно на 10% выше эффективности метода наискорейшего спуска.
4. ПОИСК МИНИМУМА В ПРОСТРАНСТВЕ
УГЛОВ ПРИЛОЖЕНИЯ
ИМПУЛЬСОВ СКОРОСТИ
Минимизация в пространстве углов
приложения импульсов скорости (на множестве F) является
более сложной из-за того, что область минимизации может состоять из нескольких
отдельных областей, из-за наличия локальных минимумов и из-за того, что само
значение функционала получается в результате минимизации в пространстве
составляющих импульсов скорости. По этим причинам трудно применить какой-нибудь
эффективный численный метод и обычно используют простой перебор точек из
разрешенных интервалов, что позволяет найти глобальный минимум функционала W, но требует значительных затрат машинного времени.
Желание ускорить процесс
поиска глобального минимума заставляет искать возможность сократить число точек
множества F, для которых проводится вычисление Wm. Для этого можно одновременно использовать два метода.
Первый – геометрический, позволяющий очень быстро и просто исключить заведомо
не оптимальные точки для перелета между компланарными орбитами. Второй метод,
основанный на использовании оценки снизу величины Wm, применяется для отсеивания точек, не
оптимальных для изменения плоскости орбиты.
Для объяснения идеи
первого метода на плоскости составляющих вектора эксцентриситета построим
окружности, имеющие радиусы R1 и R2 (рис.3), соответствующие суммам трансверсальных
составляющих импульсов скорости первого и второго интервалов маневрирования (R1=DVtI, R2=DVtII) [3]. Центры окружностей расположены
в точках А(0,0) и К(Dех,Dеу). Определить величины DVtI, DVtII можно по формулам
 ,
,
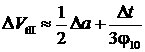 ,
,
где j10 – произвольная точка, принадлежащая
первому интервалу маневрирования. Как было показано в [3], для оптимального
решения задачи многовитковой встречи точка, соответствующая вектору
эксцентриситета орбиты ожидания (орбиты, получающейся после реализации импульсов
скорости первого интервала маневрирования), должна принадлежать области G -области пересечения кругов, имеющих
радиусы R1 и R2, приведенной на рисунке 3.

Рис.3
Таким образом, нецелесообразно использовать углы приложения импульсов
скорости первого интервала маневрирования, при которых точка, соответствующая
вектору эксцентриситета орбиты ожидания, будет принадлежать области I или II.
Область I это полуплоскость, образованная прямой, проходящей через точки С и В
(СВ перпендикулярна АК) и
не содержащая область G (рис. 3). Область II это
полуплоскость, образованная прямой, проходящей через точки D и Е (DЕ перпендикулярна АК), и также не содержащая область G.
Таким образом, набор
точек из множеств F отсеивается, если
φе+φI<φ1<φе+2p-φI и одновременно φе+φI<φ2<φе+2p-φI, или когда 0<φ3<φе+p-φII или φе+p+φII<φ3< 2p и
одновременно 0<φ4<φе+p-φII или φе+p+φII<φ4< 2pI, где
 ,
, 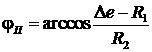 ,
,  .
.
Напомним, что углы φ1,
φ2, φ3, φ4 отрицательные,
поэтому перед проверкой этих условий их надо путем увеличения на нужную
величину 2pk привести к значению из диапазона [0,2p].
Набор точек из
пространства F также отсеивается, если углы приложения
импульсов скорости первого интервала лежат выше прямой АК, а углы приложения импульсов скорости второго интервала лежат
ниже прямой АК или наоборот.
Очевидно, что при таких углах точка, соответствующая вектору эксцентриситета
орбиты ожидания, также не будет принадлежать области G.

Рис.4
Пример решения, которое
должно быть исключено по этому критерию (вектору эксцентриситета орбиты
ожидания соответствует точка С),
приведен на рис. 4. Импульсам скорости этого решения соответствуют отрезки АВ, ВС,
СD, DК. Углы приложения импульсов скорости
первого интервала φ1, φ2
лежат выше прямой АК, а углы
приложения импульсов скорости второго интервала φ3, φ4 лежат ниже прямой АК.
Таким образом, для существования
оптимального решения не допустимо, чтобы одновременно было выполнено условие φе<φ1,φ2<φе+p, и φе+p<φ3,φ4<2p или
0<φ3,φ4<φе или наоборот φе<φ3,φ4<φе+p, и φе+p<φ1,φ2<2p или
0<φ1,φ2<φе.
Можно использовать и
другие геометрические построения, сокращающие ещё большее число точек множества
F, для которых проводится численная
оптимизация, но необходимо помнить, что алгоритм должен быть достаточно
простым, чтобы давать выигрыш по времени по сравнению с вычислением Wm.
Если окружности не
пересекаются, то точка, соответствующая вектору эксцентриситета орбиты
ожидания, должна принадлежать области D (рис.5).

Рис. 5
Используя алгоритм, аналогичный приведенному выше, также можно при переборе исключить значительное
число возможных точек множества F.
На втором этапе
происходит отсеивание точек из областей G или D, для которых решение компланарной
задачи встречи оптимально, однако имеются большие затраты на коррекцию
положения плоскости орбиты. Для отсеивания применяется алгоритм [4],
использующий оценку снизу минимизируемого функционала W и Lπτ последовательность [5] для перебора
точек из множества F. Аналитическая оценка снизу Wn, вычисление которой требует значительно меньше времени, чем
численное определение Wm, позволяет значительно сократить
общее время решения задачи. Если величина Wn больше чем минимальное значение
функционала W, найденное к этому
моменту, то численный поиск минимума в пространстве составляющих импульсов
скорости (определение Wm) для данного набора углов приложения
импульсов скорости можно не проводить.
Поясним эту процедуру на
примере, изображенном на рисунке 6. На этом рисунке значение функционала Wm показано сплошной линией, значение оценки снизу Wn - точечной. Необходимо найти минимум функционала Wm на интервале АF. Перебор точек интервала происходит с постоянным
шагом от точки А к точке F. До точки C значение Wm будет вычисляться для всех точек.
Начиная с точки С значение Wn будет больше значения Wm в точке В и все точки на интервале СD будут исключены (значение Wm для них вычисляться не будет). При
дальнейшем переборе аналогичным образом будут отброшены и точки на интервале ЕF.

Рис.6
В качестве оценки снизу для
непересекающихся орбит можно использовать величину
Wn = ![]() , (7)
, (7)
а для пересекающихся орбит величину
Wn = ![]() ,
(8)
,
(8)
где
∆а, ∆е –разность больших полуосей орбит и модуль разности их векторов
эксцентриситетов, ∆Vzi , ∆Vzk – две наиболее эффективные боковые
составляющие импульсов скорости, процедура определения которых была описана
выше.
Точки Lπτ последовательности были выбраны для перебора точек из
множества F потому,
что они позволяют наиболее эффективно использовать возможности величины Wn. Замечательным свойством Lπτ последовательности является то, что каждые 2n её точек равномерно распределены в
единичном кубе размерности N [5]. Множество F можно вписать в многомерный
прямоугольник L=L1*L2*...*LN, где Li отрезок минимальной длины, содержащий
множество Fi. Если мы возьмем 2n точек Lπτ последовательности, то из её свойств следует, что для
i-ой переменной в каждой ![]() части отрезка Li будет находиться точка Lπτ последовательности. Таким образом,
для каждого n точки последовательности равномерно
распределены по отрезку Li, а при росте n плотность распределения увеличивается.
части отрезка Li будет находиться точка Lπτ последовательности. Таким образом,
для каждого n точки последовательности равномерно
распределены по отрезку Li, а при росте n плотность распределения увеличивается.
То, что просмотр отрезка
осуществляется не с мелким постоянным шагом, начиная с какой-то его части, а
просматривается весь отрезок с каждый раз всё более уменьшающимся шагом,
позволяет быстро определить районы существования локальных минимумов. Таким
образом, текущее значение Wn будет сравниваться со значением функционала W близким к глобальному минимуму, и большее число точек будет
исключено из рассмотрения.
Эта возможность показана на рис. 7. Пусть после просмотра
первых четырех точек (они обозначены в том порядке, в каком их выдает Lπτ последовательность), равномерно распределенных
на интервале АF, в четвертой точке было вычислено минимальное текущее
значение функционала Wm4. Для всех последующих точек текущее значение Wn будет сравниваться с Wm4 и как минимум будут исключены все
точки на интервалах АВ, СD и EF.
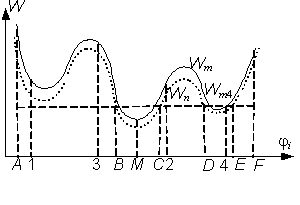
Рис.7
Если в процессе последующего
перебора одна из точек попадет в окрестность глобального минимума (т.M), это позволит в дальнейшем не вычислять Wm для ещё большего количества точек.
5. ИСПОЛЬЗОВАНИЕ ГРАФИЧЕСКОГО ДИАЛОГА
С ЗАДАЧЕЙ
Численный метод весьма универсален,
а в случае, когда число используемых составляющих импульсов совпадает с числом
терминальных ограничений, достаточно быстрый и очень надежный. Существенным его
недостатком является то, что нет объяснения, почему получили именно такое
решение, и непонятно, как будет меняться решение, например, при учете
дополнительных ограничений. Используя только численные методы, трудно выбрать
схему маневрирования, т.е. определить какое минимальное число импульсов
скорости достаточно использовать для решения задачи и в каких местах их
необходимо прикладывать.
Чтобы устранить эти недостатки можно организовать графический диалог
с задачей. Впервые графический диалог был использован Р.К.Казаковой и
А.К.Платоновым [8] при определении параметров маневров для межпланетных
перелетов, и доказал свою высокую эффективность. В процессе диалога с задачей
на экране монитора указывались моменты приложения импульсов скорости на
начальной и конечной орбитах, параметры маневров определялись с помощью решения
задачи Ламберта.
Для данной задачи импульсы скорости
удобно изображать на плоскости составляющих вектора эксцентриситета. На экране
монитора рисуется ломаная линия, соответствующая импульсам скорости найденного
численным методом решения. Рисуются также окружности, соответствующие сумме
трансверсальных составляющих импульсов скорости каждого из интервалов
маневрирования. Взаимное положение ломаной и окружностей позволяет судить,
например, насколько устойчиво решение к ошибкам знания орбит и исполнения
импульсов (насколько глубоко точка, соответствующая вектору эксцентриситета
орбиты ожидания, находится внутри области пересечения окружностей). Можно
оценить, насколько углы приложения импульсов скорости, принадлежащих первому
интервалу маневрирования, близки к углам оптимальной коррекции плоскости орбит
(это направление также изображается на экране) и т.д. На экране существует
возможность задать графически или числами новые значения каждого из углов
приложения импульсов скорости и вернуться после этого в задачу, для определения
новых значений величин импульсов скорости. Таким образом, можно учитывать
дополнительные ограничения на место приложения и величины импульсов скорости,
сокращать число используемых импульсов и т.д. Использование графического
диалога позволяет объединить возможности численного и аналитического методов.
Он особенно эффективен на стадии выбора схемы маневрирования, а также в случае
возникновения нештатных ситуаций в полете. Если полет проходит штатно и
используется давно выбранная и проверенная схема маневрирования, то можно
обойтись только численным методом, т.к. необходимо просто определить параметры
оптимальных маневров.
6. ИТЕРАЦИОННОЕ УТОЧНЕНИЕ ПАРАМЕТРОВ
МАНЕВРОВ
В сформулированной в первом
параграфе задаче используются довольно простые уравнения движения, не
учитываются нецентральность гравитационного поля, влияние атмосферы, время
работы двигателей КА и т.д. Это приводит к тому, что реальная точность
формирования конечной орбиты будет недостаточной. Чтобы решить задачу с
заданной точностью можно использовать итерационную схему [2], [6].
1. В начале очередной итерации
решается “приближенная” задача: при принятых ранее упрощающих предположениях
определяются параметры импульсов скорости, обеспечивающих формирование
“целевой” орбиты (на первой итерации “целевая” орбита совпадает с конечной
орбитой).
2. Затем, с учетом рассчитанных
импульсов скорости и всех необходимых возмущений, осуществляется “точное”
прогнозирование движения КА и находятся параметры сформированной орбиты.
3. Вычисляются отклонения
параметров сформированной орбиты от соответствующих параметров конечной орбиты.
4. Если отклонения превышают
допустимые, то параметры “целевой” орбиты меняются на величину вычисленных
отклонений, и проводится следующая итерация.
Процедура заканчивается, когда терминальные условия выполнены с заданной
точностью.
Ниже приведена
блок-схема этой итерационной процедуры.
Для “точного”
прогнозирования используются, как правило, численное и/или высокоточное
численно-аналитическое интегрирование. Возможно, на разных итерациях
использовать разные методы прогноза, но точность прогноза должна расти с ростом
номера текущей итерации.
При численном интегрировании
учитываются влияние нецентральности гравитационного поля, атмосферы, светового
давления и т.д., моделируется работа двигателей КА, поэтому, не смотря на то,
что параметры маневров и находятся на каждой итерации с использованием
простейшей модели движения, но в результате использования итерационной
процедуры они обеспечивают выход на конечную орбиту с требуемой точностью.
Заметим, что возможности такой схемы
решения весьма велики. Отклонения каждой из орбит от опорной круговой могут
достигать несколько сотен километров, а протяженность каждого из маневров
составлять два-три десятка градусов по аргументу широты, что весьма далеко от
первоначального импульсного предположения.
Конечно, возникает вопрос о строгой
оптимальности найденного решения, но, как правило, вопрос строгой оптимальности
еще более актуален для решений найденных другими методами.
Определение
элементов начальной орбиты
![]() 0 и элементов конечной орбиты
0 и элементов конечной орбиты ![]() f в
точке встречи
f в
точке встречи


Проверка выполнения
терминаль-ных условий
![]()
![]() да
да
![]()
нет

7. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
В этом параграфе рассматриваются
задачи определения параметров оптимальных маневров, которые решались в баллистическом
центре ИПМ им. М.В. Келдыша РАН при баллистико-навигационном обеспечении полета
КА «Союз ТМ-30».
В момент выхода на орбиту КА «Союз
ТМ-30» разность в угловом положении корабля и станции (разность фаз) составляла
Du»1970.
Перед первым интервалом
маневрирования решалась четырехимпульсная задача. При этом предполагалось, что
на 17 витке прикладывается фиксированный импульс величиной 2м/с.
Исходные данные и результаты расчета
четырехимпульсной задачи представлены в примере 1. В первой части примера
приведены начальные условия обоих аппаратов (в гринвической вращающейся системе
координат). Заданы F и ap
динамической атмосферы, а также, сколько гармоник разложения гравитационного
потенциала Земли будет учитываться при численном интегрировании уравнений
движения. Номером витка и аргументом широты задана прицельная точка, а также
приведено время её достижения пассивным аппаратом. Заданы прицельный вектор и
точности выполнения терминальных условий. Отличные от нуля значения
диагональных элементов матриц J и Jz
указывают, отклонения каких параметров необходимо корректировать.
Во второй части примера приведены
разрешенные для приложения импульсов скорости интервалы маневрирования (они
заданы номером витка, аргументом широты правой и левой границ) и шаги перебора
точек из этих интервалов. Отметим, что углы приложения третьего и четвертого
импульсов скорости фиксированы за виток и за пол витка до точки встречи. В
массиве VrVtVz указано, какие составляющие
импульсов скорости можно использовать для решения задачи (первая позиция
соответствует Vr, вторая - Vt, третья - Vz, «1» в соответствующей позиции
показывает, что эту составляющую надо использовать, «0» – не надо). В следующей
строке определяется, в какой системе координат фиксируется ориентация ДУ во
время реализации соответствующего маневра (0-инерциальная стабилизация,
1-орбитальная стабилизация). Эта информация указывается для каждого импульса
скорости отдельно, поскольку иногда ориентация импульсов скорости на разных
интервалах маневрирования может фиксироваться в разных системах координат.
Приводятся также ограничения на минимальную и максимальную величины импульсов
скорости, и на минимальное угловое расстояние между ними. В последней строке
приводятся значения коэффициентов ki для функционала W
В третьей части примера приведена
информация о фиксированных импульсах скорости.
В четвертой части представлены
полученные на последней итерации результаты определения параметров маневров
(составляющие импульсов скорости и аргументы широты точек их приложения). В
следующей строке указано сколько потребовалось итераций для решения задачи,
приведены значения функционала W, затрат суммарной характеристической
скорости и суммы боковых составляющих импульсов скорости, а также общее число
рассмотренных точек пространства F, и число точек отсеянных по
различным критериям.
В пятой части дается информация о
маневрах, полученная после численного интегрирования. Приводится время
включения и время работы ДУ, величина и ориентация импульсов скорости.
Поскольку ориентация ДУ фиксировалась в инерциальной системе координат, время
включения и ориентация ДУ выбирались таким образом, чтобы на расчетную точку
приложения импульса скорости приходилась середина активного участка, а
ориентация ДУ в этот момент совпадала с расчетной ориентацией импульсов
скорости. Этим объясняется наличие небольших отрицательных тангажей, величина
которых пропорциональна величине импульсов, хотя радиальные составляющие
импульсов не использовались. Этим объясняется и то, что аргументы широты
моментов включения ДУ (последний столбец) немного меньше расчетных моментов
приложения импульсов. В этой части примера приведены также отклонения корабля
от станции.
В конце примера приведены элементы
орбиты станции (ДОС) и элементы орбиты активного КА в начальный момент и после
каждого из импульсов.
Пример
1
ДОС КА Параметры атмосферы Грав. поле
виток
782. 3. F0=125.0
AP=
12.0 Ngarm=8.
дата 06.04.00 04.04.00 прицельная точка:
время
85139.26 104719.62 виток
аргм. шир.(гр) дата время
X 3.159596 5.570846 33. 344.80
06.04.00 90048.42
Y(км) -4.262639
-3.503213
приц. вектор:
Z -4.110163 .0 R, Vr, Vn, N, Z, Vz (км,м/с)
Vx 6.286519 2.291193 0. 0.
-12.5 0. 0.
0.
Vy(км/с) 1.022838
3.694669 точности: R,Vr,Vn,N,Z,Vz
(км,м/с)
Vz 3.774388 6.110578 .100
.050 .050 .500
.100 .050
S .0390 .0340 диаг. матрицы J=1. 1. 1. 1. Jz =1. 1.
интервалы маневрирования
N
импульса
1 2 3 4
виток начала интервала 3 3
32 33
аргм. широты левой границы (град) 200. 200.
344.8 164.8
аргм. широты правой границы (град) 440. 440.
344.8 164.8
шаг перебора интервала (град) 3.0 3.0
0. 0.
используемые составл-е импульса (VrVtVz) 011
011 010 010
тип стабилизации ДУ (0-инерц.,
1-орбитальн.) 0. 0.
0. 0.
огран-е на миним-ю величину импульса .5 .5
.5 .5
огран-е на максим-ю величину импульса 60. 60.
60. 60.
огр-е на мин-е раст-е между имп-сами
(град) 120. 120.
120. 120.
значения коэффициентов K .007 .007
0. 0.
фиксированные импульсы:
N
имп. виток арг.шир.(U) dV(м/с)
курс тангаж
3 17. 344.8 2. 0. 0.
Приближенное решение: составл-е имп-в и их
углы приложения
dVi(
Виток арг. шир.: 3. 263.
3. 437. 32.
344.8 33.
164.8
Nit=5. W=129.70
dVsum= 64.71 dVzsum= 16.42
Nall=821. NdV=134.
N
дата время
dV
курс танг. T(с) вит
арг.шир.
1
20000404. 115124.0 23.90
27.26 -1.94 56.6
3. 261.06
2
20000404. 123445.1 12.14
333.20 -.97 28.6
3. 436.03
3
20000405. 90615.8 2.00
0. 0. 4.7
17. 344.80
4
20000406. 73028.1 6.29
0. -.49 14.7
32. 344.31
5
20000406. 81501.2 22.38
0. -1.74 52.2
33. 163.06
Отклонения от станции: км, м/сек
R=
-0.001 Vr= .008
Vn=
-12.499 N= -.046
Z=
.0 Vz= 0.
Вит.
U Hmin
Umin Hmax Umax
w I Omg e
782
344. 329.7 7.9
341.6 308.7 41.6
51.6687 117.6062 .00082
3. 360. 192.0
61.2 238. 264.8
71.5 51.6920 130.1112 .00369
3. 264. 237.7
261.1 264.3 86.4 258.8
51.6391 129.7626 .00135
4. 78. 254.6
10.8 274.7
268.8 88.9 51.6315 129.5567 .00022
17.
345. 253.1 7.9
276.0 256.2 10.5
51.6690 123.9449 .00152
32.
345. 253.8 5.4
285.5 185.8 357.7
51.6675 117.9373 .00311
33.
166. 285.1 163.1
337.4 305.7 152.3 51.6688 117.7708 .00447
Приц-я точка: высота (км)=332.6 широта, долгота
(град)= -11.9 332.4
После реализации на третьем и
четвертом витках двух первых из рассчитанных импульсов скорости и определения
орбиты по измерениям на 13-15 витках решается трехимпульсная задача. При этом
определяются параметры маневра на 17 витке и параметры маневров на последнем
интервале маневрирования. Применение этого вначале фиксированного, а затем
уточняемого маневра на 17 витке позволяет компенсировать ошибки реализации маневров
первого интервала маневрирования. Исходные данные для решения трехимпульсной
задачи и рассчитанные параметры маневров приведены в примере 2.
После исполнения маневра на 17 витке
и последующего определения орбиты перед последним интервалом маневрирования на
31-32 витках решается двухимпульсная задача. Исходные данные для её решения и
рассчитанные параметры маневров приведены в примере 3.
Пример
2
ДОС АКА Параметры атмосферы Грв. поле
виток
782. 15. F0=125.0
AP=
12.0 Ngarm=8.
дата 06.04.00 05.04.00 прицельная точка:
время
85137.89 44135.78 виток
аргм. шир.(гр) дата время
X 3.160009 3.866979 33.
344.20 06.04.00 90037.94
Y(км) -4.262298
5.393846
приц. вектор:
Z -4.110167 .0 R, Vr, Vn, N, Z, Vz (км,м/с)
Vx 6.286416 -3.518402 0. 0.
-12.5 0. 0.
0.
Vy(км/с) 1.023499
2.514312 точности: R,Vr,Vn,N,Z,Vz
(км,м/с)
Vz 3.774374 6.081848 .100
.050 .050 .500
.100 .050
S .0390 .031559 диаг. матрицы J=1. 1. 1. 1. Jz=1. 1.
интервалы маневрирования
N
импульса
1 2 3
виток начала интервала 17
32 33
аргм. широты левой границы (град) 164. 344.2
164.2
аргм. широты правой границы (град) 410. 344.2
164.2
шаг перебора интервала (град) 1.0 0.
0.
используемые составл-е импульса (VrVtVz) 011
010 010
тип стабилизации ДУ (0-инерц.,
1-орбитальн.) 0. 0.
0.
огран-е на миним-ю величину импульса .5 1.9
1.9
огран-е на максим-ю величину импульса 60.
60. 60.
огр-е на мин-е раст-е между имп-сами
(град) 120. 120.
120.
значения коэффициентов K .007 0.
0.
Приближенное решение: составл-е имп-в и их
углы приложения
dVi(Vr,Vn,Vz): 0. .61
0. 0. 7.87
0. 0. 21.47
0.
Виток арг. шир. (U):
17. 349.0 32.
344.2 33. 164.2
Nit=
5. W= 29.95 dVsum= 29.95 dVzsum= .00
Nall= 248.
дата время dV
курс танг. T(с) вит
арг.шир.
1
20000405. 90737.9 .608
0. .11 1.4
17. 348.95
2
20000406. 73014.9 7.868
0. -.62 18.4
32. 343.5
3
20000406. 81452.0 21.471
0. -1.66 49.9
33. 162.54
Отклонения от станции: (км, м/сек)
R=
0. Vr= 0. Vn= -12.500
N= 0. Z= -.402 Vz= .052
Rev U Hmin
Umin Hmax Umax w I Omg e
782. 344.2
329.6 7.9 341.5
308.7 41.93 51.6685
117.6067 .00081
15. 0. 257.5
160.9 274.7 271.3 45.32
51.6695 124.9542 .00120
17.
349.0 255.8 13.3
275.4 270.3 29.49
51.6715 123.9506 .00107
32.
344.8 256.9 4.9
285.5 135.3 357.44
51.6686 117.9417 .00285
33.
165.9 285.1 165.9 337.3
305.0 152.20 51.6699
117.7753 .00446
Приц-я точка: высота (км)=332.7 широта, долгота
(град)= -12.4 332.1
Пример
3
ДОС АКА Параметры атмосферы Грв. поле
виток
782. 30. F0=125.0
AP=
12.0 Ngarm=8.
дата 06.04.00 06.04.00 прицельная точка:
время
84937.62 30537.89 виток
аргм. шир.(гр) дата время
X 2.379805 2.004973 33. 344.20
06.04.00 90037.64
Y(км) -4.351406
6.325135
приц. вектор:
Z -4.522517 0. R, Vr, Vn, N, Z, Vz (км,м/с)
Vx 6.709404 -4.125250 0. 0.
-14.54 0. 0.17
0.
Vy(км/с) .459303
1.300320 точности: R,Vr,Vn,N,Z,Vz
(км,м/с)
Vz 3.089667 6.083085 .100
.050 .050 .500
.100 .050
S .0390 .031063 диаг. матрицы J=1. 1. 1. 1. Jz =1. 1.
интервалы маневрирования
N
импульса
1 2
виток начала интервала
32 33
аргм. широты левой границы (град) 284.2 104.2
аргм. широты правой границы (град) 404.2 224.2
шаг перебора интервала (град) 3.0 3.0
используемые составл-е импульса (VrVtVz) 111 111
тип стабилизации ДУ (0-инерц.,
1-орбитальн.) 0. 0.
огран-е на миним-ю величину импульса .5 .5
огран-е на максим-ю величину импульса 60. 60.
огр-е на мин-е раст-е между имп-сами
(град) 120. 120.
значения коэффициентов K
.007 .007
Приближенное решение: составл-е имп-в и их
углы приложения
dVi(Vr,Vn,Vz): -2.15 5.78
-2.19 2.36 21.50
-2.29
Виток
арг. шир. (U): 32.
323.2 33. 164.2
Nit=
3. W= 29.17 dVsum= 28.30 dVzsum= 4.48 Nall= 1410.
N дата время dV курс
танг. T(с)
вит арг.шир.
1
20000406. 72513.7 6.545
20.75 -19.15 15.3
32. 323.20
2
20000406. 81518.6 21.753
6.09 6.24 50.6
33. 164.20
Отклонения от станции: (км, м/сек)
R=
-.001 Vr= .001 Vn= -14.54 N= .002
Z= .170 Vz= 0.
Rev U Hmin
Umin Hmax Umax w
I Omg e
782. 344.2
330.6 360.0 343.6 300.8
44.95 51.6680 117.6063
.00078
30.
0. 256.2 10.0 274.6
271.3 42.31 51.6707
118.9471 .00134
32.
324.2 257.5 4.4
279.7 114.9 351.86 51.6715
117.9378 .00166
33.
167.6 277.7 164.2 337.0
306.8 153.62 51.6683 117.7690
.00506
Приц-я точка: высота (км)=333. широта, долгота
(град)= -12.4 332.12
Для приведенной в примере 1
четырехимпульсной задачи проиллюстрируем возможности графического диалога для
анализа и изменения получаемого решения. На рисунке 8 изображена картинка,
которую оператор видит на экране монитора, после решения задачи на итерации с заданным
номером (в данном случае после пятой итерации).


Рис.8
Рис.9
Поскольку
углы приложения третьего и четвертого импульсов скорости фиксированы за p и 2p до
точки встречи, отрезок LM, с которого импульсами скорости второго
интервала маневрирования можно перейти в конечную точку К, параллелен оси ех
и проходит через точку К. Направлению
оптимальной коррекции плоскости орбиты соответствует пунктирная линия, проведенная
через точку A
под
углом jz к оси ех. Решению задачи
(трансверсальным составляющим импульсов скорости) соответствует ломаная ABCDK. Можно
видеть, что пунктирная линия пересекает отрезок LM. Как было показано в
[5], в этом случае оптимальным будет решение, у которого импульсы скорости
первого интервала маневрирования прилагаются в точках оптимальной коррекции
плоскости орбиты (на линии узлов), а величины боковых составляющих
пропорциональны величинам трансверсальных составляющих импульсов скорости.
Действительно, у приведенного в примере 1 решения, найденного при помощи
численного метода, модули отношений боковых составляющих импульсов скорости к
трансверсальным составляющим у первого и второго импульсов примерно равны, а
соответствующие трансверсальным составляющим импульсов отрезки АВ и ВС близки к
пунктирной прямой. Третьему импульсу скорости соответствует отрезок СD
четвертому DК.
Видно, что у оптимального решения импульсы второго интервала (отрезки СD и DК) сильно отличаются по
величине. Из рисунка также видно, что, для получения решения, у которого
импульсы скорости второго интервала маневрирования будут примерно равны по
величине, необходимо уменьшать угол приложения первого импульса скорости. В
этом случае отрезок, соответствующий первому импульсу скорости, будет
приближаться к точке К.
Это
решение (рис 9) было получено с использованием графического диалога. Параметры
импульсов скорости этого решения и их углы приложения приведены в Примере 4
Пример
4
dVi(Vr,Vn,Vz): .0
21.89 .45 .0 10.09 16.72
.0 14.11 .0
.0 14.95 .0
Виток арг. шир.: 3. 221.0 3. 440. 32. 344.8 33. 164.8
Nit= 8.
W=
70.49 dVsum= 70.49
dVzsum= 17.16
У
этого решения СD»DК.
Направление отрезка, изображающего второй импульс скорости близко к направлению
пунктирной прямой, следовательно, именно этим импульсом в основном
осуществляется коррекция плоскости орбиты (это видно и по величинам боковых
составляющих импульсов скорости). Поскольку затраты на коррекцию плоскости
орбиты у нового решения не распределены пропорционально между первым и вторым
импульсами скорости, суммарная характеристическая скорость нового решения на
5.8 м/с больше чем у решения, приведенного в примере 1.
Решение каждой из приведенных выше
задач осуществлялось с помощью итерационной процедуры, приведенной в разделе 5.
Эффективность функционирования этой процедуры хорошо видно из данных по
итерациям для четырехимпульсной задачи, приведеных в Примере 5.
Последовательно, по итерациям выведена следующая информация: номер текущей
итерации (Nit); суммарный вектор отклонений (SVD), который используется на этой
итерации в системе 1 для определения параметров маневров; вычисленные на этой
итерации составляющие импульсов скорости (dVi(Vr,Vt,Vz)), номера витков и
углы приложения импульсов скорости (Ni,Ui), а также
получающиеся после реализации маневров, отклонения элементов орбиты корабля от
элементов орбиты станции измененных на величину прицельного вектора (CD). Суммарный вектор отклонений (SVD) имеет размерность м/с (координатные
составляющие вектора отклонений умножаются на угловую скорость движения по
опорной круговой орбите). Используемый на первой итерации суммарный вектор
отклонений совпадает с вектором отклонений нескорректированной орбиты корабля
от орбиты станции, приведенным в самом начале Примера 5. Для ускорения
сходимости итерационной процедуры углы приложения импульсов скорости
фиксировались на третьей итерации. Как можно видеть из примера, итерационная
процедура позволяет быстро и с высокой точностью обеспечить выполнение
терминальных ограничений (после каждой итерации отклонения уменьшаются почти на
порядок).
Пример
5
CD
начальные отклонения корабля от станции+ прц. век. [км, м/с]:
CD: R=-141.47 VR= -11.25 VN= 95.79 N= 17538.6 Z= 2.635 VZ= 3.287
_____________________________
Nit=1
SVD: 162.504 11.250
-95.792 -20146.397 3.026
3.287
dVi(Vr,Vn,Vz): 0.
25.45 4.48 0.
9.68 .02 0.
-.77 0. 0.
32.34 0.
Ni
Ui:
3. 302.0 3.
440.0 32. 344.8
33. 164.8
CD:
R=15.48 VR=-25.47 VN=-11.89
N=-1468.2 Z=-18.07 VZ=-5.35
_____________________________
Nit=2
SVD: 144.713 36.728
-83.893 -18459.880 -17.729
-2.070
dVi(Vr,Vn,Vz):
0. 25.58
-13.28 0. 6.47
4.58 0. 5.84
0. 0. 22.92
0.
Ni
Ui:
3. 263.0 3.
437.0 32. 344.8
33. 164.8
CD:
R=-1.413 VR= 17.47 VN=1.70
N= 3.443 Z= 1.231 VZ= .310
_____________________________
Nit=3
SVD: 146.336 19.253
-85.587 -18463.836 -16.315
-1.760
dVi(Vr,Vn,Vz):
0. 21.12
-10.84 0. 10.94
5.59 0. 6.26
0. 0. 22.41 0.
Ni
Ui:
3. 263.0 3.
437.0 32. 344.8
33. 164.8
CD: R=
.170 VR= -.408 VN= -.207
N= 7.379 Z= .021 VZ= -.007
_____________________________
Nit=4
SVD: 146.140 19.661
-85.380 -18472.312 -16.291
-1.767
dVi(Vr,Vn,Vz):
0. 21.23
-10.91 0. 10.84
5.48 0. 6.29
0. 0. 22.38 0.
Ni
Ui: 3. 263.0 3.
437.0 32. 344.8
33. 164.8
CD: R=
.002 VR=-.044 VN=.001
N=-.597 Z=-.010 VZ=-.003
_____________________________
Nit=5
SVD: 146.138 19.705
-85.382 -18471.626 -16.302
-1.771
dVi(Vr,Vn,Vz):
0. 21.24
-10.94 0. 10.83 5.47
0. 6.29 0.
0. 22.38 0.
Ni
Ui:
3. 263.0 3. 437.0
32. 344.8 33.
164.8
CD:
R=-.001 VR= .008 VN= .001
N=-.046 Z= 0. VZ= 0.
8. ИСПОЛЬЗОВАНИЕ ИТЕРАЦИОННОЙ
ПРОЦЕДУРЫ ДЛЯ ТОЧНОГО УЧЕТА ОГРАНИЧЕНИЙ НА ВЫСОТУ ОРБИТЫ ОЖИДАНИЯ
Эту
же процедуру можно эффективно использовать для точного выполнения ограничений
на параметры орбиты ожидания и для многих других целей.
Рассмотрим,
например, её использование для точного учета ограничения на высоту орбиты
ожидания.
Пусть
на i–й итерации задача решалась при ограничении, что высота
орбиты ожидания h должна быть больше заданной величины hmi. Было
найдено решение, у которого вычисляемая по аналитическим формулам высота hai удовлетворяла
этому ограничению (hai>hmi). В
процессе численного интегрирования уравнений движения с учетом рассчитанных
импульсов скорости, определяется также и высота орбиты ожидания hi,
соответствующая этому решению. Определяется разница Dh=hai-hi между значениями высоты, рассчитанными при
помощи аналитического метода и численного интегрирования. На следующей i+1 итерации
в качестве ограничения по высоте используется величина hmi+1=hm+Dh, где hm – заданное
минимально возможное значение высоты орбиты ожидания.
Такой
прием позволяет использовать довольно простые формулы для вычисления высоты
орбиты ожидания и в тоже время выполнять ограничение на высоту с высокой
точностью.
Для
определения параметров маневров, удовлетворяющих ограничению на высоту hmi, можно
воспользоваться численно аналитическим методом, приведенным в [7]. Если же для
решения задачи используется численный метод, и число ограничений в виде
равенств совпадает с числом используемых составляющих импульсов, то выполнение
ограничения на высоту просто проверяется. После определения величин
составляющих импульсов для очередной точки из множества F,
проверяется выполнение ограничения hai>hmi, и, если
ограничение не выполнено, то решение отсеивается, а если выполнено, то
проверяется оптимальность найденного решения и, если оно лучше предыдущих, оно
становится текущим оптимальным решением.
Процедура
аналогичная процедуре изменения hmi используется при решении задачи,
когда только часть из терминальных отклонений требуется сделать нулевыми (Dк), а
остальные отклонения (Dp) добавляются в минимизируемый функционал в виде
штрафов.
9. ЛИТЕРАТУРА
1. Баранов А.А., Гундобин И.О., Иванов
Д.М. и др., Управление орбитальным
движением КА в программе пилотируемых полетов, Труды XVI Научных чтений по
космонавтике, М., 1992.
2. Бажинов И.К., Гаврилов В.П. и др.,
Навигационное обеспечение полета орбитального комплекса «Салют – 6» - «Союз» -
«Прогресс», М., Наука, 1985.
3. Баранов А.А., О геометрическом
решении задачи встречи на близких почтикруговых компланарных орбитах,
Космические исследования, 1989, т.27, №
6, с. 808.
4. Баранов А.А., Алгоритм расчета параметров
четырехимпульсных переходов между близкими околокруговыми орбитам,
Космические исследования, 1986, т.24, №
3, с. 400.
5. Соболь И.М., Левитан Ю.Л., Получение
точек, равномерно расположенных в многомерном кубе, препринт Института
прикладной математики АН СССР, 1976, №40.
6. Баранов А.А., Алгоритм расчета
параметров многовитковых маневров дальнего наведения, Космические исследования, 1990, т.28, № 1, с. 69.
7. Баранов А.А., О геометрическом
решении задачи импульсного многовиткового перехода между близкими
околокруговыми компланарными орбитами, препринт Института прикладной математики
им. М. В. Келдыша АН СССР, 1985, №64.
8. Платонов А.К., Казакова Р.К., Система
проектирования орбит в прикладных задачах небесной механики, препринт Института
прикладной математики АН СССР, 1976, №106.
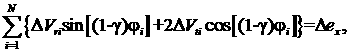

 ,
,
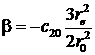
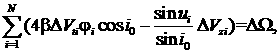


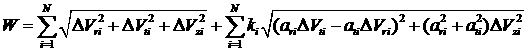 .
.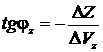 ). На рис. 1 на плоскости (
). На рис. 1 на плоскости (