Аннотация
В работе в рамках ограниченной задачи трех тел рассматривается возможность существования равновесного аккреционного
диска в двойной звездной системе. Для различных соотношений масс гравитирующих тел, образующих эту систему, найдены
и исследованы на устойчивость несамопересекающиеся периодические орбиты пробного тела вокруг одной из компонент системы.
Построены области устойчивости орбит, на основе которых может быть предложена в баллистическом приближении конфигурация
равновесного аккреционного диска.
Abstract
The opportunity of existence of equilibrium accretion disk, in double star system within restricted three-body problem
is examined in this paper. Periodic orbits without self-intersections around one of the stars were found and tested
for stability for the different values of star mass ratios. The areas of stable orbits were found, which can be used
for creating equilibrium accretion disk within ballistic approach.
Аннотация………………………………………………………………………………………2
Содержание……………………………………………………………………………………..3
1. Введение……………………………………………………………………………………...4
2. Постановка задачи и методы ее
решения…………………………………………………..6
3. Области существования и устойчивости периодических
решений при 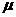 = 0.5 ……….9 = 0.5 ……….9
4. Области существования и устойчивости периодических
решений при 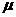 = 0.3 ………11 = 0.3 ………11
5. Результаты исследований при различных 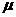 ……………………………………………..12 ……………………………………………..12
6. Влияние резонансных эффектов……………………………………………………………13
7. Заключение………………………………………………………………………………......15
Список литературы…………………………………………………………………………….16
Одна из фундаментальных проблем современной астрофизики связана с
изучением структуры, устойчивости и эволюции аккреционных дисков в двойных
звездных системах. Этому вопросу посвящено значительное количество
исследований, в том числе выполненных с помощью методов математического
моделирования. Так, например, в работах [1,2,3] показано, что в двойной системе
аккреционный диск может образовываться и существовать вблизи одной из компонент
при наличии истечения вещества с поверхности другой компоненты.
В то же время в [4] отмечено, что при отсутствии потока массы с одной из компонент
равновесный аккреционный диск в двойной звездной системе может и не
существовать. Этот результат был получен в конкретной задаче, постановка
которой сводится к следующему. Рассматривается равновесное облако газа,
вращающегося вокруг гравитирующего тела. Такие равновесные конфигурации для
двухмерного случая были получены в [5]. Самогравитация в облаке не учитывается.
В начальный момент на некотором расстоянии от тела помещается второе
гравитирующее тело. Вся система, включая газовое облако, начинает вращаться
вокруг общего центра масс с некоторой постоянной угловой скоростью, вычисляемой
на основании законов небесной механики. Газовое облако перестает быть
равновесным. Под действием гравитационных, а также «неинерциальных сил»
(центробежные силы и сила Кориолиса) начинается его распад, возникает сложная
нестационарная структура течения газа, содержащая, в частности, ударные волны и
«двухрукавные» волны плотности. Однако на поздней стадии эволюции облака
какое-либо равновесное его состояние не устанавливается ─ газ истекает на
периферию и его масса в расчетной области со временем уменьшается по
экспоненциальному закону. Заметим, что истечение вещества с поверхности второго
тела звездной системы, которое могло бы скомпенсировать отток газа из нее, в
задаче не рассматривалось.
Настоящая работа предпринята с целью установить возможность существования
равновесного газового облака (аккреционного диска) вблизи одной из компонент
двойной звездной системы, где отсутствует поток вещества между компонентами. В
качестве первого шага исследование проводится для пространственно двумерного
случая (тонкие диски) в рамках так называемого «баллистического приближения».
Газ считается холодным и его частицы при отсутствии давления, не взаимодействуя
друг с другом, движутся как «пробные частицы» в гравитационном поле двух тел,
вращающихся вокруг общего центра масс. Таким образом, в отличие от
процитированных выше работ, где использовалось приближение сплошной среды,
описываемой уравнениями газовой динамики, здесь диск рассматривается как
совокупность пробных частиц, и математическая сторона вопроса сводится к
решению плоской ограниченной задачи трех тел [6].
В рамках этого подхода мы будем искать такие замкнутые периодические
траектории частиц, из которых можно сконструировать искомый равновесный
аккреционный диск. Траектории движения частиц должны быть орбитально
устойчивыми, то есть устойчивыми по отношению к малым возмущениям орбиты. Кроме
того, они не должны пересекаться.
Следует
отметить, что в задачах об аккреционном диске двойной звездной системы
исследуются диски, вращающиеся в ту же сторону, что и двойная система. Это
связано с тем, что в большинстве двойных звездных систем, образующихся в
результате эволюции, аккреционные диски вращаются в ту же сторону, что и вторичная
компонента. Однако последние наблюдения показывают, что существуют аккреционные
диски с противоположным направлением вращения, например, звездные и газопылевые
скопления вокруг центров галактик. В некоторых спиральных галактиках звездные
или газовые диски с левым вращением сосуществуют с первичным диском с правым
вращением много большего радиуса. Представляет интерес галактика NGC 4826,
называемая «Око дьявола», в которой направление вращения газа меняет свое
направление на противоположное по мере удаления от ее центра [7]. Причиной
возникновения подобного противоположного направления вращения может являться,
например, слияние двух галактик с противоположным угловым моментом. Учитывая
сказанное, ниже рассматриваются оба направления вращения частиц, образующих
аккреционный диск.
В предыдущей работе [8] были описаны методы построения периодических решений
плоской ограниченной задачи трех тел и исследования их на устойчивость.
Приведем краткое изложение этих результатов.
Плоской
ограниченной задачей трех тел называется задача о плоском движении тела  бесконечно малой
массы, которое иногда именуется пробной
частицей, в переменном гравитационном потенциале, создаваемом системой двух
других вращающихся тел бесконечно малой
массы, которое иногда именуется пробной
частицей, в переменном гравитационном потенциале, создаваемом системой двух
других вращающихся тел 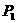 и и  ,
обладающих массами ,
обладающих массами  и и 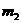 . .
В движущейся системе координат с началом в точке  (центр масс системы из (центр масс системы из 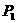 и и  )
и осью )
и осью  , проходящей через , проходящей через  и и  (рис.1), движение тела (рис.1), движение тела
 описывается следующей
системой обезразмеренных уравнений: описывается следующей
системой обезразмеренных уравнений:
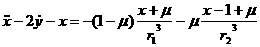
 , (1) , (1)
где  - координаты тела - координаты тела  , , 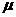 - масса тела - масса тела  , ,  - время, - время, 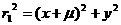 , ,  . Система уравнений (1) записана в безразмерных единицах, где
в качестве основных размерных величин, используемых для обезразмеривания,
приняты полная масса системы . Система уравнений (1) записана в безразмерных единицах, где
в качестве основных размерных величин, используемых для обезразмеривания,
приняты полная масса системы 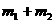 , расстояние между телами , расстояние между телами 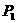 и и  и угловая скорость вокруг центра масс и угловая скорость вокруг центра масс  . Тогда . Тогда 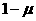 - масса тела - масса тела 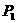 и и  . Соотношение масс . Соотношение масс  является параметром
рассматриваемой задачи. является параметром
рассматриваемой задачи.

Рис. 1
Для построения периодических решений использовался тот факт, что
траектория движения частицы  , соответствующая периодическому решению с периодом , соответствующая периодическому решению с периодом  , симметрична относительно прямой, соединяющей , симметрична относительно прямой, соединяющей 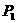 и и  , и для нее выполняются условия: , и для нее выполняются условия: 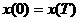 , , 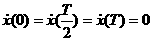 , , 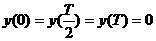 , ,  . Поэтому для нахождения периодического решения достаточно
найти . Поэтому для нахождения периодического решения достаточно
найти  и и 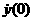 такие, что такие, что  и и  . .
Для поиска решения фиксируется
соотношение масс 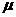 и выбирается некоторая
точка и выбирается некоторая
точка  . Ищется периодическое решение задачи, которое исходит из
этой точки. Сначала выбирается некоторое начальное приближение компоненты
скорости . Ищется периодическое решение задачи, которое исходит из
этой точки. Сначала выбирается некоторое начальное приближение компоненты
скорости  в направлении перпендикулярном линии, соединяющей в направлении перпендикулярном линии, соединяющей 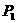 и и  ,
и полупериода ,
и полупериода 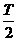 .
Для выбранного приближения .
Для выбранного приближения 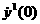 вычисляется траектория
тела вычисляется траектория
тела  и выбирается момент времени и выбирается момент времени 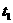 в некоторой
окрестности начального приближения полупериода в некоторой
окрестности начального приближения полупериода 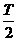 , в котором , в котором  . Иными словами, ищется точка пересечения траектории движения
тела . Иными словами, ищется точка пересечения траектории движения
тела  при заданном приближении при заданном приближении 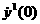 с горизонтальной осью
координат и в ней вычисляется с горизонтальной осью
координат и в ней вычисляется  . Для периодического решения необходимо, чтобы выполнялось . Для периодического решения необходимо, чтобы выполнялось  . Методом последовательных приближений достигается заданная
точность. . Методом последовательных приближений достигается заданная
точность.
Устойчивость
построенного решения определялась по методу, предложенному Deprit A. и Price J.F. в работе
[9]. В этом методе для каждой построенной орбиты вычисляется индекс
устойчивости  . Построенное периодическое решение орбитально
устойчиво тогда и только тогда, когда выполняется . Построенное периодическое решение орбитально
устойчиво тогда и только тогда, когда выполняется 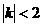 . Для нахождения индекса устойчивости путем численного
решения соответствующей системы уравнений в вариациях строится матрица
монодромии . Для нахождения индекса устойчивости путем численного
решения соответствующей системы уравнений в вариациях строится матрица
монодромии 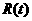 . Индекс устойчивости связан следующим соотношением с ее
следом: . Индекс устойчивости связан следующим соотношением с ее
следом:  Вычисляя индекс устойчивости для каждой построенной орбиты,
можно определить ее устойчивость или неустойчивость. Объединяя полученные
результаты, можно построить области устойчивых и неустойчивых решений. Мы будем
искать эти области при различных соотношениях масс Вычисляя индекс устойчивости для каждой построенной орбиты,
можно определить ее устойчивость или неустойчивость. Объединяя полученные
результаты, можно построить области устойчивых и неустойчивых решений. Мы будем
искать эти области при различных соотношениях масс 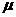 между гравитирующими телами.
В связи с тем, что параметр между гравитирующими телами.
В связи с тем, что параметр 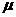 рассматривается на
интервале рассматривается на
интервале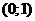 , в силу симметрии задачи достаточно изучить вращение
пробного тела , в силу симметрии задачи достаточно изучить вращение
пробного тела  вокруг только одного из
тел. вокруг только одного из
тел.
В
качестве примера рассмотрим область существования и орбитальной устойчивости (в
дальнейшем просто устойчивости) периодических решений вокруг одного из тел при 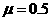 , то
есть когда массы тел , то
есть когда массы тел 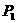 и и  одинаковы. Здесь и
далее для наглядности представляемых результатов будем использовать систему
координат с началом в одинаковы. Здесь и
далее для наглядности представляемых результатов будем использовать систему
координат с началом в 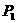 ,
так чтобы тело ,
так чтобы тело  оказалось в точке оказалось в точке 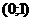 . Это позволит сравнивать искомую область существования и устойчивости периодических
решений при различных . Это позволит сравнивать искомую область существования и устойчивости периодических
решений при различных 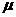 , поскольку
при данном выборе системы координат положение ее начала относительно тел , поскольку
при данном выборе системы координат положение ее начала относительно тел 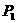 и и  не зависит от не зависит от 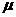 (рис. 2). (рис. 2).

Рис. 2
Мы будем строить орбиты вокруг тела 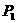 , проходящие через точку , проходящие через точку 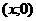 , где , где  с шагом с шагом  , определяя для каждой построенной орбиты является ли она
устойчивой или нет. Таким образом, будут получены области устойчивости
несамопересекающихся орбит. , определяя для каждой построенной орбиты является ли она
устойчивой или нет. Таким образом, будут получены области устойчивости
несамопересекающихся орбит.
Сначала рассмотрим случай прямого вращения пробного тела вокруг 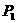 , то есть по направлению вращения двойной звездной системы.
При данном направлении вращения периодические решения без самопересечений
существуют на интервале , то есть по направлению вращения двойной звездной системы.
При данном направлении вращения периодические решения без самопересечений
существуют на интервале 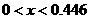 (рис. 3). Здесь и
далее пунктирной линией изображена полость Роша. Напомним, что полостью Роша
называется область в системе из двух гравитирующих тел, ограниченная
поверхностью равного гравитационного потенциала, проходящей через первую точку
Лагранжа (рис. 3). Здесь и
далее пунктирной линией изображена полость Роша. Напомним, что полостью Роша
называется область в системе из двух гравитирующих тел, ограниченная
поверхностью равного гравитационного потенциала, проходящей через первую точку
Лагранжа 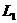 . Стрелки на рисунке обозначают направление движение
пробного тела по крайней орбите, ограничивающей область существования искомых
периодических решений. Сама область заштрихована. . Стрелки на рисунке обозначают направление движение
пробного тела по крайней орбите, ограничивающей область существования искомых
периодических решений. Сама область заштрихована.
При  периодические
решения из данного семейства перестают быть несамопересекающимися, то есть
удовлетворяющими постановке задачи. Пример самопересекающегося решения
изображен на рис. 4. периодические
решения из данного семейства перестают быть несамопересекающимися, то есть
удовлетворяющими постановке задачи. Пример самопересекающегося решения
изображен на рис. 4.
Диапазон 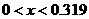 является областью
устойчивости построенных решений, далее начинается диапазон неустойчивости является областью
устойчивости построенных решений, далее начинается диапазон неустойчивости  . Затем решения становятся вновь устойчивыми ─ в
области . Затем решения становятся вновь устойчивыми ─ в
области  . Интервал, как отмечалось выше, . Интервал, как отмечалось выше,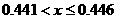 является диапазоном неустойчивости, а при является диапазоном неустойчивости, а при  периодические
решения без самопересечений построить не удается. периодические
решения без самопересечений построить не удается.
Суммируя
полученные результаты, получаем, что областью существования устойчивых
периодических решений без самопересечений является объединение двух интервалов  и и  , а неустойчивых - , а неустойчивых - 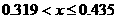 и и 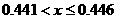 . Область устойчивых периодических решений изображена на рис. 5. На этом рисунке
видно, что траектории частиц из второго диапазона устойчивости . Область устойчивых периодических решений изображена на рис. 5. На этом рисунке
видно, что траектории частиц из второго диапазона устойчивости  слева от слева от 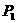 пересекаются с
траекториями из первого диапазона. Аналогично, неустойчивые траектории
пересекаются с устойчивыми из первого интервала устойчивости пересекаются с
траекториями из первого диапазона. Аналогично, неустойчивые траектории
пересекаются с устойчивыми из первого интервала устойчивости  . На рис. 5 «светлым» цветом закрашены такие области, через
которые проходят только устойчивые орбиты, а «темным» - как устойчивые, так и неустойчивые. Таким
образом, данный пример показывает, что через одну точку могут проходить две
траектории без самопересечений, принадлежащих различным диапазонам. . На рис. 5 «светлым» цветом закрашены такие области, через
которые проходят только устойчивые орбиты, а «темным» - как устойчивые, так и неустойчивые. Таким
образом, данный пример показывает, что через одну точку могут проходить две
траектории без самопересечений, принадлежащих различным диапазонам.
Теперь рассмотрим обратное вращение пробного тела вокруг 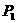 , то есть в сторону противоположную , то есть в сторону противоположную  . В этом случае чередование областей устойчивости и
неустойчивости искомых периодических решений без самопересечений происходит
большее количество раз. Области устойчивости здесь получаются . В этом случае чередование областей устойчивости и
неустойчивости искомых периодических решений без самопересечений происходит
большее количество раз. Области устойчивости здесь получаются 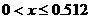 , ,  и и  , неустойчивости - , неустойчивости -  , , 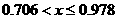 и и  (рис. 6). При (рис. 6). При 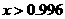 исследуемое семейство орбит перестает быть несамопересекающимся,
поэтому орбит без самопересечений при исследуемое семейство орбит перестает быть несамопересекающимся,
поэтому орбит без самопересечений при 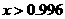 найти не удается.
Соответственно, областью существования искомых решений является интервал найти не удается.
Соответственно, областью существования искомых решений является интервал 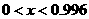 (рис. 7). (рис. 7).
Случай  интересен тем, что при
данном значении параметра интересен тем, что при
данном значении параметра 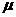 для случая прямого вращения пробного тела все построенные
несамопересекающиеся решения являются устойчивыми, то есть область
существования совпадает с областью устойчивости. Искомые решения существуют и
являются устойчивыми при для случая прямого вращения пробного тела все построенные
несамопересекающиеся решения являются устойчивыми, то есть область
существования совпадает с областью устойчивости. Искомые решения существуют и
являются устойчивыми при 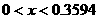 (рис. 8). (рис. 8).
При обратном направлении вращения пробного тела несамопересекающиеся
решения существуют при 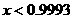 . Диапазоны устойчивости - . Диапазоны устойчивости - 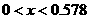 и и  (рис. 9). Соответственно область существования неустойчивых
периодических решений без самопересечений - (рис. 9). Соответственно область существования неустойчивых
периодических решений без самопересечений -  и и 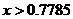 (рис. 10). При этом в окрестности точки (рис. 10). При этом в окрестности точки 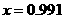 существует очень
небольшой диапазон устойчивости шириной порядка существует очень
небольшой диапазон устойчивости шириной порядка  . .
Для различных значений 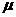 находились области существования интересующих нас
периодических несамопересекающихся решений и области их устойчивости. Как и
ранее, строились орбиты, проходящие через точку находились области существования интересующих нас
периодических несамопересекающихся решений и области их устойчивости. Как и
ранее, строились орбиты, проходящие через точку 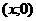 , где , где  с шагом 0.001. При
этом каждая построенная орбита исследовалась на устойчивость. с шагом 0.001. При
этом каждая построенная орбита исследовалась на устойчивость.
Рассмотрим сначала прямое вращение пробного тела  , то есть в ту же сторону, что и направление вращения
системы. В этом случае несамопересекающиеся решения существуют далеко не при всех
значениях , то есть в ту же сторону, что и направление вращения
системы. В этом случае несамопересекающиеся решения существуют далеко не при всех
значениях 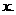 Например, как было
отмечено выше, при Например, как было
отмечено выше, при 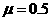 областью
существования является областью
существования является 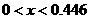 . При некоторых значениях . При некоторых значениях 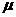 , например при , например при  , все найденные периодические решения без самопересечений
являются устойчивыми, а при других возникают области неустойчивости. Результаты
проведенных исследований показаны на рис. 11, на котором изображены области
существования и устойчивых решений в зависимости от соотношения масс , все найденные периодические решения без самопересечений
являются устойчивыми, а при других возникают области неустойчивости. Результаты
проведенных исследований показаны на рис. 11, на котором изображены области
существования и устойчивых решений в зависимости от соотношения масс 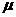 . На этом рисунке координата точки по оси абсцис
соответствует соотношению масс . На этом рисунке координата точки по оси абсцис
соответствует соотношению масс 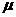 , а по оси
ординат – координате , а по оси
ординат – координате 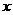 , то есть точке
пересечения орбиты с отрезком, соединяющим , то есть точке
пересечения орбиты с отрезком, соединяющим 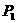 и и  .
Штрих-пунктирной линией на рисунке ограничена область существующих искомых
решений без самопересечений, а заштрихованные области соответствуют устойчивым
решениям. Как видно, для всех исследованных .
Штрих-пунктирной линией на рисунке ограничена область существующих искомых
решений без самопересечений, а заштрихованные области соответствуют устойчивым
решениям. Как видно, для всех исследованных 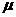 количество
областей устойчивости не превосходит
двух, при этом область существования чаще всего довольно близка к области
устойчивости. Вертикальными пунктирными линиями выделены ранее рассмотренные
случаи количество
областей устойчивости не превосходит
двух, при этом область существования чаще всего довольно близка к области
устойчивости. Вертикальными пунктирными линиями выделены ранее рассмотренные
случаи  и и  . Из рисунка видно, что при . Из рисунка видно, что при  все существующие
решения устойчивы, а при все существующие
решения устойчивы, а при  есть два интервала
устойчивости, что совпадает с ранее полученными результатами. есть два интервала
устойчивости, что совпадает с ранее полученными результатами.
Теперь
рассмотрим обратное вращение (рис. 12). В этом случае периодические решения без
самопересечений для всех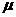 удавалось
построить практически на всем интервале (0;1),
поэтому на рис. 12 область существования не нарисована. На этом рисунке, как и
на предыдущем, в фазовом пространстве удавалось
построить практически на всем интервале (0;1),
поэтому на рис. 12 область существования не нарисована. На этом рисунке, как и
на предыдущем, в фазовом пространстве 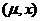 заштрихованными областями являются области
устойчивых решений, а пунктирной линией обозначены координаты первой точки
Лагранжа заштрихованными областями являются области
устойчивых решений, а пунктирной линией обозначены координаты первой точки
Лагранжа 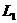 , положение которой зависит от соотношений масс , положение которой зависит от соотношений масс 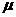 . Интересно
отметить, что при . Интересно
отметить, что при 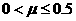 граница «внутренней» области устойчивости находится
довольно близко к точке граница «внутренней» области устойчивости находится
довольно близко к точке 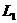 , то есть найденные области устойчивости близки к полости
Роша. При , то есть найденные области устойчивости близки к полости
Роша. При  и и 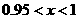 существует множество чередующихся очень «тонких»
областей устойчивых и неустойчивых решений, точное нахождение которых
достаточно трудоемко, поэтому в рамках поставленной задачи не производится. существует множество чередующихся очень «тонких»
областей устойчивых и неустойчивых решений, точное нахождение которых
достаточно трудоемко, поэтому в рамках поставленной задачи не производится.
Как видно из приведенных выше результатов, в задаче существуют области
неустойчивости орбит. Это обстоятельство можно объяснить резонансными
эффектами, возникающими при движении исследуемого тела  в переменном
гравитационном поле, создаваемом системой двух других движущихся тел в переменном
гравитационном поле, создаваемом системой двух других движущихся тел 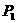 и и  .
Напомним, что резонансные эффекты возникают, когда частота периодической
возбуждающей силы совпадает с собственной частотой движения частицы или
находится с ней в простых соотношениях [10]. В случае движения пробной частицы
в системе двух тел .
Напомним, что резонансные эффекты возникают, когда частота периодической
возбуждающей силы совпадает с собственной частотой движения частицы или
находится с ней в простых соотношениях [10]. В случае движения пробной частицы
в системе двух тел 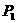 и и  резонанс является параметрическим, потому что
внешнее воздействие на пробную частицу со стороны этой системы изменяется во
времени по периодическому закону. резонанс является параметрическим, потому что
внешнее воздействие на пробную частицу со стороны этой системы изменяется во
времени по периодическому закону.
Пусть  - угловая скорость
движения тела - угловая скорость
движения тела  вокруг вокруг 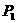 (напомним, что в нашей задаче она считается
равной единице). Для пробной частицы (напомним, что в нашей задаче она считается
равной единице). Для пробной частицы  она является частотой внешней возбуждающей силы. Если ее
собственная угловая скорость связана с она является частотой внешней возбуждающей силы. Если ее
собственная угловая скорость связана с  простыми соотношениями
1:2, 2:3, 3:4 и т.д., то на пробную частицу начинают действовать периодические
сфазированные возмущения, что приводит к
неустойчивости орбиты, так как постоянные возмущения соответствующей фазы
накапливаются и изменяют орбиту пробной частицы. Например, соотношение 1:2 означает, что на
каждые два оборота пробной частицы приходится один оборот тела простыми соотношениями
1:2, 2:3, 3:4 и т.д., то на пробную частицу начинают действовать периодические
сфазированные возмущения, что приводит к
неустойчивости орбиты, так как постоянные возмущения соответствующей фазы
накапливаются и изменяют орбиту пробной частицы. Например, соотношение 1:2 означает, что на
каждые два оборота пробной частицы приходится один оборот тела .
Чем проще данное соотношение, тем чаще пробная частица сближается с телом .
Чем проще данное соотношение, тем чаще пробная частица сближается с телом  и тем сильнее возникающие резонансные
возмущения. В результате образуются резонансные области колец, внутри которых
орбиты пробной частицы неустойчивы. и тем сильнее возникающие резонансные
возмущения. В результате образуются резонансные области колец, внутри которых
орбиты пробной частицы неустойчивы.
Важно отметить, что для достижения сильных резонансных эффектов
необходимо, чтобы скорость движения пробной частицы по орбите была постоянной. В нашей же ситуации тесной
двойной звездной системы пробная частица, двигаясь по орбите, изменяет свою
скорость. Так, например, при прямом вращении и  на границе внутренней
области устойчивости соотношение скоростей в точках апогея и перигея равно
0.91. Также отличны и радиусы орбит в этих точках. Поэтому, мы будем искать
зависимость найденных областей неустойчивости от соотношений периодов обращений на границе внутренней
области устойчивости соотношение скоростей в точках апогея и перигея равно
0.91. Также отличны и радиусы орбит в этих точках. Поэтому, мы будем искать
зависимость найденных областей неустойчивости от соотношений периодов обращений
 и и  тел тел  и и
 соответственно.
Непостоянность скорости движения пробной частицы должно приводить к тому, что
резонансные эффекты будут возникать не при всех соответствующих простых
соотношений периодов. соответственно.
Непостоянность скорости движения пробной частицы должно приводить к тому, что
резонансные эффекты будут возникать не при всех соответствующих простых
соотношений периодов.
Рассмотрим случай прямого вращения при  . Области устойчивых орбит изображены на рис. 4. Диапазон
неустойчивых орбит, соответствующий . Области устойчивых орбит изображены на рис. 4. Диапазон
неустойчивых орбит, соответствующий  возникает при возникает при 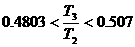 . Как видно, этот диапазон соответствует приблизительному
отношению частот вращения 1:2. Таким образом, причиной возникновения данной
области неустойчивости являются резонансные эффекты. Подобная ситуация
прослеживается и для остальных соотношений масс . Как видно, этот диапазон соответствует приблизительному
отношению частот вращения 1:2. Таким образом, причиной возникновения данной
области неустойчивости являются резонансные эффекты. Подобная ситуация
прослеживается и для остальных соотношений масс 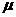 , при которых существует диапазон неустойчивых решений. , при которых существует диапазон неустойчивых решений.
Теперь рассмотрим случай обратного вращения и также  . Области устойчивых орбит изображены на рис. 3. В этом
случае узкий диапазон неустойчивых орбит, соответствующий . Области устойчивых орбит изображены на рис. 3. В этом
случае узкий диапазон неустойчивых орбит, соответствующий 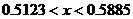 возникает при возникает при 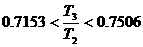 или приближенно или приближенно  . Таким образом, можно предположить, что причиной
возникновения данной области неустойчивости являются резонансные эффекты,
возникающие на границах области и влияющие на всю область из-за непостоянности
скорости движения частицы . Таким образом, можно предположить, что причиной
возникновения данной области неустойчивости являются резонансные эффекты,
возникающие на границах области и влияющие на всю область из-за непостоянности
скорости движения частицы  . Аналогичные зависимости прослеживаются и при многих других
соотношений масс . Аналогичные зависимости прослеживаются и при многих других
соотношений масс 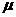 . .
В рамках ограниченной задачи трех тел
для различных значений параметра
соотношения масс  найдены области
устойчивых замкнутых, периодических и несамопересекающихся траекторий движения
пробных частиц вокруг одного из гравитирующих тел. найдены области
устойчивых замкнутых, периодических и несамопересекающихся траекторий движения
пробных частиц вокруг одного из гравитирующих тел.
Указана причина существования областей устойчивости и неустойчивости
траекторий, − резонансные эффекты, возникающие при движении пробной
частицы вокруг одного из гравитирующих тел в двойной системе, когда частота вращения
двойной системы совпадает с собственной частотой движения пробной частицы или
находится с ней в простых соотношениях.
На основе найденных устойчивых и несамопересекающихся траекторий можно
предложить структуру равновесного аккреционного диска, которая не содержит
неустойчивости и самопересекающихся орбит. Такая структура может быть
использована в качестве начальных данных в газодинамических расчетах. Подобные
расчеты дадут ответ на вопрос о возможности существования равновесных газовых
конфигураций в двойных звездных системах при отсутствии перетекания газа с
одной компоненты на другую.
Авторы выражают благодарность А.Д.Брюно и В.М.Чечеткину за полезные
обсуждения в процессе выполнения данной работы.
Работа выполнена при частичной поддержке РФФИ (проект № 06-01-00182).
1.
Боярчук
А.А., Кузнецов О.А., Попов Ю.П., Чечеткин В.М. Исследование течения газа в
двойных звездных системах. Препринт/ИПМ РАН, М.: 1990, № 120.
2. Chechetkin V.M.,
Kuznetsov O.A., Lovelace R.V E., Romanova M.M. Hydrodynamic simulations of
counterrotating accretion disks. Astron. J.,
Vol. 514, P. 691-703, 1999.
3. Maltsuda
T., Sekino N., Shima E., Sawada K., and Spruit H. Mass transfer by tidally
induced spiral shocks in an accretion disk. Astron. Astrophys, 1990, V. 235,
P.211-218.
4.
Абакумов
М.В., Мухин С.И., Попов Ю.П., Чечеткин В.М. Математическое моделирование
процессов в аккреционном диске двойной звездной системы. Препринт/ИПМ РАН, М.:
1996, № 82.
5.
Абакумов
М.В., Жданов А.А., Мухин С.И., Попов Ю.П., Чечеткин В.М. Аккреционные диски в
двойной звездной системе с переменными расстояниями между компонентами.
Математическое моделирование. Препринт/ИПМ РАН, М.: 2003, № 65.
6.
Брюно
А.Д. Ограниченная задача трех тел. Москва: Наука, 1992.
7. Rubin,
Vera C. Kinematics of NGC 4826: A
sleeping beauty galaxy, not an evil eye. Astron. J., Vol. 107, No. 1, pp.
173-183, 1994.
8.
А.В.Галактионов,
Ю.П.Попов. Построение периодических решений для ограниченной задачи трех тел.
Препринт/ИПМ РАН, М.: 2005, № 115.
9. Deprit A., and Price J.F. The computation of characteristic exponents in the planar restricted
problem of three bodies. Astron. J.,
Vol. 67, No. 10, pp. 732-739, 1962.
10.
Горькавый
Н.Н., Фридман А.М. "Физика планетных колец. Небесная механика сплошной cреды". М.: Наука, 1994.
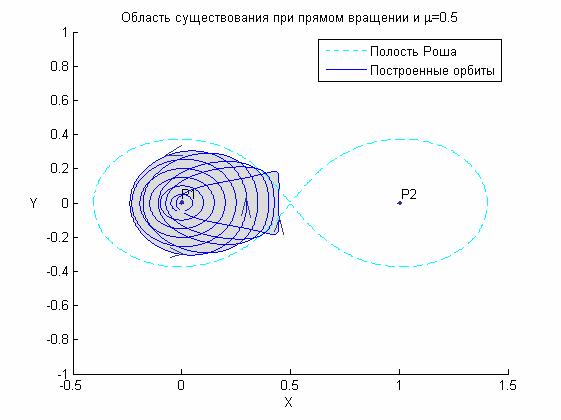
Рис. 3
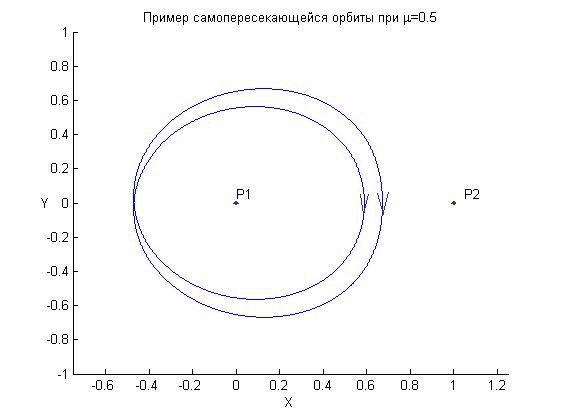
Рис. 4
-
Рис. 5
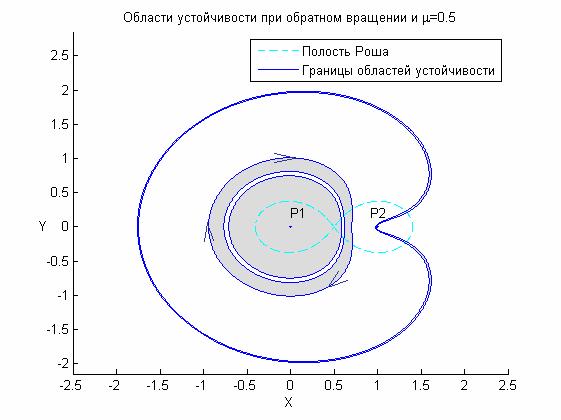
Рис. 6
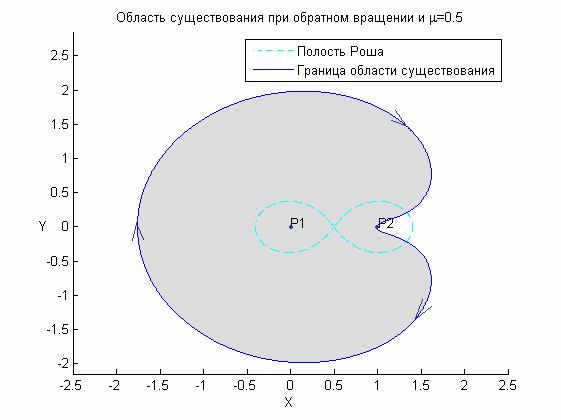
Рис. 7

Рис. 8

Рис. 9
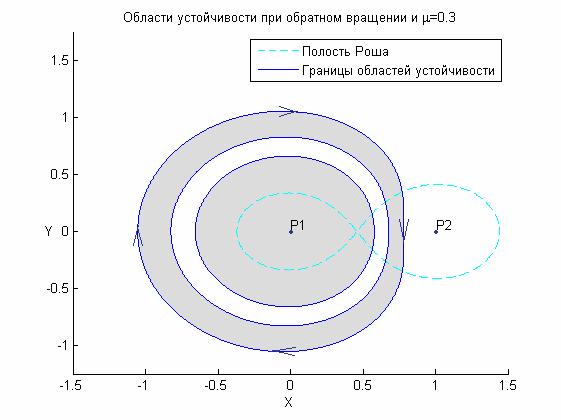
Рис. 10
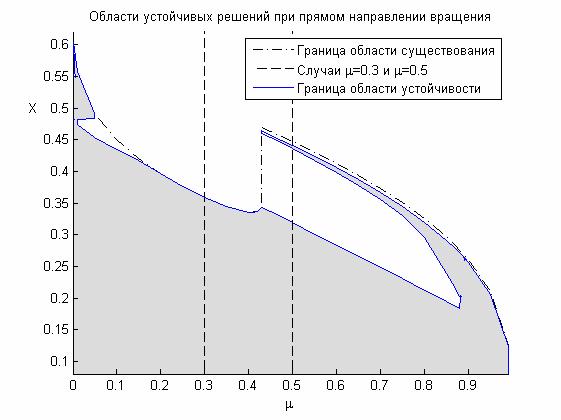
Рис. 11
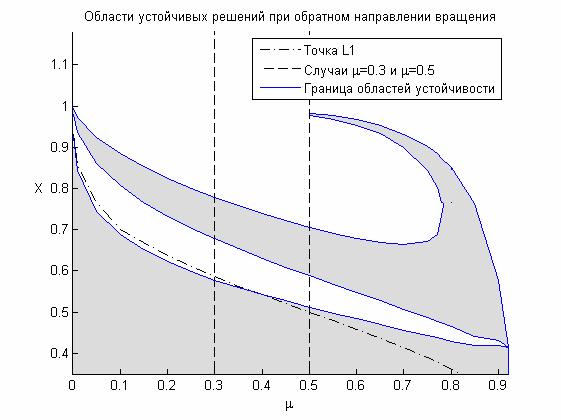
Рис. 12
|