Аннотация
В работе проводится обобщение теоремы В.В. Козлова о слабой сходимости решения бесстолкновительного
уравнения Лиувилля к равновесному распределению, однородному по пространственным переменным.
Для этого вводится принцип проектирования меры фазовом пространстве системы на меру, абсолютно непрерывную относительно
меры Лебега в координатном пространстве. В этих терминах доказывается теорема о слабом пределе распределений,
являющихся решениями однородного уравнения Лиувилля и принадлежащих новым функциональным пространствам.
Abstract
In this work the generalization of the Kozlov-Puancare diffusion theorem on weak
convergence of the collisionless Liouville equation to the equilibrium distribution,
which is homogeneous with respect to spatial coordinates. For this purpose the principal
of measure projection in the system phase state is introduced. In these terms the theorem of
existence of weak limit of distributions of Liouville equation is proved in new functional spaces.
Введение
В настоящей работе исследуются асимптотические по
времени свойства функционалов на решениях уравнения Лиувилля. Этими свойствами
определяется равновесное состояние системы.
Статистическое равновесие в газе означает в
классическом понимании, что скорости частиц имеют максвелловское распределение,
а плотность постоянна по всему объему (с точностью до флуктуаций), т.е. равна
средней плотности газа. Выравнивание же плотности означает, что имеет место
диффузия, при которой начальные неоднородные условия необратимо размываются. В
то же время уравнения динамики отдельных частиц и всей системы в целом обратимы
по времени. Согласование этих двух положений именно для случая идеального газа
представляет особую важность: может оказаться, что необратимость является
скорее математическим свойством, чем следствием физических гипотез, таких,
например, как гипотеза молекулярного хаоса в уравнении Больцмана [1].
Данная работа основывается на теоремах В.В. Козлова
[2] об асимптотическом поведении функций распределения для ряда модельных
систем статистической механики, в частности, для уравнения Лиувилля
бесстолкновительной сплошной среды. В монографии [2] были математически
корректно обоснованы идеи А. Пуанкаре [3] о представлении идеального газа как
бесстолкновительной сплошной среды, использующем аналогию между уравнением
Лиувилля для функции распределения идеального газа по координатам и скоростям и
уравнением неразрывности в механике жидкости.
В настоящей работе проводится доказательство аналога
теоремы В.В. Козлова о диффузии для случая принадлежности распределений (мер в
фазовом пространстве) классам функций, отличным от интегрируемых по Риману или
Лебегу. Именно, доказано существование слабого предела решения уравнения
Лиувилля для бесстолкновительной сплошной среды, когда распределение
принадлежит классу сингулярных обобщенных функций по пространственной
координате.
2. Постановка задачи
Введем следующую систему обозначений. Следуя [2],
движение частицы в замкнутом сосуде, например, в n-мерном
параллелепипеде, с условием упругого отражения от стенок может быть
представлено как бесстолкновительное периодическое движение на торе 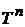 . Пусть скорость . Пусть скорость  частицы принадлежит частицы принадлежит 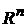 . Тогда ее движение в фазовом пространстве . Тогда ее движение в фазовом пространстве 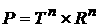 задается уравнениями задается уравнениями
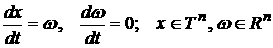 .
(1) .
(1)
Предположим теперь, что имеется континуум частиц,
которые движутся по закону (1), т.е. не сталкиваются между собой, но упруго
отражаются от стенок сосуда. Введем функцию распределения такой
бесстолкновительной сплошной среды 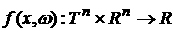 . Исследуем, сходится ли и в каком смысле эта функция
распределения при . Исследуем, сходится ли и в каком смысле эта функция
распределения при 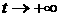 . .
Введем оператор эволюции системы
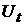 : : 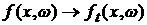 , ,
где
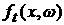 – функция
распределения через промежуток времени t: – функция
распределения через промежуток времени t: 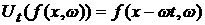 . .
Приведем формулировки теорем, доказанных В.В. Козловым
в [2] относительно асимптотических свойств функции 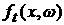 , которые обобщаются в данной работе. , которые обобщаются в данной работе.
Теорема 1 (В. В.
Козлов).
Пусть 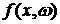 : : 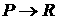 есть интегрируемая по
Лебегу функция, а есть интегрируемая по
Лебегу функция, а 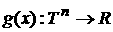 интегрируемая по
Риману функция. Введем функционал интегрируемая по
Риману функция. Введем функционал
 . (2) . (2)
Тогда
существует предел этого функционала при 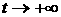 , равный , равный
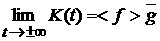 , (3) , (3)
где
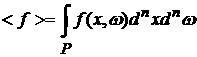 , , 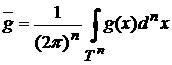 . (4) . (4)
Теорема 2 (В. В. Козлов).
Пусть 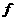 , , 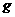 : : 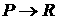 - интегрируемые по
Лебегу функции вместе со своими квадратами, т.е. - интегрируемые по
Лебегу функции вместе со своими квадратами, т.е. 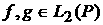 . Введем функционал . Введем функционал
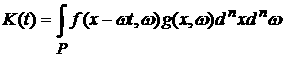 .
(5) .
(5)
Тогда существует предел этого
функционала при 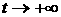 , равный , равный
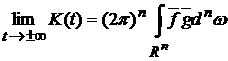 .
(6) .
(6)
В формуле (6) черта сверху означает усреднение по
тору, как и в (4). В частном случае теоремы 1, когда 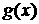 является
характеристической функцией некоторого множества является
характеристической функцией некоторого множества 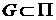 , измеримого в смысле Жордановой меры, функционал , измеримого в смысле Жордановой меры, функционал 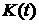 в формуле (2)
может быть представлен в виде в формуле (2)
может быть представлен в виде
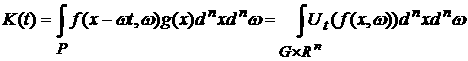 . .
Последний интеграл представляет собой долю частиц,
находящихся в момент времени 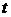 в объеме в объеме 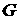 . Следовательно, указанная теорема имеет следующую
интерпретацию [2]: . Следовательно, указанная теорема имеет следующую
интерпретацию [2]:
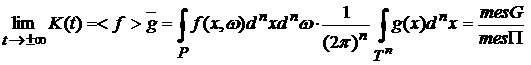 , ,
т.е.
частицы со временем стремятся равномерно заполнить сосуд.
В теореме 2 функцию распределения следует
рассматривать как линейный функционал на пространстве 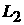 . В пространстве линейных функционалов предел . В пространстве линейных функционалов предел 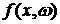 при при 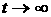 понимается в слабом
смысле, и теорема 2 позволяет найти этот предел. Именно, определим непрерывный
линейный функционал понимается в слабом
смысле, и теорема 2 позволяет найти этот предел. Именно, определим непрерывный
линейный функционал
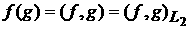 . .
Тогда
теорема 2 может быть записана в следующем виде:
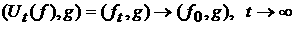 , ,
где
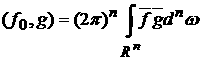 . .
Далее мы рассматриваем обобщения вышеприведенных
теорем, переходя от функций распределения к мерам в фазовом пространстве
системы.
3. Обобщение теоремы 1
Принципиально важным свойством функции плотности
распределения является ее интегрируемость по Лебегу. Отказ от этого свойства в
общем случае приводит к тому, что утверждение теоремы 1 не имеет места.
Например, пусть в системе существует конечная доля 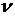 частиц с одинаковой
скоростью частиц с одинаковой
скоростью 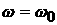 . В этом случае среднее значение некоторой функции . В этом случае среднее значение некоторой функции  по распределению по распределению  определяется как определяется как
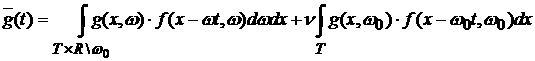 . .
В
этом выражении первое слагаемое при 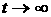 , как следует из (3)-(4), стремится к константе, а вот второе
слагаемое может являться в общем случае периодической функцией, и в результате
сумма не будет стремиться к константе. Если же существует конечный набор таких
групп частиц со скоростями , как следует из (3)-(4), стремится к константе, а вот второе
слагаемое может являться в общем случае периодической функцией, и в результате
сумма не будет стремиться к константе. Если же существует конечный набор таких
групп частиц со скоростями 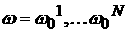 , то получающаяся в результате сумма периодических функций
является почти-периодической функцией и также не имеет предела при , то получающаяся в результате сумма периодических функций
является почти-периодической функцией и также не имеет предела при 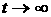 . .
Однако есть важный пример обобщения теоремы 1 на
случай, когда распределение 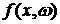 представляется в виде
линейной комбинации обобщенных функций с точечным носителем по пространственным
координатам с коэффициентами, являющимися интегрируемыми по Лебегу функциями в
пространстве скоростей. В частности, пусть представляется в виде
линейной комбинации обобщенных функций с точечным носителем по пространственным
координатам с коэффициентами, являющимися интегрируемыми по Лебегу функциями в
пространстве скоростей. В частности, пусть
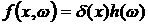 .
(7) .
(7)
Тогда
для функционала (2) получаем
 (8) (8)
Исследуем поведение 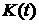 (8) при (8) при 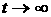 и покажем, что, как и в случае (4), частицы
со временем равномерно заполняют сосуд. Подчеркнем, что функция распределения
(7) принадлежит другому классу, чем предполагается в теореме 1. и покажем, что, как и в случае (4), частицы
со временем равномерно заполняют сосуд. Подчеркнем, что функция распределения
(7) принадлежит другому классу, чем предполагается в теореме 1.
Теорема
3.
Пусть 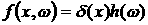 , где , где 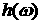 – интегрируемая по
Лебегу функция на – интегрируемая по
Лебегу функция на 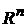 , и пусть , и пусть 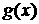 есть интегрируемая по Риману функция на есть интегрируемая по Риману функция на 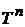 . Тогда существует предел при . Тогда существует предел при 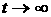 функционала функционала

(см. формулу (2)), равный
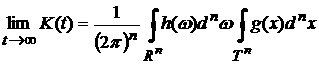 . (9) . (9)
Доказательство проводится в несколько этапов. Предварительно
заметим, что, поскольку любую интегрируемую по Лебегу функцию можно представить
как разность двух положительных функций, то доказательство достаточно провести
только для положительных функций 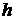 . Сначала докажем
теорему для случая, когда . Сначала докажем
теорему для случая, когда  является тригонометрическим полиномом.
Затем получим то же равенство для всех функций является тригонометрическим полиномом.
Затем получим то же равенство для всех функций  из пространства
интегрируемых по Риману на из пространства
интегрируемых по Риману на 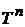 . .
1)
Пусть  . Тогда сразу же получаем формулу (9): . Тогда сразу же получаем формулу (9):
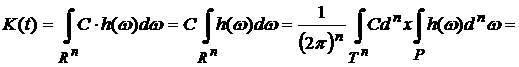
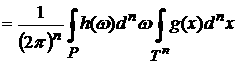 . .
2)
Пусть 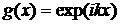 . Тогда . Тогда
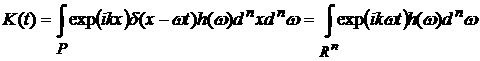 , ,
и
по теореме Римана  . В силу линейности функционала (2) отсюда следует, что
равенство (9) выполнено для всех тригонометрических полиномов. . В силу линейности функционала (2) отсюда следует, что
равенство (9) выполнено для всех тригонометрических полиномов.
3)
Пусть теперь  – функция,
интегрируемая по Риману. Тогда для любого – функция,
интегрируемая по Риману. Тогда для любого  существуют такие
тригонометрические полиномы существуют такие
тригонометрические полиномы 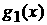 и и 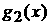 , что , что 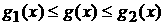 , и , и 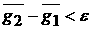 где, как и выше в (4),
чертой сверху обозначено усреднение функции по тору. где, как и выше в (4),
чертой сверху обозначено усреднение функции по тору.
Обозначим
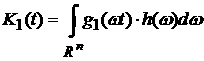 , ,  . .
Т.к.  , то , то 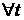 имеет место система
неравенств имеет место система
неравенств 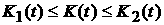 и, кроме того, и, кроме того,
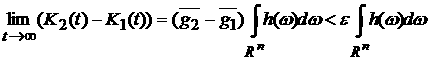 . .
Следовательно,
получаем оценку
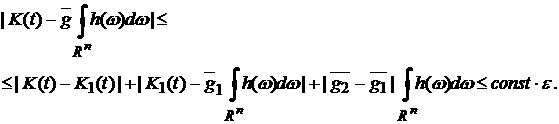
Теорема
3 доказана.
Таким образом, формулировка теоремы 1 в части
интегрируемой по Лебегу функции может быть изменена так, чтобы включить случай,
когда 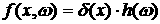 , где только , где только 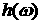 является интегрируемой
по Лебегу функцией. Теперь представляется полезным сформулировать и доказать
теорему, включающую в себя оба варианта. Для этого имеет смысл перейти от
функций распределения к мерам. является интегрируемой
по Лебегу функцией. Теперь представляется полезным сформулировать и доказать
теорему, включающую в себя оба варианта. Для этого имеет смысл перейти от
функций распределения к мерам.
4. Теорема об асимптотике меры
Заметим, что функционал 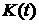 в (2) можно
рассматривать не только в виде в (2) можно
рассматривать не только в виде 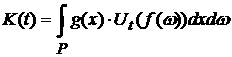 , но и перенести временную зависимость на функцию , но и перенести временную зависимость на функцию 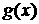 : :
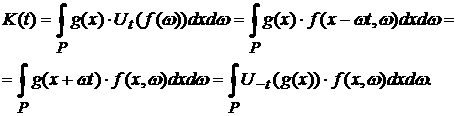
Тем самым теорема 1 может быть переформулирована в
терминах меры
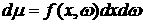 : :
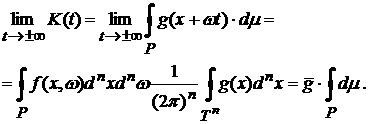
Аналогично
и функцию 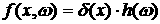 , где , где 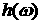 интегрируемая по
Лебегу функция, можно представить как меру интегрируемая по
Лебегу функция, можно представить как меру 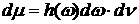 , где , где 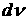 есть мера Дирака, т.е. есть мера Дирака, т.е.
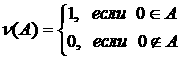 . .
В этом случае для
рассматриваемого функционала 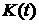 (2) получаем тот же
результат, что и в теореме 3, совпадающий формально с утверждением теоремы 1: (2) получаем тот же
результат, что и в теореме 3, совпадающий формально с утверждением теоремы 1:
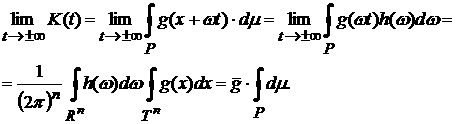
Таким образом, возникает вопрос
дальнейшего обобщения задачи: для какого класса мер можно доказать теорему 1?
Как мы уже упоминали, большое значение
имеет интегрируемость функции распределения по скоростям. Для того чтобы это
условие можно было сформулировать для произвольной меры, необходимо определить
принцип «проектирования» меры 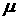 пространства пространства 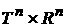 в меру в меру 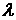 пространства пространства 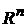 , на которую можно будет уже накладывать требования
абсолютной непрерывности относительно меры Лебега. Мы будем рассматривать
только конечные меры, определенные на борелевской , на которую можно будет уже накладывать требования
абсолютной непрерывности относительно меры Лебега. Мы будем рассматривать
только конечные меры, определенные на борелевской  - алгебре. Определим «принцип проектирования» следующим
образом: каждой интегрируемой по Риману функции - алгебре. Определим «принцип проектирования» следующим
образом: каждой интегрируемой по Риману функции 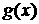 поставим в
соответствие меру поставим в
соответствие меру
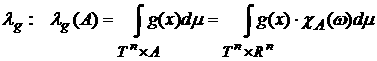 (10) (10)
для любого множества  из борелевской из борелевской  - алгебры на - алгебры на 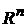 . Докажем корректность такого определения . Докажем корректность такого определения 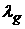 и определим
соответствующий интеграл и определим
соответствующий интеграл 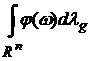 . .
Лемма. Для любой интегрируемой по Риману
функции 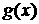 функционал функционал
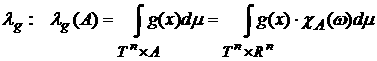
является мерой, причем для любой
ограниченной непрерывной функции 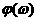 выполняется равенство выполняется равенство
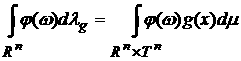 . .
Доказательство. Покажем сначала, что функционал
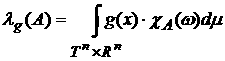
существует
и принимает конечные значения. Действительно, функция 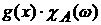 измерима относительно
борелевской измерима относительно
борелевской  - алгебры и ограничена. Следовательно, - алгебры и ограничена. Следовательно, 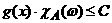 . Тогда . Тогда
 . .
Теперь
докажем, что функционал  обладает всеми
необходимыми свойствами меры, а именно: во-первых, обладает всеми
необходимыми свойствами меры, а именно: во-первых, 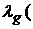 Æ) = 0; во-вторых, Æ) = 0; во-вторых,
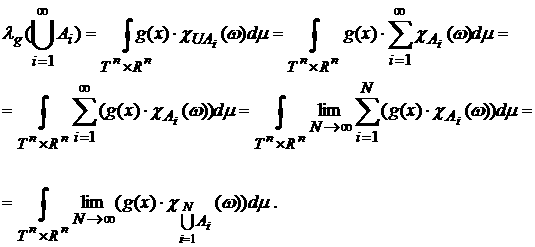
Поскольку же 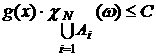 и интеграл и интеграл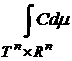 существует, то по теореме о мажорированной сходимости [4,
стр.30] написанная выше цепочка равенств может быть продолжена так: существует, то по теореме о мажорированной сходимости [4,
стр.30] написанная выше цепочка равенств может быть продолжена так:
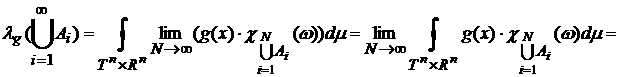
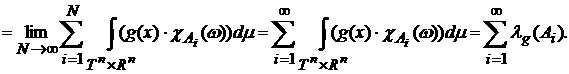
Таким образом, мера 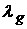 определена корректно и
является конечной. определена корректно и
является конечной.
Докажем, что любая ограниченная непрерывная функция 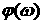 является интегрируемой
по мере является интегрируемой
по мере 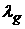 и и 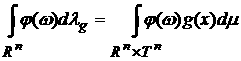 . .
Рассмотрим сначала простые функции, то есть измеримые
функции, принимающие не более чем счетное число значений. Пусть 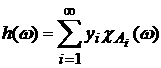 есть простая
ограниченная функция. Тогда имеем есть простая
ограниченная функция. Тогда имеем
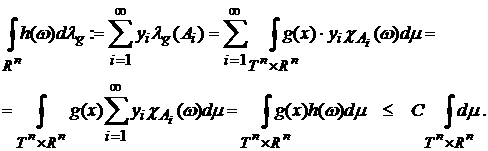
Далее, для любой ограниченной непрерывной функции 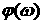 существует
последовательность равномерно сходящихся к ней простых ограниченных функций существует
последовательность равномерно сходящихся к ней простых ограниченных функций 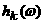 , так что , так что 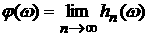 . Тогда справедлива цепочка равенств: . Тогда справедлива цепочка равенств:
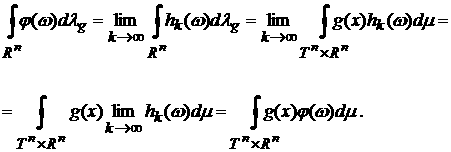
Лемма
доказана.
Таким образом, каждой интегрируемой по Риману функции 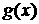 и мере и мере 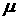 , определенной на , определенной на 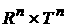 , мы ставим в соответствие меру , мы ставим в соответствие меру 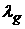 , определенную на , определенную на 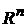 . На эту меру мы будем накладывать ограничения, которые
накладывали на функцию . На эту меру мы будем накладывать ограничения, которые
накладывали на функцию 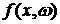 по переменной по переменной  , а именно: мера , а именно: мера 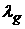 должна быть абсолютно
непрерывна относительно меры Лебега, то есть должна быть абсолютно
непрерывна относительно меры Лебега, то есть 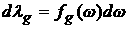 . Тогда справедливо следующее утверждение, являющееся
обобщением теоремы 1. . Тогда справедливо следующее утверждение, являющееся
обобщением теоремы 1.
Теорема 4. Пусть мера 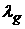 , определенная в (10), абсолютно непрерывна относительно меры
Лебега. Тогда существует предел , определенная в (10), абсолютно непрерывна относительно меры
Лебега. Тогда существует предел
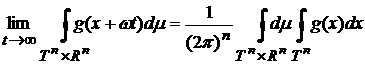 (11) (11)
Доказательство теоремы 4 проводим аналогично доказательству теоремы
3.
1).
Пусть 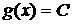 . Очевидно, что . Очевидно, что
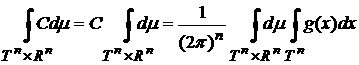 , ,
т.е.
формула (11) выполнена.
2).
Пусть 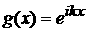 . Тогда . Тогда
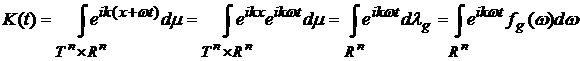 . .
Так
как 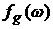 - интегрируемая по
Лебегу функция, то по теореме Римана - интегрируемая по
Лебегу функция, то по теореме Римана 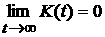 . Таким образом, формула (11) справедлива, если . Таким образом, формула (11) справедлива, если 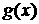 – тригонометрический
полином. – тригонометрический
полином.
3.)
Пусть теперь 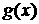 интегрируемая по
Риману функция. Тогда существуют такие тригонометрические полиномы интегрируемая по
Риману функция. Тогда существуют такие тригонометрические полиномы 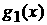 и и 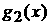 , что , что
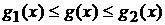 , , 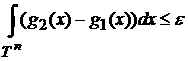 . .
Отсюда
следует, что
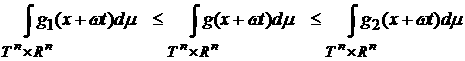 . .
4).
Из пункта 2) доказательства следует, что существует такое  , что при всех , что при всех 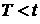 выполняется выполняется
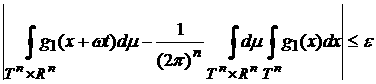 . .
Поскольку
же 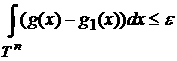 , то , то
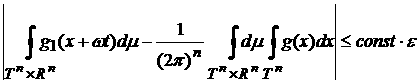 . .
Аналогичное
неравенство записывается и для 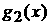 . Тогда получаем, что . Тогда получаем, что
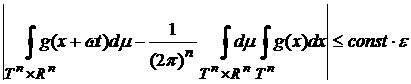 , ,
то есть
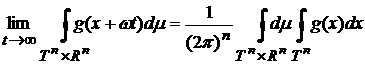 . .
Теорема
4 доказана.
5. Заключение
Итак, мы рассмотрели возможность обобщения
формулировки теоремы о слабой асимптотике функции распределения, являющейся
решением уравнения Лиувилля, переходя от распределений к мерам и вводя операцию
проектирования меры на пространство скоростей так, чтобы полученная мера была
абсолютно непрерывна относительно меры Лебега. В этот класс мер попадает и мера
в виде обобщенной функции с точечным носителем по пространственной координате.
Тем самым «теорема о диффузии» (теорема 1 В.В. Козлова) усиливается с позиций
ее физической интерпретации.
Используя теорему 2, можно сказать, что необратимая
диффузия до полностью однородного состояния идеального газа в сосуде с зеркальными
граничными условиями имеет место даже в том случае, когда первоначально газ был
собран «в одной точке», если только распределение его по скоростям является
интегрируемой по Лебегу функцией.
Представляется, что формулировка и доказательство
теоремы 1 (теорема 4) в терминах меры позволяет унифицировать метод
доказательства аналогичных утверждений для более сложных динамических систем,
чем модель (1). В то же время подчеркнем, что и бесстолкновительная модель (1)
обладает нетривиальным поведением с точки зрения стремления к равновесию.
Авторы глубоко признательны академику В.В. Козлову за
возможность обсуждения на его семинарах отдельных аспектов рассматриваемой
проблемы, связанных с термодинамической и статистической интерпретацией
полученных результатов, а также профессорам В.В. Веденяпину и М.В. Масленникову
за внимание к работе и полезные дискуссии.
Список литературы
1. Л. Больцман. Лекции по теории газов. М.: Гостехиздат,
1956.
2.
В.В. Козлов. Тепловое равновесие по Гиббсу и Пуанкаре. Москва-Ижевск: Институт
компьютерных исследований, 2002.
3.
А. Пуанкаре. Замечания о кинетической теории газов. Избранные труды, т. III.
М.: Наука, 1974.
4. М. Рид, Б. Саймон. Методы современной
математической физики. Т 1. Функциональный анализ. М.: Мир, 1977.
|