Класс обратных задач

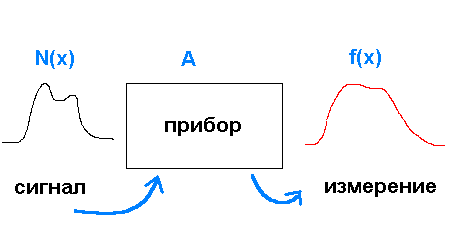
Обратные задачи наиболее типичны для экспериментальной физики. Рассмотрим типичную постановку обратных задач на примере так называемой инструментальной задачи. Пусть имеется некоторый сигнал N(x), который подвергается измерению на приборе А. Физику-исследователю доступно измерение данного сигнала, которое находится на выходе прибора (дисплее, табло или т.п.). Обозначим это измерение  f(x). Поскольку прибор вносит в сигнал, во-первых, искажения (например, в приборах типа спектрометров часто измеряются некоторые интегральные характеристики сигнала) и, во-вторых, шумовую компоненту. В результате измерения f(x) могут довольно сильно отличаться от исходного сигнала N(x) (см. рис.). В этой связи весьма актуальна задача восстановления сигнала N(x) по показаниям прибора f(x) (при наличии определенной дополнительной информации о физике измерения, т.е. об операторе , выражающем действие прибора).

Таким образом, в отличие от прямой задачи:
N(x)Ю f(x), выражающейся равуенством f(x)=А{N(x)}
обратной задачей является восстановление
N(x)Ь f(x)

Отметим, что сигнал (и, соответственно, его измерение) может зависеть от времени и/или пространственных координат. Эту зависимость мы обозначили как зависимость от х. При использовании численных методов непрерывные зависимости от х дискретизируются, заменяясь соответствующими векторами. Таким образом, задача может быть записана в векторном виде
AN= f, 
где вектор N неизвестен, а оператор (в линейном случае, матрица) А и вектор правых частей уравнений f известны..