Алгебраические уравнения > Метод Ньютона-Рафсона  

Метод Ньютона-Рафсона

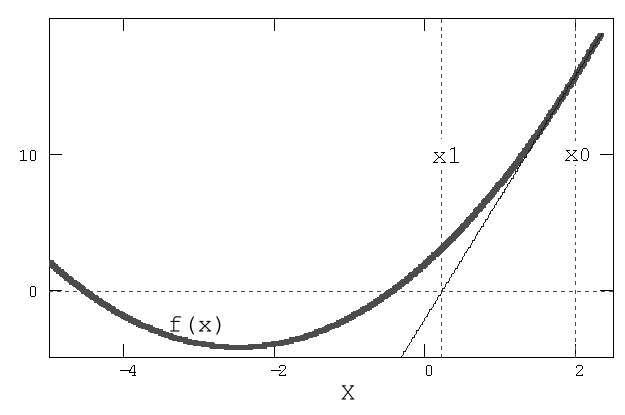
Основная идея градиентных методов состоит в последовательных приближениях к истинному решению уравнения f(x)=0, которые вычисляются с помощью производной от f(x). 

• Вводится нулевая итерация x0 

• В этой точке методом конечных разностей вычисляется производная f'(x0) 

• Пользуясь разложением Тейлора, f(x) заменяется в окрестности точки касательной – прямой линией f(x0)+f'(x0)(x-x0) 

• Определяется точка, в которой прямая пересекает ось Х

• Эта точка принимается за новую итерацию, и цикл повторяется: строится касательная, точка ее пересечения с осью и т.д., пока корень не будет найден с нужной точностью

Модификация алгоритма Ньютона для решения системы нескольких уравнений заключается в линеаризации соответствующих функций многих переменных, т. е. аппроксимации их линейной зависимостью с помощью частных производных. Например, для нулевой итерации в случае системы двух уравнений: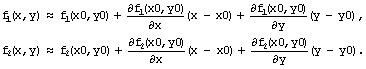

Чтобы отыскать точку, соответствующую каждой новой итерации, требуется приравнять оба равенства нулю, т.е. решить на каждом шаге полученную систему линейных уравнений.