
Решение отдельных нелинейных уравнений и систем типа представляет собой несложную, с вычислительной точки зрения, задачу. В реальных инженерных и научных расчетах очень распространена более сложная проблема: решение не одного уравнения (или системы), а целой серии уравнений, зависящих от некоторого параметра (или нескольких параметров). Для таких задач существует очень эффективные методы, которые называются методами продолжения.
Будем далее говорить об одном уравнении, имея в виду, что всегда возможно обобщение результатов на случай системы уравнений.
Пусть имеется уравнение f(a,x)=0, зависящее не только от неизвестного x, но и от параметра
a. Рассмотрим конкретный пример, аналитическое решение которого заранее известно
и зависимость уравнения от параметра a в
котором записывается следующим образом:
sin(ax)=0.
Аналитическое решение этого уравнения находится из соотношения
ax =Np, где N=0,1,2,…, т. е. имеется бесконечное количество (для каждого N) семейств решений
xN=Np/a. Несколько из семейств для N=1,2,3 показаны на рис.1
тремя сплошными кривыми. Кроме того, следует иметь в виду, что для N=0, т. е. x=0, решением является прямая, совпадающая с осью X.
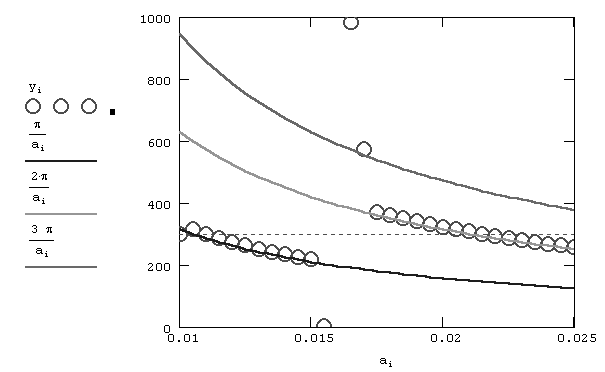
Рис.1. Решение уравнения sin(ax)=0 с нулевой
итерацией x0=300 для всех значений
параметра а
Забудем на время, что аналитическое решение известно, и подойдем к уравнению (1) как к любой другой новой задаче. Решим его,
к примеру, при помощи алгоритма секущих. Корень уравнения
требуется определить численно для каждого значения параметра a,
ради определенности, в диапазоне значений от 0.010 до 0.025 с шагом 0.0005 (эти числа взяты ради примера, Вы можете поэкспериментировать с другими значениями).
Чтобы алгоритм заработал, необходимо предварительно задать
начальное приближение к решению,
например, одно и то же начальное значение x=300 для всех
a.
Результат расчетов показан на том же рис.1 точками, причем самая левая точка отвечает начальному значению
x0=300. Обратите внимание, что, по мере увеличения a, кривая корней уравнения сначала идет по семейству решений
x=p/a, а потом (в районе a~0.17) "перепрыгивает" на другое семейство
x=2p/a. С вычислительной точки зрения такая ситуация, чаще всего, крайне неблагоприятна, поскольку хотелось бы отыскать непрерывное семейство решений. Скачки зависимости
x(a) могут вводить пользователя в заблуждение, вовсе скрывая от него существование семейства решений при a>0.17.
Почему же происходят эти скачки с одного семейства решений на другое? Конечно, причина кроется в выборе начального значения для вычисления каждого из корней. Линия начальных значений
x0=300 обозначена на рис.1 в виде пунктирной горизонтальной прямой. Для
a=0.01, и вообще для нескольких первых a начальное значение
x=300 находится ближе всего к нижнему семейству решений y=p/a. Поэтому неудивительно, что численный метод находит именно эти корни. В правой части графика на рис.1 к линии начальных значений ближе второе семейство решений y=2p/a, к ним то и приводит численный метод.
Приведенные соображения диктуют очень простой рецепт избавления от скачков и нахождения одного из семейств непрерывных решений. Для этого требуется при поиске каждого (i+1)-го корня взять начальное значение, по возможности близкое к отыскиваемому семейству. Неплохим вариантом будет выбор приближения в виде предыдущего i-го корня, который был найден для прошлого значения параметра
ai. Результат вычислений, приведенный на рис.2, разительно отличается от предыдущего. Как видно, столь малое изменение идеологии применения численного метода привело к определению непрерывного семейства корней.
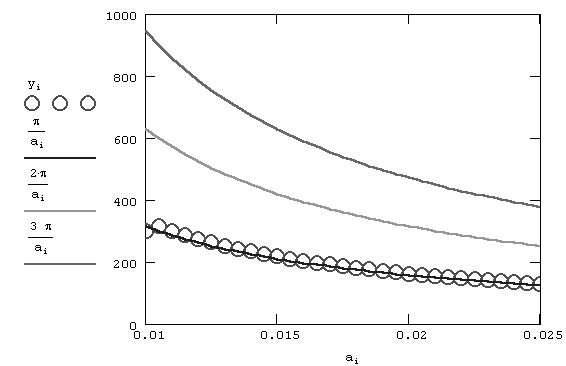
Рис.2. Решение уравнения sin(ax)=0 методом продолжения для
x0=300
Чтобы найти другое семейство решений, нужно взять соответствующее первое начальное значение, например,
600. Если взять его ближе к третьему семейству решений (например,
900), то оно и будет найдено численным
алгоритмом, и т. д.
Мы привели основную идею и наиболее простой
из возможных способов реализации метода продолжения по параметру. Безусловно, Вы можете предложить иные как математические, так и программистские решения этой проблемы. В частности, для выбора очередного начального приближения к корню можно использовать результат экстраполяции уже найденной зависимости x(a), придумать более сложные алгоритмы для ветвящихся семейств решений и т. д.