Андрей Николаевич Тихонов.
Серия Замечательные ученые физического факультета МГУ. Выпуск VIII. Москва, Физический факультет МГУ, 2004. Уравнения с малым параметром Одновременно с работами по геофизике и в Отделении прикладной математики Математического института им. В.А.Стеклова АН СССР(ОПМ) Андрей Николаевич начинает исследования по обыкновенным дифференциальным уравнениям, содержащим малый параметр при старшей производной. Хотя это не было основным направлениям его научной деятельности, тем не менее, цикл работ Андрея Николаевича положил начало большому самостоятельному направлению современной математики, в котором работали и продолжают работать многие ученые во всем мире, и которое называется теперь теорией сингулярных возмущений
К математической постановке задачи Андрея Николаевича подвела одна модель из области физической химии, по поводу которой к нему обратились за консультацией. Пусть происходит разложение вещества Y под действием катализатора Z, причем одновременно имеют место два процесса. Первый состоит в соединении вещества Y и катализатора Z с образованием при этом промежуточного продукта M и вещества, которое выделяется, например, выпадает в осадок. Второй процесс состоит в том, что вещество М, будучи неустойчивым, распадается, восстанавливая катализатор Z и образуя еще одно выделяющееся вещество. Если обозначить соответствующими малыми буквами концентрации веществ, то рассматриваемое явление будет описываться системой уравнений с начальными условиями
Здесь k и /alpha постоянные, характеризующие скорость реакции. Требуется найти концентрацию катализатора z как функцию y. Исключая m и переходя к безразмерным величинам 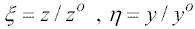 можно систему уравнений свести к одному уравнению
Практически важным является случай, когда концентрация катализатора мала по сравнению с количеством вещества /nu, т.е. /mu << 1 . Таким образом, полученная задача является задачей с малым параметром при производной.
Одной из сильных сторон Андрея Николаевича было то, что за отдельной частной задачей он умел увидеть и сформулировать общую математическую проблему. А именно, возникает следующая ситуация. Еще в 19 веке было известно, что если в правую часть дифференциального уравнения малый параметр входит достаточно гладким образом, то для того, чтобы получить приближенное решение задачи, можно положить его равным нулю и решать более простую задачу. Можно ли обращаться так же с задачей, рассмотренной выше; другими словами, можно ли найти /kci(/eta) из уравнения, полученного при /mu = 0 и считать это приближенным решением полной задачи? В общем случае нельзя, хотя бы потому, что найденное таким образом решение может не удовлетворять начальному условию. Кроме того, в силу нелинейности правой части решений при /mu = 0 может быть несколько. Какое же именно нужно выбрать для приближенного решения задачи?
В результате анализа этих вопросов Андреем Николаевичем в 1948 и 1950 годах были опубликованы работы, в которых рассматривалась система уравнений с начальными условиями, включающая уравнения с малым параметром при производной:
Были установлены условия, при которых вырожденное решение, то есть решение, полученные при /mu = 0, является пределом решения полной задачи при стремлении параметра к нулю. В частности были установлено, как выбрать корень z вырожденной системы, если их несколько. Андрей Николаевич рассмотрел случай, когда в систему входит несколько малых параметров разного порядка малости. Была дана наиболее общая формулировка понятия устойчивости решения вырожденного уравнения, имеющая прямую связь с теорией устойчивости по Ляпунову.
До работ Андрея Николаевича были отдельные статьи достаточно серьезных авторов, посвященные теме малого параметра при производных. Например, одновременно с Андреем Николаевичем аналогичной задачей занимался на механико-математическом факультете И.С.Градштейн, пришедший к близким результатам. Но такие работы не сформировали отдельного направления, что произошло в результате работ А.Н.Тихонова. По-видимому, объяснение этому заключается в том, что Андрей Николаевич был ученым, всегда работавшим в коллективе и создававшим научную школу. Каждый его результат немедленно переходил для продолжения исследования к одному из его многочисленных учеников, и процесс исследования тем самым быстро продвигался вперед. Например, А.Б.Васильевой, в дальнейшем профессору кафедры математики, Андреем Николаевичем была передана статья, находившаяся еще в рукописи, с предложением исследовать производную от решения по малому параметру. Аделаидой Борисовной была построена асимптотика, которая носит равномерный характер на всем изучаемом участке, включая пограничный слой. В отличие от случая регулярного возмущения асимптотическое разложение состоит не только из степенного ряда, но к нему добавляется ряд специального вида. А.Б.Васильева и уже ее ученики В.Ф.Бутузов, В.А Тупчиев, Н.Н.Нефедов и др. развили развили теорию сингулярных возмущений для уравнений, содержащих малые параметры при старших производных. Это было сделано как для обыкновенных дифференциальных уравнений, так и для начально-краевых задач с уравнениями в частных производных.
Другому дипломнику Андрея Николаевича, Владимиру Марковичу Волосову, в дальнейшем также профессору кафедры математики, была предложена задача, в которой условие устойчивости не было выполнено, что приводило к колебаниям высокой частоты. Из этой задачи также выросло самостоятельное направление.
| |||||
| |||||