Сплайн-интерполяция

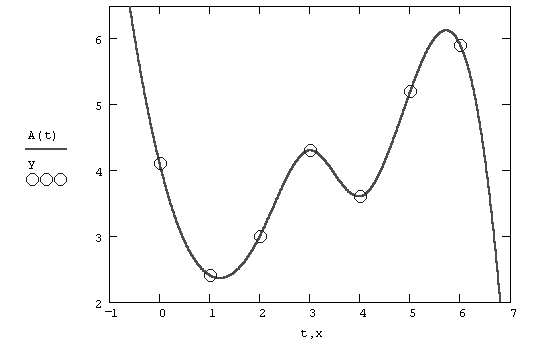В большинстве практических приложений желательно соединить экспериментальные точки (x_i,y_i)не ломаной линией, а гладкой кривой. Лучше всего для этих целей подходит интерполяция у(x) квадратичными или кубическими сплайнами, т. е. отрезками квадратичных или кубических парабол (см. рис.).

Смысл сплайн-интерполяции заключается в том, что в каждом промежутке между узловыми точками осуществляется аппроксимация в виде зависимости A(t)=a*t³+b*t²+c*t+d. Коэффициенты a,b,c,d рассчитываются независимо для каждого промежутка, исходя из значений y_i в соседних точках. Участки парабол называются сплайнами.

Сплайн-интерполяция обеспечивает равенство в узлах не только самих соседних параболических интерполирующих функций (сплайнов), но и их 1-х производных. Благодаря этому сплайн-интерполяция выглядит как очень гладкая функция.

Для построения кубической сплайн-интерполяции на i-м интервале, т.е. между узлами (t_i,t_i+1 ), используются формулы:
,

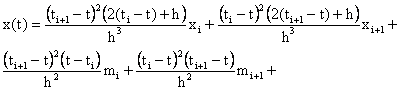где