 ,
,
ОРДЕНА ЛЕНИНА
ИНСТИТУТ ПРИКЛАДНОЙ МАТЕМАТИКИ
им.М.В.Келдыша РАН
Андрианов А.Н., Базаров
С.Б., Ефимкин К.Н.
ПРИМЕНЕНИЕ ЯЗЫКА НОРМА ДЛЯ СЕГМЕНТАЦИИ
ИЗОБРАЖЕНИЙ НА ПАРАЛЛЕЛЬНЫХ ЭВМ
Москва
Андрианов А.Н., Базаров
С.Б., Ефимкин К.Н.Применение языка НОРМА для сегментации изображений на параллельных ЭВМ.¨
Аннотация
Рассматриваются вопросы применения непроцедурного языка Норма для решения задач обработки изображений различного характера.
Язык Норма предназначен для автоматизации решения сеточных задач на вычислительных системах с параллельной архитектурой. Этот язык позволяет исключить фазу программирования, которая необходима при переходе от расчетных формул, заданных прикладным специалистом, к программе.
Приведены результаты обработки 2-х и 3-х мерных изображений.
A.N.Andrianov, S.B.Bazarov, K.N.Efimkin.
The application of NORMA language for parallel image segmentation.
Abstract
The application of nonprocedural language NORMA for the segmentation of different kind images is considered.
The Norma language is a tool aimed for automated solution of the grid-oriented problems on parallel conputer systems. This language eliminate the programming phase which is necessary to pass from computational formulas, derived by an application specialist, to a computer program.
The results of 2-D and 3-D images development are indicated.
Содержание.
Введение. *Алгоритмы сегментации.
*Программная реализация.
*Примеры обработки изображений.
*Использование методики в трехмерном случае.
*Заключение.
*Иллюстрации.
*Литература.
*Поскольку в настоящее время увеличивается использование многопроцессорных систем в численном моделировании, представляется целесообразным использование их не только для “классических” вычислительных задач, но и “сервисных” программ, одним из видов которых является обработка изображений. Использование языка НОРМА дает возможность построения программ для ЭВМ различной (в том числе параллельной) архитектурой.
Приведем описание методики, следуя в основном работе. Рассмотрим функцию
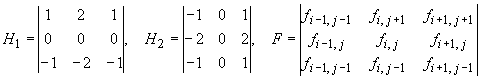 ,
,
и вычислим выражения – дискретные свертки данного окна изображения с масками
H1 и H2: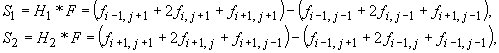
тогда величина градиента
Вычислим среднее значение градиента по всему расчетному полю:
Во множество
N1 попадают не только пиксели истинных перепадов, но и близлежащие. Для их исключения применим метод подавления немаксимумов, при котором исключается конкуренция между собой соседних точек, расположенных вдоль перепада. Принимая во внимание, чтоРассмотрим максимальную разность между значениями углов – направлений на центры соседних ячеек. Для сохранения свойства линейной протяженности перепада исключим изолированные выбросы интенсивности изображения. А именно из точек множества
N2 оставим те, в которыхДля программной реализации метода использовался транслятор-синтезатор с языка НОРМА. Приведем программу получения множества
N1 (строки, начинающиеся с восклицательного знака, являются комментариями):MAIN PART VRNOR1.
BEGIN
! Начало головной программы
GRIDSOL:((I=1..LX); (J=1..LY)).
! Сетка, на которой заданы значения интенсивности
GRID1:((I=2..(LX-1)); (J=2..(LY-1))).
! Сетка, на которой определяются значения градиента
VARIABLE F DEFINED ON GRIDSOL.
! Интенсивность изображения
VARIABLE MN1 DEFINED ON GRID1 INTEGER.
! Массив для храния признака принадлежности множеству
DOMAIN PARAMETERS LX = 125, LY = 100.
!
Размеры изображенияCOMPUTE VRRE1(LX, LY RESULT F ON GRIDSOL).
!
ФОРТРАН-подрограмма чтения массива значенийCOMPUTE VRMN1(F ON GRIDSOL RESULT MN1 ON GRID1).
!
НОРМА-процедура определения искомого множестваCOMPUTE VRWR1(MN1 ON GRID1, LX, LY).
!
ФОРТРАН-подпрограмма записи результатовEND PART.
! Конец головной программы
PART VRMN1.
! Начало процедуры определения искомого множества
F RESULT MN1
! Входной и выходной параметры процедуры
BEGIN
GRIDSOL:((I=1..LX); (J=1..LY)).
GRID1:((I=2..(LX-1)); (J=2..(LY-1))).
VARIABLE F DEFINED ON GRIDSOL.
VARIABLE MN1 DEFINED ON GRID1 INTEGER.
DOMAIN PARAMETERS LX = 125, LY = 100.
VARIABLE G DEFINED ON GRID1.
! Массив градиентов
VARIABLE SUMG REAL.
! Переменная для хранения суммы градиентов.
VARIABLE SRSUM REAL.
! Переменная для хранения среднего значения градиентов.
DISTRIBUTION INDEX I=1..15,J=1..1.
! Разбиение вычислений по 1-й координате на 15 процессов
FOR GRID1 ASSUME G = (0.125) * SQRT(
((F[I-1,J+1]+2.0*F[J+1]+F[I+1,J+1])-(F[I-1,J-1]+2.0*F[J-1]+F[I+1,J-1]))
*((F[I-1,J+1]+2.0*F[I,J+1]+F[I+1,J+1])-(F[I-1,J-1]+2.0*F[J-1]+F[I+1,J-1]))
+((F[I+1,J+1]+2.0*F[I+1,J]+F[I+1,J-1])-(F[I-1,J+1]+2.0*F[I-1]+F[I-1,J-1]))
*((F[I+1,J+1]+2.0*F[I+1]+F[I+1,J-1])-(F[I-1,J+1]+2.0*F[I-1]+F[I-1,J-1]))).
! Вычисление градиентов
SUMG=SUM((GRID1)G).
! Вычисление суммы градиентов
SRSUM=SUMG/((LX-2.0)*(LY-2.0)).
! Вычисление среднего значения градиента
GRID1T,GRID1F:GRID1/G>SRSUM.
! Определение принадлежности множеству
FOR GRID1T ASSUME MN1=1.
! Присвоение признака принадлежности множеству
END PART.
! Конец процедуры определения искомого множества
Программа транслировалась в стандарт
FORTRAN-77 (при этом оператор разбиения вычислений на несколько процессов игнорируется), в параллельный Fortran-GNS и в Fortran-MPI. Первая программа реализовывалась на ПК Pentium, вторая – на МВК-100, третья – на МВК-1000.Примеры обработки изображений.
Возьмем в качестве цифрового изображения результат численного моделирования дифракции ударной волны (число Маха 4.7,
На рис.1 приведены изолинии
f (пунктир – первоначальное положение ударной волны, стрелка – направление ее движения), а на рис.2-4 приведены точки множеств N1– N3 соответственно. То есть таким образом удалось выявить разрывы течения (в дальнейшем предполагается перенести на параллельные ЭВМ также и алгоритмы классификации разрывов).Следует отметить, что приведенная методика не требует никакой априорной информации о течении и применима к результатам расчетов, полученных любым методом сквозного счета. В случае, если численное моделирование проводилось каким-либо методом, дающим осцилляции в окрестности разрыва, возможно применение процедуры сглаживания изображения с помощью какой-либо расфокусирующей маски. В случае необходимости также возможно использование алгоритмов реставрации изображения.
Проиллюстрируем обработку экспериментальной фотографии перерасширенной сверхзвуковой струи (М=1.8). Изображение сканировалось с разрешением 300 точек на дюйм в режиме 256-ти градаций серого и сохранялось в формате “инкапсулированный ПостСкрипт”. Получающийся файл (с расширением
EPS) является текстовым и поэтому может передаваться и обрабатываться на ЭВМ другого типа. На рис.5 приведен результат сегментации, где хорошо видна бочкообразная структура течения.Применение данной методики в медицине иллюстрируется рис.6 – обработке сцинтиграммы печени (размер изображения 64*64 пиксела), позволившую выявить имеющиеся аномалии.
В заключении приведем обработку фотографии персонального компьютера, полученную цифровой камерой (с разрешением 640*480) в условиях плохого освещения – рис.7. Удалось выделить основные контуры изображения, дающие представление об объектах сцены
(корпус, клавиатура, монитор).Использование методики в трехмерном случае.
В трехмерном случае мы имеем дело с функцией интенсивности
Рассмотрим окно изображения
f размером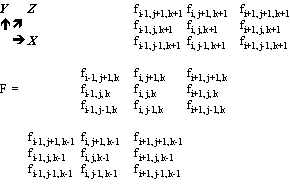
и применим к нему для вычисления составляющей градиента
Gx оператор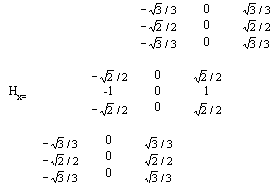
Операторы для вычисления компонент
Gy и Gz получаются при соответствующих изменениях ориентации Hx. Свойством этих операторов является то, что они дают наилучший (по методу наименьших квадратов) плоский контур между двумя областями различной интенсивности в трехмерной окрестности. Величина градиента определяется какВначале рассмотрим тестовый пример ступенчатого перепада, когда в качестве изображения берется массив данных, в котором от нуля отличны только значения в точках, лежащих на ребрах произвольного куба (для определенности полагаем все их равными единице). Те точки, в которых выполняется неравенство
Рассмотрим такую газодинамическую задачу: в начальный момент времени область, ограниченная непроницаемыми плоскостями
x=0, y=0, z=0, x=50, y=50, z=50, заполнена газом с параметрамиПоскольку заведомо известно, что использовавшиеся расчетная сетка (
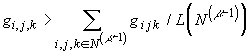 . При применении такой процедуры происходит “удаление” более слабых (по интенсивности) разрывов с одновременным утончением относительно более сильных.
. При применении такой процедуры происходит “удаление” более слабых (по интенсивности) разрывов с одновременным утончением относительно более сильных.
На рис.9 и рис.10 в двух различных ракурсах приведено множество точек
Заметим, что применение данной методике можно найти и в медицине при обработке набора томограмм – снимков слоев изучаемой области, которые “в сумме” представляют собой “трехмерное изображение”.
Описанный подход обеспечивает обработку изображений, получаемых в результате численного моделирования и физического эксперимента и повышает объективность интерпретации получаемых результатов.
Использование языка НОРМА позволяет существенно облегчить разработку соответствующих программ для многопроцессорных ЭВМ, а также повысить их переносимость. Параллелизация ускоряет процесс обработки изображения, что особенно важно в трехмерном случае.
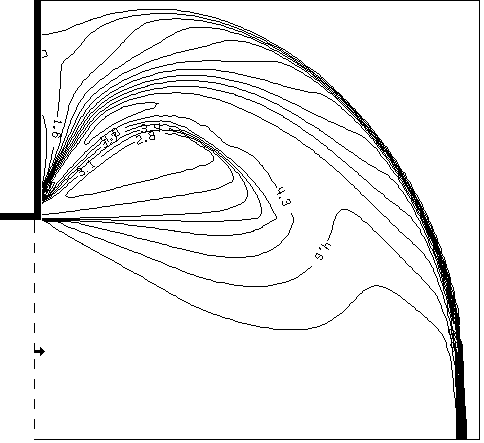
Рис.1
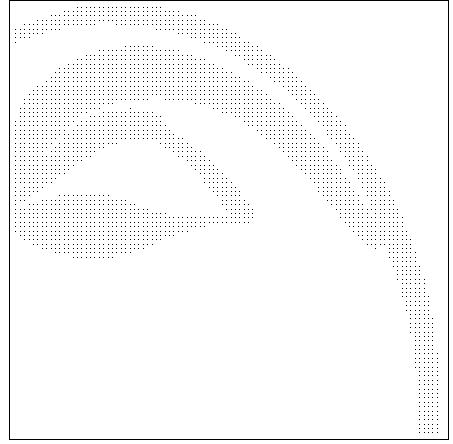
Рис.2
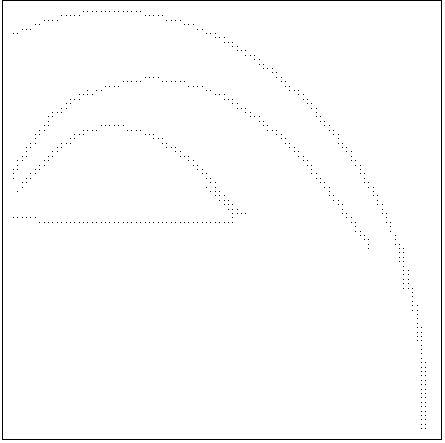
Рис.3
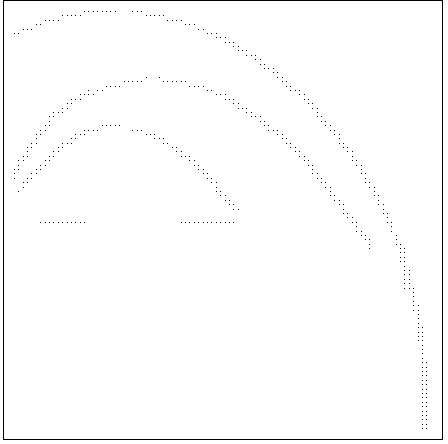
Рис.4
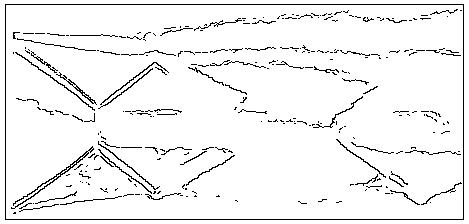
Рис.5
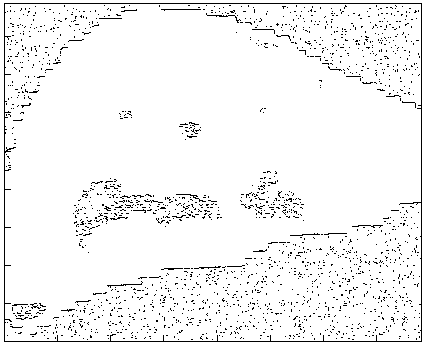
Рис.6
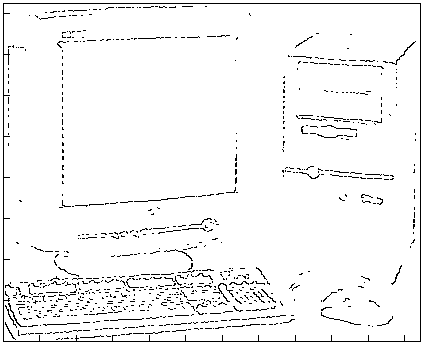
Рис.7
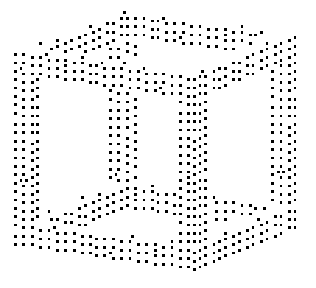
Рис.8
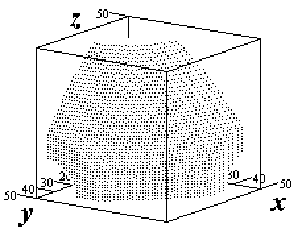
Рис.9
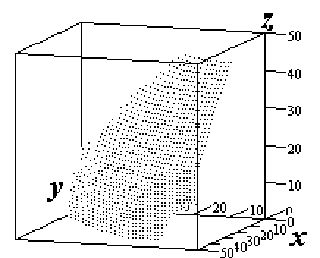
Рис.10
Базаров С.Б. Применение методов обработки изображений в вычислительной газодинамике // Труды 8-й Международной конференции по компьютерной графике и визуализации. Москва. 7-11 сентября 1998 г. с.258-264.
Shaw G.B. Local and regional edge detectors: some comparisons. Computer graphics and image processing. No.2. v.9. 1979. pp.135-149. Rosenfeld A. and Kak A.C. Digital Picture Processing. New York. Academic Press. 1976. 457 pp. Nevatia R. and Babu K.R. Linear feature extraction and description. Computer Graphics and Image Processing. No.3. v.13. 1980. pp.257-269. А.Н.Андрианов, А.Б.Бугеря, К.Н.Ефимкин, И.Б.Задыхайло. НОРМА. Описание языка. Рабочий стандарт / Препринт ИПМ им.М.В.Келдыша РАН. №120. 1995. 52с. Годунов С.К., Забродин А.В., Иванов М.Я. и др. Численное решение многомерных задач газовой динамики. М. Наука. 1976. 400 с. Альбом течений жидкости и газа. Сост. М.Ван-Дайк. М. Мир. 1986. 184с. В.З.Агранат, О.Л.Рябов, Б.В.Соколов. Способы прямого вычисления сверток матрицы чисел с некоторыми весовыми функциями / Препринт ИАЭ им.И.В.Курчатова. М. 1983. 24 с. Zucker S.W., Hummel R.A. Three-Dimensional Edge Operator. IEEE Trans. Pattern Anal. Mach. Intell. PAMI-3. No.3. 1981. pp.324-331.