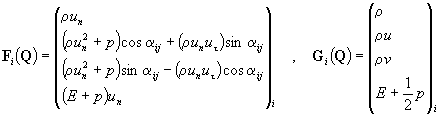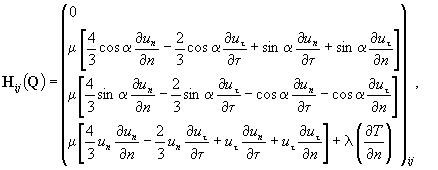ИСПОЛЬЗОВАНИЕ ПАРАЛЛЕЛЬНЫХ АЛГОРИТМОВ ДЛЯ РАСЧЕТОВ ГАЗОДИНАМИЧЕСКИХ ТЕЧЕНИЙ НА НЕРЕГУЛЯРНЫХ СЕТКАХ
А.Н. Андрианов, А.В. Жохова, Б.Н. Четверушкин
Введение
Работа посвящена моделированию сверхзвукового течения газа около тел сложной формы на параллельных вычислительных системах. Для расчетов используются кинетически-согласованные разностные схемы (КСРС)[1-2], которые легко адаптируются к архитектуре многопроцессорных ЭВМ с распределенной памятью. Кинетически-согласованный подход обеспечивает естественное обобщение разностной схемы для линейного уравнения переноса на систему нелинейных газодинамических уравнений. Аппроксимацию уравнения переноса схемой с направленными разностями можно интерпретировать как физическую модель переноса кусочно-постоянной функции распределения. Получающиеся после осреднения разностные макроуравнения в дифференциальном приближении можно рассматривать как обобщение уравнений Эйлера и Навье-Стокса.
Ранее было проведено построение КСРС для расчетов газодинамических течений на нерегулярных (треугольных) сетках [3-4]. Использование нерегулярной расчетной сетки позволяет эффективно сгустить сетку вблизи поверхности обтекаемого тела и при той же аппроксимации решения дифференциальной задачи использовать меньше узлов по сравнению со структурированными сетками. Исследование газодинамических течений в областях сложной геометрической формы также предполагает использование неструктурированных сеток.
Предыдущий опыт использования кинетических схем показал хорошее совпадение результатов как с экспериментальными данными, так и с расчетами по другим методикам. Но для подробного описания реальной картины течения при численном моделировании требуется использовать расчетные сетки, содержащие достаточно большое число узлов. Проведение расчетов на таких сетках предполагает использование соответственно больших вычислительных мощностей и, следовательно, применение параллельных вычислительных систем.
1. Кинетически-согласованная аппроксимация на нерегулярной сетке.
Кинетически-согласованный подход построения разностных схем для уравнений газовой динамики заключается в том, что вначале проводится разностная аппроксимация уравнения переноса для одночастичной функции распределения, а затем осреднение полученного разностного уравнения с сумматорными инвариантами по всем скоростям молекул. Нерегулярность сетки делает невозможной аппроксимацию производных по координатам, поэтому уравнение переноса будем аппроксимировать интегро-интерполяционным методом, интегрируя по контрольному объему Vi с центром в узле треугольной нерегулярной сетки и ограниченному отрезками медиан, идущих из центра тяжести каждого треугольника [5] (рис. 1).
Затем, интегрируя полученное разностное уравнение переноса для
локально-максвелловской функции распределения по всем скоростям молекул получим систему разностных уравнений для моделирования невязких газодинамических течений на нерегулярной сетке.
Для описания течений вязкого теплопроводного газа необходимо провести разностную аппроксимацию диссипативных потоков
[3-4]. Вязкие составляющие потоков получены следующим образом. Тензор вязких напряжений записывается в локальной
|
системе координат, полученной из исходной системы координат поворотом на угол наклона соответствующей грани ячейки. Далее, применяя теорему Остроградского к дивергенции тензора получим вязкие потоки, стоящие в разностных уравнениях движения. Для уравнения энергии проводим аналогичные действия, только вместо тензора вязких напряжений рассматриваем скалярную величину, представляющую собой диссипативную функцию в сумме с теплопроводностью. Запишем систему уравнений для моделирования течений вязкого теплопроводного газа в векторном виде: |
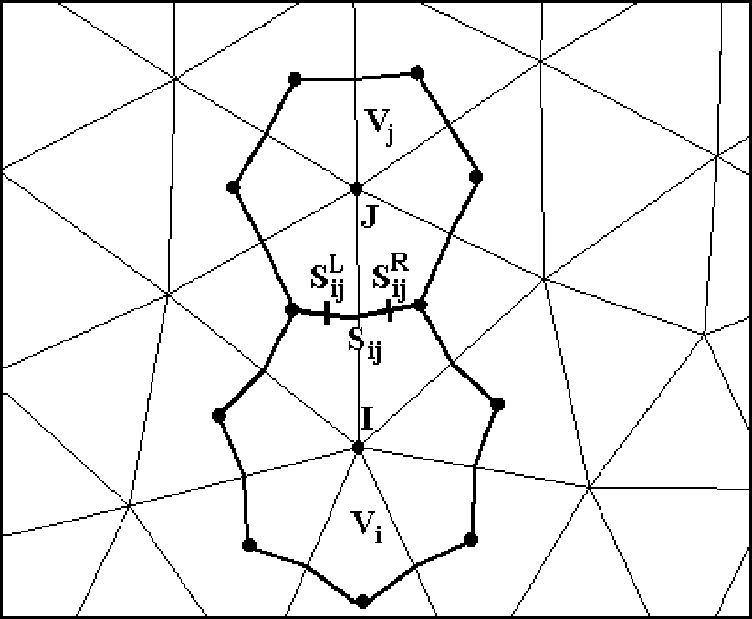
рис. 1 . Расчетная ячейка |
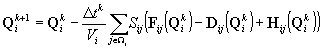 (1)
(1)
Здесь
Q=[ρ,ρu,ρv,E]T — вектор консервативных переменных, Ωi — множество соседних узлов к точке i, а Fij и Dij — конвективная и диффузионная составляющие потока:
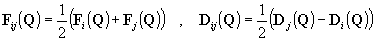 (2)
(2)
Вектор диффузии записывается следующим образом:
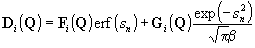 (3)
(3)
Здесь
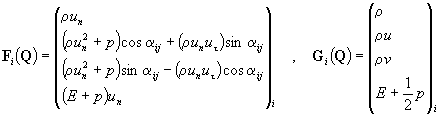
Диссипативные составляющие потока
Hij имеют следующий вид:
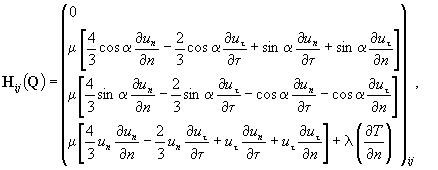
Здесь
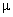 – коэффициент естественной вязкости,
– коэффициент естественной вязкости, 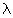 – коэффициент теплопроводности.
– коэффициент теплопроводности.
Потоковый вид записи разностной схемы упрощает ее реализацию на
вычислительной технике, в том числе и на параллельных вычислительных комплексах.
2. Моделирование сверхзвукового течения около многокомпонентного крылового профиля.
В качестве примера задач со сложной геометрической постановкой, для которых, собственно, и разрабатываются методы расчета на неструктурированных сетках, рассмотрим сверхзвуковое (
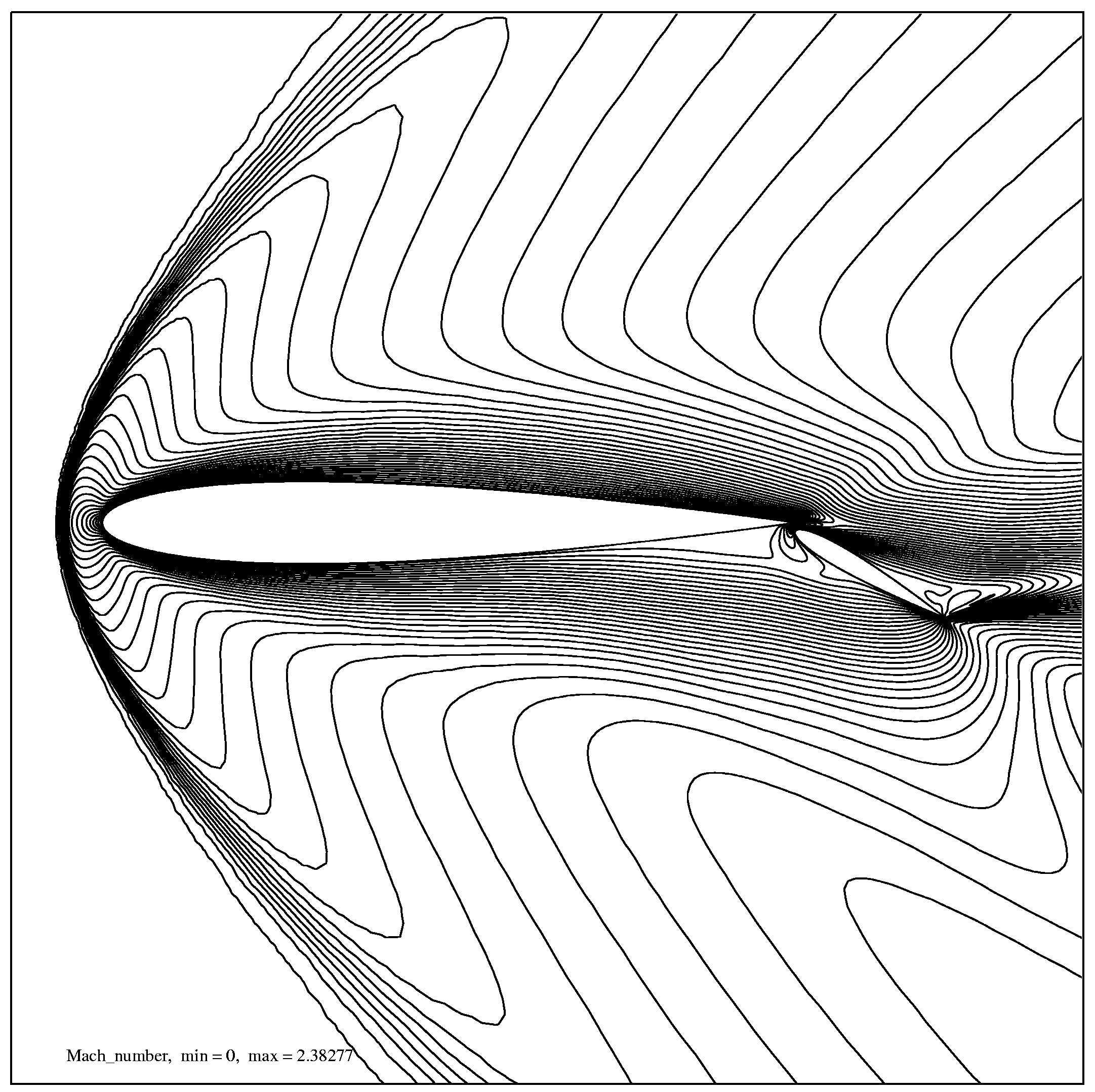
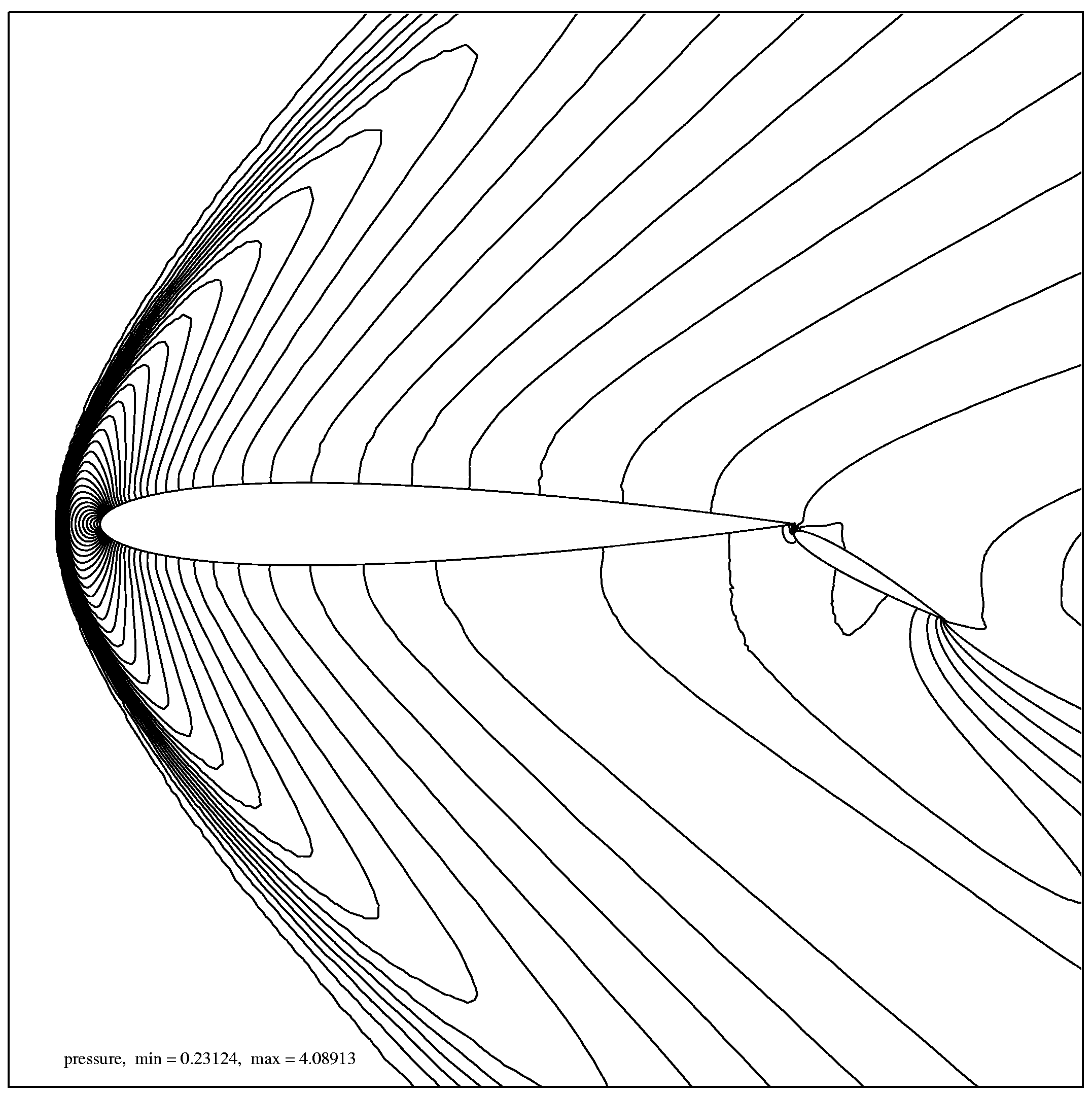
M∞=1.5) вязкое (Re∞=104) течение около многокомпонентного крылового профиля. Многоэлементное крыло состоит из двух частей, являющихся профилями NACA0012 с разной длиной хорды и под разным углом атаки. Основной крыловой профиль рассматривается под нулевым углом атаки, а закрылок, имеющий меньшую хорду, обтекается с углом атаки, равным 30°.
Сверхзвуковое вязкое течение рассматривалось в квадрате со стороной, равной десяти хордам основного крылового профиля. Расчетная сетка состоит из 150509 треугольников и содержит 75790 узлов. Около поверхности крылового профиля минимальный шаг равен
hmin=3.59´
10-5. Фрагмент установившегося течения представлен на рис. 2, рис. 3.
3. Параллельная реализация вычислительного алгоритма.
Для решения описанной выше задачи на многопроцессорной вычислительной системе
построена параллельная реализация кинетически-согласованного алгоритма. Программа для проведения расчетов была написана на языке Норма [6,7]. Язык Норма первоначально предназначался для записи решения вычислительных задач на статических структурных сетках. В последнее время широкое распространение находят и другие виды сеток. Ниже приводится классификация типов сеток, используемых при решении задач математической физики (сайт Northeast Parallel Architectures Center, Syracuse University, www.npac.syr.edu/PROJECTS/PUB/nikos/ParGG.html):
Структурные (Structured)
Статические (Static)
Неструктурные (Unstructured)
Сетки (Grids)
Вложенные (Nested)
Адаптивные (Adaptive) Движущиеся (Moving)
Неструктурные (Unstructured)
Для проведения расчетов рассматриваемой выше задачи использовалась статическая неструктурная сетка. В этом случае при разработке Норма-программы возникают две основные проблемы
:
- как задать в языке Норма вычислительную формулу при существовании зависимости одной величины от другой
, в случае использовании неструктурной сетки;
- как распределить расчетные величины между процессорами таким образом, чтобы добиться сбалансированности вычислений и минимизировать время
на обмены между процессорами. Рассмотрим эти проблемы более подробно.
Первая проблема определяется использованием неструктурных сеток и неформально может быть сформулирована следующим образом. Пусть необходимо вычислить значение расчетной величины X в точке (i,j). При вычислениях на регулярных сетках аргументы для вычисления величин обычно находятся в точках с координатами вида: (i+k,j+l), где k,l -целочисленные константы. При вычислениях на неструктурных сетках точки сетки нумеруются от 1 до N. Пусть точки, соседние к i-й точке сетки, имеют номера i1,i2,...,ik. Тогда общая структура сетки определяется матрицей neigh, состоящей из N строк, в k-й строке указываются номера точек, соседних к k-й точке. Например, если i-я строка содержит номера i1,i2,...,ik, и для вычисления значения величины X в точке i необходимо использовать значения X1 в соседних точках, то запись в программе выглядит неформально следующим образом (S - некоторая функциональная зависимость):
X(i)=S(X1(neigh(i,j)), i=1,…,N, j=1,…,ik.
Запись таких выражений в явном виде в языке Норма не предусмотрена (отсутствует понятие массива и косвенной адресации)
.
Вернемся к математической записи расчетной формулы (1), приводящей к необходимости использовать косвенную адресацию
на примере уравнения неразрывности:
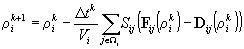 (4)
(4)
На языке Фортран такую запись обычно можно представить в следующем виде (vsn(i) - число соседей у точки с номером i):
DO i=1,N
sum=0.0
DO j=1,vsn(i)
sum=sum+F(neigh(i,j))-D(neigh(i,j))
ENDDO
ro(i)=ro(i)-dt/v(i)*
sum
ENDDO
В случае выполнения программы на распределенных вычислительных системах
косвенная адресация приводит к большим трудностям при построении эффективной параллельной программы. Это связано с тем, что нельзя явно указать номер точки, используемой в качестве аргумента выражения и, как следствие, нельзя указать номер процессора, в котором находится эта точка.
Один из способов преодоления этой трудности состоит в том, чтобы преобразовать исходную запись (4) к следующему виду
:
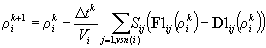 (5)
(5)
В этом случае, вместо значений
F(j) и D(j) в каждой точке, мы вводим вспомогательные переменные F1(i,j) и D1(i,j), которые строятся по следующему правилу: F1(i,j)=F(neigh(i,j)), D1(i,j)=D(neigh(i,j)), то есть "размножаем" используемые значения.
Если выражение (1) мы не могли записать на Норме, то в последнем случае такая запись возможна и имеет вид
:
FOR oi ASSUME ro =ro(it-1)-dt/v*SUM((oj) F1-D1),
где
oi : (i=1..N), oj : (j=1..8)/j<vsn(i) - используемые области изменения индексов. При этом величины F1 и D1 описываются на области oij : (oi;oj):
VARIABLE F1,D1 DEFINED ON oij.
Здесь важно отметить следующее обстоятельство. Если при программировании записи (4) вычисленные значения величин
F и D привязываются к конкретным точкам, то в случае (5) необходимо после завершения витка итерационного цикла предусмотреть распределение вычисленных значений по соответствующим местам в матрицах F1 и D1. Для этого были написаны подпрограммы, выполнение которых обеспечивает обмен данными между процессорами. Существенно, что на каждом шаге итерации обмен происходит между одними и теми же процессорами, так как сетка статическая - конфигурация сетки не изменяется на протяжении счета задачи. Конечно, нетрудно заметить, что при таком подходе значительно увеличивается размер используемой памяти. Однако, теперь для каждой точки известно, что аргументы, используемые для ее вычисления, находятся в том же процессоре, где находится и сама точка.
Вторая проблема связана с распределением расчетных точек по процессорам распределенной системы таким образом
, чтобы минимизировать время на передачу сообщений между ними. Эта проблема в последнее время интенсивно изучается (например, [8-10]) и является самостоятельной задачей, не зависящей от средств и методов разработки программ. В общем случае время, затрачиваемое на обмены информацией между процесорами, определяется двумя характеристиками. Во-первых, это количество вызовов процедур обмена, то есть, если точки, помещенные в процессор, имеют соседство с точками, размещенными в других k процессорах, то тогда необходимо обращаться к процедуре обмена k раз. Второй характеристикой является объем передаваемой информации между процессорами.
Время, необходимое для выполнения операции отправки сообщения, в общем случае, имеет вид
T=t*L+b, где L - длина сообщения в байтах, t - чистое время передачи одного байта и b - накладные расходы на вызов процедуры передачи данных (latency time). Иногда b называют временем передачи сообщения “нулевой длины”. Известно, что b>>t. Время T определяет накладные расходы, вызванные тем, что задача решается на распределенной вычислительной системе.
Минимизировать
T можно как снижением числа обращений к процедурам обмена (уменьшение k), так и уменьшением общего количества передаваемой информации.
В системах
[8-10] основное внимание уделяется сокращению общего объема передаваемой информации, причем, зачастую за счет увеличения числа обращений к процедурам обмена. К преимуществам таких систем следует отнести тот факт, что они работают очень быстро. Кроме того, уже появляются параллельные версии таких систем, которые позволяют использовать их для для динамически изменяемых сеток.
В настоящей работе был применен алгоритм сортировки (
NEW_sort), разработанный авторами. Этот алгоритм ориентирован на сокращение числа обращений к процедурам обмена данными. При этом, общий объем передаваемой информации, конечно же, может увеличиваться.
Таблица 1. METIS - распределение
|
Номер процессора |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
1 |
0 |
36 |
24 |
0 |
0 |
0 |
24 |
0 |
0 |
6 |
39 |
|
2 |
37 |
0 |
15 |
21 |
48 |
0 |
0 |
0 |
0 |
0 |
0 |
|
3 |
23 |
14 |
0 |
44 |
0 |
5 |
0 |
0 |
0 |
21 |
0 |
|
4 |
0 |
22 |
42 |
0 |
29 |
25 |
0 |
0 |
0 |
0 |
0 |
|
5 |
0 |
47 |
0 |
29 |
0 |
29 |
0 |
35 |
0 |
0 |
0 |
|
6 |
0 |
0 |
5 |
25 |
29 |
0 |
0 |
41 |
0 |
0 |
0 |
|
7 |
23 |
0 |
0 |
0 |
0 |
0 |
0 |
58 |
0 |
0 |
41 |
|
8 |
0 |
0 |
0 |
0 |
35 |
42 |
57 |
0 |
45 |
0 |
4 |
|
9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
46 |
0 |
29 |
27 |
|
10 |
7 |
0 |
21 |
0 |
0 |
0 |
0 |
0 |
29 |
0 |
55 |
|
11 |
41 |
0 |
0 |
0 |
0 |
0 |
40 |
4 |
27 |
56 |
0 |
В Таблице 1 приведена информация, полученная по результатам использования программы
METIS по распределению исходных точек по 11 процессорам. В i-строке таблицы, в позиции j, указывается число точек, находящихся в процессоре с номером j, которые являются соседними для точек из процессора с номером i.
Аналогичная информация содержится в Таблице 2. Распределение точек в этом случае получено при помощи программы, используемой авторами.
Таблица 2. New_sort
|
Номер процессора |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
1 |
0 |
192 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
194 |
0 |
189 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
3 |
0 |
188 |
0 |
193 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
4 |
0 |
0 |
193 |
0 |
185 |
0 |
0 |
0 |
0 |
0 |
0 |
|
5 |
0 |
0 |
0 |
186 |
0 |
151 |
0 |
0 |
0 |
0 |
0 |
|
6 |
0 |
0 |
0 |
0 |
154 |
0 |
142 |
0 |
0 |
0 |
0 |
|
7 |
0 |
0 |
0 |
0 |
0 |
141 |
0 |
167 |
0 |
0 |
0 |
|
8 |
0 |
0 |
0 |
0 |
0 |
0 |
164 |
0 |
150 |
0 |
0 |
|
9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
152 |
0 |
127 |
0 |
|
10 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
130 |
0 |
96 |
|
11 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
98 |
0 |
Как
видно из таблиц, общее число передач (46) для распределения, полученного по METIS-программе, превосходит общее число передач (20), полученных при помощи второго распределения. Однако, общий объем передаваемых данных во втором случае превосходит в 2.3 раза объем информации, передаваемой в первом случае. При этом общее число точек в процессоре равно 1534. При распределении исходных точек на большее число процессоров с помощью METIS распределения возрастает общее число передач (хотя объем их невелик). Кроме того, число точек, расчет которых ведется на процессоре, существенно снижается и общее число передач начинает играть значительную роль.
Ниже на рисунке 4 схематично представлено распределение точек по процессорам, полученное с помощью программы
New_sort. Прямоугольник обозначает исходную область. Все точки, находящиеся между кривыми, попадают в один процессор. Аналогично на рисунке 5 представлено распределение точек по процессорам, полученное с помощью программы METIS.
|
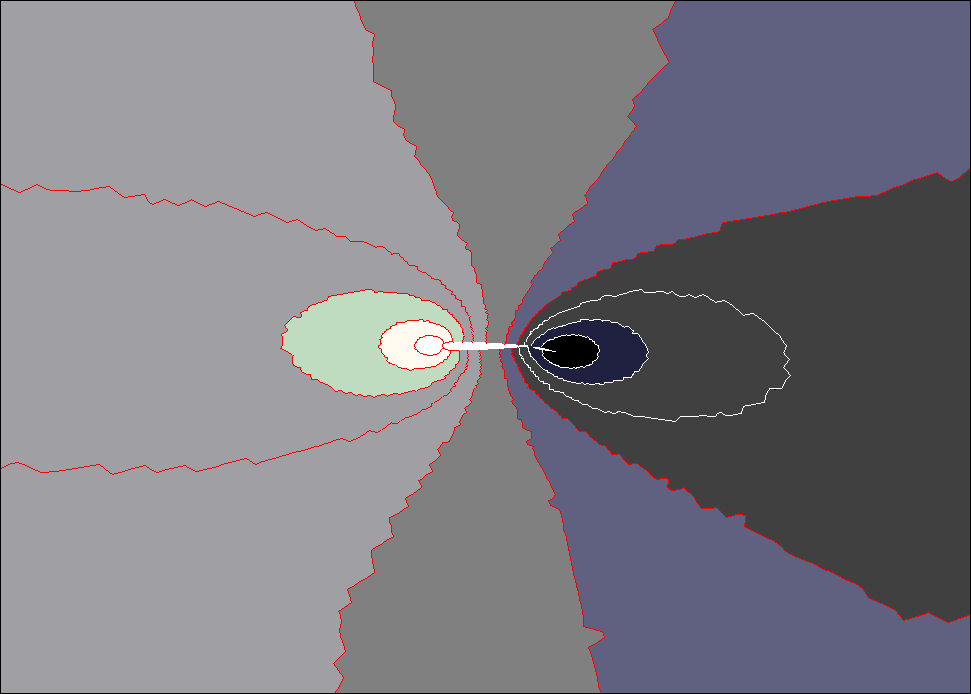
рис. 4. Распределение точек по процессорам ( New_sort). |
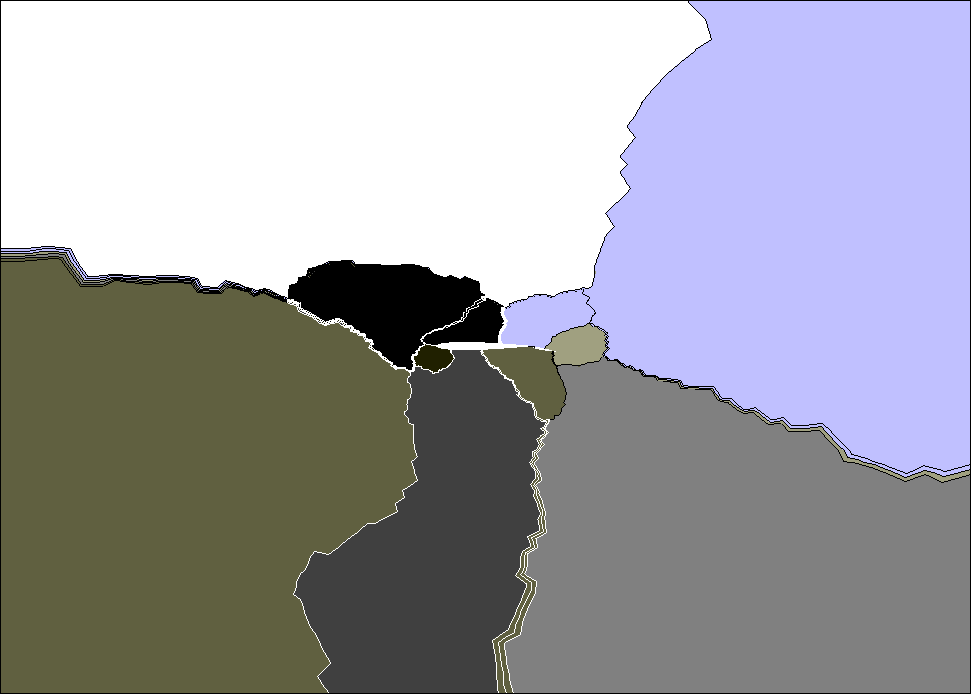
рис. 5. Распределение точек по процессорам (METIS) |
Были проведены некоторые тестовые измерения на МВС-100 для сетки, состоящей из 16864 узлов.
Таблица 3. Время выполнения 10 итераций на МВС
-100
|
Число
Процессоров |
11 |
31 |
47 |
63 |
|
New_sort |
13.59 |
5.59 |
4.38 |
4.16 |
|
METIS |
13.61 |
11.00 |
11.10 |
10.56 |
В таблице 3 указано время выполнения 10 итерационных циклов задачи на сетке из 16864 узлов. В первой строке приведены времена счета для разработанной авторами программы сортировки точек по процессорам. Во второй строке приведены времена счета, когда для распределения точек по процессорам использовалась программа
METIS. Как видно из таблицы, распределение по программе METIS с увеличением числа процессоров не позволяет сокращать время счета задачи. Это во многом определяется тем, что METIS не очень эффективен для сеток, состоящих из небольшого числа узлов при использовании распределения на большое число процессоров.
Решение задачи было запрограммировано на языке Норма. Кроме того, были написаны три программы для поддержки обмена данными между процессорами. В результате работы транслятора с языка Норма была получена программа на языке Фортран-
PVM. Выбор в качестве объектного языка Фортрана-PVM был обусловлен тем, что к моменту решения задачи, в трансляторе с языка Норма не был реализован генератор на язык Фортран-MPI. В настоящее время такой генератор реализован. Основной расчет рассматриваемой задачи проводился на ЭВМ PARSYTEC_CC–32 (использовалось 24 процессора). В результате работы алгоритма сортировки было получено такое разбиение точек по процессорам, при котором каждый процессор обменивался данными только с соседними процессорами. При этом длина максимального сообщения составляет приблизительно 20Kb (средняя длина сообщения равна ~ 13Kb). Исходные точки распределялись равномерно по процессорам, то есть каждый процессор обсчитывал 3158 точек исходной сетки.
Время счета 1000 итераций составляет
~ 920 сек. Из них процедуры обмена данными с другими процессорами занимают примерно 83 сек.
Использование языка Норма позволило автоматизировать разработку параллельной программы для рассматриваемой задачи и значительно сократить время расчета. Следует также отметить тот факт, что реализация вычислительного алгоритма в однопроцессорном варианте на сетках, состоящих из достаточно большого числа узлов (например, для задачи обтекания многокомпонентного крылового профиля, рассмотренной в п.2 сетка содержит 75790) не возможна.
Авторы благодарят Абалакина И.В. и Рубина А.Г. за помощь в проведении расчетов и обсуждение результатов.
Литература
B.N. Chetverushkin. On improvement of gas flow description via kinetically-consistent difference schemes — Experimentation, Modelling and Computation in Flow, Turbulence and Combustion, vol.2., John Wiley & Sons, Chichester, 1997, pp.27-38.
S.M. Deshpande. Kinetic flux splitting schemes — Comp. dynamic review, John Wiley & Sons, Chichester, 1995, pp.161-181.
Абалакин И.В., Жохова А.В., Четверушкин Б.Н. Кинетически согласованный алгоритм для расчета газодинамических течений на треугольных сетках — Математическое моделирование, т.10, № 4, 1998, с.51-60.
Абалакин И.В., Жохова А.В. Кинетически-согласованные схемы с коррекцией на треугольных сетках — Дифференциальные уравнения, т.34, № 7, 1998, с.904-910.
T.J. Barth, D.C. Jespersen. The design and application of upwind schemes on unstructured meshes — AIAA Paper 89-0366, 1989.
И.Б.Задыхайло, К.Н.Ефимкин. Содержательные обозначения и языки нового поколения. Информационные технологии и вычислительные системы, N2, 1996, c. 46-58.
А.Н.Андрианов, А.Б.Бугеря, К.Н.Ефимкин, И.Б.Задыхайло. Норма. Описание языка. Рабочий стандарт. Препринт ИПМ им.М.В.Келдыша РАН, N120, 1995, 50 с.
L.Oliker. PLUM: Parallel Load Balancing for Adaptive Unstructered Meshes. Journal of Parallel and Distributed Computing 52, 150-177(1998).
G.Karypis, K.Schloegel, V.Kumar. ParMETIS - Parallel Graph Partitioning and Sparse Matrix Ordering Library. Version 2.0. 1998 ( http: //www.cs.umn.edu/ ~karypis).
C.Walshaw, M.Cross. Parallel Optimisation Algorithms for Multilevel Mesh Partitioning. Tech. Rep. 99/IM/44, Univ. Greenwich, London SE18 6PF, UK, February 1999.
УДК 519.6
Андрианов
А.Н., Жохова А.В., Четверушкин Б.Н. Использование параллельных алгоритмов для расчетов газодинамических течений на нерегулярных сетках.// Проблемы математической физики. М.: Изд-во факультета ВмиК МГУ, 2000.
Работа посвящена моделированию сверхзвукового течения вязкого теплопроводного газа около тел сложной формы на параллельных вычислительных системах. Для расчетов используются кинетически-согласованные разностные схемы, которые легко адаптируются к архитектуре многопроцессорных ЭВМ с распределенной памятью. Параллельная реализация кинетически-согласованного алгоритма была написана на языке Норма.
Табл.3. Ил.5.Библиогр.10 назв.