Применение языка Норма для расчета модели дозвукового течения вязкого газа.
А.Н. Андрианов , Г.Н. Гусева, И.Б.Задыхайло
Институт математического моделирования РАН, Москва
Институт прикладной математики РАН, Москва
В работе
обсуждается возможность применения языка Норма для автоматического написания программ для многопроцессорных вычислительных систем. В качестве объекта рассмотрения используется алгоритм кинетически-согласованных разностных схем, который успешно применяется для решения задач газовой динамики. Для пространственно двумерной задачи приводятся результаты расчетов, выполненных с помощью двух многопроцессорных вычислительных систем: MBC-100 и Parsytec-CC.Norma language application in calculation of viscous gas subsonic flow model.
A.N. Andrianov, G.N. Guseva, I.B.Zadykhailo.
Institute for Mathematical Modeling, Moscow
Institute of Applied Mathematics, Moscow
A possibility of NORMA language application in software automated development for multiprocessor computing is considered in the paper. The kinetically-consistent finite difference schemes algorithm chosen as an object of the consideration is successfully being applied in solving problems related to gas dynamics. The calculation results provided herein for spatially two-dimensional problem, have been obtained by means of two multiprocessor computing systems: MBC-100 and Parsytec-CC.
1.
Математическая постановка задачи.В настоящей работе проведено моделирование дозвукового течения вязкого газа на примере обтекания воздухом квадратной каверны с движущейся в собственной плоскости верхней стенкой. Алгоритм расчета основан на использовании кинетически-согласованных разностных схем (КСРС). Схемы данного класса строятся следующим образом [1]: проводится дискретизация уравнения переноса для функции распределения числа частиц, а затем полученная разностная схема осредняется с сумматорными инвариантами.
Для записи схемы введем в расчетной области равномерную пространственную сетку с шагом h. Параметры течения постоянны внутри ячейки сетки на каждом n-том временном слое и изменяются при переходе на новый n+1 слой за промежуток времени D t. Тогда КСРС для расчета газодинамического течения в данной задаче запишется в виде:
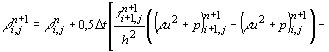
![]()
![]()
![]()
![]()
![]()
![]() (1)
(1)
![]()
![]()
![]()
![]()
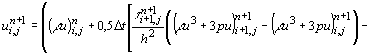
![]()
![]()
![]()
![]()
![]() (2)
(2)
![]()
![]()
![]()
![]()
![]()
![]()
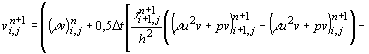
![]()
![]()
![]()
![]()
![]() (3)
(3)
![]()
![]()
![]()
![]()
![]()
![]()
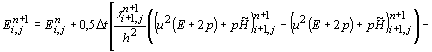
![]()
![]()
![]()
![]() (4)
(4)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Данное исследование ограничивается случаем плотных газов, когда размер ячейки пространственной сетки много больше длины свободного пробега, что позволяет не учитывать влияния диагональных ячеек и опустить смешанные производные в правых частях уравнений.
Используются следующие уравнения, связывающие параметры течения:
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]()
и степенной закон для определения вязкости
:![]() .
.
Граничные и начальные условия для разностной схемы (1)-(4) задаются следующим образом. Начальные условия для всей области:
Определение величин
![]()
Здесь вектор
Условие устойчивости разностной схемы носит курантовский характер и имеет вид
:![]() , (5)
, (5)
где
h-шаг пространственной сетки, c-скорость звука, r-число Куранта.При таком ограничении на шаг по времени для сходимости процесса на новом слое требуется небольшое число итераций (обычно
Следует отметить, что явная схема для уравнений Навье-Стокса устойчива при гораздо более жестком ограничении на шаг по времени
:![]() .
.
Мягкое ограничение (5) на шаг в сочетании с небольшим числом итераций делает объем вычислений достаточным для решения задачи на высокопроизводительных многопроцессорных вычислительных системах.
Дифференциальное приближение этих разностных уравнений носит название квазигазодинамических уравнений и имеет следующее представление
[2]:![]()
![]()
![]()
![]()
![]()
![]()
Расчет проведен при следующих параметрах внешнего потока
:![]() .
.
2.
Программная реализация на языке Норма и результаты расчетовна
многопроцессорных системах.Программа для расчетов написана на языке Норма
[3] – специализированном декларативном языке, который сначала предназначался для описания решения вычислительных задач сеточными методами, однако область его применения оказалась значительно шире.Основной тезис, который послужил первопричиной работ по проекту Норма, заключается в следующем. В большинстве случаев описание метода решения проблемы в математических терминах, используемых в определенной научной области, имеет очень высокий уровень абстракции и предоставляет большие возможности для выявления естественного параллелизма. Более того, такое описание не ориентировано на какую-либо конкретную архитектуру компьютера. По этой причине уровень описания имеет суперстабильный характер и отражает метод решения, а не его реализацию при каких-то конкретных условиях.
Язык Норма как раз и формализует ту математическую запись, которая получается в результате решения задачи вычислительного характера прикладным специалистом.
Отметим, что при описании решения задачи на Норме указываются только те правила (ограничения), которым должны удовлетворять значения переменных, при этом в записи отсутствуют понятие памяти и другие мотивы, связанные с архитектурой целевого компьютера, а также обычные элементы программ (управление, циклы, переприсваивание и т.п.).
Высокий уровень языка обеспечивает дружественный интерфейс с пользователем, так как он может использовать понятия из известной предметной области, а ошибки, которые обнаруживаются транслятером-синтезатором, также фиксируются в терминах предметной области. Автоматический синтез целевой программы по исходной Норма-программе гарантирует правильность целевой программы.
Фактически, программирование на языке Норма не требует написания программ в смысле традиционных универсальных языков программирования. Более подробно такой подход к программирования рассматривается в
[4]. Рассмотрим некоторые простейшие свойства языка, соотнося их иногда к тексту программы на Фортране и записи в математических обозначениях.|
Текст на Фортране |
Описание в математических |
Текст на Норме |
|
обозначениях |
||
|
DO j=2,nb-1 DO i=2,na-1 U(i,j)=U0 V(i,j)=0.0 P(i,j)=P0 T(i,j)=T0 RO(i,j)=P(i,j)/(R*T(i,j)) ENDDO |
|
FOR sop1 ASSUME U=U0; V=0.0; P=P0; T=T0; RO=P/(R*T). sop1((i=2..na-1);(j=2..nb-1)). |
Последняя строка в третьей колонке таблицы эквивалентна заданию некоторой двумерной сетки или области, которая в математических обозначениях имела вид
: i=2..na-1, j=2..nb-1. На языке Норма эта сетка получила название sop1. Очевидно, что в ряде случаев удобнее не выписывать каждый раз нужные диапазоны (как это сделано на Фортране и в математических обозначениях), а ссылаться на раз заданную сетку по имени.Оператор
ASSUME задает правила получения величин, стоящих в левой части. Индексы без смещения у величин могут не указываться: они однозначно восстанавливаются транслятором-синтезатором. Задание области в операторе ASSUME означает, что должны быть получены значения величин, стоящих в левой части, для всех (без исключения) точек области. В отличие от программы на Фортране, никакого порядка вычислений не предписывается. Порядок будет определен транслятором-синтезатором в зависимости от выбранной модели параллельного программирования или архитектурных особенностей вычислительной системы.Отметим некоторые другие особенности записи на Норме. Переменные
U, V, P, RO, T – это величины, определенные на сетке sop1. Такое определение делается так:VARIABLE U, V, P, RO, T DEFINED ON sop1 DOUBLE.
DOUBLE
означает, что переменные, определенные в каждой точке сетки sop1, имеют вещественные значения двойной точности. Запись видаVARIABLE U
0, V0, P0, T0 DOUBLEопределяет простые переменные с двойной точностью.
Программисты, привыкшие к Фортрану, с большим трудом понимают отличие оператора
ASSUME в Норме от оператора цикла в Фортране. Приведем следующий простой пример операторов ASSUME, который демонстрирует такое отличие (пример взят из другой программы).Текст на Норме.
Описание в математическихобозначениях.
![]()
![]()
![]()
![]()
x = 1.0
FOR DOM101 ASSUME
y = 2.0
FOR DOMOP ASSUME
![]()
![]()
Предполагается, что величины
Важное значение имеет введенная в язык Норма конструкция
ITERATION. Она определяет правила описания итерационного процесса вычислений. Например, в расчетной программе использовалось следующее описание:ITERATION U,V,P,RO,T, ttime ON time.
INITIAL time=0:
…….
END INITIAL
Эта запись означает, что итерироваться будут величины
U, V, P, RO, T, ttime, а индекс итерации time. В разделе INITIAL ... END INITIAL определяются начальные и граничные значения итерируемых переменных. Далее идет тело итерации. В нем с помощью операторов ASSUME описываются вычисления значений итерируемых переменных на новом слое по времени, определенных формулами (1)-(4).Условие окончания итерации выглядит следующим образом:EXIT WHEN (MAX((sop) ABS((U[time-1]-U[time])/U[time-1]))<eps).
END ITERATION time.
Отметим также возможность использовать в языке Норма так называемые редукционные операции, такие как суммирование, вычисление произведения, взятие минимума и максимума по всем точкам области.
Конечно, в языке Норма имеется возможность использовать части программ, подготовленные на языке Фортран.
Важно отметить, что в записи на Норме отсутствуют избыточные связи, которые обычно накладываются при программировании на процедурных языках программирования, особенно при оптимизации алгоритмов. Эти связи часто ограничивают возможности распараллеливания
: например, конструкция COMMON языка Фортран обычно делает невозможным автоматическое распараллеливание программ.Схема распараллеливания при трансляции с языка Норма кратко может быть описана следующим образом. В результате анализа информационных зависимостей между переменными Норма-программы строится граф информационных зависимостей. В результате анализа графа информационных зависимостей строится ярусно-параллельный граф алгоритма, в котором представлен
“естественный” (идеальный) параллелизм, определяемый лишь информационными зависимостями. Затем строится отображение ярусно-параллельного графа на архитектуру (модель) вычислительной системы. При построение отображения учитывается модель памяти, число процессоров, а также выполняются различные оптимизации.В настоящее время реализованы версии транслятора с языка Норма, которые позволяют получать выходные программы для распределенных параллельных вычислительных систем (модель памяти
NORMA, параллельные вычисления с передачей сообщений) и вычислительных систем с общей памятью (модели памяти NUMA, параллельные вычисления над общей памятью). Выходные программы могут быть построены на языках Фортран-77, Фортран PVM [5], Фортран GNS [6], Фортран Convex [7].Расчет модели дозвукового течения вязкого газа на примере обтекания воздухом пластины конечной длины с использованием кинетически-согласованных разностных схем (КСРС) проводился на следующих вычислительных системах
.Кратко опишем некоторые параметры рассматриваемой программы. Расчеты проводились на сетке размером
Объем данных, передаваемых между процессорами во время счета программы. составляет
62,5 Кбайт на каждом шаге итерационного процесса вычислений. Операторы отправки данных размещаются в конце итерационных циклов. Прием соответствующих данных проводится перед их первым использованием.В качестве целевых вычислительных систем использовались следующие вычислительные системы с распределенной архитектурой
.Система MВС-100
(до 64 процессоров). Эта система построена на элементах, которые выпускает фирма TRANSTECH. Каждый такой элемент (узел) состоит из пары транспьютер T800 - микропроцессор i860 (с общей памятью). В системе МВС-100 транспьютер используется в качестве элемента для передачи сообщений, а i860 – в качестве вычислителя. Несколько таких узлов обычным образом (через транспьютеры) объединяются в систему (в нашем случае – 64 узла). Тип памяти в этой системе – NORMA, а основная модель параллельных вычислений – модель передачи сообщений (message passing model). При решении задачи в качестве выходного языка Норма-транслятора использовался язык Фортран GNS [6]. Тактовая частота 50 МГц, обмен между процессорами – 1,5 Мбайт/сек.Система
Parsytec-CC (12 процессоров). Система построена на PowerPC604, тактовая частота 133 МГц, обмен между процессорами - 40 Мбайт/сек. При решении задачи в качестве выходного языка Норма-транслятора использовался язык Фортран PVM [5].Следует отметить, что Норма-транслятор позволяет получать также последовательные программы на Фортране-77 и проводить счет на ПЭВМ или рабочих станциях. Поэтому в технологической цепочке решения задачи могут быть использованы как последовательные компьютеры, так и параллельные вычислительные системы
. Любой этап в этой цепочке может оказаться, в зависимости от сложности задачи, достаточным.Время вычисления 1 внешней итерации для рассматриваемой задачи приведено в таблице
:|
ЭВМ |
Количество процессоров |
||||||||||
|
3 |
4 |
7 |
11 |
15 |
27 |
54 |
|||||
|
PARSYTEC-CC |
T |
|
2.13 |
0.83 |
|||||||
|
E |
100% |
93.2% |
|||||||||
|
МВС-100 |
T |
2.76 |
1.38 |
1.03 |
0.88 |
0.57 |
0.47 |
||||
|
E |
100% |
85.7% |
73.1% |
62.7% |
53.8% |
32.6% |
|||||
Эффективность параллелизации обычно рассчитывается по формуле
:![]() ,
,
где
Важно отметить, что программы для различных вычислительных систем (и, следовательно, для различных моделей параллельности и различных архитектур) строились автоматически транслятором.
Прикладные математики с большим трудом осваивают Норму, так как настолько свыклись с тем, что при описании решения задачи учитываются конкретные свойства языка программирования и окружения, в котором будет выполнятся программа, что часто считают невозможным (или ненужным) “чистое” математическое описание решения задачи. Однако, использование, например, понятие памяти при описании решения задачи приводит к использованию термина из совершенно другой предметной области со всеми вытекающими отсюда последствиями.
Будем надеяться, что желание
“даром” получать параллельные версии программы поможет преодолеть этот барьер.
Работа выполнена при частичном финансировании Миннауки, грант
№201011.
Список литературы.