Гравитационный маневра у луны для полета КА к сближающемуся с землей астероиду

Аннотация

В рамках анализа проблемы предотвращения астероидной опасности в работе исследуется перелет космического аппарата (КА) к астероиду, сближающемуся с Землей (АСЗ), при использовании гравитационного маневра (ГМ) у Луны. Целью полета является оказание ударного воздействия КА на АСЗ, чтобы изменить орбиту АСЗ, отклонить астероид от Земли и предотвратить их столкновение. Развиты приближенная и точная методики определения траектории полета КА от Земли к астероиду. Проведен численный анализ для сближения с астероидом Toutatis. Показано, что использование ГМ у Луны позволяет уменьшить импульс скорости разгона КА, увеличить массу КА и повысить эффективность его воздействия на астероид.

Ключевые слова: сближающиеся с Землей астероиды, астероидная опасность, космический полет к астероиду, полет к Луне, гравитационный маневр.

Abstract

In frame of the asteroid hazard mitigation problem, a space flight to near-Earth asteroid (NEA) is analysed using the lunar gravity assist. The goal of the flight is the kinetic-impact effect of the spacecraft (S/C) on the NEA to change the NEA's orbit, deflect the NEA from the Earth and prevent their collision. Approximate and exact algorithms are developed to determine the trajectory of the spacecraft to the NEA via the Moon's vicinity. A numerical analysis is performed for the flight to the asteroid Toutatis. It is shown that the using of the lunar gravity assist allows to increase the mass of S/C and efficiency of the spacecraft's effect on the NEA.

Key words: near-Earth asteroids, asteroid hazard, space flight to asteroid, space flight to Moon, gravity assist.

3.1. Определение гелиоцентрического полета КА

3.2.1. Траектория полета КА от Луны к границе сферы действия Земли

4.4. Полет КА к астероиду без гравитационного маневра у Луны

4.5. Численные результаты решения задачи в точной постановке

В работе исследуются траектории полета космического аппарата к астероиду, сближающемуся с Землей, при использовании лунного гравитационного маневра. Целью полета является оказание ударно-кинетического воздействия КА на АСЗ, в результате чего орбита АСЗ меняется, астероид отклоняется от Земли и предотвращается их столкновение. Оценки, полученные в [1], показали эффективность ударно-кинетического воздействия КА на АСЗ по сравнению с рядом других рассмотренных механических методов предотвращения столкновения АСЗ с Землей. В работах [2-5] этот метод рассмотрен более подробно для различных схем перелета КА к АСЗ. В работах [2, 3] проанализирована одноимпульсная схема перелета КА с двигательной установкой большой тяги. В работе [3] для широкого диапазона дат отлета КА от Земли и его подлета к астероиду Toutatis были построены одноимпульсные траектории перелета от Земли к астероиду и найдены локально-оптимальные (с точки зрения максимума отклонения астероида от Земли) траектории. В работе [4] рассмотрен случай перелета КА с двигателем большой тяги при возможности его двухкратного включения. В работе [5] рассмотрен случай перелета КА с двигательной установкой малой тяги. Настоящая работа является продолжением данных исследований, в ней рассматривается случай одноимпульсного перелета КА с использованием гравитационного маневра у Луны. Перелет КА к АСЗ с ГМ у Луны рассмотрен и в некоторых других работах, например, в [6, 7].

В настоящей работе анализируется данный перелет с учетом специфики воздействия КА на АСЗ. Следуя [8], где исследован перелет КА на геостационарную орбиту ИСЗ с использованием ГМ у Луны, построены приближенная и точная модели и методы анализа движения КА. В приближенной модели используются точечные сферы действия Земли, Луны и астероида. В точной модели полет КА осуществляется в соответствии с дифференциальными уравнениями движения точки в рамках проблемы 4 тел (материальная точка, Земля, Луна, Солнце) с учетом главного возмущения от несферичности гравитационного поля Земли. На основе построенных методов сделаны численные оценки характеристик траектории перелета КА к астероиду, движущемуся по орбите астероида Toutatis, для дат перелета КА, найденных в работе [3] и реализующих локально-оптимальное отклонение астероида при одноимпульсной схеме перелета для абсолютно-неупругой модели столкновения КА и астероида. Показано, что использование ГМ у Луны заметно уменьшает скорость полета к астероиду, увеличивает массу КА и эффективность его воздействия на АСЗ.

Рассматривается следующая схема полета КА (см. Рис. 1). Сначала, в некоторый момент t₀ КА разгоняется с низкой околоземной опорной орбиты (орбиты ожидания) с помощью двигателя большой тяги, включаемого импульсно около перицентра этой орбиты, и выходит на траекторию полета к Луне. После осуществления гравитационного маневра у Луны КА достигает требуемой геоцентрической скорости на бесконечности V_¥ и выходит в момент t₁⁺ на гелиоцентрический участок траектории – межпланетную траекторию перелета к астероиду. В момент t₂ КА встречается с астероидом и осуществляет ударно-кинетическое воздействие на него. В результате этого воздействия в момент времени t₃ наибольшего сближения астероида с Землей астероид отклоняется от исходной номинальной траектории. Это отклонение оценивается в картинной плоскости Земли.

Необходимо определить траекторию полета КА к астероиду с учетом ГМ у Луны и определить для нее отклонение астероида от Земли, вызванное воздействием КА на астероид. Как и в [8], анализ проведен для двух моделей движения КА. Сначала, в п.3, выполнен упрощенный анализ, основанный на моделях точечных сфер действия Земли, Луны и астероида. Затем, в п. 4, выполнен "точный" анализ, для которого используются дифференциальные уравнения движения КА в поле притяжения Земли, Луны и Солнца.

Для анализа задачи используются следующие системы координат (СК): а) O₁X₁Y₁Z₁ – гелиоцентрическая эклиптическая невращающаяся СК, СК₍₁₎; б) O₂X₂Y₂Z₂ – геоцентрическая геоэкваториальная невращающаяся СК, СК₍₂₎; в) O₃X₃Y₃Z₃ – селеноцентрическая геоэкваториальная невращающаяся СК, СК₍₃₎. При этом используются среднее равнодействие и средний геоэкватор стандартной эпохи J2000.0. Для более наглядного представления принадлежности векторов положения и скорости, а также элементов орбиты к той или иной системе координат иногда будем использовать нижние индексы (1), (2), (3), соответствующие указанным СК.

Задачу удобно рассмотреть в два этапа. На первом этапе, в п. 3.1, определяется гелиоцентрическая траектория полета КА от Земли к астероиду, на основе точечных сфер действия Земли и астероида. На втором этапе, в п. 3.2, выполнен анализ геоцентрического движения КА и оценена возможность осуществления гравитационного маневра у Луны для реализации гелиоцентрического полета. В п. 3.3 приведены результаты численной оценки характеристик полета к астероиду Toutatis для приближенного метода.

В модели точечных сфер действия Земли и астероида определение гелиоцентрической траектории перелета КА от Земли к астероиду осуществляется, как и в [2, 3], решением задачи Ламберта по заданным временам отлета от Земли t₁ и прилета к астероиду t₂. Для этого необходимо знание начального и конечного гелиоцентрических радиусов-векторов КА:

R₍₁₎(t₁) = R_E(1)(t₁), R₍₁₎(t₂) = R_A(1)(t₂); (3.1)

здесь R(t), R_E(t), R_A(t) – радиусы-векторы КА, Земли, астероида в момент t, они определяются по элементам орбит КА, Земли и астероида на соответствующий момент времени. Решением задачи Ламберта является гелиоцентрическая орбита КА с элементами

где a, e, t – большая полуось, эксцентриситет и момент прохождения перицентра орбиты, W, i, w – долгота восходящего узла, наклонение, аргумент широты перицентра – относительно плоскости эклиптики. Для оценки импульса скорости dV_A, сообщаемого астероиду в результате ударного воздействия, необходимо знание массы и вектора скорости КА при подлете к астероиду [2, 3]. Масса КА после разгона с опорной орбиты вычисляется по формуле Циолковского:

где m₀ – исходная масса КА на опорной орбите, с – скорость истечения газов из сопла двигателя КА при разгоне, DV – величина прилагаемого на опорной орбите разгонного импульса скорости:

DV = (V_¥² + 2 m_E / r_p₀)^1/2 – (m_E / p₀)^1/2 (1 + e₀). (3.4)

Здесь m_E – гравитационный параметр Земли, p₀, e₀ – фокальный параметр и эксцентриситет опорной орбиты, r_p₀ = p₀ / (1 + e₀) – ее перигейное расстояние (здесь, в п. 3 предполагается, что разгон осуществляется в перицентре опорной орбиты), V_¥ = |V_¥|, где вектор скорости на бесконечности

Здесь V(t), V_E(t) – векторы гелиоцентрической скорости КА и Земли в момент t, они определяются элементами орбит КА и Земли на этот момент.

Зная скорость КА V₍₁₎(t₂), скорость астероида V_A(1)(t₂) и массу КА m(t₂) = m₁ (в предположении постоянства массы КА после разгона), для известной модели столкновения КА и астероида можно определить вызванное воздействием КА отклонение астероида от Земли в картинной плоскости Земли на момент t₃ максимального сближения астероида и Земли [2, 3]. Если Dx, Dh - изменения координат астероида в этой картинной плоскости из-за воздействия КА, то полное отклонение астероида

После определения гелиоцентрической орбиты полета КА анализируется задача второго этапа – движение КА внутри сферы действия Земли. При этом сфера действия Луны считается точечной, а радиус сферы действия Земли принимается равным r_EI = 925 тыс. км.

На первом шаге анализа определяется геоцентрическая траектория полета КА от Луны до границы сферы действия Земли (ГСДЗ). Задача состоит в нахождении момента времени t_M и скорости v⁺(t_M) отлета КА от Луны, таких, что в момент времени t₁⁺ » t₁ КА достигает ГСДЗ, имея скорость на бесконечности V_¥, определенную в (3.5). Это можно сделать, например, следующим образом. Задаем время t_ME полета от Луны до ГСДЗ. За начальное приближение можно взять, например, величину (r_EI – a_M) / V_¥, где a_M » 385 тыс.км - большая полуось лунной орбиты. Тогда время отлета t_M = t₁⁺ - t_ME, оно определит радиус-вектор Луны r_M(t_M), и, по известной скорости V_¥, величину геоцентрической скорости КА отлета от Луны v(t_M). Последнюю скорость обозначим через v⁺(t_M), так как в модели точечной сферы действия Луны здесь будет скачок скорости КА. Определяем угол наклона этой скорости к радиусу-вектору так, чтобы по векторам r_M(t_M), v⁺(t_M) получить гиперболическую орбиту отлета от Луны с заданным вектором скорости на бесконечности V_¥. Находим для этой орбиты время полета t_ME⁺ от Луны до ГСДЗ. Должно быть выполнено равенство t_ME⁺ = t_ME. Из этого условия и определяем время t_ME, момент t_M = t₁⁺- t_ME и всю орбиту перелета. Геоцентрическая скорость v⁺(t_M) позволяет определить селеноцентрическую скорость V_¥⁺ = v⁺(t_M) – V_M(t_M), где V_M(t_M) – геоцентрическая скорость Луны в момент t_M.

Замечание. Момент t₁⁺ (»t₁) достижения ГСДЗ в процессе анализа несколько варьируется, чтобы обеспечить благоприятные условия облета Луны, хорошую сходимость итерационных процессов в п.3, п.4 и приемлемые характеристики траектории КА.

На следующем шаге определяется геоцентрическая орбита полета КА с опорной орбиты к Луне, исходя из времени подлета к Луне t_M и условия равенства модулей селеноцентрических скоростей V_¥^-, V_¥⁺ подлета к Луне и отлета от Луны, а также условия совпадения плоскостей опорной орбиты и орбиты полета к Луне. Имеем 4-параметрическую задачу: надо обеспечить (в рамках нулевой сферы действия Луны) попадание в Луну в заданный момент времени t_M и обеспечить при этом заданную величину скорости КА относительно Луны. Наклонение плоскости орбиты i совпадает с наклонением опорной орбиты i₀, оно задано, определяется космодромом. Долгота восходящего узла W определяется из условия прохождения плоскости орбиты через радиус-вектор Луны r_M(t_M). Если подлет к Луне происходит вблизи нисходящего узла орбиты КА, то имеем:

sin Du = sind_M / sini₀, cosDW = cosDu / cosd_M, W = a_M + p + DW signd_M, (3.7)

где d_M, a_M – склонение и прямое восхождение Луны в геоцентрической СК₍₂₎.

Для определения вектора скорости подлета к Луне (и, тем самым, остальных элементов орбиты полета) используем годограф подлетной скорости в плоскости орбиты КА. Множество векторов скорости КА v^-(t_M) подлета к Луне, соответствующих заданной величине селеноцентрической скорости V_¥⁺, приведено схематично на рис. 2. Оно построено в плоскости скоростей CXY (ось CX – по радиусу, ось СY – по трансверсали), которая совпадает с плоскостью орбиты КА и начало которой С есть центр Луны в момент t_M.Годограф, множество концов этих скоростей, является окружностью с центром в конце проекции V_Mp скорости Луны V_M на плоскость орбиты КА. Радиус ее

V_h = ((V_¥⁺)² – V_Mn²)^1/2 = ((V_¥⁺)² – V_M² + V_Mp²)^1/2, (3.8)

где V_Mn есть проекция скорости Луны на нормаль к орбите КА. Для определения скорости подлета КА к Луне v^-(t_M) надо на этом годографе найти точку, для которой орбита перелета КА имеет то же перигейное расстояние, что и опорная орбита [8]. После этого находятся остальные элементы геоцентрической орбиты полета к Луне: a, e, w, t, а также импульс скорости DV, время перелета от Земли к Луне t_EM, селеноцентрическая скорость подлета к Луне V_¥^- = v^-(t_M) – V_M(t_M).

В заключение необходимо проверить возможность реализации гравитационного маневра. Для этого надо определить угол d поворота селеноцентрической скорости при пролете у Луны, по нему найти расстояние r_p периселения гиперболической селеноцентрической орбиты КА и сравнить его с радиусом Луны r_M:

где m_M - гравитационный параметр Луны. Должно быть:

где Dr – допуск на ошибки навигации и управления.

В случае выполнения условия (3.10) по величине разгонного импульса скорости DV определяем массу КА m₁ (3.3). Знание этой массы и скорости V(t₂) подлета КА к астероиду позволяет определить импульс скорости, сообщаемый астероиду воздействием КА и вызываемое этим импульсом отклонение d астероида в картинной плоскости Земли. Если известны эти характеристики (m₁)₀, d₀, V₀(t₂) для траектории полета к астероиду без ГМ, то искомую величину отклонения d с учетом ГМ можно получить, используя оценку:

d= d₀ m₁ |V(t₂) - V_A(t₂)| / (m₁)₀ |V₀(t₂) - V_A(t₂)| » d₀ m₁ / (m₁)₀. (3.11)

Отметим, что полученная траектория полета КА является хорошим приближением для решения задачи в точной постановке.

Численные результаты получены для перелета КА к астероиду Тоутатис. Расчет проведен для следующих значений параметров: радиус перицентра опорной орбиты ИСЗ r_p₀ = 6671 км, ее эксцентриситет e₀ = 0,0001, наклонение i₀ = 51,5⁰, начальная масса КА m₀ = 8000 кг, скорость истечения струи c = 4,5 км/с. Время отлета от Земли в модели точечной сферы действия Земли t₁ = 2444308,886 юл. сут., время встречи с астероидом t₂ = 2444623,199 юл.сут. Время полета КА t₁₂=27,156 млн.c, время от воздействия КА на астероид до сближения с Землей t₂₃ =375,1 млн.c. Эти времена соответствуют одному из главных локально-оптимальных решений задачи без ГМ [3].

Гелиоцентрическая орбита перелета КА от Земли к астероиду (без ГМ у Луны) в системе координат СК₍₁₎ имеет следующие элементы: а = 156,7 млн.км, e = 0,0705, W = 170,11⁰, i = 0,24⁰, w = 45,48⁰, t = 2443960,0 юл.сут. Она приведена на рис. 3, где точки S, F означают отлет от Земли и подлет к астероиду. Геоцентрическая скорость на бесконечности при отлете от Земли (в СК₍₁₎) V_¥ = (1,7901; -0,9549; 0,1294) км./с. Импульс скорости разгона DV₀ = 3,388 км/с, масса КА при встрече с астероидом (m₁)₀ = 3768 кг. Отклонение астероида в картинной плоскости Земли d₀ =8100 км для модели абсолютно неупругого соударения КА и астероида.

Анализ движения КА внутри сферы действия Земли дан для момента достижения ГСДЗ t₁⁺ = t₁ + 5 сут. Время отлета от Луны t_M = 2444310,888 юл. сут»t₁⁺ - 3 сут. Геоцентрический вектор состояния КА в этот момент в СК₍₂₎: r = (138745,6; -325940,3; -118491,9) км; v⁺= (2,1350; -1,2543; -0,3687) км/c. Селеноцентрические скорости отлета от Луны и подлета к Луне : V_¥⁺ = (-0,1633, -1,9533, -0,8285) км/с, V_¥^- = (1,1897, -1,6994, -0,4745) км/с. Угол между этими скоростями d=39,02⁰. Прицельная дальность гиперболы полета у Луны b = 3055,7 км, радиус в ее периселении r_p = 2159,2 км.

Элементы геоцентрической орбиты перелета к Луне: а = -312819,4 км, W = 97,63⁰, i = 51,5⁰, w = 43,32⁰, t = t₀ = 2444309,146 юл. сут., время полета к Луне t_EM = 1,74 сут, скорость КА после схода с опорной орбиты V = 10,99 км/c. Величина импульса скорости DV=3,260 км/с, масса КА после разгона m₁=3877 кг, тогда d » 8334 км.

Сравнивая величины DV, m₁, d с величинами DV₀, (m₁)₀, d₀, видим, что траектория полета КА к астероиду с использованием ГМ у Луны является энергетически более выгодной, чем обычная, без ГМ. Импульс скорости разгона уменьшился на ~ 128 м/с, масса КА увеличилась на ~109 кг, отклонение астероида также увеличилось, ~ на 234 км.

В данном разделе дан достаточно строгий анализ задачи, основанный на исследовании движения КА в соответствии с дифференциальными уравнениями движения точки в поле притяжения Земли (с учетом главной гармоники С₂₀), Луны и Солнца. Этот анализ условно будем называть точным.

Система дифференциальных уравнений движения КА в невращающейся геоэкваториальной системе прямоугольных координат СК₍₂₎ имеет вид:

Здесь r, v – радиус-вектор и вектор скорости КА, r = |r|, a_E, a_M, a_S – возмущающие ускорения, вызванные нецентральностью поля тяготения Земли, притяжением Луны, Солнца. Эти ускорения определяются следующим образом [9 - 12]. Ускорение a_E обусловлено второй зональной гармоникой геопотенциала:

где R_e, J₂– экваториальный радиус и динамический коэффициент формы Земли, n–орт в направлении Земля–Северный полюс мира. Ускорение a_S:

где m_S, r_S – гравитационный параметр и геоцентрический радиус-вектор Солнца. Ускорение a_M:

где r_M – геоцентрический радиус-вектор Луны. Интегрирование системы (4.1 -4.4) производится методом Рунге-Кутты-Фельберга 7(8) порядка [13,12] c определением координат Луны и Солнца по JPL-эфемеридам DE200.

В момент t₂ встречи КА с астероидом радиус-вектор КА должен совпадать с радиусом-вектором астероида R_A(t₂):

Этого добиваемся, варьируя некоторые начальные данные, т.е. решая краевую задачу. В данном случае эта задача решается последовательным приближением: долготы восходящего узла опорной орбиты W₀, времени включения двигателя при разгоне Dt₀ = t₀ - t₀ относительно момента прохождения перицентра опорной орбиты и параметра d_V, который определяет величину импульса скорости при разгоне DV по отношению к исходной величине DV₀; DV = d_V DV₀. При этом элементы r_p₀, e₀, i₀, w₀, t₀ опорной орбиты задаются, причем аргумент w₀ и момент t₀, для простоты,- равными их значениям, определяемым в приближенном анализе, в п.3.2.

Точка M₀ приложения импульса скорости на опорной орбите определяется временем Dt₀ движения КА от перицентра p₀ опорной орбиты. В этой точке M₀ импульс скорости DV сообщается вдоль скорости на опорной орбите, этим полностью определяется орбита перелета к Луне, в частности, углы W, i будут теми же, что и для опорной орбиты.

Пусть X_i⁽ⁿ⁾ – вектор указанных варьируемых начальных данных (W₀, Dt₀, d_V) на n-ой итерации; X_f⁽ⁿ⁾ – вектор конечных данных, в данном случае это конечный радиус-вектор КА R(t₂), получаемый интегрированием системы (4.1–4.4) при начальных векторах положения и скорости r_i, v_i, определяемых вектором X_i⁽ⁿ⁾. Пусть А - матрица частных производных [9]:

Последовательные приближения определяются по итерационной формуле Ньютона:

DX⁽ⁿ⁾ = X_f⁽ⁿ⁾ - R_A(t₂) = R⁽ⁿ⁾(t₂) - R_A(t₂), - (4.8)

то итерационный процесс прекращается. За допустимые значения точностей попадания в астероид принято e_j = 200км. Если условие (4.9) не выполняется, то делается следующая итерация согласно (4.7). Сходимость данного метода решения краевой задачи в значительной степени определяется удачным выбором начального приближения X_i⁽⁰⁾. Примененный в настоящей работе метод определения начального приближения описан ниже, в п. 4.3.

Следуя [8], приближенные значения варьируемых параметров для решения полной краевой задачи определяются первоначальным решением более простой краевой задачи полета к Луне. В рамках строгой модели движения КА (4.1–4.4) определяется траектория полета КА к Луне, для которой в момент времени t_M^- подлета КА к сфере действия Луны вектор положения КА относительно Луны будет равен вектору прицельной дальности b для подлетной ветви гиперболической селеноцентрической орбиты КА, полученной с помощью приближенного метода, в п. 3.2. Этот вектор b задается в системе координат, связанной с картинной плоскостью Луны, проходящей через центр Луны и перпендикулярной скорости V_¥^- подлета КА к Луне. Ее ось OX направлена противоположно скорости V_¥^-, ось OY - перпендикулярно плоскости селеноцентрической орбиты:

x⁰ = - V_¥^- / V_¥^-; y⁰ = - V_¥^- ´ V_¥⁺/|V_¥^-´V_¥⁺|; z⁰ = x⁰ ´ y⁰ = - b / b. (4.10)

В этой системе координат на момент t_M^- КА должен иметь селеноцентрические координаты:

здесь r_MI = 55 тыс. км – принятый радиус сферы действия Луны. Выполнение этих условий обеспечивается варьированием прежних начальных параметров: долготы восходящего узла орбиты W, времени включения двигателя t₀, величины импульса скорости DV. При решении данной краевой задачи начальное приближение для этих варьируемых параметров и остальные элементы орбиты КА соответствуют решению задачи по приближенному методу, п. 3.2, или задаются постоянными, как элементы опорной орбиты r_p₀, e₀, i₀, w₀, t₀. Полученные значения варьируемых параметров W, t₀, DV используются как начальное приближение для полной краевой задачи, п. 4.1.

Для более полного анализа влияния ГМ на траектории полета к астероиду необходимо также определить, в рамках точной модели движения КА, и траекторию полета к астероиду без ГМ, ибо в [2, 3] такие траектории определены только в рамках упрощенной модели точечных сфер действия.

В принципе краевая задача в этом случае строится, как и в прежнем случае ГМ, в п. 4.2: обеспечивается попадание в астероид (4.5) варьированием параметров W₀, t₀, DV. Однако выбор начального приближения этих параметров осуществляется иначе, без требования прохождения траектории КА вблизи Луны. Геоцентрическая орбита отлета КА от Земли строится, как обычно, чтобы пройти через построенный в п. 3 вектор скорости на бесконечности V_¥, имея заданное наклонение i₀ и перигейное расстояние r_p₀, см, например, [9]:

sin u_¥ = sin d_¥ / sin i₀, u_¥ = p - arcsin (sin u_¥), w=u_¥ - J_¥; (4.12)

sin W = V_¥ (V_¥_y cos u_¥ - V_¥_x sin u_¥ cos i₀) / (V_¥_x² + V_¥_y²);

cos W = V_¥ (V_¥_x cos u_¥ + V_¥_y sin u_¥ cos i₀) / (V_¥_x² + V_¥_y²).

Здесь d_¥ - склонение вектора V_¥, предполагается, что |sin d_¥| £ sin i₀, скорость V_¥ находится у нисходящего узла орбиты, а участок разгона – у восходящего узла. В качестве начального приближения для времени отлета с опорной орбиты t₀ принимается его значение из приближенного решения (п.3) или точного решения с ГМ (п.4). После решения краевой задачи и определения траектории полета КА к астероиду определяется импульс скорости, сообщаемый астероиду, масса КА и отклонение астероида от Земли – для схемы полета без ГМ при расчете в рамках точной модели движения КА.

4.5. Численные результаты решения задачи в точной постановке

Сначала решается предварительная задача перелета к Луне. В таблице 1 приведены элементы опорной орбиты, характеристики траектории перелета КА к Луне (в СК₍₂₎) и элементы гиперболы полета у Луны (в СК₍₃₎), полученные на основе решения краевой задачи "выхода" КА на заданный вектор прицельной дальности на границе сферы действия Луны, согласно методу п. 4.3. Начальные данные для решения этой краевой задачи были получены на основании приближенной методики, п. 3.2. Оскуляция орбиты полета у Луны дана на момент прохождения ГСДЛ t_M^- = t_M - 0,2842 сут.

Табл. 1. Характеристики предварительной траектории полета к Луне

При движении КА по этой траектории дальше, к астероиду, промах у астероида в момент t₂ составляет 4,99 млн.км. Следовательно, данная траектория является хорошим начальным приближением для решения полной краевой задачи полета КА к астероиду с использованием ГМ у Луны.

Приведем теперь основные результаты решения полной краевой задачи полета КА к астероиду при использовании ГМ у Луны. В таблице 2 для этого случая даны параметры траектории полета КА к Луне (в СК₍₂₎) и элементы орбиты КА вблизи Луны (в СК₍₃₎). Введение ГМ уменьшило импульс скорости DV на ~ 120 м/с и увеличило массу КА на ~ 102 кг.

Табл. 2. Характеристики траектории полета к Луне

В таблице 3 приведены компоненты вектора состояния КА на момент t₂ подлета к астероиду (в СК₍₁₎ и в системе координат, связанной с картинной плоскостью астероида). Введение ГМ увеличило скорость сближения КА с астероидом на ~ 50 м/с.

Табл. 3. Вектор состояния КА при встрече с астероидом

В таблице 4 приведены элементы орбит перелета КА к астероиду с использованием ГМ и без ГМ (в СК₍₁₎, элементы получены на момент t₂).

Табл. 4. Гелиоцентрическая орбита перелета КА к астероиду

В таблице 5 приведены компоненты импульса скорости dV_A, сообщаемого астероиду (в СК₍₁₎, для модели абсолютно неупругого соударения КА и астероида). Введение ГМ увеличило этот импульс с 4,6 мм/с до 4,8 мм/с.

Табл. 5. Сообщаемый астероиду импульс скорости, в СК₍₁₎

В таблице 6 приведены компоненты импульса скорости, сообщаемого астероиду, в орбитальной системе координат астероида (RMB), оси которой направлены по номинальному радиусу r⁰, трансверсали m⁰, бинормали b⁰.

Табл. 6. Сообщаемый астероиду импульс скорости, в орбитальной СК

В таблице 7 приведены проекции отклонения астероида от номинальной траектории в момент времени наибольшего сближения с Землей t₃, в системе координат RMB.

В таблице 8 приведено отклонение астероида от номинальной траектории в момент t₃ в системе координат, связанной с картинной плоскостью Земли. Введение ГМ увеличило отклонение астероида с 8074 км до 8321 км.

Табл. 7. Вектор отклонения астероида в орбитальной СК

Табл. 8. Вектор отклонения астероида в картинной плоскости Земли

Отклонение астероида	Перелет КА с ГМ	Перелет КА без ГМ
Dx, км	8 321	8 074
Dh, км	-0,04	-0,04
d, км	8 321	8 074

Сравнивая результаты точного и приближенного расчетов, видим, что они дают очень близкие результаты - как по абсолютным параметрам полета КА, так и по оценке влияния гравитационного маневра у Луны.

Для анализа проблемы обеспечения астероидной безопасности Земли, в частности, задачи отклонения от Земли сближающегося с Землей астероида, разработаны две методики определения траектории полета КА к астероиду при использовании гравитационного маневра у Луны. Один, упрощенный метод использует точечные сферы действия Земли, Луны и астероида. Другой, достаточно точный метод, использует уравнения движения КА в поле притяжения Земли, Луны и Солнца. На основе данных методов были построены численные алгоритмы определения траектории полета КА к астероиду. Для полета к астероиду Toutatis получены численные оценки параметров траектории полета КА с использованием гравитационного маневра у Луны. Анализ работы программного комплекса показал хорошую сходимость итерационного процесса точного решения задачи. Показано также, что оба метода дают весьма близкие результаты. Использование гравитации Луны позволило для проанализированного варианта дат полета уменьшить импульс скорости при отлете от Земли на ~ 120 м/с, увеличить массу и отклонение астероида от Земли.

Авторы приносят искреннюю признательность А.В. Чернову за помощь в подготовке препринта.

1. Ивашкин В.В., Смирнов В.В. Качественный анализ некоторых методов уменьшения астероидной опасности. – Астрономический вестник. 1993. Т. 27. N 6. С. 46-54.

2. Ахметшин Р.З., Ивашкин В.В., Смирнов В.В. Анализ возможности уменьшения астероидной опасности для Земли ударным воздействием космического аппарата. – Астрономический вестник. 1994. Т. 28. N 1. С. 13-20.

3. Ивашкин В.В., Зайцев А.В. Анализ возможности изменения орбиты сближающегося с Землей астероида ударным воздействием космического аппарата. – Космические исследования. 1999. Т. 37. N 4. С. 405 - 416.

4. Ивашкин В.В., Чернов А.В., Баум Ф.И. Анализ оптимальных двухимпульсных перелетов космического аппарата к сближающемуся с Землей астероиду. – М.: Институт прикладной математики им. М.В. Келдыша РАН. 1999. Препринт N 34.

5. Ивашкин В.В., Чернов А.В. Оптимальные траектории полета КА к сближающемуся с Землей астероиду при использовании малой тяги. – Космические исследования. 2000. Т. 38. N 2. C. 151 –163.

6. Лидов М.Л., Тесленко Н.М. Об использовании гравитации Луны при полете к астероидам, сближающимся с орбитой Земли. – Письма в Астрономический журнал. 1994. Т. 20. N 1. С. 76 – 80.

7. Лидов М.Л., Тесленко Н.М. Полеты к нескольким астероидам (кометам) в окрестности земной орбиты, с использованием гравитации Луны. – Письма в Астрономический журнал. 1995. Т. 21. N 2. С. 148 - 156.

8. Ивашкин В.В., Тупицын Н.Н. Об использовании гравитационного поля Луны для выведения космического аппарата на стационарную орбиту спутника Земли. – Космические исследования. 1971. Т. 9. N 2. C. 163 – 172.

9. Основы теории полета космического аппаратов. Под. ред. Нариманова Г.С., Тихонравова М.К. - М.: Машиностроение. 1972.

10. Охоцимский Д.Е., Сихарулидзе Ю.Г. Введение в механику космического полета. - М.: Наука, 1990.

11. Марин С.Ф. К вычислению астрономической нутации в баллистических расчетах. – М.: Институт прикладной математики им. М.В.Келдыша РАН. 1993. Препринт N 5.

12. Марин С.Ф. К расчету движения высокоапогейных ИСЗ в инерциальной геоцентрической системе прямоугольных координат среднего равноденствия и среднего геоэкватора стандартной эпохи J2000.0. – М.: Институт прикладной математики им. М.В. Келдыша РАН. 1994. Препринт N 10.

13. Fehlberg E., Klassische Runge-Kutta-Formeln 5-und-7-ter Ordnung mit Schrittweiten-Kontrolle. - Computing. 1969. Vol. 4. Pp. 93 - 106.

СК₍₁₎ – гелиоцентрическая эклиптическая невращающаяся СК

СК₍₂₎ – геоцентрическая геоэкваториальная невращающаяся СК

СК₍₃₎ – селеноцентрическая геоэкваториальная невращающаяся СК

(a, e, W, i, w, t) – элементы орбиты (большая полуось, эксцентриситет, долгота восходящего узла, наклонение, аргумент широты перицентра, момент прохождения перицентра);

b, b – вектор и величина прицельной дальности селеноцентрической орбиты подлета КА к Луне;

с – скорость истечения газов из сопла двигателя КА;

d – отклонение астероида в картинной плоскости Земли;

d₀ – отклонение астероида в картинной плоскости Земли при полете без ГМ;

O₁X₁Y₁Z₁ – гелиоцентрическая эклиптическая невращающаяся система координат - СК₍₁₎;

O₂X₂Y₂Z₂ – геоцентрическая геоэкваториальная невращающаяся система координат - СК₍₂₎;

O₃X₃Y₃Z₃ – селеноцентрическая геоэкваториальная невращающаяся система координат - СК₍₃₎;

m₀, m₁ – масса КА до разгона и после разгона с опорной орбиты;

r, r_M, r_S – геоцентрические радиусы-векторы КА, Луны, Солнца;

R, R_E, R_A – гелиоцентрические радиус-векторы КА, Земли, астероида;

r_p₀ – перигейное расстояние опорной орбиты;

t₁, t₂, t₃ – времена отлета от Земли, подлета к астероиду, сближения астероида с Землей;

t₂₃ – время движения астероида от встречи с КА до сближения с Землей;

t₀, t_M^-, t_M, t_M⁺, t₁⁺ - моменты: старта с опорной орбиты, подлета к ГСДЛ, сближения с Луной, отлета от ГСДЛ, достижения ГСДЗ;

t_EM = t_M – t₀ – время полета КА от опорной орбиты до Луны;

t_ME = t₁⁺– t_M– время полета КА от Луны до ГСДЗ;

v^-(t_M), v⁺(t_M) – геоцентрические скорости подлета к Луне и отлета от Луны;

V, V_E, V_A – векторы гелиоцентрической скорости КА, Земли, астероида ;

V_h – радиус окружности – годографа скорости;

V_M, V_Mp, V_Mn – скорость Луны, ее составляющие в плоскости орбиты КА и по нормали к этой плоскости;

V_¥ - вектор геоцентрической скорости КА на бесконечности при отлете от Земли к астероиду;

V_¥^-, V_¥⁺ - селеноцентрические скорости КА при подлете к Луне и отлете от Луны;

a_M, d_M – прямое восхождение и склонение Луны;

a_¥, d_¥ – прямое восхождение и склонение вектора скорости V_¥;

d – угол поворота селеноцентрической скорости полета у Луны;

(Dr, Dm, Db) - отклонение астероида в орбитальной системе координат RMB;

Dt₀ = t₀ - t₀ – время полета от опорного перигея до точки разгона;

DV, DV – вектор и величина импульса скорости разгона с опорной орбиты;

Dx, Dh - координаты отклонения астероида в картинной плоскости Земли;

m_E, m_M, m_S – гравитационные постоянные Земли, Луны, Солнца;

r_p – расстояние до Луны в периселении орбиты.

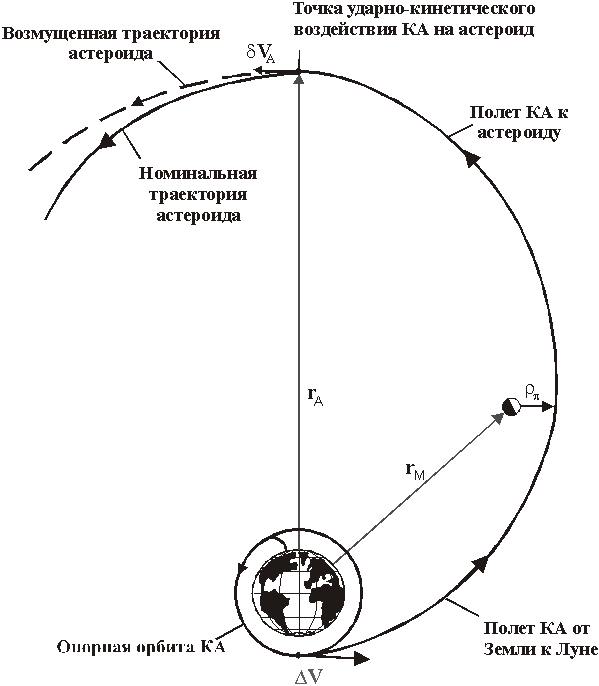
Рис. 1. Схема полета КА к астероиду с использованием гравитационного маневра у Луны.

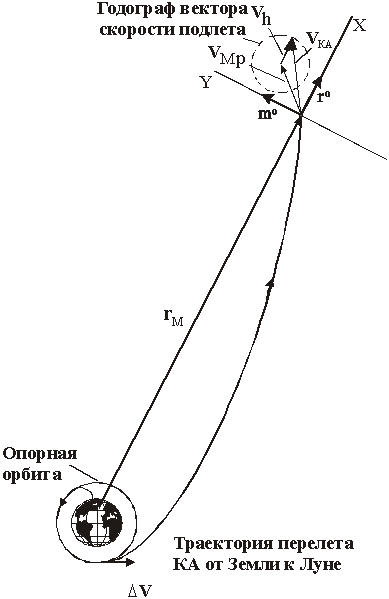
Рис. 2. Схема определения траектории полета к Луне с помощью годографа скорости

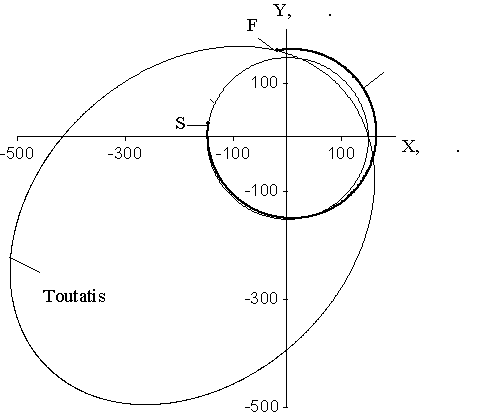
Рис. 3. Орбиты Земли, астероида Toutatis, КА в проекции на плоскость эклиптики.

Ивашкин В.В., Баум Ф.И.
(V.V.Ivashkin, Ph.I.Baum)

ИПМ им. М.В.Келдыша РАН

Москва, 2000
Работа выполнена при поддержке Российского фонда фундаментальных исследований (гранты №№ 98-01-01004, 00-15-96036)

Аннотация

Abstract

Ивашкин В.В., Баум Ф.И. (V.V.Ivashkin, Ph.I.Baum) ИПМ им. М.В.Келдыша РАН

Москва, 2000 Работа выполнена при поддержке Российского фонда фундаментальных исследований (гранты №№ 98-01-01004, 00-15-96036)

Аннотация

Abstract

Ивашкин В.В., Баум Ф.И.
(V.V.Ivashkin, Ph.I.Baum)

ИПМ им. М.В.Келдыша РАН

Москва, 2000
Работа выполнена при поддержке Российского фонда фундаментальных исследований (гранты №№ 98-01-01004, 00-15-96036)