СОДЕРЖАНИЕ

Введение                                                                                               

1.     Описание экспериментов по термометрии и теплофизические измерения на массивной свинцовой мишени.                                                

2. Расчеты нестационарных пространственных температурных полей в свинцовой мишени (сборка 1)                                                                 

Заключение                                                                                           

Литература                                                                                            

Приложение.

Расчет энерговыделения в массивной свинцовой мишени (сборка 1)

Введение

Данная работа является продолжением исследований, выполняемых Объединенным институтом ядерных исследований (ОИЯИ, г. Дубна), Институтом прикладной математики им. Келдыша РАН (ИПМ, г. Москва) и Всероссийским научно-исследовательским и проектно-констроукторским институтом атомного энергетического машиностроения Минэкономики (ВНИИАМ, г. Москва) под руководством академиков А.М. Балдина и В.И. Субботина по проблеме электроядерной энергетики и трансмутации радиоактивных отходов.

В 1998 году в ОИЯИ были проведены эксперименты с целью исследования процессов тепловыделения в мишени при ее облучении пучком высокоэнергетических протонов, получаемом на синхрофазотроне Лаборатории высоких энергий [1]. В частности, в первых экспериментах  массивная свинцовая мишень (блок с размерами 50х50х80 см**3 и массой ~ 2300 кг., сборка 1) “разогревалась” протонами с энергией 1.5 Гэв и 5 Гэв. Диапазон изменения температур в различных точках мишени не превышал нескольких десятых долей градуса. Высокоточная термометрия была проведена с использованием высокочувствительных малоинерционных  микротермопар, разработанных в ВНИИАМ. Эти эксперименты были подробно проанализированы расчетным путем в ИПМ им. М.В. Келдыша РАН.

Следует отметить, что мишень собиралась из свинцовых кирпичей 200х100х50 мм. без специальных мер по обеспечению надежного теплового контакта между ними.

В данной работе представлены результаты расчета температурных полей и их сравнение с данными термометрии в эксперименте с пучком протонов с энергией 5 Гэв .

1.     Описание экспериментов по термометрии и теплофизические измерения на массивной свинцовой мишени.

Для экспериментального исследования пространственно-временных распределений температур в свинцовой мишени использовались разработанные ВНИИАМ методика и средства термометрии. Они включают в себя высокочувствительные малоинерционные микротермопары и регистрирующую аппаратуру на основе мини-ЭВМ и специальной микро-платы. Эти средства обеспечивают точность измерения температуры 0.02-0.03^ОС.

Общий вид массивной свинцовой мишени (сборка 1) представлен на рис.1.1

В качестве мишени использовался свинцовый блок с размерами 50х50х80 см³ и весом 2300кг. Протонный пучок с энергией 5 Гэв из синхрофазотрона попадал на свинцовую мишень через углубление с размерами 10х10х20 см³. Направление бомбардирующего пучка совпадало с продольной горизонтальной осью свинцового блока.

Для термометрии использовались 10 малоинерционных высокочувствительных микротермопар. Схема размещения термопар показана на рис. 1.2

В таблице 1.1 представлен график проведения этого эксперимента. Было проведено за 1,5 часа 9 включений пучка, общее время облучения ~ 66 мин, время простоя ~24 мин. Общий флюенс протонов 3,256х10¹³ протонов, их общая энергия 26085 дж.

Таблица 1.1. Временной график эксперимента и характеристики пучка нейтронов.

Результаты эксперимента отражены на рисунках 1.3 - 1.5, на которых приведены термограммы, полученные с помощью 10 термопар.

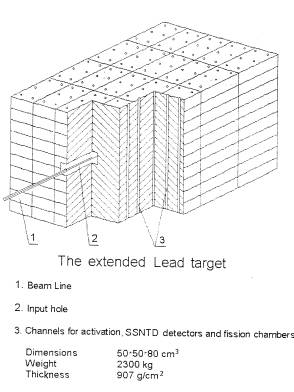
Рис.1.1 Общий вид массивной свинцовой мишени (сборка 1)

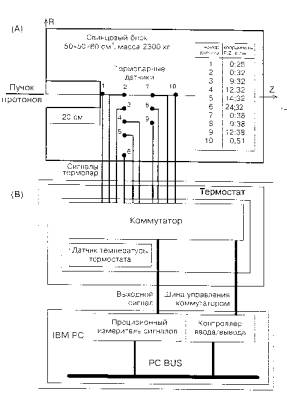
Рис. 1.2 Схема размещения термопар в эксперименте с массивной свинцовой мишенью (сборка 1)

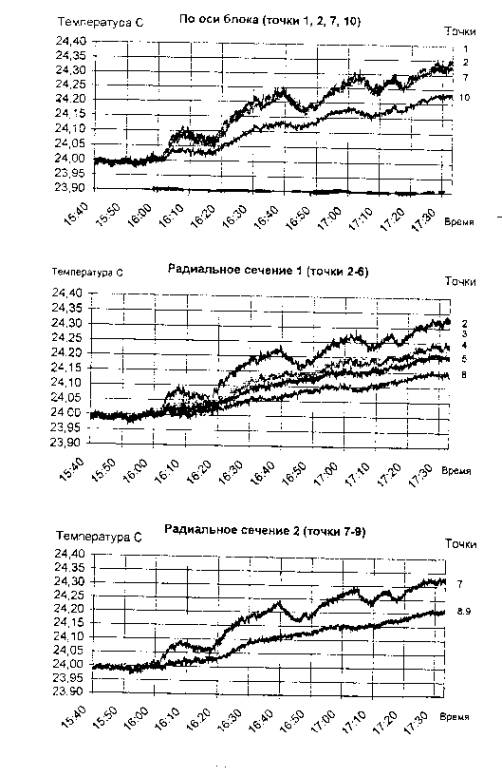
Рис 1.3-1.5 Показания термопар в первом эксперименте (сборка 1)

Обращают на себя внимание следующие факты:

1.   Вдоль протонного пучка температуры в точках 1, 2, 7  практически совпадают, происходит непрерывный рост температуры во время облучения и спад температур во время прерывания протонного пучка, общее увеличение температуры составляет ~ 0.35⁰C. Показания точки  10 по характеру такие же, только прирост температуры ~0.20⁰ C.

2.   Термопары, расположенные на различном удалении от оси пучка реагируют на прерывание пучка протонов заметно слабее (датчики 3, 4) или совсем незначительно (датчики 5, 6, 8, 9). У них происходит непрерывный плавный рост температуры, общий нагрев ~ 0.15-0.20⁰C.

2. Расчеты нестационарных пространственных температурных полей в свинцовой мишени (сборка 1)

Расчеты температурных полей были выполнены: по конечно-разностной программе ТЕМР [2].

Для нестационарных тепловых расчетов необходимо знать внешний источник энерговыделения, нарабатываемый в объеме облучаемой установки под действием пучка протонов.

Расчет внешнего источника энерговыделения представляет самостоятельную важную задачу, которая детально была решена для рассматриваемой мишени ранее с привлечением как отечественных расчетных программных комплексов SHIELD[3] и PARSE-2 [4], так и известного кода Лос-Аламосской лаборатории США LAHET [5]. Результаты расчетов по этим программам и их сравнение подробно описаны в предыдущей нашей работе [6], здесь мы приведем в приложении только расчетную модель и таблицу значений энерговыделения, насчитанные по программному комплексу LAHET, которые были использованы в расчетах полей нестационарных температур.

Прямые расчеты с использованием теоретических значений коэффициентов теплопроводности не всегда дают хорошее согласие с экспериментом. При расчете малых изменений температур (DT£0.5 ⁰С), по-видимому, нужно учитывать более детально теплофизические характеристики конкретных установок. В частности, для рассматриваемой массивной мишени, набранной из отдельных кирпичей свинца, из-за наличия контактных термических сопротивлений эффективный коэффициент теплопроводности должен быть меньше теоретического, определяемого для однородной свинцовой среды. Вычислительные эксперименты показали обоснованность такого предположения.

Целью вычислительных экспериментов являлся расчет по заданному тепловому источнику нестационарных полей температуры в объеме свинцовой мишени при ее облучении пучком протонов и сравнение полученных результатов с данными термометрии.

          Нестационарный процесс распространения тепла в неоднородном теле, включающем в себя области с различными свойствами, описывается следующим уравнением теплопроводности, записанном в цилиндрических координатах в предположении осевой симметрии задачи:

,

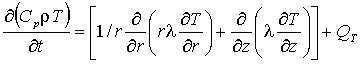где t- время, (r,z)- цилиндрические координаты , Т- температура, r - плотность, l - коэффициент теплопроводности, С_p.- теплоемкость при постоянном давлении, Q_Т – мощность теплового источника.

          Рассматриваемая область представляет собой прямоугольник в цилиндрических координатах размером 0.25 х 0.80 м, включающий в себя свинцовую мишень и заполненный воздухом вырез размером 0.05 х 0.20 м в нижней его части. На левой части области, являющейся осью симметрии, ставятся условия симметрии, остальные границы области считаются адиабатическими, т.е. на них ставятся условия нулевого теплового потока в окружающую среду.

Для решения приведенного выше уравнения теплопроводности с разрывными коэффициентами использовался эффективный численный алгоритм сквозного счета [7-10], позволяющий решать сопряженную задачу во всей рассматриваемой области, состоящей из компонент с различными свойствами.

Данный алгоритм имеет следующие особенности:

- он основан на конечно-разностных аппроксимациях;

- используется полностью неявная схема, имеющая второй порядок аппроксимации по пространству и первый - по времени;

- для решения получаемых на каждом временном слое систем алгебраических уравнений используются современные эффективные итерационные методы сопряженных градиентов с предобуславливанием: ICCG для симметричных и ORTHOMIN(1) для несимметричных матриц.

          Расчеты проводились на подробной равномерной сетке 152 х 162 узлов. Начальная температура во всей области равнялась Т=24 С. Источником  тепла является внутреннее энерговыделение, нарабатываемое в мишени за счет взаимодействия пучка протонов с веществом мишени. Энергия протонов была 5Гэв. Заданное нестационарное тепловыделение приводило к постепенному прогреванию свинцовой мишени. Тепловые свойства свинца и воздуха имели следующие значения:

            свинец:   r = 11000 кг/м3,   С_p.= 130 Дж/(кг К),     l = 35 Вт/(м К);

воздух:   r = 1,2 кг/м3,        С_p.= 1009 Дж/(кг К),   l = 0,034 Вт/(м К).

На рис. 2.1 показано поле температуры после первого интервала облучения (момент времени t=483 сек), а на рис. 2.2 – после всего сеанса облучения. Изотермы на всех рисунках построены с шагом 0.01 С, начиная со значения Т=24,01 С, что позволяет судить о динамике процесса прогрева свинцовой мишени. Более точную информацию об этом процессе дают рассчитанные временные зависимости температуры в точках расположения термопар, показанные на рис. 2.3 -2.5 для сравнения с аналогичными экспериментальными термограммами, рис. 1.3-1.6. За 9 интервалов облучения температура в этих точках поднялась на величину, примерно в 2 раза меньшую по сравнению с экспериментальными данными. Возможным объяснением таких расхождений является тот факт, что в расчетах свинцовая мишень считалась однородным телом, тогда как в реальности она была собрана из отдельных блоков, т.е. являлась анизотропным телом с коэффициентом теплопроводности, отличающимся от параметров однородного свинца. Расчеты с уменьшенным в 2 раза коэффициентом теплопроводности (l = 17,5 Вт/(м К) ) показали (см. Рис. 2.6 - 2.10), что расхождение с экспериментом в этом случае значительно уменьшилось. Уменьшение коэффициента теплопроводности в 4 раза (l = 8,75 Вт/(м К) ) дает результаты, которые в 1-ой точке измерений, расположенной на оси пучка, даже немного завышены по сравнению с экспериментом, а в остальных точках очень близки к экспериментальным термограммам (см. Рис. 2.11 - 2.15). Таким образом, очевидно, что для более точных расчетов необходимо учитывать композитную структуру мишени, которая приводит к уменьшению коэффициента теплопроводности по сравнению с чистым свинцом.

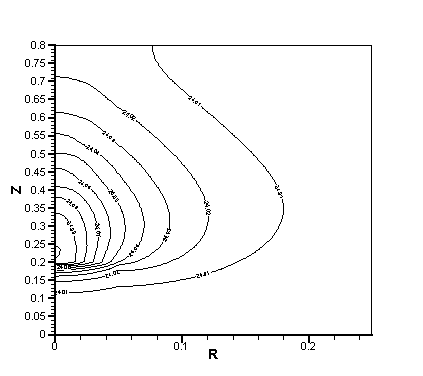
Рис. 2.1. Поле температуры после первого интервала облучения,

l = 35 Вт/(м К).

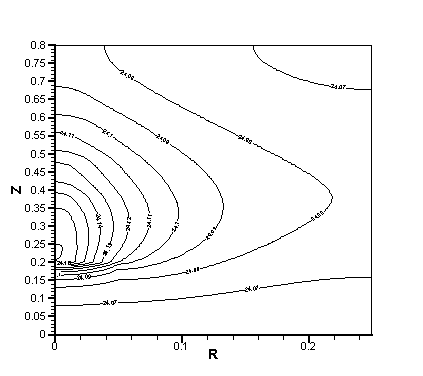
Рис. 2.2. Поле температуры после всего сеанса облучения, l = 35 Вт/(м К).

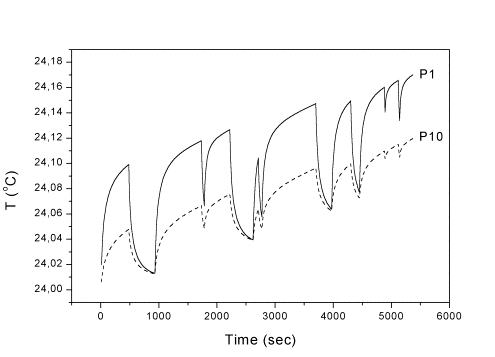
Рис. 2.3. Точки 1, 10 (по оси блока), l = 35 Вт/(м К).

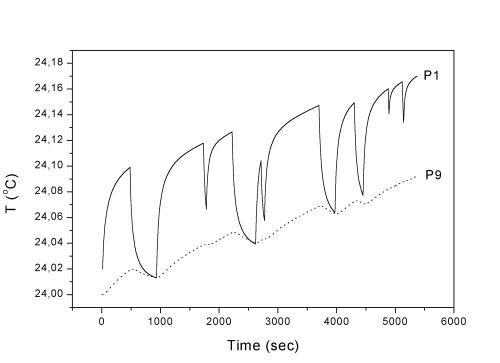
Рис. 2.4. Точки 1, 9 (радиальное сечение), l = 35 Вт/(м К).

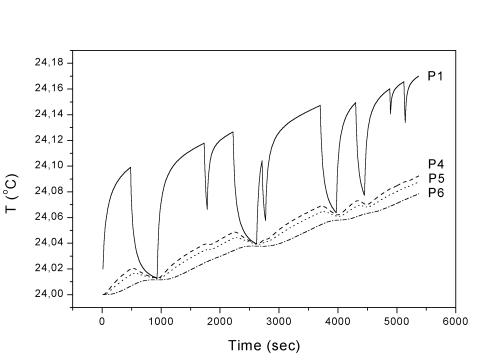
Рис. 2.5. Точки 1, 4-6 (радиальное сечение), l = 35 Вт/(м К).

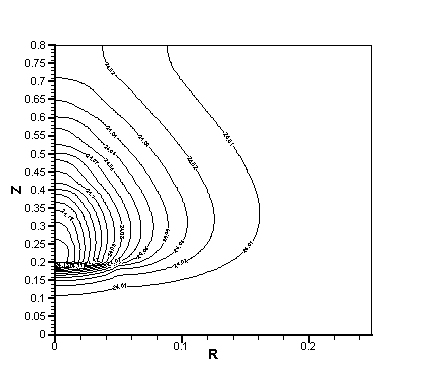
Рис. 2.6. Поле температуры после первого интервала облучения,

 l = 17,5 Вт/(м К).

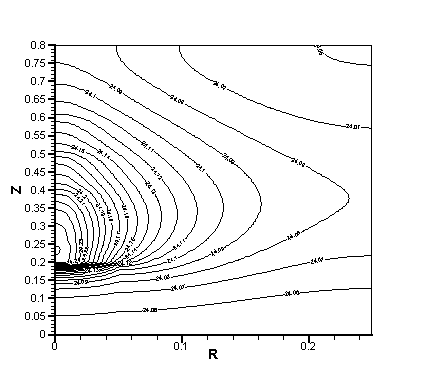
Рис. 2.7. Поле температуры после всего сеанса облучения, l = 17,5 Вт/(м К).

Рис. 2.8. Точки 1, 10 (по оси блока), l = 17,5 Вт/(м К).

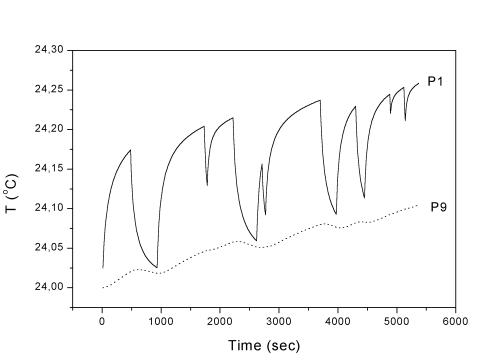
Рис. 2.9. Точки 1, 9 (радиальное сечение), l = 17,5 Вт/(м К).

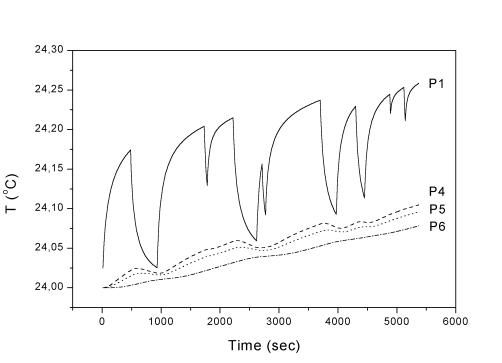
Рис. 2.10. Точки 1, 4-6 (радиальное сечение), l = 17,5 Вт/(м К).

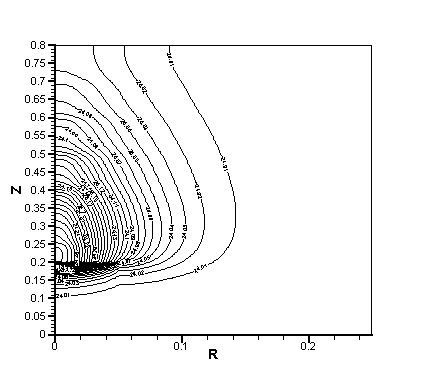
Рис. 2.11. Поле температуры после первого интервала облучения, l = 8,75 Вт/(м К).

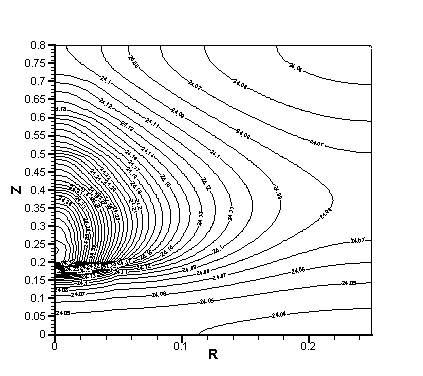
Рис. 2.12. Поле температуры после всего сеанса облучения, l = 8,75 Вт/(м К).

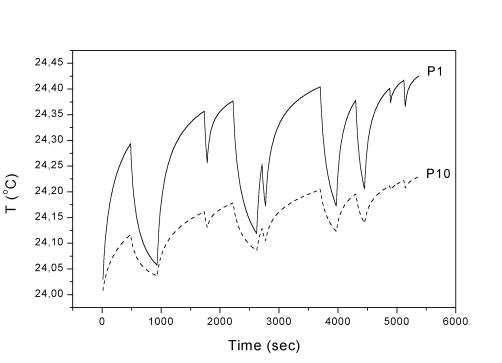
Рис. 2.13. Точки 1, 10 (по оси блока), l = 8,75 Вт/(м К).

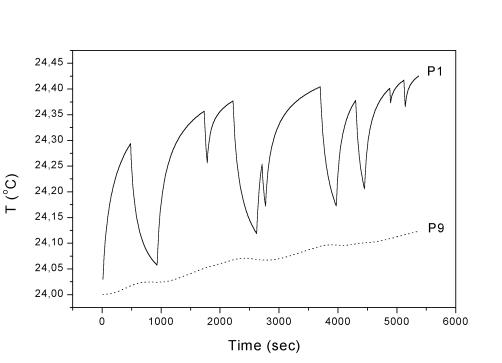
Рис. 2.14. Точки 1, 9 (радиальное сечение), l = 8,75 Вт/(м К).

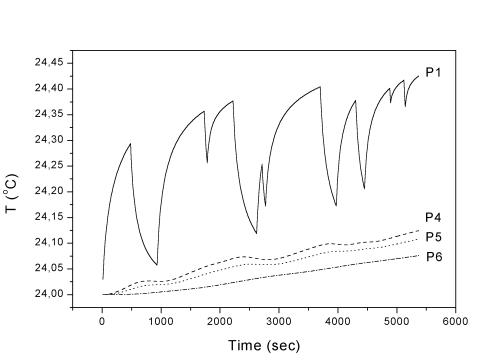
Рис. 2.15. Точки 1, 4 - 6 (радиальное сечение), l = 8,75 Вт/(м К).

Заключение

В работе проведен расчетный анализ экспериментов по термометрии массивной свинцовой мишени, проведенных в 1998 году в ОИЯИ (г. Дубна). Мишень представляет собой свинцовый блок с размерами 50х50х80 см³ и массой около 2300 кг. Мишень облучалась пучком протонов с энергией 5.0 Гэв. от синхрофазотрона Лаборатории высоких энергий, мощность пучка составляла около 7 вт, время облучения ~ 66 мин. Выделенной энергии достаточно на разогрев мишени только на несколько десятых градуса, максимальные изменения в показаниях термопар не превышают 0.35⁰С.

Проведенные расчеты нестационарных температурных полей качественно согласуются с показаниями термопар в эксперименте. Детальное согласие  с экспериментом при таких малых изменениях температур требует более точного знания теплофизических характеристик мишеней.

 В частности, для рассматриваемой сборки, собранной из отдельных свинцовых кирпичей, необходимо учесть влияние контактных термических сопротивлений на теплопроводность. Расчеты показали, что для получения совпадающих с экспериментом результатов, требуется уменьшить в модели непрерывной среды коэффициент теплопроводности примерно в 3 раза.

Литература

1.     Р. Брант, С.П. Казновский, М.И. Кривопустов и др. Исследование температурного и нейтронного полей в свинцовой среде при взаимодействии с релятивистскими протонами. Препринт ОИЯИ Р1-99-117, Дубна, 1998

2.     А.Н. Павлов, А.А. Ионкин, А.В. Воронков, А.Г. Чурбанов. “Однородный метод моделирования тепломассопереноса в областях со сложной внутренней структурой”. Препринт ИПМ им. М.В. Келдыша РАН №8, 1998.

3.     A.V.Dementyev, N.M.Sobolevsky. SHIELD - Universal Monte Carlo Hadron Transport Code: Scope and Applications. Radiation Measurements, 30 (1999) 553.

4.     Е.В. Ефремов, Н.А. Иванов, О.Б. Москалев. “PARSE-2 - комплекс программ для расчетов методом Монте-Карло адронного каскада в трехмерной геометрии”. Тезисы докладов VI Всероссийской научной конференции по защите от ИИ ЯТУ, Обнинск, 1998.

5.     R.E. Prael and H. Lichtenstein, "User Guide to LCS: The LAHET Code System", LANL report LA-UR-89-3014 (September 1989).

6.     А.В. Воронков, А.В Ефремов, Е.А. Земсков, Н.М. Соболевский, М.И. Кривопустов, С.П. Казновский. Расчетный анализ полей энерговыделения в мишенях, облучаемых пучком релятивистских протонов. Препринт ИПМ им. М.В. Келдыша РАН, 2000

7.     A.G.Churbanov, A.N.Pavlov and P.N.Vabishchevich. Operator-splitting methods for the incompressible Navier-Stokes equations on non-staggered grids. Part 1: First-order schemes. //Int. J. Numer. Methods Fluids, 1995, v.21, No.8, pp.617-640.

8.     П.Н.Вабищевич, А.Н.Павлов, А.Г.Чурбанов. Методы расчета нестационарных несжимаемых течений в естественных переменных на неразнесенных сетках. //Матем. моделирование, 1996, т.8, N 7, с.81-108.

9.     П.Н.Вабищевич, А.Н.Павлов, А.Г.Чурбанов. Численные методы решения нестационарных уравнений Навье-Стокса в естественных переменных на частично разнесенных сетках. //Матем. моделирование, 1997, т.9, N 4, с.85-114.

10. A.G.Churbanov and A.Ya.Gorbatchevski. Mathematical modeling of conjugate heat and mass transfer in a chemical reactor with incrustations. In: Proc. 2nd Int. Conf. On Finite-Difference Methods: Theory and Applications (CFDM98) (Ed. A.A.Samarskii), pp.80-84. Minsk, Belarus, 1998.

Приложение 

Расчет энерговыделения в массивной свинцовой мишени (сборка 1)

В расчете энерговыделения по программе LAHET использовалась цилиндризованная модель мишени с эквивалентным радиусом R=28.2 см. Ее расчетная схема представлена на Рис П.1.

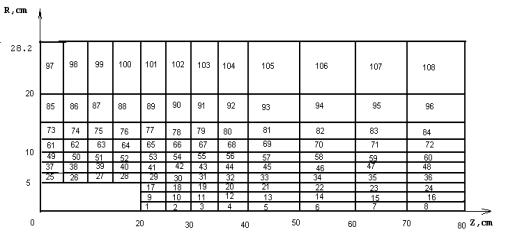
Рис П.1. Расчетная модель мишени

Детальные значения удельного энерговыделения в ячейках мишени приведены в Таблице П.1.

Таблица П.1. Удельное энерговыделение в ячейках мишени

при энергии протонов 5.0 Гэв ( Мэв/протон/ см**3).