1. Введение

Процесс взаимодействия пучка протонов с энергией порядка 1 ГэВ с мишенью из тяжелых элементов, таких, как свинец, вольфрам, природный или обедненный уран, в последнее время – ртуть, вызывает устойчивый интерес с 50^х годов. Рассматриваются различные схемы утилизации нейтронов, генерируемых пучком протонов в мишени, в целях электроядерного бридинга ядерного топлива [1,2], трансмутации отходов ядерной энергетики [3], переработки оружейного плутония [4]. Обсуждаются перспективные схемы ядерной энергетики, включающие подкритические устройства, работающие от ускорителя (ADS – Accelerator Driven Systems) [5,6]. Процесс генерации нейтронов в мишени лежит также в основе работы интенсивных импульсных источников нейтронов для исследования структуры вещества [7].

Ранее были выполнены и в настоящее время продолжаются экспериментальные и расчетно-теоретические исследования процессов генерации нейтронов и энерговыделения в тяжелых мишенях. Эти процессы определяются ядерными, и в первую очередь нейтронными свойствами материала мишени, т.е. сечениями реакций взаимодействия нейтронов и других частиц с ядрами вещества мишени. В настоящей работе рассматривается взаимодействие пучка протонов со свинцовыми мишенями разных размеров.

Выбор свинца обусловлен тем, что свинец – доступный и технологичный материал, который часто рассматривается в проектах нейтронообразующих мишеней. Для свинцовых мишеней имеется определенное количество экспериментальных данных, достаточное для верификации существенных аспектов расчетных моделей. В то же время наличие у ядер свинца небольшой делимости (~5%) под действием частиц с энергией порядка нескольких сотен МэВ позволяет ставить вопрос: не будет ли деление играть заметную роль в свинцовой мишени при высоких энергиях первичного пучка протонов, когда адронный каскад в мишени сильно разветвлен и происходит много актов неупругого взаимодействия.

В настоящей работе процесс взаимодействия пучка протонов с мишенью моделируется с помощью универсального транспортного кода SHIELD [9], который позволяет рассчитывать взаимодействие адронов и ядер со сложными макроскопическими мишенями в области энергий до 1 ТэВ. Код SHIELD является отечественным аналогом известных зарубежных транспортных кодов (см. раздел 2).

В разделе 3 приводятся некоторые результаты расчетов выхода нейтронов из свинцовой мишени с помощью кода SHIELD и их сравнение с экспериментальными данными и расчетами других авторов, что позволяет убедиться в адекватности кода SHIELD данной задаче.

В разделе 4 даны результаты расчетов взаимодействия пучка протонов с энергией 1, 10, и 100 ГэВ с цилиндрическими мишенями из свинца двух размеров: малой мишенью, (радиус R=10 см, длина L=60 см) и большой мишенью (R=50 см, L=200 см). Для сравнения выполнены также расчеты для делящейся мишени (²³⁸U). В последнем разделе 5 проводится обсуждение результатов.

2. Транспортный код SHIELD

          Транспортный код SHIELD создавался как универсальный инструмент для широкого круга исследований процесса взаимодействия частиц с веществом. Первоначальная версия кода SHIELD была разработана в ОИЯИ в начале 1970-х гг. [8]. В дальнейшем код SHIELD совершенствовался, а в 1990-х гг. был полностью переработан с учетом требований современных задач.

          Современная версия кода SHIELD [9] применяется в тех же областях исследования, что и транспортные коды HETC [11] (и его современне версии LAHET, HERMES, NMTC/JAERI) и FLUKA [12] и имеет свои оригинальные особенности и преимущества. Код SHIELD включает в себя известные отечественные модели ядерных реакций (см. ниже), обеспечивающие моделирование всех стадий неупругих ядерных взаимодействий в эксклюзивном подходе. В течение более чем 25-летнего времени жизни код SHIELD служил методической основой для решения многих задач [10].

          Транспортная часть кода SHIELD. Современная версия кода SHIELD [9] позволяет моделировать перенос нуклонов, пионов, каонов, антинуклонов и мюонов, а также ядер с произвольными значениями (A,Z) в области энергий до 1 ТэВ. Учитываются ионизационные потери энергии заряженных частиц и ионов, дополнительно возможен учет флуктуаций ионизационных потерь. При переносе пионов и каонов учитываются основные 2^х- и 3^х-частичные моды распадов. Геометрическая конфигурация мишени представляет собой произвольную комбинацию тел, ограниченных поверхностями второго порядка. Химический и изотопный состав вещества в каждой геометрической зоне мишени произволен.

          В процессе моделирования очередного адронного каскада в мишени, формируются источники нейтронов низких энергий (E_n < 14.5 MeV), а также g, e^±, и n (как продуктов распада мезонов). Все эти частицы запоминаются в специальных массивах со всеми их индивидуальными параметрами. После того, как моделирование дерева адронного каскада закончено, рассчитывается перенос частиц из источников с помощью соответствующих транспортных кодов, подключенных к SHIELD.

Перенос нейтронов с энергией ниже 14.5 MeV моделируется с помощью оригинального нейтронного транспортного кода LOENT на основе 28-групповой системы нейтронных констант БНАБ [13] (см. подробнее ниже). Для моделирования электромагнитных ливней используется известный код EGS4, который при необходимости может быть подключен к коду SHIELD с помощью специального интерфейса. Возможно подключение и других программ нейтронного и электромагнитного транспорта.

В коде SHIELD реализовано запоминание дерева адронного каскада в процессе его генерации полностью, без потери физической информации. Запоминание дерева осуществляется в специальных массивах. Запоминаются все индивидуальные параметры всех вторичных частиц во всех поколениях, а также все случаи распада, вылета из мишени и остановки из-за ионизационных потерь. Все акты упругого и неупругого ядерного взаимодействия, включая индивидуальные параметры каждого остаточного ядра (ядер), также фиксируются. Система ссылок позволяет установить, в каком поколении и в каком взаимодействии образовалась данная частица, и наоборот – какие продукты она породила. Дерево запоминается в привязке к геометрической конфигурации мишени, т.е. для каждой частицы запоминаются координаты и энергия на входе и на выходе при пересечении каждой геометрической зоны мишени. Одновременно формируются, как упоминалось выше, массивы источника нейтронов, а также g‑квантов и других продуктов распада мезонов.

В результате дерево адронного каскада запоминается без потери физической информации. Такая организация вычислений позволяет полностью разделить моделирующую и регистрирующую части кода, если требуется - накапливать деревья на внешнем носителе, облегчает визуализацию дерева и рассмотрение процесса во времени.

          В коде SHIELD предусмотрено как прямое (аналоговое) моделирование, так и использование статистических весов. Открытая архитектура кода облегчает его модификацию и развитие.

Генератор неупругих ядерных взаимодействий. Возможности транспортного кода существенно зависят от используемого генератора неупругих ядерных взаимодействий. В коде SHIELD используется генератор MSDM [14], который включает известные отечественные модели ядерных реакций. Генератор MSDM позволяет моделировать в эксклюзивном подходе адрон-ядерные и ядро-ядерные неупругие взаимодействия в области энергий до 1 ТэВ. Быстрая, каскадная стадия ядерной реакции при энергиях ниже 1 ГэВ моделируется на основе Дубнинской модели внутриядерных каскадов [15]. Выше 10 ГэВ используется модель независимых кварк-глюонных струн (QGSM) [16], а в промежуточной области 1-10 ГэВ - некоторое расширение QGSM [17]. Таким образом обеспечивается самосогласованное описание быстрой стадии ядерной реакции во всем интервале энергий первичных адронов и ядер вплоть до 1 ТэВ. Эволюция возбужденного остаточного ядра к равновесному состоянию описывается в терминах предравновесной модели, основанной на решении соответствующего мастер-уравнения методом Монте-Карло [18].

          Дальнейшее равновесное девозбуждение остаточного ядра включает несколько механизмов. Для легких ядер (A<16) используется модифицированная модель Ферми-развала [19]. Средние и тяжелые ядра при умеренных возбуждениях (E*<2 МэВ/нуклон) девозбуждаются посредством испарения частиц, включая конкуренцию испарения и деления для тяжелых ядер [19,20]. Высоковозбужденные ядра (E*>2 МэВ/нуклон) могут распадаться на несколько возбужденных фрагментов согласно Статистической модели мультифрагментации (SMM) [21] с последующей эмиссией частиц из фрагментов. Таким образом, генератор MSDM обеспечивает описание всех стадий ядерной реакции в эксклюзивном подходе.

          Необходимо отметить, что модели ядерных реакций, включенные в генератор MSDM, многократно подвергались сравнению с экспериментом [15-21]. В этих и других работах тех же авторов показано, что эти модели хорошо воспроизводят как спектрально-угловые характеристики вторичных частиц, так и выходы остаточных ядер в абсолютных единицах в широком интервале энергий снаряда и масс мишени. В частности, правильно вычисляются сечения деления и массовые распределения осколков [20] как для хорошо делящихся (U, Th), так и для слабо делящихся ядер (Bi), что важно в контексте настоящей работы.

Перенос нейтронов с энергией ниже 14.5 MeV. Перенос нейтронов моделируется с помощью оригинального нейтронного транспортного кода LOENT на основе 28-групповой системы нейтронных констант БНАБ [13]. Код LOENT может использоваться как независимо, так и совместно с кодом SHIELD, с которым он имеет общий геометрический модуль и ряд общих подпрограмм.

В коде LOENT используются следующие данные из системы констант БНАБ:

s_t‑полное сечение;

s_f‑сечение деления (n,f);

n‑среднее число нейтронов деления;

s_c‑сечение захвата (n,c);

s_in‑сечение неупругого рассеяния (n,n¢), включая реакцию (n,2n¢);

s_e‑сечение упругого рассеяния (n,n);

m‑средний косинус угла упругого рассеяния;

s_in(g,g+k)‑матрица межгрупповых переходов при неупругом рассеянии.

Соответственно, моделируются следующие реакции под действием нейтронов:

Упругое рассеяние (n,n). Угол рассеяния нейтрона определяется единственным параметром – средним косинусом в лабораторной системе координат и разыгрывается в линейно-анизотропном приближении. Энергия и импульс рассеянного нейтрона, а также ядра отдачи, вычисляются из двухчастичной нерелятивистской кинематики. При попадании нейтрона в тепловую группу предполагается, что его энергия не изменяется в дальнейших столкновениях и нейтрон переносится в тепловой группе до своего поглощения или вылета из сборки.

Захват нейтрона (n,c) означает окончание нейтронной траектории. Конкретный канал реакции – например (n,g), (n,p) или (n,a) – идентифицируется дополнительно при необходимости и наличии соответствующих сечений в групповых константах. Считается, что кинетическая энергия нейтрона выделилась локально в точке захвата.

Неупругое рассеяние (n,n'). Номер группы рассеянного нейтрона разыгрывается согласно матрице неупругих переходов. Считается, что энергия рассеянного нейтрона распределена равномерно внутри этой группы. Если нейтрон остался в той же группе, в которой находился до рассеяния, то его энергия распределена равномерно от нижней границы группы до начальной энергии. Угловое распределение рассеянных нейтронов предполагается изотропным в лабораторной системе координат. Разность энергий до и после рассеяния выделяется локально в точке рассеяния.

Реакция (n,2n) описывается той же самой матрицей неупругих переходов и конкурирует с неупругим рассеянием (n,n'). Характеристики обоих вторичных нейтронов разыгрываются тем же способом, что и в случае неупругого рассеяния.

Деление(n,f). Используя заданное среднее число нейтронов деления `n разыгрываем конкретное значение n как одно из двух соседних целых чисел. Затем энергия каждого нейтрона разыгрывается согласно спектру деления. Угловое распределение предполагается изотропным в лабораторной системе координат. Энерговыделение в точке деления задается как параметр со значением ~ 180-190 МэВ.

При работе кода LOENT нейтроны выбираются из внешнего источника последовательно, по одному, и прослеживаются до окончания траектории нейтрона. При этом нейтроны могут размножаться в реакциях (n,2n) и (n,f), поэтому для их хранения предусмотрена память достаточного объема.

Каждый нейтрон имеет статистический вес, а также кумулятивный таймер, в котором накапливается время, прошедшее с момента его выборки из внешнего источника нейтронов или рождения в адрон-ядерном взаимодействии. Статистический вес обычно равен единице, но он резервирует стандартные возможности весового моделирования.

На Рис. 1 и 2 в иллюстративных целях изображены групповые сечения для натурального свинца и изотопа ²³⁸U [13], использованные в настоящих расчетах.

3. Взаимодействие протонов со свинцовой мишенью:

сравнение расчета с экспериментом

Выход нейтронов из свинцовой мишени измерялся несколькими группами в широком диапазоне энергий первичного пучка [22-25] (ссылки на более ранние измерения собраны в обзоре В.С.Барашенкова [1]). В большинстве измерений свинцовая мишень имела цилиндрическую форму. Размеры мишени были, как правило, следующие: радиус R=10 см, длина L=60 см. Такая мишень полностью поглощает протоны с энергией 1 ГэВ, падающие вдоль ее оси, и часто встречается в экспериментальных и расчетно-теоретических исследованиях. В некоторых измерениях использовалась мишень радиусом R=5 см, для которой снижение выхода нейтронов не превышает 20% по сравнению с мишенью радиусом R=10 см.

На Рис.3 изображена зависимость выхода нейтронов с полной поверхности свинцовой цилиндрической мишени (R=10 см, L=60 см) в зависимости от энергии пучка протонов [26]. Кривая – расчет по программе SHIELD, точки – измерения разных авторов [1, 22-25]. Поскольку экспериментальные методики позволяют регистрировать, как правило, только выход нейтронов низких энергий, то в расчете регистрировались нейтроны с энергией ниже 10.5 МэВ. Выход нейтронов более высоких энергий составляет около 10% полного выхода. Вопрос о доле быстрых нейтронов в полном выходе при разных энергиях пучка будет уточнен ниже.

Чтобы выяснить, при какой энергии пучка затраты энергии на производство одного нейтрона минимальны, полезно представить кривую выхода (Рис. 3) в виде удельной кривой (Рис. 4), т.е. разделить выход на энергию пучка в ГэВ. Как видно, с точки зрения энергетической цены одного нейтрона, оптимальной является энергия протонов ~1.2 ГэВ (положение максимума удельной кривой). При меньших энергиях пучка возрастают ионизационные потери, при больших – происходит утечка энергии в электромагнитные ливни за счет генерации и распада p⁰‑мезонов. Обе эти причины снижают выход нейтронов.

Отметим, что форма энергетического спектра нейтронов, образующихся в мишени (спектра источника нейтронов) весьма устойчива и слабо зависит от энергии пучка, т.к. большинство нейтронов испускается на равновесной («испарительной») стадии реакции. Энергия первичного пучка определяет лишь интенсивность источника нейтронов, поскольку при более высокой энергии пучка происходит больше неупругих взаимодействий в мишени. Эти соображения иллюстрируются Рис. 5 [27], где представлены спектры источника нейтронов для энергии пучка 360, 600 и 1200 МэВ. Средняя энергия спектра «испарительных» нейтронов составляет около 3 МэВ.

Далее, в процессе переноса в мишени, спектр источника деформируется, и наружу из мишени выходят нейтроны с заметно более мягким спектром. Это иллюстрируется Рис. 6, где представлены спектры источника нейтронов и спектры на выходе из мишени, рассчитанные тремя разными транспортными кодами: SHIELD, LAHET и HERMES. Энергия протонного пучка равнялась 800 МэВ. Эти результаты были получены в ходе международного сравнения транспортных кодов, инициированного Nuclear Energy Agency OECD [28]. Как видно из Рис. 6, указанные выше транспортные коды дают весьма близкие результаты, чего нельзя сказать о некоторых других кодах, участвовавших в сравнении [28].

Важным вопросом при разработке нейтронообразующих мишеней является отвод тепла, т.к. энерговыделение в мишени под действием сильноточного пучка протонов с энергией порядка 1 ГэВ весьма велико. На Рис. 7 представлено распределение энерговыделения по глубине в мишенях из обедненного урана, свинца, меди и алюминия под действием пучка протонов с энергией 1 ГэВ. Все мишени имели цилиндрическую форму и одинаковые размеры (R=10 см, L=60 см). На рисунке даны результаты калориметрических измерений [29] и расчеты по коду SHIELD. Согласие расчета и эксперимента вполне удовлетворительное.

Таким образом, проведенное сравнение с экспериментом и расчетами других авторов показывает, что код SHIELD правильно воспроизводит основные закономерности взаимодействия пучка протонов со свинцовой мишенью в широком интервале энергий.

4. Взаимодействие протонов со свинцовой мишенью

разных размеров при энергиях 1, 10 и 100 ГэВ

С целью наблюдать картину взаимодействия пучка протонов с массивной свинцовой мишенью в широком диапазоне энергий, с помощью кода SHIELD были выполнены расчеты взаимодействия протонов с энергией 1, 10 и 100 ГэВ с цилиндрическими мишенями двух размеров.

Малая мишень имела такие же размеры, как в предыдущем разделе (R=10, L=60 см). Узкий пучок протонов падал вдоль оси мишени на ее торец, как и во всех случаях, рассмотренных выше.

Большая мишень изображена на Рис. 8. Ее габаритные размеры составляли: R=50 см, L=200 см. Узкий пучок протонов вводился внутрь мишени через узкий канал на глубину 50 см, чтобы исключить «альбедную» утечку нейтронов с заднего торца. Внутренняя область большой мишени (собственно мишень), имела те же размеры, что и малая мишень (R=10, L=60 см). Внешняя область большой мишени («бланкет») состояла, в одном варианте расчета также из свинца, а в другом – из урана ²³⁸U, см. Рис. 8.

Уран в качестве бланкета использовался для сравнения. Напомним, что свинец не делится нейтронами с энергией ниже 14.5 МэВ (сечение деления s_f в константах БНАБ равно нулю), но имеет небольшую делимость, около 5%, при энергиях частиц в области нескольких сотен МэВ. Изотоп ²³⁸U имеет делимость до 20% на быстрых нейтронах и более 50% под действием частиц с энергией до 1 ГэВ. Таким образом, мы получаем возможность сравнить процессы в слабо делящейся (Pb) и хорошо делящейся (²³⁸U) под действием быстрых частиц средах. Заметим, что с дальнейшим увеличением энергии протона выше 1 ГэВ делимость тяжелых ядер снижается, т.к. из ядра выбивается все больше нуклонов и остаточное ядро становится слишком легким, чтобы делиться.

Результаты расчетов представлены в Таблицах 1-3 и на Рис. 9‑11. Каждая таблица относится к одному значению энергии протонов и содержит данные для трех конфигураций: малой Pb-мишени и сборок со свинцовым и урановым бланкетом. Заливкой выделены данные, относящиеся к адронному каскаду. Данные по переносу нейтронов с энергией ниже 14.5 МэВ показаны без заливки. Все числа нормированы на 1 протон.

Адронный каскад включает, по определению, нейтроны с энергией выше 14.5 МэВ и все остальные адроны (протоны, пионы, каоны, антинуклоны). Для адронного каскада дается среднее число актов упругого рассеяния и неупругих взаимодействий в мишени и бланкете. В число неупругих взаимодействий включены реакции с делением остаточного ядра; число делений показано отдельно.

Затем дается среднее число ядер-продуктов, число нейтронов с энергией выше 14.5 МэВ, вылетевших за пределы сборки и число нейтронов с энергией ниже 14.5 МэВ (источник нейтронов), образовавшихся в ядерных реакциях. Эти данные приводятся для всей сборки суммарно (мишень+бланкет).

Как было сказано выше, перенос нейтронов с энергией ниже 14.5 МэВ моделируется на основе констант БНАБ. В таблицах дано среднее число нейтронов с энергией ниже 14.5 МэВ, вылетевших за границы сборки, а также число взаимодействий типа (n,f), (n,c), (n,n¢) и (n,2n) в мишени и бланкете отдельно.

Статистическая погрешность приведенных данных равна 1-3% при энергии протонов 1 ГэВ и несколько возрастает с ростом энергии, составляя 5-10% при энергии 100 ГэВ.

Аналогично, каждый рисунок относится к одному значению энергии протонов. Для каждой из трех конфигураций (сверху вниз: Pb-мишень, сборка с Pb-бланкетом, сборка с ²³⁸U-бланкетом ) показан спектр источника нейтронов и спектр нейтронов с энергией ниже 14.5 МэВ, вылетающих из сборки.

5. Обсуждение результатов

Первое, что следует отметить: с ростом энергии протонов каких либо качественных изменений в общей картине взаимодействия с массивной свинцовой мишенью не происходит. С ростом энергии протонов на порядок, число взаимодействий в свинцовой мишени, интенсивность источника нейтронов и выход нейтронов из мишени возрастают в 6¸8 раз. При этом форма нейтронных спектров сохраняется, возрастает лишь интенсивность.

Далее, деление ядер свинца не играет сколько-нибудь существенной роли. В свинце отсутствуют условия возникновения цепной ядерной реакции при любых энергиях инициирующих протонов из-за малости сечения деления. Положительный энергетический выход в мишени невозможен, т.к. затраты энергии на отрыв нуклонов от ядра (т.е. на образование нуклидов в реакциях глубокого расщепления) многократно превосходят энерговыделение в редких актах деления. Число реакций с делением сохраняется в пределах 0.2¸0.7% от числа всех неупругих взаимодействий для всех рассмотренных энергий протонов и размеров мишени.

Уточним вопрос о доле нейтронов с энергией выше 14.5 МэВ в спектрах нейтронов, вылетающих из мишени. Для малой Pb-мишени при энергиях 1, 10 и 100 ГэВ эта доля соответственно равна 8.9, 11.4 и 10.8%. Для большой свинцовой мишени эта доля меньше 1% при всех энергиях, т.к. практически все каскадные нейтроны (с энергией выше 14.5 МэВ) успевают испытать неупругие взаимодействия.

Наличие пика в спектре выхода нейтронов в группе №11 БНАБ для малой Pb‑мишени объясняется структурой матрицы неупругих переходов: имеется заметная вероятность перехода в группу №11 из групп №5 и 6, лежащих вблизи максимума спектра источника, тогда как переходы в группы №9 и 10 из групп №5 и 6 отсутствуют. С увеличением размеров мишени указанный пик исчезает при всех энергиях протонов, т.к. нейтроны успевают, до вылета из мишени, перейти в группы с более низкой энергией.

Наконец, различие в нейтронных свойствах Pb и ²³⁸U настолько существенно (Рис. 1 ,2), что спектры выхода для свинцового и уранового бланкета различаются радикально. В свинце, ниже порога неупругого рассеяния 0.4 МэВ, нейтроны испытавают лишь упругое замедление (плюс очень слабый захват). Соответственно спектр нейтронов, вылетающих из большой свинцовой мишени, простирается вплоть до тепловой энергии. Напротив, выход нейтронов из уранового бланкета подавлен вследствие сильного захвата.

          Настоящая публикация подготовлена в ходе работ, проводимых под руководством акад. В.И.Субботина в целях поиска возможных новых подходов и концепций развития ядерной энергетики. Авторы благодарны М.В.Масленникову, Е.В.Ефремову, Е.А.Земскову и С.П.Казновскому за интерес к работе и полезные обсуждения. Один из нас (Н.С.) благодарит авторов ядерных моделей, включенных в генератор MSDM, Н.С.Амелина, А.С.Ботвину, К.К.Гудиму и В.Д.Тонеева, предоставивших в его распоряжение современные версии компьютерных кодов.

Литература

1.     В.С.Барашенков. Ядерно-физические аспекты электроядерного метода. ЭЧАЯ, 9 (1978) 871.

2.     Р.Г.Васильков, В.И.Гольданский, В.В.Орлов. Об электрическом бридинге. УФН, 139 (1983) 435.

3.     C.Rubbia, S.Buono, Y.Kadi, J.A.Rubio. Fast Neutron Incineration in the Energy Amplifier as Alternative to Geologic Storage: the Case of Spain. CERN/LHC/97-01 (EET).

4.     C.Rubbia, S.Buono, E.Gonzales, Y.Kadi, J.A.Rubio. A Realistic Plutonium Elimination Scheme with Fast Energy Amplifies and Thorium-Plutonium Fuel. CERN/AT/95-53 (ET).

5.     R.Fernandez, P.Mandrillon, C.Rubbia, J.A.Rubio. A Preliminary Estimate of the Economic Impact of the Energy Amplifier. CERN/LHC/96-01 (EET).

6.     В.И.Субботин. Ускорители могут сделать ядерную энергетику более безопасной. Сообщение ОИЯИ Р1-99-97, Дубна, 1999.

7.     J.M.Carpenter. Pulsed Spallation Neutron Sources for Slow Neutron Scattering. NIM, 145 (1977) 91.

8.     Н.М.Соболевский. Программа расчета нуклон-мезонного каскада в веществе методом Монте-Карло. ОИЯИ, Б1-2-5458, Дубна, 1970. В.С.Барашенков, Н.М.Соболевский, В.Д.Тонеев. Атомная Энергия 32 (1972) 123, 217.

9.     A.V.Dementyev, N.M.Sobolevsky. SHIELD - Universal Monte Carlo Hadron Transport Code: Scope and Applications. Radiation Measurements, 30 (1999) 553.

10. N.M.Sobolevsky. The SHIELD Transport Code: a Tool for Computer Study of Interaction of Particles and Nuclei with Complex Media. Proc. of the 3^rd Yugoslav Nuclear Society International Conference YUNSC 2000, Belgrade, October 2-5, 2000, in print.

11. T.W.Armstrong, K.G.Chandler, Nucl.Sci.Eng. 49 (1972) 110.

12. A.Fasso, A.Ferrari, J.Ranft, P.R.Sala. New Developments in FLUKA Modeling Hadronic and EM Interactions. Proc. of 3rd Workshop on Simulating Accelerator Radiation Environments (SARE 3), KEK, Tsucuba, Japan, May 7-9, 1997. KEK Proceedings 97-5, June 1997, H/R/D, Ed. H.Hirayama, p. 32.

13. Л.Р.Абагян, Н.О.Базазянц, М.Н.Николаев, А.М.Цибуля.. Групповые константы для расчета реакторов и защиты. Энергоиздат. Москва, 1981.

14. A.S.Botvina, A.V.Dementyev, O.N.Smirnova, N.M.Sobolevsky, V.D.Toneev. MSDM - Multy Stage Dynamical Model. International Codes and Model Intercomparison for Intermediate Energy Activation Yields, by R.Michel and P.Nagel, NSC/DOC(97)-1, NEA/P&T No 14, OECD, Paris, 1997, p.307.

15. V.D.Toneev, K.K.Gudima. Nucl. Phys. A400 (1983) 173c.

16. Н.С.Амелин, К,К,Гудима, В.Д.Тонеев. Ядерная Физика 51 (1990) 1730.

17. Н.С.Амелин, К,К,Гудима, С.Ю Сивоклоков, В.Д.Тонеев. Ядерная Физика 52 (1990) 272.

18. K.K.Gudima, S.G.Mashnik, V.D.Toneev. Nucl. Phys. A401 (1983)329.

19. A.S.Botvina, A.S.Iljinov, I.N.Mishustin et al. Nucl. Phys. A475 (1987) 663.

20. Г.Д.Адеев, А.С.Ботвина, А.С.Ильинов и др. Метод расчета массово-энергетических распределений осколков деления ядер частицами средних энергий. Препринт ИЯИ РАН 816/93, Москва, 1993.

21. A.S.Botvina, A.S.Iljinov, I.N.Mishustin. Nucl. Phys. A507 (1990) 649.

22. R.G.Vassil’kov, V.I.Yurevich. Neutron emission from an extended lead target under the action of light ions in the GeV region. Proc. 11^th Meeting of International Collaboration on Advanced Neutron Sources ICANS-11, KEK, Tsukuba, Japan, October 22-26, 1990, KEK Report 90-25 (1991) vol. 1, p. 340.

23. А.Г.Акопян, Н.В.Колмычков, А.В.Кузин. АЭ, 75 (1993) 219.

24. H.Shibazaki et al. Experimental Study on Neutron Yield for 12 GeV Protons. Preprint KEK Internal 96-11, Tsukuba, 1996.

25. Yu.V.Ryabov, G.K.Matushko, V.N.Slastnikov. Z.Phys. 311 (1983) 363.

26. A.V.Dementyev, N.M.Sobolevsky, Yu.Ya.Stavissky. Neutron Yield from Extended Lead Target under Incident Protons of 0.1 to 100 GeV. Nucl. Instr. Meth. A374 (1996) 70.

27. С.Ф.Сидоркин, Н.М.Соболевский, А.Д.Перекрестенко. К вопросу о демонстрационном электроядерном стенде и исследованиях в области ядерной тренсмутации. Сборник докладов Международного совещания «Подкритические системы, управляемые ускорителем», ИТЭФ, Москва, 11-16 октября 1999 г., с. 91.

28. N.M.Sobolevsky. Conclusions of International Code Comparison for Intermediate Energy Nuclear Data. Thick Target Benchmark for Lead and Tungsten. Report NEA OECD NSC/DOC(96)15, Paris, 1996.

29. V.I.Belyakov-Bodin et al. Nucl. Instr. Meth. A295 (1990) 140; A314 (1992) 508; A335 (1993) 30. Атомная Энергия, 70 (1991) 339.

Приложение

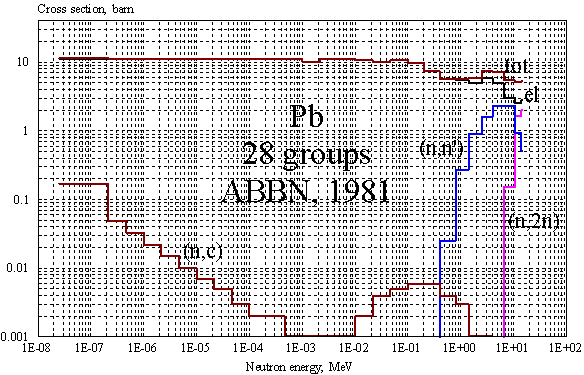
Рис. 1. 28-групповые нейтронные сечения БНАБ [13] для свинца

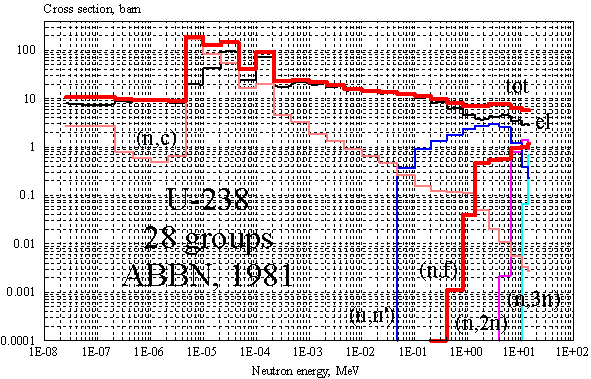
Рис. 2. 28-групповые нейтронные сечения БНАБ [13] для изотопа 238U

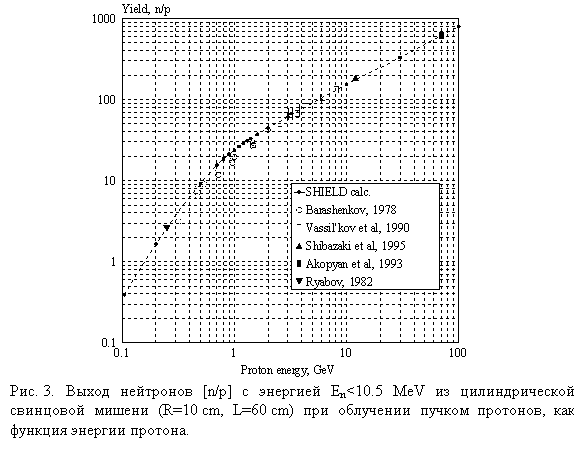
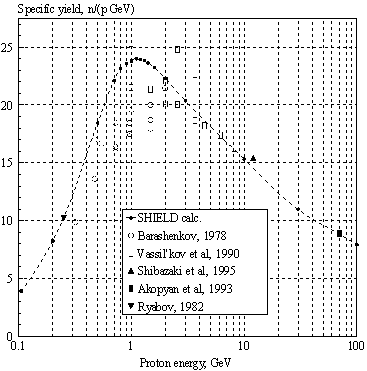
Рис. 4. Удельный выход нейтронов [n/(p GeV)] с энергией E_n<10.5 MeV из цилиндрической свинцовой мишени (R=10 cm, L=60 cm) при облучении пучком протонов, как функция энергии протона.

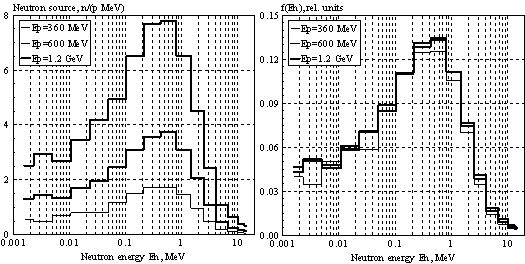
Рис. 5. Спектры нейтронов, образующихся в цилиндрической свинцовой мишени (R=10 см, L=60 см) при облучении пучком протонов с энергией 360, 600 и 1200 МэВ. Слева - спектры в абсолютной нормировке, справа - в нормировке на единичную площадь.

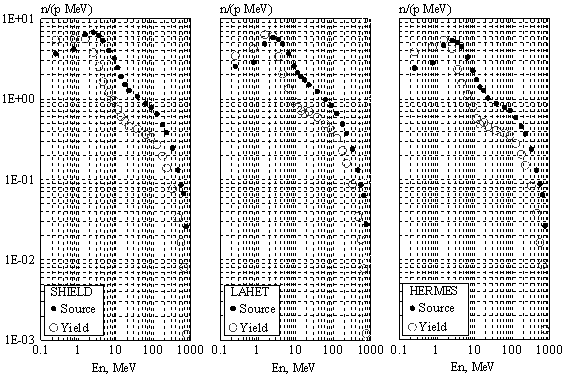
Рис. 6. Спектры нейтронов, образующихся в мишени (источник нейтронов) и вылетающих из мишени (нейтронный выход) при облучении цилиндрической свинцовой мишени (R=10 см, L=60 см), пучком протонов с энергией 800 МэВ. Расчет по программам SHIELD, LAHET и HERMES.

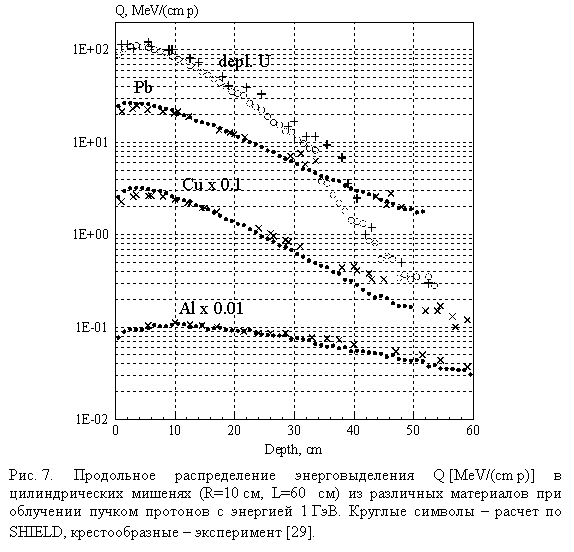
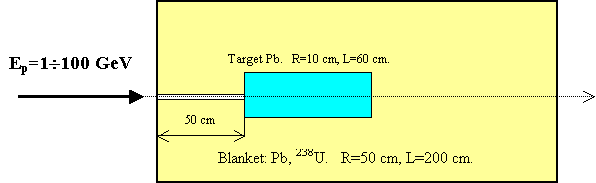
Рис. 8. Сборка из свинцовой мишени и бланкета (Pb, ²³⁸U).

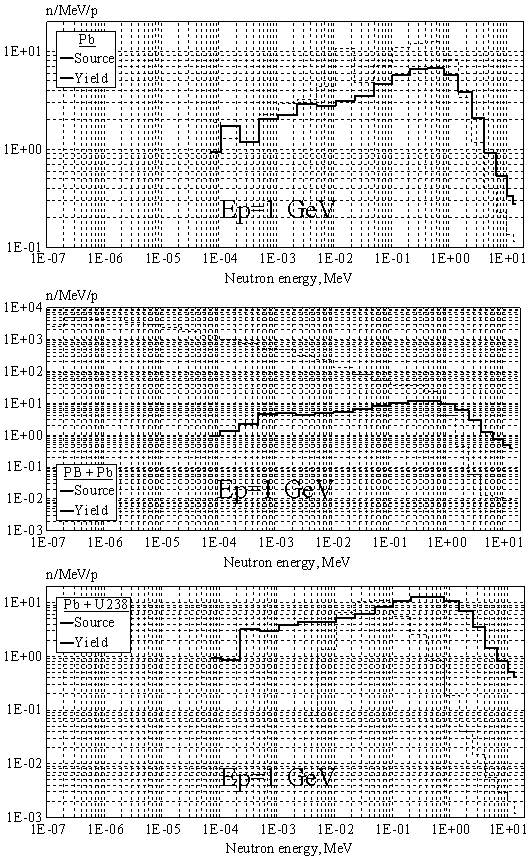
Рис. 9. Спектры источника нейтронов и выхода нейтронов с энергией ниже 14.5 МэВ для трех мишенных конфигураций при энергии протонов 1 ГэВ.

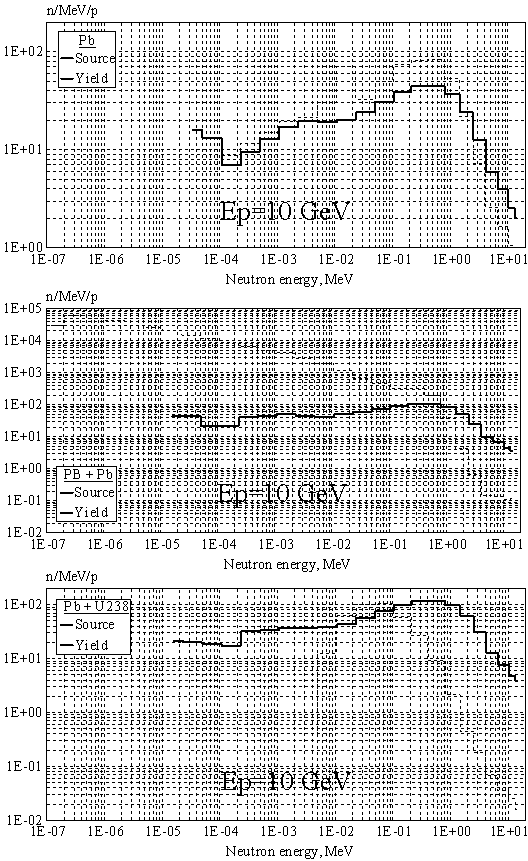
Рис. 10. То же, что на Рис. 9 для энергии протонов 10 ГэВ.

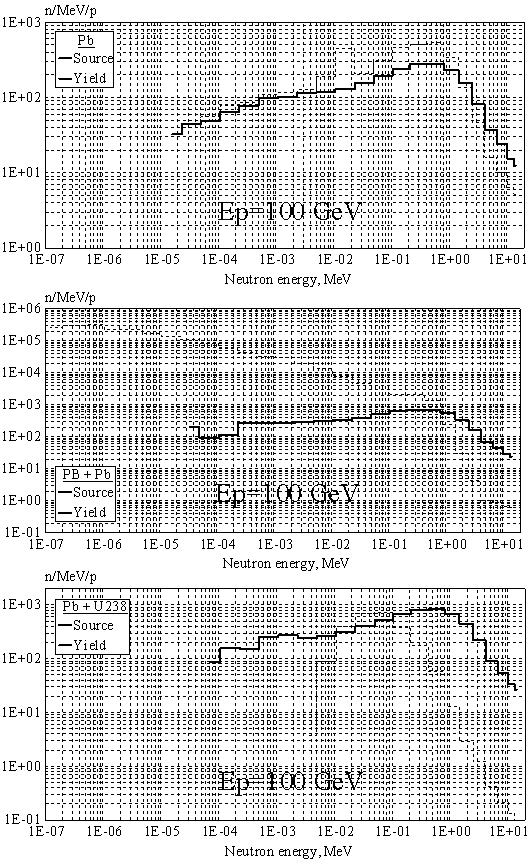
Рис. 11. То же, что на Рис. 9 для энергии протонов 100 ГэВ.

Таблица 1. Среднее число реакций и выходы нейтронов для трех конфигураций мишени. Энергия протонов 1 ГэВ. Заливкой выделены данные, относящиеся к адронному каскаду. Все числа нормированы на 1 протон.

Таблица 2. Среднее число реакций и выходы нейтронов для трех конфигураций мишени. Энергия протонов 10 ГэВ. Заливкой выделены данные, относящиеся к адронному каскаду. Все числа нормированы на 1 протон.

Таблица 3. Среднее число реакций и выходы нейтронов для трех конфигураций мишени. Энергия протонов 100 ГэВ. Заливкой выделены данные, относящиеся к адронному каскаду. Все числа нормированы на 1 протон.