Аннотация
Двумерная компьютерная модель была применена для численного расчета начальной фазы разряда
в высокочастотном поле. Модель учитывает гидродинамику газа, ионизацию, диффузию электронов
и т.д.
Abstract
A two-dimensional computer code has been developed for numerical calculation of the
initial phase of the discharge in uhf fields. The model takes into account hydrodynamics
of gas, ionization, electron diffusion etc.
Введение
Явление пробоя с последующим
развитием газоразрядного процесса давно является
предметом исследования традиционной физики в связи с широким спектром
приложений. Каждый частотный диапазон электромагнитных полей
(от постоянноточного до лазерного) обладает своим своеобразием развития
газоразрядного процесса. Особенно ярко это своеобразие проявляется в
микроволновом диапазоне (длины волн излучения от миллиметров до
дециметров). Развитие техники генерирования мощного излучения и
создание областей с весьма высокой плотностью потока энергии в сантиметровом
диапазоне (порядка МВт/cм2) позволило
наблюдать пробой и газовый разряд искрового типа при среднем давлении (доли
атмосферного) в фокусе излучения [1,2] и при высоком давлении (до
нескольких атмосфер) - в микроволновом
открытом резонаторе [3]. Разряд в фокусе
проходящего излучения представляет собой запутанную сеть очень тонких
плазменных нитей [4], заполняющую область фокуса
и распространяющуюся в сторону источника. Этот объект весьма сложен для
подробного изучения в силу отмеченных особенностей пространственного распределения.
Напротив, разряд в фокусе резонатора возникает в виде
уединенного регулярного образования. Это - тонкая яркая нить, вытянутая вдоль
вектора электрического поля, с длиной, близкой к полудлине волны излучения [5]. Геометрическая простота такого объекта уже
открывает некоторые возможности изучения детальной физики
явления.
Поскольку
микроволновый разряд обладает способностью развиваться в области с
допробойным значением поля, было сформулировано представление о
ведущей роли стримерного механизма в этом процессе [6]. Дальнейшие исследования
подтверждают это предположение. Однако работа по
построению теоретической модели встретилась со
значительными трудностями. Конечно, модель должна включать процессы
электронного баланса – ионизацию электронным ударом, рекомбинацию,
прилипание, электронную диффузию и пр. Протекание
электрического тока по плазме вызывает быстрый нагрев с последующими бурными
газодинамическими событиями
[7]. И,
что
особенно
усложняет
модель,
развитие
плазменного
образования
сильно
искажает
первоначальное,
невозмущенное,
поле. Собственно
это
искажение и
обусловливает
проявление
стримерного
эффекта.
Решение самосогласованной
электродинамической
задачи
приходится искать в
волновом
приближении,
поскольку
длина
объекта
сопоставима
с длиной волны,
а, как
известно,
дифракция
излучения
на тонком
длинном
объекте
представляет
собой
весьма
непростую
математическую
задачу.
Приведенная
в §1
математическая модель учитывает по минимуму все отмеченные факторы и,
подтверждая полученные ранее результаты, существенно дополнила представления, в
том числе и качественные.
Содержание §2 носит методический характер и оказывается очень полезным
для понимания начальной стадии разряда.
Основные результаты расчетов
описываются в §3.
§1 Постановка задачи
Взаимодействие высокочастотного электромагнитного поля E0exp(-iwt) с проводящим
плазменным облаком
описывается системой Максвелла
для амплитуд возмущения поля E, H
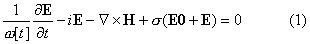
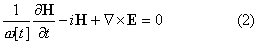
В качестве
единиц измерения используются [x]=c/w, [s]=w/4p, [t] -
характерное время изменения s. Проводимость s(t,x) определяется
уравнением непрерывности для электронной компоненты ионизуемого газа
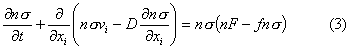
где
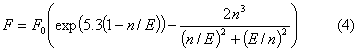
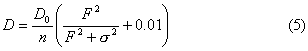
n – концентрация
газа, E =|E0+E | – амплитуда
поля, ns пропорционально концентрации
электронов. В качестве
единиц используются характерные
значения [n] и [E].
наконец,
состояние
самого газа
описывается уравнениями
гидродинамики

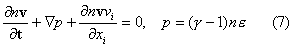

Наличие
множителя q дает свободу в выборе [t], g=1.4. В расчетах константы имеют следующие значения: w[t] »106, F0=800, f=25, D0 =0.16, q=166.Они соответствуют давлению воздуха 200 Torr и длине волны излучения 9 см.
Зависимость (4) аппроксимирует экспериментальные данные по ионизации и прилипанию (см.,
например, [8]). в
зависимости
(5)
модельно
учтен переход
на фронте ионизации
от свободной
электронной
диффузии
к амбиполярной [9].
Cамым
существенным
элементом в
рассматриваемой
модели (1)-(8) является нормированная частота ионизации -
функция nF(n,E)
(4).
Представление о ней дает рис.1, где она
изображена
как функция различных,
указанных на рисунке, аргументов: a)
при
фиксированном
значении E=0.5,
b) и c) при
фиксированном n=1.
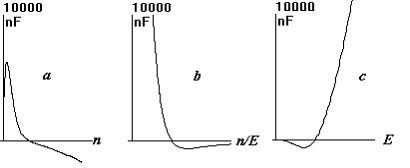
Рис.1 Нормированная частота ионизации nF(n,E): a) при E=0.5, b) и с) при n=1.
Отметим, что nF меняет знак
в районе n=E и
достигает максимума при
n » E/5.3.
§2
Одномерный
вариант
Некоторые вопросы, в особенности касающиеся
начального этапа, можно выяснить
уже на одномерном,
сферически симметричном, варианте задачи. Поскольку возмущение поля ( уравнения (1)-(2) ) такой симметрией обладать не может,
пренебрежем им и величину поля Е
будем считать заданной.
В качестве начальных данных естественно
использовать неподвижную однородную среду с
n=1,
v=0, w=1, s=0, E=E0, возмущенную наличием при r<r0 электронной компоненты, так что количество
электронов S = т nsr2dr в начальный момент равно S0>0. если E0>1, т.е. E>n, то везде F>0 и
препятствий для лавинной ионизации и последующего развития разряда нет. Здесь мы рассмотрим противоположный
случай, когда E0<1, т.е. E<n, F<0, и на начальной стадии
концентрация электронов должна уменьшаться.
Однако
имеющийся при r<r0 источник
нагрева qsE2 >0 создаст избыточное давление, выталкивающее газ из
центральной области. Падение плотности здесь
может оказаться значительным
и привести к ситуации, когда она станет меньше E, т.е. F станет положительным
и количество электронов S начнет расти. Расчеты
подтверждают
это. На рис.2а
дана
зависимость
от
времени
количества
электронов S(t) = т nsr2dr для варианта с е0=0.5, r0=0.03 и
начальным значением ns0=200(1-(r/r0)2), что
соответствует
S0=0.0007. здесь же пунктиром дана
энергия нагрева W(t) = т n(w-1)r2dr, уменьшенная
в 100 раз.
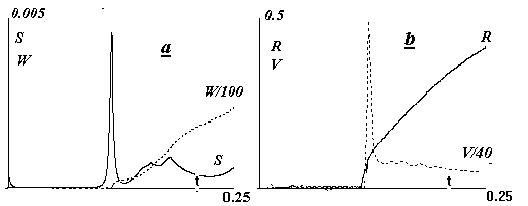
Рис2. a)
Зависимость от времени количества электронов
S(t)=т nsr2dr,
при Е0=0.5, r0=0.03, ns0=200(1-(r/r0)2).
Пунктир - энергия нагрева W(t)=т n(w-1)r2dr.
b) Траектория фронта ионизации R(t) и его скорость V(t).
отчетливо
видны фазы
поведения S: падение с образованием
разреженной
полости,
резкий
всплеск и медленное
немонотонное нарастание.
На
первом  этапе,
после падения плотности газа и практического исчезновения электронной
компоненты, происходит некоторый квазистационарный процесс, внешне себя не
проявляющий. Чтобы представить себе происходящее на этой стадии, рассмотрим
простейшую модель уравнения (3) вида этапе,
после падения плотности газа и практического исчезновения электронной
компоненты, происходит некоторый квазистационарный процесс, внешне себя не
проявляющий. Чтобы представить себе происходящее на этой стадии, рассмотрим
простейшую модель уравнения (3) вида
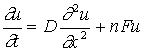  (3*) (3*)
При постоянных
D, nF она имеет решения u=exp(lt-ikx), l=nF-Dk2. это
означает, что длинноволновые
возмущения
(с
малыми к) могут
нарастать. Полагая k=1/L, где L - характерный размер
области с nF>0, получаем
условие неустойчивости нулевого решения
уравнения (3*)
l=nF -- D/L2 > 0
(*)
Это -
известное условие пробоя [8]. Очевидно, оно
же является условием инициирования процесса малыми возмущениями
электронной концентрации. Как видим (рис.2), ожидание выполнения этого условия и его
последствий может длиться довольно долго (до t=0.1).
Вторая
стадия – результат ионизации
сразу во всем
объеме r<r0, приводящая к существенному нагреву,
разлету и разрежению. Разрежение и прекращает эту фазу, т.к. nF приближается внутри каверны к нулю.
Поверхностный
слой с nF>0 отрывается от
объема, образуя фронт ионизации. Траектория
его движения R(t) и скорость V(t) изображены
на рис.2b. Что происходит на этой, основной, стадии
демонстрируют рис.3-7, на которых даны распределения величин на момент t=0.2.
Рис.3 Концентрация электронов и
проводимость при t=0.2
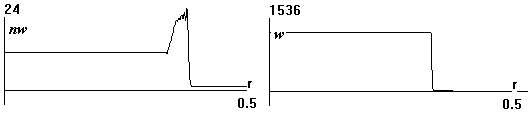
Рис.4 Плотность энергии при
t=0.2
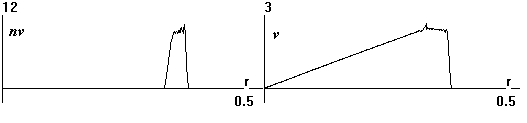
Рис.5 Импульс и скорость при
t=0.2
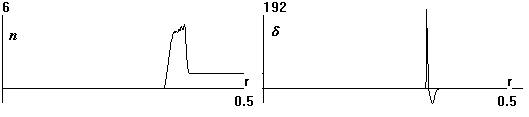
Рис.6
Плотность газа n и интенсивность ионизации d =ns(nF-fns), при t=0.2
Как видно, все происходит в узком слое между
разлетающейся ударной волной и следующей за ней волной разрежения, в которой плотность
газа падает на несколько порядков. Ситуацию внутри слоя демонстрирует рис.7, на
котором совмещены оба графика рис.6 -
радиальные распределения n и правой
части (3) d=ns(nF-fns), в растянутом (по r) масштабе. Как видно, фронт
ионизации, где d >0,
еще на порядок тоньше и располагается на тыловой поверхности волны
разрежения, где концентрация газа минимальна. Перед ним, в самой волне разрежения, d<0,
происходит прилипание электронов, появившихся здесь, очевидно, только благодаря
диффузии.
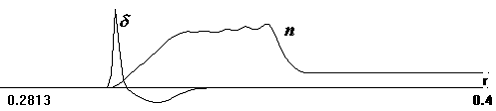
Рис.7. То же, что на рис.6, но в укрупненном масштабе в
области слоя.
Специфическая конфигурация d(r) со временем не меняется, но среднее значение d колеблется около нуля, определяя скорость изменения
S: dS/dt= тdr2dr. Нетрудно заметить, что d на рис.7 напоминает рис.1а, что неудивительно, так как на
них изображена фактически одна и та же зависимость. Отличие лишь в
аргументах: в первом - n, во втором
- r. Ясно, что ширина слоя ионизации
определяется градиентом концентрации газа в волне разрежения.
Представленный вариант
расчета, определяемый набором параметров:
E0=0.5, r0=0.03, S0=0.0007
является критическим. Если уменьшить S0,
оставляя неизменными E0, r0, то
инициация не происходит, фронт не образуется, процесс экспоненциально
затухает, S(t)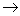 0. Увеличение же S0, естественно, все ускоряет и
усиливает. 0. Увеличение же S0, естественно, все ускоряет и
усиливает.
Интересно, что это значение S0=0.0007 оказывается критическим и для
других r0, в диапазоне 0.01< r0 <0.04, при сохранении E0=0.5. Не отличаются существенно и остальные результаты расчетов из этого
диапазона. За исключением крайнего варианта с r0=0.01. Здесь процесс
протекает вяло, с уменьшением S(t) на
два порядка, c малой скоростью фронта V=0.5 и превышением n и nw
их начальных значений всего на 20%. Объяснение этому факту – условие (*).
Действительно, используя характерные значения параметров, получаем L2>D/nF=10--4,
т.е. условие на радиус r0=L>0.01. И в расчетах, при r0<0.01, получить
положительный результат не удается. Более того, расчеты с другими значениями
коэффициента диффузии D подтверждают
справедливость условия (*).
В описанном сценарии принципиальным элементом
является локальное падение плотности газа, которое может происходить и по
другим причинам. Поэтому имеет смысл рассмотреть задачу, задав n<1 при r<r0 уже в начальный момент и исследовать последствия только
этого фактора.
Положим n=n0+(1-n0)(r/r0)2 при r<r0. Характерным значением радиуса
следует считать при этом не само r0,
а несколько меньшее - то, при котором n=E/5.3
или n=E. Первое соответствует
максимуму nF, второе - смене его
знака. Среднее значение плотности, при этом, равно 0.6+0.4n0. Увеличение
значения параметра S0 будет, конечно,
способствовать интенсификации процесса. Но, не желая смешивать роли различных
факторов, возьмем, например, S0=10--15.
Так как наличие полости с nF> 0 обеспечено уже в начальных данных, условие (*)
применимо непосредственно и определяет критический размер
полости. Грубая оценка, по порядку величин, дает и в этом случае L=0.01. Общая картина решения в этой,
второй, постановке задачи не меняется. Рис.8, аналог рис.2,
демонстрирует для варианта r0=0.05,
n0=0.1 поведение тех же величин S(t),
W(t), R(t),V(t).
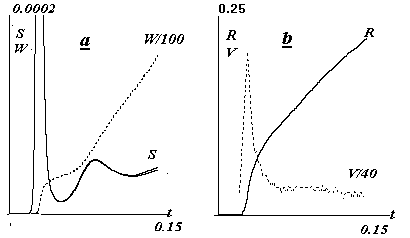
Рис.8. a)Зависимость от времени
количества электронов S(t)=тnsr2dr, при
Е0=0.5, r0=0.05, n0=0.1.
Пунктир - энергия нагрева W(t)=т n(w-1)r2dr.
b)Траектория фронта ионизации R(t) и его скорость V(t).
И
качественно, и количественно все очень похоже на прежний вариант постановки
задачи, и представленные на рис.3–7 конфигурации практически не меняются.
Сокращается первая стадия, поскольку разреженная полость уже готова.
Происходящую здесь эволюцию демонстрирует
рис.9, на котором изображены профили плотности (а) и частоты ионизации (b) на
интервале времени, когда происходит всплеск S(t).
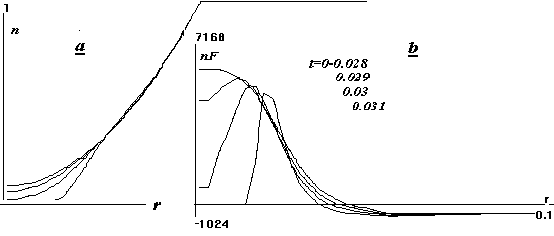
Рис.9. Радиальные профили
плотности (a) и частоты ионизации (b)
Критическим оказывается радиус r0=0.03, при котором инициирования не происходит.
Противоречия с L=0.01 нет, учитывая
отмеченную выше неоднозначность определения критического
значения.
На
рис.10a изображены траектории фронта
ионизации при различных r0,
указанных на рисунке, для
фиксированного n0=0.1.
На рис.10b – наоборот,
при различных n0 для r0=0.05.
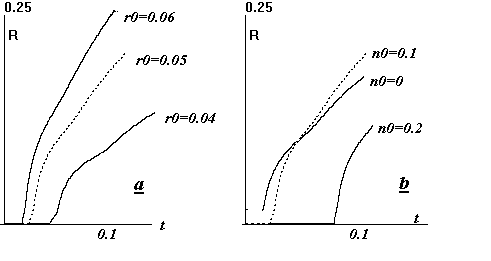
Рис.10. Траектории фронта
ионизации:
a) при различных r0, для n0=0.1, b) при
различных n0, для r0=0.05.
Зависимость
результата от параметра n0 простая.
При n0=0.25 процесс затухает. От глубины падения плотности, в диапазоне 0<n0<0.2, характеристики
решения зависят несущественно.
Заметим, что изменение n0 в этих
пределах меняет среднее значение плотности газа в пределах от 0.6 до 0.7.
§3 Двумерный
цилиндрически-симметричный вариант
Этот вариант
позволяет рассмотреть задачу
(1)-(8) в полном
объеме. Внешнее поле
в этом случае
является стоячей волной с отличной от нуля амплитудой осевой
компоненты Ez =E0×J0(r) – функцией Бесселя нулевого порядка. Ввиду малости
коэффициента 1/w[t] при производных
по времени в уравнениях (1)-(2)
пренебрежем этими членами и будем
решать полученную стационарную, при
каждом t, задачу с асимптотикой
Зоммерфельда (exp(i|x|)/|x|) на бесконечности.
Попытка инициировать
пробой локальным возмущением
электронной плотности ( ns>0 при r,|z|< r0 )
дает тот же результат, что и в
рассмотренном одномерном случае.
Возмущение «тратится» на нагрев и разлет газа. Увеличение поля на полюсах (n/E<1) несущественно и полностью
компенсируется уменьшением его внутри проводящей полости (n/E>>1). К тому же эта ситуация
кратковременна – возмущение поля
быстро исчезает вместе с проводимостью.
Таким образом, необходимым этапом
при инициировании пробоя
остается появление в газе каверны – полости с малой плотностью и не слишком малого размера.
В качестве исходных данных используем однородную
среду с n=w=1, v=s=0, E0=0.5, возмущенную наличием шаровой полости радиуса » 0.03 , где n < 0.5, S << 1. Область расчета: r>0, z>0 с очевидными условиями
симметрии на осях. На начальном этапе повторяется один из вариантов описанной
выше одномерной задачи. Поскольку проводимости практически нет, то поле не
возмущено и сферическая симметрия сохраняется. Отличия начинаются при t ˜0.03. Здесь опять происходит
взрывное экспоненциальное нарастание полного числа электронов. Однако оно
гораздо слабее. Во-первых, появляющееся возмущение поля снижает E, т.е. повышает n/E, замедляя темп ионизации. Во-вторых, эта же причина,
отодвигая n/E от нуля, ликвидирует
резкий спад S. В результате имеем
монотонный рост S(t). Все это
демонстрируют рис.11-14. На первом из них изображены S(t), она же в логарифмическом масштабе ( lnS(t) - щтрих-пунктиром) и энергия нагрева W(t) – пунктиром.
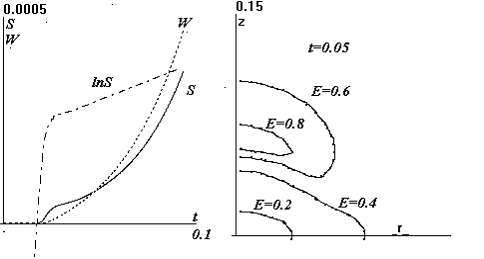
Рис.11 Зависимости от времени Рис.12 Линии уровня E(r,z)=const при t=0.05.
полного числа электронов S и
энергии нагрева W
Линейность функции lnS(t) свидетельствует об экспоненциальном характере нарастания S(t) с резкой сменой показателя – логарифмической производной dlnS/dt, уменьшением его при
t ˜0.03 в тридцать раз (с
1000 до 30).
На рис.12 изображены линии
уровня E(r,z)=const при t=0.05,
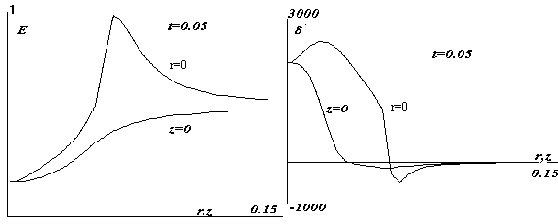
Рис.13. Профили E(r,0), E(0,z).
Рис.14. Профили d(r,0), d(0,z).
На рис.13–14 даны профили E(r,0),
E(0,z) и d(r,0),
d(0,z), соответственно, вдоль осей на момент t=0.05. Налицо существенное отличие в
распределении этих величин от сферической симметрии.
Но
главное - отрыва фронта ионизации не происходит, так как в тылу его
она не прерывается, d здесь не исчезает. Последнее и обусловливает
более интенсивную ионизацию. Концентрация и проводимость на этой стадии
практически сохраняют сферическую симметрию.
Следующий этап – спокойное вытягивание
проводящего облака вдоль оси z - демонстрируют рис.15-16. На первом
показано положение фронта ионизации (линии уровня s=1) в указанные моменты времени. Эти линии совпадают с границей волны
разрежения, следующей за ударной волной. На втором – даны профили n(0,z), E(0,z) в два момента
времени. Заметим, что в волне разрежения отношение n/E близко к единице, а внутри проводящего облака меньше 1.
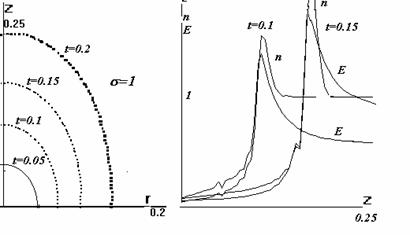
Рис.15.Положение
фронта ионизации Рис.16. Профили плотности и амплитуды поля
(линии уровня s=1)
Стоит отметить следующее. К моменту t=0.15
( рис.16 ) в картине процесса
появляется
существенная деталь – возмущение поля обгоняет ударную волну, здесь возникает ситуация n/E<1, означающая появление второго очага ионизации. Представление о
распределении величин в пространстве на этом этапе дают рис.17-19, на которых изображены линии уровня n, s, E на момент t=0.2. Качественно распределения концентрации и проводимости пока сохраняют
свои квазиодномерные конфигурации.
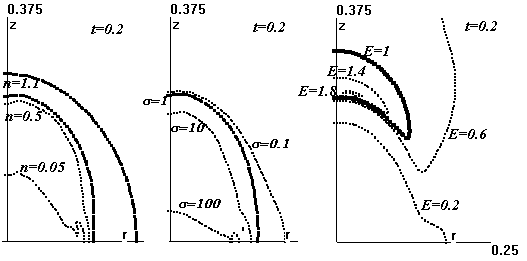
Рис.17,18,19. Линии уровня n, s, E, соответственно, на момент t=0.2.
Следующий этап процесса демонстрируют рис.20-22. На
первом изображены положения линии уровня n=1.1
для шести последовательных моментов времени (от 0.2 до 0.3). Он показывает
эволюцию сжатого (n>1.1 ). слоя.
Имевший до t=0.2 правильную простую
форму он около оси расслаивается на два, а затем и вовсе прорывается.
Объяснение этому дает рис.21, демонстрирующий форму проводящей (s >1) области для тех же
моментов. Причина – в отмеченном выше появлении нового очага ионизации на оси.
Возникнув, он дает новый импульс процессу.
Рис.20. Положения линии уровня n=1.1 для шести последовательных
моментов времени (от 0.2 до 0.3, через 0.02).
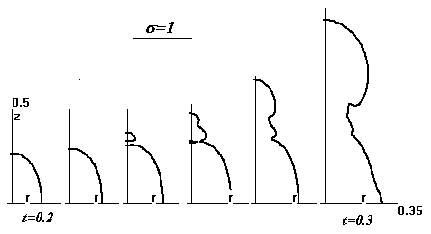
Рис.21
Положения фронта ионизации для шести моментов времени.
Рис.22 аналогичным образом показывает эволюцию формы области, где E>1.
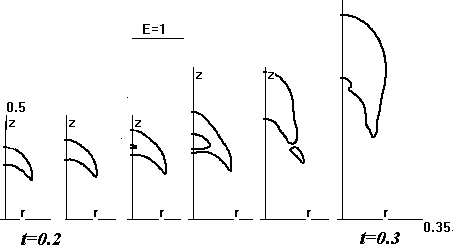
Рис.22.
Положения линии уровня E=1 для шести
последовательных моментов времени (от 0.2
до 0.3, через 0.02).
Некоторые особенности процесса на этой
стадии можно увидеть на рис.23- 24. Первый показывает n(0,z) и E(0,z) на оси
для двух моментов t=0.24 и t=0.28 (пунктиром). Существенное отличие от прежнего – ионизация происходит
в плотном газе, где E>n=1, а не
только в разреженной полости.
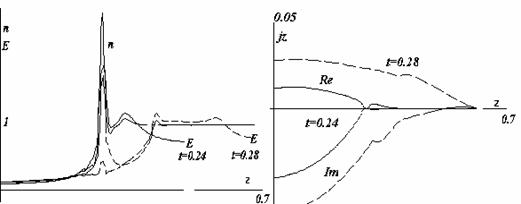
Рис.23. Профили n(0,z) и E(0,z) для Рис.24. Распределение действительной
двух
моментов t=0.24 и t=0.28 (пунктир) и мнимой части амплитуды
тока
через сечения z=const.
Рис.24 для тех же моментов дает распределение
действительной и мнимой части тока через сечения z=const.
Здесь также заметно появление второго очага ионизации. Отметим, что за
интервал Dt=0.04 размер
(по z) проводящей области удваивается. Собственно,
только на этом этапе можно говорить, что инициация произошла и пробой
состоялся.
На рис.25-26, изображающих поведение S(t),W(t) и токa j0(t) через сечение z=0,
также хорошо виднa интенсификация процесса после пробоя. В частности,
характеристический показатель – логарифмическая производная S(t) – после медленного долгого падения
от 30 до 15 на последнем интервале времени t=0.2–0.28 резко возрастает до 40.
То же и со скоростью фронта ионизации, траектория которого Z(t) изображена на рис.27. Она возрастает на порядок, от 1 до 10.
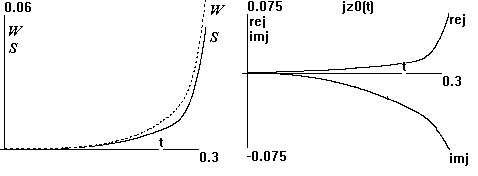
Рис.25. Зависимость от времени Рис.26. Зависимость от времени
полного числа электронов S(t) и токa j0(t) через сечение z=0
энергии нагрева W(t). .
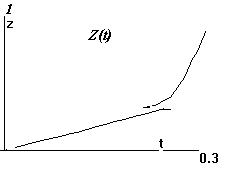
Рис.27. Траектория фронта
ионизации Z(t).
Заключение
Проведенное исследование позволяет сделать некоторые выводы.
Подтверждена стримерная природа
микроволнового разряда и его способность развиваться в поле,
меньшем пробойного ( критического).
Показано, что для инициации разряда в докритическом поле необходимо создать каверну
плотности с радиусом, не меньшем некоторого. На дне
каверны должен выполняться положительный баланс для электронов в
невозмущенном поле.
Плечи стримера
развиваются в основном за счет увеличения поля на концах стримера и только
позднее за счет нагрева канала. Горячая область стримера заметно короче
проводящих плечей.
Сферическая ударная волна, зарождающаяся на начальной стадии, по мере
роста плечей превращается
в цилиндрическую. Перед
головкой стримера ударной волны нет.
Расчет остановлен
в момент времени, когда размер стримера еще не достиг резонансного размера
(половина длины волны). Резонансный этап привнесет много новых особенностей и
потребует специальных дополнительных исследований.
Литература
[[1]] Г.М.Батанов, С.И.Грицинин, И.А.Коссый и др.
СВЧ-разряды высокого
давления. //Труды ФИАН. 1985. Т.160,
С.174-203.
[2] Л.П.Грачев, И.И.Есаков Г.И.Мишин, М.Ю.Никитин, К.В.Ходатаев.
Безэлектродный разряд в воздухе при
средних давлениях. //ЖТФ. 1985.
Т.55, Вып.2, С. 389-391.
[3] Л.П.Грачев, И.И.Есаков,
Г.И.Мишин, К.В.Ходатаев. Разряд в воздухе
в квазиоптическом СВЧ
резонаторе. // ЖТФ. 1994.Т.64, Вып.2, С.26-37
[4] Л.П.Грачев, И.И.Есаков,
Г.И.Мишин, К.В.Ходатаев. Стадии развития
безэлектродного СВЧ разряда. //ЖТФ.
1996. Т.66, Вып.7, С.32-45
[5] Л.П.Грачев, И.И.Есаков, К.В.Ходатаев.
Особенности развития импуль-
сных СВЧ
разрядов в квазиоптическом пучке
в различных газах.
//ЖТФ. 1998. Том.68, №4,
С.33-36.
[6] В.Б.Гильденбург, И.С.Гущин, С.А.Двинин,
А.В.Ким. Динамика высоко-
частотного стримера. //ЖЭТФ.
1990. Т.97, Вып.4, С.1151-1158.
[7] К.В.Ходатаев. Гидродинамические процессы в
плазме сверхмощного
высокочастотного разряда.
//Химическая физика, 1993, Т.12, Вып.3,
С.303 - 315
[8].
А.Мак-Доналд. Сверхвысокочастотный пробой в газах. “Мир”, Москва
1969.
С.38-40.
[9] К.В.Ходатаев,
Б.Р.Горелик. Диффузионный и
дрейфовый режимы
распространения
плоской волны ионизации
в СВЧ-поле.
//Физика Плазмы. 1997, Т.23, №3,
C.236-245.
|