1.Введение.

Для медицинских (клинических) задач типичен индивидуальный подход к объекту (больному). Врач лечит больного, а не болезнь. Признаки, описывающие изучаемое болезненное состояние организма, могут составлять лишь часть описания состояния организма, которое используется врачом. Эта часть обычно находится в центре внимания врача, но никогда, кроме редких случаев, внимание врача ею не ограничивается. Другие, вроде бы не участвующие непосредственно в болезненном процессе, органы и системы организма реагируют на болезнь, лечебные мероприятия или просто на больничную обстановку и непривычный режим жизни. Эта реакция различна у разных больных. Часть усилий врача уходит на стабилизацию состояния организма, компенсацию «посторонних» изменений.

Такой подход порождает определенные особенности  типичных информационных массивов. Например, наборы данных у двух больных одной болезнью могут заметно отличаться, а собранные сведения об отдельном больном, как правило, никогда нельзя уверенно считать полными. Это вносит существенные трудности в решение задачи о выделении стандартными математическими методами признаков состояния больного. Если брать все возможные сведения «по максимуму», то у большинства больных большая часть сведений будет отсутствовать. Если же брать только сведения, собранные для всех больных, почти ничего невозможно сказать о состоянии отдельного больного. Тем не менее, проблема должна иметь решение: врачи умеют ставить диагнозы и лечить по данным с такой своеобразной структурой.

Классы больных относительно некоторого заболевания, состояния организма, варианта лечения, прогноза развития ситуации, и т.п. при описанной структуре данных естественно задавать персональными списками, что обычно и делается в клинических исследованиях. Как правило, требование однородности классов заметно ограничивает их численность [1], а сама однородность оказывается неполной. При небольших классах трудно ожидать «гладких» распределений численных параметров, что ограничивает поле применения стандартных статистических методов параметрического типа. От описаний свойств классов «по большинству представителей» также приходится отказываться.

Попытки навязать медицинской задаче простую продукционную структуру, хорошо зарекомендовавшую себя в машинном доказательстве теорем, дали меньше, чем ожидалось [2-4]. Отдельные успехи в решении узких, сильно формализованных задач не облегчили работы над реальной проблематикой.

Параллельно с анализом стратегии врача можно фиксировать корреляцию наблюдаемых характеристик состояния больного с «элементарными» действиями и решениями врача.

Естественно предположить, что процесс выработки общего языка и одновременной формализации описания больных пойдет одновременно в двух направлениях. Во- первых, будет происходить дробление изучаемого класса больных на более узкие подклассы с единой врачебной тактикой. Возможно дробление процесса лечения на этапы, и т.д. Во- вторых, пойдет укрупнение самых мелких, элементарных понятий, допускающих строгую проверку и точное представление, в более крупные, регулярно используемые блоки. Этот процесс может привести к достаточно экономному описанию наблюдаемых особенностей состояния больных.

Одновременное использование этих подходов позволяет представить модель принятия решения в виде открытой совокупности подзадач, каждая из которых связана со своей структурой анализа своих данных. Подчеркнем, что подзадачи в этой модели могут использовать различные переменные. Отметим, что «общий технологический язык» врача и математика, вырабатываемый в процессе такой работы, должен способствовать лучшему взаимопониманию и может привести к частичному заимствованию структур рассуждений друг у друга.

Процессы первого типа (дробление задачи) достаточно хорошо покрываются различными вариантами диагностических игр [1,5].

Процессы второго типа (поэтапная формализация «снизу вверх») требуют некоторых нетрадиционных инструментов. Рассмотрим некоторые из них.

2. Логические симптомы.

Многообразные признаки, описывающие индивидуальный объект, могут быть приведены к совокупности дискретных переменных. Для численных признаков достаточно воспользоваться процедурами сравнения, а для текстовых -  наборами эталонов. Более того, все дискретные признаки можно свести к совокупности троичных, принимающих три значения: ДА (1), НЕТ (0) и НЕИЗВЕСТНО (?). Такие троичные признаки будем называть логическими симптомами. Троичное расширение обычной логики удобно при описании результатов наблюдений. Наблюдение состояния объекта может быть не произведено, неудачно, утеряно или искажено помехами.

Полезно использовать в этой трехзначной логике аналоги употребительных логических функций НЕ, И, ИЛИ, НТЖ (нетождественность). Дополнительно введем удобную функцию НАСЛЕДОВАНИЕ. Таблички значений для них приведем без комментариев. При отсутствии неизвестных значений все эти

функции, кроме наследования, переходят в обычные функции алгебры логики.

На этом языке каждому объекту соответствует вектор значений всех симптомов. Объекты, принадлежащие различным классам, могут иметь  различные значения координат этих векторов и, следовательно, занимать различное положение в пространстве симптомов.

Задачу классификации объектов можно сформулировать как задачу получения такого описания объектов в пространстве симптомов, которое позволило бы отнести новый объект к определенному классу. Обычно такое описание приходится строить «на примерах», т.е. используя наборы объектов, заведомо принадлежащих изучаемым классам (обучающая выборка) [6].

2.1. Симптомы в задачах классификации.

Будем считать, что справедлива гипотеза разделимости: в каждом классе найдется хотя бы один объект, не совпадающий ни с одним объектом остальных классов.

Разумеется, в практических примерах возможен случай неполной разделимости, т.е. совпадение описаний объектов, заведомо принадлежащих различным классам. В этом случае приходится либо исключать «двусмысленные» объекты, либо фиксировать отказ правила классификации. В процессе  построения правила удобнее исключать такие объекты из обучающей выборки. В дальнейшем будем считать, что в обучающей выборке «примеры» классов не имеют совпадающих объектов.

В зависимости от поставленной задачи можно выражать принадлежность объекта определенному классу либо через процедуру голосования подмножества симптомов, либо посредством логического выражения, связывающего значения симптомов. Оба варианта используют неполные описания объектов и могут порождать противоречивые ситуации – совпадение частичных описаний объектов, принадлежащих разным классам. В таком случае будем фиксировать отказ правила классификации.

Процедура голосования в простейшем случае задается списком участвующих симптомов, указанием для каждого симптома, какое его значение соответствует голосу за данный класс, и пороговым значением числа голосов, соответствующим принятию решения. В нашем формализме первые две группы сведений удобно записать в виде маски, т.е. вектора значений симптомов, соответствующих голосованию «ЗА». Координаты, значения которых безразличны, например, они принимают различные значения для объектов данного класса, будут закодированы в маске неизвестным значением (?).

Пусть  x_a = (x_a1, x_a2, … ,x_an) – вектор симптомов объекта a. Введем несколько полезных функций. Назовем элементарным совпадением функцию

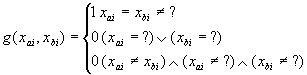
а элементарным присутствием функцию

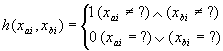
Тогда суммарное совпадение G(x_a,x_b) векторов x_a,x_b можно записать в виде

а суммарное присутствие H(x_a,x_b)  в виде

С помощью величин G и H введем определения двух величин относительной близости симптомных векторов – относительного сходства c(x_a,x_b)  = G/n и относительной неотличимости  d(x_a,x_b) = G/H. Очевидно, что . Покажем, что это же справедливо и для d(x_a,x_b). В самом деле,  только при значениях , а во всех остальных случаях они равны, следовательно G £ H и d £ 1.

Если нет неизвестных значений, суммарное совпадение G переходит в дополнение до n расстояния по Хэммингу, а суммарное присутствие в n, и обе величины близости оказываются равными  c(x_a,x_b)  = d(x_a,x_b).

Рассмотрим простейшую задачу классификации. Пусть есть два класса и каждый задан маской («идеальным вектором»), не содержащей неизвестных. Будем считать классы дополнительными друг другу, тогда маска одного есть отрицание маски другого и

Для вектора x, не содержащего неизвестных значений координат,

Для вектора, в котором доля неизвестных координат составляет 1-l,

Отсюда следует, что величины c и d ведут себя по-разному при увеличении количества неизвестных значений: c отражает количество совпадающих координат и сохраняется при замене несовпадающих значений неизвестными, а d отражает долю совпадающих среди известных и сохраняется при пропорциональной замене известных неизвестными. Шкала значений c при сохранении размерности симптомного вектора сужается пропорционально доле известных, сохраняя размер градации. Шкала для d сохраняет свой размер (0,1), но градации становятся грубее при увеличении доли неизвестных координат.

Если в маске m₁ есть неизвестные координаты, то в маске m₂  есть такое же количество неизвестных координат и занимают они  те же позиции в векторе маски, поскольку эти маски задают дополнительные классы.

Поскольку маски m₁ и m₂ связаны между собой, можно в дальнейшем использовать для классификации любую из них, например, m₁. Для каждого объекта можно вычислить величины c и d  относительно этой маски. Будем говорить, что маска разделяет объекты классов A  и B  , если распределения  p_A(x) = p(c(x_A,m₁))  и  p_B(x) = p(c(x_B,m₁))  отличаются положением, т.е. между ними существует сдвиг, обнаруживаемый соответствующими критериями (напр., Вилкоксона-Манна-Уитни, Колмогорова-Смирнова) [8,9].  Значения критериев будут характеризовать классификационную силу выбранной маски.

Практическое определение принадлежности неизвестного объекта одному из двух указанных классов удобно проводить с помощью порога наилучшего разделения, который дает критерий Колмогорова-Смирнова при сравнении распределений p_A(x) и p_B(x). Заметим, что в случае единственной маски m₁ задачу классификации можно свести к задаче с маской меньшей размерности, получаемой выбрасыванием неизвестных координат маски.

2.2. Чистые классы.

Можно выбрать порог разделения p_0A для c(x,m₁) так, чтобы значения сходства, меньшие этого порога, соответствовали только объектам класса A. Этот порог, вообще говоря, уже не будет оптимальным по Колмогорову-Смирнову. Будем говорить, что такое правило выделяет чистый подкласс A^* класса A. Аналогично можно назначить еще один порог p_0B, выше которого будут расположены только объекты класса B. Таким образом, можно с помощью двух пороговых значений для сходства выделить два чистых подкласса и промежуточный, смешанный. Заметим, что в маске m₁ могут быть использованы не все координаты. Аналогичные построения возможны для неотличимости d(x,m₁).

Рассмотрим специальный случай двух масок. Пусть первая маска m₁₁ подобрана так, чтобы обеспечить чистое выделение подкласса A^*, но в ней есть неизвестные значения. Подберем вторую маску m₁₂ и значение порога так, чтобы выделить из промежуточного подкласса только объекты, принадлежащие A. В эту маску обязательно войдут ранее неиспользованные переменные. Эта маска укажет объекты класса A, ранее не отнесенные к подклассу A^*. Теперь подкласс A* правильно классифицированных объектов класса A можно представить как объединение полученных подклассов, а их  полное описание в виде совокупности двух масок.

 Процедура допускает многократное повторение. При этом на каждом шаге в построенный по нашему правилу подкласс A^* будут включаться дополнительные объекты класса A, а его описание будет становиться все более полным.

Критерий остановки процедуры будет определяться поставленной целью. Если происходит исследование класса больных совместно с врачом, момент остановки выберет врач по своим представлениям о полноте класса больных и пригодности полученного описания для медицинской практики. Если решается более формальная задача о внешнем сходстве объектов, можно воспользоваться традиционными статистическими критериями, например хи-квадрат 2*2, точным методом Фишера или другими [10].

Таблица данных для критериев 2*2 в случае выделения чистого подкласса выглядит так:

где z_A - пороговое значение для c(x,m) , a,b,d – численности соответствующих подклассов. Нулевое количество объектов второго класса в подклассе «ниже порога» есть следствие предположения о выделении чистого подкласса. Критерий хи-квадрат для этой таблицы равен

Введем обозначения

(чувствительность и отрицательная диагностическая значимость), тогда формула примет вид

Таким образом, значение критерия увеличивается при увеличении общего числа наблюдений или отношения диагонального элемента к сумме по строке или столбцу. С учетом поправки Йейтса формула примет вид

По мере усложнения описания класса A в промежуточном подклассе будет оставаться все меньше объектов, что приведет к снижению значения критерия и выходу его за допустимую границу достоверности.

Таким образом, если совокупность симптомных векторов допускает построение последовательности чистых подклассов класса A, можно построить правило отделения этого класса от дополнительного с качеством разделения, определяемым критерием остановки процедуры.

2.3. Частичная классификация.

Если в первоначальной классификационной задаче не удается подобрать пороги p_0A и p_0B так, чтобы выделились чистые подклассы A* и B*, приходится решать классификационную задачу не для исходных классов, а для их подклассов. В этом случае найденное правило классификации решает задачу лишь «по большинству».

Вернемся к рассмотрению таблички для критериев 2*2. В общем случае она выглядит  так:

где b > 0, с > 0 и, следовательно, bс > 0. Если при этом  выборочное отношение шансов , то при с < b можно исключить из рассмотрения с объектов класса B, для которых c(x,m₁) <z_A.  Для  большей части класса A задача свелась к предыдущей. Последовательность шагов, аналогичная рассмотренной выше, дает частичную классификацию. Напомним, что теперь существует некоторое количество объектов второго класса, попадающих в первый, неизбежная ошибка классификации, тем меньшая, чем больше выборочное отношение шансов.

2.4. Построение маски по симптомам.

До сих пор процесс подбора маски не был конкретизирован. Было использовано предположение, что подбор маски с необходимыми свойствами возможен. Заполним этот пробел.

Для каждой координаты можно рассчитать значение критерия 2*2 разделения объектов двух классов по ее «известным» значениям ДА и НЕТ. Возьмем координату с наибольшим значением критерия. Если она выделяет чистый подкласс класса A, то задача решена, мы имеем подходящую маску из одного значения одной координаты. Если это не так, возьмем следующую по величине критерия координату. Для каждого из 4 сочетаний их известных значений проверяем выделение чистого подкласса класса A. Если ни одно из сочетаний не выделяет чистого подкласса, добавляем следующую координату и проверяем 8 сочетаний, и т.д. Построение маски прекращается, как только будет выделен чистый подкласс класса A или исчерпан список координат.

Результат фиксируем в форме маски:  используем известные значения координат, входящие в разделяющую комбинацию, а остальным координатам присваиваем значение «неизвестно». Полученную маску добавляем к уже имеющемуся описанию класса, а объекты, выделенные на этом шаге, исключаем из дальнейшего рассмотрения. Заметим, что такой шаг процедуры может и не привести к успеху, но предположение, что ни один из подобных шагов не завершится получением маски, будет противоречить первоначальной гипотезе о разделимости классов.

Процесс повторяем для остающихся объектов, начиная каждый раз с новой координаты до получения набора масок или исчерпания списка координат. Эта теоретическая модель иллюстрирует принципиальную возможность отыскания некоторого количества таких масок. Вычислительные трудности лишают ее практического применения.

На практике удобнее менее строгий, но более быстрый алгоритм. Выбираем некоторое количество координат по достаточно высокому значению одного из критериев 2*2, например, хи-квадрат, и затем из их списка формируем маску, добавляя каждый раз координату, если значение критерия хи-квадрат для получившейся таблицы разделения классов сочетаниями значений координат увеличивается. В этом случае каждый последующий шаг вызывает увеличение времени расчетов, поэтому есть смысл ограничить длину формально выбираемой маски. Тогда, начиная с момента заполнения в первый раз всех отведенных

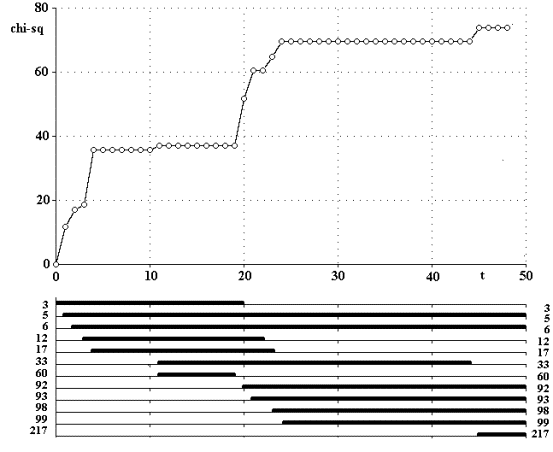
          Рис. 1. Отбор симптомов по критерию хи-квадрат.

позиций, перед возможным добавлением очередной координаты решается задача исключения одной из ранее включенных координат. Естественно исключить координату, отсутствие которой в наименьшей мере уменьшает значение критерия. Эти соображения легли в основу реализованного алгоритма отбора координат в маски. Ввиду трудности теоретических оценок проиллюстрируем работу этого алгоритма результатами численных расчетов.

На рис.1 приведен результат использования этого алгоритма в одной из прикладных задач. В  верхней части рисунка помещен график изменения значения критерия хи-квадрат по шагам алгоритма. Напомним, что на каждом шаге добавляется или исключается один симптом. Если симптом не увеличивает значение критерия, его тут же исключают, и он не сказывается на величине критерия. В нижней части дана диаграмма присутствия отдельных симптомов, дававших увеличение значения критерия. Слева и справа стоят номера симптомов. Видно, что симптомы 3,12, 17, 33, 60 были вытеснены более эффективными с точки зрения классификации.

В маске, полученной применением описанной процедуры, будут присутствовать симптомы 5, 6, 92, 93, 98, 99, 217.  Простыми преобразованиями можно редуцировать маску до маски чистого подкласса:  m₉₂ = 0, m₉₈ = 1, остальные значения – «неизвестно». Классификационная табличка 2*2 примет вид

Тем самым, искомый чистый подкласс численностью 23 объекта удалось выделить.

Применяя эту же процедуру к остатку класса A, последовательно получаем другие фрагменты чистого подкласса A*.

2.5. Построение маски наследованием.

Предположим, что существует заранее неизвестная нам маска m_A, выделяющая чистый подкласс класса A. Пусть у нас есть набор s векторов x_A1, … x_As, принадлежащих классу  A, причем d(x_Ai, m_A)=1 для всех i, т.е. маска целиком содержится в каждом векторе набора. Тогда применив к набору векторов x_A1, … x_As  поразрядную операцию наследования, мы получим новый вектор, также содержащий эту маску. Поскольку в координатах, не совпадающих с разрядами маски, возможны любые значения, а операция наследования превращает несовпадающие значения в «неизвестно», новый полученный вектор будет содержать меньше известных значений в разрядах, не совпадающих с маской. Этот простой прием позволяет при достаточно большом числе s векторов и их разнообразии обнаружить «скрытую» маску. Найденную маску следует обязательно проверить на  выделение чистого подкласса.

Заметим, что рассмотренные варианты классификационных задач были рассмотрены в терминах «чистый подкласс» – «все остальное». В литературе распространены методы получения классификационных правил, «дожимающие» правило до формальной «определенности» в любом случае [6,7]. Это позволяет строить  разнообразные оценки «оптимальности» правила. В наших задачах мы сочли это неуместным, поскольку правило строится на оценках и наблюдениях специалистов, и его неоптимальность отражает, скорее всего, пробелы в информации, доступной специалистам, или же неопределенность их выводов, что требует содержательного анализа постановки задачи.

Полученные методы легко распространить на случай произвольного числа K классов. Для этого следует решить K задач по выделению каждого класса из совокупности всех остальных. При этом мы получим K чистых подклассов и неопределенный остаток, источник отказов правила.

3. События, динамический сценарий.

Часто специалист, наблюдающий состояние объекта, принимает решение не по мгновенному состоянию объекта, а после анализа динамики поведения объекта на протяжении некоторого времени. Естественно предположить, что его решение складывается под влиянием каких-то разновременных изменений состояния объекта. Для анализа подобных ситуаций введем понятие динамического сценария изучаемого процесса.

Рассмотрим последовательность дискретных моментов времени t  (t = 1,2, … , T). Эти моменты времени не обязаны быть эквидистантными. В каждый момент времени мнение специалиста о состоянии объекта можно представить  вектором x(t) = (x₁(t), … ,x_N(t)). Каждая координата этого вектора отражает частное решение специалиста относительно одной из наблюдаемых характеристик объекта. Будем считать набор таких решений конечным, т.е. положим, что каждая координата имеет свой конечный алфавит возможных значений. Назовем сценарием процесса полную совокупность всех векторов (x(1), … , x(T)) , описывающую весь процесс. Заметим, что в каждый момент времени могут оказаться известными не все координаты. Более того, для практических приложений характерны случаи, когда большая часть координат неизвестна для большинства моментов времени. Содержательно это означает, что специалист в таких случаях не нуждается в подробной информации для этих моментов времени.

Если значение координаты x_i(t) известно, будем иногда называть его для краткости «факт i в момент t». Более общее определение факта будет дано ниже. Назовем итогом процесса некоторый факт, поддающийся независимой верификации. Назовем событием фиксированное сочетание фактов. Событие будем считать прогностическим для некоторого итога, если оно предшествует его наступлению. Достоверное прогностическое событие предшествует всегда, возможное – иногда. Моделью события будем называть формулу, описывающую некоторую совокупность событий. Как правило, модель события будем связывать с  некоторым итогом.

Задача прогнозирования некоторого итога процесса сводится к поиску моделей прогностических событий (прогнозов) для этого итога. Мы будем использовать построение прогнозов в качестве средства анализа наблюдаемых решений специалиста с целью уточнения возможного использования им различных сведений, поступающих в ходе наблюдения процесса.

Описание процесса в виде сценария допускает наглядное представление в виде таблицы из N строк и T столбцов, в клетках которой располагаются символы значений координат или пробелы в качестве значения «неизвестно».

3.1. Факты.

Введем более строго понятие факта. Назовем фактом, реализовавшимся в момент t*, последовательность s значений одной координаты x_i(t) в течение некоторого интервала времени (t_1,t₂), нестрого предшествующего моменту t*    (t₁ £ t₂ £ t*). Приведем несколько примеров различных способов задания этой последовательности.

1.     Список значений, порядок безразличен. Могут встречаться только  значения переменной, содержащиеся в заданном списке. Иные значения переменной на этом интервале не допускаются.

2.     Список исключений, порядок безразличен. Допустимо любое значение переменной, не содержащееся в заданном списке.

3.     Список нестрогий, порядок безразличен. Допустимо любое значение переменной, содержащееся в заданном списке. Возможны значения, не входящие в список, их присутствие безразлично.

4.     Нестрогая последовательность. Значения переменной, представленные в образце, встретились на интервале в том же порядке следования, что и в образце. Кроме них могут присутствовать и другие значения.

5.     Строгая последовательность. В интервале присутствуют только значения, представленные в образце, и обязательно в том же порядке.

Таким образом, факт f(t*,x_i(t),t₁,t₂,v,a) задают сочетанием следующих элементов:

1.     Момент реализации факта, момент наблюдения t*.

2.     Проверяемая координата x_i(t)  вектора x(t).

3.     Интервал времени (t₁,t₂).

4.     Образец набора значений v.

5.     Правило соответствия наблюдаемых значений значениям в образце a.

Если в интервале времени (t₁,t₂) значения проверяемой координаты x_i(t) могут быть соотнесены по правилу a значениям, приведенным в образце v, факт принимает в момент t* логическое значение «ДА» (1), во всех остальных случаях – значение «НЕТ» (0).

Заметим, что границы интервала времени в описании факта можно задавать как указанием на абсолютные моменты времени, так и в относительном виде – указанием на смещение относительно момента  наблюдения t*.

3.2. Свойства фактов.

Назовем факт f₂(t*,x_i(t),t₁,t₂,v,a)  объемлющим по отношению к  факту f₁(t*,x_i(t),t₁,t₂,v,a)  ,   если из f₁ = 1 следует f₂ = 1 (обозначим  f₁ £  f₂). Назовем два факта f₁(t*,x_i(t),t₁,t₂,v,a) и f₂(t*,x_i(t),t₁,t₂,v,a) эквивалентными (f₁ = f₂), если одновременно справедливы утверждения f₁ £  f₂  и f₂ £  f_{1 .} Например, факты эквивалентны, если совпадают все их аргументы.  Естественно считать отношение «объемлющий факт» транзитивным, т.е. из f₁ £  f₂  и f₂ £  f₃ следует f₁ £  f₃.

Конечный алфавит значений переменной x_i(t) может порождать всевозможные последовательности символов {s}. Образец v вместе с правилом a позволяют сформировать из них множество «пригодных» на интервале (t₁,t₂) последовательностей M. Условие истинности факта  f(t*,x_i(t),t₁,t₂,v,a) можно сформулировать как условие вхождения  последовательности символов s на интервале (t_1,t₂) в это множество M, т.е.    s(t_1,t₂) Î M_.  

Если вместе с каждой последовательностью во множество M входят все ее продолжения в обе стороны, будем называть такое множество расширенным и обозначать M*.

Пусть мы имеем 3 факта f₁, f₂, f₃, причем M*₁ = M*₂ = M*₃. Пусть  также  дано f₁(t*,x_i(t),t₁,t₂,v,a), f₂(t*,x_i(t),t₂,t₃,v,a), f₃(t*,x_i(t),t₁,t₃,v,a), причем t₁ £ t₂ £ t₃, т.е. факты с одинаковыми расширенными множествами последовательностей символов определены на смежных интервалах.  Покажем, что f₁ £ f₃. Поскольку меньший интервал (t₁,t₂) входит в (t₁,t₃), а множества последовательностей одинаковы, то всякая последовательность, делающая факт истинным в меньшем интервале, автоматически делает его истинным и в большем. Так как все возможные продолжения этой последовательности также принадлежат M*, то дополнительные символы, которые могут оказаться в интервале (t₂,t₃), не нарушат истинности факта. Тривиальное следствие: если интервал (t₂,t₃) не содержит ни одного символа, то f₁ = f₃, т.е. к рассматриваемому интервалу можно добавлять произвольные смежные «пустые» интервалы. Аналогично можно показать f₂ £ f₃. Верно также f₁ + f₂ £ f₃. Неравенство сохраняется потому, что возможна последовательность, содержащаяся в большем интервале, и такая, что ни одна ее часть, попадающая в каждый из меньших интервалов, может не входить в M*.

Рассмотрим  два факта  f₁(t*,x_i(t),t₁,t₂,v₁,a), f₂(t*,x_i(t),t₁,t₂,v₂,a),  у которых совпадают интервалы времени и правила использования образцов, а сами образцы отличаются, причем v₁ Í v ₂, т.е. первый образец является частью второго. Пусть также M*₁ = M*₂. Тогда  f₂ £ f₁ , поскольку последовательности меньшего образца допускают продолжение символами, не входящими в больший образец.

Мы видим, что особую важность приобретают такие типы фактов, у которых последовательности символов допускают произвольное продолжение. В этих случаях можно ограничиться локальной проверкой в интервале (t₁,t₂). Один из классов фактов, отвечающих этому требованию – класс фактов, правила a в которых не содержат явных запретов на определенные символы. В приведенных выше примерах этим свойством обладают правила 3 и 4 (нестрогий список и нестрогая последовательность).

3.3. Факты для прогнозирования итога.

Пусть у нас есть два набора сценариев: сценарии, приводящие к итогу I₁, и сценарии, приводящие к итогу  I₂. Задача состоит в том, чтобы сформировать факты, связанные с этим итогом, из предшествующих итогу значений переменных. Разумеется, построенные факты будут представлять собой лишь нашу гипотезу о закономерностях наблюдаемого процесса. Добавление еще одного сценария может изменить наше представление о прогностической пригодности того или иного факта.

Тем не менее, воспользуемся приведенной выше формулировкой задачи, считая наборы сценариев фиксированными. Выберем переменную x_i(t), для которой будем строить факт. Зададимся правилом проверки. Выберем такое значение этой переменной, которое встречается достаточно часто в сценариях 1 класса и как можно реже – в сценариях второго класса. В качестве второго символа выберем такое значение, которое как можно реже встречается у сценариев второго класса, еще не отбракованных первым символом. Аналогично можно выбрать третий символ, также редко встречающийся в еще не отбракованных сценариях второго класса. Продолжая этот процесс, мы можем получить последовательность, не встречающуюся в сценариях второго класса, или последовательность, не соответствующую ни одному объекту первого класса, или превысить максимальную длину последовательности, встречающуюся в заданных наборах сценариев. В любом случае, конечность числа использованных сценариев гарантирует завершение работы алгоритма за конечное число шагов. Если мы получили последовательность, встречающуюся только в первом классе сценариев, задача решена, и мы имеем реализацию последовательности значений выбранной переменной, начинающуюся с заданного символа и приводящую к искомому итогу I₁. Заметим, что, по построению, эта последовательность имеет минимальную длину.

На этом принципе основан алгоритм генерации последовательностей символов, реализованный в виде программы, строящей эти последовательности по наборам сценариев. Программа получает наборы сценариев, принадлежащих различным классам, и выбирает из них последовательности символов, специфичные для каждого класса. Каждый набор снабжается оценкой хи-квадрат качества различения.

Совокупность таких последовательностей, полученных при различных вариантах выбора участвующих в них символов, служит материалом для формулирования правила a, входящего в факт. Если существуют содержательные соображения, продиктованные спецификой задачи, их следует использовать на этом этапе построения факта. Во многих случаях опытному исследователю удается угадать подходящее условие. К сожалению, построить полностью формальную процедуру получения этого правила пока не удалось.

Легко формализуемый вариант «один символ – один факт»  переносит трудности анализа последовательностей символов в область построения событий, заметно увеличивая подлежащие проверке наборы событий. В некоторых случаях приходится идти на это, несмотря на повышение трудоемкости работы.

В качестве интервала времени естественно взять объемлющий интервал, т.е. такой, в котором размещаются все реализации полученной последовательности во всех сценариях.

При ручном построении правила можно использовать сформулированные выше свойства смежных интервалов и увеличенных наборов символов на совпадающих интервалах. Эти преобразования заметно упрощают процедуру построения правила.

Заметим также, что отбор фактов требует определенной осторожности, поскольку отдельный факт, сам по себе дающий плохое различение сценариев, может войти в событие, хорошо прогнозирующее искомый итог.

3.4. События.

Описание сценария в виде набора фактов подразумевает внесение некоторой структуры в совокупность решений специалиста, зарегистрированных в сценарии. Во- первых, в факты могут войти не все значения переменных сценария. Во- вторых, в наборе должны присутствовать факты, теснее связанные с определенным итогом процесса, чем исходные значения переменных. Как всякая структурированная запись, набор фактов может дать более экономное представление части процесса, предшествующей данному итогу.

Уточним понятие события. Будем называть событием совокупность фактов, присутствующих или отсутствующих в сценарии и имеющих общий момент реализации t*, к которому и будет отнесено событие. Поскольку событие оперирует лишь наличием фактов, его можно представить логической функцией e(f₁. … .fn)  входящих в него фактов. Согласно определению, факт является истинным (1) тогда и только тогда, когда последовательность наблюдаемых значений переменной соответствует образцу согласно правилу сравнения. Отсутствие факта по любой причине всегда соответствует его ложному значению (0).

События удобны для прогнозирования некоторого итога процесса, наступающего в момент времени t**. Если момент события t* < t**, то в некоторых случаях возможно активное воздействие на процесс, изменяющее его дальнейшее течение. В медицинских задачах эта ситуация соответствует возможности лечения. Тем самым, можно поставить задачу отыскания логической функции от набора фактов дающей предсказание возможного итога процесса.

Прогностическую силу события e можно оценивать с помощью обычных критериев 2*2  на основе таблицы сопряженности

Будем строить событие в форме конъюнкции фактов e = f₁ & f₂ & … & f_k. На шаге j будем получать конъюнкцию длины j £ k   e_j = f₁ & …& f_j. Эта конъюнкция будет истинна на a_j сценариях с итогом I₁ и b_j сценариях с итогом I₂. Вследствие минимального свойства конъюнкции при добавлении новых членов количество объектов, для которых она истинна, не увеличивается:   a_j+1 £ a_j и b_j+1 £ b_j. Зададимся константой a₀ и будем  на каждом шаге искать конъюнкцию, удовлетворяющую условиям  a_j+1 ³ a₀  и b_j+1 < b_j. Конечный набор фактов гарантирует конечность процесса построения конъюнкции. В результате мы можем получить чистую конъюнкцию (без противоречий, b_j = 0), конъюнкцию с минимальным, но не нулевым количеством противоречий, или процесс остановится из-за исчерпания набора фактов. Только первый из этих исходов будем считать успешным. Остальные сигнализируют о неполноте набора фактов для прогноза итога I₁. Часто причиной этого оказывается недостаточная подготовка задачи на стадии содержательного анализа первоначального набора показателей.

Если нам удалось построить некоторый набор чистых конъюнкций, объединим их операцией дизъюнкции. Вследствие максимального свойства этой операции набор сценариев, на которых она истинна, будет не меньше каждого из наборов сценариев использованных конъюнкций, т.е. a будет максимально, а b будет, по- прежнему, равно нулю.

Заметим, что, в отличие от предыдущего раздела, мы теперь рассматриваем факты, относящиеся ко всем переменным сценария.

Мы получили алгоритм построения модели события, предшествующего итогу I₁ или прогноза этого итога. Разумеется, прогноз, построенный по ограниченному, а часто даже по малому массиву данных, представляет собой лишь нашу гипотезу, которая должна найти подтверждение либо среди фундаментальных данных предметной области (у нас: медицины), либо в специальном более широком исследовании. Во всяком случае, этот прогноз отражает определенную сторону профессиональной деятельности изучаемого специалиста.

4. Программная реализация.

Описанные выше методы укрупнения элементарных понятий реализованы в виде пакетов программ. Входная информация извлекается из полей базы данных структуры dBASE III (.dbf).

Перекодировка содержимого базы в симптомы происходит автоматически по заранее подготовленному описанию.  Укрупнение симптомов (образование новых, вторичных) происходит в режиме диалога с оператором, которому программа предъявляет все необходимые оценки.

Алфавитная кодировка переменных сценария производится заранее, а символы размещаются в той же база данных. Программа позволяет наблюдать индивидуальные сценарии процесса для каждого больного как в первоначальных переменных, так и «в событиях». В пакет включены программы анализа сценариев с выделением предполагаемых событий, сравнением классов.

Использование этих средств существенно облегчило и ускорило решение ряда медицинских задач [11-13].

Л И Т Е Р А Т У Р А

1.     И.М. Гельфанд, Б.И. Розенфельд, М.А. Шифрин. Очерки о совместной работе   математиков и врачей. - М., Наука, 1989.- 272 с.

2.     Построение экспертных систем. Пер. с англ. / Под ред. Ф.Хейеса-Рота, Д.Уотермана, Д.Лената.-М.: Мир,1987.-441с.

3.     Pople H.E.Jr. Heuristic methods for imposing structure on ill-structured problems: The structuring of medical diagnostics./ In: P. Szolovitz, ed., Artificial intelligence in medicine. American Association for the Advancement of Science. Boulder Colo: Westview Press, 1981, pp. 119-185.

4.     Shortliffe E.H. Computer-based medical consultation: MYCIN. New York: American Elsevier, 1976.

5.     А.В. Алексеевский, И.М. Гельфанд, М.Л. Извекова, М.А. Шифрин. О роли формальных методов в клинической медицине: от цели к постановке задачи. // Информатика и медицина. –М.: Наука, 1997. с. 70-71.

6.     Э.М. Браверман, И.Б. Мучник. Структурные методы обработки эмпирических данных. – М.: Наука. Главная редакция  физико-математической литературы. 1983, - 464 с.

7.     Алгоритмы и программы восстановления зависимостей. Под ред. В.Н. Вапника.- М.: Наука. Главная редакция физико-математической литературы, 1984.-816с.

8.     Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. – М.: Наука. Главная редакция физико-математической литературы, 1983, -416с.

9.     Холлендер М., Вульф Д.А. Непараметрические методы статистики. – М., Финансы и статистика, 1983. – 518с.

10. Флейс Дж. Статистические методы для изучения таблиц долей и пропорций. – М.: Финансы и статистика, 1989, -319с.

11. Котов Ю.Б. Федорова М.В. Шалаев О.Н. Минимизация размерности описания объекта при выборе тактики в медицинской задаче. V Всероссийская конференция "Нейрокомпьютеры и их применение", сб. докл.,  М.:1999,с.310-313.

12. Ю.Б. Котов М.В. Федорова М.В. Троицкая. Оценка состояния новорожденного у матери с сахарным диабетом. Научная сессия МИФИ-2000. Сб. научных трудов М.,2000, т. 5, с.20-21.

13. Ю.Б. Котов Построение шкалы оценки состояния организма новорожденных у матерей с сахарным диабетом. Инженерная физика N 2, 2000г. с.60-65.