Аннотация
Показана возможность использования режима одноосной солнечной ориентации на спутнике,
находящемся на почти круговой орбите с высотой около 900 км и несущем солнечный парус. Спутник
(вместе с парусом) представляет собой осесимметричную конструкцию, причем его ось симметрии
является главной центральной осью максимального момента инерции. Центр давления паруса лежит
на этой оси и смещен относительно центра масс спутника. Спутник выставляется осью симметрии
на Солнце так, чтобы его центр масс располагался между Солнцем и центром давления, и
закручивается вокруг этой оси с угловой скоростью несколько градусов в секунду. Под действием
гравитационного момента и момента сил светового давления ось симметрии спутника медленно
прецессирует. Хотя максимальные значения модулей этих моментов сравнимы по величине, момент
сил светового давления доминирует и направляет прецессию таким образом, что ориентация оси
симметрии на Солнце сохраняется. Оценены влияние на рассматриваемый режим отсутствия части
солнечного паруса из-за неполного развертывания последнего и возмущающее действие создаваемого
парусом пропеллирующего момента.
Abstract
Possibility of using the single axis solar orientation is substantiated for the satellite with
a solar sail. The satellite orbit is nearly circular one with the altitude about 900 km.
The satellitite (together a sail) has an axially symmetric structure, its symmetry axis being
central principal axis of the maximal moment of inertia. The sail pressure center lies
in the axis and don’t coincide with the satellite barycenter. The satellite is directed by
its symmetry axis towards the Sun so that its barycenter lies between the sun and the pressure
center. Then the satellite is twisted around the symmetry axis with angular rate equal
a few degrees per second. The axis performs a slow precession under the action of gravitational
and solar pressure torques. The solar pressure torque predominates and directs a pression
so that the orientation of the symmetry axis towards the Sun is preserved. Estimation of
orientation error is obtained for the case when the solar sail was not developed completely
and influence of the sail propeller tourqe on the oriented satellite motion is evaluated.
1.
Введение. В данной работе изучается возможность
длительного применения режима одноосной солнечной ориентации на искусственном
спутнике Земли, снабженном солнечным парусом. Орбита спутника близка круговой и
имеет высоту около 900 км. Основными факторами, определяющими движение
спутника относительно центра масс, являются гравитационный момент, момент сил
светового давления и эволюция орбиты.
Спутник (вместе с парусом) представляет
собой осесимметричную конструкцию, причем его ось симметрии является главной
центральной осью максимального момента инерции. Центр давления паруса лежит
на этой оси и смещен относительно центра масс спутника. Ось симметрии
направляется на Солнце так, чтобы центр масс спутника располагался между
Солнцем и центром давления. Затем спутник закручивается вокруг этой оси с
угловой скоростью несколько градусов в секунду. Такое вращение устойчиво, и
если бы на спутник не действовали внешние моменты, то ось симметрии сохраняла
бы неизменное направление в абсолютном пространстве. Внешние моменты, прежде
всего, гравитационный и момент сил светового давления вызывают прецессию оси
симметрии, что в общем случае должно приводить к нарушению ориентации этой
оси на Солнце. Однако в случае рассматриваемого спутника действие момента сил
светового давления направляет прецессию таким образом, что эта ориентация
сохраняется.
Если бы спутник не испытывал возмущающего
действия гравитационного момента, то угол между его осью симметрии и
направлением на Солнце не превышал бы нескольких градусов. Действие этого
момента приводит к погрешности ориентации около 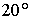 . Возможность солнечной ориентации рассматриваемого
спутника следует считать несколько неожиданной. Во-первых, максимальное
значение приложенного к спутнику гравитационного момента составляет примерно
70% от максимального значения момента сил светового давления (эти максимумы
достигаются на разных положениях спутника). Во-вторых, при некоторых
положениях орбиты спутника относительно направления на Солнце на орбите
имеется теневой участок, на котором момент сил светового давления отсутствует
и возмущающее действие гравитационного момента особенно велико. . Возможность солнечной ориентации рассматриваемого
спутника следует считать несколько неожиданной. Во-первых, максимальное
значение приложенного к спутнику гравитационного момента составляет примерно
70% от максимального значения момента сил светового давления (эти максимумы
достигаются на разных положениях спутника). Во-вторых, при некоторых
положениях орбиты спутника относительно направления на Солнце на орбите
имеется теневой участок, на котором момент сил светового давления отсутствует
и возмущающее действие гравитационного момента особенно велико.
Возможность реализации режима одноосной
солнечной ориентации обосновывается в рамках анализа уравнений вращательного
движения спутника, усредненных по регулярной прецессии Эйлера. Описывающие
этот режим решения усредненных уравнений построены численно и исследованы с
помощью существующего в данной задаче адиабатического инварианта. Исследовано
влияние на рассматриваемый режим отсутствие части солнечного паруса из-за
неполного развертывания последнего и возмущающее действие создаваемого парусом
пропеллирующего момента.
2. Момент сил светового давления. Спутник
представляет собой небольшое центральное тело, к которому прикреплен
солнечный парус. Парус состоит из восьми одинаковых плоских лепестков, имеющих
форму равнобедренного треугольника. Все лепестки без перекрытия можно
уложить в правильный восьмиугольник. Форму паруса опишем следующим образом.
Пусть указанный восьмиугольник расположен в координатной плоскости 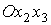 системы координат системы координат 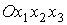 , образованной главными центральными осями инерции спутника,
причем точка , образованной главными центральными осями инерции спутника,
причем точка 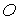 является центром
восьмиугольника, а ось является центром
восьмиугольника, а ось 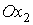 проходит через середину
одной из его сторон. Лепестки последовательно занумеруем числами 1, 2, … , 8,
приписав номер 1 лепестку, содержащему отрезок положительной полуоси проходит через середину
одной из его сторон. Лепестки последовательно занумеруем числами 1, 2, … , 8,
приписав номер 1 лепестку, содержащему отрезок положительной полуоси 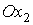 , номер 2 лепестку, содержащему биссектрису первого квадранта
системы координат , номер 2 лепестку, содержащему биссектрису первого квадранта
системы координат 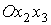 , и т. д. Лепестки с нечетными номерами перенесем вдоль оси , и т. д. Лепестки с нечетными номерами перенесем вдоль оси 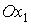 параллельно самим
себе в плоскость параллельно самим
себе в плоскость 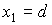 , лепестки с четными номерами перенесем точно также в
плоскость , лепестки с четными номерами перенесем точно также в
плоскость 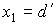 , , 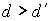 . Затем каждый лепесток повернем на угол . Затем каждый лепесток повернем на угол 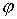 вокруг прямой, проходящей
через вершину лепестка на оси вокруг прямой, проходящей
через вершину лепестка на оси 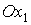 параллельно его
противолежащей стороне. Поворот выполним в сторону отрицательной полуоси параллельно его
противолежащей стороне. Поворот выполним в сторону отрицательной полуоси 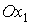 . Получим солнечный парус. . Получим солнечный парус.
Приведем
некоторые геометрические характеристики такого паруса. Нормаль
к лепестку с номером 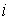 обозначим обозначим 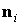 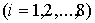 и положим и положим 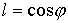 , , 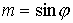 . Тогда в системе координат . Тогда в системе координат 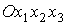 будем иметь будем иметь
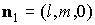 , , 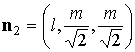 , , 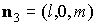 , , 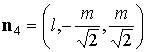 , ,
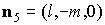 , , 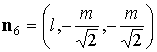 , , 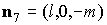 , , 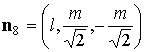 . .
Радиус-вектор
геометрического центра  -го лепестка (точки пересечения медиан соответствующего
треугольника) относительно точки -го лепестка (точки пересечения медиан соответствующего
треугольника) относительно точки 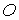 обозначим обозначим 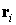 . В системе . В системе 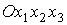
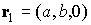 , , 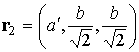 , , 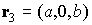 , ,  , ,
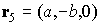 , , 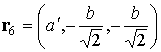 , , 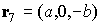 , , 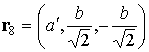 . .
Здесь 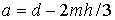 , , 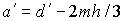 , , 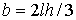 , , 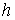 – высота лепестка-треугольника,
опущенная на его основание. – высота лепестка-треугольника,
опущенная на его основание.
Перейдем к вычислению главного момента
действующих на спутник сил светового давления. В качестве полюса выберем точку 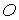 . Поскольку центральное тело мало, будем учитывать действие
света только на парус. Примем, что доля . Поскольку центральное тело мало, будем учитывать действие
света только на парус. Примем, что доля 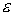 попавших на парус
фотонов отражается от него зеркально, доля фотонов попавших на парус
фотонов отражается от него зеркально, доля фотонов 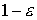 полностью им
поглощается. Будем рассматривать только такие положения спутника, в которых угол
между осью полностью им
поглощается. Будем рассматривать только такие положения спутника, в которых угол
между осью 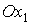 и ортом и ортом 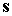 направления на Солнце
меньше направления на Солнце
меньше 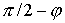 . Взаимное затенение лепестков учитывать не будем. При сделанных
предположениях главный момент приложенных к парусу сил светового давления
определяется формулами . Взаимное затенение лепестков учитывать не будем. При сделанных
предположениях главный момент приложенных к парусу сил светового давления
определяется формулами
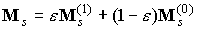 , ,
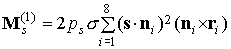 , , 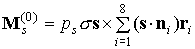 . .
Здесь 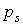 – давление света на
плоское идеальное зеркало, расположенное перпендикулярно солнечным лучам в
точке – давление света на
плоское идеальное зеркало, расположенное перпендикулярно солнечным лучам в
точке 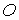 , , 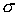 – площадь одного лепестка паруса. Выписанные
суммы вычислялись в системе координат – площадь одного лепестка паруса. Выписанные
суммы вычислялись в системе координат 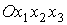 . Суммирование проводилось раздельно по четным и нечетным
индексам. При этом выражения для сумм по четным индексам получаются из
выражений для сумм по нечетным индексам заменой . Суммирование проводилось раздельно по четным и нечетным
индексам. При этом выражения для сумм по четным индексам получаются из
выражений для сумм по нечетным индексам заменой 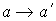 . После несложных, но громоздких выкладок для момента сил
светового давления была получена формула . После несложных, но громоздких выкладок для момента сил
светового давления была получена формула
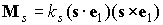 , ,
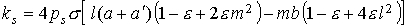 . .
Здесь 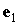 – орт оси – орт оси 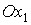 . .
Приведем числовые оценки. На
орбите Земли 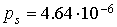 Н/м Н/м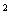 . Параметры конструкции паруса возьмем следующие: . Параметры конструкции паруса возьмем следующие: 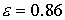 , , 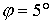 , ,  м, м, 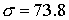 м м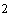 (основание лепестка-треугольника несколько меньше (основание лепестка-треугольника несколько меньше  – стороны
упоминавшегося выше восьмиугольника), – стороны
упоминавшегося выше восьмиугольника), 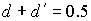 м. В этом случае м. В этом случае  Нм. Нм.
Полученные
формулы относятся к освещенному Солнцем участку орбиты спутника. В тени Земли
действующий на спутник момент сил светового давления равен нулю. Условие
пребывания спутника в тени Земли запишем в предположении, что Земля представляет
собой шар радиуса 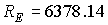 км. Это условие
выражается неравенствами км. Это условие
выражается неравенствами 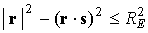 , , 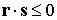 , где , где  – геоцентрический
радиус-вектор спутника. Выполнение первого неравенства означает, что спутник
находится в прямом круговом цилиндре, касающемся поверхности Земли по окружности
большого круга, перпендикулярного орту – геоцентрический
радиус-вектор спутника. Выполнение первого неравенства означает, что спутник
находится в прямом круговом цилиндре, касающемся поверхности Земли по окружности
большого круга, перпендикулярного орту 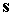 . Солнце лежит на оси этого цилиндра. Выполнение второго неравенства
означает, что спутник и Солнце лежат в указанном цилиндре по разные стороны
от Земли. Введем геоцентрическое
расстояние спутника . Солнце лежит на оси этого цилиндра. Выполнение второго неравенства
означает, что спутник и Солнце лежат в указанном цилиндре по разные стороны
от Земли. Введем геоцентрическое
расстояние спутника 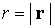 и орт его радиуса-вектора и орт его радиуса-вектора
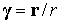 . Тогда условие пребывания спутника в тени Земли можно выразить
неравенством . Тогда условие пребывания спутника в тени Земли можно выразить
неравенством
 . .
3. Гравитационный
момент. Действующий на спутник гравитационный момент
можно представить в виде [1]
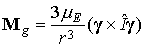 . .
Здесь 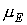 – гравитационный
параметр Земли, – гравитационный
параметр Земли, 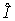 – тензор инерции спутника. Рассматриваемый
спутник осесимметричен, и в системе координат – тензор инерции спутника. Рассматриваемый
спутник осесимметричен, и в системе координат 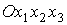 , образованной его
главными центральными осями инерции, тензор , образованной его
главными центральными осями инерции, тензор 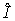 имеет матрицу diag имеет матрицу diag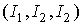 . Здесь . Здесь  и и 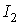 – осевой и
экваториальный моменты инерции спутника. Следующие выкладки проведем в системе – осевой и
экваториальный моменты инерции спутника. Следующие выкладки проведем в системе
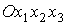 . Пусть в этой системе . Пусть в этой системе 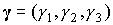 . Тогда . Тогда
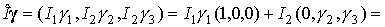 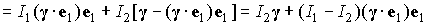 . .
Подставим найденное выражение для 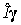 в формулу
гравитационного момента. Получим в формулу
гравитационного момента. Получим
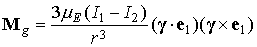 . .
Приведем
числовые оценки. Орбита рассматриваемого спутника близка к круговой. В случае
круговой орбиты последняя формула принимает вид
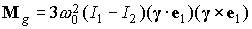 , ,
где 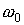 – среднее движение
(орбитальная частота) спутника. В рассматриваемом случае – среднее движение
(орбитальная частота) спутника. В рассматриваемом случае 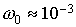 с с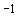 , , 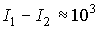 кгм кгм и и 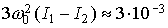 Нм. Из приведенных
оценок следует, что максимальные значения гравитационного момента и момента
светового давления сравнимы по величине. Нм. Из приведенных
оценок следует, что максимальные значения гравитационного момента и момента
светового давления сравнимы по величине.
4. Уравнения вращательного движения спутника. Спутник считаем
твердым телом. Его уравнения вращательного движения под действием момента сил
светового давления и гравитационного момента запишем в виде
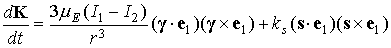 , , 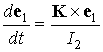 . (1) . (1)
Здесь 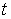 –
время, –
время, 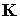 –
кинетический момент спутника в его движении относи- тельно центра масс. Первое
уравнение выражает обшую теорему динамики об изменении этого момента, второе
уравнение – следствие кинематического уравнения Пуассона для орта –
кинетический момент спутника в его движении относи- тельно центра масс. Первое
уравнение выражает обшую теорему динамики об изменении этого момента, второе
уравнение – следствие кинематического уравнения Пуассона для орта 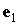 . Исходная форма уравнения Пуассона . Исходная форма уравнения Пуассона
 , ,
где 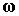 – угловая скорость
спутника. Поскольку – угловая скорость
спутника. Поскольку 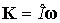 , то (ср. приведенную выше формулу для , то (ср. приведенную выше формулу для 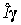 ) )  и и
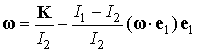 . .
Подстановка последнего
соотношения в выписанное кинематическое уравнение приводит ко второму уравнению
(1).
Уравнения
(1) не дают полного описания вращательного движения спутника. Они описывают
только изменение его собственного кинетического момента и движение оси 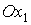 . Однако для описания режима одноосной солнечной ориентации
спутника – движений, в которых ось . Однако для описания режима одноосной солнечной ориентации
спутника – движений, в которых ось  составляет малый угол
с ортом составляет малый угол
с ортом 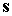 , – эти уравнения достаточны. , – эти уравнения достаточны.
Уравнения
(1) допускают первый интеграл 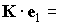 const и интегральное соотношение const и интегральное соотношение 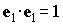 . Для численного интегрирования эти уравнения
записывались во второй геоэкваториальной системе координат . Для численного интегрирования эти уравнения
записывались во второй геоэкваториальной системе координат 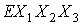 , связанной со средним экватором эпохи даты. Точка , связанной со средним экватором эпохи даты. Точка 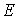 – центр Земли, оси – центр Земли, оси 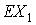 и и 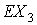 направлены в
соответствующие точку весеннего равноденствия и северный полюс мира, ось направлены в
соответствующие точку весеннего равноденствия и северный полюс мира, ось 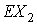 дополняет систему до
правой. Эта система координат считалась инерциальной. Геоцентрическое
движение Солнца рассчитывалось по формулам [2], в качестве орта дополняет систему до
правой. Эта система координат считалась инерциальной. Геоцентрическое
движение Солнца рассчитывалось по формулам [2], в качестве орта 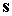 принимался орт
направления “Земля – Солнце”. Движение центра масс спутника рассчитывалось по
формулам задачи двух тел, в которых учитывались вековые изменения элементов
орбиты, обусловленные « принимался орт
направления “Земля – Солнце”. Движение центра масс спутника рассчитывалось по
формулам задачи двух тел, в которых учитывались вековые изменения элементов
орбиты, обусловленные «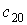 ». ».
Для реализации одноосной
солнечной ориентации спутника на длительных интервалах времени предлагается
использовать движения с достаточно большим собственным кинетическим моментом.
Эти движения близки регулярной прецессии Эйлера осесимметричного твердого
тела, и при изучении этих движений внешние моменты можно рассматривать как
малые возмущения. Для приближенного интегрирования первого уравнения (1) в
такой ситуации воспользуемся методом усреднения. А именно, усредним правую
часть этого уравнения по регулярной прецессии Эйлера, считая положение Солнца
и положение спутника на орбите неизменными. Замена точных уравнений усредненными
допустима, если за период прецессии кинетический момент спутника практически
не меняется. Приемы использования метода усреднения в рассматриваемой ситуации
разработаны в [1].
Выполнение усреднения начнем
с рассмотрения регулярной прецессии Эйлера. В этом движении 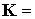 const, изменение орта const, изменение орта 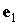 описывается вторым
уравнением (1), и в силу этих двух соотношений описывается вторым
уравнением (1), и в силу этих двух соотношений 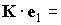 const. Для описания регулярной прецессии введем новый ортонормированный базис const. Для описания регулярной прецессии введем новый ортонормированный базис
 , , 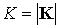 , , 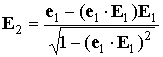 , , 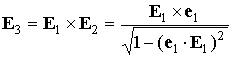 . .
Орт 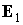 сохраняет неизменное
направление в пространстве и образует посто-янный угол с ортом сохраняет неизменное
направление в пространстве и образует посто-янный угол с ортом 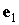 , орты , орты 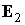 и и 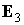 вращаются вокруг вращаются вокруг 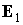 с постоянной угловой
скоростью с постоянной угловой
скоростью 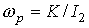 . Последнее утверждение следует из соотношений . Последнее утверждение следует из соотношений
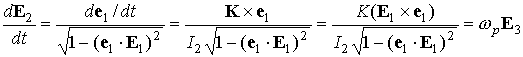 , ,
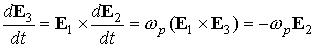 . .
Перейдем к усреднению правой части первого уравнения (1).
Начнем с гравитационного момента. Операцию усреднения некоторой функции 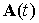 по регулярной
прецессии Эйлера будем обозначать угловыми скобками с индексом 1: по регулярной
прецессии Эйлера будем обозначать угловыми скобками с индексом 1: 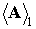 . Поскольку при усреднении величины . Поскольку при усреднении величины 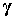 и и 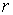 считаются
неизменными, имеет место соотношение считаются
неизменными, имеет место соотношение
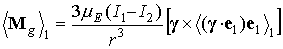 . .
Дальнейшие вычисления
основаны на равенствах
 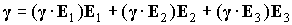 , ,
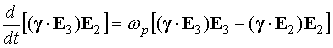 . .
Первое из них – следствие
ортонормированности базиса 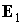 , ,  и и 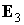 , при выводе второго следует учесть, что здесь , при выводе второго следует учесть, что здесь 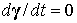 и воспользоваться
приве-денными выше выражениями для производных и воспользоваться
приве-денными выше выражениями для производных 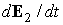 и и 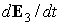 . Усредним эти равенства по регулярной прецессии Эйлера и
учтем, что среднее значение полной производной по времени должно быть равно
нулю [3]. Получим . Усредним эти равенства по регулярной прецессии Эйлера и
учтем, что среднее значение полной производной по времени должно быть равно
нулю [3]. Получим
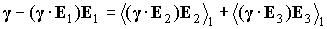 , , 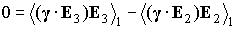 . .
Отсюда находим
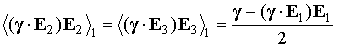 . .
Так как 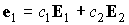 , , 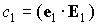 , , 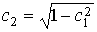 , то , то
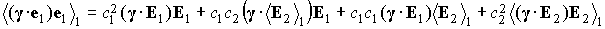 . .
Имеем также 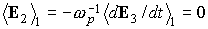 , поэтому , поэтому
 . .
Окончательно получаем
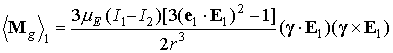 . .
Структура
зависимости моментов 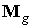 и и 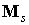 от от 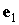 одинакова, поэтому
аналогичные выкладки позволяют установить соотношение одинакова, поэтому
аналогичные выкладки позволяют установить соотношение
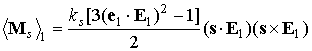 . .
Усредненное
уравнение, описывающее изменение кинетического момента спутника, имеет вид
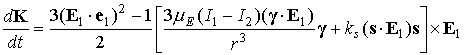 , ,
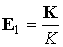 , , 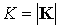 . .
Левую часть выписанного уравнения представим следующим образом
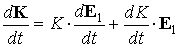 . .
Умножим это соотношение скалярно на 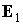 . Поскольку . Поскольку 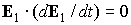 и в силу усредненного
уравнения и в силу усредненного
уравнения 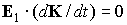 , получаем , получаем 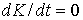 , , 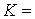 const. Как уже говорилось, уравнения (1)
допускают первый интеграл const. Как уже говорилось, уравнения (1)
допускают первый интеграл 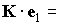 const, поэтому const, поэтому
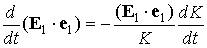 . .
Усредняя правую часть последнего соотношения по регулярной прецессии
Эйлера, устанавливаем неизменность скалярного произведения 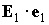 . С учетом сделанных замечаний усредненное уравнение запишем
в виде . С учетом сделанных замечаний усредненное уравнение запишем
в виде
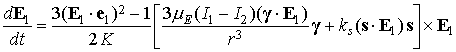 , (2) , (2)
и величины 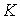 и и 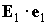 будем считать
параметрами, характеризующими прецессию,
по которой выполнялось усреднение. Описание вращательного движения спутника
выглядит теперь следующим образом. Это движение представляет собой быструю
регулярную прецессию Эйлера с параметрами будем считать
параметрами, характеризующими прецессию,
по которой выполнялось усреднение. Описание вращательного движения спутника
выглядит теперь следующим образом. Это движение представляет собой быструю
регулярную прецессию Эйлера с параметрами 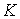 и и 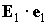 . Ось прецессии, задаваемая ортом . Ось прецессии, задаваемая ортом 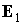 , медленно изменяет свое направление в соответствии с уравнением (2). , медленно изменяет свое направление в соответствии с уравнением (2).
Уравнения (1), (2) записаны в предположении, что спутник освещен Солнцем.
В тени Земли члены этих уравнений, содержащие коэффициент 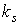 , должны быть отброшены. Для удобства будем
считать, что в этих уравнениях указанные члены присутствуют всегда, но , должны быть отброшены. Для удобства будем
считать, что в этих уравнениях указанные члены присутствуют всегда, но 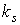 –
кусочно-постоянная функция времени: на освещенном участке орбиты –
кусочно-постоянная функция времени: на освещенном участке орбиты  , в тени Земли , в тени Земли 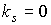 . .
Уравнения
(2) допускают дальнейшее упрощение. А именно, если за время одного оборота
спутника по орбите его собственный кинетический почти не меняется, то
уравнения (2) можно усреднить по орбитальному движению [1]. При усреднении
орбитальное движение спутника следует считать кеплеровым эллиптическим, орты 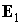 и и 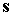 неизменным. Операцию
усреднения по орбитальному движению будем обозначать угловыми
скобками с индексом 2. Справедлива формула [1] неизменным. Операцию
усреднения по орбитальному движению будем обозначать угловыми
скобками с индексом 2. Справедлива формула [1]
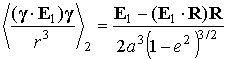 . .
Здесь 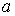 и и 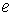 – большая полуось и
эксцентриситет орбиты спутника, – большая полуось и
эксцентриситет орбиты спутника, 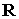 – орт орбитального
кинетического момента (нормаль к плоскости орбиты). – орт орбитального
кинетического момента (нормаль к плоскости орбиты).
Эксцентриситет орбиты
рассматриваемого спутника мал, поэтому при усреднении по орбитальному движению
величины  орбиту будем считать
круговой с радиусом, равным большой полуоси исходной орбиты. Тогда орбиту будем считать
круговой с радиусом, равным большой полуоси исходной орбиты. Тогда 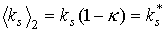 , где , где
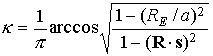 при при 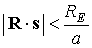 , , 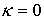 при при 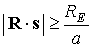 . .
Величина  представляет собой
отношение длины отрезка орбиты, находящегося в тени Земли, к длине всей
орбиты. Для наибольшего затенения номинальной орбиты представляет собой
отношение длины отрезка орбиты, находящегося в тени Земли, к длине всей
орбиты. Для наибольшего затенения номинальной орбиты 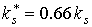 . .
Усредненное по орбитальному движению
уравнение (2) имеет вид
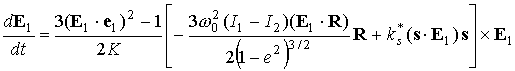 . (3) . (3)
Здесь 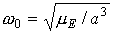 – среднее движение
спутника. – среднее движение
спутника.
Для численного
интегрирования уравнения (2) и (3) записывались во второй
геоэкваториальной системе координат.
Сравним результаты
интегрирования уравнений (1) – (3). Начальный
момент 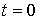 отнесем к отнесем к 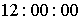 декретного
московского (зимнего) времени 22.09.2001. Полагаем, что спутник в этот момент
находится в восходящем узле орбиты. Параметры орбиты возьмем следующие:
большая полуось декретного
московского (зимнего) времени 22.09.2001. Полагаем, что спутник в этот момент
находится в восходящем узле орбиты. Параметры орбиты возьмем следующие:
большая полуось  км, эксцентриситет км, эксцентриситет 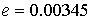 , наклонение – , наклонение – 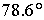 , начальное значение аргумента широты перигея – , начальное значение аргумента широты перигея – 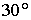 . Начальное значение . Начальное значение 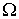 долготы восходящего узла
варьировалось. Для выбранного момента долготы восходящего узла
варьировалось. Для выбранного момента 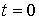 целесообразно принять целесообразно принять
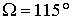 или или 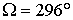 . Это позволяет получить длительные начальные участки
движения спутника без захода в тень Земли. Параметры паруса возьмем, как в разделе
2; будем использовать два варианта значений моментов инерции спутника: 1) . Это позволяет получить длительные начальные участки
движения спутника без захода в тень Земли. Параметры паруса возьмем, как в разделе
2; будем использовать два варианта значений моментов инерции спутника: 1)  1620 кгм 1620 кгм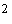 , , 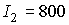 кгм кгм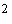 , 2) , 2) 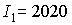 кгм кгм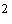 , , 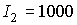 кгм кгм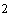 . Примем, что в нчальный момент времени . Примем, что в нчальный момент времени 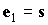 , , 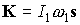 , , 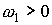 . Эти соотношения задают начальные условия уравнений (1).
Из них же получаем начальное условие . Эти соотношения задают начальные условия уравнений (1).
Из них же получаем начальное условие 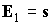 для уравнений (2),
(3) и значения параметров этих уравнений для уравнений (2),
(3) и значения параметров этих уравнений 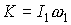 , , 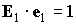 . .
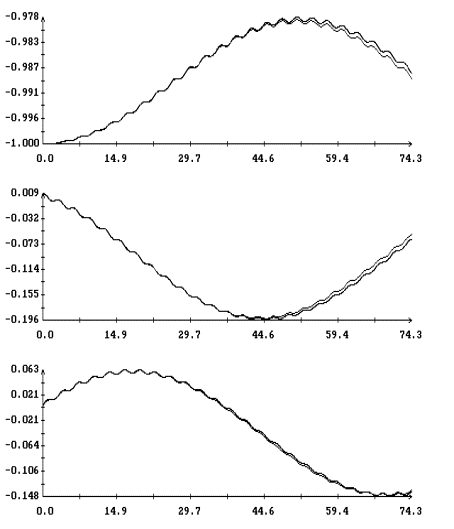
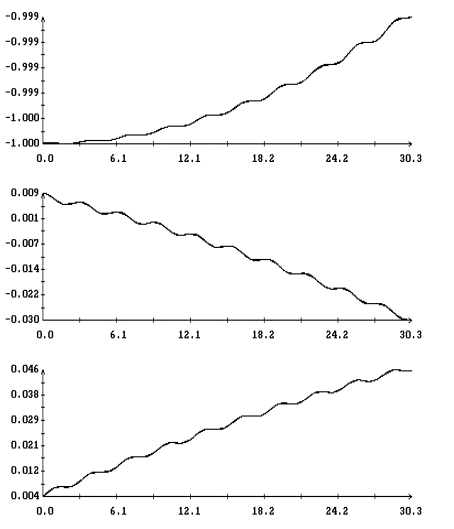
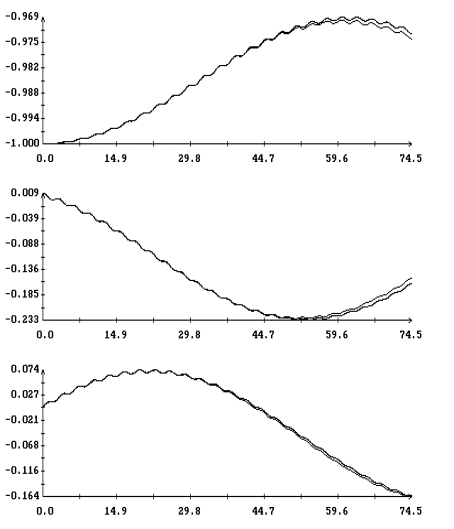
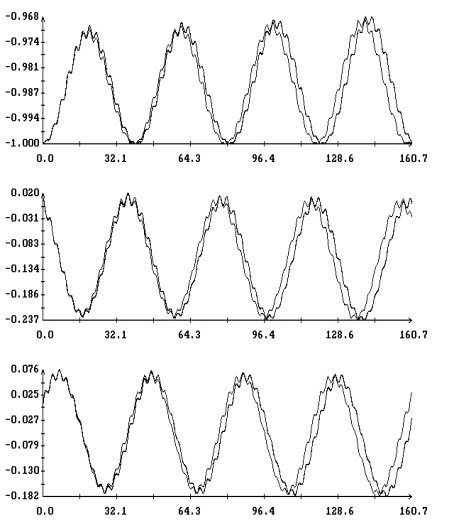
При
сравнении результатов интегрирования уравнений (1) и (2) решения этих уравнений
будем представлять графиками зависимости от времени ком-понент орта 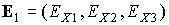 во второй
геоэкваториальной системе коор-динат. Для решений уравнений (1) во второй
геоэкваториальной системе коор-динат. Для решений уравнений (1) 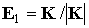 . Результаты интегрирования приведены на рис. 1, 2. Здесь
графики решений обоих уравнений изображены в одних и тех же координатных осях.
Вычисленные решения достаточно хорошо совпадают по амплтудам и вековому
изменению переменных . Результаты интегрирования приведены на рис. 1, 2. Здесь
графики решений обоих уравнений изображены в одних и тех же координатных осях.
Вычисленные решения достаточно хорошо совпадают по амплтудам и вековому
изменению переменных 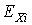 , но при малых значениях , но при малых значениях 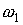 и больших значениях и больших значениях 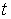 фазы этих переменных заметно
отли-чаются. Полученные результаты согласуются с типичными оценками
погреш-ности метода усреднения. фазы этих переменных заметно
отли-чаются. Полученные результаты согласуются с типичными оценками
погреш-ности метода усреднения.
При
сравнении результатов интегрирования уравнений (2) и (3) решения этих уравнений
будем представлять графиками зависимости от времени углов 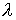 , , 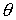 , , 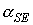 . Углы . Углы 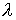 и и 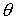 служат для задания
компонент орта служат для задания
компонент орта 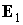 во второй
геоэкваториальной системе координат: во второй
геоэкваториальной системе координат: 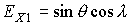 , , 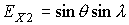 , , 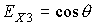 ; ; 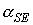 –
угол между ортами –
угол между ортами 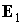 и и 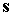 : : 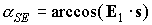 . Результаты интегрирования приведены на рис. 3, 4. Графики
решений обоих уравнений изображены на этих рисунках в одних и тех же
координатных осях. Полученные результаты можно характеризовать также, как и в
предыдущем случае. При малых значениях . Результаты интегрирования приведены на рис. 3, 4. Графики
решений обоих уравнений изображены на этих рисунках в одних и тех же
координатных осях. Полученные результаты можно характеризовать также, как и в
предыдущем случае. При малых значениях 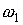 и больших значениях и больших значениях 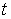 вычисленные решения
заметно расходятся по фазе, но они всегда достоточно хорошо совпадают по
амплтудам и вековому изменению переменных. вычисленные решения
заметно расходятся по фазе, но они всегда достоточно хорошо совпадают по
амплтудам и вековому изменению переменных.
Проведенное
сравнение показывает, что уравнение (3) в общем случае не пригодно для
предсказания деталей движения спутника на срок в несколько суток (или десятков
суток, в зависимости от значения 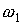 ), но оно позволяет правильно оценить погрешность ориентации,
исследовать эволюцию движения и решать другие подобные задачи, требующие знания
амплитуд различных характеристик движения, а не их фаз. Ниже при изучении
движения спутника на длительных интервалпх времени будет использоваться только
уравнение (3). Преимущество этого уравнения перед уравнениями (1) и отчасти
уравнением (2) – ничтожно малое время интегрирования на длительных интервалах
времени и возможность качественного исследования. ), но оно позволяет правильно оценить погрешность ориентации,
исследовать эволюцию движения и решать другие подобные задачи, требующие знания
амплитуд различных характеристик движения, а не их фаз. Ниже при изучении
движения спутника на длительных интервалпх времени будет использоваться только
уравнение (3). Преимущество этого уравнения перед уравнениями (1) и отчасти
уравнением (2) – ничтожно малое время интегрирования на длительных интервалах
времени и возможность качественного исследования.
5. Исследование усредненных уравнений. Будем считать, что 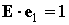 , и введем обозначения , и введем обозначения
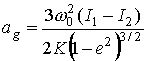 , , 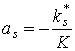 , , 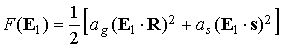 . .
Тогда уравнение (3) можно записать в виде
 , (4) , (4)
и в виде
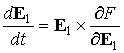 . (5) . (5)
Последняя форма рассматриваемого уравнения и
соотношение 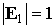 позволяют
преобразовать это векторное
уравнение к гамильтоновой системе двух скалярных уравнений. Воспользуемся введенными выше углами позволяют
преобразовать это векторное
уравнение к гамильтоновой системе двух скалярных уравнений. Воспользуемся введенными выше углами 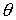 и и  . В качестве независимых
переменных примем . В качестве независимых
переменных примем 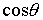 и и 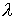 . Тогда уравнение (5) можно привести к виду . Тогда уравнение (5) можно привести к виду
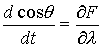 , ,  . (6) . (6)
В данном случае 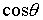 выступает в роли обобщенной
координаты, выступает в роли обобщенной
координаты, 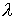 – в роли обобщенного
импульса. Указанное свойство уравнения (4) позволяет провести его приближенное
аналитическое исследование. – в роли обобщенного
импульса. Указанное свойство уравнения (4) позволяет провести его приближенное
аналитическое исследование.
Это исследование основано на
следующих оценках. Скорость изменения орта 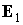 характеризуется коэффициентами характеризуется коэффициентами
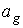 и и 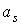 . При . При 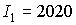 кгм кгм , , 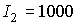 кгм кгм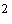 и и 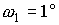 /с эти коэффициенты имеют значения /с эти коэффициенты имеют значения 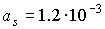 с с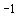 , , 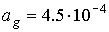 с с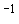 . В то же время скорость изменения орта . В то же время скорость изменения орта 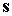 составляет пример-но составляет пример-но 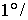 сут, т. е. сут, т. е. 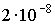 с с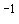 , скорость изменения , скорость изменения 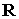 примерно на порядок
больше. Следовательно, орты примерно на порядок
больше. Следовательно, орты 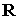 и и 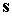 – весьма медленно
меняющиеся функции времени. – весьма медленно
меняющиеся функции времени.
Предположим
сначала, что эти орты неизменны. Такое предположение оправдано при изучении
движения спутника на интервале времени в несколько суток. При сделанном
предположении уравнение (4) допускает первый интеграл 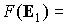 const, и его траектории представляют собой замкнутые кривые,
являющиеся линиями пересечения единичной сферы const, и его траектории представляют собой замкнутые кривые,
являющиеся линиями пересечения единичной сферы  и прямого эллиптического
цилиндра и прямого эллиптического
цилиндра 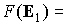 const. Ось этого цилиндра проходит через центр сферы вдоль
вектора const. Ось этого цилиндра проходит через центр сферы вдоль
вектора 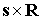 . Пусть . Пусть 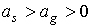 и в начальный момент
времени и в начальный момент
времени 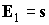 . Тогда максимальный угол между ортами . Тогда максимальный угол между ортами 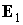 и и  достигается в
моменты времени, когда орт достигается в
моменты времени, когда орт 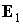 проходит через
плоскость, натянутую на орты проходит через
плоскость, натянутую на орты 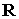 и и 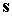 . Этот угол задается формулой . Этот угол задается формулой
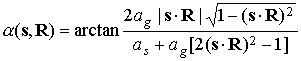 . .
Максимизируя правую часть
последней формулы по скалярному произведению 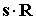 , найдем, что при любом взаимном расположении векторов , найдем, что при любом взаимном расположении векторов 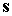 и и 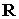 продольная ось
спутника и направление на Солнца будут составлять угол, не превосходящий продольная ось
спутника и направление на Солнца будут составлять угол, не превосходящий
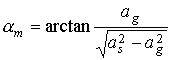 . .
Отношение 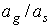 , определяющее углы , определяющее углы 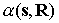 и и 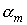 не зависит от не зависит от 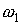 , но зависит от продолжительности теневого участка. , но зависит от продолжительности теневого участка.
Пусть 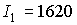 кгм кгм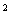 , , 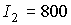 кгм кгм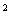 . Если орбита не имеет теневых участков, то в этом случае . Если орбита не имеет теневых участков, то в этом случае 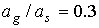 и и 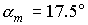 . Для наибольшего затенения . Для наибольшего затенения 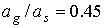 и и 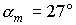 . Пусть теперь . Пусть теперь 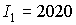 кгм кгм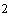 , , 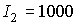 кгм кгм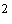 . Тогда для орбиты без теневых участков . Тогда для орбиты без теневых участков 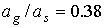 и и 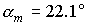 . В случае наибольшего затенения . В случае наибольшего затенения  и и 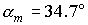 . .
Рассмотрим случай медленно
меняющихся ортов 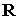 , , 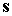 и коэффициента и коэффициента 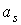 . Функция . Функция 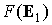 теперь не
будет первым интегралом уравнения (4), и здесь следует воспользоваться
указанной выше возможностью сведения этого урав-нения к гамильтоновой системе
(6). Система (6) допускает адиабатический инвариант теперь не
будет первым интегралом уравнения (4), и здесь следует воспользоваться
указанной выше возможностью сведения этого урав-нения к гамильтоновой системе
(6). Система (6) допускает адиабатический инвариант
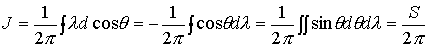 . .
Выписанная цепочка
соотношений интерпретируется следующим образом. Первые два интеграла цепочки –
определение адиабатического инварианта [3]. Они
вычисляются по траекториии системы (6) в предположении, что 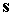 , , 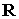 и и 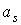 неизменны, т.
е. по кривой, задаваемой уравнением неизменны, т.
е. по кривой, задаваемой уравнением 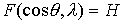 ( (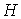 – обозначение постоянной в соответствующем первом интеграле).
Таким образом – обозначение постоянной в соответствующем первом интеграле).
Таким образом 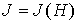 . Последний интеграл берется по области, ограниченной кривой . Последний интеграл берется по области, ограниченной кривой  в плоскости в плоскости 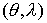 . Как следует из вида этого интегра-ла, он равен площади . Как следует из вида этого интегра-ла, он равен площади 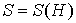 области на единичной
сфере области на единичной
сфере 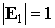 , ограниченной траекторией уравнения (4), которая отвечает
значению первого интеграла , ограниченной траекторией уравнения (4), которая отвечает
значению первого интеграла 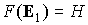 . Адиабатический инвариант можно считать приблизительно
неизменным на всем интервале времени, на котором оказывается достаточно точным
(по амплитудам) уравнение (4). . Адиабатический инвариант можно считать приблизительно
неизменным на всем интервале времени, на котором оказывается достаточно точным
(по амплитудам) уравнение (4).
Существование
адиабатического инварианта можно использовать так. Пусть для примера 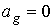 – гравитационный
момент не учитываем. Тогда первый интеграл – гравитационный
момент не учитываем. Тогда первый интеграл 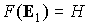 дает дает 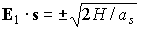 . Траектория орта . Траектория орта 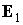 на единичной сфере
представляет собой окружность, центр которой лежит на радиусе сферы,
параллельном орту на единичной сфере
представляет собой окружность, центр которой лежит на радиусе сферы,
параллельном орту 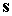 . Рассмотрим траекторию, отвечающую знаку «+» в последнем соотношении.
В этом случае . Рассмотрим траекторию, отвечающую знаку «+» в последнем соотношении.
В этом случае 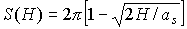 , , 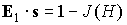 . Сохранение адиабатического инварианта . Сохранение адиабатического инварианта 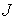 означает, что угол означает, что угол 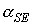 между ортами между ортами 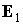 и и 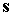 остается неизменным в
течение всего времени движения спутника несмотря на изменение со временем
направления орта остается неизменным в
течение всего времени движения спутника несмотря на изменение со временем
направления орта 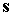 . Отсюда следует возможность односной солнечной ориентации
спутника в случае, когда на него действует один лишь момент сил светового
давления. . Отсюда следует возможность односной солнечной ориентации
спутника в случае, когда на него действует один лишь момент сил светового
давления.
Аналогичная
ситуация имеет место и при  , только форма кривой, по которой движется конец орта , только форма кривой, по которой движется конец орта 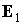 , более сложна. Чтобы упростить
использование адиабатического инварианта в этом случае, заменим
площадь области, ограниченной кривой , более сложна. Чтобы упростить
использование адиабатического инварианта в этом случае, заменим
площадь области, ограниченной кривой 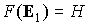 , на единичной сфере площадью проекции этой области на
плоскость, перпендикулярную орту , на единичной сфере площадью проекции этой области на
плоскость, перпендикулярную орту 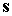 . Поскольку интерес представляют траектории уравнения (4),
лежащие в окрестности конца этого орта, ошибка должна быть приемлемой. Введем
систему коодинат . Поскольку интерес представляют траектории уравнения (4),
лежащие в окрестности конца этого орта, ошибка должна быть приемлемой. Введем
систему коодинат 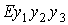 так, чтобы ось так, чтобы ось 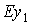 была направлена вдоль
орта была направлена вдоль
орта 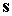 и орт и орт 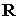 лежал в первом или
втором квадранте плоскости лежал в первом или
втором квадранте плоскости 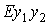 . В этой системе . В этой системе 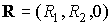 , где , где 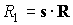 , , 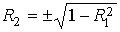 . Искомая область в плоскости . Искомая область в плоскости  будет близка
внутренности эллипса, задаваемого уравнением будет близка
внутренности эллипса, задаваемого уравнением
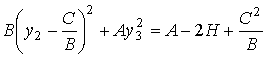 ,
(7) ,
(7)
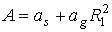 , ,  , , 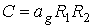 . .
Выписанное уравнение
получено из точного уравнения границы искомой области отбрасыванием членов
третьей и более высокой степени относительно 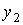 и и 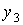 . В данном случае . В данном случае
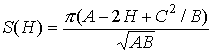 , ,  . .
Пусть
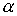 - максимальный угол
между ортами - максимальный угол
между ортами 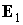 и и  на кривой на кривой  . На кривой (7) соответствующему экстремальному положению орта . На кривой (7) соответствующему экстремальному положению орта 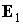 отвечает
точка отвечает
точка
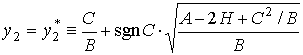 , , 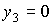 , ,
причем в рассматриваемом
приближении 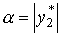 . С помощью адиабатичес-кого инварианта указанный
максимальный угол можно представить следую-щим образом . С помощью адиабатичес-кого инварианта указанный
максимальный угол можно представить следую-щим образом
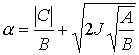 . (8) . (8)
Функция (8) медленно
меняется во времени и должна служить достаточно точной оценкой сверху угла 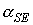 . Эта функция ограничена, причем из построения указанной выше
оценки . Эта функция ограничена, причем из построения указанной выше
оценки 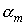  следует неравенство следует неравенство 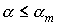 . Значение . Значение 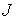 в (8) определяется по
начальным условиям решения уравнения (4). Для решения с начальным условием в (8) определяется по
начальным условиям решения уравнения (4). Для решения с начальным условием 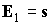 имеем имеем
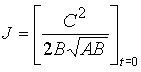 . .
Из
полученных оценок угла 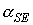 , следует, в частности, возможность реализации одноосной солнечной
ориентации при , следует, в частности, возможность реализации одноосной солнечной
ориентации при 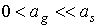 . Эти оценки можно использовать и для тестирования программ
интегрирования уравнений движения спутника. . Эти оценки можно использовать и для тестирования программ
интегрирования уравнений движения спутника.
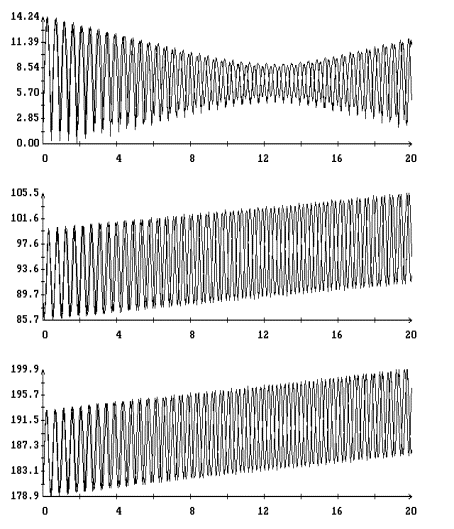
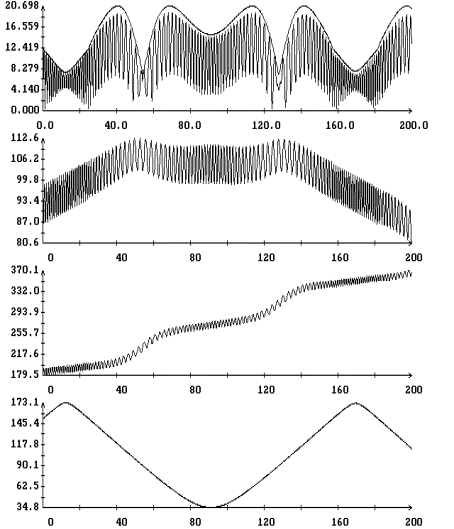
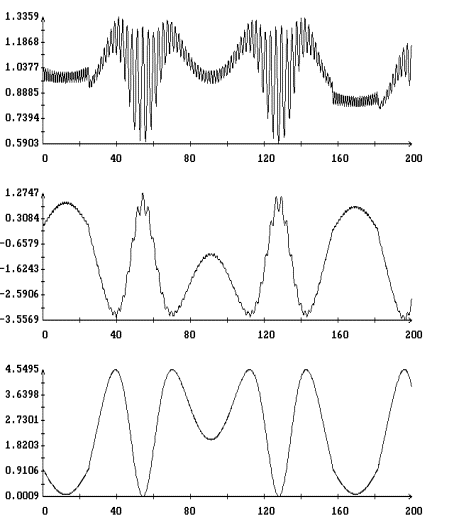
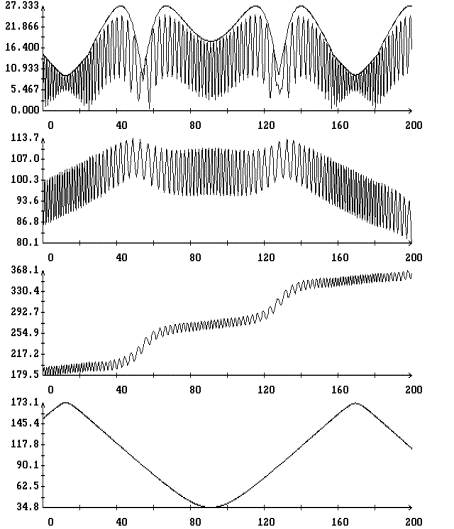
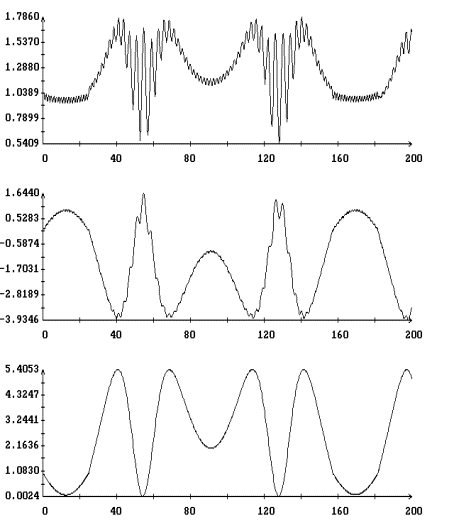
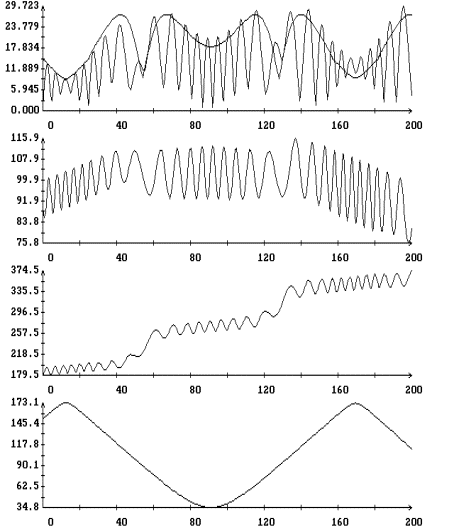
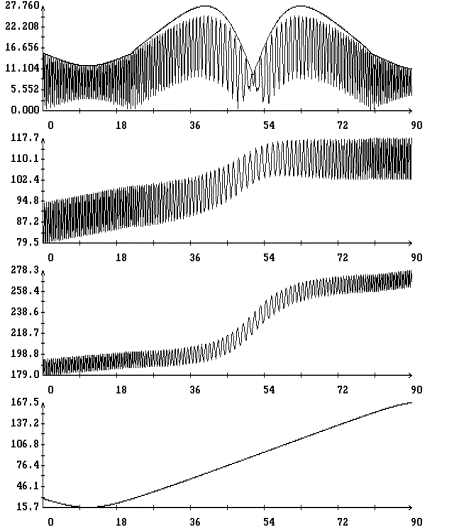
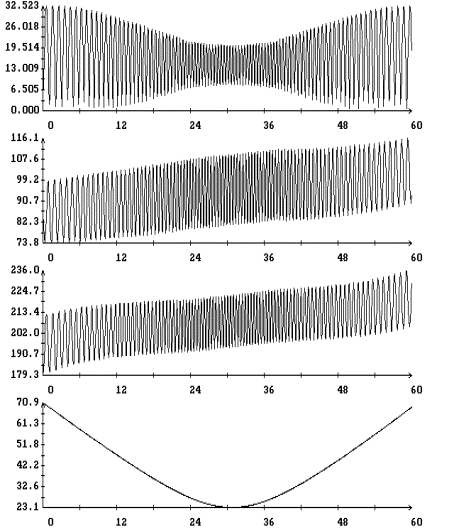
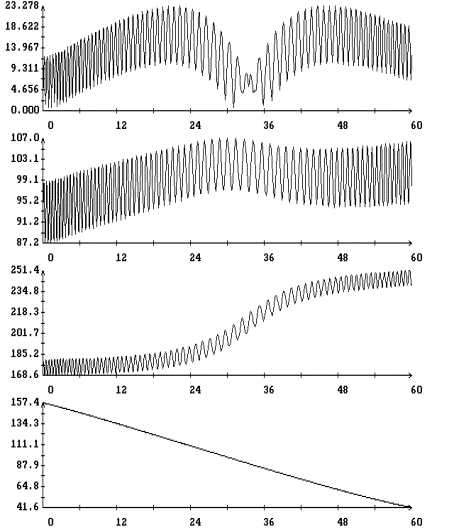
Результаты
интегрирования уравнения (4) на продолжительных интервалах времени при
различных значениях моментов инерции спутника и угловой скорости закрутки
приведены на рис. 5 – 9. Эти результаты получены при указанных выше элементах
орбиты и параметрах паруса. На рисунках изображены графики зависимости от
времени углов  , , 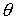 , , 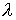 и функции (8), а
также аналогичный график для угла и функции (8), а
также аналогичный график для угла 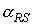 между ортами между ортами 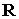 и и 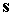 . Графики угла . Графики угла 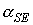 и функции (8) приведены
в одних и тех же координатных осях. Графики угла и функции (8) приведены
в одних и тех же координатных осях. Графики угла 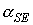 сильно осциллируют, графики
функции (8) – представляют собой плавные кривые. Во всех представленных
вариантах расчетов, за исключением части решения, приведенного на рис. 8,
функция (8) является достаточно точной оценкой сверху угла сильно осциллируют, графики
функции (8) – представляют собой плавные кривые. Во всех представленных
вариантах расчетов, за исключением части решения, приведенного на рис. 8,
функция (8) является достаточно точной оценкой сверху угла 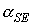 . Чтобы проиллюстрировать сохранение адиабатического инварианта,
на рис. 5 – 8 приведены графики зависимости от времени величины . Чтобы проиллюстрировать сохранение адиабатического инварианта,
на рис. 5 – 8 приведены графики зависимости от времени величины 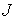 и ее составляющих и ее составляющих
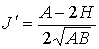 , , 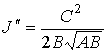 , ,  . .
Для удобства на графиках
представлены не сами величины 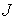 , , 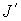 и и 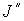 , а их отношения к значению , а их отношения к значению 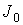 адиабатического
инварианта в начальный момент времени. Сопоставление этих графиков показывает
нетривиальность факта существования адиабатического инварианта. адиабатического
инварианта в начальный момент времени. Сопоставление этих графиков показывает
нетривиальность факта существования адиабатического инварианта.
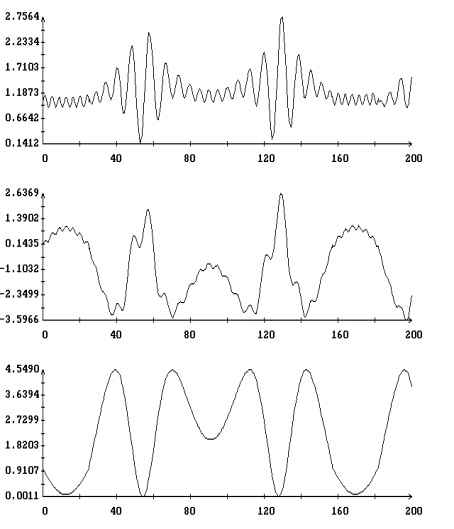
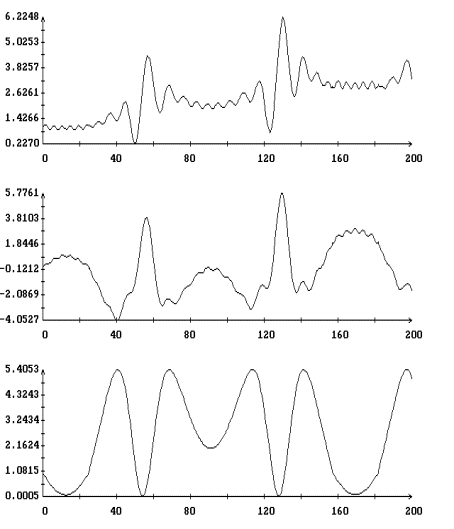
Согласно
теории адиабатических инвариатов [3] их постоянство не является таким точным, как
постоянство первых интегралов. Сохранение адиабатического инварианта
означает лишь отсутствие в нем монотонно меняющейся с течением времени
составляющей. Иными словами, допускаются колебания значений адиабатического
инварианта относительно некоторого неизменного среднего уровня. Если последние слова трактовать широко, то
их можно считать справедливыми для функций 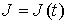 , чьи графики представлены на рис. 5 – 7, но они явно не
относятся к графику на рис. 8. На этом рисунке хорошо видны изменения среднего
значения , чьи графики представлены на рис. 5 – 7, но они явно не
относятся к графику на рис. 8. На этом рисунке хорошо видны изменения среднего
значения 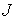 , связанные с наличием на орбите теневых участков, точнее, с
обусловленной их возникновением или исчезновением негладкостью функции , связанные с наличием на орбите теневых участков, точнее, с
обусловленной их возникновением или исчезновением негладкостью функции 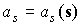 . Впрочем, влияние этой негладкости заметно и на рис. 5 –
7. Следует также напомнить, что формула, определяющая . Впрочем, влияние этой негладкости заметно и на рис. 5 –
7. Следует также напомнить, что формула, определяющая 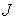 , является приближенной, причем ее ошибка тем больше, чем
дальше от конца орта , является приближенной, причем ее ошибка тем больше, чем
дальше от конца орта 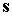 удалена траектория решения
уравнения (4). удалена траектория решения
уравнения (4).
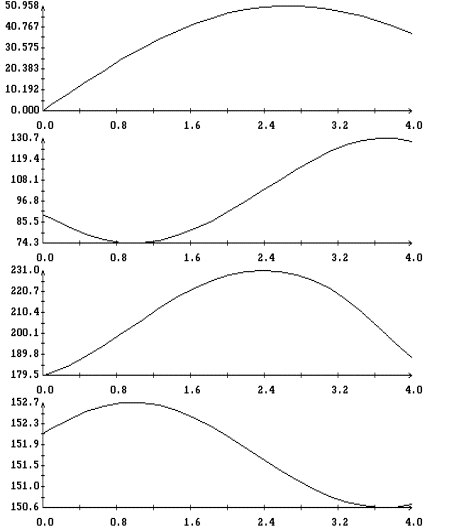
Как видно из приведенных
оценок и рис. 5 – 9, экстремальные значения угла 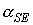 практически не
зависят от угловой скорости закрутки практически не
зависят от угловой скорости закрутки 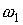 . Важно лишь, чтобы абсолютная величина этой скорости была
достаточно большой и можно было использовать уравнение (4). Однако начальная
долгота восходящего узла орбиты может оказывать на эти значения существенное
влияние (см. рис. 10, 11). . Важно лишь, чтобы абсолютная величина этой скорости была
достаточно большой и можно было использовать уравнение (4). Однако начальная
долгота восходящего узла орбиты может оказывать на эти значения существенное
влияние (см. рис. 10, 11).
Полученные результаты
показывают, что парус позволяет реализовать режим одноосной солнечной
ориентации спутника, хотя (см. разделы 2, 3) максимальные значения
гравитационного момента и момента светового давления сравнимы по величине.
Чтобы показать, что солнечная ориентация обусловлена именно моментом
светового давления, на рис. 12
приведены графики решений уравнения (4) при  . На этом рисунке . На этом рисунке  – угол между ортами – угол между ортами 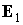 и и 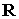 . Рисунок построен при значении . Рисунок построен при значении 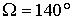 , обеспечивающем практически максимальное влияние гравитационного
момента. Для значения , обеспечивающем практически максимальное влияние гравитационного
момента. Для значения  графики зависимости
угла графики зависимости
угла  от времени выглядят
так же. Вид представленных на рис. 12 графиков определяется не величинами
моментов инерции спутника от времени выглядят
так же. Вид представленных на рис. 12 графиков определяется не величинами
моментов инерции спутника 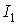 и и 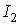 , а их отношением , а их отношением 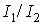 . Поскольку для обоих принятых вариантов значений этих моментов . Поскольку для обоих принятых вариантов значений этих моментов
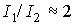 , рис. 12 иллюстрирует оба эти варианта. Как видно из
рисунка, без учета влияния момента светового давления режим одноосной
солнечной ориентации не существует. Графики зависимости от времени угла , рис. 12 иллюстрирует оба эти варианта. Как видно из
рисунка, без учета влияния момента светового давления режим одноосной
солнечной ориентации не существует. Графики зависимости от времени угла 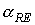 показывают, что орт показывают, что орт 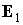 (фактически ось (фактически ось 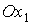 ) движется так, что
угол между ним и ортом ) движется так, что
угол между ним и ортом 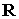 (нормалью к плоскости
орбиты) остается практически неизменным. Неизменность этого угла следует из
существования в рассматриваемой задаче адиабатического инварианта и
обосновывается точно также, как выше была обоснована неизменность угла (нормалью к плоскости
орбиты) остается практически неизменным. Неизменность этого угла следует из
существования в рассматриваемой задаче адиабатического инварианта и
обосновывается точно также, как выше была обоснована неизменность угла 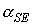 в случае в случае 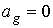 . Другое доказательство неизменности угла . Другое доказательство неизменности угла 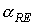 приведено в [1]. Там же показано, что
движение орта приведено в [1]. Там же показано, что
движение орта 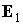 вокруг орта вокруг орта  происходит с
постоянной угловой скоростью. В свою очередь вследствие регрессии узла орбиты
орт происходит с
постоянной угловой скоростью. В свою очередь вследствие регрессии узла орбиты
орт 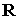 вращается, но существенно
медленнее с постоянной угловой скоростью вокруг оси вращается, но существенно
медленнее с постоянной угловой скоростью вокруг оси 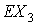 . Результирующее сложное движение орта . Результирующее сложное движение орта 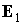 , описываемое графиками зависимости от времени углов , описываемое графиками зависимости от времени углов 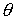 и и 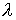 на рис. 12, служит
причиной разрушения режима солнечной ориентации. на рис. 12, служит
причиной разрушения режима солнечной ориентации.
6. Движение спутника при неполном раскрытии паруса. Исследуем
вращательное движение спутника в случае, когда один лепесток паруса не раскрыт. Пусть это будет
лепесток с номером 1. Примем, что
отсутствие одного лепестка не влияет на положение главных центральных осей
инерции спутника относительно раскрытых лепестков. Момент сил светового
давления, действующий на спутник в рассматриваемой ситуации, представим в виде
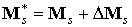 , ,
где слагаемое 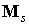 определено формулой
из раздела 2 для паруса со всеми лепестками, определено формулой
из раздела 2 для паруса со всеми лепестками,
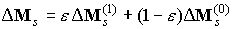 , ,
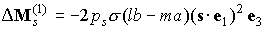 , ,
 , ,
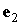 и и 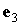 – орты осей – орты осей 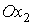 и и 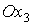 . .
При учете дополнительного
слагаемого 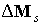 в уравнениях (2) и
(3) его необходимо усреднить по регулярной прецессии Эйлера. Это – несколько более
сложная задача, чем та, которая рассматривалась в разделе 4. В данном случае
усреднение выполняется независимо по двум движениям спутника – по его вращению
вокруг оси в уравнениях (2) и
(3) его необходимо усреднить по регулярной прецессии Эйлера. Это – несколько более
сложная задача, чем та, которая рассматривалась в разделе 4. В данном случае
усреднение выполняется независимо по двум движениям спутника – по его вращению
вокруг оси 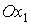 и по прецессии этой
оси относительно вектора собственного кинетического момента спутника. В
разделе 4 вследствие симметрии усредняемых моментов выполнялось только второе
усреднение. Первое усреднение (обозначим его и по прецессии этой
оси относительно вектора собственного кинетического момента спутника. В
разделе 4 вследствие симметрии усредняемых моментов выполнялось только второе
усреднение. Первое усреднение (обозначим его 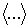 ) выполняется примерно также и приводит к результату ) выполняется примерно также и приводит к результату
 , (9) , (9)
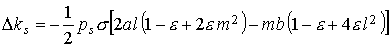 . .
Вычисления
показывают, что для рассматриваемого паруса 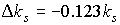 . Приведенные соотношения остаются верными, если вместо
лепестка 1 отсутствует один из лепестков 3, 5 или 7. Чтобы получить формулу,
описывающую отсутствие одного из лепестков с четным номером, надо в (9)
заменить . Приведенные соотношения остаются верными, если вместо
лепестка 1 отсутствует один из лепестков 3, 5 или 7. Чтобы получить формулу,
описывающую отсутствие одного из лепестков с четным номером, надо в (9)
заменить 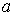 на на 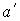 . В этом случае . В этом случае 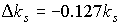 . Если приближенно принять . Если приближенно принять 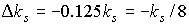 , то формулой (9) можно пользоваться при отсутствии любого
лепестка. , то формулой (9) можно пользоваться при отсутствии любого
лепестка.
Формула (9) имеет ту же структуру, что и формула
момента светового давления,
действующего на полный парус (см. раздел 2). В результате отсутствие
одного лепестка описывается уменьшением модуля коэффициента 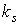 на 1/8 его величины.
Дальнейшее усреднение дополнительного слагаемого в формуле момента светового
давления можно не выполнять, ограничившись указанной коррекцией коэффициента на 1/8 его величины.
Дальнейшее усреднение дополнительного слагаемого в формуле момента светового
давления можно не выполнять, ограничившись указанной коррекцией коэффициента 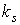 . Примеры решений уравнения (4) в для скорректированного
таким образом значения . Примеры решений уравнения (4) в для скорректированного
таким образом значения 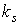 приведены на рис.
13. На этом рисунке представлены два
решения, оба для случая приведены на рис.
13. На этом рисунке представлены два
решения, оба для случая 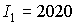 кгм кгм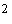 , , 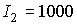 кгм кгм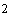 , , 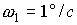 . Одно решение отвечает значению . Одно решение отвечает значению 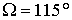 , другое – значению , другое – значению 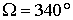 , при котором достигаются наибольшие значения , при котором достигаются наибольшие значения 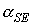 . .
7. Пропеллирующий момент паруса. Солнечный
парус, рассматривавшийся в предыдущих разделах, обладает одним замечательным
свойством – создаваемый им момент светового давления 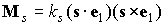 потенциален. А именно,
этот момент можно представить в виде потенциален. А именно,
этот момент можно представить в виде
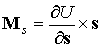 , , 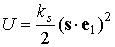 , ,
если рассматривать
векторы 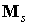 , , 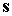 и и 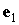 в системе координат в системе координат 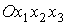 , и в виде , и в виде
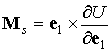
с той же самой
силовой функцией 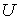 , если рассматривать те же векторы в системе , если рассматривать те же векторы в системе 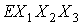 . Разница между этими способами представления состоит в том,
что в системе . Разница между этими способами представления состоит в том,
что в системе 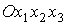 орт орт 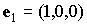 =const, и дифференцировать по нему силовую функцию нельзя. Орт =const, и дифференцировать по нему силовую функцию нельзя. Орт 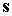 в этой системе –
независимая переменная, и производная в этой системе –
независимая переменная, и производная  имеет смысл. В
системе имеет смысл. В
системе 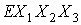 наоборот, орт наоборот, орт 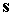 задан, а орт задан, а орт 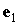 – независимая
переменная. – независимая
переменная.
Погрешности в изготовлении и установке
солнечного паруса могут привести к нарушению свойства потенциальности
действующего на спутник момента светового давления. Движение спутника в этом
случае может заметно отличаться от движения, исследованного выше. В качестве
примера рассмотрим изменение способа установки лепестков паруса, приводящее к
возникновению так называемого пропеллирующего момента. Для простоты расчетов
будем считать, что это изменение одинаково для всех лепестков. Предположим,
что все лепестки повернуты на один и тот же угол в одну и ту же сторону
вокруг своих осей симметрии. При этом указанные в разделе 2 радиусы-векторы 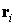 центров лепестков
остаются прежними, а нормали к лепесткам принимают вид центров лепестков
остаются прежними, а нормали к лепесткам принимают вид
 , , 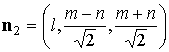 , , 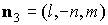 , ,
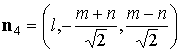 , , 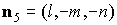 , , 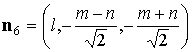 , ,
 , , 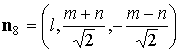 . .
Здесь 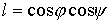 , , 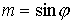 , , 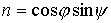 , , 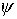 – угол поворота
лепестка относительно его продольной оси. Для момента сил светового давления
справедлива формула – угол поворота
лепестка относительно его продольной оси. Для момента сил светового давления
справедлива формула
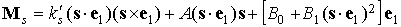 , ,
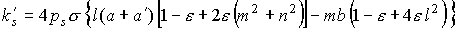 , ,
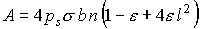 , , 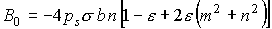 , ,
 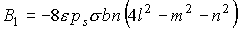 . .
Эта формула отличается от формулы для 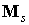 в разделе 2
измененным выражением для коэффициента в первом слагаемом и наличием двух
дополнительных слагаемых. При в разделе 2
измененным выражением для коэффициента в первом слагаемом и наличием двух
дополнительных слагаемых. При 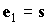 прежняя формула дает прежняя формула дает 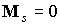 , новая формула дает , новая формула дает
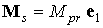 , , 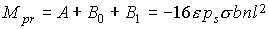 . .
Последнее соотношение означает, что если
продольная ось спутника направлена на Солнце, то на спутник относительно этой
оси действует постоянный момент. Спутник подобен вертушке, раскручиваемой
ветром. Усредненные уравнения, описывающие вековое изменение вектора
собственного кинетического момента спутника при новом выражении для момента
сил светового давления, запишем для случая 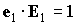 и орбиты без теневого
участка. Эти уравнения имеют вид и орбиты без теневого
участка. Эти уравнения имеют вид
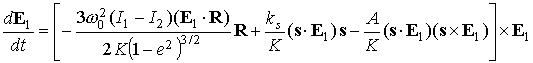 , (10) , (10)
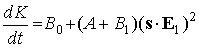 . .
Теперь модуль кинетического момента
испытывает вековое изменение. Для оценки этого изменения положим 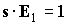 . Будем иметь . Будем иметь 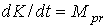 . Удобнее рассматривать не модуль кинетического момента
спутника . Удобнее рассматривать не модуль кинетического момента
спутника 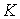 , а его угловую скорость относительно продольной оси , а его угловую скорость относительно продольной оси 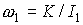 . Вековое изменение этой угловой скорости описывается
уравнением . Вековое изменение этой угловой скорости описывается
уравнением
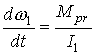 . .
Приведем числовые оценки.
Примем прежние значения параметров паруса, 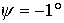 и и 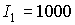 кгм кгм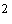 . В этом случае . В этом случае 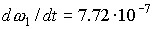 с с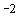 . Пусть в начальный момент времени . Пусть в начальный момент времени 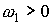 . Тогда кинетический момент спутника возрастает, и
уравнения (11) остаются справедливыми. При указанном угловом ускорении увеличение . Тогда кинетический момент спутника возрастает, и
уравнения (11) остаются справедливыми. При указанном угловом ускорении увеличение
 на на  происходит за происходит за 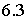 ч. Разумеется, рассмотренная
конфигурация паруса весьма маловероятна. Однако при ч. Разумеется, рассмотренная
конфигурация паруса весьма маловероятна. Однако при 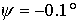 увеличение угловой
скорости на увеличение угловой
скорости на  происходит за 63 ч,
т. е. менее чем за 3 сут. Увеличение происходит за 63 ч,
т. е. менее чем за 3 сут. Увеличение 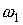 в первые несколько
суток ориентированного движения не скажется на точности солнечной ориентации
спутника – последний член в квадратных скобках уравнения (11) существенно
меньше первых двух членов. в первые несколько
суток ориентированного движения не скажется на точности солнечной ориентации
спутника – последний член в квадратных скобках уравнения (11) существенно
меньше первых двух членов.
Если угол 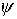 положителен, то при
начальном значении положителен, то при
начальном значении 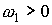 происходит
замедление вращения. В этом случае режим солнечной ориентации может весьма
быстро разрушиться. При начальном значении происходит
замедление вращения. В этом случае режим солнечной ориентации может весьма
быстро разрушиться. При начальном значении
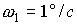 время существования
режима может оказаться менее суток. время существования
режима может оказаться менее суток.
Для борьбы с пропеллирующим
эффектом целесообразно предусмотреть возможность управления углом 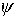 . Например, во время полета спутника можно систематически
измерять его угловую скорость относительно оси . Например, во время полета спутника можно систематически
измерять его угловую скорость относительно оси 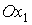 и корректировать ее
значение изменением этого угла. и корректировать ее
значение изменением этого угла.
8. Заключение. Исследована возможность
длительного применения режима одноосной солнечной ориентации на искусственном
спутнике Земли, снабженном солнечным парусом в виде восьми одинаковых
треугольных лепестков. Рассмотрены два
варианта значений главных центральных моментов инерции спутника. Эти значения
характеризуют приложенный к спутнику гравитационный момент, который в данном
случае выступает в роли возмущения. Чем меньше
моменты инерции при заданных размерах паруса, тем точнее ориентация. В
худшем (по точности ориентации)
варианте максимальное значение модуля гравитационного момента составляет около
70% максимального значения модуля момента сил светового давления, погрешность
ориентации на наиболее выгодных орбитах не превышает 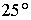 в течение 60 сут.
Если один из лепестков паруса не будет раскрыт, то погрешность ориентации на
таких орбитах не превысит в течение 60 сут.
Если один из лепестков паруса не будет раскрыт, то погрешность ориентации на
таких орбитах не превысит 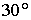 . Пропеллирующий момент, обусловленный неточностью установки
паруса может оказать определяющее влияние на вращательное движение спутника,
поэтому следует принять меры по его компенсации. . Пропеллирующий момент, обусловленный неточностью установки
паруса может оказать определяющее влияние на вращательное движение спутника,
поэтому следует принять меры по его компенсации.
Литература
1. Белецкий
В.В. Движение искусственного спутника относительно центра масс. М., Наука,
1965.
2. Меес
Ж. Астрономические формулы для калькуляторов. М., Мир, 1988.
3. Ландау
Л.Д., Лифшиц Е.М. Механика. М., Наука, 1973.
|
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
![]() (1000 с)
(1000 с)
![]() (1000 с)
(1000 с)![]() кгм
кгм![]() ,
, ![]() кгм
кгм![]() ;
; ![]() , справа
, справа ![]()
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
![]() (1000 с)
(1000 с)
![]() (1000 с)
(1000 с)![]() кгм
кгм![]() ,
, ![]() кгм
кгм![]() ;
; ![]() , справа
, справа ![]()
![]() (град.) Углы
(град.) Углы ![]() (град.)
(град.)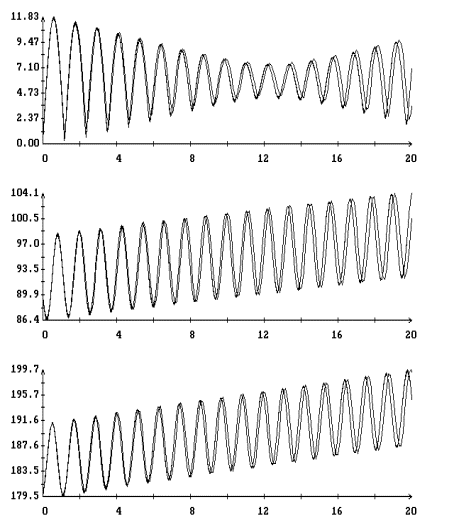

![]() (сут)
(сут)
![]() (сут)
(сут)![]() кгм
кгм![]() ,
, ![]() кгм
кгм![]() ;
; ![]() , справа
, справа ![]()
![]() (град.) Углы
(град.) Углы ![]() (град.)
(град.)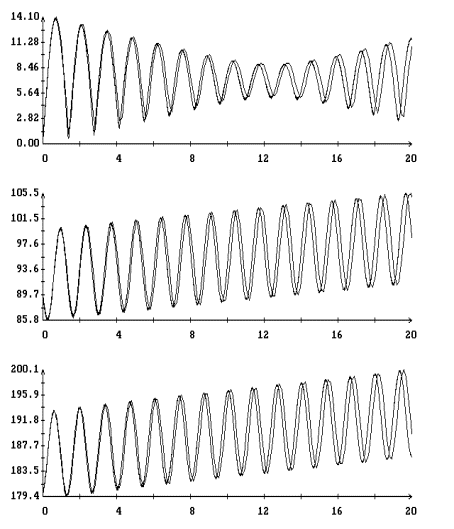
![]() (сут)
(сут)
![]() (сут)
(сут)![]() кгм
кгм![]() ,
, ![]() кгм
кгм![]() ;
; ![]() , справа
, справа ![]()
![]() (град.)
(град.) ![]() ,
, ![]() ,
, ![]()
![]() (сут)
(сут)
![]() (сут)
(сут)![]() кгм
кгм![]() ,
, ![]() кгм
кгм![]() и
и ![]() .
. ![]() (град.)
(град.) ![]() ,
, ![]() ,
, ![]()

![]() (сут)
(сут)
![]() (сут)
(сут)![]() кгм
кгм![]() ,
, ![]() кгм
кгм![]() и
и ![]() .
. ![]() (град.)
(град.) ![]() ,
, ![]() ,
, ![]()
![]() (сут)
(сут)
![]() (сут)
(сут)![]() кгм
кгм![]() ,
, ![]() кгм
кгм![]() и
и ![]() .
. ![]() (град.)
(град.) ![]() ,
, ![]() ,
, ![]()
![]() (сут)
(сут)
![]() (сут)
(сут)![]() кгм
кгм![]() ,
, ![]() кгм
кгм![]() и
и ![]() .
. ![]() (град.) Углы
(град.) Углы ![]() (град.)
(град.)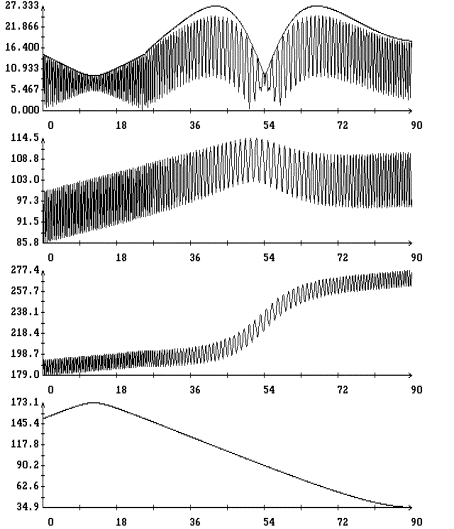
![]() (сут)
(сут) ![]() (сут)
(сут)![]() кгм
кгм![]() ,
, ![]() кгм
кгм![]() и
и ![]() ;
; ![]() , справа
, справа ![]() .
. ![]() (град.) Углы
(град.) Углы ![]() (град.)
(град.)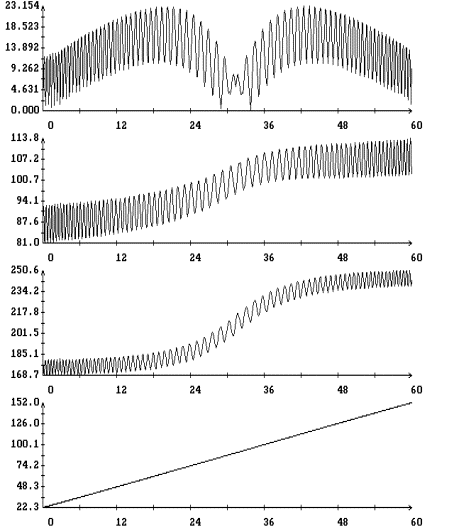
![]() (сут)
(сут) ![]() (сут)
(сут)![]() кгм
кгм![]() ,
, ![]() кгм
кгм![]() и
и ![]() ;
; ![]() , справа
, справа ![]() .
. ![]() (град.) Углы
(град.) Углы ![]() (град.)
(град.)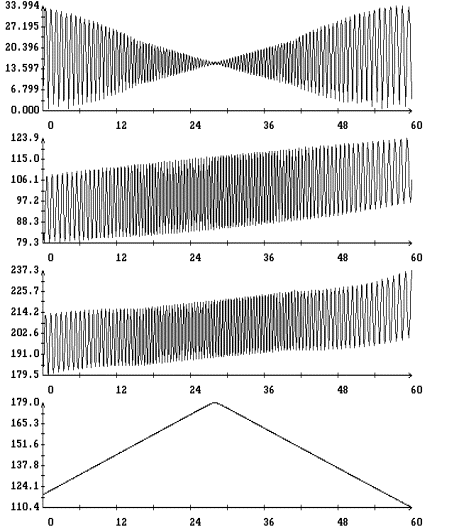
![]() (сут)
(сут) ![]() (сут)
(сут)![]() кгм
кгм![]() ,
, ![]() кгм
кгм![]() и
и ![]() ;
; ![]() , справа
, справа ![]() .
. ![]() (град.) Углы
(град.) Углы ![]() (град.)
(град.)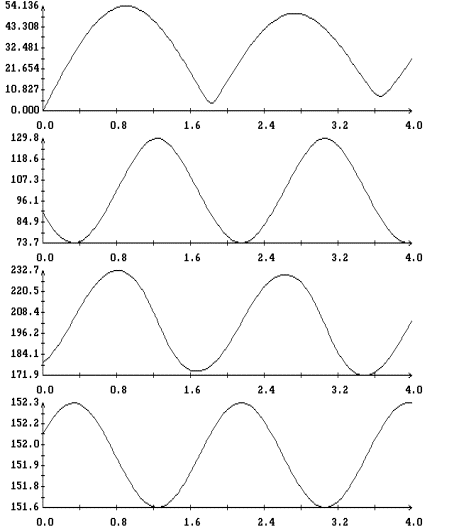
![]() (сут)
(сут) ![]() (сут)
(сут)![]() кгм
кгм![]() ,
, ![]() кгм
кгм![]() ,
, ![]() и
и ![]() ;
; ![]() , справа
, справа ![]() .
. ![]() (град.) Углы
(град.) Углы ![]() (град.)
(град.)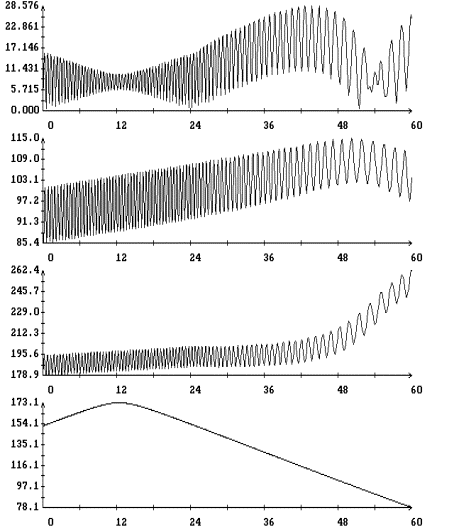

![]() (сут)
(сут) ![]() (сут)
(сут)![]() кгм
кгм![]() ,
, ![]() кгм
кгм![]() ,
, ![]() и отсутствии
и отсутствии ![]() , справа
, справа ![]() .
.