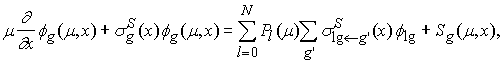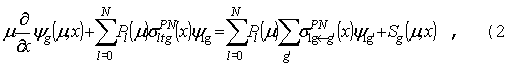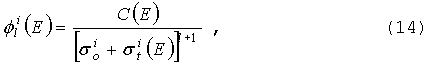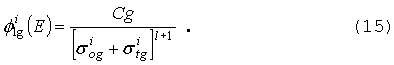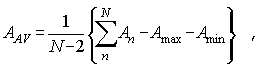GNPDL-30/19: БИБЛИОТЕКА НЕЙТРОННО-ФОТОННЫХ ГРУППОВЫХ КОНСТАНТ ДЛЯ РАСЧЕТА ПОДКРИТИЧЕСКИХ СИСТЕМ С ВНЕШНЕЙ ПОДСВЕТКОЙ
Часть 2. Подготовка макроконстант

(GNPDL-30/19: LIBRARY OF NEUTRON-PHOTON GROUP CONSTANTS FOR ADS CALCULATIONS
Part 2. Preparation of macroconstants
Preprint, Inst. Appl. Math., the Russian Academy of Science)

ОГЛАВЛЕНИЕ

1.  Введение                                                                                                       

2.   Константы уравнения Больцмана                                                                  

2.1 Многогрупповое уравнение переноса                                                     

2.2 Транспортные приближения                                                                   

2.3 Учет резонансной самоэкранировки                                                       

2.4 Поправки на гетерогенность                                                                   

2.5 Поправка в сечение замедления                                                               

2.6 Сопряженная задача                                                                                 

3.   Файл макроконстант и скоростей процессов                                                

3.1 Структура макроконстат                                                                           

3.2 Программа расчета макроконстант TRANSX                                         

3.3 Программы сопровождения и доступа                                                   

4.   Тестовые расчеты                                                                                          

4.1 Критические эксперименты                                                                     

4.2 Подкритический реактор ADS                                                                 

4.3 Сферические пропускания                                                                       

     Литература                                                                                                    

ПРИЛОЖЕНИЕ. Структура файла макроконстант GOXS                           

1.ВВЕДЕНИЕ

Подготовка макроконстант является ответственным этапом переработки данных для использования в задачах расчета переноса излучения, требующим умения учесть геометрические и физические особенности рассчитываемой системы. Это умение базируется на знании физики процесса переноса излучения и методов учета различных эффектов в рамках используемой математической модели. Обычно эти модели закладываются в алгоритмы программ расчета макроконстант, которые оставляют пользователю выбор той или иной опции и заданием соответствующих параметров. В настоящей работе приводится описание методов расчета макроскопических сечений и скоростей реакций, реализованных в программе TRANSX[1]. Эта программа была разработана в Лос-Аламосской национальной лаборатории США для обеспечения ядерными данными программ решения мультигруппового уравнения переноса методом дискретных ординат: ANISN[2], ONEDANT/TWODANT[3], и т.п. Она базируется на формате MATXS, который используют в библиотеке микроконстант GNPDL-30/19.

Ниже изложены основные сведения, необходимые для пользования этой программой TRANSX и корректного внесения поправок на основные физические и геометрические эффекты. В ней также приведены результаты расчетов некоторых бенчмарков, которые здесь следует рассматривать как демонстрационные, а не валидационные, поскольку они не систематизированы и не полны. Описание программы и методов расчета взяты из работы [1].

2. КОНСТАНТЫ УРАВНЕНИЯ БОЛЬЦМАНА

2.1. Многогрупповое уравнение переноса

Мультигрупповое S_N - уравнение переноса в одномерной плоской геометрии имеет вид:

     (1)

где m - косинус угла рассеяния, х - пространственная координата,
f_g(m,x)- поток в группе g, f_lg - l-момент потока, P_l(m) - полином Лежандра,

S_g(m,x)- источник нейтронов в группе.  Сечения в уравнении (1) доджны быть опеределены таким образом, чтобы поток f_g  был максимально приближен к решению уравнения Больцмана. Соответственно мультигрупповое P_N  - уравнение может быть записано в виде:

где P_N - сечения даются следующими выражениями:

 
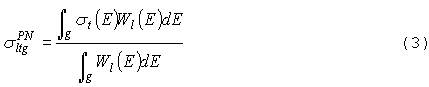
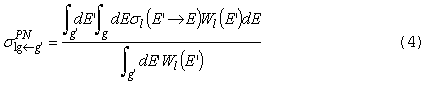
В этих формулах  и  - полное сечение и сечение рассеяния, W_l(E)- весовая функция, максимально приближенная к функции y. Требуемые P_N - сечения содержатся в MATXS - файлах. Из  уравнений (1) и (2) следует, что:

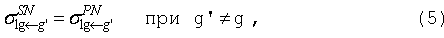
и

где  не определено. Выбор  составляет суть “транспортного приближения”, для которого предусмотрены следующие альтернативы.

2.2. Транспортные приближения

          Удобно переписать уравнение (6) в виде:

          и

Поправочный член в скобках (…) вносит поправку на анизотропию в сечение полного взаимодействия в уравнении Больцмана, выбор параметра  производится таким образом, чтобы минимизировать эффект пренебрежения членами разложения при l=N.

P-согласованное приближение:

P-несогласованное приближение:

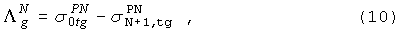
Дигональное транспортное приближение:

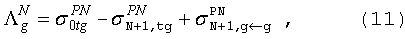
Белл-Хансен-Сэндмайера или расширенное транспортное приближение:

"Обобщенное"транспортное приближение:

Первые два приближения лучше использовать рассеяние порядка выше N мало, причем P-несогласованное приближение устраняет большую часть вклада от дельта-функции рассеяния вперед путем внесения поправки в анизотропию полного рассеяния и обычно сходится лучше, чем согласованное.

Диагональное и Белл-Хансен-Сэндмайера (BHS) приближения корректируют анизотропию в матрице рассеяния и особенно эффективны в случае преимущественного рассеяния вперед. Лучше использовать BHS приближение, но в случаях, когда оно приводит к отрицательным решениям, его следует заменить на диагональное.

"Обобщенное" транспортное приближение позволяет сделать N+1 член P_N-разложения исчезающе малыми, но требует хорошего знания N+1 моментов потока из предварительных расчетов. Это приближение сводится к BHS для систем, находящихся в детальном равновесии (например, в тепловой области). Диффузионное уравнение, использующее  "обобщенное" приближение, эквивалентно P1-транспортному уравнению. Эти поправки требуют данные для (N+1)-го момента сечения.

2.3             Учет резонансной самоэкранировки

          Использование мультигруппового приближения, огрубляющее резонансное поведение сечений, приводит к необходимости учета эффекта резонансной самоэкранировки. В общем случае этот эффект является сложной функцией геометрии и композиции системы. Широкое распространение получила простая модель, получившая название метода Бондаренко, основанная на понятии сечения разбавления. Несмотря на простоту, она дает удивительно хорошие результаты для многих приложений. Согласно этой модели поток для усреднения сечения изотопа i в группе может быть записан в виде (если в смеси присутствуют другие изотопы):

Влияние полного сечения в знаменателе состоит в моделировании провала в потоке в пике резонанса сечения, а сечение разбавления задает относительную глубину провала.

Зависимость от l применима для больших систем с почти изотропным рассеянием (B₀ - приближение) и содержится в данных MATXS. Выражение (14) основано на приближении узкого резонанса и является не вполне корректным для широких низкоэнергетических резонансов, что несущественно для быстрых систем.

Для бесконеченых гомогенных систем соответствующее сечение разбавления вычисляется из уравнения:

где N_i - ядерная концентрация i-го изотопа. Поскольку s_t зависит от s_0,  значение s₀ вычисляется итерациями.

В мультигрупповой форме поток имеет вид:

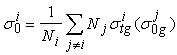                                         (16)

Если некоторое тело из резонансного материала поместить в большую замедляющую среду, утечка нейтронов из него также увеличит сечение разбавления. Это дополнительное сечение утечки описывается формулой:

где ` - средняя длина хорды для тела, вычисляемая по формуле:

V и S - объем и площадь поверхности тела (например, для цилиндра  =2r )

Средняя хорда  может быть вычислена из соотношения (18) с учетом наличия других тел (поправка Данкова ) или, исходя из вероятности - уравнение (17) (фактор Белла). Программа TRANSX обеспечивает вычисление этих поправок исходя из значения параметра `.

          Уравнения (16) и (17)  показывают, что имеется  своего рода эквивалентность между эффектом самоэкранировки вследствии гомогенного присутствия замедлителя, и эффектом, обусловленным конечным размером образца (гетерогенный эффект). Физически для узких резонансов это означает, что если появился нейтрон с энергией, попадающей на поглощающий резонанс изотопа i , он может избежать поглощения либо замедлившись на рассеивающем материале j, либо вылетев за границы образца. Очевидно, что эти эффекты аддитивны, а следовательно для их описания можно использовать один параметр - сечение разбавления.

2.4             Поправки на гетерогенность

          Если тела, стержни или пластины, содержащие резонансный топливный материал, находятся недалеко друг от друга, имеется веоятность, что нейтрон покинув один стержень пройдет сквозь заполняющий материал и прореагирует с топливом в другом стержне. Такое событие эквивалентно тому, как если бы нейтрон вообще не покидал топливного материала. Вероятность утечки при этом уменьшается. Для учета этого эффекта используется поправка Данкова. В программе TRANSX предусмотрены следующие опции:

Аппроксимация Белла для цилиндра:

Аппроксимация Зауэра для цилиндра в гексагональной решетке

          где

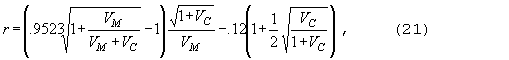
Аппроксимация Зауэра для цилиндра в квадратной решетке:

где

Аппроксимация Белла для плоской ячейки:

E₃ аппроксимация вероятности столкновений для плоской ячейки:

          В этих выражениях l - оптический путь в области замедлителя, , l_L и l_R - оптический пути слева и справа от области, содержащей материал i к слоям с тем же материалом, V_M и V_C - отношения объема замедлителя и оболочки к объему топлива, E₃ - эллиптический интеграл третьего порядка.

Сечение утечки с поправка Данкова в этих случаях имеет вид:

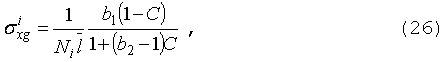
где b₁ и b₂ - так называемые поправки Данкова (обычно принимаемые равными 1.09 для слоя и 1.35 для цилиндра). Если b₁ = b₂, эту константу обычно обозначают A и называют "фактор Левина".

2.5  Поправка в сечение замедления

          Для получения библиотеки групповых констант (2), (3), (4) необходимо выбрать модельную весовую функцию. Реальный поток в рассчитываемых системах может существенно отличаться от принятой модели. Задача усложняется для многозонных системах, в которых поток меняется от области к области. Для векторных сечений (сечений захвата, деления), влияние отличия модельного от реального потока можно уменьшить, сделав группы достаточно узкими. Это не справедливо для упругого замедления на тяжелых ядрах, которое происходит в узком интервале вблизи нижней границы группы. Введем параметр r - отношение потока вблизи нижней граница группы к среднегрупповому потоку. Сечение увода из группы в результате упругого рассеяния очень чувствительно к этому параметру, который может сильно отличаться для модельного и реального потоков. Пренебрегая локальными отличиями этого параметра в группах, в которых проявляются индивидуальные особенности отдельных резонансов, оценим эффективную производную потока в интервале, охватывающим несколько групп. Для многих важных функционалов, например k_эфф , это приближение оказывается достаточно хорошим.

          Запишем увод из группы g в группу g':

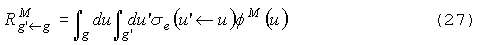
где u - летаргия, s_e -дифференциальное сечение упругого рассеяния, f^M-модельный поток. Запишем отличие истинного потока на нижней границе группы от модельного потока в виде линейного множителя:

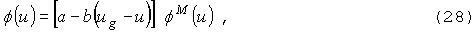
Тогда для скорости увода нейтронов из группы получим:

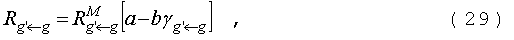
где

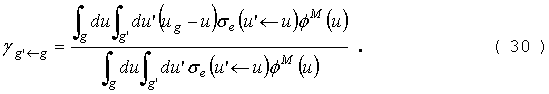
Представим сглаженное отношение потоков в группе g в виде:

Величина   представляет собой константу замедления g используемую для коррекции матрицы упругого рассеяния.

Коэффициенты x₀, x₁, x₂ можно определить методом наименьших квадратов по значениям средних потоков, приписывая их центральным точкам некоторого количества групп, окружающих выделенную группу ( скажем, три сверху и три снизу). Параметры a и b, вычисленные на нижней границе группы и значение сглаженного отношения потоков в центре группы позволяют вычислить искомую поправку в скорость увода.

2.6 Сопряженная задача

Решение сопряженного уравнения переноса используется для вычисления изменений функционалов системы при малых возмущениях, а также для расчета величины возмущения, необходимого для получения требуемого изменения функционала. Сопряженные потоки чаще всего используются для расчета чувствительности функционала к изменениям основных сечений.

Сопряженное уравнение переноса может быть получено из прямого  путем транспонирования матриц рассеяния и деления. Однако при этом рассеяние "вниз" становится рассеянием "наверх". Если обратить порядок подгрупп и одновременно изменить вектор направления на противоположный, нахождение сопряженного потока может быть найдено решением прямого уравнения. Связь прямого и сопряженного решений дается выражением:

3. ФАЙЛ МАКРОКОНСТАНТ И СКОРОСТЕЙ ПРОЦЕССОВ

3.1 Структура макроконстант

Как было показано выше, для решения S_N уравнения (1) требуются набор сечений:

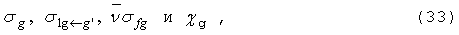
называемый базовым набором (индекс SN  для краткости опущен). Традиционно программы решения уравнения переноса методом SN используют также сечение баланса частиц (или сечение "поглощения"), определяемое как:

Это сечение становится отрицательным, если количество частиц, образующихся в реакциях (n,xn) превосходит количество поглощенных в реакциях (n,g),(n,p),(n,a) и др.

         После того, как поток найден, часто возникает необходимость вычислить такие функционалы, как тепловыделение, смещение на атом, образование газообразных продуктов, образование фотонов, дозу и пр. Для этого в исходной библиотеке помимо базовых, непосредственно входящих в уравнения переноса, должны содержаться некоторые дополнительные сечения, обозначаемые ниже . Традиционно всю эту информацию представляют в форме "транспортных таблиц":

Таблица 1. Структура транспортной таблицы

NED    = число дополнительных сечений (NED і0)

NUP    = максимальное число групп с рассеяние наверх

NTABL  = длина таблицы (NED+4+NUP Ј NTABL Ј NED+4+NUP+NGROUP)

NGROUP = число энергетических групп

IPTOT  = NED+3 = позиция полного сечения

         Транспортные таблица подобного рода требуются для каждой группы, момента, материала. По способу их упорядочивания различают таблицы "материал-группы" и  "группа-материалы". Упорядочивание по материалам естественно в процессе получения групповых констант. Однако, в расчетных программах данные требуются по группам. Схема решения S_N уравнения такова, что сначала требуются все материалы и моменты для 1-й (верхней по энергии) группы, затем для 2-й, и далее, в порядке возрастания номеров групп. При разработке форматов файлов- интерфейсов учитывается эта особенность доступа к данным.

         Одним из наиболее распространенных форматов хранения транспортной таблицы является формат GOXS [2]. Полное описание формата можно найти в Приложении. Здесь же приводятся его краткие характеристики. 

GOXS формат разработан в рамках СССС-стандартов и совместим с форматом MACRXS, используемым в программах ONEDANT/TWODANT. Данные в нем упорядочены по типу "группа-материалы". Так же, как и формат MATXS, материалы и типы взаимодействия именуются в нем с помощью текстовых констант. Количество типов  сечений в нем произвольно и практически неограниченно. Наличие имен позволяет разработчикам программ обеспечивать легко читаемую выдачу результатов.

Матрица рассеяния в файле GOXS упаковывается таким образом, чтобы минимизировать количество нулей.

Такие программы, как ONEDANT/TWODANT используют эту возможность.

3.2    Программа расчета макроконстант TRANSX

Программа TRANSX предназначена для получения таблиц констант для решения многогруппового уравнения переноса нейтронов, фотонов и других частиц методом дискретных ординат (SN) и диффузионного уравнения. Входной библиотекой для нее служит библиотека в формате MATXS. При получении констант учитываются эффекты гомогенной и гетерогенной резонансной самоэкранировки, рассеяние в области термализации, деление на мгновенных нейтронах и в установившемся процессе; предусмотрено использование различных поправок в транспортное сечение, в упругое рассеяние. Имеется возможность получения скоростей комбинации процессов как для отдельных материалов, так и их смесей, свертки групп с заданным потоком, гомогенизация сечений, получение констант для сопряженной задачи.

 Исходные данные

  карта 1   заголовок задачи -

             текст до 72 символов без ограничителей

            stop - остановка задания

  карта 2   опции

   iprint   печать (0=полная/1=сокращенная)

   iout     выходной формат

             0   не требуется

             1   типа card (6e12)

             2   claw - сard с вынесенным в начало блоком сечений

             3   fido - компактная запись повторяющихся чисел

             4   anisn - fido с фактором 2*l+1

             5   goxs - бинарный упорядоченный по группам

             6   isotxs - бинарный упорядоченный по материалам, стандарт cccc-iv

             7   anisnb - бинарный anisn

             8   anigif - упорядоченный по группам бинарный anisn

   iprob    задача (0=прямая/1=сопряженная)

   iset     iset=i - простая таблица констнат для частицы типа i,

              iset=ij - составная таблица констант для частиц i и j,

              iset=ijk - составная таблица константd для 3-х частиц и т.д.

   iform    iform - тип упорядоченности: 1=по материалам/2=по группам

   itime    время деления (1=стационарное/2=мгновенное)

   idecay   время распада (не используется)

   itrc     транспортная поправка

             0   отсутствует

             1   p-согласованная

             2   диагональная

             3   Bell-Hansen-Sandmeier

             4   «обобщенная»

             5   p-несогласованная

   icoll    свертка (0=нет/nfine=да)

   initf    способ ввода потока для свертки

             0   использовать блиотечный для p0 потока

             1   прочитать p0 поток с карт

             2   файл rtflux -полный поток в стандарте cccc-iv

             3   файл rzmflx - моменты потока по зонам

             4   rzflux - поток в зонах в стандарте cccc-iv

           12-14 признак ввода карты соответствий поток-область

            -n   ввести поправку на форму спектра внутри группы в сечение
                 рассеяния

        для последних 5 пунктов, по умолчанию активен первый пункт

  карта 3   параметры

   ngroup   число групп в таблице

             ngroup<0 - материалы заданы в виде отдельных файлов

   nl       число моментов

   ntabl    длина таблицы

   nup      число групп с рассеянием наверх

   nthg     число тепловых групп

   nmix     число материалов или смесей на выходе
   nreg     число областей

   nmixs    число описателей смеси

   ned      число дополнительных выходных величин

   neds     число описателей выходных величин

  карта 3a (если ngroup < 0)

   mpath    путь к директории с файлами matxs ( до 24 символов)

  карта 4   имена смесей

   hmixn    nmix тексовых имен mix (до 6 символов)

  карта 5   описание областей и гетерогенности

   hregn    имя области (до 6 символов)

   rtemp    температура области (k) (по умолчанию=300)

   rvol     объем области  (по умолчанию=1.)

   ihet     тип гетерогенности (по умолчанию=0=самоэкранировка отсутствует)

             0   самоэкранировка отсутствует
             1   постоянное сечение утечки

             2   аппроксимацией Белла для цилиндра

             3   цилиндр в гексогональной решетке с аппроксимацией Зауера

             4   цилиндр в квадратной решетке с аппроксимацией Зауера

             5   плоская ячейка с аппроксимацией Белла (отражение)

             6   плоская ячейка с  аппроксимацией (отражение)

             7   плоская ячейка с аппроксимацией Белла (периодическая)

             8   плоская ячейка с  аппроксимацией (периодическая)

            -n   продолжение описания ячейки

          последущие параметры на карте 5 определяются значением ihet.
          Эти величины задаются только для первой области каждой ячейки.

   -- ihet=1 -- утечка постоянная

   chord    - длина средней хорды (см)

   -- ihet=2 до 8 -- поправка Данкова

   bell1    поправка Белла для рациональной аппроксимации.

   bell2    поправка Белла в знаменателе

        повторить карту 5 nreg раз

  карта 6   карта соответствий ( |initf| і 12)

            для потоков в точках, зонах, областях из входного файла
            указываются соответствия каждой области (nreg целых)

  карта 7   описание смесей

   imix     номер смеси (от 1 до nmix)

   ireg     номер области

   hmix     имя изотопа в библиотеке matxs

   dens     множитель (концентрация или плотность) (по умолчанию=1)

   hinc     имя тепловых данных по неупругому рассеянию (по умолчанию=пробел),
            или признак принадлежности сечения

            ("rc" - принадлежит области,  "cc" - ячейке)

   hcoh     имя тепловых данных по упругому рассеянию (по умолчаниюl=пробел)

   hmod     тип взаимодействия для матрицы (по умолчанию=пробел=полная)

         поторить карту 7 nmixs раз

  карта 8   имена выходных величин

   hed      ned  текстовых имен (не более 6 символов)

  карта 9  описания величин

   jedpos   ее положение в списке (обычно в диапазоне от 1 до ned)

             (-n означает влючение запаздывающих фотонов в группу n
              составной таблицы констант)

   hednam   имя типа взаимодействия в библиотеке matxs

   edfact   множитель (по умолчанию=1)

   hedmat   имя изотопа в библиотеке MATXS (по умолчанию=пробел)

            если пробел - используются макроданные (сумма по всем изотопам)

         повторить карту 9 neds раз

  карта 10   описание свертки ( icoll > 0 )

        указывается число узких групп в каждой широкой группе

  карта 11  поток - весовая функция (если initf=1)

   inwt     поток в узких группах для всех моментов и областей

  специальные имена

   hed=*chi*      спектр деления chi

   hednam=*chi*   то же самое

   hed=*trd*      транспортное сечение для уравнения диффузии. Если задан или
                  рассчитан момент потока p1, используется inflo определение,

                  в противном случае - outflo.

   hednam=*trd*   то же самое

   hed=*gam*      первое из ngg данных для фотонов.

3.3    Программы сопровождения и доступа

Для расширения области применимости предлагаемой системы констант и облегчения ее адаптации к другим вычислительным системам, для выходных файлов констант разработано программное обеспечение аналогичное тому, которое имелось для файлов MATXS.
Mod_goxs - программа модификации типа представления бинарный/текстовый и наоборот; запрашиваемый параметр  nmod определяет тип выходного файла goxs:
 nmod = 0 - бинарный,

  = 1 - текстовый.
Используемые файлы:
  goxs - бинарный файл,
  text - текстовый файл.

Get_goxs- процедура поиска данных в файле GOXS и записи нужного фрагмента в буферный массив. Контрольные параметры данных  заносятся в область данных

COMMON /BGETGOXS/  NMAT,NGROUP,NORD
NMAT        - число материалов,
NGROUP - число групп,

NORD         - число моментов.

Вызов процедуры:

call Get_goxs(NAME,kg,ig,l,array)
Входные параметры
NAME - текстовая константа (A8) - имя данных, может принимать одно из следующих значений:
energy  - групповые границы (эB)

d       - коэффициент диффузии

siy     - сечение увода

nsf     - `ns_f

chi     - спектр деления

sit     - полное сечение

sie     - сечение упругого рассеяния

sif     - сечение деления

sic     - сечение захвата

siz0    - сечение замедления

sigs    - сечение расcеяния "в себя"

sigtr0  - матрица замедления P₀  

sigtr1  - матрица замедления P₁

sigpq   - матрица замедления P_N

sigel0  - матрица упругого рассеяния P₀

micro   - дополнительные сечения
         (специальные величины, скорости реакций и пр.)

kg - номер группы

Выходные данные:

ig - номер верхней по энергии группы-источника
     (только для матриц рассеяния)                    

l - длина вектора данных

array(l) - вектор данных

4. ТЕСТОВЫЕ РАСЧЕТЫ

4.1 Критические эксперименты

Расчеты критических экспериментов проводились по программе ANISN-OR в P5/S16 приближении.  Сравнивались эффективные коэффициенты размножения и центральные спектральные индексы. Обозначения: F- деление, 23-²³³U, 25-²³⁵U, 28-²³⁸U, 37-²³⁷Np, 49-²³⁹Pu. В скобках при названиях сборок указаны их идентификационные номера в соответствии с документом [4].

GODIVA (HEU-MET-FAST-001): сфера из обогащенного урана без отражателя.

Состав:

   Имя элемента    Ядерная концентрация в  ×10²⁴

        ²³⁴U                        4.9184-4
        ²³⁵U                        4.4994-2
        ²³⁸U                        2.4984-3
Радиус сферы: R = 8.741 см

                    эксперимент                 расчет 
Kэфф          1.000 ± 0.001                   0.9987
F23/F25       1.59                                1.5900
F28/F25       0.1647                            0.1582
F37/F25       0.837                              0.8029

F49/F25       1.402                              1.3785

JEZEBEL (PU-MET-FAST-001): сфера из металлического плутония без отражателя;

Cостав:

Имя элемента       Ядерная концентрация в  ×10²⁴

        ²³⁹Pu             0.03705

        ²⁴⁰Pu             0.001751

        ²⁴¹Pu             0.000117

        Ga                0.001375

Радиус сферы: R = 6.385 см

                    эксперимент                 расчет 
Kэфф          1.000 ± 0.002                   0.9972
F28/F25       0.2137± 0.0023                0.2044
F23/F25       1.578 ± 0.027                   1.5773
F37/F25       0.962 ± 0.016                   0.9295

F49/F25      1.448 ± 0.029                   1.4188

4.2 Подкритический реактор ADS

           Подкритический реактор  ADS c топливом ²³³U+²³²Th и свинцовым теплоносителем был принят в качестве бенчмарка в международном тесте, в котором принимали участие ряд европейских стран - Франция, Италия, Германия, Нидерланды, Швеция, а также Россия и Япония. Условия теста подробно описаны в работе [5], ниже приведена только часть, касающаяся первого пункта, а именно:

определение относительной концентрации ²³³U в топливных зонах реактора I,II  в смеси ²³³U+²³²Th, обеспечивающей при начальной загрузке реактора критичность 0.94, и 0.98.          Расчеты проводились на основе сформированной 30-групповой библиотеки групповых констант  GNPDL-30/19 в P1/S8 приближении. Файл макроскопических констант готовился с помощью программы TRANSX. В качестве расчетной программы  была использована программа TWODANT[3]. 

          На рис.1 приведены размеры и расположение зон реактора ADS при температуре 20°C. Состав зон 1-5 указан в таблице 1. В таблице 2 приведены относительные концентрации ²³³U в смеси ²³³U+²³²Th, полученные различными участниками теста, их среднее значение и результаты настоящей работы. Как видно из таблицы, полученные концентрации наиболее близки к среднему значению (при усреднении результаты настоящей работы не учитывались):

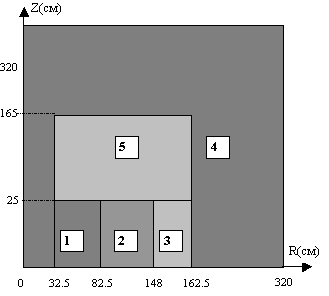
       Рис.1 Геометрия реактора ADS при 20°С

Таблица 1. Ядерные концентрации при 20°С×10²⁴

Таблица 2. Обогащение ²³³U в областях 1,2 при начальной загрузке реактора ADS (%)

Таблица 2. Продолжение

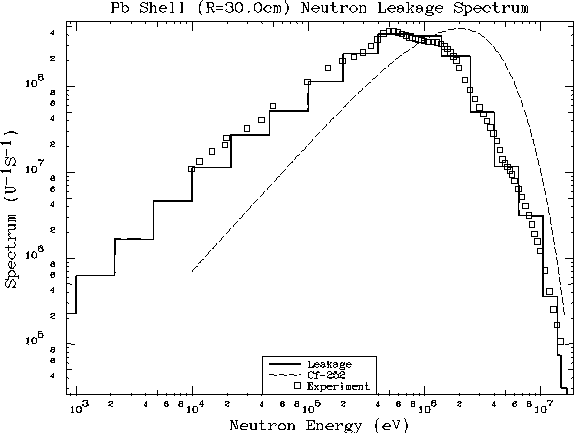
4.3    Защитные эксперименты

ЛИТЕРАТУРА

1.  R.E.MacFarlane "TRANSX-2: A Code for Interfacing   MATXS   Cross-Section     Libraries to  Nuclear  Transport  Codes",LA-12312-MS(1992)

2.  W.W.Engle,Jr.,"A User's Manual for ANISN: A One-Dimensional Discrete Ordinates Transport Code with Anisotropic Scattering", Oak Ridge Gaseous Diffusion Plant Computing Technology Center report K-1693(1967)

3.  “TWODANT - One- and Two- Dimensional, Multigroup, Discrete-Ordinates Transport Code System”,  - RSIC Computer Code Collection, Code Number CCC-547, ORNL,1990

4.  “Evaluated Criticality Safety Benchmark Experiments”, Handbook NEA/NSC/DOC(95)03

5.  “IAEA-ADS benchmark(Stage 1). Results and preliminary analysis”.
Proc. RCM-Meeting, Bologna, March 24-26,1997

Приложение. Структура файла макроконстант GOXS.

 cs          структура файла

cs

cs              тип записи                          наличие

cs              ==============================    ===============

cs              заголовок файла                     всегда

cs              параметры файла                     всегда

cs              данные файла                        всегда

cs   *************(в цикле по группам)

cs   *          групповая структура                 всегда

cs   *          сечения                             всегда
cs   *          параметры рассеяния                 всегда
cs   *          данные рассеяния                    всегда
cs   *************

c

c  ---------------------------------------------------------------

сr               заголовок файла
с

cl       hname,(huse(i),i=1,2),ivers
c
cw     1+3*mult
c
cs      format(4h 0v ,a8,1h*,2a8,1h*,i6)

c

cd      hname - текстовое имя файла - GOXS - (A8)

cd      huse  - текстовое имя пользователя (A8)

cd      ivers   - номер версии файла

cd      mult   - параметр двойной точности

cd                         1- A8 - одинарное слово

cd                         2- A8 - двойное слово
с
c  ---------------------------------------------------------------

с
c  ---------------------------------------------------------------

сr               параметры файла
c
cl       ngroup,nmat,nord,ned,idpf,lng,maxup,maxdn,nprin,i2lp1
c       
cw     10
c
cd      ngroup - число групп
cd      nmat  - число материалов
cd      nord   - порядок разложения по полиномам Лежандра
cd      ned    - число требуемых сечений
cd                         ( дополнительно к базовым )
cd      idpf    - признак двойной точности для сечений и матриц
cd                         (1/2 = одинарная/двойная)
cd      lng     - номер последней нейтронной группы для составных таблиц
cd      maxup         - максимальное число групп с рассеяниям вверх
cd      maxdn         - максимальное число групп с рассеянием вниз
cd      nprin  - число базовых сечений (0,4 или 6)
cd      i2lp1  - наличие в данных множителя 2l+1 (0/1 = нет/да)
c
c-----------------------------------------------------------
c

c-----------------------------------------------------------
cr                          данные файла
c
cl       (hmat(i),i=1,nmat),)hed(j),j=1,nedt),(vel(k),k=1,ngroup),
cl   1(eg(k),k=1,ngroup),emin
c
cw     (nmat)+ned)*mult+2*ngroup+1
c
cd      hmat(i) - текстовое имя материала
cd      hed(j)  - текстовые имена дополнительных сечений
cd      vel(k)  - средняя скорость для группы k (см/сек)
cd      eg(k)    - верхняя граница энергии для группы k (эВ)
cd      emin     - нижняя граница энергии для группы k (эВ)
cd      nedt     - ned+nprin
c
c-----------------------------------------------------------
c
c-----------------------------------------------------------
cr                          сечения
c
cl       ((edxs(i,j),i=1,nmat),j=1,nedt_
c
cw     nmat*nedt
c
cd      edxs(i,j) - сечения. В зависимости от признака NPRIN
cd                         всегда присутствуют следующие типы сечений:
cd               NPRIN=4
cd                         TOTAL  - полное транспортное сечение
cd                         ABS  - балансное сечение поглощения
cd                         NUSIGF - произведение ns_f
cd                         CHI   - спектр деления
cd               NPRIN=5 дополнительно к перечисленным задается
cd                         TRD  - диффузионное транспортное сечение
c
c--------------------------------------------------------------
c
c--------------------------------------------------------------
cr                          параметры данных по рассеянию
c
cl       ((njj(l,i),l=1,nord),i=1,nmat),
cl   1((ijj(l,i),l=1,nord),i=1,nmat)
c
cw     2*nord*nmat
c
cd      njj(l,i) - число групп в блоке
cd      ijj(l,i)  - первая группа в блоке
c
c-------------------------------------------------------------
c
c-------------------------------------------------------------
cr                          данные по рассеянию
c
cl       (scat(i),i=1,ntab)
c
cw     ntab
c
cd      scat(k)         - данные по рассеянию
cd      ntab             - сумма njj(l,i) по l от 1 до lord
cd                                               и по i от 1 до nmat
c
c------------------------------------------------------------