Динамика инвестиционного процесса: анализ и прогноз

Введение

Задача прогнозирования хода торгов на фондовом рынке не теряет своей актуальности с момента возникновения самого фондового рынка и биржи, как механизмов организации и управления инвестиционными процессами. На сегодняшний день традиционными подходами к построению биржевых прогнозов считаются технический и фундаментальный анализ. Однако прогнозы, полученные на основе классических методов технического анализа, зачастую противоречат друг другу и ставят потенциального инвестора в тупик. Кроме того, кризисные ситуации, возникающие в последнее время на различных финансовых рынках по всему миру, свидетельствуют об отсутствии эффективных методов управления фондовым рынком.

Таким образом, создание методики достоверного прогнозирования хода инвестиционного процесса преследует две цели:

а) поддержка принятия решений отдельными участниками торгов при проведении операций на фондовом рынке;

б) принятие адекватных мер по управлению самим рынком.

Одним из наиболее эффективных подходов к построению предсказывающей системы является создание математической модели исследуемого процесса. Однако при анализе сложных явлений традиционные методы математического моделирования оказываются неприменимыми. В первую очередь, это связано с необходимостью формального описания поведения большого количества людей – сложных рефлексирующих субъектов, алгоритмы поведения которых, вообще говоря, неизвестны. В подобных исследованиях все большую популярность в последнее время приобретает синергетика (теория самоорганизации) [3]. Основная идея этого междисциплинарного подхода состоит в том, что многие сложные явления могут быть описаны с помощью сравнительно небольшого числа “главных” переменных – параметров порядка, которые и определяют динамику процесса в целом. При этом с течением времени остальные переменные “подстраиваются” под главные. Возникает явление самоорганизации.

Такая концепция, действительно, кажется крайне привлекательной: при рассмотрении реальных ситуаций, таких как хаотическое взаимодействие большого количества людей в ходе инвестиционного процесса, выделение основных групп (параметров порядка) из огромной массы участников торгов могло бы существенно упростить модель исследуемой ситуации. Попытки разделить множество биржевых игроков на группы со сходным поведением предпринимались и в техническом анализе. Так, биржевая толпа условно делилась на “быков”, которые поднимали цену, скупая акции, и ”медведей”, которые толкали рынок вниз.

Что же касается хаотичности исследуемого процесса, то в нелинейной динамике показано, что хаотическое поведение может быть описано с помощью довольно простых детерминированных систем. Качественные и количественные характеристики хаоса подробно рассмотрены, например, в [1]. С позиций нелинейной динамики удается исследовать различные явления в физике, химии, биологии, социологии, экономике и многих других областях современной науки, рассматривая лишь простейшие базовые модели. Кроме того, на основе методов нелинейной динамики разработаны эффективные алгоритмы анализа временных рядов, что позволяет надеяться на возможность определения характеристик системы исходя только из экспериментальных данных.

Однако при рассмотрении реальных ситуаций зачастую возникает необходимость существенного увеличения размерности фазового пространства (пространства решений). При этом традиционные методы нелинейной динамики, позволяющие определить важнейшие характеристики динамических систем (размерность аттрактора, энтропии, ляпуновские показатели) оказываются неприменимыми [2]. При анализе временных рядов возникают проблемы построения достаточно сложных отображений в многомерных пространствах. Эти отображения практически невозможно построить аналитическими методами. На помощь приходит компьютерное моделирование. С помощью нейронных сетей, смоделированных на ПК, удается строить сколь угодно сложные функциональные зависимости. Точнее сказать, сложность создаваемого отображения ограничивается только техническими возможностями ЭВМ. Нейронная сеть в таком случае работает как автомат, способный самостоятельно находить функцию зависимости ответа от нескольких входных параметров: [7, 9].

В настоящей работе предпринята попытка объединения идей синергетики, нелинейной динамики и нейронауки. На основе представлений синергетики удается сформировать концептуальную картину хода инвестиционного процесса, как процесса хаотического взаимодействия людей, в котором проявляются как организующее начало, так и самоорганизация. Принципиальная возможность прогнозирования хода такого процесса показана в нелинейной динамике. В качестве инструмента построения краткосрочных прогнозов используется многослойная нейронная сеть, которую можно рассматривать также и в качестве математической модели исследуемого процесса. Предложенная в настоящей работе методика проходит тестирование на одной из базовых моделей нелинейной динамики – системе Лоренца, а затем применяется и для прогнозирования хода торгов по акциям РАО ЕЭС России и индексам Доу Джонса. Результаты прогнозирования сравниваются с результатами, полученными на основе традиционных методов технического анализа. Кроме того, исследуется возможность составления смешанных обучающих выборок, а также оценки размерности предполагаемого аттрактора на основе результатов обучения нейросети. 

1. Постановка задачи

Исходные данные представляют собой обыкновенную базу данных – электронную таблицу, в которой содержатся ежедневные котировки акций, включающие цены открытия и закрытия торгов, минимальную, максимальную и среднюю цену акции, зафиксированные в течение торгового дня, а также объем торгов. Таблица содержит около 600 записей (строчек), что соответствует временному периоду около двух лет (Табл. 1).

…………………………………………………………………………

Табл.1. Исходные данные

Проблема состоит в определении цены акции на несколько дней вперёд, исходя из имеющихся данных за прошедший временной период. Не менее важным результатом считается оценка возможности возникновения тренда.

В графическом виде данные представлены на рис.1.1. Традиционно объем торгов представляется в виде столбчатой диаграммы, а цены – в виде вертикальных штрихов с отметками значения закрытия торгов.

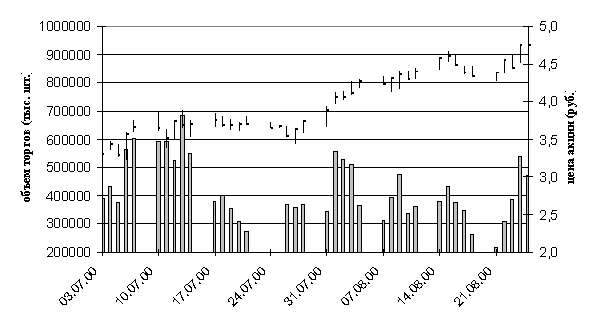
Рис. 1.1 Графическое представление исходных данных

Далее приводится формализованная постановка задачи, которая предполагает возможность описания процессов, протекающих на фондовом рынке посредством динамической системы с хаотическим поведением.

Пусть дан некоторый объект, описываемый системой уравнений вида

, , .                  (1)

Пусть одну из характеристик этой системы, например, s-ю компоненту вектора  (вообще говоря, некоторую функцию состояния системы ) мы измеряем в моменты времени . Это даёт временной ряд наблюдений  Задача прогноза или задача построения предиктора по временному ряду состоит в определении  по множеству . Число l будем называть горизонтом прогноза или дальновидностью предиктора.

Данные, приведенные в Табл. 1., представляют собой временные ряды некоторых характеристик исследуемого явления. Таким образом, мы имеем дело с задачей анализа свойств системы по ее временному ряду.

Существенные успехи, связанные с анализом временных рядов, были достигнуты в нелинейной динамике [1]. Рассмотрим некоторые методы нелинейной динамики более подробно.

2. Подход нелинейной динамики

Существует множество задач, где интегрирующихся уравнений написать невозможно, а проблема поведения решения на сколь угодно больших временах остается. В этом случае можно попытаться выяснить свойства решений дифференциального уравнения, не решая его. Основным понятием такой теории становится динамическая система (ДС), которая является по сути обобщением автономной системы дифференциальных уравнений и включает в себя два основных компонента: фазовое пространство P, точки которого представляют решение системы уравнений на различных начальных данных и однопараметрическую непрерывную или дискретную группу его преобразований  или ,  или Z. Переход к геометрической трактовке приводит к тому, что многие основные термины носят геометрический смысл - траектория, множество, многообразие, размерность и т. д. Одним из основных терминов является понятие аттрактора – притягивающего множества в фазовом пространстве, к которому сходятся траектории ДС на асимптотической стадии.

Наличие аттрактора у исследуемой системы является следствием процесса самоорганизации: c течением времени все переменные системы “подстраиваются” под главные – параметры порядка, которые задают положение и форму аттрактора. При рассмотрении реальных явлений, когда из множества возможных характеристик явления в распоряжении исследователя оказывается лишь временной ряд, существование аттрактора можно только предполагать. Далее можно применить методы нелинейной динамики и сопоставить полученный результат с теорией. Поступим именно таким образом.

2.1. Основные черты хаотических режимов

Поверхностный анализ исходных данных нашей задачи оставляет впечатление “хаотичности” исследуемого процесса (несмотря на это некоторые игроки все же пытаются отыскать циклические закономерности на бирже, такие попытки, как правило, не имеют успеха). Однако в нелинейной динамике существует множество примеров динамических систем, когда за видимой простотой исследуемой модели скрывается полная непредсказуемость ее поведения. Получается, что динамическая система объединяет в себе глобальную устойчивость (траектория не уходит из области аттрактора) с локальной неустойчивостью – малые погрешности начальных данных нарастают, близкие траектории расходятся. Расстояние l между траекториями при малых l обычно увеличивается экспоненциально, , где  называется ляпуновским показателем. Таким образом, если в начальный момент времени мы знали состояние системы достаточно точно, с малой ошибкой, то со временем ошибка начнет нарастать, и спустя некоторое время, зависящее от , окажется, что на больших временах характеризовать систему можно только указав вероятность появления траектории в окрестности некоторой точки.

 Итак, мы обнаруживаем существование принципиальных ограничений на горизонт прогноза. Различные оценки времени предсказуемости , в основном, сводятся к соотношению:

,

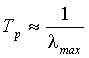где  - старший ляпуновский показатель исследуемой динамической системы.

Существует ли принципиальная возможность предсказания поведения динамической системы по временному ряду?

2.2. Теорема Такенса и возможность достоверного прогноза

Рассмотрим ДС вида  в предположении, что через любую точку фазового пространства x проходит только одна траектория, и если в момент  траектория оказалась в точке , то в момент  она окажется в точке , причём зависит от  и , но не от . Т. е. существует отображение , переводящее  в : .

Тогда члены обрабатываемого временного ряда

можно представить как

……………………………………………

Т. о. если ввести новый m-мерный вектор

,

то должна существовать функция , зависящая только от исходной динамической системы (т. е. функций f или ) и параметров m и , такая что .

Возникает вопрос, нельзя ли обратить функцию , т. е. выразить неизвестный вектор  через известный z? Аналитически это сделать не удаётся, но Ф. Такенсом была доказана теорема, которая утверждает, что почти для всех  и , где d – размерность аттрактора, отображение  будет взаимно однозначным и непрерывным. Если же в пространстве z-векторов выделить множество, на которое отображаются вектора x, то на этом множестве отображение будет обратимым, и можно условно записать .

Подставив выражение для x в соотношение , мы получим

для всех k.

Найти саму функцию F аналитическими методами не удаётся. Важно, однако, что такая функция в принципе существует, и её свойства можно попытаться определить по измеренному временному ряду.

При моделировании ДС на основе нейронной сети временной ряд данной системы рассматривается в качестве исходных данных. Цель обучения нейросети – определить свойства функции F и вычислить m-ю компоненту временного ряда по m-1 предыдущим.

2.3. Построение предиктора

Пусть требуется построить предсказывающую систему (предиктор) с дальновидностью 1 шаг по исходной выборке, т. е. требуется вычислить N+1-ю величину  временного ряда  данной системы по N предыдущим. Для решения задачи будем применять трёхслойную нейронную сеть с   нейронами на входном слое и  нейроном на выходном. В таком случае входные данные представляется в виде m-1-мерных z-векторов. Компоненты z-векторов  подаются на  входных нейронов соответственно (k в процессе обучения выбирается произвольно по выборке на каждом шаге обучения). На выходной нейрон в качестве желаемого результата в процессе обучения подаётся величина . Согласно теореме Такенса, для некоторых значений m должна существовать такая функция F, что

Таким образом, после завершения процесса обучения нейронная сеть предположительно “умеет” вычислять функцию F. Теперь, если мы хотим продолжить временной ряд, достаточно подать на вход сети  компоненты временного ряда и получить на выходе искомую величину - .

Далее, если ставится задача более долгосрочного прогноза, т. е. нахождения величин , можно поступать следующим образом: каждое полученное на выходе значение h использовать в качестве входного на следующем шаге при тестировании. Например, для получения значения  требуется подать на вход величины  и т. д.

При тестировании с целью проверки качества обучения нейросети значения , полученные в качестве прогноза, сравниваются с заранее известными значениями временного ряда.

3. Прогнозирование временного ряда системы Лоренца

Хаотическое поведение может наблюдаться в весьма простых системах, таких как система трех обыкновенных дифференциальных уравнений. В исследованиях по динамическому хаосу основной моделью и объектом испытания множества методик служит т. н. “система Лоренца”:

Траектории этой системы при всех положительных значениях параметров  входят в некоторую сферу в фазовом пространстве X, Y, Z, т. е. у системы существует аттрактор и находится он внутри этой сферы.

При численных расчетах для значений параметров  можно наблюдать нерегулярные колебания. Несложно также составить временной ряд наблюдений данной системы, вычисляя, скажем, x-координату через одинаковые промежутки времени .

На рис. 3.1 и 3.2 представлен нормированный временной ряд системы Лоренца, а также результаты прогнозирования значений ряда, полученные с применением трёхслойной нейронной сети, обучаемой по алгоритму обратного распространения ошибки [ФАК].

С помощью этого предиктора удается довольно точно предсказывать значения временного ряда на протяжении около 28 витков аттрактора системы Лоренца, однако дальше траектории расходятся вследствие хаотичности поведения. Величина горизонта прогноза определяется старшим показателем Ляпунова, а также точностью, с которой вычислялись значения временного ряда. Таким образом, число 28 является горизонтом прогноза системы Лоренца для точности вычисления значений временного ряда 8-ого порядка.

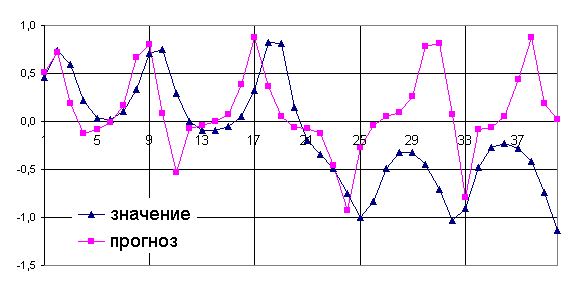
Рис. 3.1 Прогнозирование значений временного ряда системы Лоренца

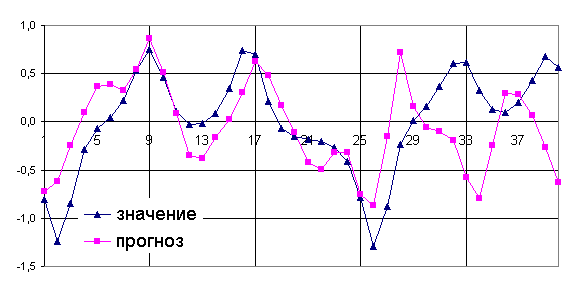
Рис. 3.2 Прогнозирование значений временного ряда системы Лоренца

Удовлетворительные результаты прогнозирования поведения одной из базовых моделей нелинейной динамики – системы Лоренца вселяют надежду в успех применения методики к анализу других временных рядов. Проведенный эксперимент также подтверждает возможность применимости нейросетевых методов для краткосрочного прогнозирования хода хаотических процессов.

4. Прогнозирование курса акций РАО ЕЭС России

Рассмотренная выше методика была применена для создания предсказывающей системы, предназначенной для прогнозирования курса акций РАО “ЕЭС России”. В качестве предиктора использовалась трехслойная нейронная сеть, обучаемая по алгоритму обратного распространения ошибки (см. приложение 1).

Методика проходила тестирование в режиме реального времени на протяжении около 6 месяцев. Опытным путем был установлен оптимальный горизонт прогноза – одна неделя. После сравнения недельного прогноза с реальными данными, сеть “подучивалась” на выборке, включающей данные за прошедшую неделю. Далее строился прогноз на следующую неделю.

На рисунках 4.1-4.4 представлены результаты прогнозирования дневной цены закрытия торгов по акциям РАО “ЕЭС России”. В качестве обучающей выборки использовался временной ряд цен закрытия за прошедший временной период.

Рис. 4.1 Прогнозирование курса акций РАО “ЕЭС России”

Т. к. число обучающих параметров и нейронов модели невелико, мы описываем динамическую систему сравнительно небольшой размерности. Детальный анализ результатов тестирования позволяет сделать вывод применимости такого подхода и возможности описания взаимодействия людей в ходе инвестиционных процессов как процесса самоорганизации. Однако, в некоторых случаях ход этого процесса может нарушаться под воздействием “сторонней силы”, появление которой невозможно выявить исходя лишь из имеющихся данных.

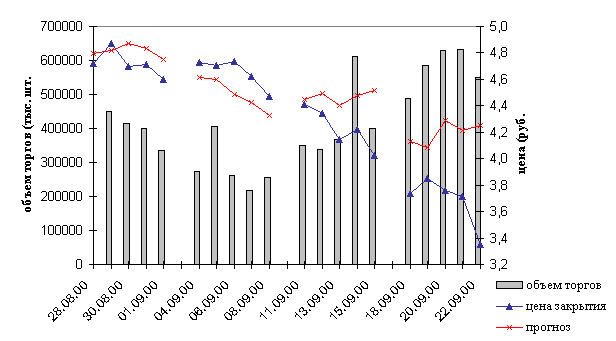
Рис. 4.2 Прогнозирование курса акций РАО “ЕЭС России”

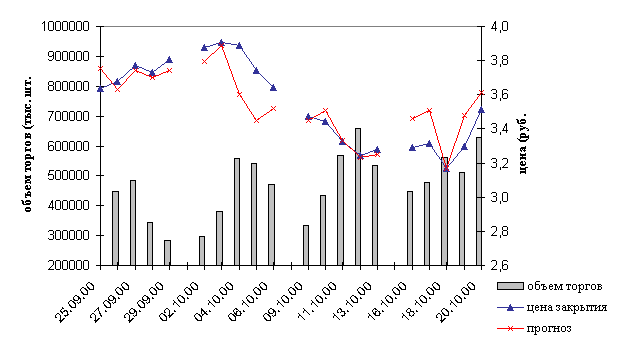
Рис. 4.3 Прогнозирование курса акций РАО “ЕЭС России”

В качестве объяснения возникавших в некоторых случаях несоответствий прогноза реальным данным можно выдвинуть следующие гипотезы:

1)      Вмешательство в ход самоорганизационного процесса государства, как организующей силы. Примерами этого могут служить периодически появляющиеся в СМИ сообщения, касающиеся изменений в политике или экономике государства.

2)      Вмешательство крупных сторонних инвесторов, действия которых не были включены в обучающую выборку и, следовательно, не могли учитываться при обучении нейросети.

Характерными примерами проявления подобных несоответствий можно считать ситуации, возникшие на рынке 14-ого и 19-ого сентября 2000-ого года (Рис. 4.2). Оптимистический прогноз на рост в течение всего дня подтверждался и увеличением объема торгов, однако, далее следовал “откат”, вызванный продажей крупных пакетов акций.

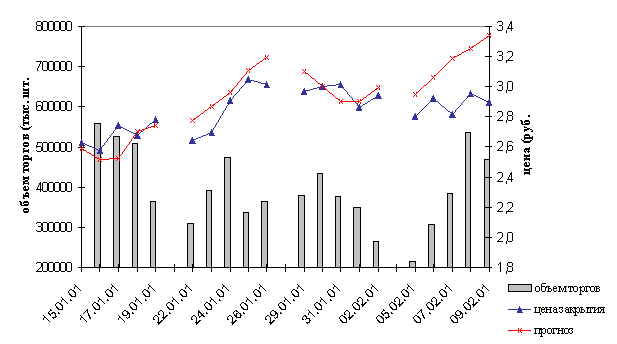
Рис. 4.4 Прогнозирование курса акций РАО “ЕЭС России”

В остальных случаях можно наблюдать качественное сходство прогнозируемого и реального хода событий. Вероятность успешного определения возникновения недельного тренда оценивается как 75-80%, при этом отличие прогнозируемого значения цены от реального составляет не более 3%.

В ходе эксперимента результаты нейросетевого прогноза сравнивались с прогнозами, полученными с помощью традиционных методов технического анализа (гистограммы рассогласований, индикатора направлений, стохастического индикатора, релятивно-силового индекса, различных скользящих средних, индикатора баланса объемов и др.) [10]. Несмотря на то, что противоречивые показания индикаторов технического анализа не позволяют дать количественную оценку их точности, следует отметить существенное превосходство нейросетевых методов.

При исследовании возможностей нейросетей различных конфигураций, были “пойманы” основные негативные эффекты, затрудняющие процесс обобщения данных: переучивание, застревание в локальных минимумах, недостаточность параметров и входных сигналов, а также реализованы алгоритмы их предотвращения. Для решения “проблемы переучивания” применялся алгоритм перекрестной проверки (см. приложение 2). Для вывода процесса обучения из локальных минимумов – увеличение шага обучения.

5. Прогнозирование индекса Доу Джонса

Предложенная методика применялась также для прогнозирования индекса Доу Джонса. Обучающая выборка была составлена на основе временного ряда ежедневных значений индекса и охватывала временной период, соответствующий одному году. На рис. 5.1 приводятся результаты прогнозирования в период с 16-ого мая по 1-ое июля 2000-ого года.

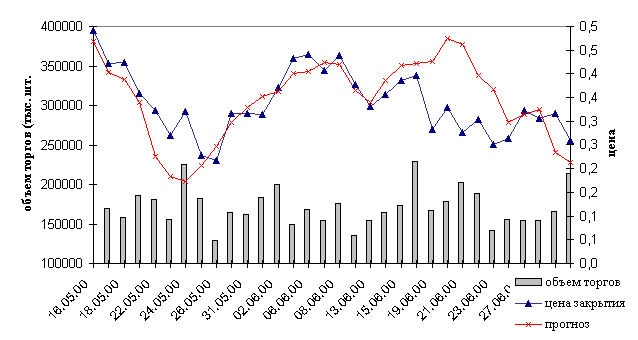
Рис. 5.1 Прогнозирование индекса Доу Джонса

Следует заметить, что дальновидность предиктора при прогнозировании индекса Доу Джонса значительно превосходит горизонт прогноза для акций РАО “ЕЭС России” и достигает 20-ти и более торговых дней. Этот факт является подтверждением мнения о большей стабильности западного рынка ценных бумаг. Однако в некоторых случаях можно также наблюдать характерные расхождения прогноза с реальным ходом событий. Так 16-ого июня (см. рис. 5.1) увеличивающийся объем торгов свидетельствовал о поддержке участниками торгов тенденции на рост цен, о том же говорил и прогноз, но реальный ход событий оказался противоположным: последовал сильный откат.

6. Оценка размерности аттрактора

Одним из самых популярных алгоритмов нелинейной динамики для временных рядов считается алгоритм расчета т. н. “корреляционной размерности” исследуемого аттрактора, предложенный в 1983 г. П. Грассбергером и И. Прокаччиа. Алгоритм основан на определении корреляционного интеграла

Методика оценки размерности D состоит в линейной аппроксимации зависимости  по “наиболее линейному” участку.

 Нейросетевые методы позволяют по-новому взглянуть на поиск размерности аттрактора системы по временному ряду данной системы. Очевидно, что не при любом количестве m входных нейронов сети удается находить функциональную зависимость

.

Но m – суть размерность входных z-векторов, которая, следуя Такенсу, должна соответствовать неравенству , где d – размерность аттрактора. Таким образом, увеличивая количество нейронов входного слоя начиная с некоторой малой величины и наблюдая за результатами процесса обучения сети, можно сделать выводы относительно минимального m, для которого процесс обучения сходится за конечное время и, следовательно, дать оценку размерности d сверху.

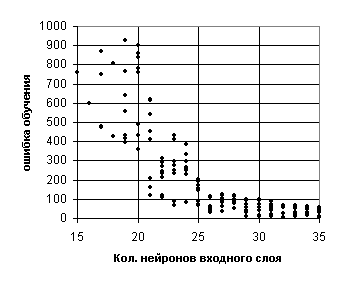
Рис. 6.1 Зависимость ошибки обучения от количества входных нейронов

Рассмотрение инвестиционного процесса с позиций теории самоорганизации позволяет предположить существование аттрактора или множества аттракторов фондового рынка, которые имеют сравнительно небольшую размерность, и попытаться определить их размерность на основе предлагаемой методики.

Практическое применение данной схемы на обучающих выборках, составленном из исходных данных по РАО ЕЭС позволяет дать оценку d как 12-15, что находится в хорошем соответствии с результатами, полученными на основе алгоритма расчета корреляционного интеграла. На рис. 6.1 представлена зависимость ошибки обучения нейросетей различных конфигураций от количества нейронов входного слоя этих сетей. Как видно из графика, начиная с некоторого количества нейронов входного слоя (25-30), ошибка резко убывает.

Таким образом, в ходе торгов по акциям РАО “ЕЭС России” можно выделить до 15 самоорганизованных групп участников торгов, определяющих динамику инвестиционного процесса в целом. При отсутствии вмешательства “извне” эта динамика довольно точно прогнозируется на основе приведенной выше методики.

7. Прогнозирование цены по объему

В определении временного ряда явно не уточняется, какую именно величину h системы следует измерять. Следовательно, один и тот же результат мы должны получать, измеряя практически любую величину h. Для проверки данной гипотезы можно попытаться представлять сети в качестве обучающей выборки не цены, а, скажем, объем торгов. При этом в качестве желаемого результата по-прежнему остается цена.

На рис 7.1 представлены результаты тестирования сети, обученной именно таким образом.

Рис. 7.1 Прогнозирование по объему

Если предположить, что объём торгов отражает настроение участников торгов, их вовлечённость в биржевую игру, то на этом фоне нейросети успешно удаётся строить отображение: настроение->цена со временным сдвигом, равным горизонту прогноза.

Выводы

Самоорганизация людей в ходе торгов на фондовом рынке приводит к образованию нескольких групп участников инвестиционного процесса, определяющих динамику процесса в целом. В отсутствие вмешательства “извне” эта динамика является легко предсказуемой. Примерами такого вмешательства могут быть сообщения в СМИ, а также действия крупных инвесторов, которые не были учтены в обучающей выборке.

Достоверное прогнозирование возможно только в пределах горизонта прогноза, величина которого определяется степенью хаотичности процесса. Для прогнозирования курса акций РАО “ЕЭС России” горизонтом прогноза является временной период 5-10 дней.

В качестве инструмента прогноза подходит стандартная трехслойная нейронная сеть, обученная на временных рядах предсказываемой величины. Количество нейронов входного слоя является главным параметром сети и определяется опытным путем на основе предложенной методики. Количество нейронов скрытого слоя принципиального значения не имеет.

Точность прогнозирования хода торгов по акциям РАО “ЕЭС России”  достигает 80%, при этом отклонение прогнозироуемого значения цены от реального составляет не более 3%, что показывает явное превосходство данного метода над традиционными методами технического анализа. Результаты были получены на различных показателях отечественного, а также зарубежного рынков ценных бумаг, что подтвердило возможность использования метода и построения краткосрочных прогнозов (до 10 дней) с большой степенью достоверности.

Были обнаружены интересные эффекты, связанные с возможностью прогнозирования одних характеристик системы (цены) через другие (объем торгов), а также предложена методика поиска размерности предполагаемого аттрактора на основе сопоставления результатов, полученных при обучении нейросетей различных конфигураций.

В качестве перспектив данного метода можно отметить:

а) более точное определение границ предсказуемости на основе расчета ляпуновских показателей;

б) исследование возможностей составления смешанных обучающих выборок, включающих дополнительную информацию о системе;

в) создание предсказывающей системы по принципу классификатора.

Благодарности

Автор пользуется приятной возможностью поблагодарить своих учителей Малинецкого Георгия Геннадьевича и Потапова Алексея Борисовича, а также Бахура Андрея Борисовича за полезное обсуждение и помощь при подготовке настоящей статьи.

Приложение 1.

Конфигурация нейросети

Во всех экспериментах использовалась стандартная трехслойная нейронная сеть, обучаемая по алгоритму обратного распространения ошибки [9].

Работа сети определяется в соответствии с формулами функционирования многослойной нейронной сети:

,

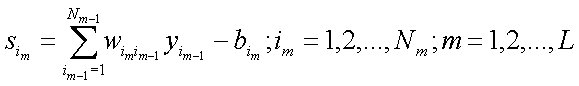
где s - выход сумматора, w - вес связи, y - выход нейрона, b - смещение, i - номер нейрона, N - число нейронов в слое, m - номер слоя, L - число слоев, f - функция активации.

В качестве функции активации на скрытом слое используется сигмоидальная функция вида:

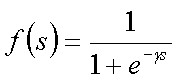
Синаптические веса настраиваются в соответствии с формулой:

,

где  - вес от нейрона i или от элемента входного сигнала i к нейрону j в момент времени t, - выход нейрона i или i-ый элемент входного сигнала, r - шаг обучения, - значение ошибки для нейрона j.

Если нейрон с номером j принадлежит последнему слою, то

,

где - желаемый выход нейрона j, - текущий выход нейрона j.

Если нейрон с номером j принадлежит одному из слоев с первого по предпоследний, то

,

где k пробегает все нейроны слоя с номером на единицу больше, чем у того, которому принадлежит нейрон j.

Приложение 2.

Алгоритм перекрестной проверки

Алгоритм обратного распространения решает по существу задачу минимизации ошибки. При этом, располагая достаточным количеством параметров сети, ошибку можно сделать сколь угодно малой величиной.

Такой процесс обучения можно условно разбить на два этапа:

На первом этапе сеть пытается обобщить вводимые данные. Происходит усреднение данных, выделение основных тенденций. Сеть улавливает и обобщает наиболее важные элементы выборки.

На втором этапе сеть начинает настройку на шум. Поскольку в реальных данных всегда содержится некоторый шум, сеть начинает настраиваться на этот шум, пытаясь минимизировать суммарную ошибку. Т. к. шум является уникальным на разных выборках, после такого обучения сеть показывает плохие результаты на неизвестной (не участвовавшей в обучении) выборке. Возникает т. н. “проблема переучивания”.

Решение этой проблемы состоит в своевременной остановке процесса обучения. Обучение должно остановиться в момент перехода с первого этапа на второй.

Для определения момента остановки применяется алгоритм перекрёстной проверки. Основная идея алгоритма состоит в разделении всей обучающей выборки на множество обучения, которое используется для настройки параметров сети и множество проверки, с помощью которого выбирается момент остановки обучения.

На каждом шаге обучения из множества N входных векторов произвольным образом выбирается k-й вектор (k=random(N)), который не участвует в процессе обучения, а играет роль “оценщика” качества работы сети. После того, как данный шаг обучения завершен, измеряется величина ошибки на k-ом векторе e и сравнивается с предыдущим значением ошибки k-ого вектора error[k] (каждому i-му вектору из N соответствует ошибка error[i], измеренная ранее для i=k, или заведомо большая ошибка, в случае когда такое измерение ещё не успело произойти). Обучение останавливается в случае, когда  e>error[k] с раз подряд. Параметр с определяется опытным путем.

Используемая литература:

1.          Малинецкий Г.Г., Потапов А.Б., “Современные проблемы нелинейной динамики”. М., УРСС, 2000, 336 с.

2.          Малинецкий Г.Г., Потапов А.Б. Русла и джокеры: о новых методах прогноза поведения сложных систем. ИПМ им. М.В.Келдыша РАН (препринт), 1998. N32. 20 c.

3.          “Новое в синергетике. Загадки мира неравновесных структур”, М. Наука, 1996.

4.          Ахромеева Т. С., Курдюмов С. П., Малинецкий Г. Г., Самарский А. А., “Нестационарные структуры и диффузионный хаос”. М. Мир, 1982.

5.          Сб. “Странные аттракторы”. М. Мир, 1980

6.          Малинецкий Г.Г., “Хаос, структуры, вычислительный эксперимент”. М. Мир, 1997.

7.          А. Н. Горбань, Д. А. Россиев, “Нейронные сети на персональном компьютере”, Новосибирск. Наука, 1996.

8.          Andreas S. Weigend, Bernardo A. Huberman, David E. Rumelhart, “Predicting the Future: A Connectionist Approach”.

9.          Internet: ftp://ftp.sas.com/pub/neural/FAQ.html Copyright 1997, 1998, 1999, 2000 by Warren S. Sarle, Cary, NC, USA.

10.      А. Элдер. “Как играть и выигрывать на бирже”. М. КРОН-ПРЕСС, 1996.