Аннотация
Описывается универсальная методика ускорения вычислений в задачах математического моделирования
процесса структурообразования биологических макромолекул, синтезируемых в живой клетке
(нуклеиновые кислоты, белки). Развитие таких процессов определяется соотношением скорости
удлинения растущей молекулярной цепи и скорости распада и образования структурных связей в ней.
Вычислительная сложность моделирования здесь оценивается как N5, где N – полная длина
молекулярной цепи. Задача сводится к многократному построению локально-минимального пути на
ориентированном динамически меняющемся графе, описывающем возможные межструктурные переходы.
Множество таких переходов для каждой вершины графа монотонно растет вместе с ростом
молекулярной цепи. Это свойство позволяет снизить вычислительные затраты до N4. Проводится
доказательство корректности методики, анализируются ее возможные варианты. Методика
использовалась при математическом моделировании и изучении прицесса образования вторичных
структур рибонуклеиновых кмслот (РНК) различных типов.
Abstract
Universal method is described of calculations acceleration in tasks of mathematical
simulation of biological macromolecules structures formation process in living cell
(nucleic acids, proteins). The way of such processes running is determined by the ratio of
velocity of molecular chain lengthening and the velocity of structure bonds breaking and
arising. Computational complication of simulation in this task is estimated as N5, where
N – is full length of molecular chain. The task is reduced to multiple calculations of
locally optimal path on an oriented and dynamically changed graph, which describes possible
inter-structural transitions. The set of such transitions in every graph vertex monotonously
growth according to the growth of molecular chain. This property allows us to decrease
computational expenditures up to N4. The proof of method correctness is given. The method
possible variants are analyzed. This method has used in mathematical simulation and
investigation of process of various ribonucleic acids (RNA) secondary structures formation.
Содержание
1. Введение............................................................................................... 3
2. Вторичные структуры РНК и моделирование их
образования.......... 5
3. Общая модель процесса образования вторичной
структуры РНК.... 8
4. Методика ускорения вычислений...................................................... 12
5. Анализ эффективности....................................................................... 18
ЛИТЕРАТУРА....................................................................................... 20
Определение геометрической структуры таких биологических макромолекул как
белки и нуклеиновые кислоты (их геометрической формы, топологии межатомных
связей) является фундаментальной проблемой молекулярной биологии. Эти молекулы
представляют собой длиныые цепочки однотипных элементов – нуклеотидов для
нуклеиновых кислот или аминокислот для белков. Молекулярная цепь образуется и
растет путем постепенного добавления к ней этих однотипных элементов в ходе
соответствующего процесса, происходящего в живой клетке – трансляции (для
белков), транскрипции или репликации (для нуклеиновых кислот). Функциональные
свойства биологической макромолекулы в значительной степени определяются той
формой (или структуой), в которую сворачивается ее молекулярная цепь.
В связи с большим количеством
(тысячи) известных к настоящему времени различных биологических макромолекул и
сложностью прямых физических и
биохимических методов распознавания их структур особый интерес представляет
разработка математических моделей структурообразования биологических
макромолекул и определение структур реальных макромолекул методом
математического моделирования.
Биологическая макромолекула,
сворачиваясь, приобретает структуру, которой соответствует локальный минимум ее
свободной энергии. Линейные (продольные) связи вдоль молекулярной цепи
достаточно сильны, поэтому в ходе структурообразования молекулярная цепь не разрывается, молекула
принимает энергетически локально -
минимальную форму за счет изгибов молекулярной цепи и образования поперечных,
более слабых, связей.
Гибкость молекулярной цепи и способность образовывать поперечные связи
определяется ее составом или, как принято говорить, ее первичной структурой.
Однотипные элементы, составяющие молекулярную цепь могут отличаться друг от
друга. Молекулярная цепь рибонуклеиновой кислоты (РНК) составляется из нуклеотидов четырех видов, то же имеет
место и для дезоксироибонуклеиновых кислот (ДНК). Белковая молекулярная цепь составляется из аминокислот двадцати
различных видов. Первичная структура молекулы определяется тем, какие и в какой
последовательности однотипные элементы составляют молекулярную цепь.
Целью математического моделирования процесса структурообразования биологических макромолекул является
определение пространственной структуры в которую сворачивается молекулярная
цепь по ее первичной структуре. В данной работе рассматриваются методы такого
математического моделирования для
процесса структурообразования РНК. Однако, в силу общности основных черт
механизмов роста цепи биологических макромолекул и их структур, эти методы могут найти применение применимы и для
математического моделирования процессов
структурообразования биологических макромолекул других типов.
Число потенциально возможных устойчивых структур для биологической
макромолекулы велико. Сворачивание
макромолекулы в ту или иную структуру зависит не только от ее первичной структуры, но и от условий, в
которых образуется молекулярная цепь.
Математическая модель процесса
структурообразования должна учитывать эти условия. Характерной особенностью синтеза нуклеиновых кислот и
белков в живой клетке является то, что
макромолекула образуется постепенно;
молекулярная цепь ее растет с некоторой конечной скоростью (скорость элонгации). При этом на уже
синтезированном участке молекулы
постоянно идут процессы структурообразованияи и, как показали наши исследования для РНК [1 - 3], развитие структуры определяется соотношением скорости элонгации
и скорости структурообразования (т.е.
образования новых и распада старых
поперечных структурных связей в
молекуле). Численную меру этого
соотношения мы назвали периодом стуктуризации T. В нашей модели величина T
определяется, как число нуклеотидов, на
которые удлиняется молекулярная цепь за время структуризации уже образовавшегося участка молекулярной
цепи. В связи с тем, что данная
молекула РНК может порождаться как часть более длинной молекулярной цепи (т.н. первичного
транскрипта), процесс ее
структурообразования может начинаться не сразу (с появления первого нуклеотида), а тогда, когда
молекулярная цепь уже имеет в своем
составе некоторое число (L0) нуклеотидов.
При неизвестных заранее значениях T и L0
вычислительная сложность математического моделирования процесса
структурообразования оценивается как N5, где N – полная длина
молекулярной цепи (число нуклеотидов в ней). В данной работе описывается универсальная методика ускорения
вычислений. Задача сводится к многократному построению локально-минимального
пути на ориентированном динамически меняющемся графе, описывающем возможные межструктурные переходы. Множество таких переходов для каждой вершины графа
монотонно растет вместе с ростом
молекулярной цепи. Это свойство позволяет
снизить вычислительные затраты до N4. Проводится
доказательство корректности методики,
анализируются ее возможные варианты.
Методика использовалась при математическом моделировании и изучении прицесса образования вторичных
структур рибонуклеиновых кмслот (РНК)
различных типов.
Как уже говорилось, молекулярная цепь
рибонуклеиновой кислоты (РНК) составляется из нуклеотидов четырёх видов. Это
адениновая, гуаниловая, цитидиловая и уридиловая кислоты. Основания этих кислот
обозначаются символами: A – аденин, G – гуанин, C – цитозин, U – урацил.
Первичная структура РНК описывает последовательность нуклеотидов в молекулярной
цепи; её можно представить как строку текста составленного из указанных четырёх
букв. Среди поперечных связей, которые образуются при сворачивании молекулярной
цепи в пространственную структуру, наиболее сильными являются водородные
Уотсон-Криковские связи, возникающие между основаниями некоторых нуклеотидов.
Такие связи могут возникать между A и U, между C и G и между G и U. Пары
оснований A-G и C-G называются классическими, комплементарными; пара
G-U – неклассической. Пары
оснований, между которыми возникли Уотсон-Криковские связи, называются
спаренными. Связь C-G – самая сильная, связь
G-U – самая слабая и может
возникать только при некоторых условиях.
В естественной молекуле РНК часть оснований
находится в спаренном, а часть в неспаренном, свободном состоянии. Это
определяет т.н. вторичную структуру РНК и вторичные (Уотсон-Криковские)
взаимодействия в молекуле. При сворачивании молекулы РНК в пространстве могут
возникать добавочные (более слабые) связи между её атомами. Это определяет т.н.
третичную структуру РНК и третичные взаимодействия в молекуле. Первичная
структура у молекулы РНК одна, а возможных вторичных (и третичных) структур
много.
Формально, вторичная структура РНК – это описание
всех спаренных и свободных оснований в молекулярной цепи. Пронумеруем
последовательно нуклеотиды в молекулярной цепи так, что нуклеотид,
присоединяющийся к растущей цепи позже, имеет больший номер. Отрезок [n1,
n2] свободных оснований в молекулярной цепи называется однонитевым.
Отрезки [n1, n2] и [n3, n4]
спаренных оснований так, что n1 спарен с n4, n1 +1 с n4 -1,…, n2 с n3 образуют
двухнитевый или двуспиральный участок во вторичной структуре РНК. Однонитевые
участки также называются петлями, а двухнитевые – стеблями. Стебель можно
представить себе, как участок винтовой лестницы, где ступеньки – это
поперечные, Уотсон-Криковские связи. Длиной стебля называется чсло пар
оснований в нём: n2 - n1 + 1 = n4
- n3 + 1.
Таким образом , вторичная структура РНК – это
совокупность стеблей и петель. Других элементарных составляющих во вторичных
структурах реальных РНК к настоящему времени не обнаружено.
Общее число возможных стеблей для данной молекулы
РНК оценивается как N2, где N – число нуклеотидов в цепи РНК.
Получим эту оценку для случая, когда разрешено только классическое спаривание C-G и A-U (случай с G-U рассматривается аналогично). Вероятность того,
что наугад выбранная пара оснований окажется классической коплементарной равна ¼ (четыре пары A-U, U-A, C-G, G-C из 16 возможных
комбинаций). Число различных пар оснований в цепи РНК равно 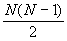 . Поэтому число стеблей длины 1 оценивается как . Поэтому число стеблей длины 1 оценивается как 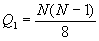 . Вероятность того, что наугад выбранные k пар оснований все
окажутся комплементарными равна (¼)k. Число четверок (n1,
n2, n3, n4) таких, что n1 £ n2 < n3 £ n4 и
n2 - n1 + 1 = n4 - n3 + 1= k, не превосходит . Вероятность того, что наугад выбранные k пар оснований все
окажутся комплементарными равна (¼)k. Число четверок (n1,
n2, n3, n4) таких, что n1 £ n2 < n3 £ n4 и
n2 - n1 + 1 = n4 - n3 + 1= k, не превосходит 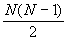 . Поэтому число стеблей длины k в среднем не превосходит . Поэтому число стеблей длины k в среднем не превосходит 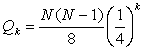 . Поскольку . Поскольку 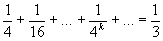 , то среднее число стеблей m можно теперь оценить так: , то среднее число стеблей m можно теперь оценить так:
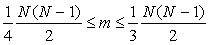 , ,
что и требовалось показать.
Отметим, что вероятности появления нуклеотидов
любого типа (или их цепочек) здесь предполагались равными. Обратный случай
рассматривается аналогично.
В работах [1 – 4 ] моделируетсяя процесс
образования вторичной структуры РНК, развивающийся по пути локальной минимизации
свободной энергии молекулы. Процесс является пошаговым и отражает
последовательный рост молекулярной цепи РНК. На первом шаге длина молекулярной
цепи (т.е. число нуклеотидов в ней) полагается равной некоторой величине L0,
называемой начальной длиной. На каждом шаге сначала моделируется
структуризация, т.е. процесс образования вторичной структуры РНК в пределах уже
выросшего участка молекулярной цепи. ”Выращивание” структуры производится
повторяющимся добавлением к ней новых стеблей так, чтобы обеспечивался
минимальный отрицательный прирост свободной энергии молекулы. По окончании
структуризации молекулярная цепь удлиняется на некоторое постоянное число
нуклеотидов T и происходит переход к следующему шагу. Параметр T называется
периодом структуризации. Он равен величине удлинения молекулярной цепи за время
её структуризации и, таким образом, характеризует отношение скоростей двух
процессов – элонгации (роста молекулярной цепи) и структуризации (роста
вторичной структуры).
Моделирование проводилось для четырёх
опубликованных моделей свободной энергии вторичной структуры РНК: G1
– [5], G2 – [6], G3 – [7], G4 – [8]. Модель
свободной энергии – это семейство термодинамических параметров, позволяющих
вычислить приращение свободной энергии DG молекулы по её
нуклеотидной последовательности. Во всех этих моделях свободная энергия
вторичной структуры РНК складывается из
суммы свободных энергий её элементов – свободной энергии стеблей и свободной
энергии образования (инициации) петель. Параметры в этих моделях были
определены экспериментально (в простейшей модели G1 этого не
требовалось).
Исследования проводились в полной области
целочисленных значений параметров T, L0. Для каждой молекулы РНК
моделировалось 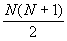 вариантов процесса
структурообразования (N – полная длина молекул, значение L0 лежит в
пределах 0 £ L0 £ T – 1). Вычислительную сложность
моделирования одного варианта можно оценить как N4. Она складывается
из следующих величин: N – число шагов процесса, N2 – число стеблей,
перебираемых на каждом шаге процесса, N – сложность вычисления приращения
свободной энергии DG при добавлении к структуре
нового стебляя. Таким образом, общая сложность моделирования процесса
образования вторичной структуры РНК достигала N6. В следующих
разделах данной работы описывается методика вычислений для данной задачи,
которая позволила понизить сложность до N4. вариантов процесса
структурообразования (N – полная длина молекул, значение L0 лежит в
пределах 0 £ L0 £ T – 1). Вычислительную сложность
моделирования одного варианта можно оценить как N4. Она складывается
из следующих величин: N – число шагов процесса, N2 – число стеблей,
перебираемых на каждом шаге процесса, N – сложность вычисления приращения
свободной энергии DG при добавлении к структуре
нового стебляя. Таким образом, общая сложность моделирования процесса
образования вторичной структуры РНК достигала N6. В следующих
разделах данной работы описывается методика вычислений для данной задачи,
которая позволила понизить сложность до N4.
В данном разделе дается математическая модель процесса образования
вторичной структуры РНК в несколько более общем виде, чем в [1 – 5]. Введём
некоторые обозначения. Нуклеотиды в молекулярной цепи РНК пронумеруем начиная с
единицы последовательно, в порядке её роста. Пусть L – длина РНК, т.е. число
нуклеотидов в полной цепи. S(n) обозначает вторичную структуру на отрезке
молекулярной цепи состоящем из нуклеотидов 1, 2, 3,…, n. S(n) – это множество
пар (i, j), означающих, что нуклеотид i образовал Уотсон-Криковскую связь
(спарен) с нуклеотидом j. Там, где это ясно, или не важно, мы будем обозначать
вторичную структуру просто S, не
указывая значения n. Совпадение вторичных структур понимается в
теоретико-множественном смысле. Формула S1 = S2 означает,
что множества пар (i, j) спаренных нуклеотидов для обоих структур совпадают.
Обозначим n0(S) – максимальный номер
спаренного нуклеотида:
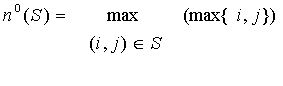 
Данная структура S может реализоваться только
тогда, когда число нуклеотидов в молекулярной цепи станет не меньшим, чем n0(S).
Для всех n: n0(S) £ n £ L, имеем S(n0) = S(n)
= S(L).
Стебель С – это четвёрка целых чисел C = (n1,
n2, n3, n4), n1 £ n2 £ n3 £ n4, таких, что
нуклеотиды n1, n1 + 1, n1 + 2,…, n2
могут образовывать Уотсон-Криковские связи (спариваться) соответственно с
нуклеотидами n4, n4 –
1, n4 – 2,…, n3.
Длина стебля l(C) – это число пар оснований в нём: l(C) = n2 – n1
+ 1. Любую Уотсон-Криковскую пару (n1, n2) можно
рассматривать как стебель длины 1: (n1, n1, n2,
n2). В дольнейшем мы не будем различать пару (n1, n2)
и соответствующий ей стебель.
Стебель можно определить и как вторичную
структуру, состоящую из Уотсон-Криковских пар вида (n1, n4),
(n1 + 1, n4 – 1), (n1 + 2, n4 –
2),…, (n2, n3). В этом смысле выражение CÍ S означает, что все пары
оснований из C спариваются в структуре S. Выражение n0(C) означает
максимальный номер нуклеотида спаренного в стебле, т.е. n0(C) = n4.
Два стебля C1 и C2 называются совместимыми, если они
могут одновременно участвовать в какой-либо вторичной структуре S: C1Í S и C2 Í S. Не любые два стебля C1
и C2 совместимы. Например, если (n, p) Î C1, (n, q) Î C2 и p ¹ q, то стебли C1 и C2
несовместимы, поскольку в данной вторичной структуре основание n может быть
спарено только с одним основанием.
Часто используется стерическое условие
совместимости [9]. Пары (p1, p2) и (q1, q2)
стерически совместимы, если их связи не “перекрещиваются”, т.е. выполнено одно
из условий:
либо [p1, p2] Í [q1, q2],
либо [q1, q2] Í [p1, p2],
либо [p1, p2] Ç [q1, q2] =
Æ,
где [n, m] – это целочисленный отрезок от n до m.
Два стебля стерически совместимы, если совместимы любые две составляющие их
Уотсон-Криковские пары.
Условия совместимости могут быть разнообразными.
Мы не будем их конкретизировать здесь, поскольку это не влияет на излагаемый
здесь материал.
В ходе роста вторичной структуры в ней исчезают
(разрываются) некоторые старые Уотсон-Криковские связи и возникают новые. В
описываемой математической модели это достигается добавлением к структуре тех
или иных стеблей. Множество допустимых стеблей, которые можно добавлять к
структуре S(n) обозначается D(S, n). Операцию добавления будем условно
обозначать знаком +. При добавлении к структуре S(n) стебля C Î D(S, n) возникает некая новая
структура S1(n):
S + c = S1
Операция добавления может происходить по-разному.
В основном случае из структуры S сначала удаляются пары (i, j) несовместимые с
C (разрыв Уотсон-Криковских связей), а затем добавляются пары (i, j) ÎC (возникновение новых
Уотсон-Криковских связей). В других вариантах, например, возникновение связей
или их разрушение может быть опущено. Трактовка операции добавления
регулируется признаком, который приписывается стеблю при формировании множества
допустимых стеблей D(S, n).
Формирование множества допустимых стеблей D(S, n)
происходит по правилам модели процесса структурообразования. Допускаются
различные модели. В работах [1 – 5] рассматривалась простейшая модель, в
которой не допускались перестройки структур с разрушением Уотсон-Криковских
связей. В этом случае D(S, n) состоит из всех стеблей C совместимых с S и
таких, что n0(C) £ n (если n0(C)
> n, то не все Уотсон-Криковские пары в стебле могут возникнуть). В другом
(предельном) случае также рассмотренном в этих работах допускаются любые
перестройки и в D(S, n) включаются любые стебли C, у которых n0(C) £ n. Можно также, например,
запретить все стебли, содержащие неклассические пары G–U и т.п.
Выше уже говорилось, что рост вторичной структуры
РНК направляется локальной минимизацией её свободной энергии. Пусть молекулярная
цепь имеет длину n нуклеотидов. Будем обозначать DG(S, n) – приращение свободной энергии при
переходе молекулярной цепи из свободного однонитевого состояния, в котором нет
спаренных оснований, в состояние со структурой S(n). Отметим, что хотя S(n1)
= S(n2) (для n1, n2 ³ n0(S)), но в
некоторых моделях свободной энергии может быть DG(S, n1) ¹ DG(S, n2) при n1 ¹ n2.
Введём функцию локального приращения свободной
энергии F. Пусть S(n) – некая структура, к которой добавляется стебель C, тогда
F(S, C, n) = DG(S + C, n) – DG(S , n)
Отметим
свойство использующееся в следующем разделе. Для всех моделей энергии G1,
G2, G3 значение F не зависит от длины молекулярной цепи:
F(S, C, n) = F(S, C, m), " m ³ n
Для модели G4 можно полагать
F(S, C, n) £ F(S, C, m), " m ³ n
В этой модели свободная энергия зависит от галичия или отсутствия одного
свободного нуклеотида в конце цепи (справа). Поэтому
F(S, C, n0(C)) ¹ F(S, C, n0(C) + 1),
Но
F(S, C, n0(C)) = F(S,
C, m), " n, m ³ n0(C) + 1.
В этом случае каждый стебель C берётся в двух
экземплярах C и C*, при этом экземпляр C считается допустимым при n ³ n0(C) + 1 и величина
F для него берётся как обычно; экземпляр C* считается доаустимым при
n ³ n0(C), но
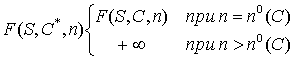
Обозначим
 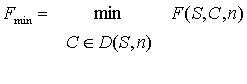
Fmin – минимальное приращение свободной энергии при добавлении к
структуре S стебля из множества допустимых стеблей. Множество стеблей , на
которых F = Fmin обозначим Dmin:
 Dmin(S, n) = {C Î D(S, n): F(S, C, n) = Fmin}. Dmin(S, n) = {C Î D(S, n): F(S, C, n) = Fmin}.
Если Fmin > Eact, т.е.
больше энергии активации, то Dmin = Æ.
Если Dmin(S, n) = Æ, то это означает, что
структурные перестройки возможны только при поступлении дополнительной энергии,
т.е. что структура S энергетически устойчива.
Введём также
D~(S, n) = {C Î D(S, n): F(S, C, n) < Eact},
Тогда Dmin Í D~.
Введём граф межструктурных переходов. Вершины
графа – это вторичные структуры, рёбра – переходы от структуры к структуре при
добавлении какого-либо стебля. Этот граф меняется с ходом времени. В каждый
момент времени t молекулярная цепь имеет длину n(t). При этом в графе могут
существовать только те вершины S, у которых n0(S) £ n(t). У каждой существующей
вершины S графа имеется множество допустимых переходов: {S –> S + c, " C Î D(S, n(t)}.
Моделирование процесса структурообразования
начинается в момент t = 0 из пустой вторичной структуры S0 при
исходной длине молекулярной цепи равной L0 нуклеотидов. Строится
путь на графе межструктурных переходов. Это отражает рост молекулярной цепи и
вторичной структуры на ней. Если в момент t молекулярная цепь имеет длину n(t)
и мы находимся в вершине S графа (т.е. имеем вторичную структуру S), то
выбирается стебель C, обеспечивающий минимальный прирост свободной энергии C Î Dmin(S, n(t)) и
делается переход S –> S* = S + C. Если Dmin = Æ (пустое), то делается переход S
–> S* = S, причём считается, что на это затрачивается время Dt, в течение которого молекулярная цепь удлиняется
на Dn нуклеотидов.
Модели элонгации (роста молекулярной цепи) могут
быть разнообразными. В простейшем случае, как в [1 – 5]
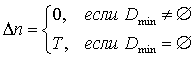
т.е. структура полностью формируется в пределах
выросшего участка молекулярной цепи, а когда этот процесс кончается,
молекулярная цепь удлиняется на T нуклеотидов. В другой модели
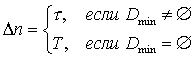
т.е. за время добавления любого стебля
молекулярная структура вырастает на t нуклеотидов. Если же
структура стабилизировалась, то молекулярная цепь растёт с постоянной скоростью
T нуклеотидов за единицу времени. Интересны модели, в которых время
переформирования структуры (и, следовательно, Dn) растёт по мере сложности происходящих
переформирований.
Процесс структурообразования кончается, когда
молекулярная цепь дорастает до конца (n = L) и структура стабилизируется (Dmin
= Æ).
В данном разделе представляется методика ускорения
вычислений при математическом моделировании процесса образования вторичной
структуры РНК. Модель процесса описана в предыдущем разделе.
Основное время при моделировании уходит на вычисление
множества энергетически минимальных допустимых стеблей Dmin(S, n)
для данной вторичной структуры S при длине молекулярной цепи n нуклеотидов.
Поскольку процесс моделируется при разных значениях начальной длины L0
молекулярной цепи и периода структуризации T , то мы можем попадать в данную
структуру S много раз (порядка L2 в ходе моделирования). Основное время при вычислении Dmin
уходит на определение приращений свободной энергии F(S, C, n) = DG(S + C, n) – DG(S , n) для различных стеблей C. В
использовавшихся моделях свободной энергии величина F либо вовсе не зависит от
n (при n ³ n0(C)), либо
не зависит от n при n ³ n0(C) + 1
(модель G4 [9]). Поэтому очень эффективным оказался следующий метод.
Метод 1. При попадании в структуру S
вычисляется и заполняется
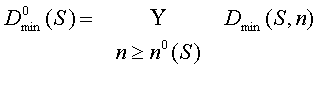
Кроме того заполняются значения F(S, C, n) для
всех n ³ n0(C) и C Î D0min(S).
При дальнейших попаданиях в структуру S множество Dmin(S, n)
отыскивается как подмножество D0min(S). Заметим, что
число стеблей, реально попадавших в D0min(S) оказалось
достаточно малым (порядка N/10).
Метод 1 универсален. Он не использует специальных
черт моделируемого процесса, однако требует определённой памяти. Обратимся
теперь к методам, использующим специфику и за счёт этого ускоряющих вычисления
или уменьшающих размер требуемой памяти.
Свойство 1. Монотонность локального
приращения свободной энергии при росте молекулярной цепи.
F(S, C, n) £ F(S, C, m), " m > n.
Это свойство означает, что если молекулярная цепь увеличивается, а набор
Уотсон-Криковских связей остаётся неизменным, то свободная энергия неубывает,
т.е. вторичная структура не становится стабильнее. Это свойство имеет место для
всех исследовавшихся нами математических моделей структурообразования (см. п. 2).
Оно даёт возможность использовать следующий метод ускорения вычислений.
Метод 2. Обозначим
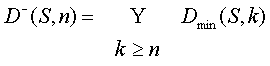
Нетрудно видеть, что " m > n имеем
 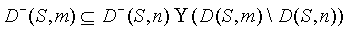 (4.1) (4.1)
В самом деле, пусть 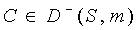 . Если C Ï D(S, n), то C Î D(S, m) \ D(S, n), если
С Î D(S, n), то . Если C Ï D(S, n), то C Î D(S, m) \ D(S, n), если
С Î D(S, n), то
F(S, C, n) £ F(S, C, m) < Eact
и, значит, 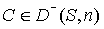 , что и доказывает
(4.1). , что и доказывает
(4.1).
Поскольку 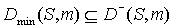 , то поиск Dmin можно вести на стеблях из
множества, стоящего в правой части (4.1), что значительно сокращает поиск. Это
особенно выигрышно, если структура S стабильна при длине молекулярной цепи n.
Тогда , то поиск Dmin можно вести на стеблях из
множества, стоящего в правой части (4.1), что значительно сокращает поиск. Это
особенно выигрышно, если структура S стабильна при длине молекулярной цепи n.
Тогда
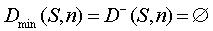 , ,
и
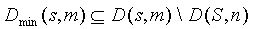
При малых скоростях роста молекулярной цепи может
оказаться, что m = n + Dn близко к n и, что D(S,
m) = D(S, n). Тогда Dmin(S, m) Í Æ, и перебор полностью
отсутствует.
Свойство 2. Отметим важное свойство
множеств допустимых стеблей, которое нам понадобится в дальнейшем. Это свойство
монотонности по отношению к длине молекулярной цепи:
если n < m, то D(S, n) Í D(S, m) (4.2)
Оно означает, что с ростом молекулярной цепи
множество структур, в которые можно перейти из структуры S, растёт. Именно на
этом свойстве основаны описанные ниже методы ускорения вычислений при
математическом моделировании. В исследовавшихся нами математических моделях
процесса структуризации это свойство имело место.
В связи с этим свойством можно ввести числовую функцию
d(C) – предел допустимости для стебля
C. Это минимальное n, при котором C Î D(S, n). Величина d(C)
зависит от структуры S, но мы не будем её указывать, т.к. это не приводит к
двусмысленности. Ясно, что d(C) ³ n0(C), таким
образом, стебель C допустим в диапазоне d(C) £ m £ L.
Свойство 3. Имеет место для моделей
свободной энергии G1, G2, G3 :
F(S, C, n) = F(S, c, m), " m ³ n (4.3)
(см. п.2).
Метод 3. Этот метод применим для моделей
свободной энергии G1, G2, G3, для которых
выполнено (4.3) и (4.2).
Имеем " m ³ n
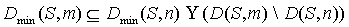 (4.4) (4.4)
В самом деле, пусть C Î Dmin(S, m) и C Î D(S, n). Из свойства 2 следует,
что Dmin(S, n) Í D(S, m). Тогда F(S, C,
m) £ F(S, C*, m) и, из
(4.3) имеем F(S, C, n) £ F(S, C*, n)
и, значит C Î Dmin(S, n),
что и требовалось доказать.
Использование (4.4) вместо (4.1) ещё более
сокращает перебор.
В дальнейшем будем использовать следующее
обозначение. Если D – некое множество стеблей, то D½n = {C Î D : d(C) £ n} – подмножество стеблей из D,
которые допустимы на молекулярной цепи длиной n и выше. Пусть также
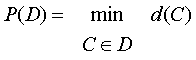
Утверждение 1. Пусть Pn = P(Dmin(S,
n)), тогда
Dmin(S, m) = Dmin(S,
n)½m, " m: max{Pn, n0(S))
£ m £ n
Доказательство. Докажем, что Dmin(S,
n)½m Í Dmin(S, m). Пусть C Î Dmin(S, n)½m, тогда d0(C) £ m и F(S, C) £ F(S, C*), " C* Î D(S, n). Но D(S, m) Í D(S, n), значит F(S, C) £ F(S, C*), " C* Î D(S, m). Поскольку d0(C)
£ m, то C Î Dmin(S, m).
Докажем, что Dmin(S, m) Î Dmin(S, n)½m. Возьмём C* Î Dmin(S, n)½m Î Dmin(S, m), тогда " С Î Dmin(S, n) имеем F(S,
C) = F(S, C*). Значит
F(S, C*) £ F(S, C’), " C’ Î D(S, n)
Кроме того d(C*) £ m £ n, поэтому C* Î D(S, m) Í D(S, n), значит C* Î Dmin(S, n), что и
требовалось доказать.
Нетрудно видеть, что верно следующее следствие.
Следствие 1. Пусть n0(S) £ m £ n. Если Dmin(S, n)½m = Æ, то Dmin(S, m) = Dmin(S,
n)½m.
Сформулируем теперь два метода ускорения
вычислений, опирающихся на это утверждение.
Метод 4. Для каждой структуры S, которая
возникла при моделировании вычисляется и сохраняется множество стеблей 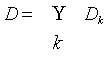 и значения локального
приращения свободной энергии F(S, C). Множества Dk определяются
рекуррентными соотношениями: и значения локального
приращения свободной энергии F(S, C). Множества Dk определяются
рекуррентными соотношениями:
D1 = Dmin(S,
L), n1
= P(D1)
Dk+1 = Dmin(S,
nk – 1), nk+1 =
P(Dk+1)
Нетрудно видеть, что " n
Dmin(S, n) Í {C Î D: d(C) £ n}
В отличие от метода 1 здесь не надо вычислять Dmin(S,
n) для всех значений n, а только для n = nk – 1, k = 1, 2,… Это
существенно ускоряет вычисления.
Прежде, чем описывать следующий метод ускорения
вычислений, определим множество N(S). В ходе математического моделирования (для
различных значений L0, T) мы можем попадать в данную структуру S
неоднократно. Длина молекулярной цепи n при разных попаданиях может быть
различной. Обозначим её ni для i-го попадания в структуру S.
Обозначим Nk(S) – множество содержащее величины ni для i
= 1, 2, …, k: Nk(S) = {n1,
n2,… ,nk}.
Метод 5. Для каждой вторичной структуры
S, в которую мы попали в ходе математического моделирования в k-й раз, хранится
множество Dk :
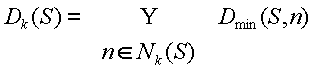
Помимо этого множества для любого стебля C Î Dk(S) хранится величина
nmax(C) – максимальная длина молекулярной цепи из Nk, при
которой стебель C давал минимальный локальный прирост свободной энергии (и,
следовательно, мог участвовать в переформировании структуры):
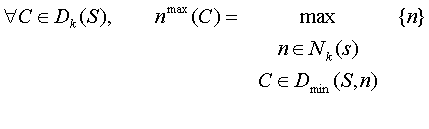
Вся эта информация накапливается рекуррентным
образом:
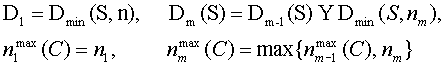
(если C Î Dmin(S, nm)).
Пусть теперь мы попали в структуру S в k + 1-й
раз, при длине молекулярной цепи РНК равной nk+1. Определим
множество Q стеблей из Dk(S) допустимых для данной длины цепи РНК:
Q = {C Î Dk(S): d(C) £ nk+1} = Dk(S)½nk+1.
Если Q не пусто (Q ¹ Æ), то определим
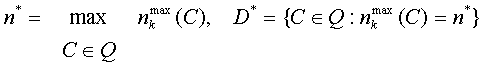
Если Q = Æ, то положим D* =
Æ, n* = –¥. Если n* ³ nk+1, то это
означает, что на предыдущих шагах моделирования мы попадали в структуру S при
длине молекулярной цепи n* ³ nk+1 и,
значит, Dmin(S, n*) Í Dk. При этом
Dmin(S, n*)½nk+1 ¹ Æ.
Значит (см. Следствие 1 из Утверждения 1)
Dmin(S, nk+1)
= Dmin(S, n*)½nk+1.
Поэтому
Dmin(S, nk+1)
= D* (4.5)
Если n* < nk+1 или Q = Æ, то
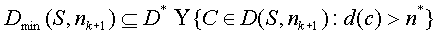 (4.6) (4.6)
В силу определения D* Í D(S, nk+1) и, кроме
того, D* Í D(S, n*),
причём F(S, C*) £ F(S, C), " C* Î D* и " C Î D(S, n*) и
F(S, C*) £ F(S, C), " C* Î D* и " C Î D(S, n*) \ D* (4.7)
Если C Î D(S, nk+1) и
d(C) £ n*, то C Î D(S, n*). Если C Ï D*, то из (4.7) C Ï Dmin(S, nk+1).
Таким образом, Dmin(S, nk+1)
определяется либо из (4.5), либо из (4.6). И то, и другое значительно сокращает
перебор.
Эффективность рассматриваемой методики во многом
зависит от конкретного вида моделируемого процесса: от того, какие перестройки
структуры допустимы, какие временные задержки они вызывают и т.п. Поскольку
именно этим определяется сложность или простота, разбросанность или
компактность семейства путей на графе межструктурных переходов, по которым
будет развиваться процесс для различных значений (T, L0). Поэтому
здесь мы сможем дать только довольно грубую аналитическую оценку, и дополнить
её некоторыми числовыми данными, полученными при математическом моделировании.
Напомним обозначения:
L – полная длина молекулы
РНК,
T – период структуризации.
Если считать, что, грубо, процесс развивается так:
сначала структура наращивается, затем молекулярная цепь удлиняется, то число
шагов в развитии процесса составляет 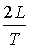 . При этом возникают последовательно . При этом возникают последовательно 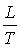 структур. На каждом
шаге процесса, при текущей длине РНК –
n нуклеотидов, имеем порядка ~0.3n2 стеблей, которые можно добавить
к структуре. Для выбора энергетически минимального стебля надо затратить
порядка ~0.3n2t времени, где t – время
расчёта свободной энергии для одного стебля. Модели свободной энергии таковы,
что t ~n. Таким образом, общее время
счёта на одном шаге процесса составляет ~n3. Просуммировав это по ~ структур. На каждом
шаге процесса, при текущей длине РНК –
n нуклеотидов, имеем порядка ~0.3n2 стеблей, которые можно добавить
к структуре. Для выбора энергетически минимального стебля надо затратить
порядка ~0.3n2t времени, где t – время
расчёта свободной энергии для одного стебля. Модели свободной энергии таковы,
что t ~n. Таким образом, общее время
счёта на одном шаге процесса составляет ~n3. Просуммировав это по ~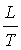 шагам процесса, получим, что моделирование одного варианта
процесса структурообразования требует времени ~ шагам процесса, получим, что моделирование одного варианта
процесса структурообразования требует времени ~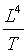 . Поскольку для данного T мы моделируем процесс на различных
значениях начальной длины молекулы L0 = 0, 1, 2, …, T – 1, то для
данного T (на всех L0) моделирование требует времени ~L4.
Поскольку T также меняется от 1 до L (с шагом 1), то общее время моделирования
для одной молекулы РНК без применения методки ускорения оценивается как ~L5. . Поскольку для данного T мы моделируем процесс на различных
значениях начальной длины молекулы L0 = 0, 1, 2, …, T – 1, то для
данного T (на всех L0) моделирование требует времени ~L4.
Поскольку T также меняется от 1 до L (с шагом 1), то общее время моделирования
для одной молекулы РНК без применения методки ускорения оценивается как ~L5.
Методы ускорения вычисления, изложенные в п.4
можно разбить на две группы. Это метод 2, не требующий памяти, и остальные (1,
3 – 5), использующие дополнительную память ЭВМ. Рассмотрим сначала метод 2.
Сокращение времени здесь происходит за счёт того, что после стабилизации
структуры, при удлинении молекулярной цепи РНК, перебор происходит для стеблей,
возникших на участке цепи от n до n + T нуклеотидов. Число их можно оценить как
~0.3((n + T)2 – n2) ~ nT, а число таких шагов ~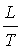 . Таким образом, время вычислений для этих шагов (при
фиксированных T и L0) можно оценить как ~L3. А при всех
(T, L0), как ~L5. Значит, в этом методе время вычислений,
хотя и сокращается, но всё равно имеет порядок L5. Реальные
эксперименты с этим методом показали, что, для молекул РНК длиной около 100
нуклеотидов, этот метод уменьшает время вычислений в полтора – два раза. . Таким образом, время вычислений для этих шагов (при
фиксированных T и L0) можно оценить как ~L3. А при всех
(T, L0), как ~L5. Значит, в этом методе время вычислений,
хотя и сокращается, но всё равно имеет порядок L5. Реальные
эксперименты с этим методом показали, что, для молекул РНК длиной около 100
нуклеотидов, этот метод уменьшает время вычислений в полтора – два раза.
Обратимся теперь к группе методов с памятью. Здесь
основное время вычислений приходится на анализ новых (ещё не возникавших)
структур. Общее число возможных структур на отрезке молекулярной цепи длиной L
можно оценить как ~L3 (экспериментальная оценка). Оценка каждой
структуры требует время ~L, а в целом получается ~L4. После того,
как структуры оценены, остаётся расчет ~L2 вариантов (для всех T и L0).
Это время добавляется к предыдущему и в целом получается ~L4.
Работа выполнена при финансовой поддержке Российского фонда
фундаментальных исследований (проект 99-01-00029).
1. Кугушев Е.И., Козлов Н.Н. Компьютерное
моделирование структурообразующих свойств плюс- и минус-цепей ДНК, кодирующих
5s р РНК и тРНК. (1993), Доклады Академии Наук, 333 (1), стр. 107 – 111.
2. Kozlov N.N., Kugushev E.I.
(1993), Computer simulation of tRNA
secondary structure folding.
CABIOS, v. 9, p. 253 - 258.
3. Кугушев Е. И.,
Козлов Н.Н. (1995), Моделирование влияния структурных перестроек на
процесс образования вторичной структуры РНК. Доклады Академии Наук, 340 (2),
стр. 263 – 267.
4. Козлов Н. Н.,
Кугушев Е.И., Энеев Т. М. (1998), Структурообразующие характеристики
транскрипционного процесса. Математическое моделирование, 10(6), стр. 3 – 19.
5. Туманян В.Г., Сотникова Л.Е., Холопов А.Е. (1966), Об определении
вторичной структуры РНК по последовательности нуклеотидов. Докл. АН СССР, т.
166, N 6, с. 1465 - 1468.
6. Salser,W.
(1977), Globin mRNA sequences: Analysis of base pairing
and evolutionary implications. Cold
Spring Harbor Symp. Quant. Biol., v. 42, p. 985 - 1002.
7. Jacobson A.B. Good L., Simonetti J., Zuker M.
(1984), Some simple
computational methods to improve the folding of large RNAs. Nucleic Acids
Res., v. 12, N 1, p 45 - 52.
8. Freier,S.M., Kierzek,R., Jalger,J.A.,
Sugimoto,N., Caruthers,M.H.,
Neilson,T., and Turner,D.H. (1986), Improved free-energy parameters
for predictions of RNA duplex stability.
Proc. Natl. Acad. Sci. USA, 83, 9373–9377.
9. Ninio,J., (1979), Biochimic, 61, 1133-1150.
|