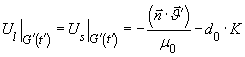Исследование динамики фазового перехода при направленной
кристаллизации металла в переохлажденный расплав на основе
модели фазового поля
|
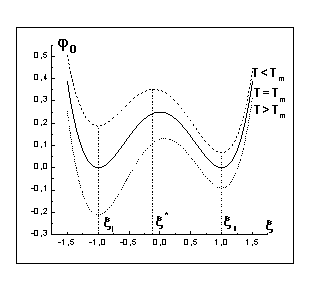 |
Рис.
1
Как это видно из рис.1, при ![]() фаза
фаза ![]() (твердая) находится в стабильном состоянии, фаза
(твердая) находится в стабильном состоянии, фаза![]() (расплав) находится в метастабильном состоянии. При равновесной температуре
фазового превращения
(расплав) находится в метастабильном состоянии. При равновесной температуре
фазового превращения ![]() , и как расплав, так и твёрдая фаза являются стабильными состояниями
системы.
, и как расплав, так и твёрдая фаза являются стабильными состояниями
системы.
Плотность
энтропии ![]() и энтальпии
и энтальпии ![]() системы,
соответствующие потенциалу (9), имеют вид
системы,
соответствующие потенциалу (9), имеют вид
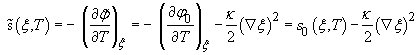 (10)
(10)
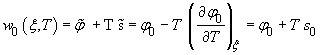 .
(11)
.
(11)
Полагая теплоёмкость
среды

величиной постоянной, независящей от
![]() , плотность энтальпии будет
, плотность энтальпии будет
![]() , (12)
, (12)
где ![]() - температурно-независимая часть энтальпии и
- температурно-независимая часть энтальпии и ![]() - скрытая теплота
фазового перехода единицы объёма.
- скрытая теплота
фазового перехода единицы объёма.
В
соответствии с первым началом термодинамики количество тепла, полученного
единицей объёма системы ![]() , где
, где ![]() - плотность
внутренней энергии системы и
- плотность
внутренней энергии системы и ![]() при постоянной
плотности. Предполагая кондуктивный механизм теплопереноса,
т.е. закон Фурье для теплового потока
при постоянной
плотности. Предполагая кондуктивный механизм теплопереноса,
т.е. закон Фурье для теплового потока
![]() ,
(13)
,
(13)
тогда ![]() и учитывая, что
и учитывая, что
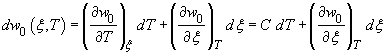 ,
,
можно получить уравнение
сохранения энергии (уравнение для температуры) континуальной
модели
![]() . (14)
. (14)
Для вывода уравнения эволюции параметра порядка рассматривается изменение энтропии![]() в произвольном объёме
в произвольном объёме ![]() двухфазной системы с
течением времени [29,31,34]
двухфазной системы с
течением времени [29,31,34]
![]()
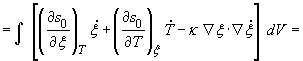
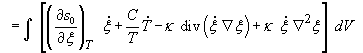 (15)
(15)
Поскольку из (14)
следует соотношение
![]() ,
,
а из (11),(12)
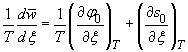 ,
,
учитывая так же, что
![]() ,
,
соотношение (15) преобразуется
к виду
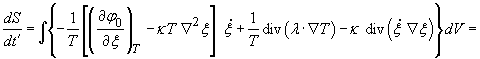
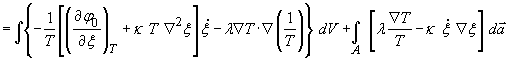 , (16)
, (16)
где ![]() поверхность объёма
поверхность объёма ![]() . Используя (13), для уравнение (16) окончательно можно получить
. Используя (13), для уравнение (16) окончательно можно получить
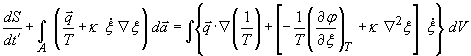 . (17)
. (17)
Интеграл в левой
части (17) представляет собой поток энтропии через границу ![]() объёма
объёма ![]() , обусловленный теплопроводностью (плотность потока энтропии
, обусловленный теплопроводностью (плотность потока энтропии ![]() ) и движением фазового перехода (плотность потока энтропии
) и движением фазового перехода (плотность потока энтропии ![]() [31]). Интеграл в правой
части является источником энтропии в объёме
[31]). Интеграл в правой
части является источником энтропии в объёме ![]() . Производство энтропии обусловлено теплопереносом
. Производство энтропии обусловлено теплопереносом
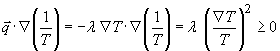
и процессом
релаксации системы к равновесию. Мощность релаксационного источника энтропии
должна быть, в соответствии со вторым началом термодинамики, так же
неотрицательна
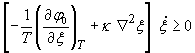 . (18)
. (18)
Наиболее простое
уравнение, удовлетворяющее условию (18), которым описывается процесс релаксации
двухфазной системы к равновесию, будет
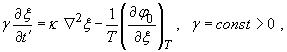 (19)
(19)
Уравнение
эволюции поля параметра порядка типа
(19) известно как временное уравнение Ландау-Гинзбурга [44]
или
Кана-Хиллиарда [46,47], хотя подобное уравнение использовалось и раннее
для описания эволюции неравновесных систем [38].
Свободная
энергия Гиббса всей системы определяется функционалом
![]() (20)
(20)
где ![]() объём, занимаемый системой. При адиабатических условиях на границе
(отсутствие потока тепла и градиента параметра порядка) изменение свободной
энергии с течением времени будет
объём, занимаемый системой. При адиабатических условиях на границе
(отсутствие потока тепла и градиента параметра порядка) изменение свободной
энергии с течением времени будет
![]()
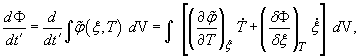 (21)
(21)
где
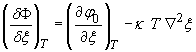 (22)
(22)
вариационная
производная функционала ![]() . В изотермическом случае из уравнения (21) с учетом
(19),(22) следует
. В изотермическом случае из уравнения (21) с учетом
(19),(22) следует
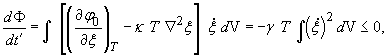
что находится в
соответствии с известной теоремой об убывании свободной энергии
адиабатически-изолированной системы при необратимом изотермическом процессе [45]. В состоянии
равновесия свободная энергия системы достигает минимального значения и ![]() .
.
Неизвестные
параметры модели ![]() в уравнение (19) можно связать с физически-измеряемыми
свойствами системы, задавая плотность термодинамического потенциала
в уравнение (19) можно связать с физически-измеряемыми
свойствами системы, задавая плотность термодинамического потенциала ![]() в явном виде.
Предполагая, что
в явном виде.
Предполагая, что
![]()
где ![]() температурно-независимая часть плотности энтропии, для
плотности термодинамического потенциала с учётом (11),(12) можно получить
температурно-независимая часть плотности энтропии, для
плотности термодинамического потенциала с учётом (11),(12) можно получить
![]()
Уравнения
модели (14),(19), для безразмерной температуры, преобразуются к виду
![]()
![]() (23)
(23)
![]() (24)
(24)
где
![]()
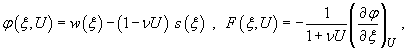
![]()
При равновесной
температуре фазового превращения ![]() предполагается, что
предполагается, что
![]() (25)
(25)
где ![]() - расплав,
- расплав,![]() - твердая фаза. Для плоского фазового перехода в состоянии
равновесия, уравнение для параметра порядка (24) с учётом (25) будет
- твердая фаза. Для плоского фазового перехода в состоянии
равновесия, уравнение для параметра порядка (24) с учётом (25) будет
![]() (26)
(26)
Решение этого
уравнения с граничным условиям
![]()
![]()
известно
![]() (27)
(27)
и параметр ![]() можно интерпретировать как ширину фазового перехода в
равновесном состоянии.
можно интерпретировать как ширину фазового перехода в
равновесном состоянии.
Энергия
поверхностного натяжения на фазовом переходе равна избытку свободной энергии,
обусловленному гетерогенностью. В случае плоского фазового перехода в состоянии
равновесия, энергия поверхностного натяжения на единицу площади будет
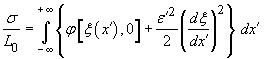 .
(28)
.
(28)
Поскольку, как это
следует из (25),(27),

то из (28)
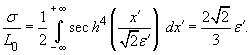 (29)
(29)
Ширина фазового
перехода ![]() является характерным масштабом длины поля параметра порядка.
Характерная длина теплового поля
является характерным масштабом длины поля параметра порядка.
Характерная длина теплового поля ![]() , где
, где ![]() скорость фазового перехода. Когда межфазное число Пекле
скорость фазового перехода. Когда межфазное число Пекле![]() , ширина фазового перехода много меньше длины теплового поля и фазовый
переход можно рассматривать как изотермический. В этом случае методом
согласованных асимптотических разложений для модели (23),(24) можно показать [28,55,57], что с точностью до
членов порядка
, ширина фазового перехода много меньше длины теплового поля и фазовый
переход можно рассматривать как изотермический. В этом случае методом
согласованных асимптотических разложений для модели (23),(24) можно показать [28,55,57], что с точностью до
членов порядка![]() малости для разности тепловых потоков на границах межфазной
области выполняется уравнение (2), а температура межфазной области связана со
скоростью её перемещения уравнением
малости для разности тепловых потоков на границах межфазной
области выполняется уравнение (2), а температура межфазной области связана со
скоростью её перемещения уравнением
![]() (30)
(30)
Из (3),(30) следуют
соотношения связывающие параметры модели фазового поля![]() с физически-измеряемыми макроскопическими свойствами
межфазной поверхности
с физически-измеряемыми макроскопическими свойствами
межфазной поверхности
![]() (31)
(31)
или
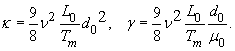
Теплофизические
параметры чистого никеля, расплав которого может находиться в состоянии
сильного переохлаждения, достаточно хорошо известны [52]
![]()
![]()
и параметры модели
(31) для Ni ![]()
§2.
Постановка задачи для плоского фронта кристаллизации.
В одномерном случае (плоский фронт) кристаллизации в переохлаждённый
расплав для неограниченной области ![]() уравнения модели
(23), (24) в безразмерных переменных
уравнения модели
(23), (24) в безразмерных переменных ![]() имеют вид
имеют вид
![]() (32)
(32)
![]() (33)
(33)
где
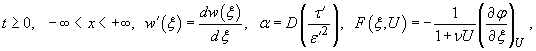
![]() .
.
Функция ![]() - температурно-независимая часть энтальпии может быть выбрана
различными способами [31,34,35,54-60], в дальнейшем используется
- температурно-независимая часть энтальпии может быть выбрана
различными способами [31,34,35,54-60], в дальнейшем используется
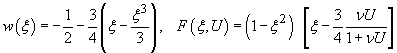 .
(34)
.
(34)
Граничные условия
для уравнений (32), (33) задаются соотношениями
![]() (35)
(35)
![]() (36)
(36)
При невысокой
степени переохлаждения ![]()
![]() . Начальные условия для температуры соответствуют
автомодельному решению (5)-(7) задачи Стефана
. Начальные условия для температуры соответствуют
автомодельному решению (5)-(7) задачи Стефана
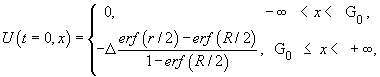 (37)
(37)
где
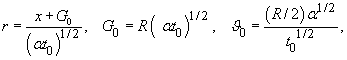
![]() произвольная постоянная. Если постоянная
произвольная постоянная. Если постоянная ![]() выбрана, так что
длина теплового поля (37) в начальный момент времени
выбрана, так что
длина теплового поля (37) в начальный момент времени ![]() , то фазовый переход можно рассматривать как изотермический
и, полагая температуру межфазной области близкой к равновесной, задавать в
качестве начальных условий для поля параметра порядка равновесное решение (27)
, то фазовый переход можно рассматривать как изотермический
и, полагая температуру межфазной области близкой к равновесной, задавать в
качестве начальных условий для поля параметра порядка равновесное решение (27)
![]() (38)
(38)
В этом случае можно
ожидать, что решение задачи (32)-(38) будет близко к решению задачи Стефана
(1)-(3), и при ![]() выходить на
автомодельное решение (5)-(7) классической задачи Стефана кристаллизации в
переохлаждённый расплав.
выходить на
автомодельное решение (5)-(7) классической задачи Стефана кристаллизации в
переохлаждённый расплав.
При
гиперохлаждении ![]() задача (32)-(36)
может иметь квазистационарное решение [37,56], т.е. фазовый переход
движется с постоянной скоростью
задача (32)-(36)
может иметь квазистационарное решение [37,56], т.е. фазовый переход
движется с постоянной скоростью![]() После замены переменных
После замены переменных![]() уравнения (32), (33) приводятся к виду
уравнения (32), (33) приводятся к виду
![]() (39)
(39)
![]() (40)
(40)
![]() (41)
(41)
а граничные условия
(35), (36) будут
![]() (42)
(42)
![]() . (43)
. (43)
Интегрирование
уравнения (39) приводит к соотношению
![]()
и полагая ![]() , получаем уравнение, связывающее температуры расплава и
твёрдой фазы
, получаем уравнение, связывающее температуры расплава и
твёрдой фазы
![]() . (44)
. (44)
Поскольку![]() , то необходимым условием квазистационарного решения задачи
(32)-(36) является
, то необходимым условием квазистационарного решения задачи
(32)-(36) является ![]() и, поскольку
и, поскольку ![]() , то
, то ![]() .
.
Начальное
условие для температуры задается в соответствии с квазистационарным решением
(8) задачи Стефана
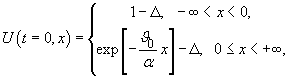 (45)
(45)
где ![]() .
.
Для
постановки начального условия поля параметра порядка используется известное
изотермическое ![]() решение задачи (40),(41),(43)
решение задачи (40),(41),(43)
![]()
(46)
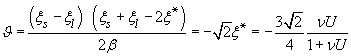
Если ![]() то, длина теплового поля (45)
то, длина теплового поля (45) ![]() и изотермическое приближение справедливо. Полагая в (41)
и изотермическое приближение справедливо. Полагая в (41) ![]() , из (46) следует
, из (46) следует
![]() .
.
Таким
образом, если ![]() то, задавая начальные условия для параметра порядка в виде (38),
а для температуры (45) можно ожидать, что квазистационарное решение задачи
(32)-(35) будет близко к квазистационарному решению (8) задачи Стефана кристаллизации
в гиперохлаждённый расплав.
то, задавая начальные условия для параметра порядка в виде (38),
а для температуры (45) можно ожидать, что квазистационарное решение задачи
(32)-(35) будет близко к квазистационарному решению (8) задачи Стефана кристаллизации
в гиперохлаждённый расплав.
§3. Разностная схема
и алгоритм адаптации сетки к решению.
Основная
трудность, связанная с численным решением задачи (32)-(36), заключается в том,
что ширина межфазной области, где параметр порядка заметно меняется, может быть
много меньше длины теплового поля. Для аппроксимации пространственных
производных поля параметра порядка в этой области с необходимой точностью, шаг
сетки должен быть достаточно малым.
Поскольку межфазная область является подвижной, шаги пространственной сетки
должны изменятся с течением времени, адаптируясь к этой особенности решения
задачи [65]. Эффективным алгоритмом построения адаптивных сеток
для нестационарных задач с большими градиентами является метод динамической
адаптации [61-64].
В
основе метода лежит переход от исходной системы координат ![]() физического
пространства к нестационарной системе координат
физического
пространства к нестационарной системе координат ![]() расчетного
пространства, в котором область больших градиентов решения неподвижна. Полагая,
что
расчетного
пространства, в котором область больших градиентов решения неподвижна. Полагая,
что ![]() соотношение перехода от физического пространства к расчётному
и что существует обратное невырожденное преобразование
соотношение перехода от физического пространства к расчётному
и что существует обратное невырожденное преобразование ![]() , для частных производных можно получить соотношения
[61]
, для частных производных можно получить соотношения
[61]
![]() (47)
(47)
где
функции![]() -метрический коэффициент,
-метрический коэффициент,![]() -скорость движения системы координат, связаны между собой
соотношением
-скорость движения системы координат, связаны между собой
соотношением
![]() . (48)
. (48)
Уравнения модели и
граничные условия (32)-(36) в новых независимых переменных ![]() расчетного пространства
имеют вид
расчетного пространства
имеют вид
![]() (49)
(49)
![]() (50)
(50)
![]() (51)
(51)
![]() (52)
(52)
где ![]() - энтальпия,
- энтальпия,
![]() ,
, 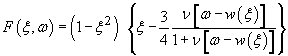 ,
,
![]() ;
; ![]() - координаты границ расчетной области
- координаты границ расчетной области
![]() . (53)
. (53)
Дополнительное
уравнение для функции скорости узлов ![]() , которое определяет механизм адаптации сетки к решению и
замыкает систему уравнений (48)-(50), определяется из требования квазистационарности
[63-64] энтальпии в расчетном пространстве. Нестационарная система координат
, которое определяет механизм адаптации сетки к решению и
замыкает систему уравнений (48)-(50), определяется из требования квазистационарности
[63-64] энтальпии в расчетном пространстве. Нестационарная система координат ![]() выбирается таким
образом, чтобы
выбирается таким
образом, чтобы ![]() . Из уравнения (49) следует требуемое уравнение для функции
. Из уравнения (49) следует требуемое уравнение для функции ![]()
![]() (54)
(54)
Для
конечно-разностной аппроксимации используется дивергентная форма уравнений
(48)-(50)
![]() ,
(55)
,
(55)
![]() ,
(56)
,
(56)
![]() ,
, ![]() ,
(57)
,
(57)
где
![]() .
.
Сетка
в расчетном пространстве выбирается равномерной по пространственной координате ![]() ,
, ![]() -число шагов сетки,
-число шагов сетки, ![]()
![]()
![]()
![]()
![]() координаты целых и полуцелых узлов.
Шаг интегрирования по времени
координаты целых и полуцелых узлов.
Шаг интегрирования по времени ![]() может меняться в
процессе вычислений
может меняться в
процессе вычислений ![]() . К целым узлам относятся функции
. К целым узлам относятся функции![]() , к полуцелым узлам относятся
, к полуцелым узлам относятся ![]()
![]()
![]()
![]() . Для конечно-разностной аппроксимации уравнений модели (55)-(57)
используется схема с центральными разностями второго порядка точности [66]
. Для конечно-разностной аппроксимации уравнений модели (55)-(57)
используется схема с центральными разностями второго порядка точности [66]
![]()
![]() , (58)
, (58)
![]()
![]() , (59)
, (59)
![]() , (60)
, (60)
![]()
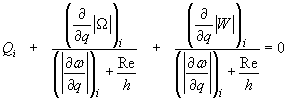 ,
(61)
,
(61)
где ![]() - регуляризирующий параметр [63],
- регуляризирующий параметр [63],
![]()
![]()
![]() .
.
Система (58)-(61)
разностных нелинейных алгебраических уравнений решалась методом Ньютона. На
каждой итерации лианеризованная система уравнений (58)-(61) “расщеплялась” по физическим
процессам. В начале, с помощью прогонки, решалась “энтальпийная” часть задачи, т.е.
уравнение (58) при заданном поле параметра порядка. Затем, так же прогонкой,
решалось “релаксационное” уравнение (59) параметра
порядка при заданной энтальпии. Итерация заканчивается вычислением значений
функций ![]() из уравнений
(60),(61). Такая процедура решения линеаризованных уравнений с помощью
раздельных прогонок оказывается более экономичной, чем с использованием
матричной прогонки. Шаг интегрирования по времени
из уравнений
(60),(61). Такая процедура решения линеаризованных уравнений с помощью
раздельных прогонок оказывается более экономичной, чем с использованием
матричной прогонки. Шаг интегрирования по времени ![]() выбирался автоматически, изменяясь в зависимости от количества
итераций.
выбирался автоматически, изменяясь в зависимости от количества
итераций.
§4. Результаты
тестовых расчетов.
Модель фазового поля (32),(33)
является более общей моделью процесса кристаллизации, чем модели Стефановского
типа. При невысокой скорости движения фронта кристаллизации ![]() , длина теплового поля для типичных металлов много больше ширины
фазового перехода, т.е.
, длина теплового поля для типичных металлов много больше ширины
фазового перехода, т.е.![]() . В этом случае, использование модели Стефана для
описания процесса кристаллизации является вполне оправданным и результаты
расчета динамики фазового перехода на основе модели фазового поля должны быть
близки к решению задачи Стефана (1)-(3). Это означает, что ширина фазового
перехода (ширина профиля параметра порядка) должна слабо меняться со временем,
а скорость его движения и температурное поле вне области фазового перехода
должны совпадать с достаточно высокой
. В этом случае, использование модели Стефана для
описания процесса кристаллизации является вполне оправданным и результаты
расчета динамики фазового перехода на основе модели фазового поля должны быть
близки к решению задачи Стефана (1)-(3). Это означает, что ширина фазового
перехода (ширина профиля параметра порядка) должна слабо меняться со временем,
а скорость его движения и температурное поле вне области фазового перехода
должны совпадать с достаточно высокой
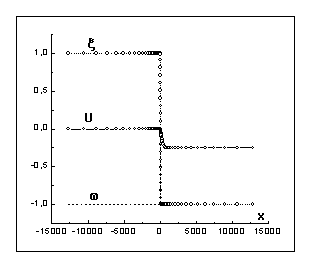
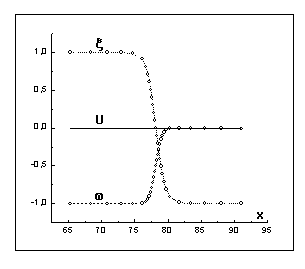
Рис. 2
Рис. 3
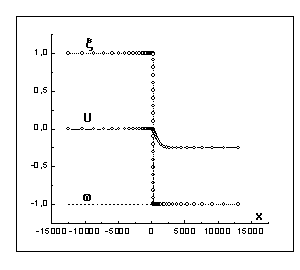
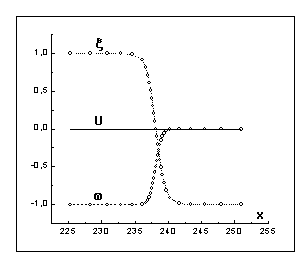
Рис. 4
Рис. 5
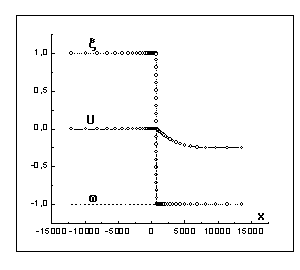
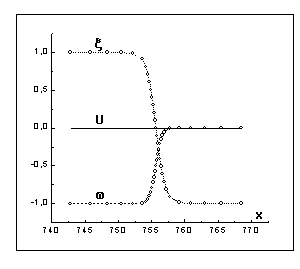
Рис. 6
Рис. 7
точностью со
скоростью движения межфазной поверхности и распределением температуры задачи Стефана.
Для проверки модели фазового поля
(32),(33) и алгоритма динамической адаптации, использованного для её численной
реализации, было проведено два тестовых расчета процесса кристаллизации металла
для плоского фронта (одномерная геометрия) в переохлажденный расплав в условиях
когда ![]() .
.
На рис.2-7 представлены результаты
расчета процесса кристаллизации металла в слабо переохлажденный расплав ![]() . Граничные и начальные условия для параметра порядка и
температуры задавались в виде (35)-(38) и определялись параметра
. Граничные и начальные условия для параметра порядка и
температуры задавались в виде (35)-(38) и определялись параметра ![]() .
.
На
рис. 2,3 изображены графики зависимостей параметра порядка ![]() , энтальпии
, энтальпии ![]() , и температуры
, и температуры ![]() от координаты
от координаты ![]() для момента времени
для момента времени ![]() в различном
координатном масштабе, а на рис. 4,5; 6,7 представлены графики тех же
функций, но для моментов времени
в различном
координатном масштабе, а на рис. 4,5; 6,7 представлены графики тех же
функций, но для моментов времени ![]() . Маркерами на рисунках обозначены положения узлов адаптивной
сетки. Как это видно из приведенных результатов, профиль
параметра порядка практически не меняется с течением времени, т.е. его движение
носит волновой характер, а температура слабо меняется по ширине фазового
перехода. При этом, как показали расчеты, скорость движения фазового перехода и
температурное поле вне фазового перехода совпадают с автомодельным решением
задачи Стефана (5),(6) с точностью до 1% когда
. Маркерами на рисунках обозначены положения узлов адаптивной
сетки. Как это видно из приведенных результатов, профиль
параметра порядка практически не меняется с течением времени, т.е. его движение
носит волновой характер, а температура слабо меняется по ширине фазового
перехода. При этом, как показали расчеты, скорость движения фазового перехода и
температурное поле вне фазового перехода совпадают с автомодельным решением
задачи Стефана (5),(6) с точностью до 1% когда ![]() становится порядка 10. Параметр
становится порядка 10. Параметр ![]() слабо влияет на динамику фазового перехода при выходе на
автомодельный режим.
слабо влияет на динамику фазового перехода при выходе на
автомодельный режим.
На
рис. 8,9 представлены результаты расчета процесса кристаллизации металла в
сильно-переохлажденный расплав (гиперохлаждение) ![]() . Граничные и начальные условия для поля параметра порядка и
температуры задавались в виде (35),(36), (38),(45) и определялись параметрами
. Граничные и начальные условия для поля параметра порядка и
температуры задавались в виде (35),(36), (38),(45) и определялись параметрами ![]() .
.
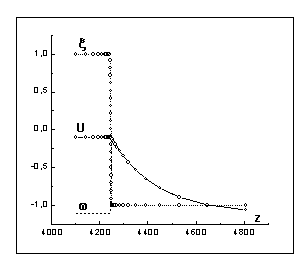

Рис. 8
Рис. 9
Как показали расчёты, решение выходит на квазистационарный режим, т.е.
представляет собой волну кристаллизации, двигающуюся с постоянной скоростью ![]() . Графики зависимостей параметра порядка
. Графики зависимостей параметра порядка ![]() , температуры
, температуры ![]() и энтальпии
и энтальпии![]() от переменной
от переменной ![]() , после установления квазистационарного режима
кристаллизации, представлены в различном координатном масштабе на рис. 8,9.
Скорость движения волны кристаллизации и распределение температуры вне фазового
перехода совпадают с квазистационарным решением задачи Стефана с точностью до
1%.
, после установления квазистационарного режима
кристаллизации, представлены в различном координатном масштабе на рис. 8,9.
Скорость движения волны кристаллизации и распределение температуры вне фазового
перехода совпадают с квазистационарным решением задачи Стефана с точностью до
1%.
§5.
Анализ результатов моделирования динамики плоского фронта
кристаллизации
при гиперохлаждении расплава.
На основе модели фазового поля (32),
(33) были выполнены расчёты динамики плоского фронта кристаллизации при
различной степени переохлаждения расплава ![]() . Граничные и начальные условия задавались в виде (35), (36),
(45), (46) и определялись параметрами
. Граничные и начальные условия задавались в виде (35), (36),
(45), (46) и определялись параметрами ![]() Во всех случаях решение
выходит на квазистационарный режим кристаллизации.
Во всех случаях решение
выходит на квазистационарный режим кристаллизации.
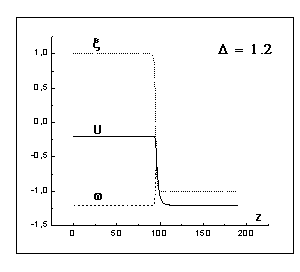
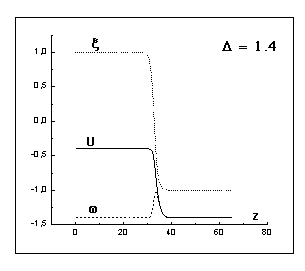
Рис. 10
Рис. 11
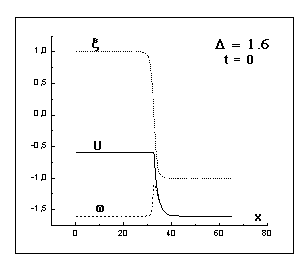
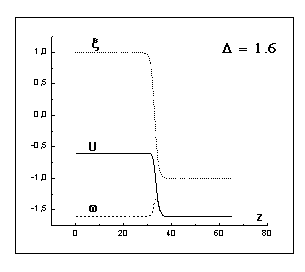
Рис. 12
Рис. 13
Графики зависимостей параметра
порядка ![]() , температуры
, температуры ![]() и энтальпии
и энтальпии ![]() от переменной
от переменной ![]() (
(![]() -скорость движения фронта кристаллизации) после
выхода на квазистационарный режим представлены на рис. 10, 11, 13, 15, а на
рис. 16 изображён график зависимости скорости движения фронта кристаллизации
-скорость движения фронта кристаллизации) после
выхода на квазистационарный режим представлены на рис. 10, 11, 13, 15, а на
рис. 16 изображён график зависимости скорости движения фронта кристаллизации ![]() от величины
переохлаждения
от величины
переохлаждения ![]() для модели фазового
поля (кривая 1) и модели Стефана (линия 2).
для модели фазового
поля (кривая 1) и модели Стефана (линия 2).
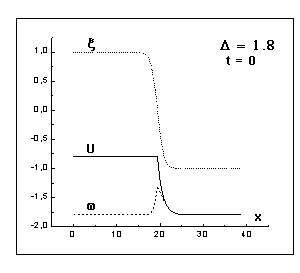
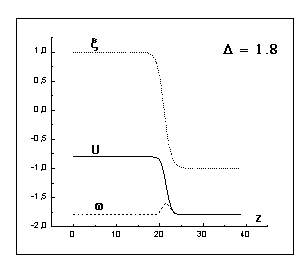
Рис. 14
Рис. 15
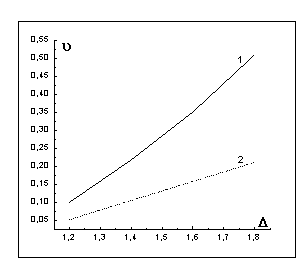
Рис. 16
При невысокой степени гиперохлаждения ![]() функции
функции ![]() (рис. 10,11) мало
отличаются (~5%) от соответствующих им начальных условий, хотя
скорость фронта кристаллизации отличается от скорости фронта квазистационарного
решения модели Стефана (рис. 16) значительно. По мере увеличения глубины
переохлаждения, отклонение квазистационарного решения модели фазового поля
(рис. 13, 15) от соответствующего квазистационарного решения задачи Стефана
(рис. 12, 14) нарастает, так же как и различие в скорости движения фронта
кристаллизации.
(рис. 10,11) мало
отличаются (~5%) от соответствующих им начальных условий, хотя
скорость фронта кристаллизации отличается от скорости фронта квазистационарного
решения модели Стефана (рис. 16) значительно. По мере увеличения глубины
переохлаждения, отклонение квазистационарного решения модели фазового поля
(рис. 13, 15) от соответствующего квазистационарного решения задачи Стефана
(рис. 12, 14) нарастает, так же как и различие в скорости движения фронта
кристаллизации.
Заключение.
Проведённое численное исследование
процесса направленной кристаллизации металла в переохлаждённый расплав на
основе модели фазового поля показало:
1. результаты
моделирования с достаточно высокой точностью согласуются с решениями задачи
Стефана в условиях, когда ширина фазового перехода много меньше длины теплового
поля, т.е. ![]() ;
;
2. при высокой степени
переохлаждения расплава ![]() фазовый переход
движется с постоянной скоростью (квазистационарный режим кристаллизации) и
скорость его движения, в отличие от квазистационарного решения задачи Стефана,
нелинейным образом зависит от величины переохлаждения.
фазовый переход
движется с постоянной скоростью (квазистационарный режим кристаллизации) и
скорость его движения, в отличие от квазистационарного решения задачи Стефана,
нелинейным образом зависит от величины переохлаждения.
Численное
исследование процесса кристаллизации для различных модельных потенциалов и
сравнение результатов с существующими экспериментальными наблюдениями
планируется выполнить в дальнейшем.
Автор считает своим долгом выразить благодарность Мажукину В.И. за
полезные обсуждения численной методики и интерес к работе.
Литература
1. Мейерманов А.М. Задача Стефана. –
Новосибирск: Наука, 1986, 240с.
2. Langer
J.S. Instabilities and pattern formation
in crystal growth. – Rev. Mod. Phys.1980, v. 52, pp.1-28.
3. Kessler
D.A., Koplik J., Levine H. Pattern
selection in fingered growth phenomena. – Adv.
Phys.1988, v. 37, pp.255-339.
4. Уманцев А.Р. Движение плоского фронта при кристаллизации. - Кристаллография, 1985, т. 30, с. 153-160.
5. Борисов В.Т. О механизме нормального роста кристаллов. - ДАН СССР, 1963, т. 151, с. 1311-1314.
6.
Coriell S.R.,
Parker R.L. Interface kinetics and the shape of a solid sphere growing from the
melt. – In “Crystal growth”. Ed. Peiser H.S. Pergamon, Oxford, 1967, pp.
703-708.
7. Glicksman
M.E.,
Shaefer R.J. Investigation of solidification interfaces
temperatures via isenthalpic solidification. - J. Cryst. Grow.1967, v. 1, pp.
297-310.
8.
Shaefer R.J.,
Glicksman M.E. Fully time-dependent theory for the growth of spherical crystal
nuclei. - J. Cryst. Grow. 1969, v. 5, pp. 44-58.
9.
Mikheev L.M.,
Chernove A.A. Mobility of a diffuse simple crystal-melt interface-J. Cryst.
Grow. 1991, v.112, pp.591-596.
10.
Langer J.S. Model
of pattern formation in first-order phase transition. – In “Directions in
condense matter physics”. Eds. Grinstein G., Mazenco G. Word Scientific,
Singapore, 1986, pp. 164-186.
11.
Langer J.S.
Lectures on the theory of pattern formation. – In “Chance and matter”.
Proceedings of the Les Houches summer school of theoretical physics. Les
Houches, 1986. Eds. Souletie J., Vanniemeus J., Stora R. North-Holland, New
York, 1987, pp.629-711.
12.
Brener E.A.,
Temkin D.E., Dendritic growth at deep undercooling and transition to planar
front. – Europhys. Let. 1989,v. 10, pp. 171-175.
13.
Mishbah C.,
Muller-Krumbhaar H., Temkin D.E. Interface structure at large undercooling. -
J. Physique. 1991, ser.1, v.1, pp. 585-601.
14.
Ben Amar M.
Dendritic growth rate at arbitrary undercooling. –Phys. Rev. A. 1990, v. 41,
pp. 2080-2091.
15.
Umantsev A.,
Davis S.H. Growth from a hypercooled melt near absolute stability. – Phys. Rev.
A. 1992, v.15, pp. 7195-7201.
16.
Sarocka D.C.,
Bernoff A.J. An intrinsic equation of interfacial motion for the solidification
of a pure hypercooled melts. - Physica D. 1985, v.85, pp. 348-374.
17.
Strain J.
Velocity effect in unstable solidification. - SIAM J. Appl. Math. 1990, v. 52,
pp.1-15.
18.
Chadam J., Caginalp G. Stability of interface with
velocity correction term. – Rock. Mount. J. Math. , 1991, v. 21, pp.617-629.
19.
Sullivan
J.M.,Jr., Lynch D.R., O’Neill K. Finite element simulation of planar
instabilities during solidification of undercooled melt. - J. Comput. Phys.
1987, v. 69, pp. 81-111.
20. Sullivan J.M.,Jr., Lynch D.R. Non-linear simulation of dendritic solidification of an undercooled melt. - Int. J. Num. Meth. Engin. 1988, v. 25, pp.415-444.
21.
Strain J. A
boundary integral approach to unstable solidification. - J. Comput. Phys.1989,
v. 85, pp.342-389.
22.
Sethian J.A.,
Strain J. Crystal growth and dendritic solidification. - J. Comput. Phys.1992,
v.92, pp. 231-253.
23.
Chan S. -K.
Steady-state kinetics of diffusionless first order phase transitions. - J. Chem. Phys.1977, v.67, pp.6755-6762.
24.
Gunton J.D., San
Miguel M., Sahni P.S. The dynamics of first-order phase transition. - In “Phase
transition and critical phenomena”. Eds. Domb C., Lebowitz J.L. Academic Press,
London, 1983, v. 8, pp. 267-482.
25.
Fix G. Phase
field models for free boundary problems. - In “Free boundary problems: theory
and applications”. Eds. Fasano A., Primicerio M. Pittman, London, 1983, pp.
580-589.
26. Caginalp
G. Surface tension and supercooling in solidification theory. - In “Application
of field theory to statistical mechanics”. Lecture notes in physics, №
216. Ed. Garrido L. Springer, Berlin, 1984, pp. 216-226.
27.
Collins J.B.,
Levine H.I. Diffuse interface model of diffusion-limited crystal growth. –
Phys. Rev. B, 1985, v. 31, pp. 6119-6122.
28.
Caginalp G. An
analysis of phase field model of a free boundary. – Arch. Ration. Mech. Anal. , 1986, v. 92, pp.
205-245.
29. Уманцев А.Р.,
Ройтбурд А.Л. Неизотермическая релаксация в нелокальной среде. – ФТТ, 1988, т. 30, с. 1124-1131.
30. Collins
J.B., Chakrabari A., Gunton J.D. Dynamics of phase separation in a model for diffusion-limited
crystal growth. – Phys. Rev. B, 1989, v. 39, pp. 1506-1511.
31.
Penrose O., Fife
P.C. Thermodynamically consistent models of phase-field type for the kinetic of
phase transitions - Physica D, 1990, v. 43, pp. 44 - 62.
32. Schofield
S.A.,
Oxtoby D., Diffusion disallowed crystal growth. I.
Landau-Ginzburg model. - J. Chem. Phys., 1991, v. 94, pp. 2176-2186.
33.
Lowen H.,
Bechhoefer J., Tuckerman L. Crystal growth at long time: Critical behavior at
the crossover from diffusion to kinetic-limited regimes. – Phys. Rev. A, 1992,
v. 45, pp. 2399-2415.
34.
Wang S. -L.,
Sekerka R.F., Wheeler A.A., Murray B.T., Coriell S.R., Braun R.J., McFadden
G.B. Thermodynamically consistent phase-field models for solidification.
-Physica D, 1993, v.69, pp.189-200.
35.
Penrose O., Fife
P. On the relation between the standard phase-field model and a
“thermodynamically consistent” phase-field model. -Physica D, 1993, v.69,
pp.107-113.
36.
Caginalp G.,
Jones J. A derivation and analysis of phase field models of thermal alloys. –Annal.
Phys., 1995, v.237, pp.66-107.
37.
Bates P.W., Fife
P.C., Gardner R.A., Jones C.K.R.T. The existence of travelling wave solution of
a generalized phase-field model. – SIAM J. Math. Anal, 1997, v.96, pp.60-93.
38.
Мандельштам Л.И.
, Леонтович М.А. К теории поглощения звука в жидкостях. –ЖЭТФ, 1937, т. 7, с.
438-449.
39.
Ландау Л. К
теории фазовых переходов. – ЖЭТФ, 1937, т. 7, с. 19-32.
40. Ландау
Л.Д. К теории фазовых переходов. II – ЖЭТФ, 1937, т. 7, с. 627-632.
41.
Гинзбург В.Л. ,
Ландау Л.Д. К теории сверхпроводимости. – ЖЭТФ, 1950, т. 20, с. 1064-1082.
42.
Cahn J.W.,
Hilliard J.E. Free energy of nonuniform system. I. Interfacial free energy. –
J. Chem. Phys., 1958, v. 28, pp. 258-267.
43.
Cahn J.W.,
Hilliard J.E. Free energy of nonuniform system. III. Nucleation in a
two-component incompressible fluid. – J. Chem. Phys., 1959, v. 31, pp. 688-699.
44.
Ландау Л.Д., Халатников И.М. Об
аномальном поглощении звука вблизи точек фазового перехода второго рода. – ДАН СССР, 1954, т. 96, с. 469-473.
45. Леонтович
М.А. Введение в термодинамику. Статистическая физика. – М.: Наука, 1983, 416 с.
46.
Cahn J.W. Theory
of crystal growth and interface motion in crystalline materials. – Acta Metall.,
1960, v. 8, pp. 554-562.
47.
Cahn J.W. On
spinodal decomposition. –Acta Metall., 1961, v. 9, pp. 795-801.
48. Уайт Р., Джабелл Т.
Дальний порядок в твердых телах. – М.: “Мир”,1982, 448с.
49. Halperin
B.I., Hohenberg
P.C., Ma S. – K.
Renormalization group method for critical dynamics. 1. Recursion
relations and effects of energy conservation. – Phys. Rev. B, 1974, v. 10, pp.
139-153.
50.
Hohenberg P.C.,
Halperin B.I. Theory of dynamic critical phenomena. – Rev. Mod. Phys., 1977, v.
49, pp. 435-479.
51.
Metiu H.,
Kitahara K., Ross J. Statistical mechanical theory of the kinetics of phase
transitions. - In “Fluctuation phenomena. Studies in statistical mechanics”.
Eds. Montroll E.W., Lebowitz J.L. North-Holland Publish. Comp. , Amsterdam,
1979, v. 7, pp. 229-291.
52.
Desai P.D.
Thermodynamic properties of nickel. -
Int. J. Thermophys., 1987, v.8, pp.763-780.
53.
Bassler B.T.,
Hofmeister W.H., Carro G., Bayuzick J. The velocity of solidification of highly
undercooled nickel. - Metall. Mater. Trans., 1994, v. 25A, pp.1301-1308.
54.
Umantsev A.
Thermodynamic stability of phases and transition kinetics under adiabatic conditions.
- J. Chem. Phys., 1992, v. 96, pp.
605-617.
55.
Fife P.C.,
Penrose O. Interfacial dynamics for thermodynamically consistent phase-field models
with nonconserved order parameter. – Electron. J. Diff. Equ. , 1995, v. 1995,
pp. 1-49.
56.
Bates P.W., Fife
P.C., Gardner R.A., Jones C.K.R.T. Phase field model for hypercooled solidification.
– Physica D, 1997, v. 104, pp. 1-31.
57.
Braun R.J.,
McFadden G.B., Coriell S.R. Morphological instability in phase-field models of
solidification. -Phys. Rev., 1994, v. 49, pp. 4336-4352.
58.
Wang S. -L.,
Sekerka R. Computational of the dendritic operating state at large
supercoolings by the phase-field model. – Phys. Rev. E, 1996, v. 53, 3750-3776.
59.
Karma A., Rappel
W. -J. Quantitative phase-field modeling of dendritic growth in two and three
dimensions. – Phys. Rev. E, 1998, v.
57, pp. 4323-4349.
60.
Fabbri M., Voller
V.R. The phase-field method in the sharp-interface limit: a comparison between
model potentials. – J. Comput. Phys., 1997, v.130, pp. 256-265.
61. Мажукин В.И.,
Самарский А.А., Кастельянос О., Шапранов А.В. Метод динамической адаптации для
нестационарных задач с большими градиентами. –
Мат. Моделирование. , 1993, т. 5, с. 33-56.
62.
Мажукин В.И., Самарский А.А., Шапранов
А.В. Метод динамической адаптации в проблеме Бюргерса. – ДАН, 1993, т. 333, с. 165-169.
63.
Mazhukin V.I.,
Shapranov A.A. Numerical solution of transient combustion problem on the grid
dynamically adaptive to the solution. – In “Finite-difference methods: theory
and applications”. Proceedings of second international conference. Ed.
Samarskii A.A., Belarus, Minsk, 1998, v. 3, pp. 19-26.
64. Дёмин М.М., Мажукин
В.М., Шапранов А.А. Метод динамической адаптации в проблеме ламинарного
горения. – ЖВМ и МФ ( в
печати), 2001, т. 41.
65.
McCarthy J.F.
One-dimensional phase field models with adaptive grids. – J. Heat Trans., 1998, v. 120, pp. 956-964.
66. Самарский
А.А. Теория разностных схем. – М. : Наука, 1989, 616 с.