Аннотация
Рассматриваются процессы генерации электромагнитного поля от источника ионизирующего
излучения в воздухе и исследуется искажение этих полей, вызванное присутствием проводящего
объекта. Представлен ряд типичных задач о радиационном возбуждении электромагнитных полей
в окрестности объектов, находящихся в разреженном воздухе. Для объектов цилиндрической и
конической форм построены самосогласованные аксиально-симметричные двумерные модели,
учитывающие влияние объекта на поля и влияние этих полей на кинетику электронов в условиях
плазменных колебаний. Сформулированы граничные условия на проводящих поверхностях этих
объектов, с использованием которых разработана единообразная численная методика и алгоритмы
для проведения численных исследований на многопроцессорной вычислительной технике.
Проведен анализ особенностей генерации полей вблизи объектов, необходимый для построения
эффективного алгоритма численного решения рассматриваемых задач. В частности, определены
амплитудно-временные характеристики полей, оценены пространственные масштабы переходных слоев
между искаженным и невозмущенным полем, а также амплитудные и частотные параметры полей
внутри объекта при наличии у него электропрозрачных участков.
Abstract
The electromagnetic field generation by an ionizing radiation source in air and the distortion
of these fields caused by a conducting object present are considered. The self-consistent
axially symmetric 2D models taking into account the object effect on EMF generated and the
influence of these fields on electron kinetics under plasma oscillations are developed
for the cylindrical and conic objects. The boundary conditions for conducting surfaces
of these objects allowing creation the uniform numerical method and the parallel codes
to perform numerical experiments by using multiprocessor computers are formulated.
The algorithms developed are used to investigate the distortions of the electromagnetic
field with an object present. In particular, amplitude and frequency features of the fields
are analyzed, values of the transition layers from the distorted to the undisturbed fields
are estimated, as well as amplitude and frequency parameters of the fields inside an object
with electrically transparent areas are calculated.
Введение.
Характеристики электромагнитного поля, генерируемого в окрестности
проводящего объекта, находящегося в воздухе, существенно зависят от физических
свойств окружающей объект пространственной области, от
пространственно-временных параметров потоков заряженных частиц, порожденных
ионизирующим излучением, и свойств воздушной плазмы, образующейся в результате
ионизации воздуха этими частицами.
С учетом этого задачи о радиационном возбуждении электромагнитных полей
в воздухе можно условно разбить на две группы:
- задачи о
формировании токов и полей в неоднородной атмосфере с учетом геомагнитного
поля, ионизации воздуха, эффектов самосогласования и других важных факторов,
влияющих на условия протекания соответствующих физических процессов,
- задачи о взаимодействии этих полей с объектами, находящимися в
пространственных областях с различными физическими свойствами (плотность воздуха,
взаимное расположение объекта и источника ионизирующего излучения и др.).
При решении задач первой группы анализируются параметры генерируемых
полей в зависимости от свойств среды в местах расположения источника излучения
и точки наблюдения. Исследуется влияние характеристик источника излучения и
различных физических факторов (изменение плотности воздуха по одной из
пространственных переменных, геомагнитное поле, обратное влияние генерируемых
полей на кинетику электронов воздушной плазмы, порожденной ионизирующим
излучением и т.д.) на пространственно-временное распределение этих полей.
Характерные пространственные масштабы в этих задачах определяются масштабом
неоднородности атмосферы, длиной пробега квантов ионизирующего излучения,
размером области формирования электромагнитного излучения и составляют до
десятков километров. Для описания рассматриваемого явления были разработаны
физические модели [1], получены квадратурные формулы для токов релятивистских
электронов, порожденных ионизирующим излучением [2], предложены модели
воздушной плазмы, возникающей при рассеянии первичных электронов в воздухе
[1,3]. Разработаны методики [4-6], программные комплексы и проведены численные
исследования характеристик электромагнитных полей в различных пространственных
областях с учетом физических эффектов, характерных для рассматриваемых
процессов (см., например, [7-9]).
Проведенные исследования основных особенностей формирования и анализ
характеристик электромагнитных полей в конкретных физических условиях
определяют подход к решению задач второй группы о генерации этих полей в
окрестности объекта. Модель для описания процессов возбуждения
электромагнитного поля вблизи проводящего объекта строится на основе работ
[1,2] с использованием различных приближений (приближение плотной среды,
локально однородного поля и т.д.) и с учетом свойств окружающего объект
пространства. Характерные пространственные масштабы в этих задачах определяются
размерами объектов и масштабами «искажений» электромагнитного поля,
обусловленных присутствием объекта, и составляют до десятков метров. Такие
масштабы позволяют рассматривать поток квантов ионизирующего излучения как
плоский, а «невозмущенное» поле (т.е. поле в отсутствии объекта) считать
однородным. Размеры области искажений электромагнитного поля определяются главным
образом частотными характеристиками невозмущенного поля [10], что существенно
используется для задания расчетной области, постановки внешних граничных
условий при решении задач второй группы в ограниченной области, а также при определении
параметров дискретизации по пространственным переменным при разработке
численной методики.
Ниже рассмотрены
вопросы выбора модели, построения численной методики и реализации параллельных
вычислений на многопроцессорной системе МВС-1000 для математического
моделирования процессов генерации электромагнитных полей в окрестности
проводящих объектов.
Физическая модель и используемые приближения. Модель
рассматриваемого явления строится на основе самосогласованного описания процесса
генерации электромагнитных полей нестационарными уравнениями Максвелла и
кинетики электронов в формирующихся полях.
В процессе формирования электромагнитного поля от ионизирующего
источника в окрестности проводящего объекта существенно влияние последнего на
характеристики генерируемого поля. Наиболее заметным это влияние будет в
случае, когда длина волны поля не превосходит по порядку величины характерных
размеров объекта (порядка метра). При возбуждении электромагнитного сигнала в
воздухе характерные длительности полей определяются масштабом неоднородности
атмосферы (порядка нескольких километров), радиусом закручивания электронов в
геомагнитном поле (сотни метров), а также длиной волны плазменных колебаний электрического
поля в облаке электронов воздушной плазмы [10]. Эти колебания возникают в
разреженном воздухе при достаточно высокой концентрации электронов (когда
частота столкновений электронов воздушной плазмы с молекулами воздуха меньше
ленгмюровской частоты). Длина волны соответствующих колебаний электрического
поля может быть порядка нескольких сантиметров.
Ниже рассматриваются процессы генерации электромагнитных полей в
окрестности объекта в условиях, когда высокочастотная составляющая этого поля
определяется плазменными колебаниями. В этом случае поле в окрестности точки
наблюдения можно считать пространственно однородным (приближение локально
однородного поля [2]), а закручиванием электронов в магнитном поле земли можно
пренебречь. Тогда, пренебрегая междуэлектронными соударениями, уравнение для
плотности тока быстрых электронов можно записать в виде [2,10]
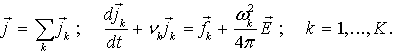
K – количество линий спектра ионизирующего
излучения.
В этом уравнении 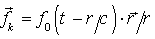 - плотность
источников первичных электронов; nk – частота столкновений электронов с молекулами
воздуха; wk – плазменная частота. - плотность
источников первичных электронов; nk – частота столкновений электронов с молекулами
воздуха; wk – плазменная частота.
При вычислении плотности тока медленных вторичных электронов воздушной
плазмы предполагается, что основным (помимо генерируемого поля) фактором,
влияющим на величину тока, является изменение направления импульса этих
электронов при упругих столкновениях с молекулами воздуха. В настоящей работе
используется приближение, в котором сечение этого процесса не зависит от
скорости электрона (как в [3, 11]), что позволяет получить уравнение для
плотности вторичного тока путем усреднения соответствующего кинетического
уравнения [1,10] по энергетическому распределению. Это уравнение имеет вид
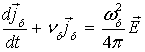 , ,
где:
плазменная частота  ; частота столкновений νδ ; частота столкновений νδ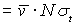 , , 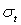 - транспортное
сечение упругого рассеяния, - транспортное
сечение упругого рассеяния, 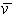 - средняя по
распределению скорость вторичных электронов; N – концентрация нейтральных молекул воздуха. - средняя по
распределению скорость вторичных электронов; N – концентрация нейтральных молекул воздуха.
Концентрация вторичных электронов 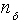 определяется из
уравнений баланса (см., например, [3]), в которых учитываются следующие
процессы взаимодействия этих электронов со средой: трехчастичное и
диссоциативное прилипание электронов к молекулам кислорода, ионизация молекул
азота и кислорода электронами, разогнанными электрическим полем, рекомбинация
электронов и отрицательных ионов с положительными ионами. Скорости этих
процессов, являющиеся коэффициентами в уравнениях баланса, подробно рассмотрены
в [3]. определяется из
уравнений баланса (см., например, [3]), в которых учитываются следующие
процессы взаимодействия этих электронов со средой: трехчастичное и
диссоциативное прилипание электронов к молекулам кислорода, ионизация молекул
азота и кислорода электронами, разогнанными электрическим полем, рекомбинация
электронов и отрицательных ионов с положительными ионами. Скорости этих
процессов, являющиеся коэффициентами в уравнениях баланса, подробно рассмотрены
в [3].
Постановка задачи.
 1. Рассмотрим
идеально проводящий цилиндрический объект радиуса R и высотой H, находящийся в
воздухе. Как указывалось выше поток квантов ионизирующего излучения в окрестности
объекта можно считать плоским, а невозмущенное поле пространственно однородным.
Пусть ось объекта параллельна направлению распространения квантов (рис.1). В
этом случае задача обладает аксиальной симметрией. В цилиндрической системе
координат, ось z которой совпадает с
осью симметрии объекта, уравнения Максвелла для ненулевых компонент
электромагнитного поля имеют вид
1. Рассмотрим
идеально проводящий цилиндрический объект радиуса R и высотой H, находящийся в
воздухе. Как указывалось выше поток квантов ионизирующего излучения в окрестности
объекта можно считать плоским, а невозмущенное поле пространственно однородным.
Пусть ось объекта параллельна направлению распространения квантов (рис.1). В
этом случае задача обладает аксиальной симметрией. В цилиндрической системе
координат, ось z которой совпадает с
осью симметрии объекта, уравнения Максвелла для ненулевых компонент
электромагнитного поля имеют вид
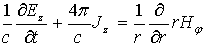 ; ;
 ; ;
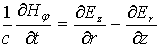 ; ;  . .
На поверхности объекта выполняются условия равенства нулю касательных
компонент электрического поля.
Очевидно, что на
больших расстояниях от объекта, значительно превышающих его размеры,
электромагнитное поле совпадает с невозмущенным полем. С учетом этого вводится
цилиндрическая «внешняя» граница, окружающая расчетную область, на которой
ставятся внешние краевые условия. На боковой поверхности (r=rmax) продольная компонента
электрического поля Ez равна
электрическому полю e, генерируемому в данной
области пространства без объекта (невозмущенное поле). Электрическое поле e является решением локальной по пространству задачи 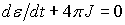 , где J есть решение
уравнений (1.1), (1.2) с Ez=e и нулевыми начальными
условиями. На верхней и нижней границах расчетной области (z=0, z=zmax) ставятся условия
«излучения», которые физически эквивалентны отсутствию проникновения внешнего
электромагнитного сигнала внутрь рассматриваемой области [12,13]. , где J есть решение
уравнений (1.1), (1.2) с Ez=e и нулевыми начальными
условиями. На верхней и нижней границах расчетной области (z=0, z=zmax) ставятся условия
«излучения», которые физически эквивалентны отсутствию проникновения внешнего
электромагнитного сигнала внутрь рассматриваемой области [12,13].
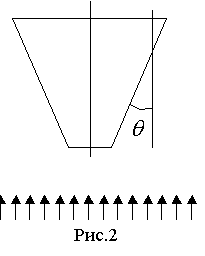 2. Представляет интерес задача о генерации полей, когда ионизирующее
излучение падает под углом к боковой поверхности объекта. Оценку влияния
«наклонного» падения излучения на характеристики полей вблизи объекта можно
провести в следующей аксиально-симметричной постановке. Рассмотрим объект в
форме усеченного конуса (рис.2), на который параллельно оси симметрии падает
ионизирующее излучение. Угол между образующей конуса и осью вращения - q. В этом случае
тангенциальные (по отношению к поверхности объекта) составляющие электрического
поля Et являются комбинацией
компонент полей Ez, Er, входящих в систему уравнений
(2.1). Краевые условия на боковой поверхности усеченного конуса можно записать,
используя равенство нулю на этой поверхности Et и интегральную
форму уравнения Максвелла
2. Представляет интерес задача о генерации полей, когда ионизирующее
излучение падает под углом к боковой поверхности объекта. Оценку влияния
«наклонного» падения излучения на характеристики полей вблизи объекта можно
провести в следующей аксиально-симметричной постановке. Рассмотрим объект в
форме усеченного конуса (рис.2), на который параллельно оси симметрии падает
ионизирующее излучение. Угол между образующей конуса и осью вращения - q. В этом случае
тангенциальные (по отношению к поверхности объекта) составляющие электрического
поля Et являются комбинацией
компонент полей Ez, Er, входящих в систему уравнений
(2.1). Краевые условия на боковой поверхности усеченного конуса можно записать,
используя равенство нулю на этой поверхности Et и интегральную
форму уравнения Максвелла
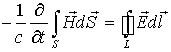
или
соотношение  ( (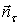 - единичный вектор вдоль образующей конуса) вблизи боковой поверхности
объекта. - единичный вектор вдоль образующей конуса) вблизи боковой поверхности
объекта.
 3. Рассмотрим также
задачу о генерации полей в окрестности и внутри объекта при наличии у него
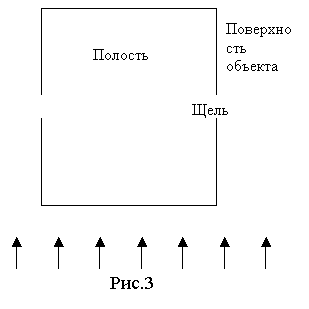
электропрозрачных участков. Пусть полый объект цилиндрической формы состоит из
двух одинаковых частей, изображенных на рис.3. Вокруг объекта – воздушная плазма,
порожденная ионизирующим излучением, в полости – не ионизованный воздух. Оценка
характеристик электромагнитных полей в этом случае проводится путем решения
задачи (2.1, 1.1, 1.2) о генерации электромагнитного поля вне и внутри объекта.
При этом снаружи и внутри на проводящих поверхностях объекта выполняются
граничные условия: равенство нулю касательных компонент электрического поля.
3. Рассмотрим также
задачу о генерации полей в окрестности и внутри объекта при наличии у него
электропрозрачных участков. Пусть полый объект цилиндрической формы состоит из
двух одинаковых частей, изображенных на рис.3. Вокруг объекта – воздушная плазма,
порожденная ионизирующим излучением, в полости – не ионизованный воздух. Оценка
характеристик электромагнитных полей в этом случае проводится путем решения
задачи (2.1, 1.1, 1.2) о генерации электромагнитного поля вне и внутри объекта.
При этом снаружи и внутри на проводящих поверхностях объекта выполняются
граничные условия: равенство нулю касательных компонент электрического поля.
Расчетная методика. Разностная
аппроксимация задачи (2.1, 1.1, 1.2) основана на использовании модифицированной
схемы «крест» и строится аналогично [12]: магнитное поле приписывается центру
прямоугольной пространственно-временной ячейки, электрические поля – ребрам, а
токи соответствующим граням этой ячейки.
При дискретизации
расчетной пространственной области необходимо учитывать основные характерные
пространственные масштабы задачи, в частности, размеры расчетной области
(десятки метров) и объекта (порядка метра), пространственные масштабы изменения
электромагнитного поля (от одного до нескольких десятков сантиметров), а также
размеры «щелей» и других особенностей геометрии объекта. Очевидно, что величина
шага разностной сетки по пространственным переменным определяется минимальным
из указанных пространственных масштабов, а число этих шагов – максимальным. При
этом следует также учитывать различный характер изменения решения задачи по
разным пространственным переменным. Так, например, в рассматриваемой постановке
фронт ионизирующего излучения распространяется вдоль оси z, что обусловливает резкое изменение полей по
этой оси в окрестности указанного фронта. В то же время по переменной r вне области «влияния» объекта электромагнитные
поля меняются слабо.
Для учета краевых
условий на поверхности объекта расчетная сетка выбирается таким образом, чтобы
торцевые и боковые (цилиндрическая либо коническая) части этой поверхности
проходили через центры пространственных разностных ячеек. В этом случае с
использованием (2.2) краевые условия записываются единообразно для всех типов
указанных постановок задач в виде уравнений относительно магнитного поля Hj (нестандартные
формулы расчета в краевых «полуячейках»). Отметим, что для задачи с объектом в
виде усеченного конуса его боковая поверхность проходит по диагонали
пространственной ячейки, что обусловливает необходимость согласования шагов Dr и Dz расчетной сетки.
В качестве примера
приведем формулу для расчета магнитного поля Hj в краевой «полуячейке» на
боковой конической поверхности объекта для задачи 2:
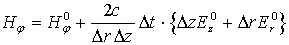 , где верхним индексом «0» обозначены поля, рассчитанные на
предыдущем шаге по времени. , где верхним индексом «0» обозначены поля, рассчитанные на
предыдущем шаге по времени.
Реализованная
численная методика, учитывающая вышеуказанные особенности, позволила, в
частности, проанализировать распределение электромагнитных полей в окрестности
объекта для различных углов падения ионизирующего излучения на его боковую
поверхность.
Важно отметить, что
численное решение рассматриваемых задач является весьма ресурсоёмким, что
обусловлено в значительной степени необходимостью расчета токов электронов и
концентраций электронов воздушной плазмы в каждой пространственной точке.
Оценка количества пространственных ячеек, проведенная с учетом вышеуказанных
особенностей показывает, что для качественной аппроксимации решения (с точки
зрения достаточной точности передачи характерных закономерностей поведения
искомых функций и малости погрешности амплитудных значений полей) число шагов
по каждой из пространственных переменных может быть порядка 103, по
временной переменной - 104, а по спектру ионизирующего излучения
порядка нескольких десятков. В этих условиях проведение численного анализа
процессов генерации полей для различных типов объектов и разных расчетных
ситуаций требует значительных вычислительных ресурсов и больших временных
затрат. С целью повышения эффективности исследований разработаны алгоритмы
распараллеливания вычислений для проведения расчетов на многопроцессорной
вычислительной технике.
Особенностью
рассматриваемой постановки задачи (характерной для всех типов упомянутых выше
объектов) является то обстоятельство, что фронт ионизирующего излучения
распространяется вдоль оси z. Это
порождает резкую пространственную неоднородность решения
вдоль этой оси, обусловленную наличием границы между ионизованной и неионизованной
областями окружающего объект пространства. Причем эта граница перемещается в
пространстве.
Вместе с тем, протекание во времени процессов генерации достаточно
однородно по переменной r. Это
позволяет эффективно использовать вариант «геометрического» принципа
организации параллельного счета на линейке процессоров, каждый из которых
связан обменами лишь с двумя соседними (аналогично [7,10]). Пространственная
расчетная область разбивается по переменной r
на ряд подобластей, разделенных соосными цилиндрами. При этом разбиение
пространственной области определяется количеством используемых процессоров.
Объем обмениваемой информации (два одномерных вектора Hj и Ez) существенно меньше всей
совокупности рассчитываемых в каждом процессоре физических величин: полей,
токов, концентраций электронов. Это обусловливает незначительность временных
потерь на обменные операции на фоне вычислительных затрат.
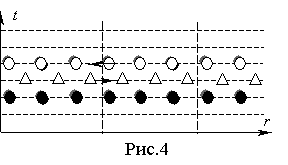 В каждом из
процессоров (за исключением первого и последнего) расчет проводится по одному и
тому же алгоритму. Расчет одного временного слоя происходит в два этапа:
сначала рассчитываются магнитные поля, и осуществляется передача необходимой
информации от левых процессоров правым, затем рассчитываются электрические
поля, и требуемые величины передаются от правых процессоров левым (на рис.4
треугольники - Hj , кружки - Ez, закрашенные кружки
соответствуют полям, рассчитанным на предыдущем слое). Очевидные отличия работы
алгоритма для крайних процессоров обусловлены наличием объекта и внешней
границы расчетной области. В рамках описанного подхода реализован параллельный
вариант расчетной программы на многопроцессорной вычислительной системе
МВС-1000, который обеспечил с использованием 30-50 процессоров численное
решение трудоёмких вариантов разностной задачи в пределах одного – двух часов.
Это позволяет с приемлемыми временными затратами проводить математическое моделирование
исследуемых процессов и подробный анализ электромагнитной обстановки в окрестности
объектов для различных расчетных ситуаций.
В каждом из
процессоров (за исключением первого и последнего) расчет проводится по одному и
тому же алгоритму. Расчет одного временного слоя происходит в два этапа:
сначала рассчитываются магнитные поля, и осуществляется передача необходимой
информации от левых процессоров правым, затем рассчитываются электрические
поля, и требуемые величины передаются от правых процессоров левым (на рис.4
треугольники - Hj , кружки - Ez, закрашенные кружки
соответствуют полям, рассчитанным на предыдущем слое). Очевидные отличия работы
алгоритма для крайних процессоров обусловлены наличием объекта и внешней
границы расчетной области. В рамках описанного подхода реализован параллельный
вариант расчетной программы на многопроцессорной вычислительной системе
МВС-1000, который обеспечил с использованием 30-50 процессоров численное
решение трудоёмких вариантов разностной задачи в пределах одного – двух часов.
Это позволяет с приемлемыми временными затратами проводить математическое моделирование
исследуемых процессов и подробный анализ электромагнитной обстановки в окрестности
объектов для различных расчетных ситуаций.
Примеры результатов
численных исследований.
1. Проводящий объект
существенно влияет на пространственное распределение электромагнитных
полей в области его расположения. При
формировании электромагнитного поля в окрестности такого объекта вблизи его
боковой поверхности возникает переходный пространственный слой, в котором
продольное электрическое поле Ez меняется от нуля на
поверхности до значений, близких к невозмущенному полю e при удалении от
объекта. Амплитуда магнитного поля меняется при этом от максимальной до
пренебрежимо малой.
Упомянем, что оценка
величины переходного слоя h важна при постановке
внешних граничных условий, а также при выборе размеров расчетной области. Кроме
того, эта оценка необходима на этапе дискретизации задачи по пространственным переменным.
Анализ результатов
расчетов показывает, что в разреженном воздухе при достаточно большой плотности
потока ионизирующего излучения, когда затуханием из-за столкновений электронов
с молекулами воздуха можно пренебречь по сравнению с плазменными колебаниями (n в (1.1) и (1.2)
много меньше ω), генерируется
поле Ez, частота которого
определяется плазменной частотой. В этой ситуации h обратно пропорциональна
частоте поля и составляет величину порядка длины волны λ. Частоту генерируемого поля можно оценить путем решения
локальной по пространству задачи для электрического поля ε.
Очевидно, что радиус
rmax цилиндрической
расчетной области следует выбирать много большим, чем h. Кроме того, границы расчетной области следует выбирать так,
чтобы внешние краевые условия не влияли на решение задачи в окрестности объекта
за время наблюдения. На практике это время составляет обычно величину порядка 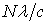 , N ~ 10 – 50. С учетом
этого rmax можно брать
порядка Nλ. Для определения
полей на внешних границах расчетной области одновременно с основной двумерной
задачей решается пространственно локальная задача о генерации поляризационных
электрических полей ε
(невозмущенных полей) в воздухе в отсутствие объекта. , N ~ 10 – 50. С учетом
этого rmax можно брать
порядка Nλ. Для определения
полей на внешних границах расчетной области одновременно с основной двумерной
задачей решается пространственно локальная задача о генерации поляризационных
электрических полей ε
(невозмущенных полей) в воздухе в отсутствие объекта.
Для хорошей точности
передачи пространственной структуры полей минимальный шаг дискретизации следует
выбирать меньшим, чем λ, что,
очевидно, достаточно для приемлемой аппроксимации переходных слоев.
2. Оценку влияния «наклонного» падения ионизирующего излучения на
объект дает сравнительный анализ характеристик электромагнитных полей в
окрестности объектов цилиндрической и конической форм. Такой анализ, проведенный
по результатам расчетов полей для объектов с различным углом θ между образующей и осью симметрии (рис. 2),
показал, что пространственно-временные параметры нормальных и тангенциальных к
поверхности объекта полей слабо зависят от формы указанных выше аксиально
симметричных объектов.

Рис.5
На рис.5 в
качестве примера приведены двумерные распределения амплитуды азимутального
магнитного поля для объектов цилиндрической и конической форм. Темные участки
на этой иллюстрации соответствуют меньшим амплитудам поля, светлые - большим.
Числами по краям изображения отмечены геометрические размеры в сантиметрах.
Видно, что как по величине амплитудных значений (яркость светлых участков), так
и по характерным пространственным масштабам переходных слоев в окрестности объекта
отличия изображений для конуса и цилиндра малы. Эти иллюстрации подтверждают
вывод о слабом влиянии на «внешнюю» электромагнитную обстановку в окрестности
объекта наклонного падения ионизирующего излучения.
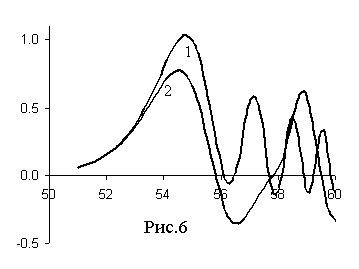 3. В случае, когда проводящий объект имеет электропрозрачные участки,
внутри него формируются электромагнитные поля. Для оценки амплитудно-временных
характеристик этих полей проведены
расчеты в геометрии, описанной выше (рис.3). Анализ результатов этих расчетов
показал, в частности, что внутри объекта генерируются резонаторные
электромагнитные поля, частота которых определяется геометрическими размерами
объекта. На рис.6 приведен пример временных разверток продольного
электрического поля Ez
снаружи (кривая 1) и внутри (кривая 2) объекта. По оси абсцисс отложено время в
наносекундах, по оси ординат – Ez
в относительных единицах. Эти графики показывают, что частота внутренних полей
меньше характерной частоты внешних и определяется поперечным размером объекта
(длина волны поля внутри объекта имеет величину порядка диаметра цилиндра).
Амплитудные значения внутренних полей зависят от расположения точки наблюдения
внутри объекта и меняются от максимальных величин вблизи щели до минимальных у
стенок.
3. В случае, когда проводящий объект имеет электропрозрачные участки,
внутри него формируются электромагнитные поля. Для оценки амплитудно-временных
характеристик этих полей проведены
расчеты в геометрии, описанной выше (рис.3). Анализ результатов этих расчетов
показал, в частности, что внутри объекта генерируются резонаторные
электромагнитные поля, частота которых определяется геометрическими размерами
объекта. На рис.6 приведен пример временных разверток продольного
электрического поля Ez
снаружи (кривая 1) и внутри (кривая 2) объекта. По оси абсцисс отложено время в
наносекундах, по оси ординат – Ez
в относительных единицах. Эти графики показывают, что частота внутренних полей
меньше характерной частоты внешних и определяется поперечным размером объекта
(длина волны поля внутри объекта имеет величину порядка диаметра цилиндра).
Амплитудные значения внутренних полей зависят от расположения точки наблюдения
внутри объекта и меняются от максимальных величин вблизи щели до минимальных у
стенок.
Заключение.
В работе рассмотрен
ряд типичных задач о радиационном возбуждении электромагнитных полей в
окрестности объектов, находящихся в разреженном воздухе. При этом используется
самосогласованное описание электромагнитных полей и кинетики первичных
электронов, порожденных ионизирующим излучением, и вторичных электронов
воздушной плазмы, возникающей в результате ионизации воздуха первичными
электронами. Проведен анализ особенностей генерации полей вблизи объектов,
необходимый для построения эффективного алгоритма численного решения
рассматриваемых задач. Исследовано влияние формы аксиально-симметричного
объекта на характеристики генерируемых полей. Проведена оценка параметров полей
формирующихся внутри объекта, имеющего электропрозрачные участки.
Для указанных
процессов характерна существенная разномасштабность изменения искомых функций
как по пространственным, так и по временной переменным, обусловленная наличием
распространяющегося фронта ионизирующего излучения, а также возникновением
тонких переходных слоев вблизи поверхности объекта. Это диктует необходимость
использования весьма подробной дискретизации расчетной области для достаточно
точной передачи пространственной структуры генерируемых полей. Кроме того,
рассмотрение объектов, границы которых не совпадают с координатными
поверхностями, а также наличие небольших по размеру электропрозрачных участков
накладывают дополнительные ограничения на величину шага пространственной сетки.
Отмеченные
особенности определяют потребность использования высокопроизводительных
многопроцессорных вычислительных систем для эффективного решения задач
генерации электромагнитных полей и их взаимодействия с различными объектами.
Проведенные
исследования показывают возможность эффективного распараллеливания алгоритмов
решения рассмотренных задач радиационного возбуждения электромагнитных полей на
многопроцессорной системе МВС-1000, которая обеспечивает практические
потребности решения таких задач при использовании 50 - 100 процессоров.
Авторы выражают свою
признательность А.В.Забродину за поддержку и постоянное внимание к работе.
Литература.
1. М.Е.Жуковский. Самосогласованная квазитрехмерная модель радиационного возбуждения
электромагнитных полей. Математическое моделирование, том 8, №4, 1996, с.3-20.
2. М.Е.Жуковский. Плотность тока релятивистских комптоновских электронов, порожденных
нестационарным источником гамма-квантов, находящимся в неоднородном воздухе, в
присутствии внешнего электромагнитного поля. Математическое моделирование, том
5, №10, 1993, с.67-78.
3. И.И.Евстигнеев, М.Е.Жуковский. Самосогласованная модель радиационного возбуждения продольных
электрических полей в воздухе. Математическое моделирование, том 1, №5, 1989,
с.60-70.
4. Г.Д.Васильков, И.И.Евстигнеев,
М.Е.Жуковский. Методика расчета электромагнитных полей
в квазитрехмерной модели. ЖВМ и МФ, том 28, №4, 1988, с.568-579.
5. М.Е.Жуковский, С.Г.Пономарев. Численная методика решения задачи о радиационном возбуждении
электромагнитных полей в воздухе в двумерной самосогласованной модели.
Математическое моделирование, том 2, №9, 1990, с.3-9.
6. Г.Д.Васильков, М.Е.Жуковский,
В.П.Загонов, Е.Г.Лукьянова. Конструирование
параллельных алгоритмов численного решения задач электродинамики в собственном
времени. Препринт Института прикладной математики им. М.В.Келдыша РАН, №87,
1994.
7. М.Е.Жуковский, В.П.Загонов,
С.Г.Чубукова. Исследование способов распараллеливания
алгоритмов решения нелинейных задач генерации электромагнитных полей в
собственном времени. Препринт Института прикладной математики им. М.В.Келдыша
РАН, №103, 1996.
8. Г.Д.Васильков, В.А.Горячев,
С.Г.Чубукова. Расчет электромагнитного сигнала от
нестационарного гамма-источника в условиях барометрической неоднородности
воздуха. Препринт Института прикладной математики им. М.В.Келдыша РАН, №32,
1991.
9. Р.Г.Высоцкая, М.Е.Жуковский. Численное моделирование радиационного возбуждения электромагнитных
полей в воздухе. Препринт Института прикладной математики им. М.В.Келдыша РАН,
№6, 1996.
10. М.Е.Жуковский, С.Г.Чубукова. Математическое моделирование высокочастотных электромагнитных полей в
воздухе в присутствии объекта. Препринт Института прикладной математики им.
М.В.Келдыша РАН, №83, 1997.
11. Г.Д.Васильков, М.В.Скачков. Генерация
высокочастотных электромагнитных полей в опытах по оценке электромагнитного
воздействия. Модель «теплой» плазмы. Препринт Института прикладной математики
им. М.В.Келдыша РАН, №34, 1995.
12. Г.Д.Васильков, М.В.Скачков. Генерация высокочастотных электромагнитных полей в опытах по оценке
электромагнитного воздействия. Двумерная методика и результаты расчетов.
Препринт Института прикладной математики им. М.В.Келдыша РАН, №36, 1995.
13. Г.Д.Васильков, Е.Г.Лукьянова. О математической модели эксперимента по оценке воздействия
высокочастотных электромагнитных полей на объект. Препринт Института прикладной
математики им. М.В.Келдыша РАН, №68, 1994.
|