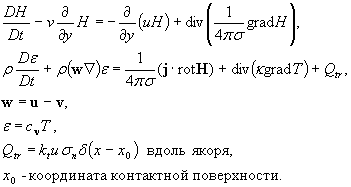Аннотация
В работе представлена прикладная программа EML, обеспечивающая автоматизацию проведения
вычислительных экспериментов для изучения процесса электродинамического разгона проводящих
макротел в ускорителе типа рельсотрон в пространственно двумерном приближении. Приведена
соответствующая физико-математическая модель и кратко описан используемый численный алгоритм.
Применение данной пользовательской оболочки проиллюстрировано на примере исследования влияния
анизотропии электропроводности материала проводников на картину протекания тока в рельсотроне.
Основные преимущества проведения серий расчетов при помощи прикладной программы EML – удобство
задания области со сложной геометрией и подобластями с различными физическими свойствами,
а также значительное упрощение процедур хранения и обработки результатов расчетов и подготовки
исходных данных.
Abstract
In the paper, there is presented the software application EML, which is used for automation
of the process of numerical experiments for studying electromagnetic launch of conducting
macroscopic objects in an accelerator of a railgun type in a spatially two-dimensional
approximation. The corresponding physical-mathematical model is presented and the numerical
algorithm used is described in brief. The use of this application is illustrated by an example
of the study of effects of anisotropy of electric conductivity of a material of conductors
on a distribution of current in a railgun. Main advantages of the conducting of series of
calculations with the help of application EML is the convenience of specifying an area of
complicated geometry and sub-areas with different physical properties, as well as significant
simplification of storage and processing of results of calculations and preparation of input
data.
Содержание
Введение.
Постановка задачи
§ 1.
Прикладная программа EML.
1.1.
Общая структура приложения EML
1.2.
Задание геометрии области сложного вида
1.3.
Задание физических свойств и параметров вычислений
§ 2.
Пример применения программы EML.
Заключение
Литература
Введение.
Постановка задачи
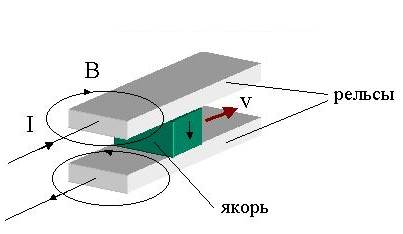
Рис. 1. Принципиальная схема рельсотрона.
Рассмотрим
электродинамический ускоритель типа рельсотрон (см. рис. 1) [1, 2]. Магнитное
поле с индукцией В, создаваемое
током I,
протекающим по рельсам и якорю, вызывает появление ускоряющей силы Лоренца
(Ампера). Направление ее действия соответствует обычному правилу вычисления
векторного произведения [j
´
B]. Сила Лоренца разгоняет якорь, движущийся
вдоль рельсов и диэлектрических направляющих (они на рисунке не показаны). С
электротехнической точки зрения рельсотрон представляет собой линейный
электрический двигатель постоянного тока. Фундаментальная проблема организации
работы подобного устройства и достижения высоких и сверхвысоких скоростей
макротел [1 - 3] состоит в том, что через скользящий контакт якорь / рельс
приходится пропускать токи до нескольких миллионов Ампер. Экспериментальная
практика показала, что после достижения якорем некоторой скорости (обычно около
1 км/с) контакт якорь / рельс теряет свойства чисто металлического и
превращается в смешанный (появляется электродуговой разряд, т.е. плазма). Это
приводит к разрушению как якоря, так и рельса, и не позволяет эффективно
преобразовать электрическую энергию, запасенную в источнике, в кинетическую
энергию якоря. Переход электрического контакта из электрического в плазменный
обычно приводит к тому, что ускорение якоря резко падает. Очевидно, что для
принятия технологических решений при проектировании реальных устройств
необходимо правильное физико - математическое моделирование процессов на
контакте.
Основным
инструментом исследования явления электромагнитного ускорения, применяемым в
данной работе, является обычная математическая модель [4, 5] в пространственно
двумерном приближении. Модель соответствует геометрии, показанной на рис. 2.
Так как устройство симметрично, то моделирование достаточно вести в половине
(верхней) приведенной области. Начало системы координат лежит на оси симметрии
рельсотрона напротив левого торца рельса. Модель представляет собой систему,
состоящую из уравнений диффузии магнитного поля и энергии (в форме уравнения
теплопроводности):


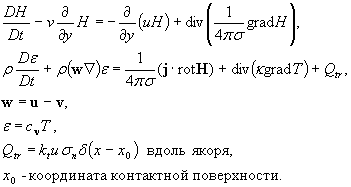
Здесь использованы
обычные обозначения: r - плотность, e - удельная внутренняя энергия,
H – напряженность магнитного поля (единственная
ненулевая компонента вектора H, направленная
перпендикулярно плоскости рисунка, при этом напряженность электрического поля E имеет две ненулевые компоненты, лежащие в плоскости рисунка), s -
удельная электропроводность материала, u
- скорость движения вещества, v -
скорость движения якоря, k -
коэффициент теплопроводности, T -
температура, Qtr -
мощность тепловыделения за счет трения на контактной поверхности, cV - удельная теплоемкость
при постоянном объеме, kt
- коэффициент трения, sn - нормальное механическое давление на
контакте, d
- дельта – функция
Дирака, x0 – координата контакта якорь – рельс (по x). Кроме
уравнений (1), в модель входит обычное уравнение Ньютона, описывающее
координату, скорость и ускорение тела, меняющиеся под действием интегральных
сил Лоренца и трения. Оно здесь для краткости опущено. Задача решается в
половине пространственной области, изображенной на рис. 2, при t > 0.
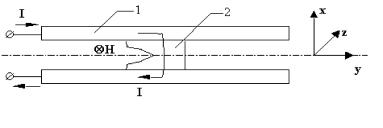
Рис. 2. Постановка пространственно двумерной задачи.
Начальные условия задачи таковы:
температура везде одинакова и задана, напряженность магнитного поля везде равна
нулю, начальная скорость якоря задана:
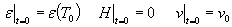 . (2) . (2)
Граничные условия
задачи состоят в следующем: на всех границах области, кроме отрезков прямых x = 0 и y = 0 и левого межрельсового пространства, напряженность магнитного
поля H равна нулю; в пространстве между рельсами
слева от якоря напряженность магнитного поля H задана
(в виде зависимости от величины полного протекающего тока); на оси симметрии x = 0 внутри якоря в силу симметрии отсутствует тангенциальная
компонента напряженности электрического поля; на торце рельса отсутствует
тангенциальная компонента напряженности электрического поля в системе
координат, где вещество покоится (отсутствие тока поперек рельса):

(3)
Тепловой поток на
всех внешних границах (кроме правого торца рельса) области равен нулю: 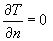 , на правом торце рельса , на правом торце рельса 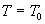 . .
Система уравнений
записана с применением смешанных эйлерово - лагранжевых переменных (СЭЛ).
Производная 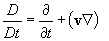 означает производную по времени при фиксированных СЭЛ -
переменных. Мощность тепловыделения за счет трения моделируется соотношением,
включающим коэффициент трения, скорость скольжения и нормальное механическое
напряжение на контакте. означает производную по времени при фиксированных СЭЛ -
переменных. Мощность тепловыделения за счет трения моделируется соотношением,
включающим коэффициент трения, скорость скольжения и нормальное механическое
напряжение на контакте.
Численный алгоритм
для реализации модели на ЭВМ основан на методе конечных элементов [4 - 8] и
удовлетворяет требованиям полной консервативности и квазимонотонности. Для
аппроксимации неизвестного решения задачи использовались два семейства
аппроксимирующих функций, соответствующих разбиению области на треугольники и
ячейки Дирихле. Первое семейство – это плоскость в пределах треугольника,
проходящая через 1 в одной из вершин и 0 в двух других. Второе – это
характеристическая функция ячеек Дирихле – то есть 1 внутри ячейки и 0 вне
ячейки. Алгоритм получения системы алгебраических уравнений для амплитуд конечных
элементов подробно описан в [4, 5].
Полученная система
уравнений даже в рассматриваемом пространственно двумерном случае, вообще
говоря, является нелинейной. Нелинейность системы вызвана зависимостью электро
– и теплофизических параметров от температуры, которая в свою очередь
определяется через джоулево тепловыделение в результате протекания
электрического тока и выделения тепла в результате трения.
Для нахождения
решения нелинейной системы алгебраических уравнений устроен итерационный
процесс, называемый внешним. При этом уравнения электродинамики и кинематики
решаются при фиксированных значениях температуры, взятых с предыдущей итерации.
Известными также считаются и значения теплофизических параметров в уравнении
теплопроводности. Для прекращения внешних итераций используется некоторый
критерий обрыва итераций в зависимости от величины относительного изменения
решения на двух последовательных итерациях.
На каждой внешней
итерации для нахождения приближенного решения необходимо решить две системы
линейных алгебраических уравнений (для H
и T). Для нахождения H используется метод неполной
декомпозиции Холесского с применением метода сопряженных градиентов [9, 10].
Приближенные значения температуры в силу малости коэффициента теплопроводности
на данных характерных временах находятся с помощью метода Зейделя. Наличие
фазовых переходов в системе учитывается с помощью однородного метода [11].
Некоторые другие подробности организации итерационных процессов приведены в
[5].
Целью данной работы
является разработка и применение специальной пользовательской оболочки,
предназначенной для организации расчета задач указанного типа в областях
сложной геометрической формы с неоднородными электро – и теплофизическими
свойствами.
На первых стадиях
работы над данной программой в этой деятельности принимал участие П.Ю. Бородин.
§ 1. Прикладная
программа EML
Описанная во
введении численная модель реализована в прикладной программе EML. Программа EML позволяет
автоматизировать процесс проведения вычислительных экспериментов. Будучи
создана на языке Microsoft FORTRAN, она является
приложением MS - DOS. В связи с особенностями библиотеки графических подпрограмм и функций
компилятора Microsoft FORTRAN Powerstation 1.0 приложение EML.exe из операционной
системы Windows должно запускаться ярлыком, в котором на вкладке "Программа"
следует щелкнуть левой клавишей мыши по кнопке "Дополнительно" и
установить флажок “Не давать программе обнаружить Windows”. Если в
конфигурации компьютера отсутствует мышь, то программа не запускается.
Оболочка
пользователя предусматривает следующие основные сценарии проведения
вычислительного эксперимента:
а) задание новой
геометрии области;
б) загрузка из
файла существующей геометрии области;
в) построение
новой сетки;
г) загрузка из
файла существующей для данной расчетной области сетки;
д) задание новых
тепло - и электрофизических параметров;
е) загрузка из
файла существующего набора физических параметров;
ж) решение задачи
с заданного начального момента времени;
з) продолжение
решения с момента, в который был остановлен предыдущий сеанс счета.
Сценарии реализуются предоставлением
возможности сохранять соответствующие файлы на жестком диске и загружать данные
из этих файлов.
Основное преимущество, которое дает
применение пользовательской оболочки EML – возможность
интерактивного задания геометрии области сложного вида. Организация хранения
данных на жестком диске облегчает проведение серий расчетов (вычислительных
экспериментов). Ход решения отображается на экране, позволяя лучше понимать
влияние тех или иных параметров на решение и на вычислительный процесс.
1.1. Общая структура приложения EML.
После запуска
оболочки на экране монитора возникает главное меню. Вид меню приведен на рис.
3. Название каждого пункта главного меню полностью соответствует его
назначению. Ниже приведена структура меню приложения EML (основные окна).
Краткие описания работы с различными окнами приведены в пунктах 1.1 и 1.2.

Рис. 3. Главное меню - появляется при запуске приложения EML.
Геометрия области
задается в окне, которое появляется при выборе в главном меню пункта
"Сетка" – см. рис. 4.
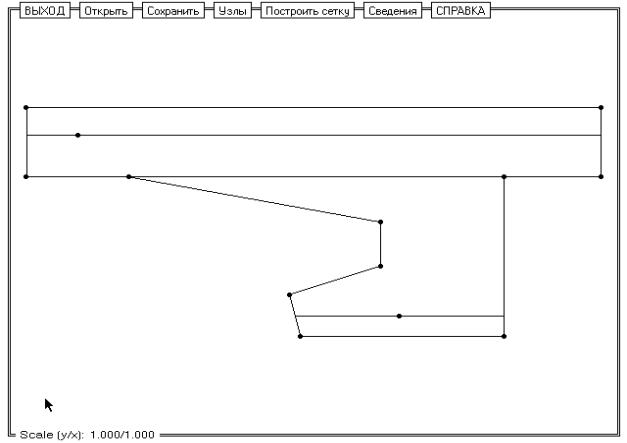
Рис. 4.
Окно, которое появляется при выборе в главном меню пункта "Сетка".
Сетка, которая возникает при выборе пункта
"Построить сетку", показана на следующем рисунке (рис. 5). Процесс
задания геометрии и построения сетки подробно рассматривается ниже в разделе
1.2.
При выборе пункта главного меню
"Исходные данные" появляется окно со списком величин, которые
используются в задаче – в основном это физические свойства материалов якоря и
рельса (причем и якорь, и рельс, могут состоять из двух материалов каждый,
материал верхнего слоя якоря – находиться в различных фазовых состояниях).
Подробнее об этом рассказано в разделе 1.3. Пример набора таких параметров
приведен на рис. 6.
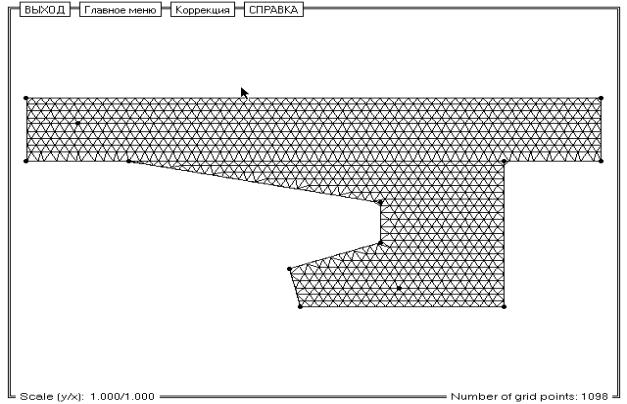
Рис. 5. Окно с вновь созданной сеткой.

Рис. 6. Окно, которое появляется при выборе в главном меню
пункта "Исходные данные".
Следующий по
порядку в главном меню пункт – "Счет". Соответствующее окно показано
на рис. 7. Назначение пунктов меню этого окна очевидно, оно полностью
соответствует названию.
 Рис. 7 - окно, которое появляется при открытии пункта
главного меню "Счет".
Рис. 7 - окно, которое появляется при открытии пункта
главного меню "Счет".
Несколько параметров, отражающих
особенности численного метода, а также параметры вывода результатов решения
задачи на экран монитора и их записи на жесткий диск можно менять в окне,
возникающем при выборе в главном меню пункта "Параметры управления
счетом". Набор таких параметров показан на рис. 8. Более подробно см. в
разделе 1.3.

Рис. 8. Окно, которое появляется при выборе в главном меню
пункта "Параметры управления счетом".
В каждом из окон при открытии пункта меню "Справка" на экран
выводится контекстная справка.
Для навигации по
экрану (то есть либо открытия других окон, либо запуска расчетных и других
процедур, соответствующих пунктам меню) применяется мышь. При помощи клавиатуры
производятся следующие действия:
Esc - отмена при работе с диалоговыми окнами;
Enter – подтверждение при работе с диалоговыми окнами;
“+” – укрупнение масштаба по вертикали (х)-(величина масштаба
отображается в левом нижнем углу экрана) при задании геометрии области;
“-” - измельчение масштаба по вертикали при задании геометрии;
ввод чисел при задании исходных данных;
ввод имен файлов при сохранении данных на жестком диске.
1.2.
Задание геометрии области сложного вида.
Как уже упоминалось
выше, основное преимущество, которое дает применение пользовательской оболочки EML – возможность
интерактивного задания геометрии области сложного вида. Область может состоять
из четырех подобластей с различными физическими свойствами. При этом
пользователю предоставляется возможность проверить разбиение области на
конечные элементы, и, если требуется, вручную корректировать разбиение.
Рассмотрим
процедуру задания геометрии с помощью пользовательской оболочки EML более подробно. При
открытии пункта главного меню "Сетка" возникает окно, показанное на
рис. 4. Границы областей задаются при помощи мыши перемещением маркеров.
Маркеры – это кружочки на рис. 4 и аналогичных ему. Одиннадцать маркеров в
углах области определяют ее границы, и два маркера внутри области – разбиение рельса
и якоря на подобласти из различных материалов (слои на поверхности). Маркер
перемещается при его перетаскивании мышью (щелчок левой клавиши мыши по маркеру
и перемещение мыши, удерживая левую клавишу нажатой). При щелчке правой
клавишей мыши по маркеру возникает окно с координатами этого кружочка, которые
можно отредактировать с клавиатуры. Имеется возможность задавать шаг разбиения
области на элементы (щелчок по пункту "Узлы" и нажатие клавиши "Enter" на
клавиатуре). Включение пункта "Сведения" выводит на экран информацию
о координатах выделенного маркера, курсора и о максимальных размерах области.
После того, как
границы области и ее разбиение на подобласти заданы, щелчком по пункту меню
"Построить сетку" проводится разбиение области на конечные элементы.
Появляется окно, показанное на рис. 5.
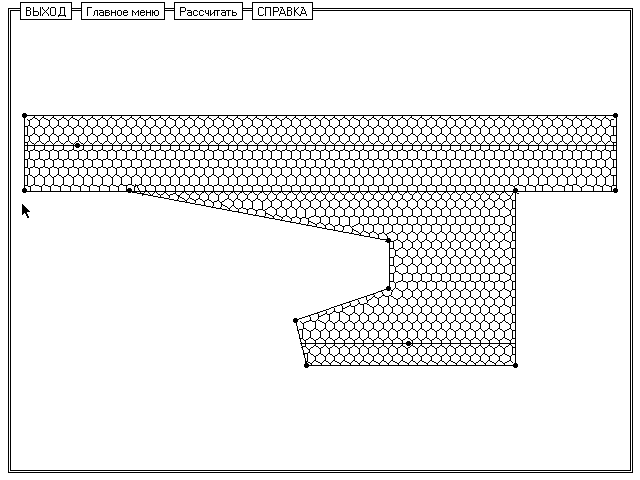
Рис. 9. Окно, которое появляется при открытии пункта главного
меню "Ячейки Дирихле" и щелчка левой клавиши мыши по
"Рассчитать".
Необходимость в
коррекции сетки вручную возникает, если, например, при визуальном просмотре
построенной сетки обнаруживаются дефектные места. Это чаще всего могут быть
тупоугольные треугольники. Наиболее распространенной причиной их появления
являются невыпуклые области, в которых необходимо решать задачу. В этом случае
вручную возможно модифицировать построенную сетку и устранить дефектные
треугольники. Аналогичная необходимость может возникнуть при наличии в
рассматриваемой области точек, в окрестности которых решение задачи имеет какие
– либо особенности. В этом случае желательно сгустить сетку вблизи такой точки.
Это также можно сделать вручную в рамках данного приложения.
Пример невыпуклой
области с построенной дефектной сеткой, которая нуждается в ручном
редактировании, показан на рис. 10. При щелчке по "Коррекция"
появляется приглашение выделить область для редактирования, что делается с
помощью щелчка левой клавиши и перетаскивания. Возникает окно, показанное на
рис. 11, причем коррекция сетки проводится при помощи мыши в окне, где сетка
изображена в увеличенном масштабе.
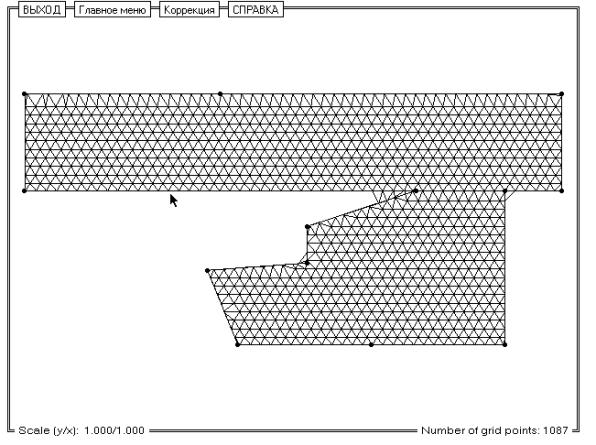
Рис. 10. Сетка, которая требует редактирования вручную.
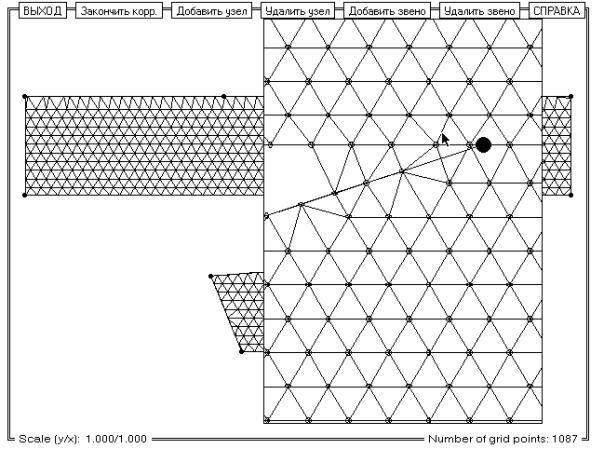
Рис. 11. Окно коррекции сетки (до
коррекции).
На рис. 12 показана отредактированная сетка,
из которой удалены лишние звенья.
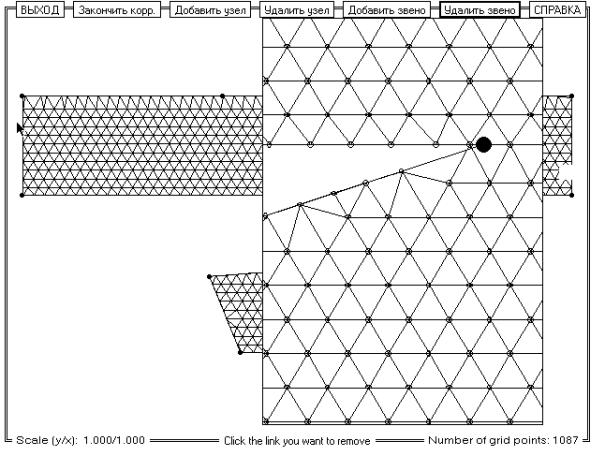
Рис. 12. Окно коррекции сетки (после коррекции).
После того, как
пользователь сделал необходимые исправления, необходимо вернуться в главное
меню (рис. 3) и открыть пункт "Ячейки Дирихле". Тогда возникает окно,
показанное на рис. 9. Щелчок по пункту "Рассчитать" приводит к выводу
на экран разбиения области на ячейки Дирихле (при этом на жесткий диск
записываются файлы с геометрической информацией, необходимой для запуска
расчета электромагнитного поля и температуры). Работа с геометрией области на
этом заканчивается.
Результатом работы
подпрограммы построения сетки является следующий набор массивов:
1. целочисленный
массив Ind (4, N) – граф связности сетки, где N – число точек сетки, 4 –
максимальное число соседей данной точки с номерами, не меньшими ее самой; первой
хранится информация о самой точке, далее – номера соседей, с которыми связана
данная точка; значение, меньшее 0, указывает на граничную точку, большее нуля –
на внутреннюю; если Ind = 0, то такой связи не существует;
2. целочисленный
массив Ip (3, NN) – описатель вершин данного сеточного треугольника
(упорядоченных по возрастанию), где NN – число треугольников (ограничено сверху
величиной 2N); содержит номера вершин данного треугольника вместе с информацией
об их принадлежности к границе или внутренности аналогично предыдущему массиву;
3. целочисленный
массив Jp (6, N) – описатель номеров треугольников, имеющих данную точку сетки
своей вершиной, где 6 – максимальное число таких треугольников, если Jp = 0, то
такого треугольника не существует;
4. массив
действительных чисел XY (2, N), в котором хранятся координаты точек сетки,
первой - x, второй – y;
5. массив
действительных чисел Cor (2, 3, NN), в котором хранятся координаты всех трех
вершин данного треугольника, первой - x, второй – y;
6. массив действительных
чисел Dir (2, 4, NN), в котором хранятся координаты трех середин сторон данного
треугольника и центра описанной вокруг него окружности, первой - x, второй – y.
1.3.
Задание физических свойств и параметров вычислений.
Для задания
физических свойств подобластей и параметров, управляющих вычислительным
процессом, включая параметры записи результатов расчета, в оболочке
предусмотрены два окна, показанных на рис. 6 и рис. 8.
Все исходные
данные задаются в системе СГС. В Таблице 1 приведен список исходных параметров
с их кратким описанием (номера параметров в соответствии с рис. 6). На рисунке
13 показаны номера материалов, соответствующие подобластям задачи. Рельс может
состоять из двух материалов 4 и 6, которые неизменно находятся в твердом фазовом
состоянии. Якорь может состоять из двух материалов 1, 2, 3 и 5. Предполагается,
что материал верхнего слоя якоря может локально находиться в газообразном
состоянии (индекс 1), жидком (2) и твердом (3). На рисунке 14 показана форма
импульса тока, определяющего и временную зависимость напряженности магнитного
поля в межрельсовом пространстве.
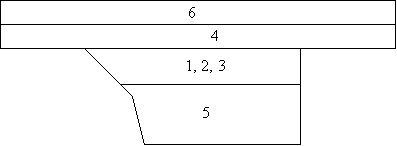
Рис. 13. Индексы материалов подобластей задачи.
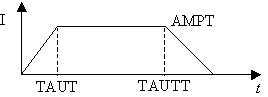
Рис. 14. Форма токовой кривой (параметры 7-9
в таблице 1).
Таблица 1. Параметры задачи для приложения EML.
|
Номер пара- метра на рис. 6
|
Наименование параметра
|
Единица измерения
|
|
1
|
Ширина рельса в направлении оси z
|
см
|
|
2
|
Масса якоря
|
г
|
|
3
|
Ширина δ – функции
|
см
|
|
4
|
Относительная ошибка – величина допустимого
отклонения от нуля Е00
|
-
|
|
5
|
Предельная относительная ошибка внутренних итераций
ЕI
|
-
|
|
6
|
Предельная относительная ошибка внешних итераций ЕE
|
-
|
|
7
|
Время выхода зависимости полного протекающего тока
на постоянное (амплитудное) значение – TAUT
на рис. 14
|
с
|
|
8
|
Время начала спада тока - TAUTT на рис. 14
|
с
|
|
9
|
Амплитуда тока – AMPT
на рис. 14
|
А
|
|
10
|
Плотность материала 1
|
г/см3
|
|
11
|
Плотность материала 2
|
г/см3
|
|
12
|
Плотность материала 3
|
г/см3
|
|
13
|
Плотность материала 4
|
г/см3
|
|
14
|
Плотность материала 5
|
г/см3
|
|
15
|
Плотность материала 6
|
г/см3
|
|
16
|
Теплоемкость материала 1
|
эрг/(г.К)
|
|
17
|
Теплоемкость материала 2
|
эрг/(г.К)
|
|
18
|
Теплоемкость материала 3
|
эрг/(г.К)
|
|
19
|
Теплоемкость материала 4
|
эрг/(г.К)
|
|
20
|
Теплоемкость материала 5
|
эрг/(г.К)
|
|
21
|
Теплоемкость материала 6
|
эрг/(г.К)
|
|
22
|
Электропроводность материала 1
|
1/с
|
|
23
|
Электропроводность материала 2
|
1/с
|
|
24
|
Электропроводность материала 3
|
1/с
|
|
25
|
Электропроводность материала 4
|
1/с
|
|
26
|
Электропроводность материала 5
|
1/с
|
|
27
|
Электропроводность материала 6
|
1/с
|
|
28
|
Температурный коэффициент электропроводности
материала 1
|
1/К
|
|
29
|
Температурный коэффициент электропроводности
материала 2
|
1/К
|
|
30
|
Температурный коэффициент электропроводности
материала 3
|
1/К
|
|
31
|
Температурный коэффициент электропроводности
материала 4
|
1/К
|
|
32
|
Температурный коэффициент электропроводности
материала 5
|
1/К
|
|
33
|
Температурный коэффициент электропроводности
материала 6
|
1/К
|
|
34
|
Коэффициент теплопроводности материала 1
|
эрг/(см.с.К)
|
|
35
|
Коэффициент теплопроводности материала 2
|
эрг/(см.с.К)
|
|
36
|
Коэффициент теплопроводности материала 3
|
эрг/(см.с.К)
|
|
37
|
Коэффициент теплопроводности материала 4
|
эрг/(см.с.К)
|
|
38
|
Коэффициент теплопроводности материала 5
|
эрг/(см.с.К)
|
|
39
|
Коэффициент теплопроводности материала 6
|
эрг/(см.с.К)
|
|
40
|
Температура плавления материала 1-2-3
|
К
|
|
41
|
Удельная теплота плавления материала 1-2-3
|
эрг/г
|
|
42
|
Температура кипения материала 1-2-3
|
К
|
|
43
|
Удельная теплота кипения материала 1-2-3
|
эрг/г
|
|
44
|
Коэффициент трения CTRS
|
-
|
|
45
|
Коэффициент трения CTRS0
|
-
|
|
46
|
Коэффициент трения CTRV
|
-
|
|
47
|
Коэффициент трения CTRV0
|
-
|
|
48
|
Коэффициент трения STTR
|
-
|
|
49
|
Начальная скорость ускоряемого тела
|
см/с
|
|
50
|
Начальное положение
|
см
|
|
51
|
Начальная температура
|
К
|
В программе
использована следующая температурная зависимость электропроводности σ от
температуры T: 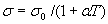 , где σ0
и a
параметры из пунктов 22 - 33 Таблицы 1. Для вычисления коэффициента трения
использовалась зависимость , где σ0
и a
параметры из пунктов 22 - 33 Таблицы 1. Для вычисления коэффициента трения
использовалась зависимость 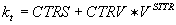 (см. [1, 2]) при T
ниже температуры плавления данного материала, а при T выше температуры
плавления использовалась совершенно аналогичная зависимость с параметрами с
нулем в конце идентификатора. (см. [1, 2]) при T
ниже температуры плавления данного материала, а при T выше температуры
плавления использовалась совершенно аналогичная зависимость с параметрами с
нулем в конце идентификатора.
Редактирование
данных осуществляется выбором пункта меню "Правка" и вводом с
клавиатуры. При этом на жесткий диск записываются файлы с исходными данными.
В Таблице 2
приведен список параметров управления вычислительным процессом.
Таблица 2. Параметры управления вычислительным процессом в приложении EML.
|
Номер параметра на рис. 8
|
Наименование параметра, ед. изм.
(если величина имеет размерность)
|
|
1
|
Размерность рабочих массивов, используемых подпрограммой решения СЛАУ
|
|
2
|
Вариант метода решения СЛАУ (из [10])
|
|
3
|
Предельная длина рельсотрона, см
|
|
4
|
Периодичность (число временных слоев) вывода информации о состоянии
счета на экран
|
|
5
|
Периодичность (число временных слоев) записи информации о решении на
жесткий диск
|
|
6
|
Максимальное число внешних итераций
|
|
7
|
Максимальное число внутренних итераций
|
|
8
|
Коэффициент увеличения шага по времени от слоя к слою (в зависимости
от числа итераций)
|
|
9
|
Коэффициент уменьшения шага по времени от слоя к слою (в зависимости
от числа итераций)
|
|
10
|
Относительная (по отношению к числу неизвестных в СЛАУ) длина цикла
итераций метода сопряженных градиентов, используемого при решении СЛАУ в
случае отсутствия сходимости метода неполной декомпозиции
|
|
11
|
Относительная (по отношению к длине цикла итераций метода сопряженных
градиентов) предельная величина числа итераций метода неполной декомпозиции,
при превышении которой происходит переход на решение СЛАУ методом сопряженных
градиентов
|
Запуск счета или
продолжение предыдущего сеанса счета осуществляются из окна, показанного на
рис. 7. Приложение EML не позволяет продолжить счет, если были изменены исходные данные,
редактируемые в пункте "Исходные данные" (рис. 3).
§
2. Пример применения программы EML.
На рис. 15, 16 показана
область (узлы и ячейки Дирихле), в которой решалась задача при исследованиях
эффекта применения анизотропно - резистивных материалов в качестве электродов
рельсотрона [12]. Как уже говорилось во введении, критическим для рельсотрона
является так называемый кризис металлического контакта, ограничивающий диапазон
достижимых скоростей. Одним из возможных путей преодоления или затягивания
наступления кризиса является применение таких нетрадиционных материалов.

Рис. 15. Треугольная сетка в вычислительном эксперименте по
изучению влияния анизотропной электропроводности.
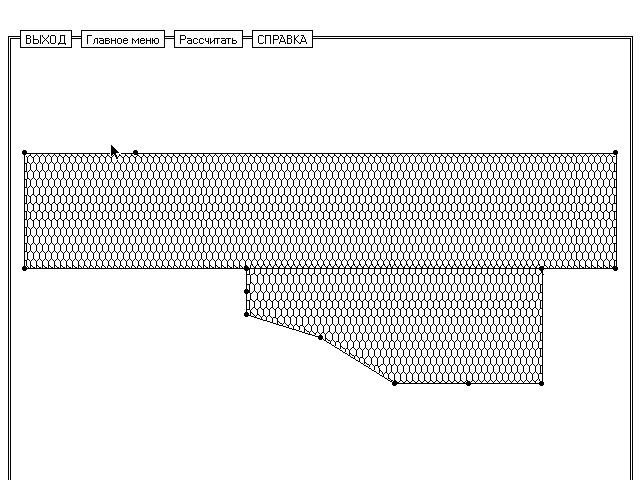
Рис. 16. Ячейки Дирихле в вычислительном эксперименте по
исследованию влияния анизотропной электропроводности.
На рис. 17
показаны полученные на данной сетке решения (линии уровня T и H) для случаев
традиционного материала рельса (медь), анизотропия электропроводности в котором
отсутствует, и для случая рельса из пирографита – электропроводность в
направлении, параллельном движению якоря, в 1000 раз выше, чем в
перпендикулярном ему.

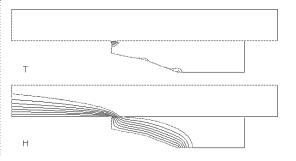

Рис. 17. Влияние анизотропии
электропроводности на картину протекания тока.
На левой половине
рис. 17 хорошо видно, что ток фактически втекает в одну точку на заднем конце
якоря вследствие наличия скоростного скин – слоя. Это ведет здесь к
значительному увеличению плотности тока с последующим плавлением и испарением
материала. Для данной ситуации испарение началось при скорости 685 м /сек.
Правая половина рис. 17 соответствует использованию реального материала
пирографита с его реальными характеристиками. Коэффициент анизотропии материала
составляет К = 1000. Такое
соотношение дает рекордную критическую скорость среди всех просчитанных. Кризис
контакта наступил при скорости 2250 м / с. Рис. 17 показывает соответствующие
кривые распределения T и H на момент, близкий точке кризиса.
Благодаря огромной анизотропии электропроводности рельса, глубина проникновения
магнитного поля в электрод в продольном направлении намного больше глубины
проникновения в поперечном. За счет этого и происходит значительное увеличение
критической скорости. Некоторые дополнительные подробности см. в [3].
Заключение
В работе представлена
прикладная программа EML, предназначенная для автоматизации проведения
вычислительных экспериментов, в основе которых лежит двумерная физико -
математическая модель электромагнитных и тепловых процессов, происходящих в
электродинамическом ускорителе типа рельсотрон.
Основным преимуществом
применения программы является удобство ввода информации о геометрии расчетной
области, а также ввода параметров рельсотрона и свойств материалов. При этом
обеспечивается возможность контролировать процесс разбиения области на
треугольники вручную – тем самым задачу можно решать на областях сложной формы
без ущерба точности.
Программа
применялась на практике, в частности, для проведения вычислительных
экспериментов по исследованию возможностей применения анизотропно - резистивных
материалов в качестве электродов рельсотрона.
Литература
1. "Материалы
I Всесоюзного семинара по динамике сильноточного дугового разряда в магнитном
поле" (Новосибирск, 10 - 13 апреля 1990 г.), под ред. М.Ф. Жукова,
Новосибирск, изд. Инст. Теплофизики СО АН СССР, 1990, 350 с.
2. "Материалы
II Всесоюзного семинара по динамике сильноточного дугового разряда в магнитном
поле" (Новосибирск, 4-6 декабря 1991г.), под ред. В.Е. Накорякова,
Новосибирск, изд. Инст. Теплофизики СО РАН, 1992, 367 с.
3. М.П. Галанин,
А.Д. Лебедев, А.П. Лотоцкий, К.К. Миляев. Тепловые и электромагнитные процессы
на контактах электродинамического ускорителя // Препр. Ин. прикл. матем. им.
М.В. Келдыша РАН. 2000. N 42. 32 с.
4. М.П. Галанин.
Задача о скоростном скин - слое и квазимонотонная конечноэлементная схема для
ее численного решения. // Препр. Ин. прикл. матем. им. М.В.Келдыша РАН. 1995. N
21. 29 с.
5. М.П. Галанин,
Ю.П. Попов. Квазистационарные электромагнитные поля в неоднородных средах. М.,
Наука, 1995, 320 с.
6. Г.И. Марчук,
В.И. Агошков. Введение в проекционно-сеточные методы. М., Наука, 1981, 416 с.
7. Д. Норри, Ж. де
Фриз. Введение в метод конечных элекментов. М.: Мир. 1981, 304 с.
8. Сильвестер П.,
Феррари Р. Метод конечных элементов для радиоинженеров и инженеров -
электриков. М.: Мир. 1986.
9. А.Л. Гончаров. К
применению градиентных методов для решения разреженных несимметричных систем
алгебраических уравнений. // Препр. Ин. прикл. матем. им. М.В. Келдыша АН СССР.
1987, № 130, 16 с.
10. А.Л. Гончаров. Комплекс
программ решения разреженных систем алгебраических уравнений. // Отчет Ин. прикл.
матем. им. М.В. Келдыша АН СССР. 1987, 53 с.
11. А.А. Самарский, Б.Д.
Моисеенко. Экономичная схема сквозного счета для многомерной задачи Стефана. //
ЖВМ и МФ. 1965. Т. 5. № 5. С. 816 - 827.
12. M.P. Galanin, A.D. Lebedev, K.K. Milyaev. An Investigation of the
Effects of Some Properties of Materials on the Characteristics of Armature
Acceleration in a Railgun. // IEEE Transactions on Magnetics. Vol. 37, No. 1,
January 2001.
|
![]() , где σ0
и a
параметры из пунктов 22 - 33 Таблицы 1. Для вычисления коэффициента трения
использовалась зависимость
, где σ0
и a
параметры из пунктов 22 - 33 Таблицы 1. Для вычисления коэффициента трения
использовалась зависимость ![]() (см. [1, 2]) при T
ниже температуры плавления данного материала, а при T выше температуры
плавления использовалась совершенно аналогичная зависимость с параметрами с
нулем в конце идентификатора.
(см. [1, 2]) при T
ниже температуры плавления данного материала, а при T выше температуры
плавления использовалась совершенно аналогичная зависимость с параметрами с
нулем в конце идентификатора.